Numerical Simulations of Wave-Induced Flow Fields around Large-Diameter Surface-Piercing Vertical Circular Cylinder
Abstract
:1. Introduction
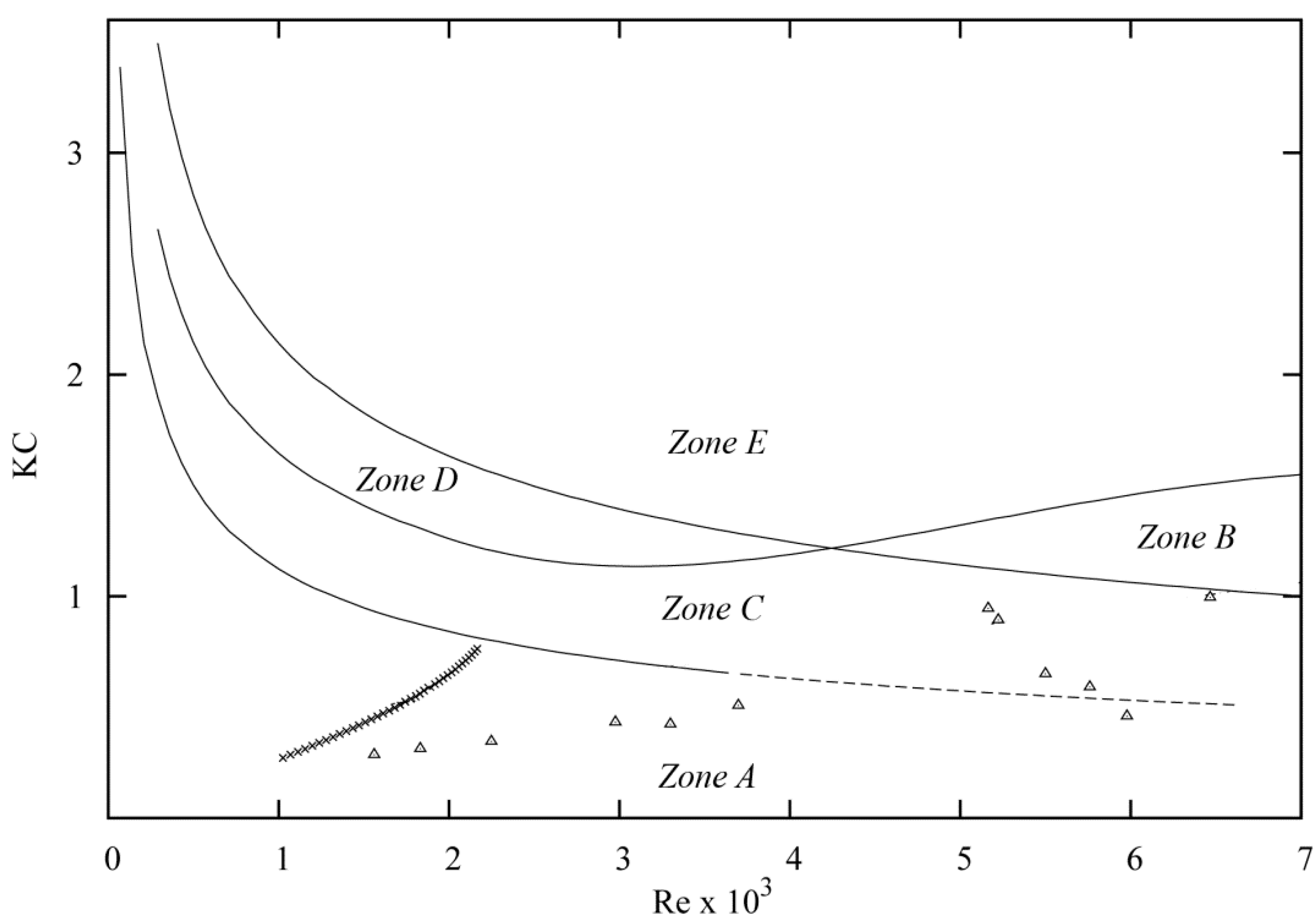
2. Wave Regimes
2.1. Overview of Wave Regimes
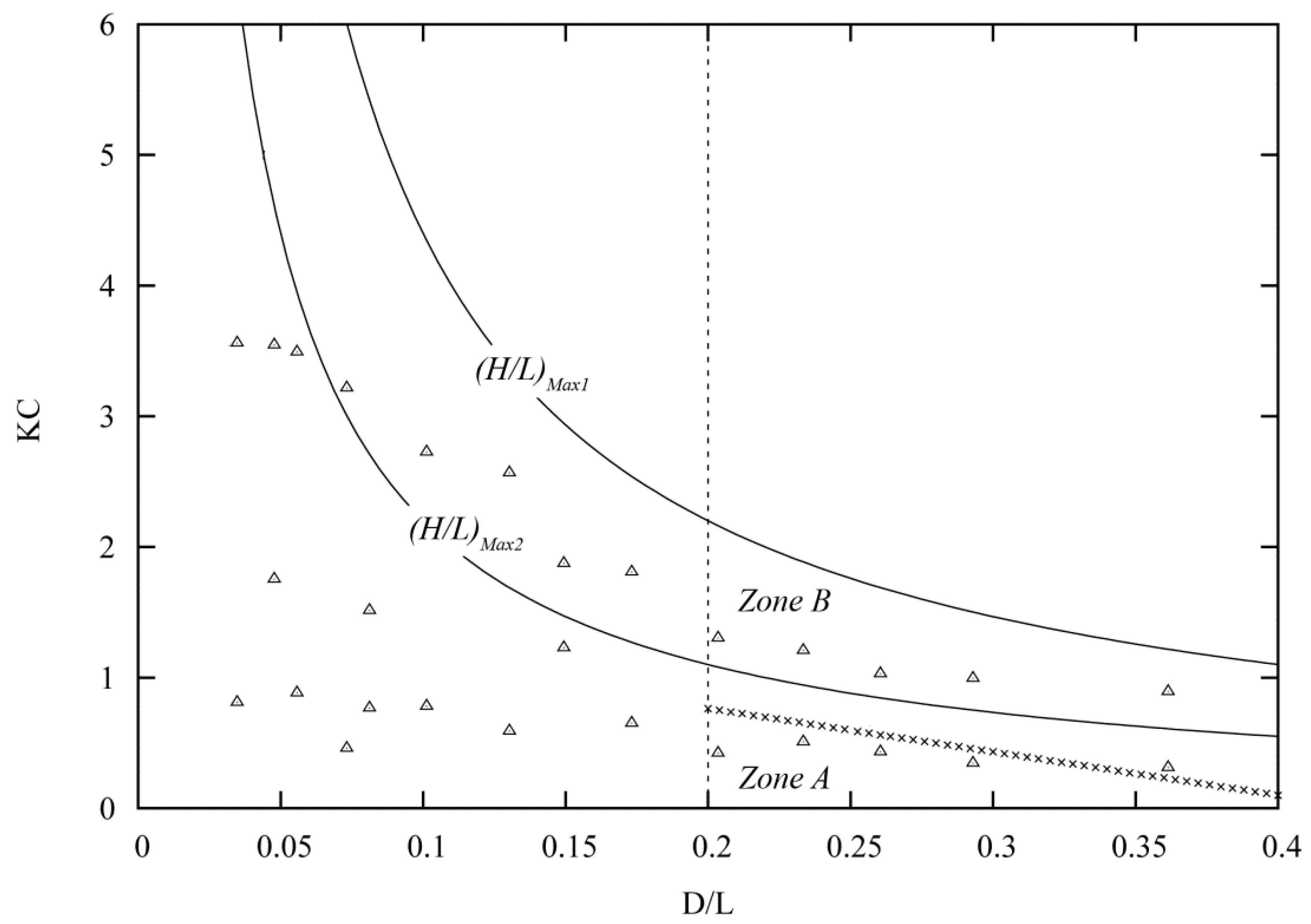
2.2. Viscous-Fluid Wave Framework
3. Numerical Techniques
3.1. Velocity-Potential Solution
| D/L | KC | d/L | kd | ||
|---|---|---|---|---|---|
| 0.2–0.4 | 0.10–0.76 | 0.480–0.064 | 0.40–0.80 | 2.51–5.03 | 0.63–1.26 |
3.2. Numerical Integration of the Euler Equations
| Field Parameters | ||||||
| KC | D [m] | H [m] | L [m] | T [s] | ||
| 0.70 | 12.0 | 2.65 | 45.11 | 5.41 | ||
| d [m] | [m] | |||||
| 18.0 | 6.0 | 0.266 | 0.44 | 0.059 | ||
| kd | ||||||
| 0.138 | 0.069 | 0.40 | 2.51 | 0.84 | ||
| Computational Parameters | ||||||
| = [m] | [m] | = | = [m] | [m] | ||
| 90.22 | 36.0 | 450 | 360 | 0.20 | 0.10 | |
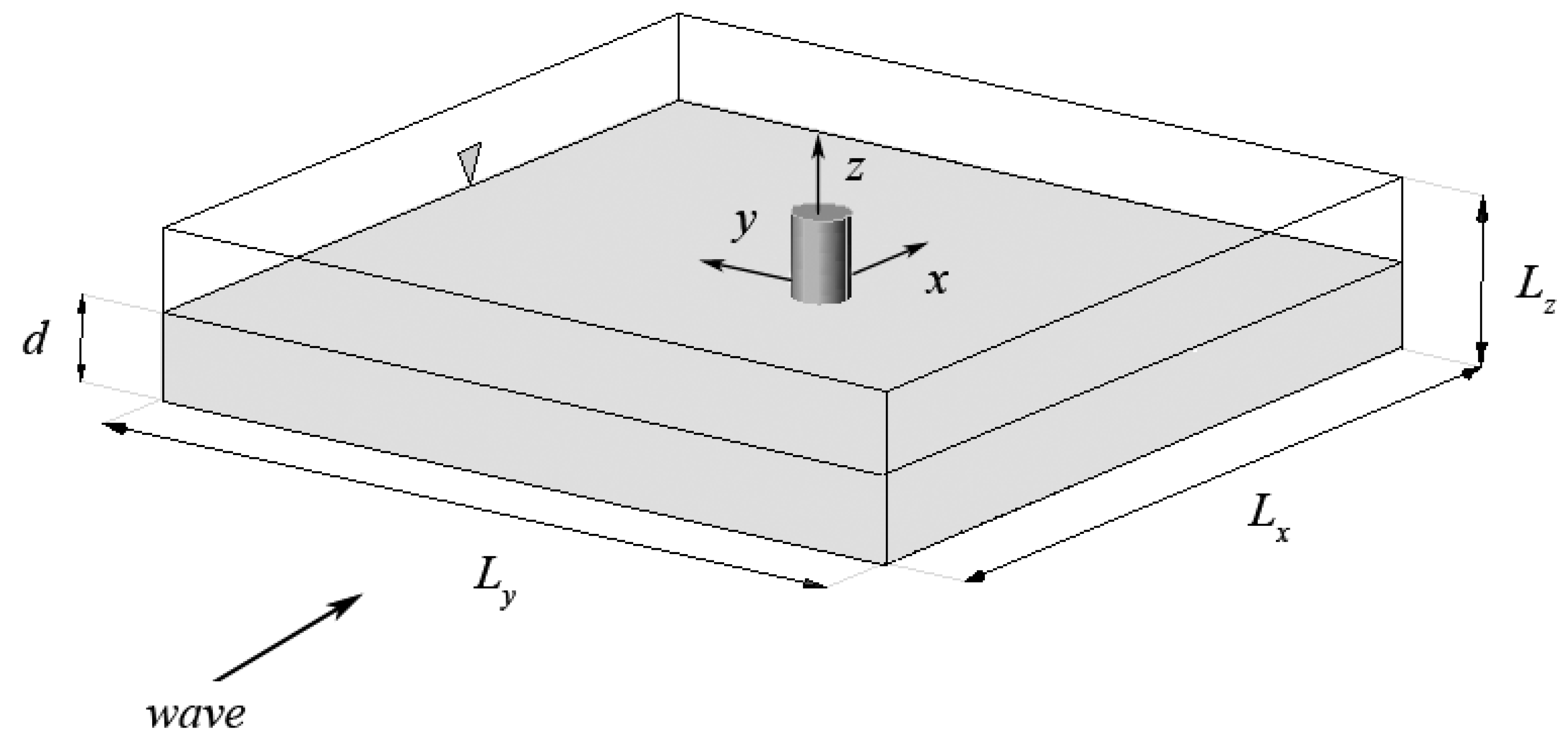
3.3. Numerical Integration of the Navier-Stokes Equations
3.3.1. Validation of the Navier-Stokes Solver

| Domain Dimensions (, ) | |||||
| 2512 | 400 | 1256 | |||
| Computational Grid for the Reference Navier-Stokes Solver | |||||
| 256 | 181 | 256 | |||
| Multi-Bolck Computational Grid for the Flow-3D Navier-Stokes Solver | |||||
| Block-subdivision along y | |||||
| 3040 | 5 | 1520 | 23.1 | ||
| 1520 | 13 | 760 | ≈ 15.1 | ||
| 760 | 18 | 380 | ≈ 5.2 | ||
| 380 | 107 | 190 | ≈ 7.7 | ||
| 760 | 18 | 380 | ≈ 5.2 | ||
| 1520 | 13 | 760 | ≈ 15.1 | ||
| 3040 | 5 | 1520 | ≈ 23.1 | ||
| 11020 | 179 | 5510 | ≈ 94.4 | ||
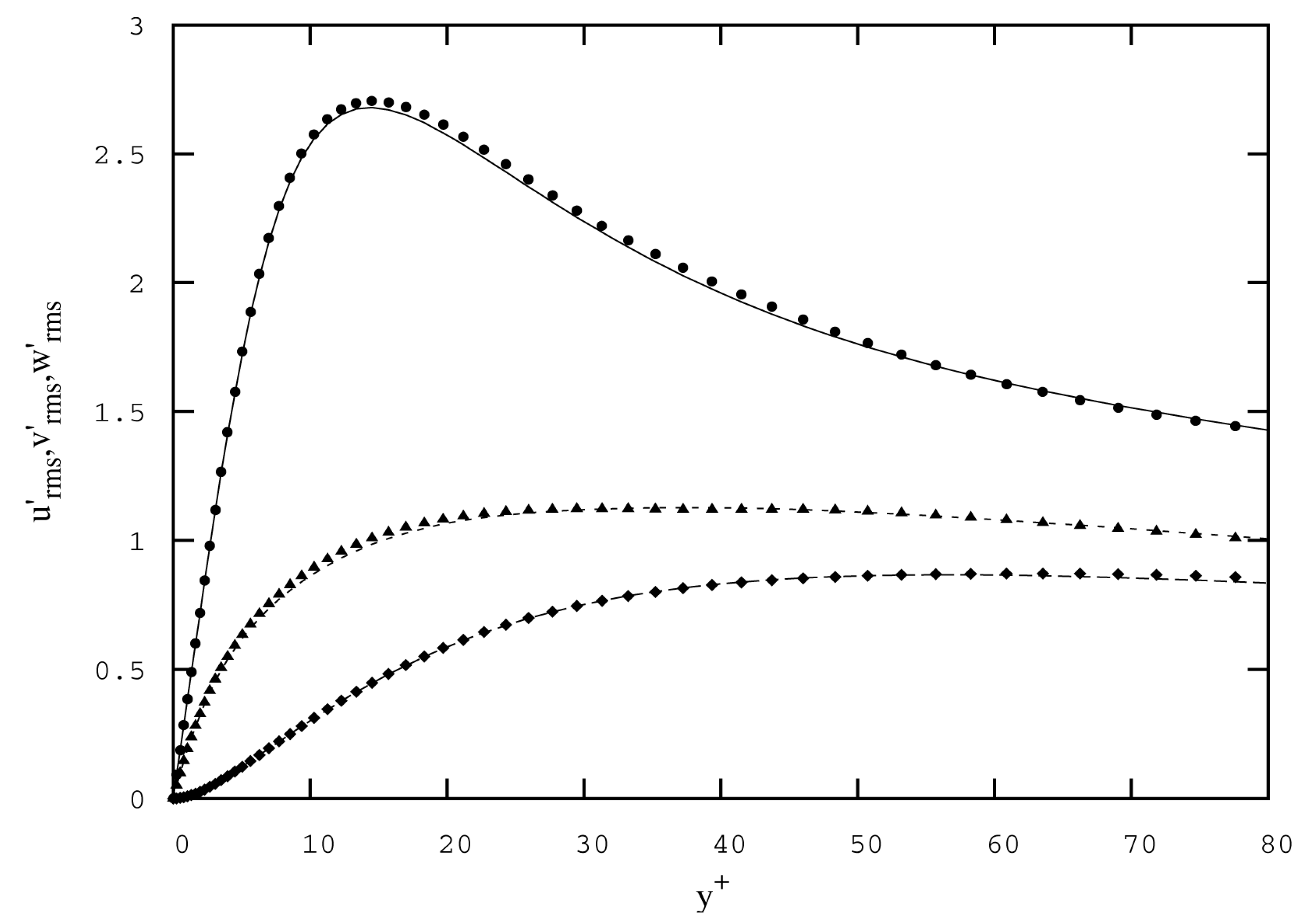

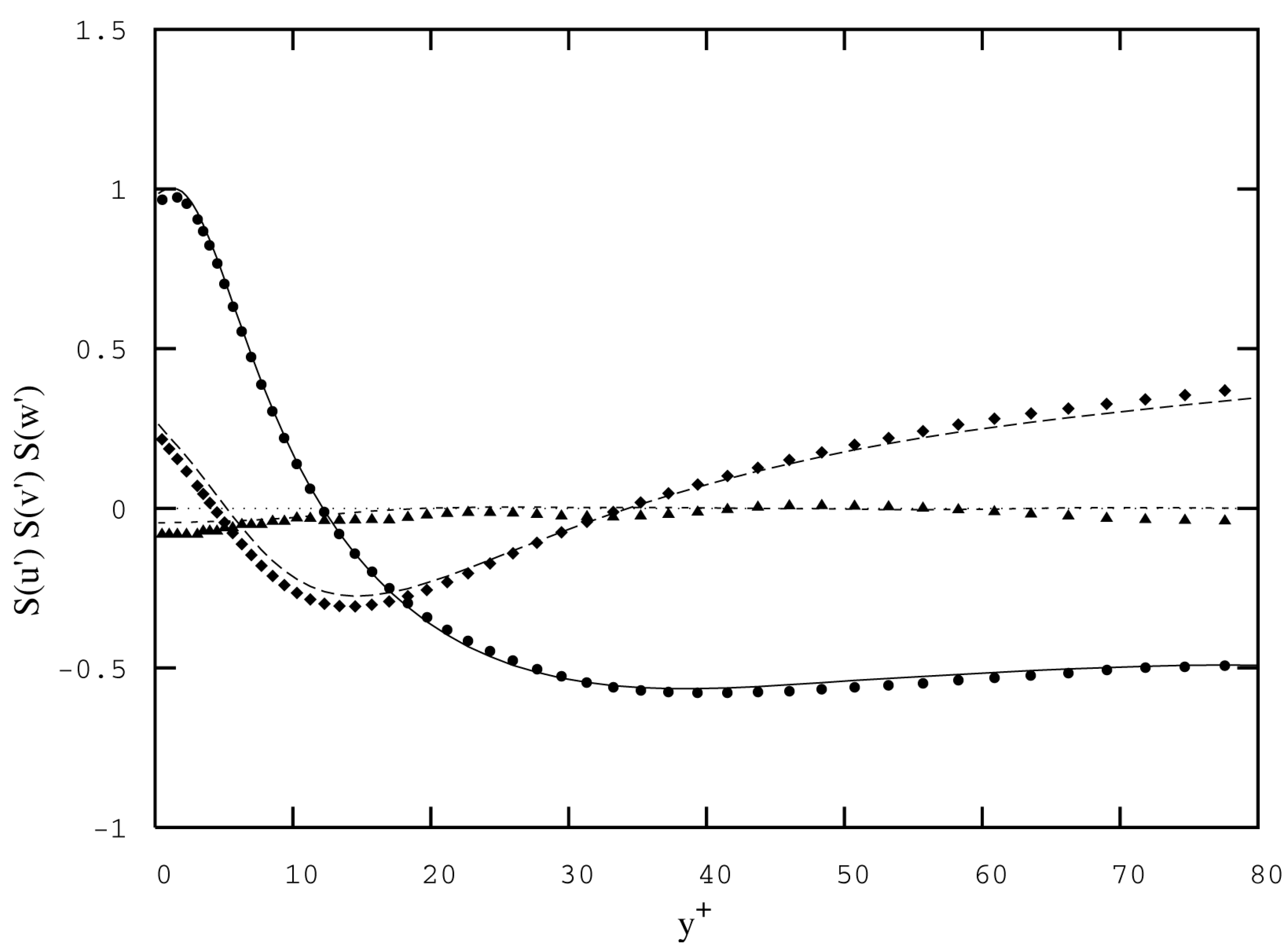
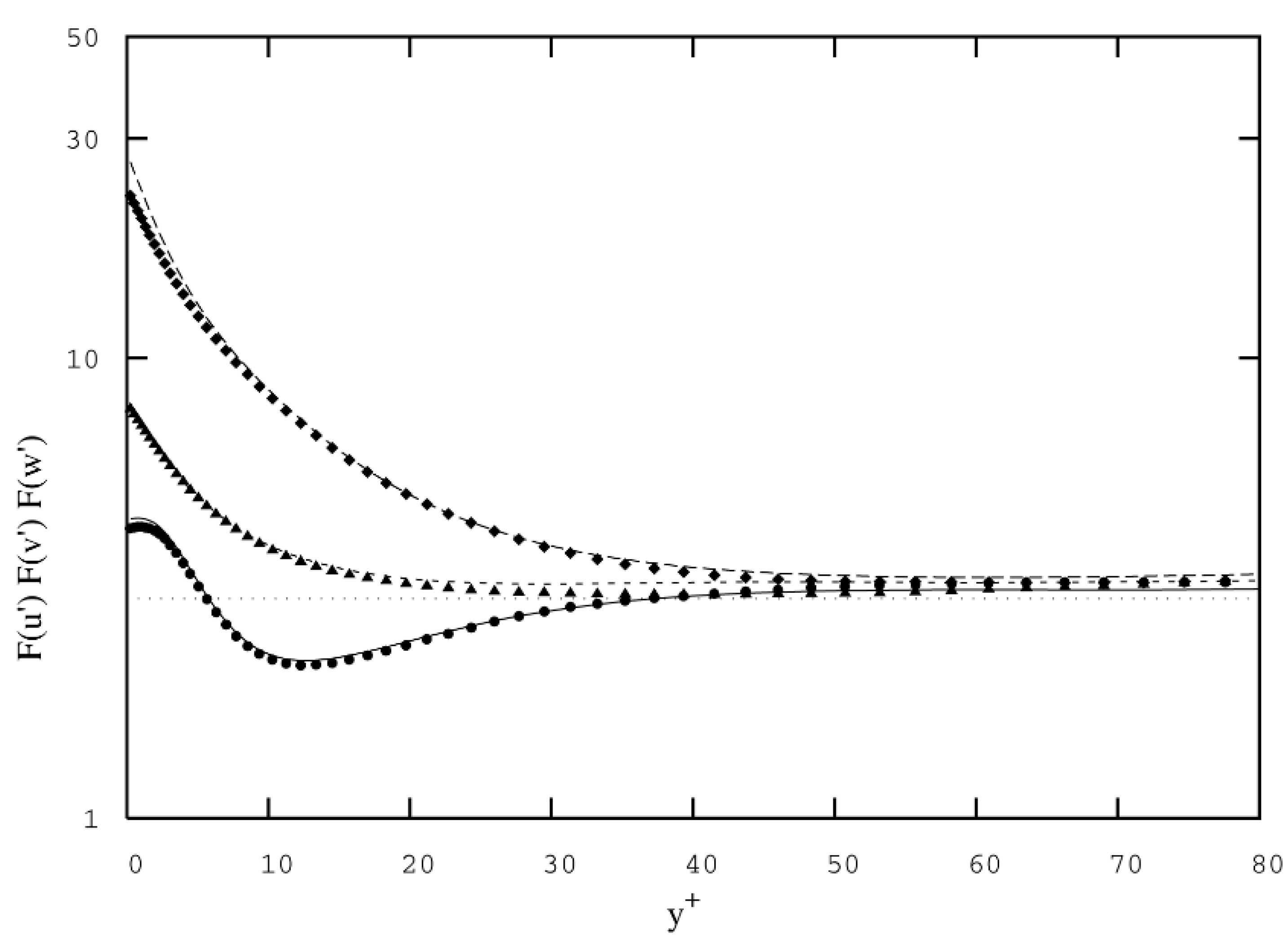
3.3.2. Accuracy of Calculations and Computing Procedures
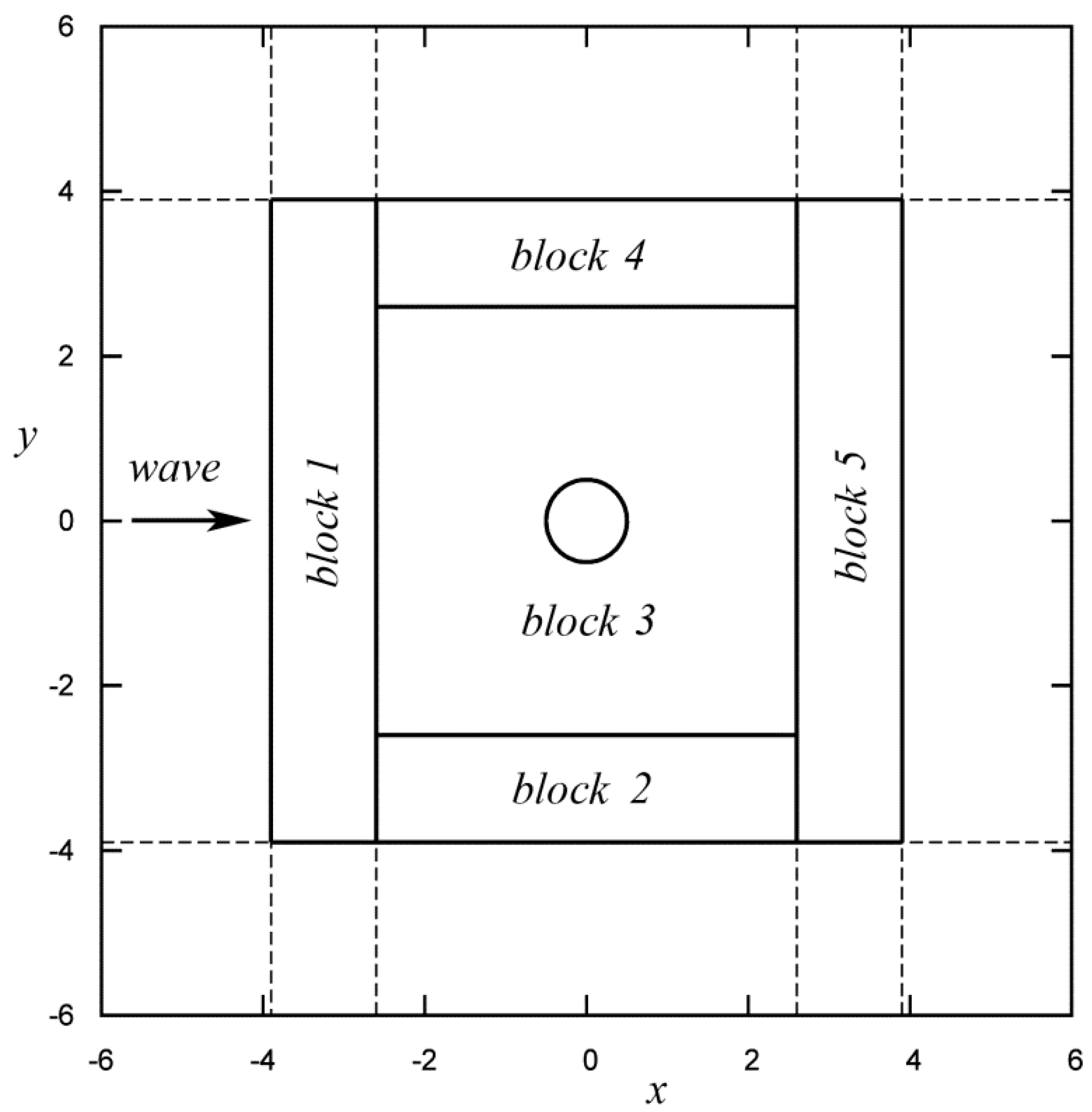
| Field Parameters (, , ) | |||||
| D | L | H | a | d | |
| [D units] | [D units] | [D units] | [D units] | [D units] | [D units] |
| 1 | 3.906 | 0.183 | 0.0915 | 2 | 0.50 |
| T | |||||
| [D units] | [ units] | [ units] | [ units] | ||
| 0.0147 | 4.962 | 3.450 | 0.116 | 0.256 | 0.367 |
| kd | |||||
| 0.047 | 0.139 | 0.0696 | 0.512 | 3.217 | 0.809 |
| Computational Parameters [D Units] | |||||
| 7.8 | 7.8 | 3.0 | 1.3 | 2.1 | |
| block 1 | 1,156,200 | ||||
| block 2 | 702,240 | ||||
| block 3 | 14,953,080 | ||||
| block 4 | 702,240 | ||||
| block 5 | 1,156,200 | ||||
| blocks 1-5 | 18,669,960 | ||||
| Space and Time Resolutions [ and Units] | |||||
4. Flow-Field Analysis
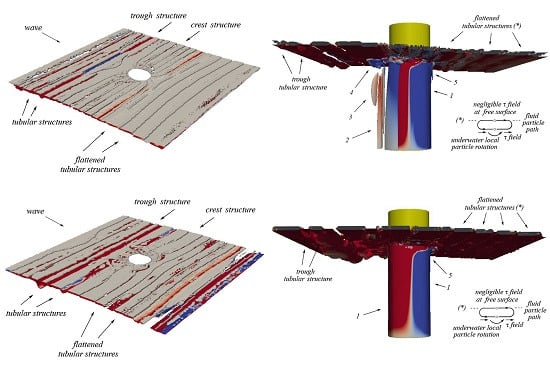
4.1. Overview of Swirling-Strength Criterion for Flow-Structure Extraction
4.2. Overview of Karhunen-Loève Decomposition Technique
| Instant Number () | Instant ( Units) | Instant ( Units) |
|---|---|---|
| 1 | 0.000 | 0.000 |
| 2 | 0.876 | 0.144 |
| 3 | 2.481 | 0.500 |
| 4 | 3.722 | 0.750 |
| 5 | 4.962 | 1.000 |
| Mode Number | Energy Fraction | Energy Sum |
|---|---|---|
| 1 | 0.87818 | 0.87818 |
| 2 | 0.10770 | 0.98588 |
| 3 | 1.2271 | 0.99815 |
| 4 | 5.0327 | 1.00 |
| 5 | 2.6852 | 1.00 |
| 6 | 9.2960 | 1.00 |
| 7 | 5.5663 | 1.00 |
| 8 | 1.2803 | 1.00 |
| 9 | 3.5057 | 1.00 |
| 10 | 2.1537 | 1.00 |
5. Results
5.1. Forces and Runups
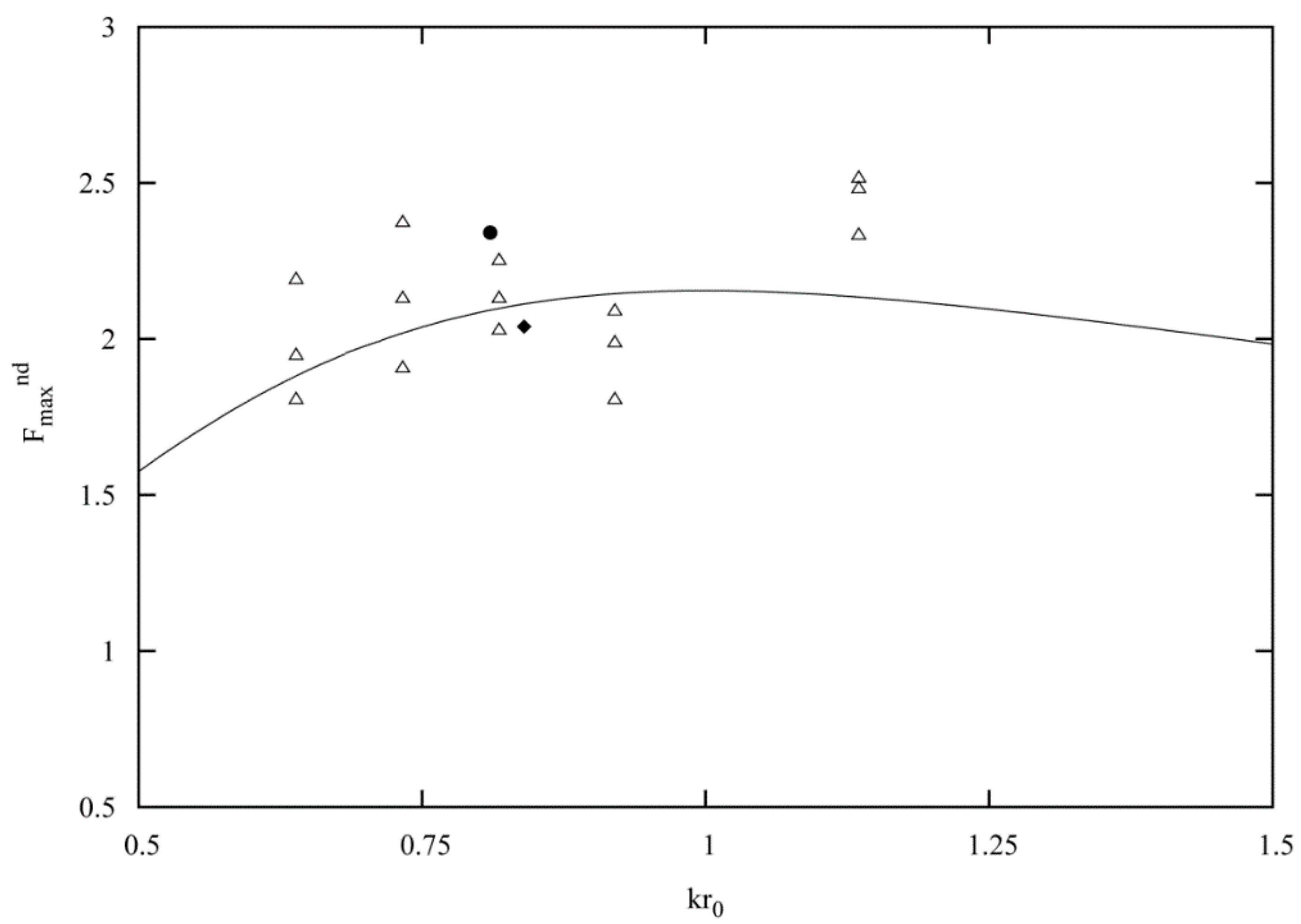
5.2. Velocity Potential
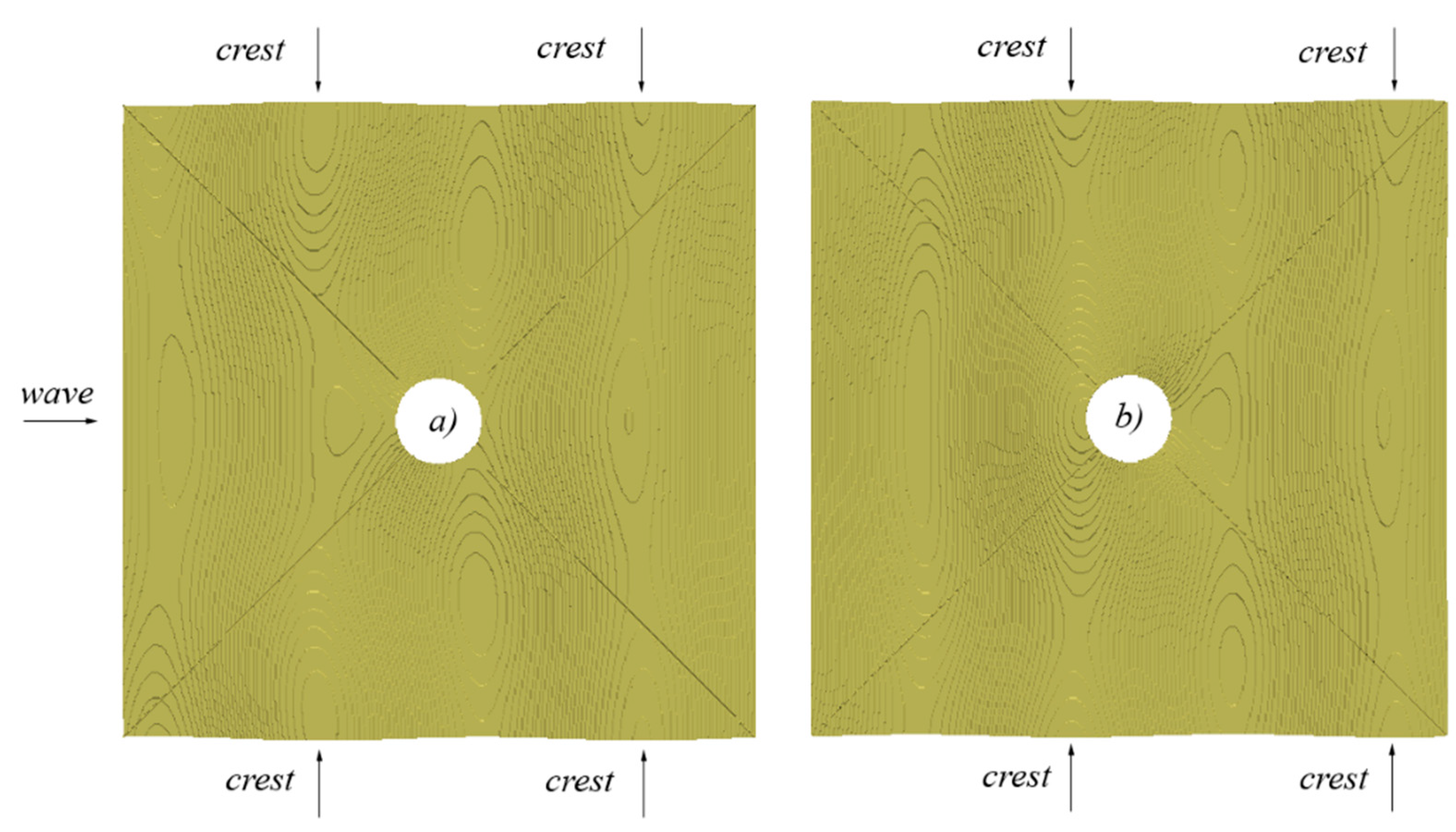
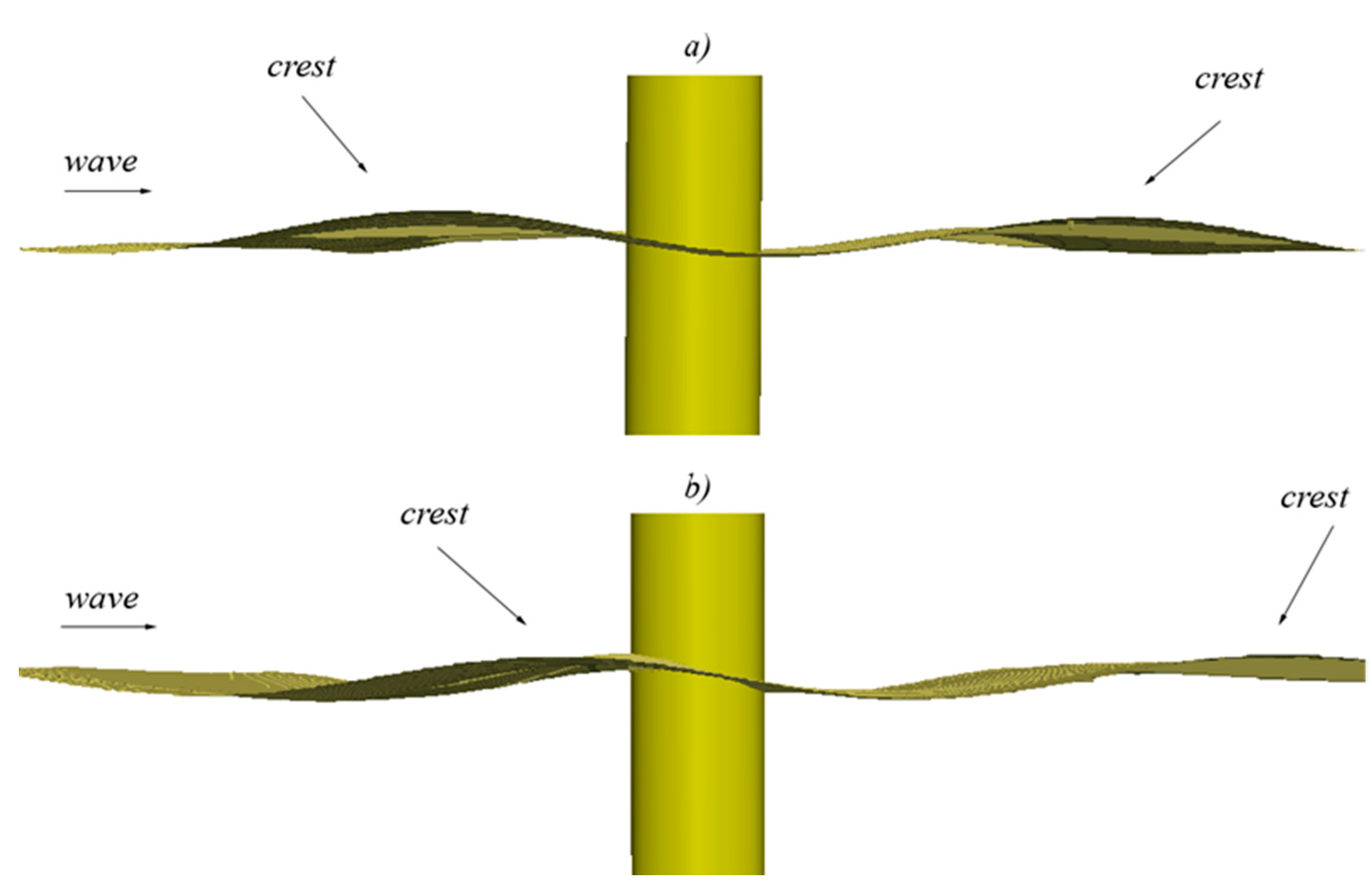
5.3. Euler Equations

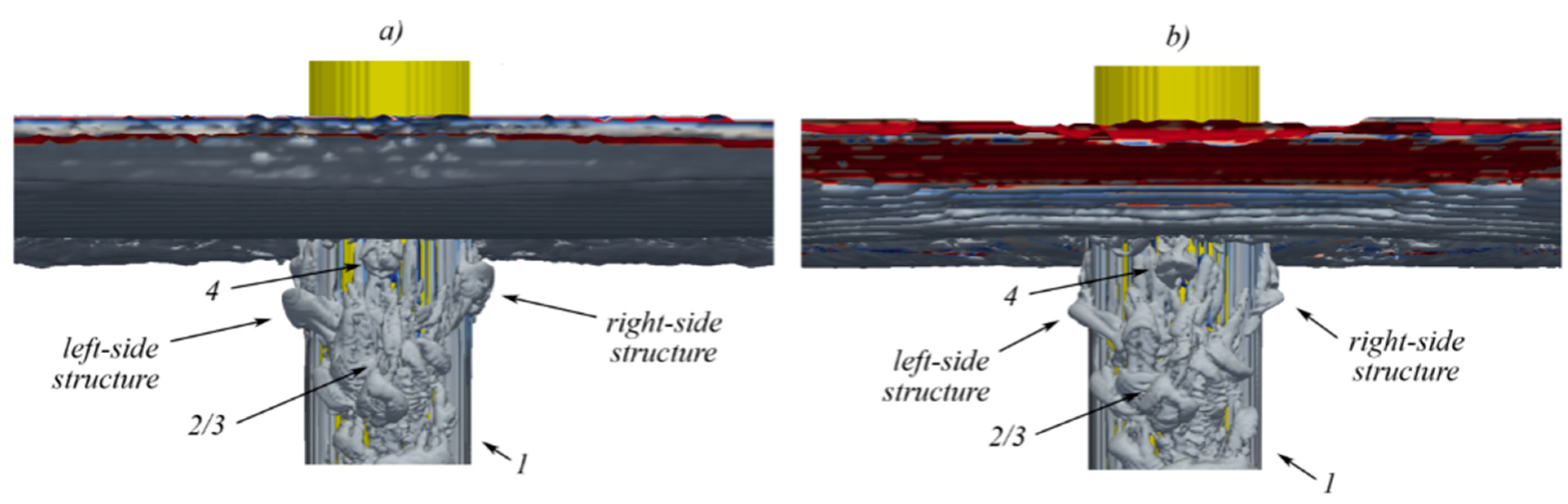
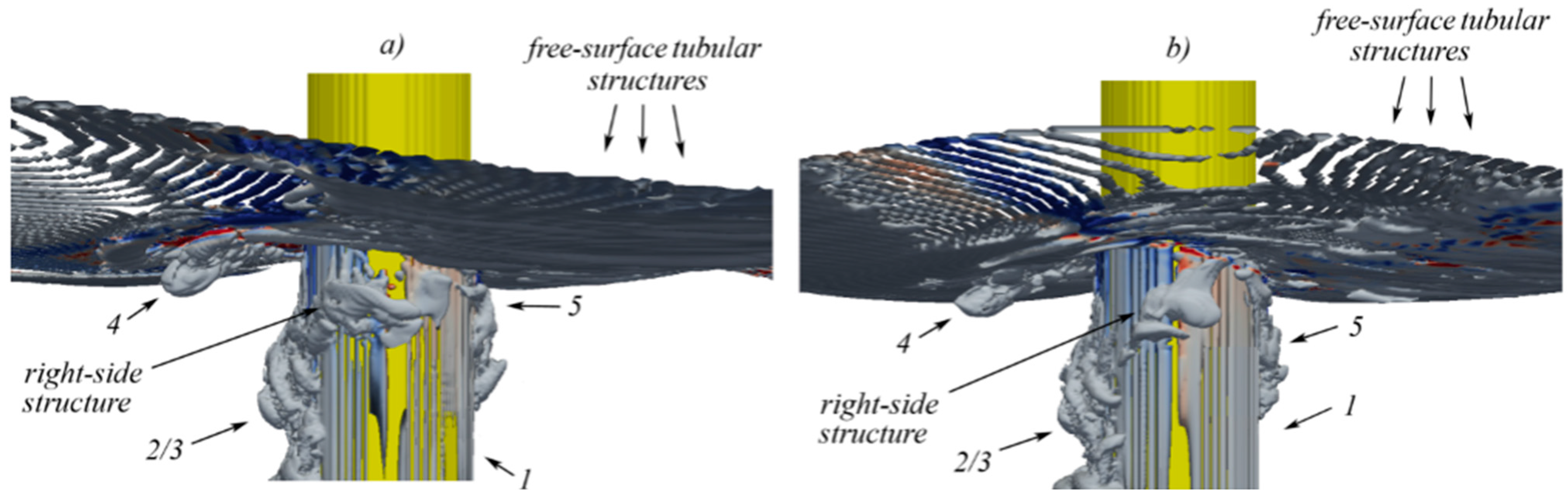
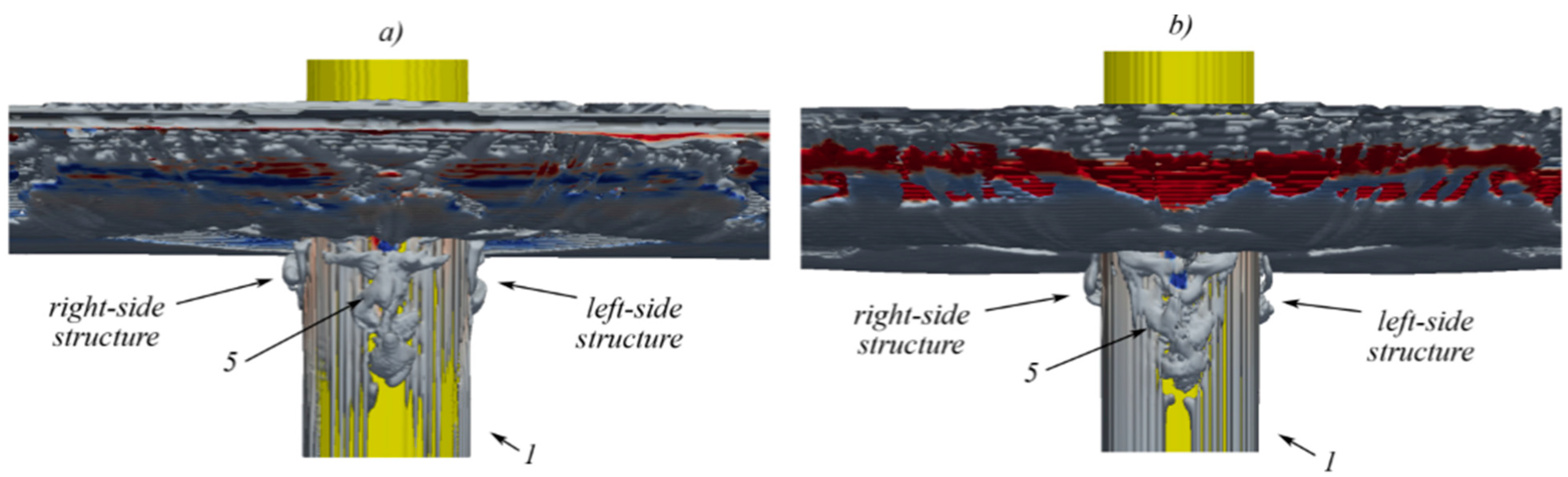
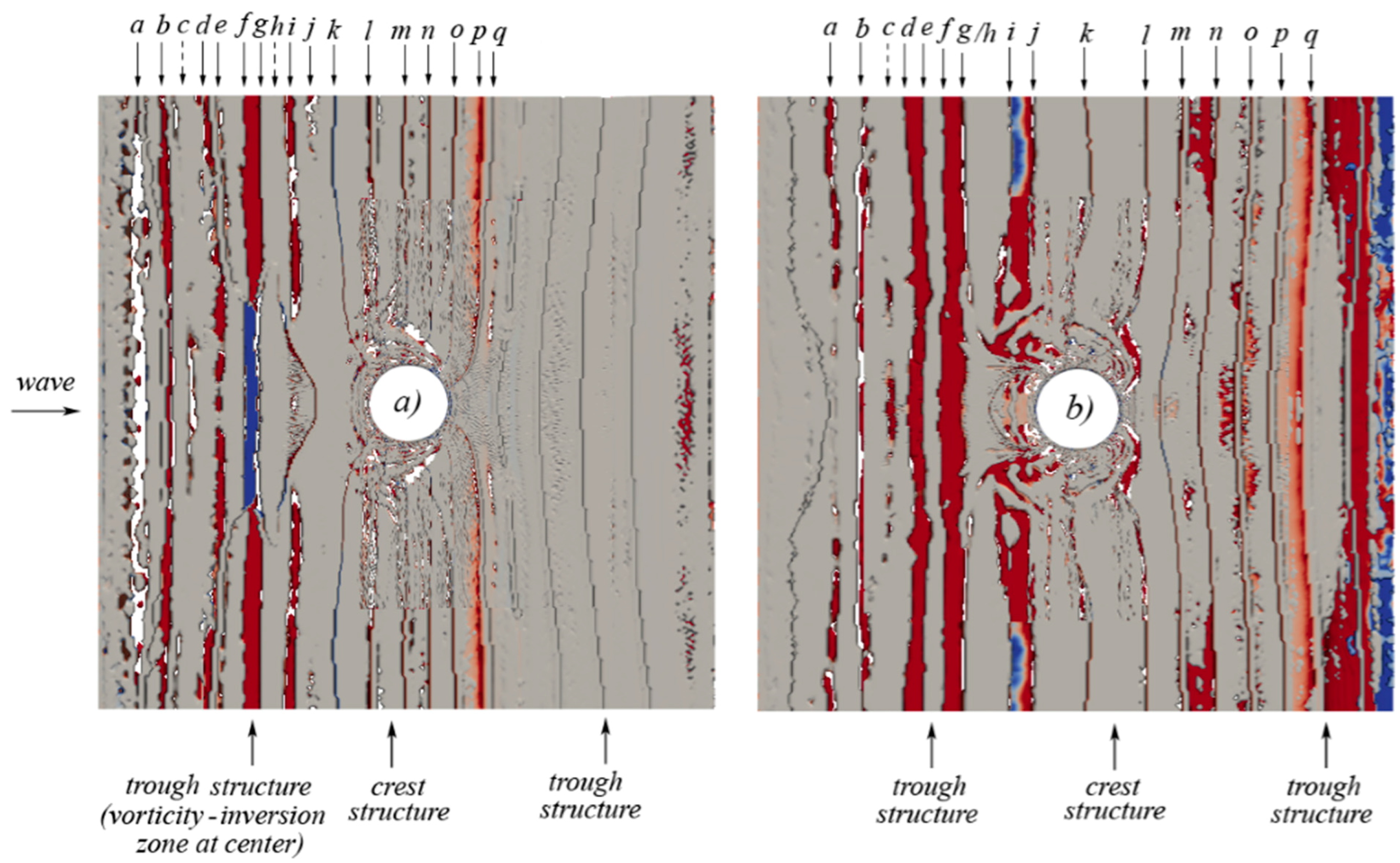
5.4. Navier Stokes Equations
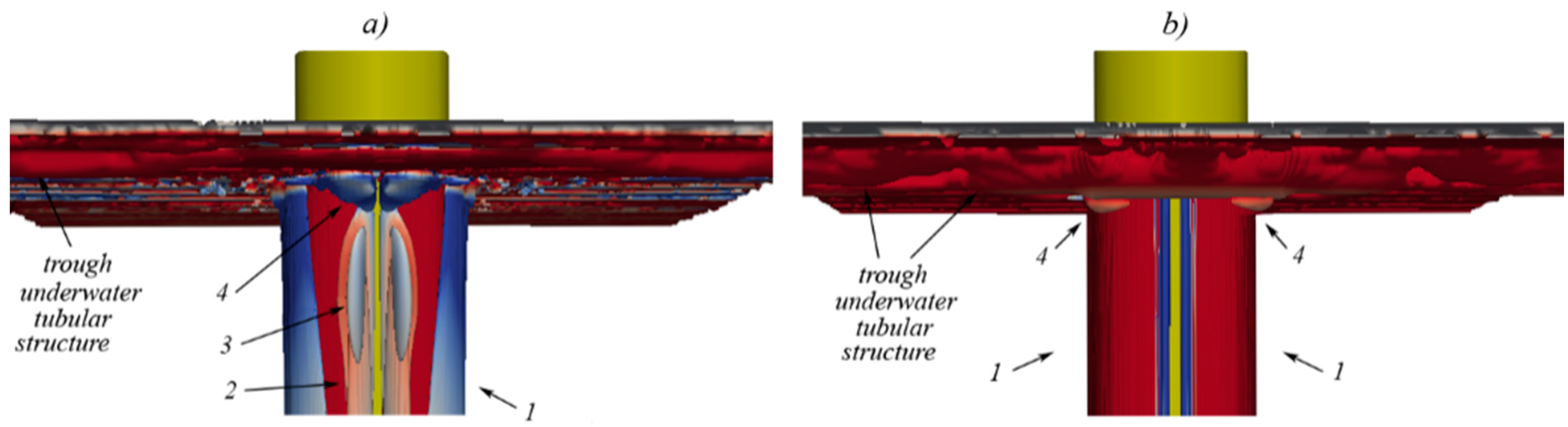
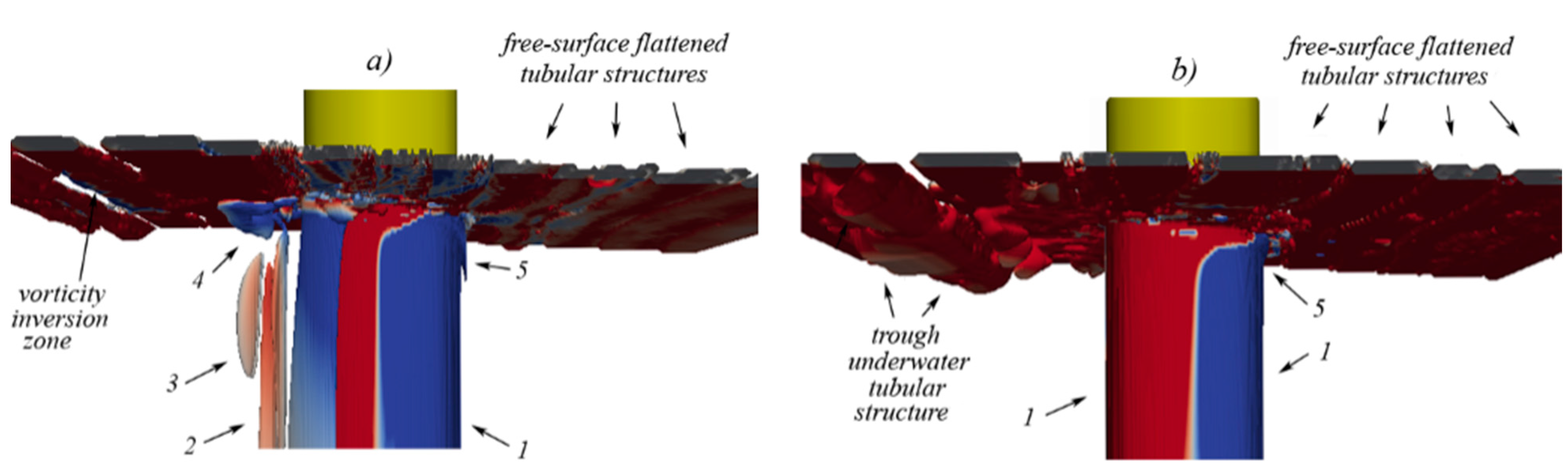
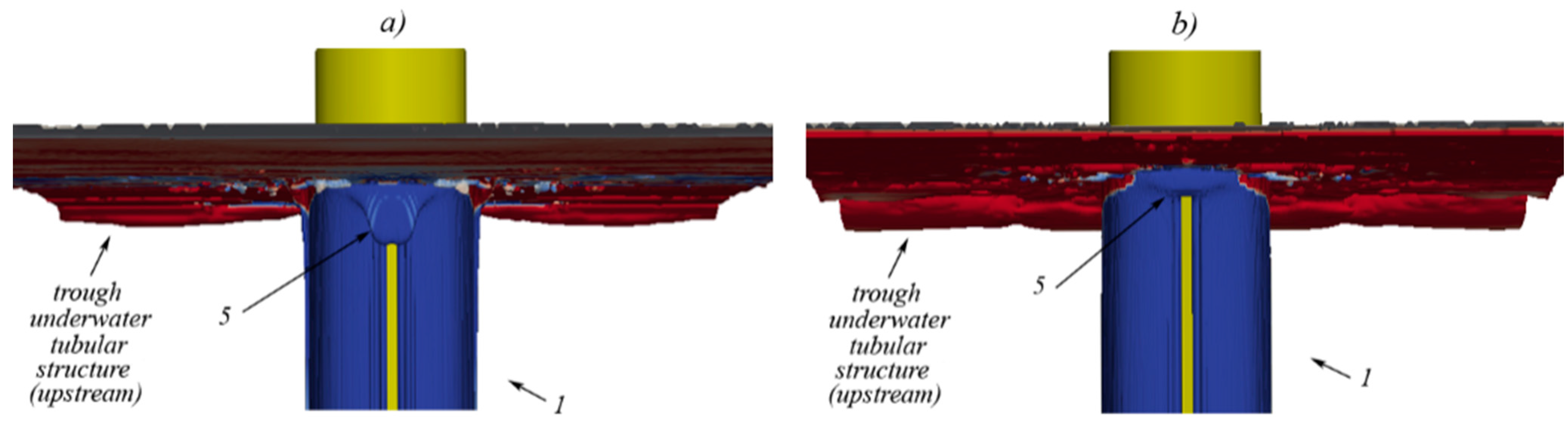


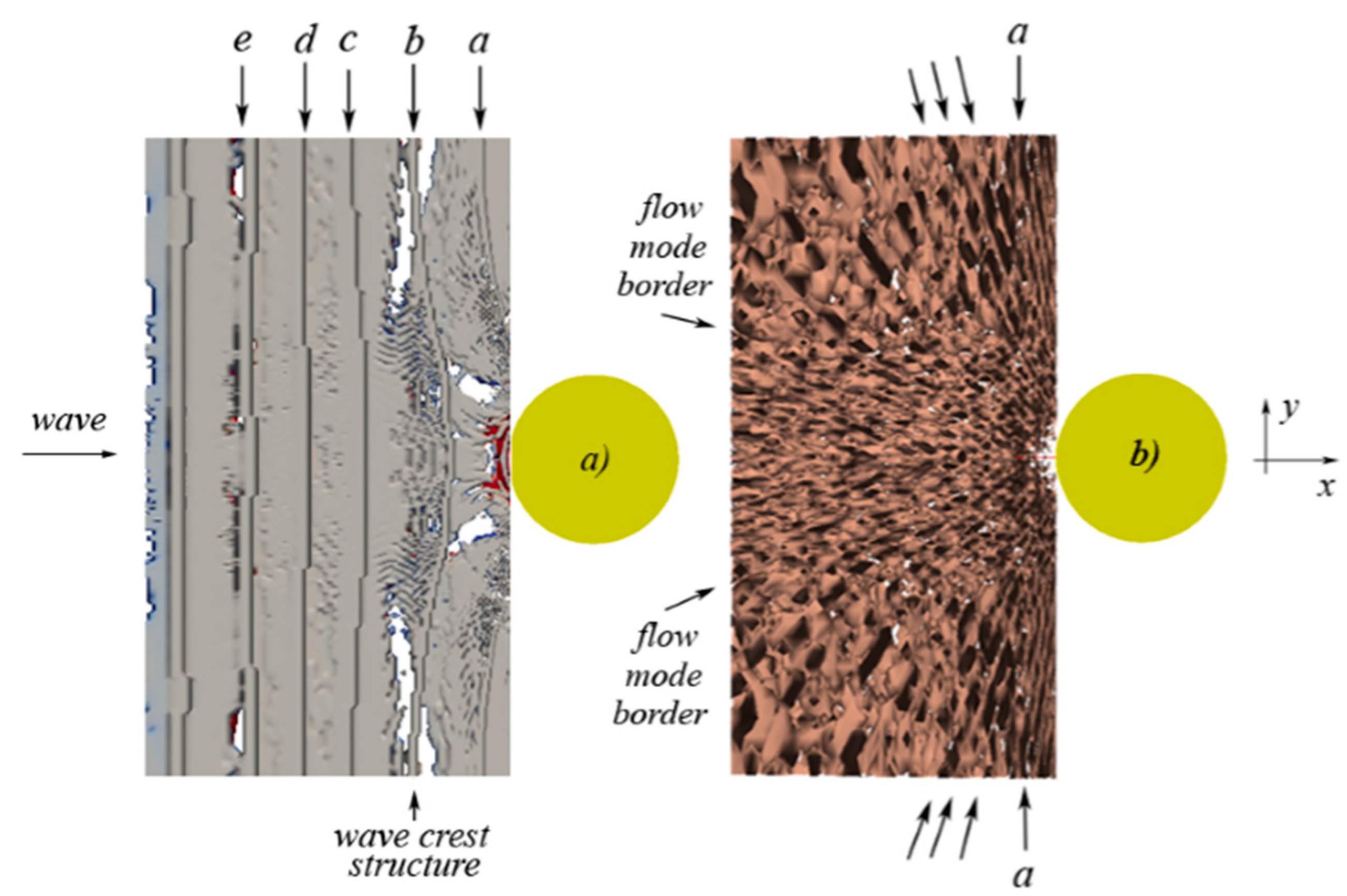
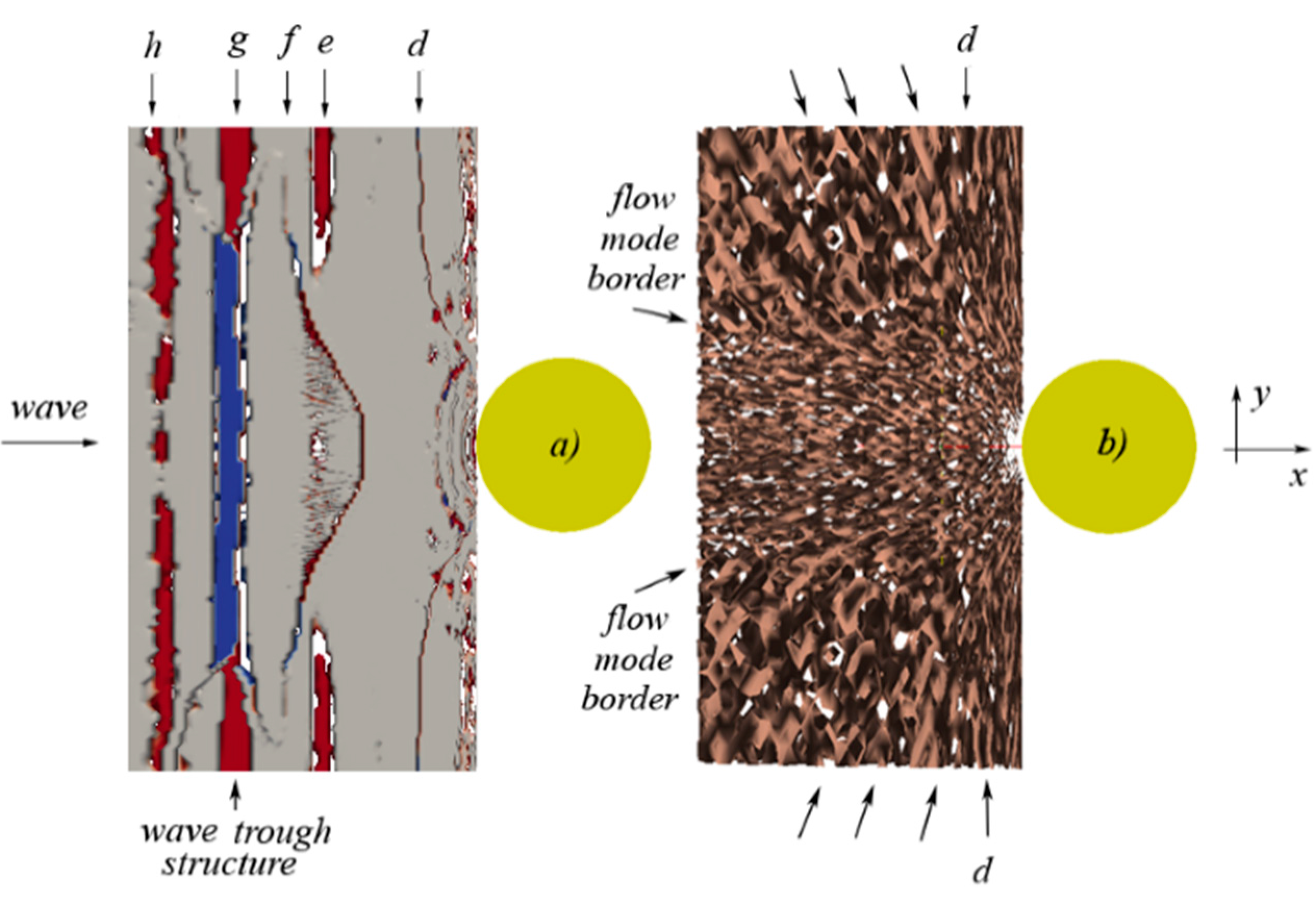
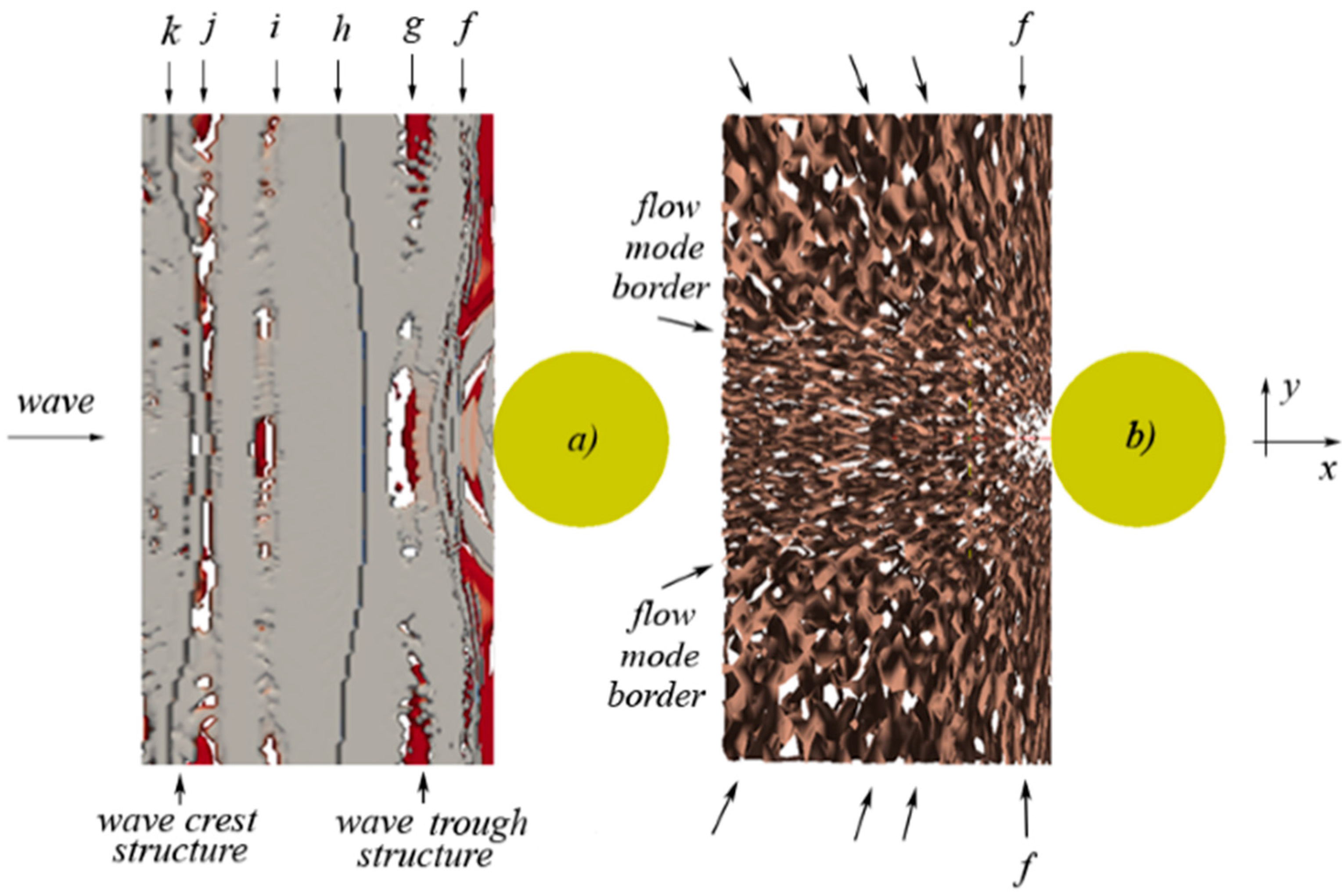
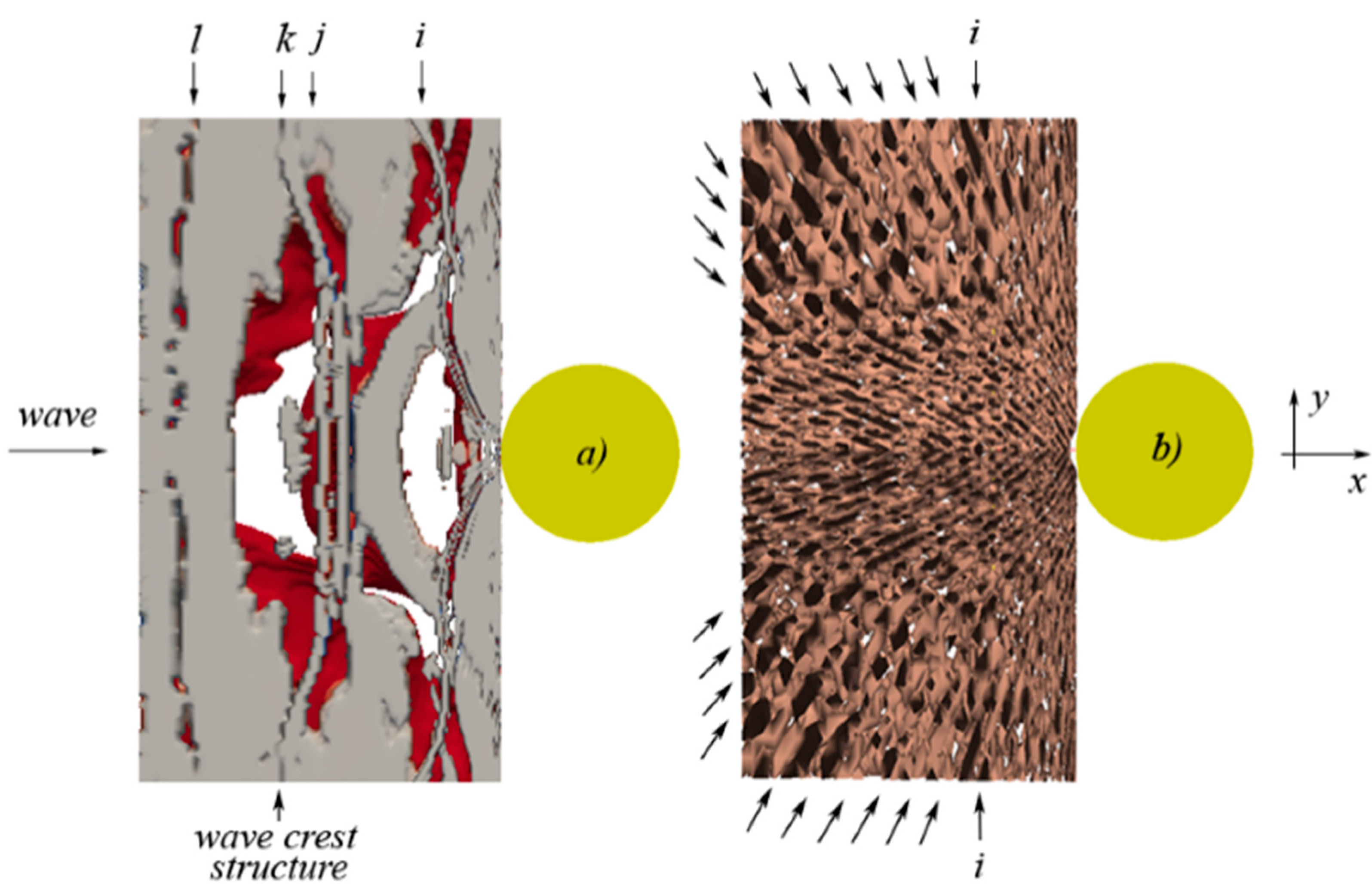

6. Concluding Remarks
Conflicts of Interest
Nomenclature
Roman Symbols (Upper Case)
velocity-gradient tensor | |
cylinder diameter | |
| Dsc | discriminant of characteristic equation |
portion-due-to-friction of force on cylinder | |
maximum force on cylinder | |
maximum force on cylinder (nondimensional) | |
| H | wave height |
Hankel function of first kind (order p) | |
first derivative of | |
Bessel function of first kind (order p) | |
first derivative of | |
| KC | Keulegan-Carpenter number |
wave length | |
dimensions of computing domain along (x,y,z) | |
dimensions of computing domain along (x,y,z) in wall units (test case) | |
number of grid points in the computing domain along (x,y,z) | |
total number of grid points in the computing domain | |
| P,Q,R | scalar invariants of velocity-gradient tensor |
| PP | parameter in hyperbolic-tangent grid-stretching law |
parameter in hyperbolic-tangent grid-stretching law | |
maximum runup at cylinder surface | |
maximum runup at cylinder surface (nondimensional) | |
wave-field Reynolds number | |
Reynolds number resulting from nondimensionalization of Navier-Stokes equations | |
friction-velocity Reynolds number (test case) | |
wave period | |
Bessel function of second kind (order p) | |
first derivative of |
Roman Symbols (Lower Case)
| a | wave amplitude |
| d | still-water level |
| g | acceleration due to gravity ( ) |
| h | channel half-width (test case) |
| k | wavenumber |
| p | pressure (also index) |
| real | real part of complex quantity |
| r,,z | cylindrical coordinate system |
cylinder radius | |
| t | time coordinate |
time at which the Euler-equations-derived verifies | |
time at which the Euler-equations-derived verifies | |
time at which the Navier-Stokes-equations-derived verifies | |
time at which the Navier-Stokes-equations-derived verifies | |
time at which the -derived verifies | |
time at which the -derived verifies | |
velocity components along (x,y,z) | |
fluctuating-velocity components along (x,y,z) (test case) | |
maximum value of | |
cartesian coordinates (x is wave direction, z is vertical direction) |
Greek Symbols (Upper Case)
time resolution of calculations | |
space resolution of calculations along (x,y,z) |
Greek Symbols (Lower Case)
phase angle | |
Kronecker delta | |
average rate of dissipation of kinetic energy per unit mass | |
alternating-unit tensor | |
eigenvalue | |
real eigenvalue | |
real part of complex eigenvalue | |
imaginary part of complex eigenvalue pair (swirling strength) | |
threshold value of swirling strength | |
Kolmogorov length scale | |
fluid kinematic viscosity | |
mean shear stress at the wall | |
Kolmogorov time scale | |
velocity-potential | |
fluid density | |
wave angular frequency | |
vorticity vector | |
spanwise component of vorticity |
Acronyms (Upper Case)
| ADI | Alternating Direction Implicit (scheme) |
| DNS | Direct Numerical Simulation (technique) |
| FAVOR | Fractional Area Volume Obstacle Representation (technique) |
| GMRES | Generalized Minimal Residual (method) |
| KL | Karhunen-Loève (decomposition technique) |
| RANS | Reynolds Averaged Navier-Stokes (equations) |
| RNG | Renormalization Group (theory) |
| VOF | Volume Of Fluid (method) |
Acronyms (Lower Case)
| lhs | left-hand side (of equation) |
| rhs | right-hand side (of equation) |
References
- MacCamy, R.C.; Fuchs, R.A. Wave forces on piles: A diffraction theory. Available online: http://acwc.sdp.sirsi.net/client/search/asset/1007800 (accessed on 25 August 2015).
- Mansour, A.M.; Williams, A.N.; Wang, K.H. The diffraction of linear waves by a uniform vertical cylinder with cosine-type radial perturbations. Ocean Eng. 2002, 29, 239–259. [Google Scholar] [CrossRef]
- Roy, P.D.; Ghosh, S. Wave force on vertically submerged circular thin plate in shallow water. Ocean Eng. 2006, 33, 1935–1953. [Google Scholar] [CrossRef]
- Kim, N.H.; Park, M.S.; Yang, S.B. Wave force analysis of vertical circular cylinder by boundary element method. KSCE J. Civil Eng. 2007, 11, 31–35. [Google Scholar] [CrossRef]
- Helstrom, B.; Rundgren, L. Model tests on Oland Sodva Grund light-house. Available online: https://www.kth.se/en (accessed on 27 August 2015).
- Laird, A.D.K. A model study of wave action on a cylindrical island. Trans. Am. Geoph. Union 1955, 26, 279–285. [Google Scholar] [CrossRef]
- Bonnefille, R.; Germain, P. Wave Action on isolated Vertical Cylinders of Large Dimension; IAHR Congress: London, UK, 1963. [Google Scholar]
- Isaacson, M. Wave runup around large circular cylinder. ASCE J. Waterw. Harb. Coast. Eng. Div. 1978, 104, 69–79. [Google Scholar]
- Galvin, C.J.; Hallermeier, R.J. Wave run-up on vertical cylinders. In Proceedings of the 13th ASCE International Conference Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972; pp. 1955–1974.
- Hallermeier, R.J. Nonlinear flow of wave crests past a thin pile. ASCE J. Waterw. Harb. Coast. Eng. Div. 1976, 102, 365–377. [Google Scholar]
- Haney, J.P.; Herbich, J.B. Wave flow around thin piles and pile groups. J. Hydr. Res. 1982, 20, 1–14. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Tam, W.A. Wave height distribution around vertical cylinder. ASCE J. Waterw. Harb. Coast. Eng. Div. 1975, 101, 225–230. [Google Scholar]
- Niedzwecki, J.M.; Duggal, A.S. Wave run-up and wave forces on a truncated cylinder. In Proceedings of the 22nd Offshore Technology Conference, Houston, TX, USA, 7–10 May 1990; pp. 593–600.
- Niedzwecki, J.M.; Duggal, A.S. Wave run-up and forces on cylinders in regular and random waves. ASCE J. Waterw. Port Coast. Ocean Eng. 1992, 118, 615–632. [Google Scholar] [CrossRef]
- Niedzweki, J.M.; Huston, J.R. Wave interaction with tension leg platforms. Ocean Eng. 1992, 19, 21–37. [Google Scholar] [CrossRef]
- Martin, A.J.; Easson, W.J.; Bruce, T. Runup on columns in steep, deep water regular waves. ASCE J. Waterw. Port Coast. Ocean Eng. 2001, 127, 26–32. [Google Scholar] [CrossRef]
- Mase, H.; Kosho, K.; Nagahashi, S. Wave runup of random waves on a small circular pier on sloping seabed. ASCE J. Waterw. Port Coast. Ocean Eng. 2001, 127, 192–199. [Google Scholar] [CrossRef]
- Morris-Thomas, M.T.; Thiagarajan, K.P. The run-up on a cylinder in progressive surface gravity waves: harmonic components. Appl. Ocean Res. 2004, 26, 98–113. [Google Scholar] [CrossRef]
- De Vos, L.; Frigaard, P.; de Rouck, J. Wave run-up on cylindrical and cone shaped foundations for offshore wind turbines. Coast. Eng. 2007, 54, 17–29. [Google Scholar] [CrossRef]
- Choi, B.H.; Kim, D.C.; Pelinovsky, E.; Woo, S.B. Three-dimensional simulation of tsunami run-up around conical island. Coast. Eng. 2007, 54, 618–629. [Google Scholar] [CrossRef]
- Alfonsi, G. Reynolds-averaged Navier-Stokes equations for turbulence modeling. Appl. Mech. Rev. 2009, 62, 040802. [Google Scholar] [CrossRef]
- Alfonsi, G. Results of numerical integration of the Navier-Stokes equations in the field of direct simulation of turbulence. J. Flow Vis. Image Proc. 2011, 18, 91–135. [Google Scholar] [CrossRef]
- Alfonsi, G. On direct numerical simulation of turbulent flows. Appl. Mech. Rev. 2011, 64, 020802. [Google Scholar] [CrossRef]
- Sarpkaya, T.; Isaacson, M. Mechanics of Wave Forces in Offshore Structures; Van Nostrand Reinhold: New York, NY, USA, 1981. [Google Scholar]
- Isaacson, M. Wave induced forces in the diffraction regime. In Mechanics of Wave-Induced Forces on Cylinders; Pitman: London, UK, 1979. [Google Scholar]
- Honji, H. Streaked flow around an oscillating circular cylinder. J. Fluid Mech. 1981, 107, 509–520. [Google Scholar] [CrossRef]
- Sarpkaya, T. Force on a circular cylinder in viscous oscillatory flow at low Keulegan-Carpenter numbers. J. Fluid Mech. 1986, 165, 61–71. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Hydrodynamics around Cylindrical Structures; World Scientific: Singapore, 1999. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Flow-3D User Manual; Flow Science, Inc.: Santa Fe, NM, USA, 2004.
- Alfonsi, G.; Ciliberti, S.A.; Mancini, M.; Primavera, L. Performances of Navier-Stokes solver on a hybrid CPU/GPU computing system. Lect. Notes Comp. Sci. 2011, 6873, 404–416. [Google Scholar]
- Alfonsi, G.; Ciliberti, S.A.; Mancini, M.; Primavera, L. GPGPU implementation of mixed spectral-finite difference computational code for the numerical integration of the three-dimensional time-dependent incompressible Navier-Stokes equations. Comp. Fluids 2014, 102, 237–249. [Google Scholar] [CrossRef]
- Alfonsi, G.; Muttoni, L. Performance evaluation of a Windows NT based PC cluster for high performance computing. J. Syst. Arch. 2004, 50, 345–359. [Google Scholar] [CrossRef]
- Alfonsi, G. Analysis of time dependent vortex shedding by means of streamfunctions’ strictly rotational component. J. Flow Vis. Image Proc. 2003, 10, 67–103. [Google Scholar]
- Alfonsi, G. Unsteady development of vortical structures in the symmetric near wake of a cylinder. J. Flow Vis. Image Proc. 2005, 12, 45–72. [Google Scholar]
- Alfonsi, G. Numerical visualization of unsteady vortex shedding. J. Flow Vis. Image Proc. 2005, 12, 105–110. [Google Scholar] [CrossRef]
- Alfonsi, G.; Giorgini, A. Nonlinear perturbation of the vortex shedding from a circular cylinder. J. Fluid Mech. 1991, 222, 267–291. [Google Scholar]
- Alfonsi, G.; Giorgini, A. Temporal evolution of high-order vortices in the nonsymmetric wake of a circular cylinder. Fluid Dyn. Res. 2002, 31, 13–39. [Google Scholar]
- Alfonsi, G. Coherent structures of turbulence: methods of eduction and results. Appl. Mech. Rev. 2006, 59, 307–323. [Google Scholar]
- Alfonsi, G. Techniques of research and results in the field of coherent structures of wall-bounded turbulence. In Vorticity Turbulence Effects Fluid Structure Interaction; Wessex Institute of Technology Press: Southampton, UK, 2006; pp. 1–27. [Google Scholar]
- Kocaman, S.; Seckin, G.; Erduran, K.S. 3D model for prediction of flow profiles around bridges. J. Hydr. Res. 2010, 48, 521–525. [Google Scholar] [CrossRef]
- Cho, S.M. Foundation design of the Incheon bridge. Geotech. Eng. J. 2010, 41, 1–16. [Google Scholar]
- Jin, J.; Meng, B. Computation of wave loads on the superstructures of coastal highway bridges. Ocean Eng. 2011, 38, 2185–2200. [Google Scholar] [CrossRef]
- Kim, C.; Kim, J.; Kang, J. Analysis of the cause for the collapse of a temporary bridge using numerical simulation. Sci. Res. 2013, 5, 997–1005. [Google Scholar] [CrossRef]
- Kayser, M.; Gabr, M.A. Assessment of scour on bridge foundations by means of in situ erosion evaluation probe. J. Transp. Res. Board 2013, 2335, 72–78. [Google Scholar] [CrossRef]
- Alfonsi, G.; Passoni, G.; Pancaldo, L.; Zampaglione, D. A spectral-finite difference solution of the Navier-Stokes equations in three dimensions. Int. J. Numer. Meth. Fluids 1998, 28, 129–142. [Google Scholar] [CrossRef]
- Passoni, G.; Alfonsi, G.; Tula, G.; Cardu, U. A wavenumber parallel computational code for the numerical integration of the Navier-Stokes equations. Parall. Comp. 1999, 25, 593–611. [Google Scholar] [CrossRef]
- Passoni, G.; Cremonesi, P.; Alfonsi, G. Analysis and implementation of a parallelization strategy on a Navier-Stokes solver for shear flow simulations. Parall. Comp. 2001, 27, 1665–1685. [Google Scholar] [CrossRef]
- Passoni, G.; Alfonsi, G.; Galbiati, M. Analysis of hybrid algorithms for the Navier-Stokes equations with respect to hydrodynamic stability theory. Int. J. Numer. Meth. Fluids 2002, 38, 1069–1089. [Google Scholar] [CrossRef]
- Alfonsi, G.; Primavera, L. Direct numerical simulation of turbulent channel flow with mixed spectral-finite difference technique. J. Flow Vis. Image Proc. 2007, 14, 225–243. [Google Scholar]
- Mochizuki, S.; Nieuwstadt, F.T.M. Reynolds-number-dependence of the maximum of the streamwise velocity fluctuations in wall turbulence. Exp. Fluids 1996, 21, 218–226. [Google Scholar] [CrossRef]
- Alfonsi, G. Analysis of streamwise velocity fluctuations in turbulent pipe flow with the use of an ultrasonic Doppler flowmeter. Flow Turbul. Combust. 2001, 67, 137–142. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, Z.; den Toonder, J.M.J.; Nieuwstadt, F.T.M. Origin of high kurtosis level in the viscous sublayer. Direct numerical simulation and experiment. Phys. Fluids 1996, 8, 1938–1944. [Google Scholar] [CrossRef]
- Alfonsi, G. Evaluation of radial velocity fluctuations in turbulent pipe flow by means of an ultrasonic Doppler velocimeter. J. Flow Vis. Image Proc. 2003, 10, 155–161. [Google Scholar] [CrossRef]
- Alfonsi, G.; Brambilla, S.; Chiuch, D. The use of an ultrasonic Doppler velocimeter in turbulent pipe flow. Exp. Fluids 2003, 35, 553–559. [Google Scholar] [CrossRef]
- Alfonsi, G.; de Bartolo, S.; Gaudio, R.; Primavera, L. Reliability of 5-beam LDV fiberoptic probe for turbulence measurements in the wall region of open channel flow. J. Flow Vis. Image Proc. 2009, 16, 255–277. [Google Scholar] [CrossRef]
- Bakewell, H.P.; Lumley, J.L. Viscous sublayer and adjacent wall region in turbulent pipe flow. Phys. Fluids 1967, 10, 1880–1889. [Google Scholar] [CrossRef]
- Bearman, P.W.; Downie, M.J.; Graham, J.M.R.; Obasaju, E.D. Forces on cylinders in viscous oscillatory flow at low Keulegan-Carpenter numbers. J. Fluid Mech. 1985, 154, 337–356. [Google Scholar] [CrossRef]
- Morison, J.R.; O’Brien, M.P.; Johnson, J.W.; Shaag, S.A. The forces exerted by surface waves on piles. AIME J. Petrol. Technol. 1950, 189, 149–154. [Google Scholar] [CrossRef]
- Alfonsi, G.; Primavera, L. Vortex identification in the wall region of turbulent channel flow. Lect. Notes Comp. Sci. 2007, 4487, 9–16. [Google Scholar]
- Alfonsi, G.; Primavera, L. On identification of vortical structures in turbulent shear flow. J. Flow Vis. Image Proc. 2008, 15, 201–216. [Google Scholar]
- Zhou, J.; Adrian, R.J.; Balachandar, S.; Kendall, T.M. Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 1999, 387, 353–396. [Google Scholar] [CrossRef]
- Alfonsi, G. On vorticity-field evolution in viscous- and inviscid-fluid wave-diffraction cases. J. Flow Vis. Image Proc. 2013, 20, 209–225. [Google Scholar]
- Alfonsi, G.; Primavera, L. Determination of the threshold value of the quantity chosen for vortex representation in turbulent flow. J. Flow Vis. Image Proc. 2009, 16, 41–49. [Google Scholar]
- Alfonsi, G.; Primavera, L. Temporal evolution of vortical structures in the wall region of turbulent channel flow. Flow Turbul. Comb. 2009, 83, 61–79. [Google Scholar] [CrossRef]
- Alfonsi, G.; Ciliberti, S.A.; Mancini, M.; Primavera, L. Hairpin vortices in turbulent channel flow. Proc. Comp. Sci. 2011, 4, 801–810. [Google Scholar] [CrossRef]
- Alfonsi, G.; Ciliberti, S.A.; Mancini, M.; Primavera, L. Turbulent events in a wall-bounded turbulent flow. J. Flow Vis. Image Proc. 2012, 19, 139–160. [Google Scholar]
- Alfonsi, G.; Lauria, A.; Primavera, L. Flow structures around a large-diameter circular cylinder. J. Flow Vis. Image Proc. 2012, 19, 15–35. [Google Scholar] [CrossRef]
- Alfonsi, G.; Lauria, A.; Primavera, L. Structures of a viscous-wave flow around a large-diameter circular cylinder. J. Flow Vis. Image Proc. 2012, 19, 323–354. [Google Scholar]
- Alfonsi, G.; Lauria, A.; Primavera, L. A study of vortical structures past the lower portion of the Ahmed car model. J. Flow Vis. Image Proc. 2012, 19, 81–95. [Google Scholar]
- Liang, Y.C.; Lee, H.P.; Lim, S.P.; Lin, W.Z.; Lee, K.H.; Wu, C.G. Proper orthogonal decomposition and its applications, Part I: Theory. J. Sound Vibr. 2002, 252, 527–544. [Google Scholar]
- Lumley, J.L. Stochastic Tools in Turbulence; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Sirovich, L. Turbulence and the dynamics of coherent structures, Part I: Coherent structures, Part II: Symmetries and transformations, Part III: Dynamics and scaling. Quart. Appl. Math. 1987, 45, 561–590. [Google Scholar]
- Alfonsi, G.; Primavera, L. Coherent structure dynamics in turbulent channel flow. J. Flow Vis. Image Proc. 2002, 9, 89–98. [Google Scholar]
- Alfonsi, G.; Primavera, L. Description of turbulent events trough the analysis of POD modes in numerically simulated turbulent channel flow. Lect. Notes Comp. Sci. 2005, 3514, 623–630. [Google Scholar]
- Alfonsi, G.; Primavera, L. Dynamics of POD modes in wall-bounded turbulent flow. Lect. Notes Comp. Sci. 2006, 3991, 465–472. [Google Scholar]
- Alfonsi, G.; Primavera, L. The structure of turbulent boundary layers in the wall region of plane channel flow. Proc. R. Soc. A 2007, 463, 593–612. [Google Scholar] [CrossRef]
- Alfonsi, G.; Lauria, A.; Primavera, L. Proper orthogonal flow modes in the viscous-fluid wave-diffraction case. J. Flow Vis. Image Proc. 2013, 20, 227–241. [Google Scholar]
- Alfonsi, G.; Primavera, L.; Felisari, R. On the behavior of POD modes of the flow past a perforated plate. J. Flow Vis. Image Proc. 2003, 10, 105–117. [Google Scholar]
- Alfonsi, G.; Restano, C.; Primavera, L. Coherent structures of the flow around a surface-mounted cubic obstacle in turbulent channel flow. J. Wind Eng. Ind. Aerodyn. 2003, 91, 495–511. [Google Scholar]
- Carbone, V.; Lepreti, F.; Primavera, L.; Pietropaolo, E.; Berrilli, F.; Consolini, G.; Alfonsi, G.; Bavassano, B.; Bruno, R.; Vecchio, A.; et al. An analysis of the vertical photospheric velocity field as observed by Themis. Astr. Astrophys. 2002, 381, 265–270. [Google Scholar]
- Vecchio, A.; Carbone, V.; Lepreti, F.; Primavera, L.; Sorriso-Valvo, L.; Veltri, P.; Alfonsi, G.; Straus, T. Proper Orthogonal Decomposition of solar photospheric motions. Phys. Rev. Lett. 2005, 95, 061102. [Google Scholar]
- Zhang, X.; Pan, C.; Shen, J.Q.; Wang, J.J. Effect of surface roughness element on near wall turbulence with zero-pressure gradient. Sci. China Phys. Mech. Astron. 2015, 58, 064702. [Google Scholar]
- Alfonsi, G.; Primavera, L. A parallel computational code for the eduction of coherent structures of turbulence in fluid dynamics. Lect. Notes Comp. Sci. 2005, 3606, 381–392. [Google Scholar]
- Alfonsi, G.; Primavera, L. A parallel computational code for the Proper Orthogonal Decomposition of turbulent flows. J. Flow Vis. Image Proc. 2007, 14, 267–286. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfonsi, G. Numerical Simulations of Wave-Induced Flow Fields around Large-Diameter Surface-Piercing Vertical Circular Cylinder. Computation 2015, 3, 386-426. https://doi.org/10.3390/computation3030386
Alfonsi G. Numerical Simulations of Wave-Induced Flow Fields around Large-Diameter Surface-Piercing Vertical Circular Cylinder. Computation. 2015; 3(3):386-426. https://doi.org/10.3390/computation3030386
Chicago/Turabian StyleAlfonsi, Giancarlo. 2015. "Numerical Simulations of Wave-Induced Flow Fields around Large-Diameter Surface-Piercing Vertical Circular Cylinder" Computation 3, no. 3: 386-426. https://doi.org/10.3390/computation3030386
APA StyleAlfonsi, G. (2015). Numerical Simulations of Wave-Induced Flow Fields around Large-Diameter Surface-Piercing Vertical Circular Cylinder. Computation, 3(3), 386-426. https://doi.org/10.3390/computation3030386