Abstract
The development of parallel Computational Fluid Dynamics (CFD) codes is a challenging task that entails efficient parallelization concepts and strategies in order to achieve good scalability values when running those codes on modern supercomputers with several thousands to millions of cores. In this paper, we present a hierarchical data structure for massive parallel computations that supports the coupling of a Navier–Stokes-based fluid flow code with the Boussinesq approximation in order to address complex thermal scenarios for energy-related assessments. The newly designed data structure is specifically designed with the idea of interactive data exploration and visualization during runtime of the simulation code; a major shortcoming of traditional high-performance computing (HPC) simulation codes. We further show and discuss speed-up values obtained on one of Germany’s top-ranked supercomputers with up to 140,000 processes and present simulation results for different engineering-based thermal problems.
1. Introduction
Due to ever-increasing advances in hardware, nowadays, high-performance computing (HPC) systems consist of several thousands to millions of cores, raising the necessity for sophisticated data structures and parallelization approaches in order to exploit the underlying computing power. The efficient ‘orchestration’ of hundreds of thousands of processes is one of the main challenges for high-fidelity applications to utilize massive parallel systems and, thus, leverage petaflop performance within multi-scale, multi-physics problems. In our approach, the focus was on coupling Computational Fluid Dynamics (CFD) simulations with thermal comfort assessment for complex engineering-based scenarios to be computed on modern HPC systems. Therefore, we have developed a hierarchical data structure that inherently supports distributed computing and combines state-of-the-art (numerical) solvers with efficient load-balancing techniques for fluid flow applications. This approach could be successfully tested on different HPC systems, including one of Germany’s three top-ranked supercomputers, up to a total of 140,000 processes solving a problem with close to one trillion (1012) unknowns.
Moreover, as the computed data have to be processed and analyzed in order to draw the necessary conclusions from the given problem statement, methods have to be devised to cope with the huge amount of data generated from a large run. Hence, the data structure is designed to handle interactive data exploration during runtime or to write a smaller, coarser data file for a subsequent offline post-processing. This issue is of major concern when it comes to analyzing HPC simulation data, as the problem sizes typically restrict data exploration and analysis. The work at hand provides a viable solution strategy.
There exist several state-of-the-art frameworks for problem solving environments (PSE), such as Chombo [1] or SCIRun [2], as well as open source CFD programs, such as OpenFOAM [3], which could have been used as foundations for algorithm development regarding an interactive data exploration. Furthermore, work has been done in the broad research area of in situ visualization (e.g., the state-of-the-art analysis by Rivi et al. [4]). The applications range from visualizing combustion problems (Yu et al. [5]) to general procedures and software solutions (Fabian et al. [6]) and extreme-scale scientific analysis (Bennett et al. [7]). From reviewing these platforms and concepts, the authors decided to develop a new data structure, allowing one to solve some of the mentioned shortcomings and to provide a flexible environment for further model implementations.
This paper, where parts are excerpts from Frisch [8] and rewritten in a condensed way in order to give a good overview over the strategies applied, describes ideas in order to create a computational fluid dynamics simulation program for indoor airflow purposes able to run on massive parallel systems, such as supercomputers and large clusters. In the following, the necessary mathematical concepts are introduced, based on the Navier–Stokes equations coupled to a temperature convection-diffusion equation by the Boussinesq approximation in order to model the thermal transport phenomena. The specifically tailored data structure, including the data exchange, is described, and efficient solving mechanisms based on a multi-grid-like solver for the pressure Poisson equation are introduced. A dedicated section treats the code validation and verification according to standard benchmarks, such as the Rayleigh–Bénard convection, before looking into engineering-based examples generated from everyday engineering needs using complex temperature boundary conditions, as well as a complex geometric setup.
2. Mathematical Modeling and Discretization
Starting from the conservation of mass, momentum and energy principles, the Navier–Stokes equations can be derived, which serve as a basis for the numerical modeling. A complete and extensive derivation, as well as the historical impact of the equations can be found in standard literature, such as [9–11]. The governing equations for an incompressible Newtonian fluid comprise three sets of equations. The first equation set, written in differential form, is called the continuity equation:
where
describes the velocity of the fluid using u1, u2, u3 as the three velocity components in the three spatial directions x1, x2, x3, respectively This equation has to be satisfied at every time step all over the domain. The second set, called the momentum equations, can be written for every direction i ∈ {1,2,3} as:
where t represents the time, ρ∞ the density of the fluid assumed constant over the complete domain and µ the dynamic viscosity p represents the pressure, β the thermal expansion coefficient of the fluid, T the temperature, T∞ the temperature of the undisturbed fluid at rest and gi the gravitational force in direction i. Here,
represents the unit vector in direction i.
The last term ρ∞ · β · (T — T∞)gi in the momentum conservation equation couples the effects of the temperature field to the momentum equations and is commonly known as the Boussinesq approximation. It is valid, if changes in the density occur only due to changes in the temperature, and can be described by a linear correlation between both variables. In other words, the density is everywhere assumed to be ρ∞, and the last term ρ∞ · β · (T − T∞)gi modifies the density due to buoyancy effects.
The last equation set describes the energy conservation equation in order to model the thermal heat transport. Using the generic convection-diffusion equation and adapting it to a heat transfer problem results in:
where α = k/(ρ∞ · cp) represents the heat diffusion coefficient, k the heat conduction coefficient, cp describes the specific heat capacity at constant pressure and qint the internal heat generation.
This equation is valid under the assumption that the variations of pressure are small enough in order to have no influence on the thermodynamic properties of the fluid. Following Lienhard and Lienhard [12], this assumption holds for most Newtonian fluids moving at moderate velocities slower than a third times the speed of sound, which is the case for indoor airflow scenarios. Furthermore, fluid properties, such as the thermal conductivity k or the dynamic viscosity µ, do not depend on changes in the temperature field. Moreover, the viscous dissipation of energy in the fluid must not heat up the fluid significantly.
Hence, under these conditions, Equation (3) models heat transport phenomena, such as convection and diffusion, along a given flow field
. As the temperature field has again an influence on the flow field in Equation (2), a coupling strategy has to be applied.
Furthermore, by analyzing Equations (1)–(3), it can be seen that there is no independent equation for the pressure p. The momentum equations include the pressure gradient ∇p, whereas the incompressible continuity equation and the energy conservation equation do not contain p at all. Nevertheless, a solution for incompressible flows can be found by applying so-called pressure correction methods, proposed by Harlow and Welch [13] in their marker and cell method (MAC) for the solution of free surface flows or in the fractional step method (or projection method) introduced by Chorin [14]. The basic idea is to iterate between velocity and pressure fields, where the pressure field acts as a correction in order to fulfil the continuity equation for the velocity field. As Equation (2) only contains the pressure gradient, the absolute value of the pressure is not relevant, and thus, the pressure term p in the incompressible equations is often referred to as ‘working pressure’.
By applying the fractional step method and choosing an explicit Euler time discretization for the temporal derivative ∂/∂t, the momentum conservation equations in the direction i for an intermediate time step⋆ can be written:
by omitting the pressure gradient. Δt denotes the time step size, and the superscriptn denotes the current time step n and the superscript⋆ an intermediate time step between n and n + 1. The pressure term is now taken into account during a second step:
While summing up the two Equations (4) and (5), it can be seen that Equation (2) results, where the velocity is treated explicitly (i.e., at time step n) and the pressure implicitly (i.e., at time step n + 1).
Using the divergence operator on Equation (5) leads to:
As the pressure term has to lead to a divergence-free velocity field at time step n + 1 with respect to the continuity Equation (1), the equation for determining the pressure at time step n+1 can be written as:
representing a Poisson equation for the pressure, which has to be solved in every time step.
The temporal discretization can be enhanced using a second order explicit multi-level Adams–Bashforth method, introduced in detail by Schwarz [15], for example. A very detailed analysis of other time derivative approaches can be found in Ferziger [16]. Kim and Moin [17], for example, use a mixture of semi-implicit and explicit methods, where the convective terms in Equation (4) are discretized using a second order explicit Adams–Bashforth method. The viscous terms, however, are discretized using a semi-implicit Crank–Nicolson method, which eliminates some numerical stability problems. Choi and Moin [18] use a similar approach, but incorporate a predictor-corrector method.
Similar to a temporal discretization, a spatial discretization has to be introduced in order to describe and prepare the domain for a numerical simulation. Popular, well-established methods, such as the finite difference method (FDM), the finite volume method (FVM) or the finite element method (FEM), could be used. This work focuses on the finite volume and finite difference approach for discretizing the spatial domain. A good description of FDM and FVM methods in fluid mechanics can be found in Ferziger and Peric´ [10] or Hirsch [11], for example. In FDM, spatial derivatives are approximated using discretized notations of a certain order on a given grid. These derivatives can be used in equations expressed in differential form. In FVM, volume and surface integrals are computed by approximations of a certain order and used in equations expressed in an integral form. If finite volume methods are used on a regular Cartesian grid, it can be shown that the finite volumes degenerate into finite differences, which can be handled by a fast computational stencil, for example.
As an explicit time discretization method was chosen here, numerical stability issues have to be taken into account. Courant and Friedrichs [19] analyzed this problem in the 1920s and proposed using an upwind-difference for the convection term and central differences for the diffusive term. Peyret and Taylor [20] give a good overview on a detailed stability analysis for explicit finite difference methods.
3. Data Structure and Data Exchange
In order to store the relevant information required to simulate an airflow scenario, for example, a lean and efficient data structure has to be used. Furthermore, as the targeted hardware comprises supercomputers of all kinds, it is mandatory to design the data structure with a parallel implementation in mind, including consistent data synchronization mechanisms.
Hence, an efficient, parallel data structure is of utmost importance if computations on massive parallel systems shall be performed. The following sections will introduce the data structure and the necessary data synchronization and distribution mechanisms. Moreover, the basic idea of interactive data exploration enabled by the implemented data structure is introduced, highlighting the basic idea behind the chosen data structure concept. Furthermore, an efficient solving technique based on a multi-grid-like method is described, and scaling results from supercomputers will be discussed.
3.1. Data Structure
The data structure is based on non-overlapping, block-structured, hierarchical, orthogonal, regular grids. A logical, purely topological grid management (called ‘l-grids’) is responsible for all hierarchic information, such as parents and children relations, while data grids (called ‘d-grids’) contain the actual data arrays.
Figure 1 gives an overview of both data structure parts. In the middle part, the nested construction of the non-overlapping grids can be seen. A root l-grid, located per definition at depth zero, is refined by
in the respective directions. The new resulting child l-grids can be refined again by
until the desired depth d is reached. Currently,
and
can be chosen independently out of the interval [1, 7]. Furthermore, while creating the newly refined child l-grids, the coarse l-grid will be defined as their parent l-grid. Hence, each l-grid can only have one parent l-grid.
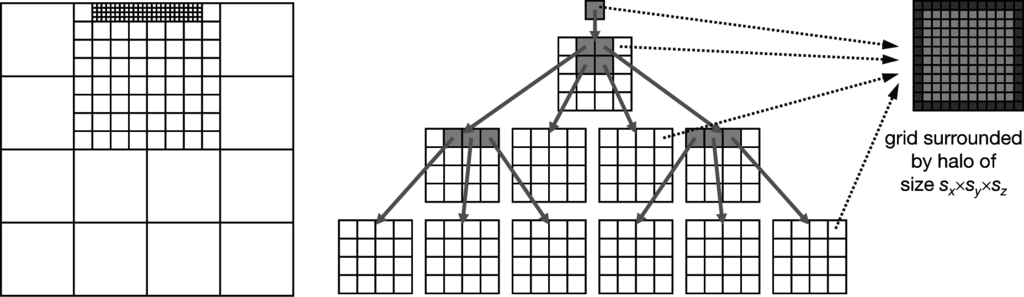
Figure 1.
Schematic representation of the construction of the hierarchic grid data structure (based on Frisch [8]): resulting (topological) grid on the left-hand side and logical l-grid (l, logic) structure in the middle and one d-grid (d, data) with a ghost halo on the right-hand side.
The second major part of the data structure is the d-grids (i.e., the data grids). Every d-grid stores the necessary variables, such as velocities, pressure or temperature values, in a matrix of cells. Thus, a cell is comparable to one finite volume or the control volume. It is surrounded by a halo of ghost cells necessary for the proper functioning of the structure. One of these d-grids can be seen on the right-hand side of Figure 1. It has a size of sx, sy, sz (not counting the halo), which can be chosen arbitrarily with one constraint: in order to avoid non-conforming setups, si has to be divisible without any remainder by
and by
. This restriction guarantees that coarse d-grid boundaries will always coincide with refined d-grid boundaries. Furthermore, each l-grid contains exactly one link to one d-grid.
Hence, due to the flexible structure of the logical grid management, complex, adaptive domain setups can be generated by combining regular blocks. By applying this type of data structure together with a finite volume approach for the spatial discretization, a few special points can be noted here.
One d-grid is constructed in such a way that it has an equidistant orthogonal spacing. In this case, it can be shown that the finite volume approach using the mid-point rule and linear interpolation degenerates into a finite difference approach. Thus, on one d-grid, a simple finite difference scheme, such as a six-point stencil in 3D, can be used. This allows a separation into two phases: a computation phase and a communication phase. In the computation phase, the finite difference approach in the form of a stencil, for example, is evaluated on every d-grid. In the communication phase, a halo update is performed filling the ghost cells with neighboring values in order to apply a Schwarz method [21]. Usually, a communication phase is only necessary for a computation running on a distributed system, but for this structure, it is required even in serial cases.
One difference between this data structure and data structures used by other codes is the retaining of the parent l-grids after a refinement into sub-grids. This generates an additional amount of data, which has to be stored, but this strategy poses great advantages in working with adaptive grids and during visualization post-processing, which will be presented in Section 3.4 after the data exchange and solving techniques are properly introduced.
3.2. Data Exchange
As the d-grids do not know anything about their neighbors and can purely compute on their local values, all other information, such as neighboring and parental relations, have to be provided by the logical grid management structure. Hence, the logical grid management has to take care of flux conservation across boundaries of d-grids, especially in the case of adaptive refinements, such as depicted in Figure 1. Therefore, complex data exchange mechanisms have to be provided by the logical grid management framework in order to guarantee data consistency and integrity.
In order to uniquely identify grids distributed over different processes, a UID (unique grid identifier) was introduced, composed out of a 64-bit integer. The first 32 bits contain the rank of the process on which the grid resides. The last 32 bits are used as a tag and encode in 22 bits the grid ID (GID), as well as in nine bits the location of this grid in the corresponding parent grid. Details of the tag encoding can be found in [8]. This coding proves quite convenient while using the message passing interface (MPI) libraries for communication, as the rank and tag can be immediately used for communication purposes.
In [22], the basic communication routines were introduced, and they are displayed in Figure 2. The parallelization, of logical grids to different processes, where the data grids can use their internal finite difference stencil and the ghost halos are exchanged at specific times.
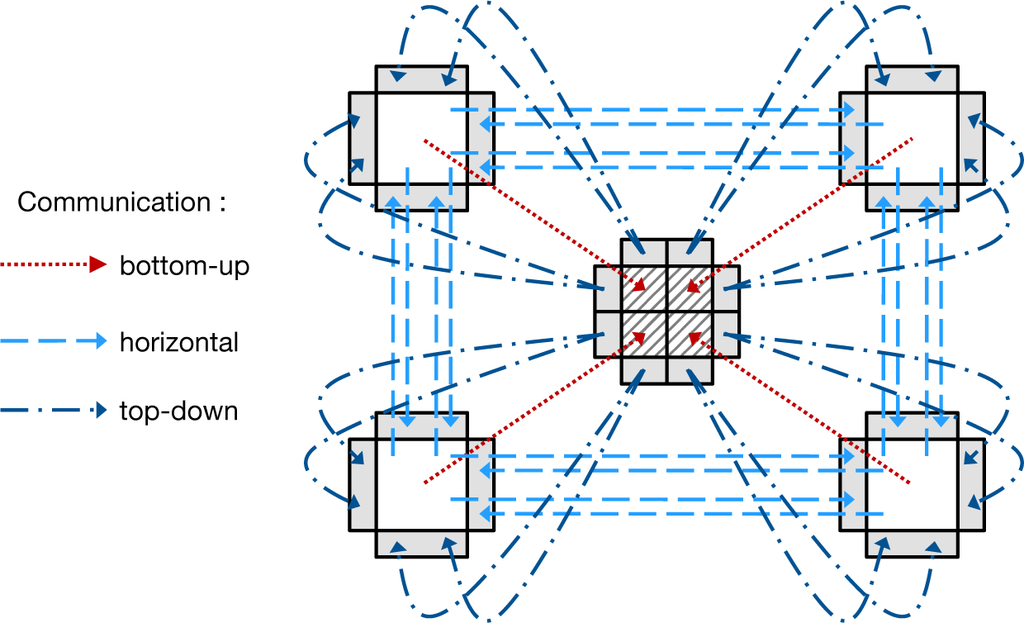
Figure 2.
Communication structure grouped into three different phases (based on Frisch [8]).
The distribution to different processes is managed by a special dedicated process called the neighborhood server. It is described in detail in [8]. The basic idea is to have one dedicated server keeping track of the logical structure for all grids (without having knowledge of the data content) and to organize the distribution to different processes by a space-filling curve in order to keep neighboring grids as close together as possible. Performance measurements showed very good results in terms of grid-to-grid communication for the distribution.
In order to ensure a consistent data exchange, a certain order has to be maintained during the exchange phase. In a serial computation, a synchronization is implicitly given by the ordering of the lines of code, and, obviously, it is necessary that data have to be available in the ghost halo before the stencil can use them for computing updated values or further exchanging them with neighboring grids.
In the case of a parallel computation, the same prerequisites have to be fulfilled: data must have been exchanged completely in all ghost halos of one d-grid, before a computation can start. Thus, synchronization mechanisms have to be implemented, preventing a computation before all necessary data have been exchanged. In a distributed parallel computation, synchronization is performed due to the existence of messages, i.e., by explicit message exchanges between different processes.
Generally, the communication is distributed into three phases: in the first stage, a bottom-up phase aggregates data from child grids and stores them in their corresponding parent grid. As soon as a parent receives data from all of its child grids, it aggregates its own data and sends them to its parent, and so on, until the root grid is updated. As the data are moving from the bottom to the top, the phase is dubbed bottom-up. In the next phase, direct neighbors exchange their values and store them in the corresponding ghost halos of their neighbors. In the case of an adaptive grid setup, it is important to do this data exchange only after the first phase finishes, as otherwise, inconsistent data storage could arise. In the last step, all ghost halos that did not receive any data from neighboring grids (thus, there was no neighboring grid at the same level) are filled with data from their corresponding parent grid. Once this step is finished, a complete and correct data exchange is done, and the computation step can work on the exchanged data.
From a technical point of view, all communications are managed by the MPI library, and data synchronization is achieved by combining blocking and non-blocking communication calls at the right places in the code.
In order to evaluate the behavior of the exchange mechanisms using large setups, tests were performed on different machines for different depths of the hierarchical data structure. Figure 3 shows the times for one ghost halo exchange of the complete grid structure. The measurements were performed on three testing systems: Shaheen ( http://www.hpc.kaust.edu.sa), a 16-rack IBM Blue Gene/P supercomputer installed at King Abdullah University of Science and Technology (KAUST) in the Kingdom of Saudi Arabia, the MAC Cluster ( http://www.mac.tum.de), a heterogeneous research cluster installed by the Munich Centre of Advanced Computing at Technische Universität München in Germany, and SuperMUC ( http://www.lrz.de/services/compute/supermuc/systemdescription), a 155,656 processor core large IBM System iDataPlex supercomputer installed at the Leibniz Supercomputing Centre (LRZ) in Garching, Germany.
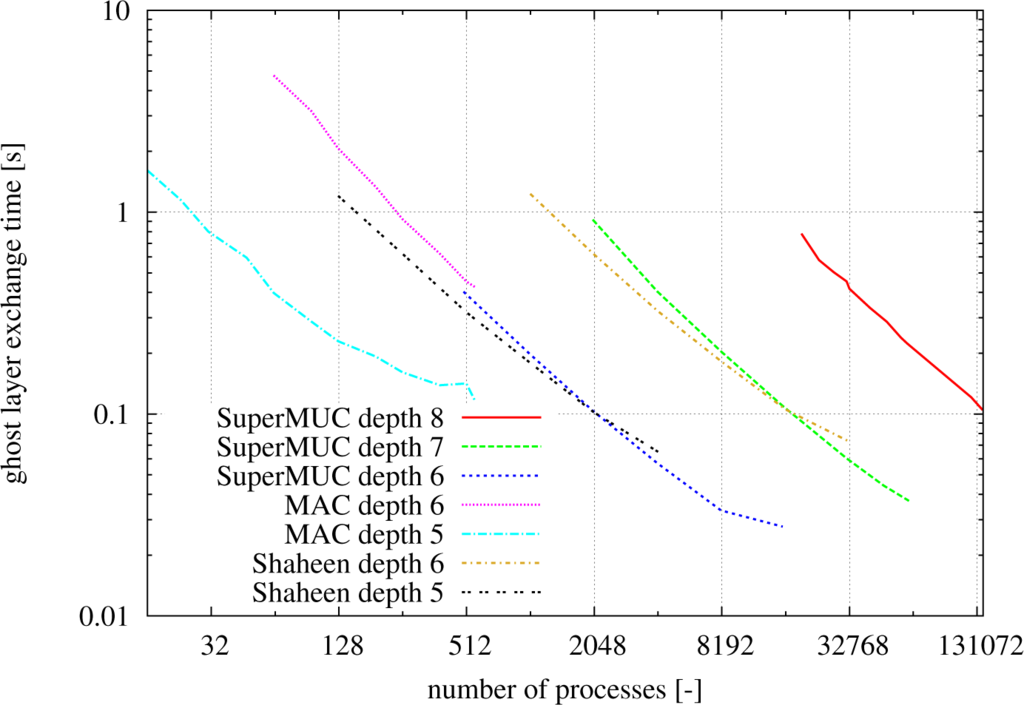
Figure 3.
Communication times for a total ghost layer exchange of nine independent variables per cell in seconds on three different computing platforms for a 3D domain of fully-refined l-grids with a refinement level (2,2,2) up to depth eight and a d-grid size of (16,16,16) (from [8]).
All curves show a tendency of decreased exchange time with increased amount of processes. The curves for depth eight describe a uniformly-refined domain using approximately 78.5 billion cells, and more than 707 billion variables are exchanged across more than 140,000 processes on SuperMUC. Hence, the data structure in its current form is extremely flexible and is well suited for massive parallel machines.
3.3. Multi-Grid-Like Solver for the Pressure Poisson Equation
Geometric multi-grid solvers were introduced in the 1970s by Brandt [23] as multi-level methods. The general idea is based on the fact that many iterative methods, such as Jacobi or Gauss–Seidel, have a smoothing effect on the error if they are applied to elliptic problems (cf. Trottenberg et al. [24]), where high-frequency components of the error will be damped much more than low-frequency components. Hence, using only a smoothing method requires a long time to reduce the overall error below a certain tolerance. Fortunately, it can be shown that by approximating a quantity to a coarser grid, the smooth behavior will become oscillatory again, and the smoothing strategy can be reapplied. As soon as the coarsest grid is small enough, it can be solved by a direct solver, for example. Once a solution is available, the error correction can be forwarded from coarse grid to a fine grid, until the finest grid is updated.
The passing from a fine to a coarse grid is called restriction and from a coarse to a fine grid prolongation. Different restriction and prolongation operators can be found in Briggs et al. [25], for example.
By comparing the data flows of restriction and prolongation operators to the previously described phases of the communication, many similarities can be seen. Hence, a cell-centered, multi-grid like solver was implemented using the already existing communication routines. Different smoothing strategies were analyzed and compared, in order to find suitable settings, working for the intended types of problems. Details can be found in [26], for example.
As the first testing example, a Laplacian equation was used, as this equation is similar to the pressure Poisson equation, which has to be solved at every time step in order to account for the pressure correction and guarantees the validity of the continuity equation. The Laplacian problem:
is defined on a 1 × 1 × 1 m cubic domain, where fixed Dirichlet boundary conditions were applied on the east and west side according to:
whereas all other sides were set to p = 0. This equation describes a pure diffusion process and could be used as well for modeling a stationary temperature diffusion problem without any convective influences or internal loads.
Before doing a large-scale analysis of the code’s performance for the Laplacian problem on a supercomputer, such as SuperMUC, small-scale analyses were performed in order to determine an optimal data grid size for this type of problem and the given hardware. As mentioned in the section describing the data structure, the overall domain discretization is dependent on the chosen grid refinement
and
, but also on the chosen data grid size si. In order to assess the influence of the data grid size on the performance, the Laplacian problem was solved for different data grid sizes on a Blue Gene/P system of Universitatea de Vest din Timişoara (UVT) in Romania and on the TUM MAC Cluster using 256 processes.
Figure 4 plots the number of solved cells per second (in millions) over the data grid size. Two facts can be observed from the resulting plot: there exists somewhere an optimal setting for the data grid size, lying around 163 cells per data grid. Moreover, it can be seen that the Blue Gene/P is around an order of magnitude slower than the MAC Cluster. This can be well explained by the hardware differences of the systems. While the Blue Gene/P uses PowerPC processors with a clock speed of 850 MHz, the MAC Cluster and SuperMUC use Sandy-Bridge processors with 2.7 GHz. Furthermore, measurements of the network interconnect showed a speed difference of a factor six in favor of the MAC Cluster. Additionally, other effects, such as different cache sizes or memory bandwidths, have to be taken into consideration. Hence, a factor of 10 can be justified from a hardware-based point of view.
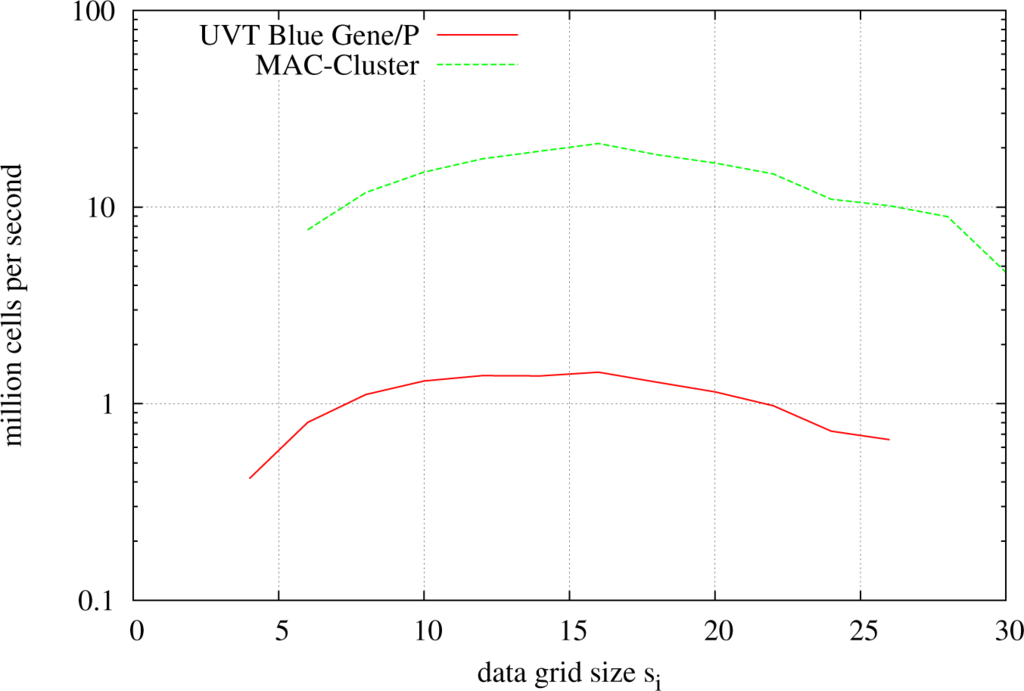
Figure 4.
Number of cells solved per second plotted over the chosen data grid size (si, si, si) for a uniform l-grid setup using a recursive bisection up to depth five and computed using 256 processes on two different systems.
Table 1 shows the number of l-grids and the total number of cells in the domain, if a uniform grid refinement up to a certain depth and a data grid size of 163 is applied. Furthermore, the total amount of required memory is listed in the last column of the table. Thus, a uniform refinement up to depth eight will generate a total of around 20 million l-grids and more than 78.5 billion cells, requiring 28 TB of main memory for storing all relevant data. Thus, on SuperMUC with around 1.5 GB of memory per core available to applications, a problem using Level 8 requires at least 20,000 processes to run.

Table 1.
Domain sizes for measurements using a recursive bisection and a data grid size of 163.
Figure 5 shows the strong speed-up results measured on SuperMUC and on Shaheen. While Figure 5a gives a complete overview of the complete range of scaling up to 140,000 processes on SuperMUC, Figure 5b zooms into the area of up to 8192 cores. On SuperMUC, depth eight with 78.5 billion cells can still show a parallel efficiency of 64% at 140,000 computing cores. Similar results can be seen for depth seven at 32,000 processes. At some point, the curves start to level off, and the parallel efficiency decreases. In a strong speed-up case, this is well known, as the communication overhead increases with a constant amount of computations. Hence, knowing the performance curves for a given hardware architecture, the amount of processes and refinement levels can be chosen in a way to maximize the throughput for a specific problem size.
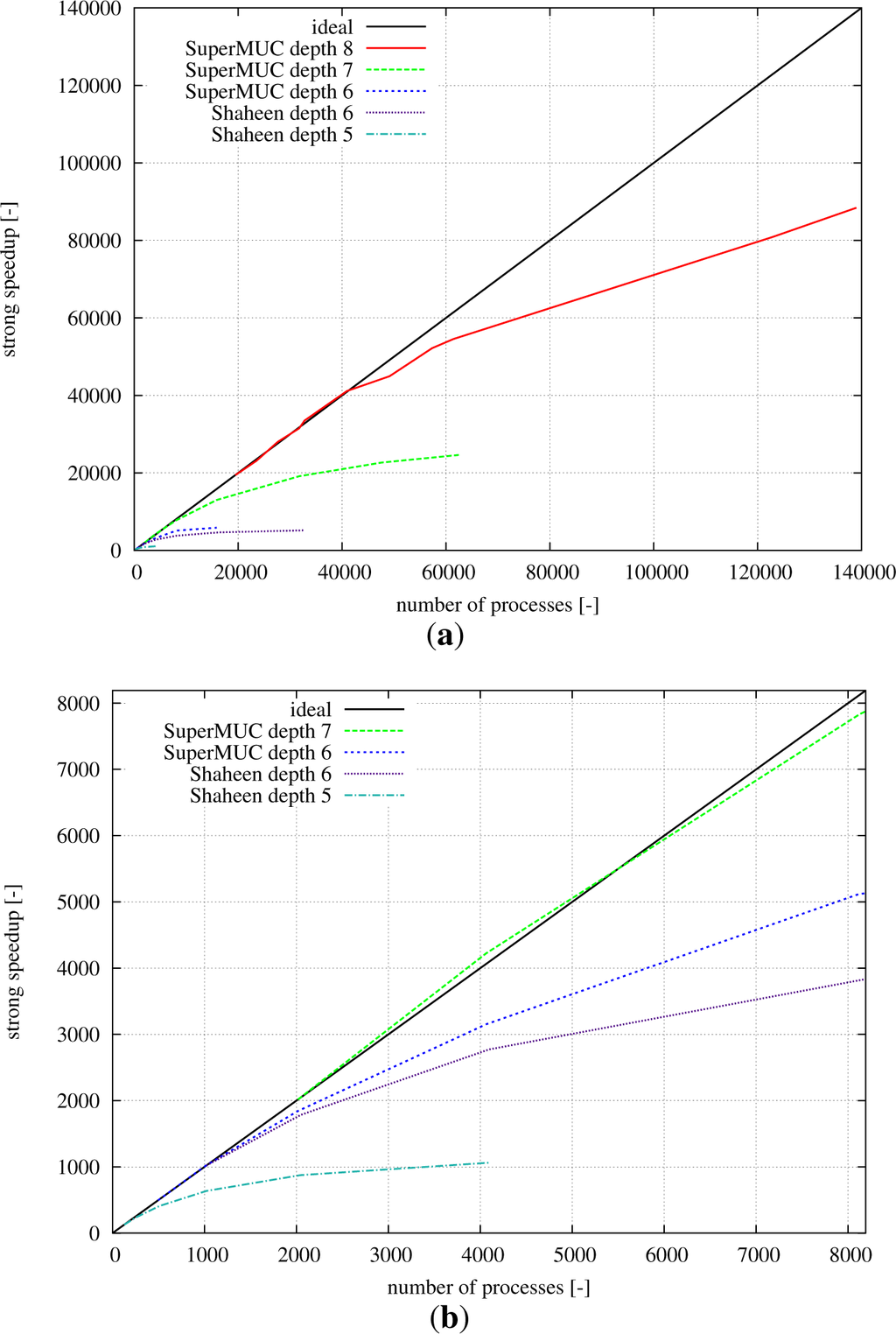
Figure 5.
Strong speedup results on two supercomputing platforms for a 3D domain of fully-refined l-grids with a refinement level (2,2,2) up to depth 5, 6, 7 or 8 and a data grid size of 163. (a) Strong speedup from one to 139,008 processes (all); (b) strong speedup from one to 8192 processes (zoom).
Further measurements on adaptive grid setups (i.e., where not all of the levels are refined uniformly) were performed and showed very similar behavior and results regarding time to solution and ghost cell exchange times. The interested reader is referred to [8] for further details.
3.4. Visualization Strategies
In order to cope with the tremendous data advent generated by CFD simulations, special consideration has to be given to data visualization and interpretation.
Standard methods dump the generated data to hard disks to perform an offline post-processing. In the case of the above-mentioned large example for depth eight computed on SuperMUC having a memory footprint of over 28 terabytes, such a ‘standard’ solution is unfeasible.
Hence, new solutions have to be used in order to tackle this ‘Big Data’ problem. One goal during the design phase of the given data structure was to provide interactive data exploration capabilities. The general and technical context is explained in detail in Mundani et al. [27] and will be briefly introduced here.
The main idea of the interactive data exploration is based on a constant bandwidth approach, where the data density is kept constant. Hence, if only a small region in the computational domain is currently of interest, only this part is visualized at full resolution. If a larger domain should be regarded, the bounding box around the window of interest is increased, while taking only every second data point into consideration and, thus, keeping the data density constant. This window of interest can be moved around in order to visualize different regions of the domain and, hence, yields to the name ‘sliding window approach’. If the complete domain should be visualized, only a coarse representation is returned, giving a general idea of the flow patterns, but omitting details from the finer grids.
Technically, the process is fully integrated into the data structure itself and requires fully populated data grids on all levels, which are generated automatically during the synchronization process. Figure 6 depicts the schematic process. The user contacts a collector server, requests visualization information and sets a sliding window bounding box. The collector contacts the neighborhood server(s) and orders a visualization of certain areas. As the neighborhood server knows the topological allocation of grids, it orders (only) the involved computing processes to send visualization data directly to the collector process, which receives the single parts, compresses them in a data stream and passes them on to the user. The communication between collector and user is based on pure TCP/IP socket communication and does not require any MPI involvement. Hence, a user can connect to the collector from any computer at any time, visualize data and disconnect. The introduced data structure poses multiple advantages. Due to the neighborhood server design, only processes where data grids are touched by the sliding window will be contacted for delivering results to the collector process. Hence, it is not necessary to engage in an all-to-all communication. Furthermore, as the communication structures provide already aggregated data at different levels in the data structure, the data can be used immediately at every level for visualization and do not require any post-processing in order to generate coarsened data.
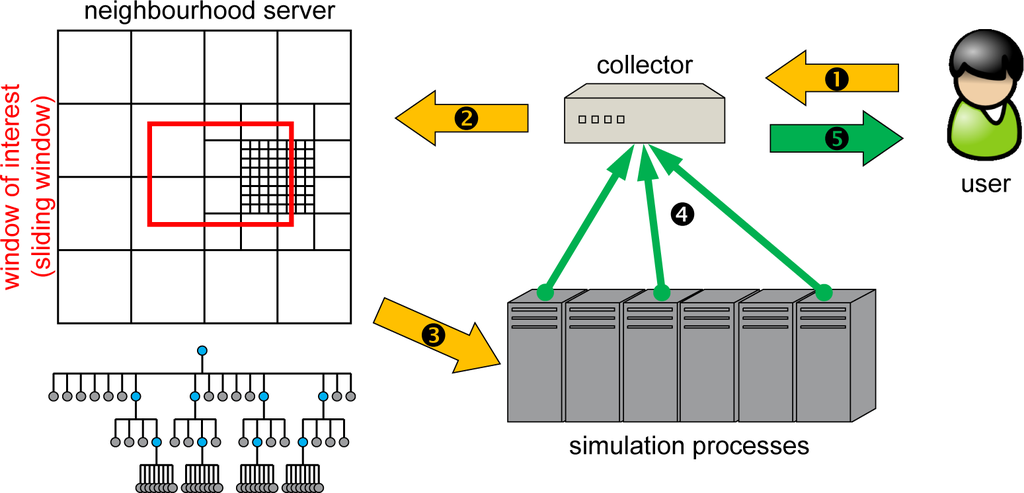
Figure 6.
Sliding window visualization concept (based on Frisch [8]).
In case a supercomputing center does not allow interactive connections to the machines running the code, the same procedures can be used to dump data only partially to disk for a subsequent post-processing analysis, exactly as in the case of the interactive visualization.
In the next stage, the same data structure could be used to enable computational steering capabilities, where boundary conditions, fluid properties or geometry definitions could be changed during runtime, and an effect could be instantaneously observed in the simulation results (see Mulder et al. [28]).
4. Verification and Validation
Validations and verifications were performed for different standard benchmarks and test examples, such as the lid-driven cavity example in 2D and 3D, a pure channel flow in 2D and 3D and a von Kármán vortex street according to the Schäfer–Turek benchmark described in the DFG (Deutsche Forschungsgemeinschaft) priority research program ‘Flow Simulation on High-Performance Computers’ [29]. These benchmarks were used to test the behavior for isothermal settings, i.e., without a thermal coupling using the Boussinesq approximation, and will not be described here. The interested reader is referred to [8] for further details and results.
In order to test the thermal coupling, natural convection scenarios due to heated side-walls and due to heated floors and ceilings were analyzed. Although these two configurations seem quite similar, the flow patterns are completely different.
4.1. Test Case: Heated Side-Walls
As the first case, heated side-walls are analyzed, where the fluid flow is purely driven by natural convection phenomena. The fluid properties are described by the Prandtl number Pr, indicating the ratio of momentum diffusivity to thermal diffusivity, and the Rayleigh number Ra, describing if the heat transfer process is dominated by conduction or convection effects. All benchmark examples use a Prandtl number of Pr = 0.71 (properties of air), whereas the Rayleigh number is varied in order to model different fluid viscosities. The left-hand wall of the square cavity is heated, whereas the right-hand wall of the cavity is cooled and modeled by fixed Dirichlet boundary conditions. The top and bottom walls are perfectly isolated and regarded as adiabatic (i.e., using homogeneous Neumann boundary conditions). The gravitation vector is pointing downwards and, thus, is parallel to the heated and cooled walls.
Figure 7 shows the isothermal profiles indicating the temperature distribution in the cavity for different Rayleigh numbers on a 2562 domain resolution. Comparisons to results published by De Vahl Davis [30], Phillips [31], Eggels et al. [32] or van Treeck [33] are in excellent agreement with the simulated results.
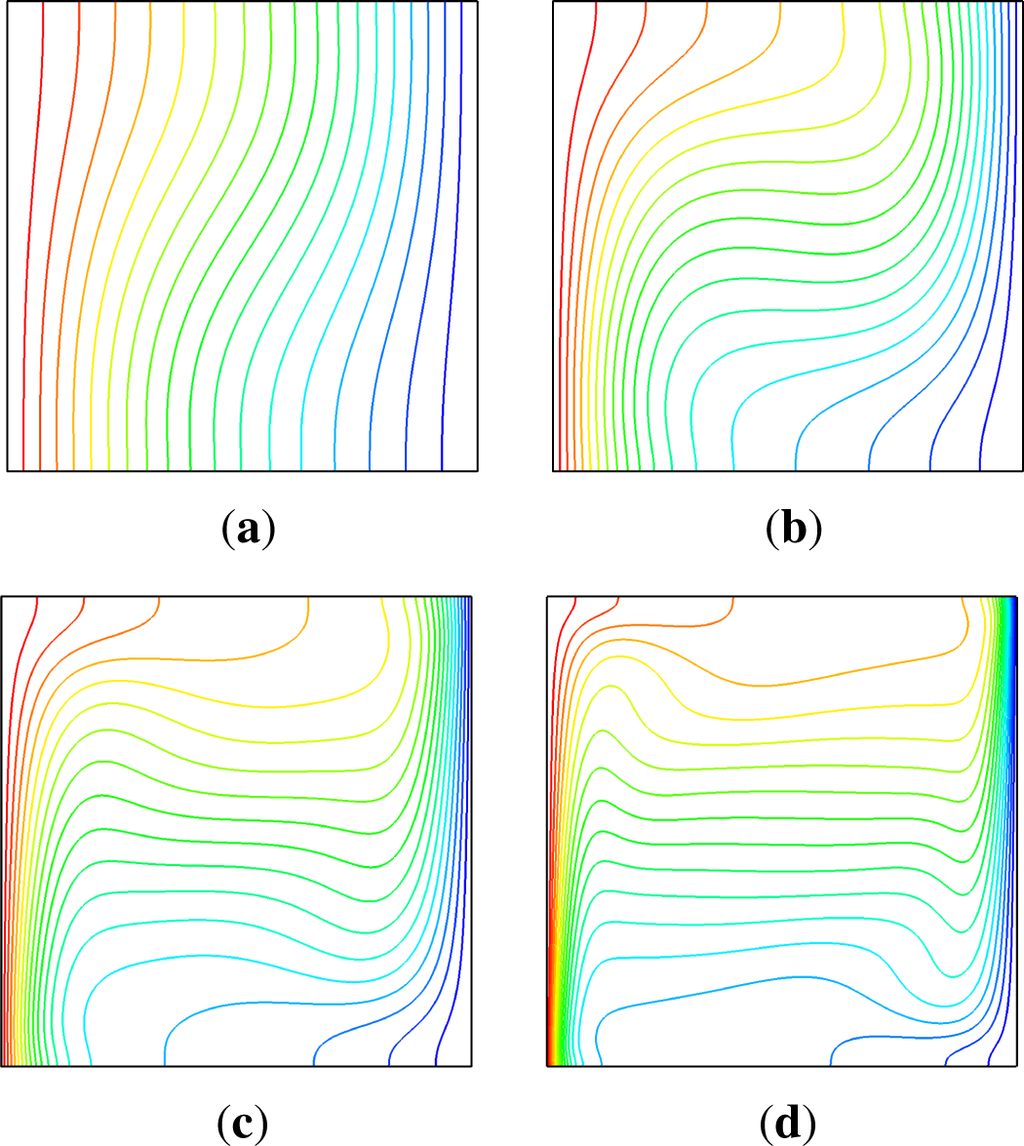
Figure 7.
Isothermal profiles for a square cavity with heated side-walls (left-hand side warm, right-hand side cold) at Pr = 0.71 for different Rayleigh numbers computed on a 2562 domain resolution. (a) Ra = 103; (b) Ra = 104; (c) Ra = 105; (d) Ra = 106.
In order to obtain a better quantification, the Nusselt number Nu for the hot wall at x = 0 can be calculated for this benchmark according to Eggels et al. [32] by:
where a higher order approximation following Phillips [31] is used for the temperature gradient discretization:
where Δx is the cell width used for the current discretization. The Nusselt number characterizes the ratio of convective heat transfer to conductive heat transfer.
Table 2 shows the results of the simulation and reference values from the literature. When comparing the simulated results to the values published by De Vahl Davis [30] up to Ra = 106, the errors for the domain discretization of 2562 range between 0.06% and 0.32%, which shows great agreement with the given reference solutions.

Table 2.
Comparison of simulated Nusselt numbers at the hot wall (x = 0) to results published in the literature.
For higher Rayleigh numbers of 107, however, an error of around 3.7% for a discretization of 2562 is relatively high. This is probably due to the fact that the current simulation kernel uses only a standard central difference approximation for the convective terms in the momentum equations. Here, a donor-cell scheme, as described by Hirt et al. [36], can remedy the situation by mixing central differences with upwind differences for the convective terms.
By normalizing the velocity
in the y-direction, as defined according to Eggels et al. [32]:
the analysis can be compared to the literature results. ly represents here the height of the cavity.
Figure 8 shows the influence of refining the grid discretization. The x-axis displays the width of one simulation cell, while keeping the total length constant. Hence, there exists a quadratic convergence characteristic towards finer mesh widths. Furthermore, it can be seen that different simulation models indicated in the literature have different characteristics, but converge towards a similar value.
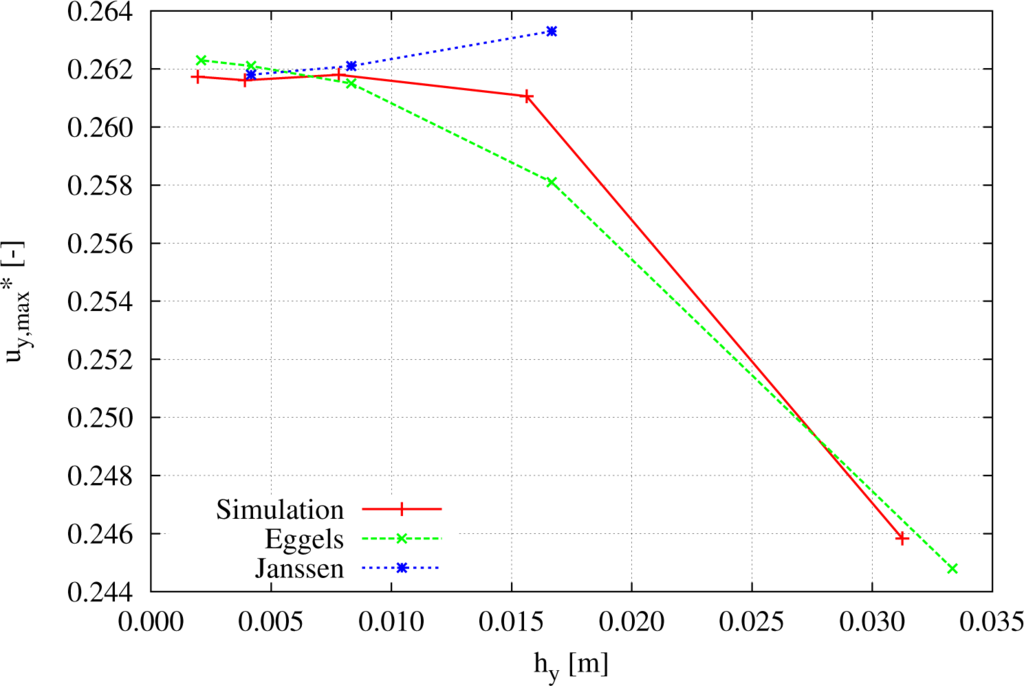
Figure 8.
Normalized maximum velocity
for Ra = 106 in the y-direction measured at a horizontal cut-line at y = 0.5 for the simulated results and two comparisons from the literature [8].
While measuring and comparing the normalized maximum velocity
for Ra = 106 and a discretization of 2562 to the references
given by Janssen [37] for a discretization of 2402, the error lies in the area of 0.07% and indicates good agreement of the simulated values using the above-described code and data structure.
4.2. Test Case: Rayleigh–Bénard Convection
In the second example, the heated and cooled surfaces are not side-walls, but the floor and the ceiling. As an infinitely long example should be regarded, the side-walls are modeled as periodic boundary conditions, connecting the left-hand side and right-hand side walls. The gravitational force is pointing downwards; thus, the temperature gradient is acting now against the gravitational force, and the resulting flow pattern is called Rayleigh–Bénard convection, analyzed by Bénard in [38] and by Lord John William Strutt, Third Baron Rayleigh.
The fundamental difference between the previous benchmark using heated side-walls and the Rayleigh–Bénard convection is that a critical threshold of the Rayleigh number has to be reached before the fluid is set in motion by convection phenomena. If the domain is sufficiently long and wide, the critical Rayleigh number is according to Pellew and Southwell [39]:
In Figure 9, two typical flow profiles can be seen. In the case of Ra = 1100, a sub-critical case, a thermal stratification can be observed. Hence, the fluid is at rest, and the heat is transported by conduction through the medium from the warm to the cold side. In case of Ra = 8000, a super-critical case, Rayleigh–Bénard convection cells are formed, and the isotherms show hot plumes rising up, getting cooled and descending to the bottom again.
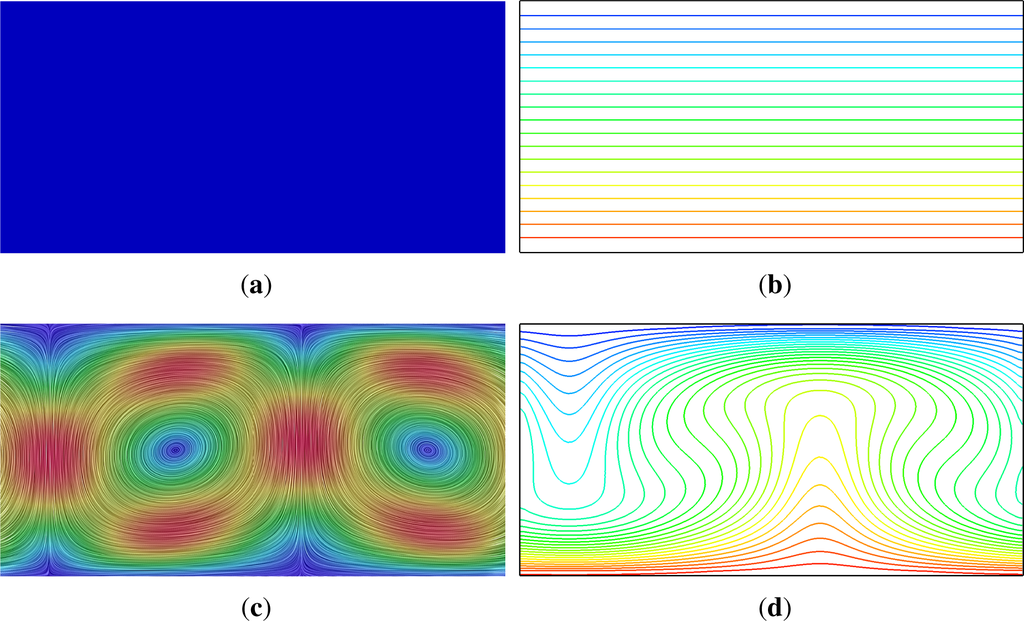
Figure 9.
Velocity and isothermal profiles for a 2:1 cavity with heated floor and cooled ceiling (Rayleigh–Bénard convection setup) at Pr = 0.71 for Ra = 1100 and Ra = 8000 computed on a 64 × 32 domain resolution. NB: the velocity and temperature color profile is chosen to be exactly the same for both settings, ranging from
m/s to T ∈ [−1,1] (from [8]). (a) velocity profile Ra = 1100; (b) isotherms Ra = 1100; (c) velocity profile Ra = 8000; (d) isotherms Ra = 8000.
In order to determine the critical Rayleigh number using the simulation results, the kinetic energy in the system is evaluated for several simulations using different Rayleigh numbers. The kinetic energy is computed by Ekin = 1/2 · m · v2, where m represents the mass and v the velocity of the system. By expressing the mass m by the density ρ and the volume V, the kinetic energy can be rewritten as Ekin = 1/2 · ρ · V · v2. By evaluating the kinetic energy of every cell and summing up all of the contributions, the total kinetic energy Ekin of the system at the time step t can be computed by:
In order to achieve fast convergence towards the quasi-stationary solutions, all simulations used as their starting point the quasi-stationary solution of a simulation performed for Ra = 8000, which lies above the critical Rayleigh number Racrit.
Figure 10 shows exemplarily for a few selected Rayleigh numbers the evolution of the total kinetic energy in (J/m) (as this is a 2D computation, the kinetic energy is in Joules per meters of depth) in the system during a simulation run when starting with the end state of Ra = 8000. When Ra ≪ Racrit, the system converges quickly to a low level of kinetic energy, and for Ra ≫ Racrit to a higher final level of kinetic energy. For Ra ≈ Racrit, i.e., the Rayleigh number is close to the critical value, the system needs much more time to converge to a certain level of kinetic energy.
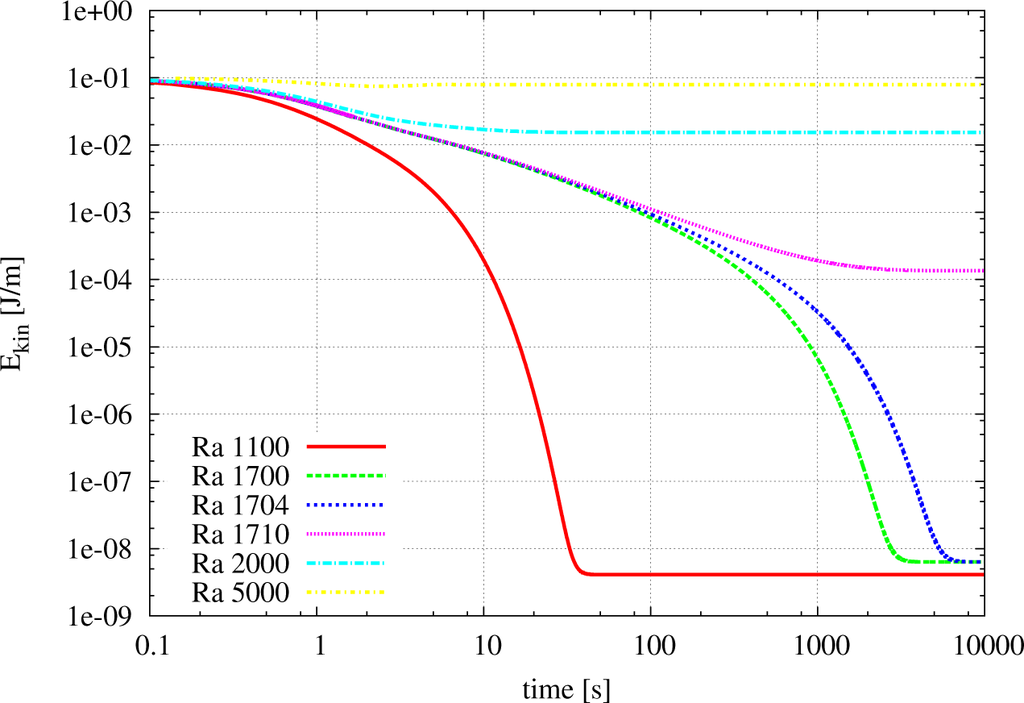
Figure 10.
Time evolution of the total kinetic energy in the system for different Rayleigh numbers (from [8]).
Figure 11 shows the evolution of the total kinetic energy in the system for different Rayleigh numbers derived at a quasi-static end of the simulation (t > 5000 s) of Figure 10, plotted over the Rayleigh number itself. The sudden increase of kinetic energy indicates the starting of the fluid motion in the system between Ra = 1704 and Ra = 1710. By interpolation, the critical Rayleigh number would be at approximately 1707, which fits well with the theoretical prediction of [39].
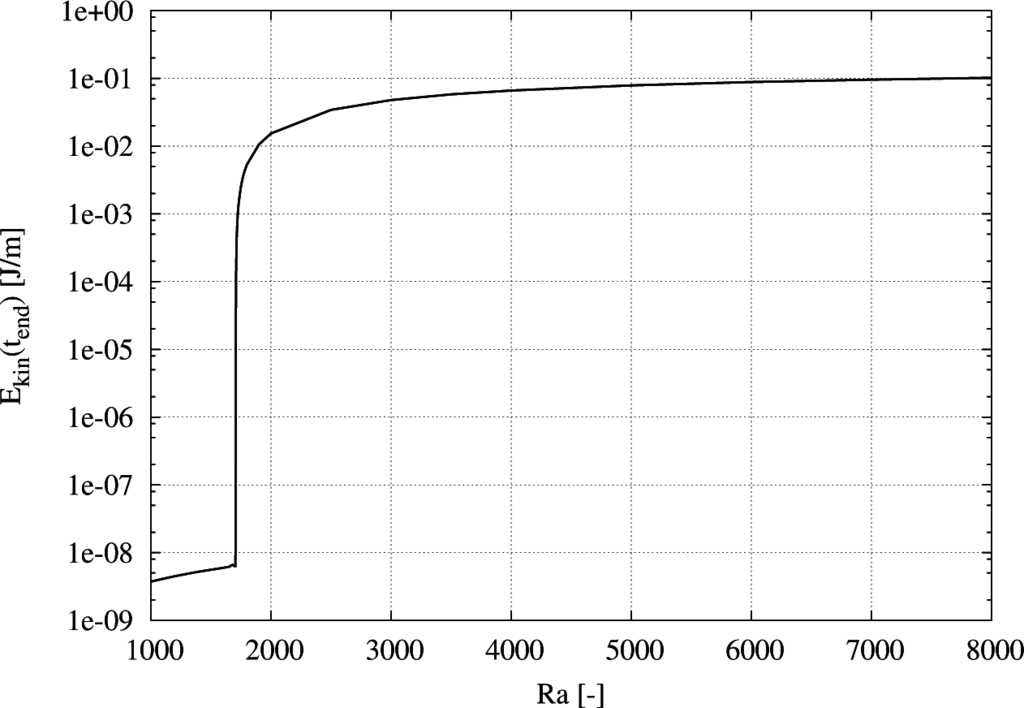
Figure 11.
Total kinetic energy in the system at a quasi-stationary state at tend for different Rayleigh numbers (from [8]).
5. Examples
In the following section, two examples will be presented, offering a high complexity in terms of geometry, as well as boundary conditions. In order to represent the geometry in the block-structured data structure, a ‘voxelization’ is performed, transforming a surface mesh, described by a b-rep (boundary representation) triangular surface model, into a volume model, where the cells in the data blocks are marked as either solid or fluid.
5.1. Scenario: Human in Climate Chamber
As the first complex example, a human manikin is analyzed standing in the middle of a test room with a geometric setup defined by the room from VDI 6020 [40], measuring 5 m in length, 3.5 m in width and 3 m in height. The front surface (at x = 0) has a window spanning the complete width of the room with a surface of 7 m2 and is exposed to outside weather conditions specified in the test reference year (TRY) data for Region 5 (Franconia and northern Baden-Württemberg, Station Number 10655). All other walls are connected adiabatically at the outer wall construction hull, whose material composition is specified in detail in Appendix A of VDI 6020 [40]. The numerical manikin represents a standard male test subject with a height of 1.70 m.
As temperature boundary conditions for the room, the results of a whole-year zonal computation are used. Thermal single- or multi-zone models are usually based on anisotropic finite volume models according to Clarke [41]. They have a coarse spatial refinement, but the building mass is modeled correctly with specific wall, floor and ceiling construction parameters, for example. The thermodynamic conservation equations are solved in every time step, while taking the influence of boundary conditions, such as weather parameters, solar irradiation, internal heat sources, and the interaction with the building energy system into account. If multiple connected zones are present, the mass flow rates in between the zones have to be evaluated, as well, using the Bernoulli equations, for example. Usually, if the zones have a considerable size, results for whole-year simulations can be delivered in the order of one hour or less computation time depending on the degree of spatial and temporal refinement.
The human manikin in the room is coupled to a thermoregulation model, able to predict sector-wise resulting surface temperatures of the human body. The model proposed by Fiala (cf. [42,43]) takes reactions of the central nervous system into account, which are triggered by multiple signals from core and peripheral sensors. Significant indicators are the mean skin temperature Tsk,m, the mean skin temperature variation over time ∂Tsk,m/∂t and the hypothalamus core temperature Thy. The central nervous system can actively react to the surrounding thermal conditions with active measures in order to compensate a heat surplus or deficit. Therefore, the skin blood flow can be changed by vasoconstriction and vasodilatation. Evaporative heat loss can be achieved by activating the sweating mechanism, and shivering can produce heat by increasing the metabolism in the muscles.
A geometry model, containing the surrounding room and the human manikin, is set up, with wall temperatures fixed to surface values delivered from a zonal computation at the interface of wall to air, ranging from 17.10 to 18.44 °C, depending on the wall selected. The surface temperatures for the human manikin, ‘insulated’ with winter clothing, are fixed in every sector of the model by applying results from the thermoregulation model. The head has an elevated surface temperature, as no insulation is present, and much metabolic heat is produced at this specific place according to physiological measurements represented in Fiala’s modeling.
There are no forced in- or out-flows out of the room, and the fluid motion is purely based on natural convection processes. The computation is performed for a Rayleigh number of 107 and a Prandtl number of 0.71. The numerical discretization on the CFD side uses a bisection in every direction up to depth four and a block size of (12,16,12), leading to a domain having 4681 logical management grids and a total of 10.8 million cells.
Figure 12 shows the velocity and temperature profiles resulting from the simulation. The manikin is heating up the immediate surroundings, and a plume of hot air is rising above the manikin due to the hot head. Furthermore, air is descending close to cold walls, similar to the standard benchmark cases. In order to quantify the results, a detailed analysis of the plume of hot air was performed.
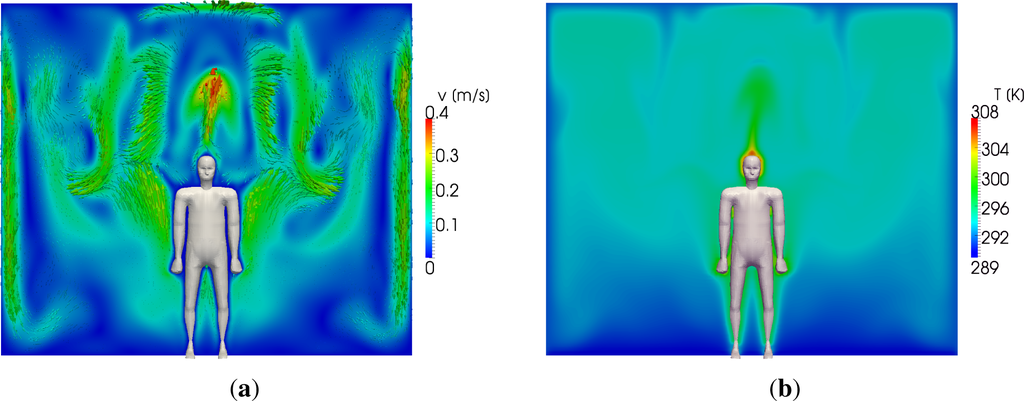
Figure 12.
Standing manikin in the middle of the VDI6020 test room configuration under pure natural convection processes. (a) Velocity profile; (b) temperature profile.
Figure 13 shows the numerically-determined values for a cut-line starting from the head of the manikin (at z = 0) and going to the ceiling of the test room (at z = 1.3 m over the head of the manikin). Furthermore, it shows an interpolated polynomial function of fourth order valid in the region z ∈ [0, 0.15] meters, which corresponds to the area of interest for the convective heat exchange with the manikin’s head. The interpolated function can be determined as:
and has a correlation coefficient R2 = 0.9952 in its region of definition.
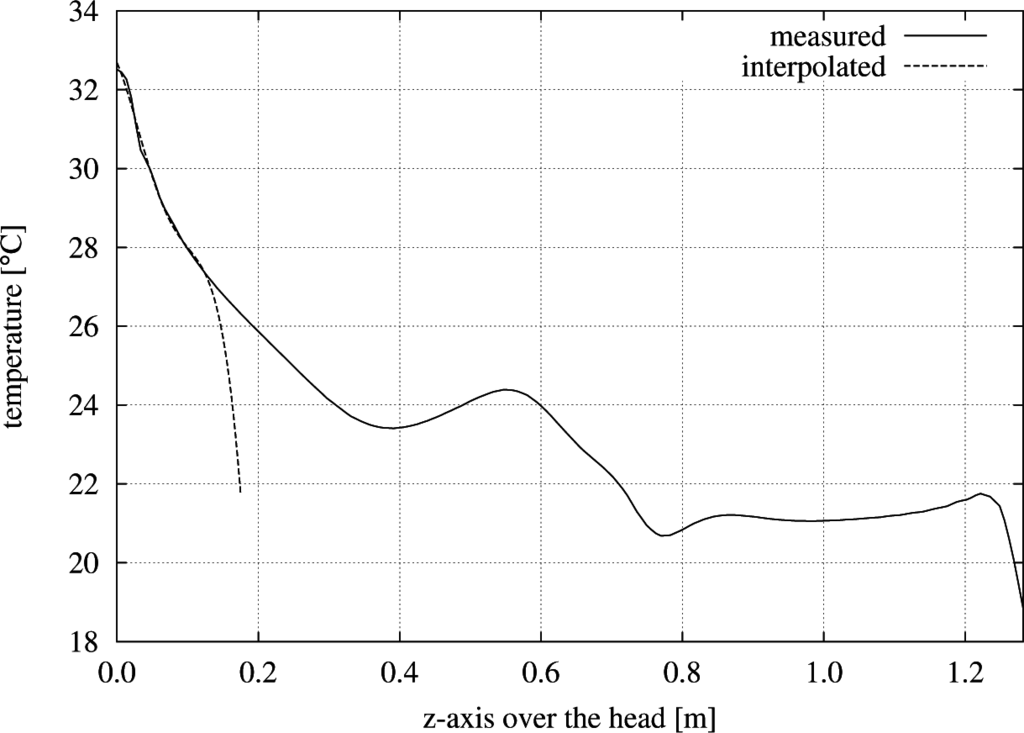
Figure 13.
Temperature distribution in °C in the z-direction starting at the top of the head of the manikin until the ceiling is reached. The interpolated polynomial function of fourth order is valid in the range [0, 0.15] m.
The derivative of the interpolated function T(x, y, z) can be determined analytically and evaluated at the position z = 0 in order to compute the convective heat transfer coefficient hc according to Bejan [44] as:
where k is the heat conduction coefficient in (W/(m·K)), T0 the temperature of the surface in (K) (in this case, the temperature of the manikin’s head) and T∞ the temperature of the fluid at rest in (K). Thus, for this specific problem setup and simulation results, the heat transfer coefficient for the manikin’s head can be computed as:
Experimental investigations made by [45] using a regression analysis for a standing person in a room yielded a convective heat transfer coefficient of:
which results in an experimentally-determined convective heat transfer coefficient of:
and corresponds very well to the results obtained, keeping in mind that the simulation was performed for ν = 4.6433 · 10−4 (m2/s) (Ra = 107) instead of real air, which would have ν = 0.150 · 10−4 (m2/s). Furthermore, no turbulence model is applied in the simulation at the moment, and thus, the simulated hc value is comparable to an averaged value over several time steps, where turbulent fluctuations were eliminated.
5.2. Scenario: Classroom
A second example is more realistic than a single manikin in a confined room and consists of a classroom containing 30 students and a teacher. The room itself has the dimensions of 10.3 × 6.4 × 3.4 meters and is discretized using 37,449 logical grids on depth five with a recursive bisection and a data grid size of (24,16,8), resulting in 115 million cells (of which 92 million are fluid cells). Hence, the cell resolution in the room is in the order of 1.3 cm.
As fluid properties, Ra = 107 and Pr = 0.71 were used. The boundary conditions were again modeled by fixed wall temperatures of 17.0 °C, and the humans are defined with surface temperatures of 28.0 °C for the body and 34.0 °C for the head, as much of metabolic heat is produced at this place.
Figure 14 shows an overview of the classroom and two characteristic temperature slices through the domain, while Figure 15 shows two details from different viewing angles. The rising heat plumes over the heads of the students can be observed exceptionally well. Furthermore, it can be seen that the different plumes of the students interact with each other and have quite a significant influence on each other. The thermal plume over the teacher, however, is nearly not affected by such interactions.
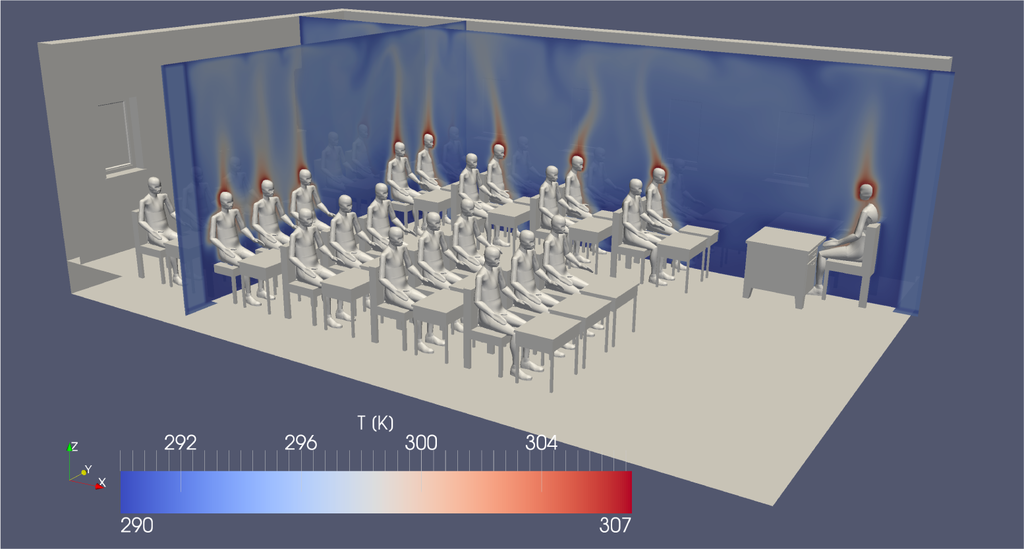
Figure 14.
Overview of a class room simulation using Ra = 107 at 86 s of simulated time.
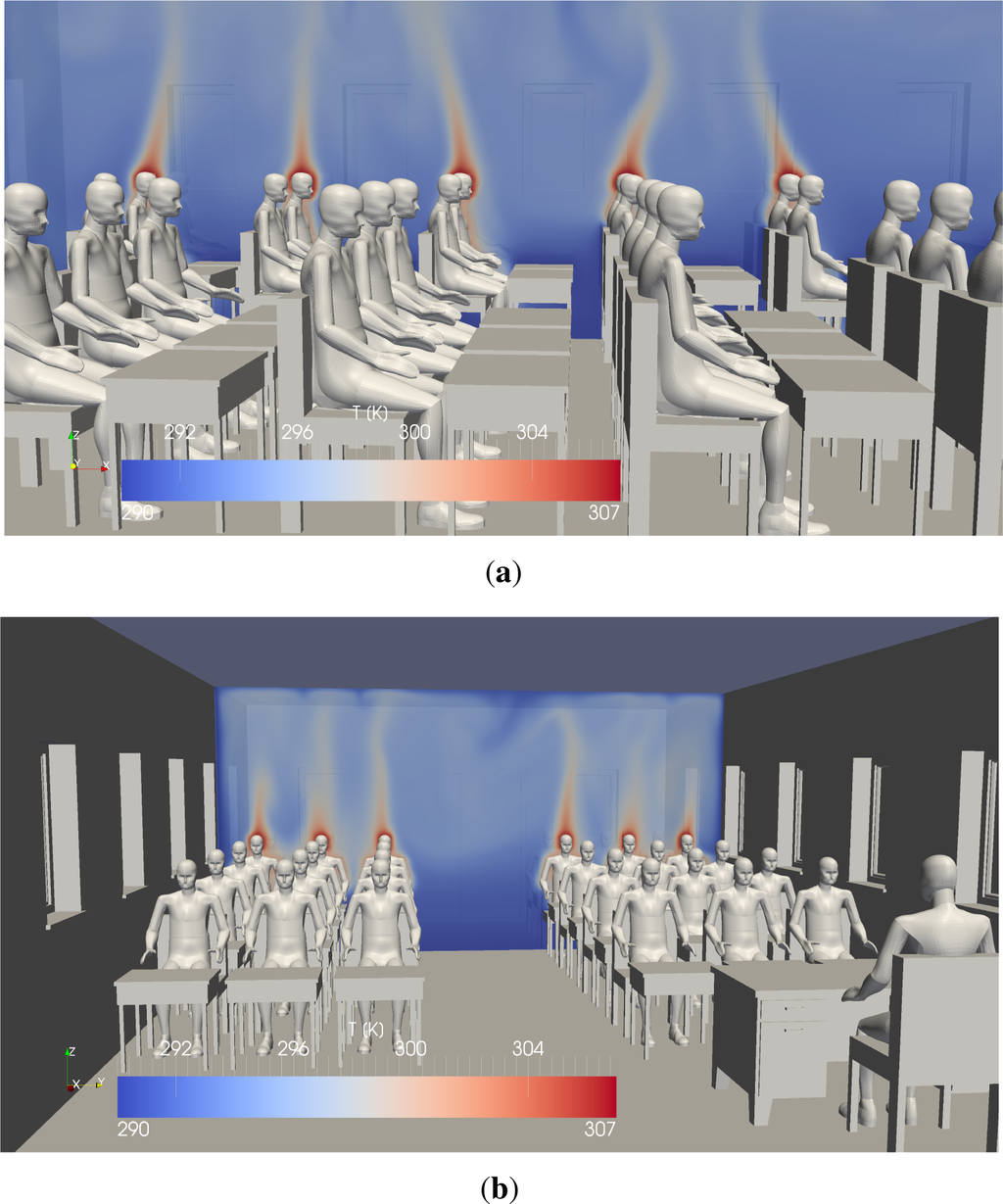
Figure 15.
Details of a class room simulation using Ra = 107 at 86 s of simulated time. (a) Side view; (b) front view.
Figure 16 shows cut-lines over every student, starting immediately above the head and going 1 m straight up into the air. The plot does not currently display which line belongs to which student in order to keep it readable and to avoid overloading it with textual information. The most important information that can be gathered from this plot is the fact that the classroom scenario has highly complex 3D flow properties. Thirty centimeters above the head of a student, temperature differences in the order of 8 °C could be observed. It should be mentioned at this place that in order to visualize the temperature values displayed in Figure 16, the data were extracted at a higher level in the data structure in order to cope with the large amount of data available at the deepest level. However, this procedure automatically introduces an averaging process due to the nature of the data structure itself, and thus, local fluctuations are smoothed in the process for the scope of visualization, which does not affect the overall solution.
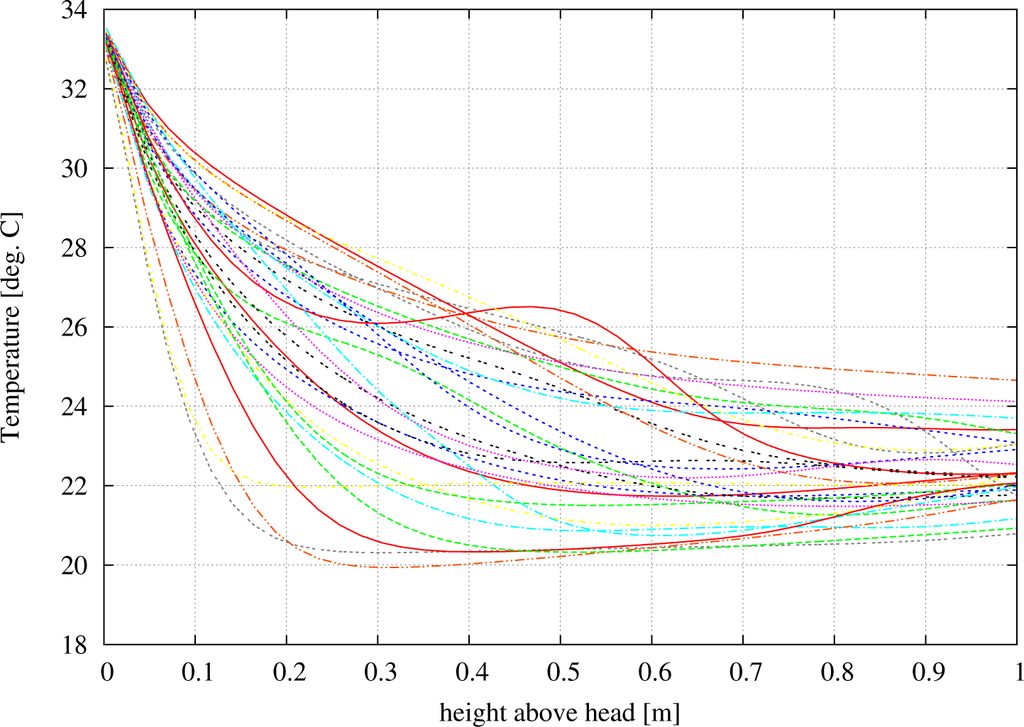
Figure 16.
Heat profile simulated above the head of every student sitting in the virtual classroom at 86 s of simulated time. The x-axis depicts the height over the head of the respective student, plotted against the temperature in °C.
Furthermore, asymmetries can be clearly seen in Figure 15b. While the student sitting in the middle between two colleagues is much better ‘isolated’, the student sitting next to the corridor is exposed to cooler air on the isle side.
As shown in the paper of Urlaub et al. [46], the indoor climate can have a significant impact on the occupants’ working performance, as well as their health. As the simulations indicate, the usage of one global indoor temperature might be very inaccurate in order to assess the possible human performance effects in a classroom.
Further possible assessments regarding indoor thermal comfort can be made by evaluating the local mean votes (LMV), as described by van Treeck et al. [47]. The LMVs can be generated for different body sectors of different students at different locations in the classroom. Hence, efficient hybrid ventilation scenarios, specifically designed to account for a complete classroom, could be devised in order to counteract negative impacts from a pure natural airflow in the room. Furthermore, additional transport equations could be coupled to the thermal simulations, enabling the monitoring of CO2 concentrations or ‘air age’ in buildings of this type.
Hence, a broad variety of different evaluation routines or post-processing tools could be used, building on the generated results from different high-performance simulation runs.
6. Conclusions
This paper presented a data structure capable of running efficiently on modern supercomputers, such as SuperMUC in Germany or Shaheen in the Kingdom of Saudi Arabia, and which is able to compute complex indoor airflow scenarios. The mathematical formulations based on the Navier–Stokes equations for the simulation of indoor airflows were introduced, and the basic ideas of the data structure, as well as the solving mechanisms were sketched. Scaling plots showed the efficient usage of the introduced strategies on SuperMUC and Shaheen. Furthermore, validation examples and complex indoor airflow scenarios were presented in order to highlight the possibilities that the code currently provides.
Moreover, it is planned to enhance the existing code structure with further features, such as turbulence modeling and immersed boundary methods for a more accurate geometric description. The porting of parts of the code to hardware accelerators could also enhance the performance greatly and enable a more efficient execution on supercomputers drawing most of their computing resources from accelerator hardware, such as graphic cards or the Intel Xeon Phi architecture. Larger examples can be targeted or an increase in resolution of the already available ones could be performed using the same amount of time.
Acknowledgments
This publication is partially based on work supported by Award No. UK-c0020, made by KAUST. Furthermore, the authors would like to thank LRZ in Germany for the support and usage of SuperMUC during their ‘Extreme Scaling Workshop’, held in June 2014, and UVT in Romania for the support and usage of their BlueGene/P.
Author Contributions
The main contribution of this paper is based on the doctoral dissertation of J. Frisch. R.-P. Mundani, in his function as head of the ‘Efficient Algorithms’ group at the Chair for Computation in Engineering in Munich, accompanied the thesis as an advisor. E. Rank and C. van Treeck acted as advisors and examiners of the thesis and contributed ideas and comments throughout the complete work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Adams, M.; Colella, P.; Graves, D.T.; Johnson, J.N.; Keen, N.D.; Ligocki, T.J.; Martin, D.F.; McCorquodale, P.W.; Modiano, D.; Schwartz, P.O.; et al. Chombo Software Package for AMR Applications—Design Document; Technical Report LBNL-6616E; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2014. [Google Scholar]
- Parker, S.G.; Johnson, C.R. SCIRun: A Scientific Programming Environment for Computational Steering, Proceedings of the 1995 ACM/IEEE Conference on Supercomputing, San Diego, CA, USA, 3–8 December 1995.
- OpenFOAM—Free Open Source CFD Software Package. Available online: http://www.openfoam.org accessed on 14 May 2015.
- Rivi, M.; Calori, L.; Muscianisi, G.; Slavnic, V. In-situ visualization: State-of-the-art and some use cases; PRACE White Paper; PRACE: Brussels, Belgium, 2012. [Google Scholar]
- Yu, H.; Wang, C.; Grout, R.; Chen, J.; Ma, K.L. In Situ Visualization for Large-Scale Combustion Simulations. Comput. Graph. Appl. IEEE 2010, 30, 45–57. [Google Scholar]
- Fabian, N.; Moreland, K.; Thompson, D.; Bauer, A.; Marion, P.; Geveci, B.; Rasquin, M.; Jansen, K. The ParaView Coprocessing Library: A scalable, general purpose in situ visualization library, Proceedings of the 2011 IEEE Symposium on Large Data Analysis and Visualization (LDAV), Providence, Rl, USA, 23–24 October 2011; pp. 89–96.
- Bennett, J.C.; Abbasi, H.; Bremer, P.T.; Grout, R.; Gyulassy, A.; Jin, T.; Klasky, S.; Kolla, H.; Parashar, M.; Pascucci, V.; et al. Combining in-situ and in-transit processing to enable extreme-scale scientific analysis, Proceedings of the 2012 International Conference for High Performance Computing, Networking, Storage and Analysis (SC), Salt Lake City, UT, USA, 10–16 November 2012; pp. 1–9.
- Frisch, J. Towards Massive Parallel Fluid Flow Simulations in Computational Engineering. Ph.D. Thesis, Technische Universitat, Munchen, Germany, 2014. [Google Scholar]
- Batchelor, G. An Introduction to Fluid Dynamics; Cambridge Mathematical Library, Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ferziger, J.H.; Peric´, M. Computational Methods for Fluid Dynamics, 3rd ed; Springer-Verlag: Berlin, Germany, 2002. [Google Scholar]
- Hirsch, C. Numerical Computation of Internal and External FlowsVolume 1, 2nd ed; Butterworth-Heinemann: Oxford, UK, 2007. [Google Scholar]
- Lienhard, J., IV; Lienhard, J., V. A Heat Transfer Textbook, 4th ed; Dover Publications: Mineola, NY, USA, 2011. [Google Scholar]
- Harlow, F.H.; Welch, J.E. Numerical Calculation of Time-Dependent Viscous Incompressible Flow of Fluid with Free Surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar]
- Chorin, A.J. Numerical solution of the Navier-Stokes equations. Math. Comput 1967, 22, 745–762. [Google Scholar]
- Schwarz, H.R.; Kockler, N. Numerische Mathematik, 8th ed; Vieweg + Teubner: Wiesbaden, Germany, 2011. [Google Scholar]
- Ferziger, J.H. Numerical Methods for Engineering Applications; Wiley-Interscience Publication, Wiley; New York, NY, USA, 1998. [Google Scholar]
- Kim, J.; Moin, P. Application of a fractional-step method to incompressible Navier-Stokes equations. J. Comput. Phys 1985, 59, 308–323. [Google Scholar]
- Choi, H.; Moin, P. Effects of the computational time step on numerical solutions of turbulent flow. J. Comput. Phys 1994, 113, 1–4. [Google Scholar]
- Courant, R.; Friedrichs, K.; Lewy, H. Uber die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann 1928, 100, 32–74. [Google Scholar]
- Peyret, R.; Taylor, T. Computational Methods for Fluid Flow; Springer Series in Computational Physics; Springer-Verlag: Berlin, Germany, 1983. [Google Scholar]
- Schwarz, H.A. Uber einen Grenzubergang durch alternierendes Verfahren. Vierteljahrsschr. Naturforschenden Ges. Zur 1870, 15, 272–286, In German. [Google Scholar]
- Frisch, J.; Mundani, R.P.; Rank, E. Communication Schemes of a Parallel Fluid Solver for Multi-Scale Environmental Simulations, Proceedings of the 13th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), Timis¸oara, Romania, 26–29 September 2011; pp. 391–397.
- Brandt, A. Multi-Level Adaptive Solutions to Boundary-Value Problems. Math. Comput 1977, 31, 333–390. [Google Scholar]
- Trottenberg, U.; Oosterlee, C.W.; Schüller, A. Multigrid; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Briggs, W.L.; Henson, V.E.; McCormick, S.F. A Multigrid Tutorial, 2nd ed; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Frisch, J.; Mundani, R.P.; Rank, E. Parallel Multi-Grid like Solver for the Pressure Poisson Equation in Fluid Flow Applications, Proceedings of the IADIS International Conference—Applied Computing, Fort Worth, TX, USA, 23–25 October 2013; pp. 139–146.
- Mundani, R.P.; Frisch, J.; Varduhn, V.; Rank, E. A sliding window technique for interactive high-performance computing scenarios. Adv. Eng. Softw 2015, 84, 21–30. [Google Scholar]
- Mulder, J.D.; van Wijk, J.J.; van Liere, R. A Survey of Computational Steering Environments. Future Gener. Comput. Syst. Spec. Issue Sci. Vis 1999, 15, 119–129. [Google Scholar]
- Schafer, M.; Turek, S. Benchmark Computations of Laminar Flow around a Cylinder. In Flow Simulation with High-Performance Computers II; Vieweg: Wiesbaden, Germany, 1996; pp. 547–566. [Google Scholar]
- De Vahl Davis, G. Natural convection of air in a square cavity: A benchmark numerical solution. Int. J. Numer. Methods Fluids 1983, 3, 249–264. [Google Scholar]
- Phillips, T.N. Natural convection in an enclosed cavity. J. Comput. Phys 1984, 54, 365–381. [Google Scholar]
- Eggels, J.G.M.; Somers, J.A. Numerical simulation of free convective flow using the Lattice-Boltzmann scheme. Int. J. Heat Fluid Flow 1995, 6, 357–64. [Google Scholar]
- Van Treeck, C.; Rank, E.; Krafczyk, M.; Tolke, J.; Nachtwey, B. Extension of a hybrid thermal LBE scheme for large-eddy simulations of turbulent convective flows. Comput. Fluids 2006, 35, 863–71. [Google Scholar]
- Le Quere, P. Accurate solutions to the square thermally driven cavity at high Rayleigh number. Comput. Fluids 1991, 20, 29–41. [Google Scholar]
- Van Treeck, C. Gebaudemodell-Basierte Simulation von Raumluftstromungen. Ph.D. Thesis, Technische Universitat, Munchen, Germany, 2004. [Google Scholar]
- Hirt, C.W.; Nichols, B.D.; Romero, N.C. SOLA: A numerical solution algorithm for transient fluid flows; Technical Report LA-5852; Los Alamos National Laboratory: Los Alamos, NM, USA, 1975. [Google Scholar]
- Janssen, R.J.A. Instabilities in Natural-Convection Flows in Cavities. Ph.D. Thesis, Technische Hogeschool, Delft, The Netherlands, 1994. [Google Scholar]
- Bénard, H. Les Tourbillons Cellulaires Dans une Nappe Liquide Propageant de la Chaleur par Convection, en Régime Permanent; Gauthier-Villars: Paris, France, 1901; In French. [Google Scholar]
- Pellew, A.; Southwell, R.V. On Maintained Convective Motion in a Fluid Heated from below. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci 1940, 76, 312–343. [Google Scholar]
- VDI 6020 Part 1. Requirements on Methods of Calculation to Thermal and Energy Simulation of Buildings and Plants; Verein Deutscher Ingenieure: Düsseldorf, Germany, 2001. [Google Scholar]
- Clarke, J.A. Energy Simulation in Building Design, 2nd ed; Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar]
- Fiala, D.; Lomas, K.J.; Stohrer, M. A computer model of human thermoregulation for a wide range of environmental conditions: The passive system. J. Appl. Physiol 1999, 87, 1957–1972. [Google Scholar]
- Fiala, D.; Lomas, K.J.; Stohrer, M. Computer prediction of human thermoregulatory and temperature responses to a wide range of environmental conditions. Int. J. Biometeorol 2001, 45, 143–159. [Google Scholar]
- Bejan, A. Convection Heat Transfer, 4th ed; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Kurazumi, Y.; Tsuchikawa, T.; Ishii, J.; Fukagawa, K.; Yamato, Y.; Matsubara, N. Radiative and convective heat transfer coefficients of the human body in natural convection. Build. Environ 2008, 43, 2142–2153. [Google Scholar]
- Urlaub, S.; Werth, L.; Steidle, A.; van Treeck, C.; Sedlbauer, K. Methodik zur Quantifizierung der Auswirkung von moderater Warmebelastung auf die menschliche Leistungsfahigkeit. Bauphysik 2013, 35, 38–44, In German. [Google Scholar]
- Van Treeck, C.; Frisch, J.; Pfaffinger, M.; Rank, E.; Paulke, S.; Schweinfurth, I.; Schwab, R.; Hellwig, R.; Holm, A. Integrated thermal comfort analysis using a parametric manikin model for interactive real-time simulation. J. Build. Perform. Simul 2009, 2, 233–250. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).