1. Introduction
The Time-Dependent Self-Consistent-Field equations together with models that include some portion of the Hartree-Fock (HF) exchange admit control over the range of self-interaction in the optical response [
1,
2,
3,
4], and are related to new models of electron correlation based on the Random Phase Approximation (RPA) [
5,
6,
7,
8]. Solving the TD-SCF equations is challenging due to an unconventional
J-symmetric structure of the naive molecular orbital (MO) representation,
where
and
are Hermitian blocks corresponding to 4th order tensors spanning transitions between occupied and virtual sub-spaces,
ω is the real excitation energy and
is the corresponding transition density. By construction, the MO representation allows strict separation between the dyadic particle-hole (
ph) and hole-particle (
hp) solutions,
and
, for which specialized algorithms exist. Nevertheless, convergence of the naive
J-symmetric problem is typically much slower than the corresponding Hermitian Tamm-Dancoff approximation (TDA),
, which is of reduced dimensionality in the MO representation.
Several TD-SCF eigensolvers are based on the oscillator picture
with
and
the Hermitian potential and kinetic matrices, and the dual
corresponding to position and momentum. This picture avoids the imbalance
whilst admitting conventional solutions based on the Hermitian matrix
as shown by Tamara and Udagawa [
9] and extended by Narita and Shibuya with second order optimization of the quotient
[
10]. More recently, Tsiper [
11] considered the quotients
and developed a corresponding dual channel Lanczos solver. Subspace solvers in this dual representation have recently been surveyed by Tretiak, Isborne, Niklasson and Challacombe (TINC) [
12], with comparative results for semi-empirical models.
Another challenge is dimensionality and scaling. Writing Equation (
1) in the general form
, admitting arbitrary representation, the superoperator matrix
is a ∼
tetradic, with
N the number of basis functions, assumed proportional to system size. In practice the action of
onto
is carried out implicitly as
, using an existing framework for construction of the effective Hamiltonian (Fockian)
F, where
is the one-particle reduced density matrix,
is a screening operator involving Coulomb, exchange and/or exchange-correlation terms and the correspondence between superoperator and functional notation is given by a tensorial mapping between diadic and matrix,
.
Recent efforts have focused on addressing the problem of dimensionality by employing linear scaling methods that reduce the cost of
within Density Functional Theory (DFT) to
. However, this remains an open problem for the Hartree-Fock (HF) exchange, an ingredient in models that account for charge transfer in the dynamic and static response, including the Random Phase Approximation (RPA) at the pure HF level of theory. Likewise, scaling of the TD-SCF eigenproblem remains formidable due to associated costs of linear algebra, even when using powerful Krylov subspace methods. Underscoring this challenge, one of the most successful approaches to linear scaling TD-DFT avoids the matrix eigenproblem entirely through explicit time-evolution [
13,
14].
Linear scaling matrix methods exploit quantum locality, manifest in approximate exponential decay of matrix elements expressed in a well posed, local basis; with the dropping of small elements below a threshold,
, this decay leads to sparse matrices and
complexity at the forfeit of full precision [
15,
16,
17]. Likewise, linear scaling methods for computing the HF exchange employ an advanced form of direct SCF, exploiting this decay in the rigorous screening of small exchange interactions bellow the two-electron integral threshold
[
18]. The consequence of these linear scaling approximations is an inexact linear algebra that challenges Krylov solvers due to nested error accumulation, a subject of recent formal interest [
19,
20]. Consistent with this view, TINC found that matrix perturbation (a truncation proxy) disrupts convergence of Krylov solvers with slow convergence,
i.e., Lanczos and Arnoldi for the RPA, but has less impact on solvers with rapid convergence,
i.e., generically for the TDA or Davidson for the RPA. Relative to semi-empirical Hamiltonians, the impact of incompleteness on subspace iteration may be amplified with first principles models and large basis sets (ill-conditioning).
An alternative is Rayleigh Quotient Iteration (RQI), which poses the eigenproblem as non-linear optimization and is variational with respect to matrix perturbation. Narita and Shibuya [
10] considered optimization of the quotient
with second order methods, but these are beyond the capabilities of current linear scaling technologies and also, convergence may be slower by a power of ½. For semi-empirical Hamiltonians, TINC found that optimization of the Thouless functional
corresponding to the solution of Equation (
1), was significantly slower for the RPA relative to the TDA, and also compared to subspace solvers. For first principles models and non-trivial basis sets, this naive RQI can become pathologically slow as shown in
Figure 1. On the other hand, the Tsiper formulation exposes the underlying pseudo-Hermitian structure of the TD-SCF equations. Here, this structure is exploited with QUasi-Independent Rayleigh Quotient Iteration (QUIRQI), involving dual channel optimization of the Tsiper quotients coupled only weakly through line search. Although this work was first placed in the arXiv some time ago [
21], it is offered here after review and revision, with changes primarily in the concluding remarks.
2. Theoretical Development
Our development begins with a brief review of the representation independent formulation developed by TINC, which avoids the
cost of rotating into an explicit
p-h,
h-p symmetry. Instead, this symmetry is maintained implicitly via annihilation,
, with
P the first order reduced density matrix and
its compliment. Likewise, the indefinite metric associated with the
J-symmetry of Equation (
1) is carried through the generalized norm
. Introducing the operator equivalents,
and
, the Tsiper functional becomes
Transformations between the transition density and the dual space involves simple manipulations and minimal cost, allowing Fock builds with the transition density and optimization in the dual space. The splitting operation is given by
and
. Likewise,
and
. The back transformation (merge) from dual to density is
. This framework provides the freedom to work in any orthogonal representation, and to switch between transition density and oscillator duals with minimal cost.
QUIRQI is given in Algorithm 1. It begins with a guess for the transition density, which is then split into its dual (lines 2–3). The choice of initial guess is discussed later. Lines 4–24 consist of the non-linear conjugate gradient optimization of the nearly independent channels: In each step, the flow of information proceeds from optimization of the duals to builds involving the density and back to the duals in a merge-annihilate-truncate-build-split-truncate (MATBST) sequence. For the variables
v,
p and
q this sequence is comprised by lines 22–23 and 5–7, and lines 15–19 for the corresponding conjugate gradients
,
and
. Truncation is carried out with the
filter operation as described in Reference [
17] and also below, with cost and error determined by the matrix threshold
.
| Algorithm 1 QUIRQI |
- 1:
procedure QUIRQI() - 2:
guess v - 3:
, - 4:
while and and do - 5:
- 6:
, - 7:
- 8:
, , - 9:
, - 10:
- 11:
- 12:
, - 13:
, , - 14:
, - 15:
, - 16:
- 17:
- 18:
, - 19:
- 20:
- 21:
, - 22:
, - 23:
- 24:
end while - 25:
end procedure
|
The Tsiper functional is the sum of dual quotients and , determined at line 8, followed by the gradients and computed at line 9. After the first cycle, the corresponding relative error (10) and maximum matrix element of the gradient (11) are computed and used as an exit criterion at line 4, along with non-variational behavior
Next, the Polak-Ribiere variant of non-linear conjugate gradients yields the search direction in each channel, and (12–14). The action of on to and is then computed, again with a MATBST sequence (15–19), followed by a self-consistent dual channel line search at line 20, as described below. With steps and in hand, minimizing updates are taken along each conjugate direction (22), and the cycle repeats with the MATBST sequence spanning lines 21–23 and 5–7.
Optimization of the Tsipper functional
involves a two dimensional line-search (line 20) corresponding to minimization of
with coupling entering through terms in the denominator such as
. A minimum in Equation (
3) can be found quickly to high precision by alternately substituting one-dimensional solutions one into the other until self-consistency is reached. This semi-analytic approach starts with a rough guess at the pair
(eg. found by a coarse scan) followed by iterative substitution, where for example the
p-channel update is
with an analogous update for the
q-channel obtained by swapping subscripts. As the solution decouples (
,
and
become small) the steps are found independently.
3. Results and Discussion
QUIRQI has been implemented in FreeON [
22], which employs the linear scaling Coulomb and Hartree-Fock exchange kernels QCTC and ONX with cost and accuracy controlled by the two-electron screening threshold
[
18].
N-scaling solution of the QUIRQI matrix equations is achieved through “sparsification” (In previous works [
15], this process has been loosely referred to as SpAMM, involving both truncation and dynamic dropping of small row-column contributions from the sparse matrix multiply based on the BCSR data structure. See Section IVA3 of Reference [
15]. In this work, only truncation in the BCSR data structure has been used, but was incorrectly referred to as SpAMM in a previous instance [
21]. In more recent developments, SpAMM refers to recursive, hierarchical truncation in the product space [
23,
24], rather than the row-column approach outlined in Reference [
15].), of the underlying vector space, where the
filter operation is applied to drop atom-blocks with norm smaller than a drop tolerance
in a block-CSR data structure (BCSR) [
15,
16,
17]. All calculations were carried out with version 4.3 of the gcc/gfortran compiler under version 8.04 of the Ubuntu Linux distribution and run on a 2GHz AMD Quad Opteron 8350.
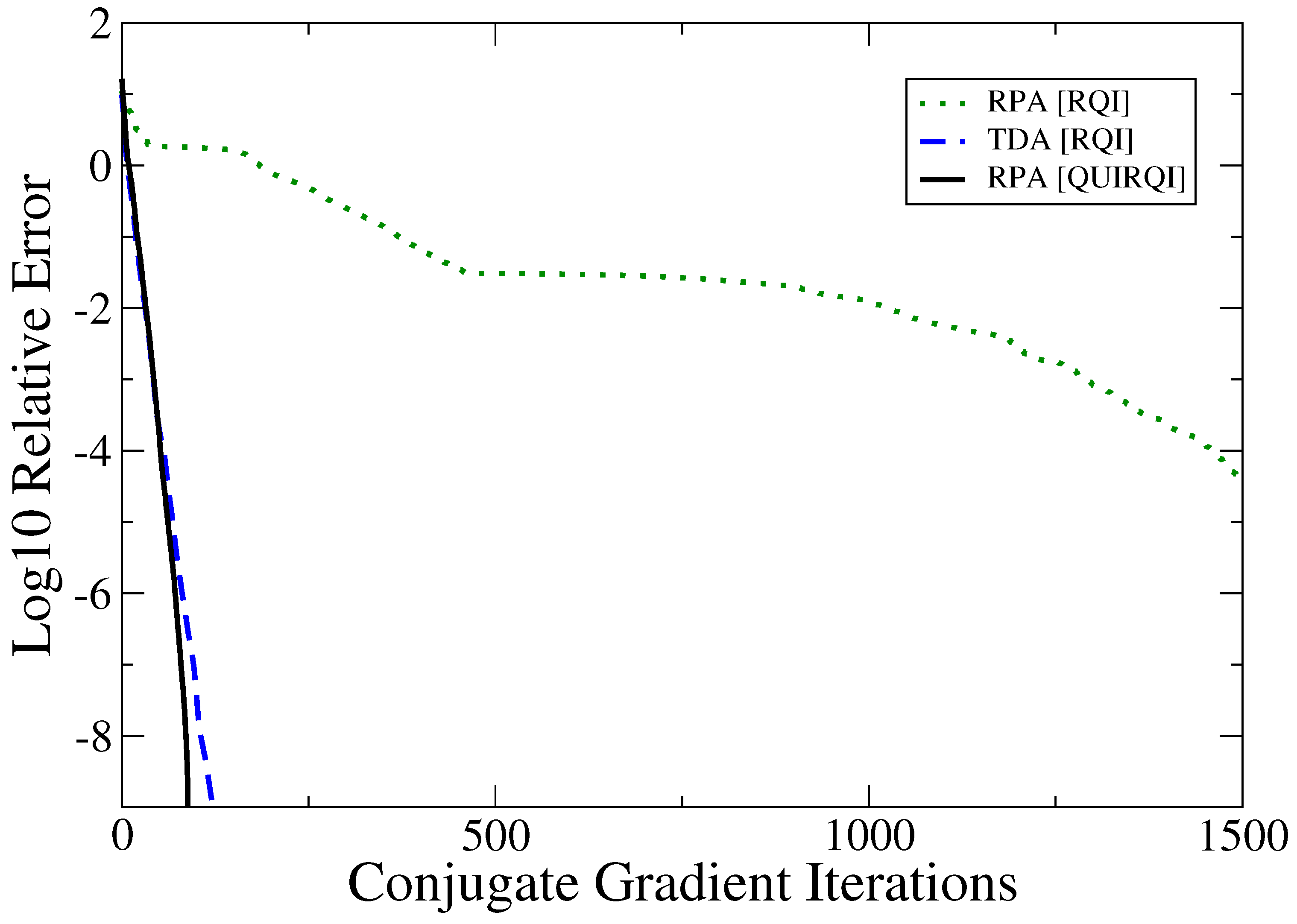
For systems studied to date, QUIRQI is found to converge monotonically with rates comparable to the TDA as shown in
Figure 1. Based on the comparative performance presented by TINC, the TDA rate of convergence appears to be a lower bound for RPA solvers. In addition to the convergence rate, performance is strongly determined by the initial guess. The following results have been obtained using the polarization response density along the polymer axis [
12], which can be computed in
by Perturbed Projection [
25]. Also, a relative precision of 4 digits in the excitation energy is targeted with the convergence parameters
and
, with exit from the optimization loop on violation of monotonic convergence (
due to precision limitations associated with linear scaling approximations).
Figure 1.
Convergence of RHF/3-21G Tamm-Dancoff approximation (TDA) and Random Phase Approximation (RPA) with the Rayleigh Quotient Iteration (RQI) and QUasi-Independen RQI (QUIRQI) algorithms for linear decaene (CH). Calculations were started from the same random guess, and tight numerical thresholds were used throughout. In the representation independent scheme, the cost per iteration is the same for TDA and RPA.
Figure 1.
Convergence of RHF/3-21G Tamm-Dancoff approximation (TDA) and Random Phase Approximation (RPA) with the Rayleigh Quotient Iteration (RQI) and QUasi-Independen RQI (QUIRQI) algorithms for linear decaene (CH). Calculations were started from the same random guess, and tight numerical thresholds were used throughout. In the representation independent scheme, the cost per iteration is the same for TDA and RPA.
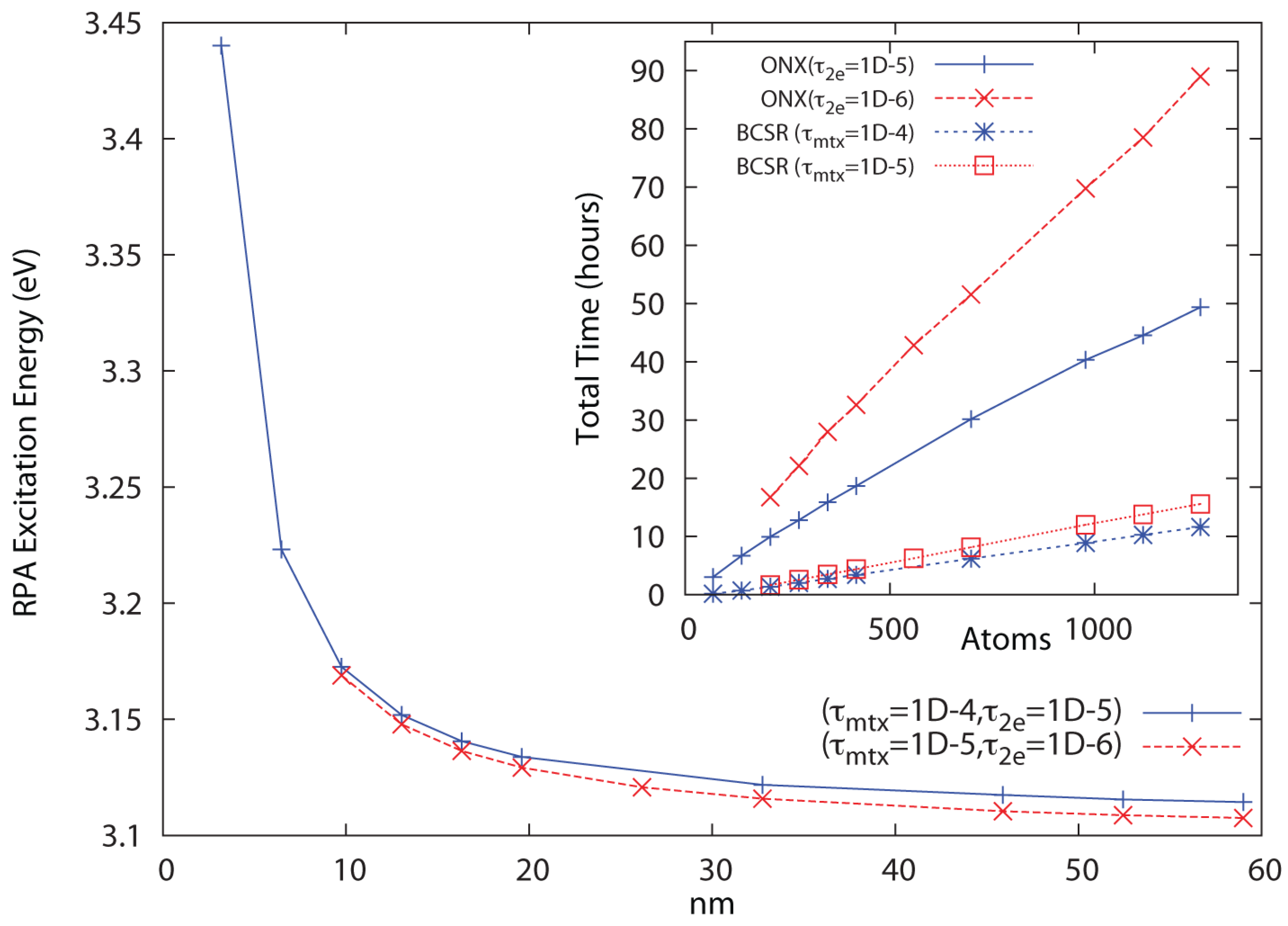
In
Figure 2, linear scaling and convergence to the bulk limit are demonstrated for a series of polyphenylene vinylene (PPV) oligomers at the RHF/6-31G** level of theory for the threshold combinations
and
. Significantly more conservative thresholds have been used for the Coulomb sums, which incur only minor cost. Convergence is reached in 24–25 iterations, with the cost of Coulomb summation via QCTC comparable to the cost of BCSR(
). In
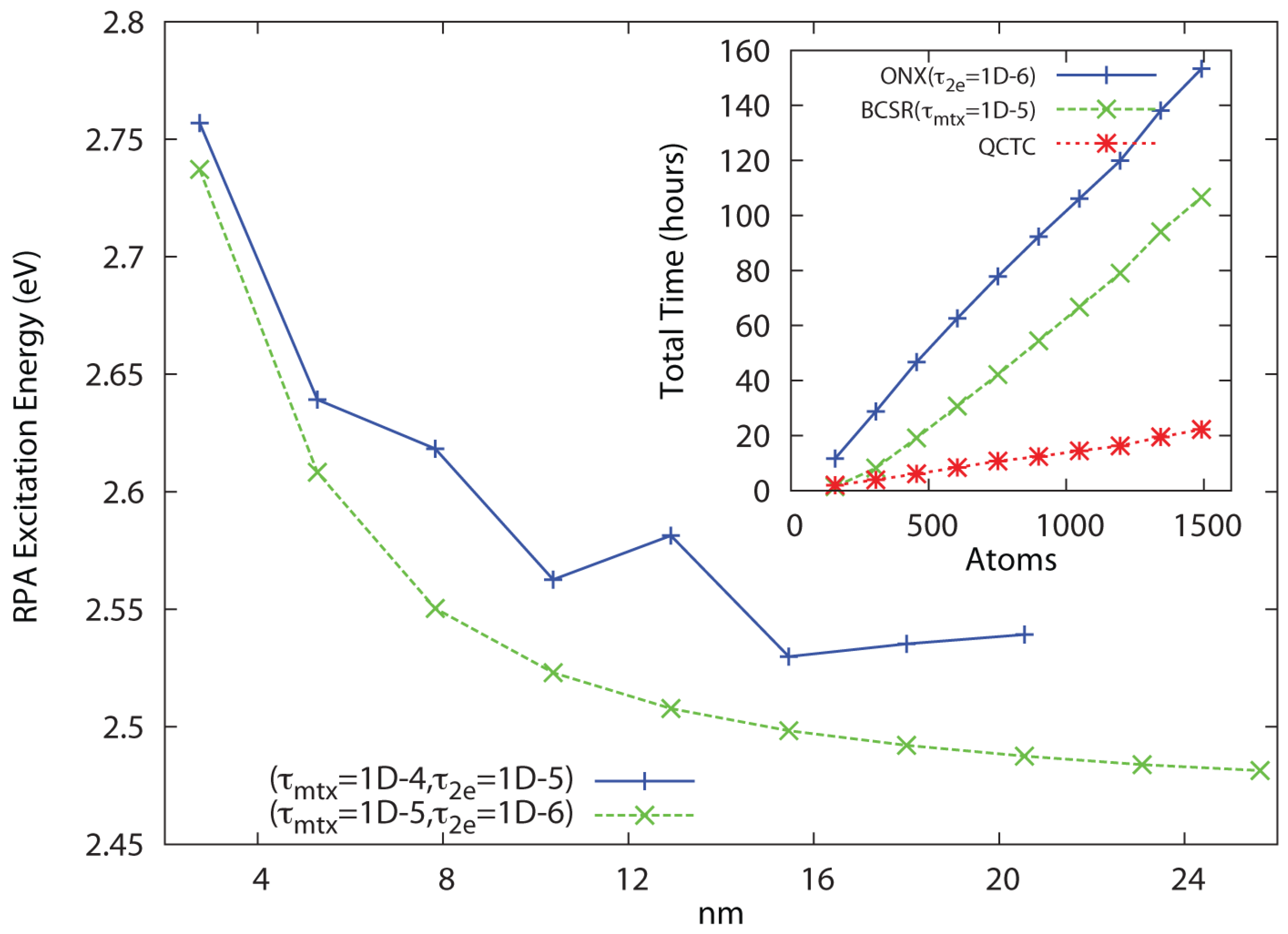
Figure 3, linear scaling and convergence to the bulk limit are demonstrated for a series of (4,3) carbon nanotube segments at the RHF/3-21G level of theory for the same threshold combinations, again with convergence achieved in about 24–25 cycles. In both cases, tightening the pair
leads to a systematically improved result. While the
thresholds that work well for PPV lead to a non-monotone behavior with respect to extent for the nanotube series, dropping one more decade to
leads to a sharply improved behavior. Dropping thresholds further to
yields identical results to within the convergence criteria (∼four digits) across the series, also scaling with
N but at roughly twice the cost.
These results demonstrate that QUIRQI can achieve both systematic error control and linear scaling in solution of the RPA eigenproblem for systems with extended conjugation. Relative to PPV, the greater numerical sensitivity encountered with the nanotube series is consistent with the ground state problem, where a smaller band gap and greater atomic connectivity typically demand tighter thresholds.
Figure 2.
Approach to the bulk limit of the polyphenylene vinylene (PPV) first excited state at the 6-31G**/RPA level of theory, with inset showing linear scaling cost for Hartree-Fock (HF) exchange (ONX) and sparse linear algebra (BCSR). The cost of Coulomb sums with much tighter thresholds are comparable to those for the BCSR.
Figure 2.
Approach to the bulk limit of the polyphenylene vinylene (PPV) first excited state at the 6-31G**/RPA level of theory, with inset showing linear scaling cost for Hartree-Fock (HF) exchange (ONX) and sparse linear algebra (BCSR). The cost of Coulomb sums with much tighter thresholds are comparable to those for the BCSR.
Figure 3.
Approach to the bulk limit of the first excited state of the (4,3) carbon nanotube segment at the 3-21G/RPA level of theory, with inset showing linear scaling cost for HF exchange (ONX), sparse linear algebra (BCSR) and Coulomb sums (QCTC).
Figure 3.
Approach to the bulk limit of the first excited state of the (4,3) carbon nanotube segment at the 3-21G/RPA level of theory, with inset showing linear scaling cost for HF exchange (ONX), sparse linear algebra (BCSR) and Coulomb sums (QCTC).
4. Conclusions
Since this note appeared some time ago in arXiv [
21], several related efforts have appeared that deserve comment: (A) single channel optimization with radial cutoffs [
26] and (B) conventional algebra with a four channel line search [
27,
28]. In the first instance, the ONETEP group have implemented a single channel quotient scheme for the TDA and demonstrated linear scaling for a number of systems using the radial cutoff approach to achieve reduced complexity. In the radial cutoff approach, portions of the vector space are eliminated from the linear algebra when the Cartesian distance between associated atoms becomes greater than some cutoff radius (Going a step further, new technologies are emerging that achieve reduced complexity without truncation in the vector space [
23,
24].). The ONETEP paper is recommended by their careful discussion of radial cutoffs leading to artificial truncation in cases of long range charge transfer, e.g., Reference [
26] Figure 5. In the current implementation, the
filter operation eliminates elements of the vector space that are numerically small; in the case of long range charge transfer, extended conjugation,
etc., an unphysical truncation does not occur. For problems without long range charge transfer or extended conjugation, for example large problems with well localized chromophores as in References [
29,
30], the complexity of QUIRQI with respect to system size becomes
.
In the second instance, the QUIRQI method has been extended to include two additional channels in the line search [
27,
28];
. The authors claim without elaboration that “the solution by our 4D search is and can be much better (than the dual channel approach)” [
28]. As shown in
Figure (1), QUIRQI decouples in the first few steps achieving convergence equivalent to TDA[RQI],
in Equation (
3), so it is hard to understand this unsupported claim, considering also the imperative that
to maintain normalization. These claims are also undercut by apparently slow rates of convergence; compare for example
Figure (1) of this work with Reference [
27], especially
Figure 3. These authors further claim without explanation that “dual channel optimization are not readily extensible to the subspace search” [
28]. Again, its hard to understand how the dual channel case isn’t extensible to subspace schemes for finding multiple eigenvalues; the equivalent of (single channel) block RQI has been demonstrated in the ONETEP paper [
26], and no obvious problems are foreseen with more sophisticated methods such as LOBPCG [
31] for single or dual channel approaches.
To summarize, the QUIRQI method is characterized by two innovations: First, dual channel optimization separates the Tsipper functional into two, nearly independent quotients that cannot be further improved by additional channels in the line search. Reflecting this separation, convergence of the TD-SCF matrix eigenproblem with QUIRQUI is found to be equivalent to the single quotient matrix eigenproblem in the Tamm-Dancoff approximation, as shown in
Figure 1. Second, the method is variational with respect to an incomplete linear algebra, controlled in this work through the
filter threshold
[
15,
16,
17], as shown in
Figure 2 and
Figure 3. While QUIRQI is not variational with respect to the screening parameter
, the solution can be systematically improved by tightening
[
18], in comparison to nested subspace methods that encounter an iterative accumulation of errors [
19,
20]. Indeed, eigensolution posed as optimization provides considerable flexibility in choosing a path to solution, offering opportunities for mixed precision GPU acceleration [
32] and variable thresholding (tightening the parameter
during convergence).