Abstract
TM@ZnS nanoclusters have been characterized by means of the Density Functional Theory, in which Transition Metal (TM) stands from Y to Cd, and i = 12 and 16. These two nanoclusters have been chosen owing to their highly spheroidal shape which allow for favored endohedral structures as compared to other nanoclusters. Doping with TM is chosen due to their magnetic properties. In similar cluster-assembled materials, these magnetic properties are related to the Transition Metal-Transition Metal (TM-TM) distances. At this point, endohedral doping presents a clear advantage over substitutional or exohedral doping, since in the cluster-assembled materials, these TM would occupy the well-fixed center of the cluster, providing in this way a better TM-TM distance control to experimentalists. In addition to endohedral compounds, surface structures and the TS’s connecting both isomers have been characterized. In this way the kinetic and thermal stability of endohedral nanoclusters is predicted. We anticipate that silver and cadmium endohedrally doped nanoclusters have the longest life-times. This is due to the weak interaction of these metals with the cage, in contrast to the remaining cases where the TM covalently bond to a region of the cage. The open-shell electronic structure of Ag provides magnetic properties to Ag@ZnS clusters. Therefore, we have further characterized (Ag@ZnS) and (Ag@ZnS) dimers both in the ferromagnetic and antiferromagnetic state, in order to calculate the corresponding magnetic exchange coupling constant, J.
1. Introduction
The recent explosion of research in nanoclusters has been driven in part by the wide-ranging of applications in nanotechnology, due to their novel properties that usually differ from those of the bulk matter. The size and composition dependent properties, which arise from the quantum confinement effect, promise new materials with novel properties. Likewise, during the last decade interest in II-VI nanocompounds has increased notably, as they have potential applications in photovoltaic solar cells, optical sensitizers or quantum devices [1,2,3,4,5]. In addition, nanoclusters made of these materials can be doped changing their properties at will. For instance, doping the nanoclusters with transition-metals can affect their magnetic properties [6,7,8,9]. In this context, spherical hollow clusters provide the chance for endohedral doping, namely, the dopant is placed inside the cavity of the hollow nanoparticle [10,11,12,13,14]. So far, few II-VI nanoclusters doped with transition-metals have been explored. Yadav et al. studied the properties of Cr-doped (ZnTe) clusters by first principles density functional calculations, concluding that it is energetically most favorable for Cr atoms to substitute at Zn sites [15]. Moreover, a theoretical investigation on (ZnSe) (n = 6–13) nanoclusters doped with manganese atoms, revealed that Mn atoms prefer to substitute Zn atoms in the doped compound [16].
(ZnO) nanoclusters doped with one and two Mn atoms were studied taking into account the substitutional, exohedral and endohedral doping [9]. The calculations suggested that, for the monodoped clusters, the substitutional isomer is energetically favorable, and an exohedral isomer may appear as a low-lying metastable state. The endohedral bi-doped isomer, however, is found to be a stable local minimum. The structural and magnetic properties of (ZnO) nanoclusters substitutionally doped with 3d transition-metals were also studied theoretically [17]. It was found that doping of TM at the Zn site is energetically more favorable than doping it at O site. Other studies on Cu-doped (ZnO) (n = 3, 9, 12) [18], Mn-doped (ZnS) [19], and Cr-doped (CdS) determined that, among the substitutional, exohedral and endohedral doping, the substitutional mono- and bi-doped clusters are the most stable ones. Likewise, Chen and co-workers found that substitutional isomer is the most favorable in energy for monodoped clusters, while the exohedral isomers are the most favorable for bidoped clusters [20].
Additionally, (ZnS) and (ZnS) nanostructures have been doped endohedrally with first-row transition-metals [21]. Both clusters were chosen due to their high symmetry [22] and highly spheroidal shape, that allow for more favorable endohedral doping as compared to other nanoclusters [23]. Nevertheless, although the theoretically characterized endohedral TM@ZnS (i = 12 and 16) structures were predicted to be thermodynamically stable, a later work [8] showed that most of them may not be thermally stable. The reason is that the dopant atom tends to move from the inner part of the cluster to the surface, giving rise to the so-called surface-doped structures [8]. However, the exceptions were Zn-doped endohedral (ZnS) and (ZnS) nanoclusters, which were predicted to have a very long lifetimes.
Nevertheless, although substitutional doping is in general more stable than endohedral doping, the latter presents a very important feature in dealing with the magnetic properties of cluster-assembled materials. In fact, the magnetic properties of such materials have been found to be related with the Transition Metal-Transition Metal (TM-TM) distances in related materials [17]. At short distances, the antiferromagnetic coupling is favored, while the enlargement of this distance leads to a near-degeneracy of both AF and F states. The advantage of endohedral doping over substitutional doping is that the TM-TM distances can be easily fixed, since the dopant atoms are localed at the center of the clusters. Therefore, in the assembled materials, the TM-TM distance would be fixed. In substitutional doping, the TM-TM distances would be different in the assembled materials, depending on the location of the TM at the cluster surface. More interestingly, the assembled materials of small clusters would lead to short TM-TM distances with antiferromagnetic properties, while large enough clusters would lead to materials with ferromagnetic properties. Therefore, it appears interesting to find sufficiently stable endohedrally doped materials, in order to design materials with well fixed magnetic properties. Unfortunately, no experimental works have been carried out on such structures yet.
In this work, we focus on endohedrally doped second-row transition-metals TM@ZnS nanoclusters (i = 12, 16), where TM stands for the second-row transition-metals (Y-Cd), with the aim of unveiling whether some of these endohedral compounds may be stable and, thus, experimentally detectable. Bearing in mind the previous experience, we have not only characterized the endohedral TM@ZnS structures, but we have also analyzed their thermal stability. With this purpose, we have additionally characterized the surface-doped structures for all compounds, along with the TS’s connecting both isomers. In this manner we have estimated the lifetime of each endohedral nanocluster by estimating the energy barriers for the endohedral-doped to surface-doped transitions. Specifically, the Eyring model has been used,
where k is the reaction rate constant, T is the absolute temperature, is the free energy barrier, the Boltzmann constant, h is the Planck’s constant and R is the constant of the ideal gas. The lifetime of each endohedral nanocluster is then calculated as the inverse of the reaction rate constant. We must emphasize that the reaction rate constants are very sensitive with respect to the activation energies. Consequently, the data obtained with this methodology should not to be taken quantitatively, but qualitatively. Nevertheless, we must emphasize that the obtained results are very conclusive. Thus, we anticipate that silver and cadmium-doped endohedral nanoclusters are the only ones that have very long lifetimes. Since Cd does not have magnetic properties because it is a closed-shell transition metal, we have focused on silver doped nanoclusters, i.e., Ag@ZnS and Ag@ZnS. Silver atoms have a doublet electronic ground state and, therefore, two silver atoms may couple in a ferromagnetic way, with parallel spins, or in an antiferromagnetic manner, with antiparallel spins. Accordingly, we have further characterized (Ag@ZnS) and (Ag@ZnS) magnetic dimers and have calculated their exchange coupling constant, J. In this respect, it is noteworthy that the antiferromagnetically coupled systems require a multideterminantal treatment, such as the complete space self consistent field (CASSCF) method. However, these kind of methods are not amenable for so big systems. Thus, we have used the spin-unrestricted approximation and the broken-symmetry solution (BS) within the DFT framework, that showed to provide a good description of weakly bonded metal-metal interactions [6,24].
To interpret the magnetic properties, we have used the Heisenberg-Dirac-van Vleck spin-Hamiltonian:
where is the local spin of Ag and is the local spin of Ag. The exchange coupling constant, J, in Equation (2) quantifies the strength of the interaction between magnetic centers. When the exchange coupling constant is positive the coupling is ferromagnetic. Conversely, a negative value of J represents an antiferromagnetic coupling. Then, in order to estimate the magnetic exchange coupling constant, we have used the formulation proposed by Yamaguchi and co-workers [25,26]:
where stands for the energy of the high-spin state, namely the ferromagnetic state, and for the energy of the broken symmetry state, i.e., antiferromagnetic state.
2. Methods
All geometries have been fully optimized using the gradient corrected hybrid B3LYP [27,28,29] functional within the Kohn-Sham formulation [30] of density functional theory [31]. Harmonic vibrational frequencies are determined by analytical differentiation of gradients, in order to determine whether the structures found are true minima or transition states, and to extract enthalpy and entropy contributions to Gibbs free energy, G, at room temperature. The relativistic compact effective core potentials and shared-exponent basis set [32] of Stevens, Krauss, Basch and Jasien (SKBJ) have been used for Zn and S, as described in the study of the isolated clusters [33], and the fully relativistic multielectron fit pseudopotentials, with 10 electrons in the core, developed by Dolg et al., were used for the trapped atoms [34,35]. The reliability of this method was checked in a previous work [8]. Note that pure angular momentum functions were used throughout this study. All the geometry optimizations and frequency calculations were carried out with the Gaussian03 package (Gaussian Inc., Wallingford, CT, USA) [36]. The transition states between the characterized endohedral nanoclusters and their corresponding surface-doped structures have been calculated using the Synchronous Transit-Guided Quasi-Newton method (STQN) for locating transition structures [37]. Intrinsic reaction coordinate (IRC) calculations [38,39] are further performed to assess that the calculated transition states connect the appropriate reactants and products. All the atomic charges are calculated from the trace of the atomic polar tensor. The spin densities shown in the text are the Mulliken atomic spin densities, as calculated in Gaussian 03 [36], which are defined as the difference of the Mulliken charges of spin-up and spin-down electrons. The sum over the Mulliken spin densities equals the total spin of the system [40].
In order to calculate the magnetic exchange coupling in silver-doped dimers, we have performed single-point density functional theory calculations using the ORCA package developed by Neese and co-workers [41] . Ahlrichs’ valence triple-ξ basis set [42] with two sets of polarization functions, TZV(pp), were used for all the atoms. All calculations were carried out with an integration grid of 4.0 and employed the gradient corrected hybrid B3LYP [27,28,29] functional.
3. Results
First of all, in Subsection 3.1, we present the characterized endohedrally doped structures, along with their electronic and geometrical features. In Subsection 3.2, we focus on the surface-doped structures. In Subsection 3.3, the characterized transition states between the endohedral and surface-doped structures are shown and their properties discussed. Then the estimated lifetimes of each endohedral transition-metal-doped nanocluster are given and discussed too. Finally, in Subsection 3.4 we focus on the magnetic properties of (Ag@ZnS) dimers.
3.1. Endohedral TM@ZnS Nanoclusters
In this subsection the characterized TM@ZnS nanoclusters, in which TM stands for the second-row transition-metals from Y to Cd and i = 12 and 16, are shown and their properties discussed. For each transition-metal the two lowest-lying spin states have been considered. In Figure 1, TM@ZnS and TM@ZnS endohedral nanoclusters are shown. Observe that the transition metal is located close to the center of each nanocluster. In Table 1, the geometrical properties (the distance of the TM with respect to the geometrical center of the nanocluster, R, and the cavity radius of the cluster, r) and electronic properties (the charge, q, and spin densities of the TM, ) are shown for TM@ZnS and TM@ZnS respectively. The encapsulation energies, ΔG, in kcal/mol are given too. The cavity radii together with their standard deviations are calculated as in [12,14].
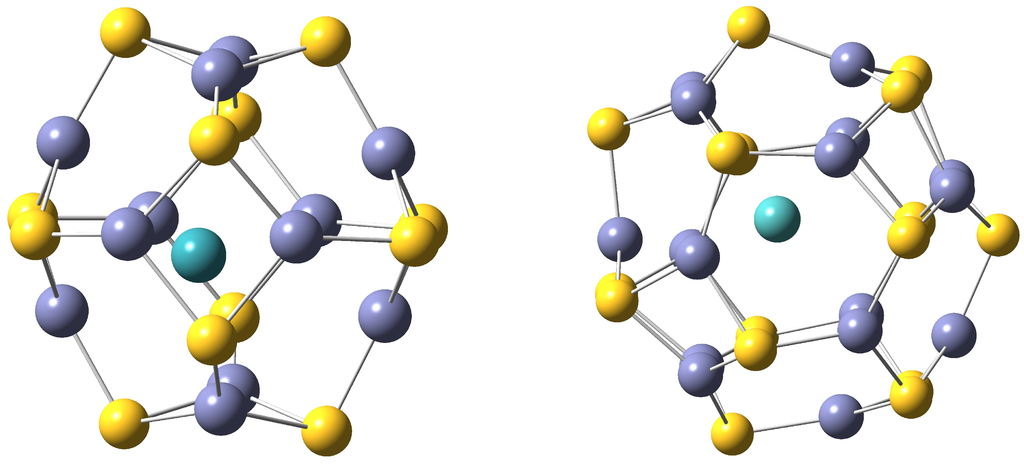
Figure 1.
On the left TM@ZnS and on the right TM@ZnS endohedral nanoclusters. S atoms are drawn in yellow, Zn atoms in violet and TM in blue.
The cavity radii of bare ZnS and ZnS are 2.53 Å and 3.10 Å respectively, with standard deviations of 0.00 and 0.03 (see [14]). This indicates that these two clusters are spherical.

Table 1.
R stands for the distance of the TM with respect to the center of the clusters and r is the cavity radius of the cluster (standard deviation in parentheses), in Å. The charge () and the spin density () is the transition-metals are given along with the encapsulation free energy, ΔG(kcal/mol).
| ZnS | ZnS | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2S + 1 | R | r | Sym | q | ΔG | R | r | Sym | q | ΔG | ||||
| Y | D | - | - | - | - | - | - | 0.00 | 3.15 (0.03) | S | 0.49 | 0.88 | −4.31 | |
| Y | F | 0.97 | 2.56 (0.20) | C | 0.19 | 1.67 | −25.75 | 1.54 | 3.09 (0.22) | C | 0.24 | 1.82 | −32.11 | |
| Zr | F | - | - | - | - | - | - | - | - | - | - | - | - | |
| Zr | F | 0.81 | 2.55 (0.13) | C | 0.18 | 3.18 | −26.05 | 1.49 | 3.09 (0.15) | C | −0.08 | 3.20 | −33.16 | |
| Nb | F | 0.97 | 2.56 (0.17) | C | 0.04 | 2.86 | −35.09 | - | - | - | - | - | - | |
| Nb | D | 0.001 | 2.53 (0.05) | C | 0.12 | 4.33 | −24.86 | 1.04 | 3.08 (0.06) | C | 0.13 | 4.42 | −27.22 | |
| Mo | S | 0.80 | 2.55 (0.14) | C | 0.04 | 3.74 | −19.15 | 0.88 | 3.14 (0.08) | C | 0.08 | 3.92 | −13.91 | |
| Mo | S | 0.02 | 2.53 (0.01) | C | 0.46 | 5.18 | −9.17 | 0.25 | 3.14 (0.02) | C | 0.26 | 5.64 | −11.15 | |
| Tc | D | 1.01 | 2.54 (0.09) | C | −0.06 | 2.91 | −36.97 | 1.56 | 3.09 (0.16) | C | −0.02 | 3.00 | -33.43 | |
| Tc | S | 0.77 | 2.53 (0.09) | C | 0.26 | 4.45 | −15.01 | 1.38 | 3.09 (0.07) | C | 0.12 | 4.62 | −17.80 | |
| Ru | F | 1.03 | 2.53 (0.07) | C | −0.03 | 1.87 | −45.82 | 1.67 | 3.10 (0.11) | C | -0.05 | 1.90 | -43.66 | |
| Ru | F | 0.94 | 2.52 (0.08) | C | 0.21 | 3.49 | −20.78 | - | - | - | - | - | - | |
| Rh | F | 0.98 | 2.53 (0.10) | C | −0.01 | 0.85 | −40.49 | 1.69 | 3.10 (0.09) | C | −0.08 | 0.87 | −39.64 | |
| Rh | F | 0.98 | 2.52 (0.08) | C | 0.1 3 | 2.40 | −17.96 | 1.56 | 3.09 (0.06) | C | 0.06 | 2.54 | −18.68 | |
| Pd | S | 0.51 | 2.51 (0.03) | C | 0.09 | - | −31.51 | 1.46 | 3.09 (0.07) | C | 0.01 | - | −27.22 | |
| Pd | F | 0.77 | 2.51 (0.07) | C | 0.15 | 1.32 | −21.29 | 1.59 | 3.08 (0.10) | C | −0.07 | 1.33 | −23.07 | |
| Ag | S | 0.08 | 2.52 (0.01) | C | 0.36 | 0.78 | 3.47 | 0.65 | 3.14 (0.03) | C | 0.20 | 0.86 | 2.94 | |
| Cd | S | 0.005 | 2.55 (0.00) | C | 0.34 | - | 23.41 | 0.00 | 3.13 (0.02) | D | 0.16 | - | 11.27 | |
Comparing the r and the standard deviations of the calculated endohedrally-doped compounds with respect to the isolated nanoclusters, it is observed that the nanoclusters do not get distorted appreciably upon encapsulation. However, if we compare these data with the data of first-row transition-metal endohedrally-doped nanoclusters [8], we can notice that here the standard deviations are slightly larger. In addition, the spin densities are localized on the TM and the charges of these guest atoms are small indicating that the charge and spin transfer from the TM to the nanocluster are negligible. In order to unveil how strong the interaction between the TM and the cluster is, we have performed a natural bond orbital (NBO) analysis [43] for two selected cases. The first one is Y(F)@ZnS, where yttrium moves 0.97 Å from the center in the ZnS cluster and 1.54 Å when it is encapsulated within the ZnS cluster. In these two compounds the transition-metal was found to be bounded to two adjacent Zn atoms of the ZnS cage and to four Zn atoms of the ZnS cage, through the d orbitals of the metal and the p orbitals of the Zn atoms. However, in the case of Ag@ZnS (R = 0.08 Å) and Ag@ZnS (R = 0.65 Å) we found that silver does not make any bond. Indeed, NBO analysis shows that there are only second order interactions between the most diffuse lone-pairs of silver and empty orbitals belonging to Zn atoms, which are oriented toward the center of the cage. Therefore, the interaction between the host and the caged atom depends on the distance of the TM from the center of the nanocluster. As a consequence, one may conclude that most of the second-row transition metals interact strongly with the host nanocluster, with the exception of Nb, Mo, Ag and Cd.
Observing the distances with respect to the center of mass of the nanoclusters, R, it is worth noticing that in the TM@ZnS, the distance is larger than in TM@ZnS clusters, because the matching between the size of ZnS cluster and the trapped atom is more appropriate and the mobility of the TM inside this nanocluster decreases. Observe that again the Nb, Mo, Ag and Cd TM show the smallest R.
Let us consider now the encapsulation energies, ΔG. It must be emphasized that all of these endohedrally doped compounds are thermodynamically stable (ΔG are negative) with two exceptions: Ag@ZnS and Cd@ZnS. Besides, the ΔG indicate that the most stable clusters are those where the corresponding TM are in low-spin state, except for Y metal.
3.2. Surface-Doped Structures
An alternative way for doping the ZnS nanoclusters is to place the TM on the surface of the clusters. As a consequence, these compounds do not resemble the square-hexagon structure of spheroids any more. Indeed, the insertion of the transition-metal in the surface of these nanoclusters breaks their original structure, due to the formation of the new covalent bonds between the TM and the S and Zn atoms adjacent to them. Such structures are called hereafter surface-doped structures. In this subsection the surface-doped nanoclusters will be analyzed and their properties will be discussed. For each TM, the two lowest-lying spin states have been considered, as for the endohedrally doped ones. In Table 2 the geometrical, electronic and energetic properties of the characterized local minima are given. The coordination number of the metal, given in Table 2, is calculated considering that the TM bonds to a neighbor atoms when the distance between them is smaller than the sum of the van der Waals radii of both atoms.

Table 2.
Surface structures and properties. stands for the atomic charge, for the spin density and the coordination number (CN), of the TM. ΔG is the formation free energy and the energy difference between the endohedral and surface isomers (kcal/mol).
| ZnS | ZnS | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2S + 1 | C.N. | ΔG | C.N. | ΔG | ||||||||
| Y | 2 | 0.72 | 0.05 | 4 | −60.88 | - | 0.72 | 0.94 | 3 | −59.72 | 55.42 | |
| Y | 4 | 0.57 | 0.84 | 8 | −73.18 | 47.45 | 0.51 | 1.52 | 5 | −54.20 | 22.11 | |
| Zr | 3 | 0.50 | 1.33 | 6 | −77.89 | - | 0.33 | 1.48 | 4 | −68.69 | ||
| Zr | 5 | 0.24 | 2.68 | 5 | −50.97 | 24.92 | 0.32 | 2.71 | 4 | −44.79 | 11.62 | |
| Nb | 4 | 0.33 | 2.80 | 6 | −77.45 | 42.35 | 0.64 | 3.05 | 3 | −73.53 | - | |
| Nb | 6 | 0.01 | 4.05 | 6 | −38.35 | 13.49 | 0.08 | 4.01 | 5 | −32.24 | 5.05 | |
| Mo | 5 | 0.16 | 4.05 | 4 | −51.59 | 32.42 | 0.38 | 4.02 | 3 | −49.05 | 35.13 | |
| Mo | 7 | 0.32 | 4.89 | 4 | −8.48 | −0.682 | 0.40 | 5.23 | 2 | −8.51 | −2.62 | |
| Tc | 4 | 0.09 | 3.10 | 4 | −63.08 | 26.082 | 0.19 | 3.11 | 4 | −62.61 | 29.15 | |
| Tc | 6 | 0.39 | 4.45 | 3 | −29.63 | 14.65 | 0.44 | 4.67 | 2 | −31.86 | 14.04 | |
| Ru | 3 | −0.05 | 1.92 | 5 | −60.13 | 14.30 | 0.11 | 1.86 | 4 | −57.15 | 13.50 | |
| Ru | 5 | 0.26 | 3.07 | 4 | −26.81 | 6.00 | 0.39 | 3.42 | 2 | −25.96 | ||
| Rh | 2 | −0.07 | 0.89 | 4 | −50.46 | 9.96 | −0.05 | 0.85 | 4 | −45.04 | 5.41 | |
| Rh | 4 | 0.27 | 2.03 | 4 | −19.78 | 1.81 | 0.31 | 2.31 | 2 | −17.80 | −0.87 | |
| Pd | 1 | −0.13 | - | 4 | −29.94 | −1.60 | −0.05 | - | 2 | −25.14 | −2.06 | |
| Pd | 3 | 0.25 | 0.93 | 4 | −26.49 | 5.21 | 0.23 | 1.10 | 2 | −27.34 | 4.24 | |
| Ag | 2 | 0.26 | 0.42 | 2 | 2.72 | 0.778 | 0.28 | 0.40 | 2 | 2.13 | 0.81 | |
| Cd | 1 | 0.30 | - | 2 | 15.95 | 7.47 | 0.35 | - | 2 | 14.60 | −3.32 | |
Different local minima have been characterized for each TM, from 2-coordinated to 6-coordinated structures. Two representative cases are depicted in Figure 2. For the sake of clarity the properties presented here are those corresponding to the most stable isomers. For Tc(D), Rh(F), Ag(S) and Cd(S) the coordination number is the same in both ZnS and ZnS compounds. However, in the rest of the nanoclusters, the coordination number is bigger in TM-ZnS.
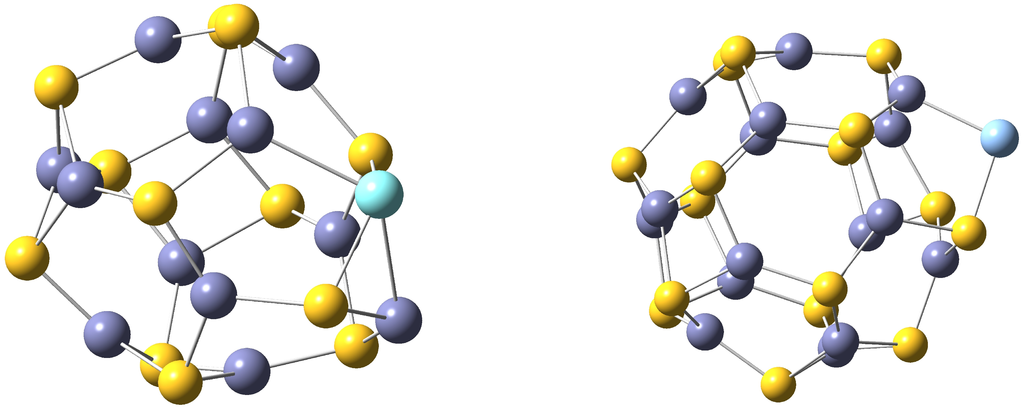
Figure 2.
4-Coordinated TM-ZnS is depicted on the left and 2-coordinated TM-ZnS surface-doped structure is shown on the right. S atoms are drawn in yellow, Zn atoms in violet and TM in blue.
Comparing the data of the endohedral nanoclusters given in Table 1 and the properties of surface structures shown in Table 2, it is observed that, in general, the spin densities and charges of TM’s are larger and smaller, respectively, in the endohedral structures. This is due to the much larger interaction between TM and the remaining atoms in the surface-doped structures. Hence, in these compounds the interaction between the host and the guest atoms is larger.
The ΔG’s are negative for all structures except for the compounds formed by Ag and Cd, which are predicted to be thermodynamically unstable. The values of ΔG indicate that the low spin states are more stable than high spin states, as it happens in the endohedral structures.
The ΔG = G − G reveal that the surface-doped structures are thermodynamically more stable than the corresponding endohedral compounds. For this reason, we have searched a transition state connecting these two isomers, in order to analyze the thermal stability of the endohedral nanoclusters. The obtained results are shown and discussed in the next subsection.
3.3. Transition States
The endohedral and surface-doped structures are connected by a transition state (TS), as it was observed in a previous work [8]. In this subsection we have characterized these transition states in order to analyze the kinetic and thermal stability of the endohedral compounds. Although surface-doped structures are thermodynamically more stable, large enough barriers would prevent endohedral compounds to rearrange into the surface-doped structures. In Table 3, the energy barriers between the endohedral structures and the TS, , the reaction rate constants (k) and the lifetimes of the endohedral compounds are given. The calculated energy barriers, , are calculated as . These values are further used to estimate the reaction rate constants (k), at room temperature, using the Eyring equation (see Subsection 1). The lifetime of each endohedral nanocluster is then calculated as the inverse of the reaction rate constant.

Table 3.
Characterized transition states between endohedral compounds and surface compounds for TM@ZnS and TM@ZnS. (kcal/mol) is the energy difference between the TS and the endohedral structure, k (s) stands for the calculated reaction rate constant and and τ (s) are the calculated lifetimes of the endohedral isomers.
| TM@ZnS | TM@ZnS | |||||||
|---|---|---|---|---|---|---|---|---|
| 2S + 1 | k | τ | k | τ | ||||
| Y | 2 | - | - | - | - | - | - | |
| Y | 4 | - | - | - | - | - | - | |
| Zr | 3 | - | - | - | - | - | - | |
| Zr | 5 | −0.66 | - | - | 9.19 | 1.14 × 10 | 8.78 × 10 | |
| Nb | 4 | −0.59 | - | - | - | - | - | |
| Nb | 6 | 9.74 | 4.50 × 10 | 2.22 × 10 | 13.20 | 1.31 × 10 | 7.64 × 10 | |
| Mo | 5 | 7.51 | 1.94 × 10 | 5.15 × 10 | - | - | - | |
| Mo | 7 | 14.65 | 1.13 × 10 | 8.83 × 10 | 17.12 | 1.75 | 0.57 | |
| Tc | 4 | 6.53 | 1.01 × 10 | 9.85 × 10 | 0.96 | 1.23 × 10 | 8.14 × 10 | |
| Tc | 6 | 5.30 | 8.09 × 10 | 1.24 × 10 | 6.30 | 1.50 × 10 | 6.68 × 10 | |
| Ru | 3 | 8.63 | 2.93 × 10 | 3.41 × 10 | 5.03 | 1.28 × 10 | 7.84 × 10 | |
| Ru | 5 | 7.22 | 3.17 × 10 | 3.15 × 10 | - | - | - | |
| Rh | 2 | −0.84 | - | - | 3.30 | 2.37 × 10 | 4.22 × 10 | |
| Rh | 4 | 14.00 | 3.39 × 10 | 2.95 × 10 | 9.11 | 1.30 × 10 | 7.67 × 10 | |
| Pd | 1 | 13.93 | 3.82 × 10 | 2.62 × 10 | 10.63 | 1.00 × 10 | 9.98 × 10 | |
| Pd | 3 | 5.69 | 4.19 × 10 | 2.39 × 10 | 2.72 | 6.30 × 10 | 1.59 × 10 | |
| Ag | 2 | 21.26 | 1.62 × 10 | 6.18 × 10 | 24.44 | 7.55 × 10 | 1.32 × 10 | |
| Cd | 1 | 27.07 | 8.91 × 10 | 1.12 × 10 | 39.70 | 4.92 × 10 | 2.03 × 10 |
At first glance, it is worth noting that most of the calculated lifetimes are very small, although most of them are predicted to be large enough as to enable experimental detection. Zr(F)@ZnS, Nb(F)@ZnS and Rh(F)@ZnS are not kinetically stable at all, as there is not any energetic barrier protecting these endohedral structures. Conversely, we must emphasize that the lifetimes of Ag(S)@ZnS and Cd(S)@ZnS are extremely large, despite their are positive (see Subsection 3.1). Thus, these compounds are predicted to be metastable. Note that in these two cases, (also inNb and Mo), the TM is located near the center of the nanocluster. Therefore, calculated life-times are related with the distance the trapped atom is from the center of the cage. In fact, in those cases NBO analysis showed that there is a weak interaction between the cage and the host atom. Note that the 4s3d shells are (almost) half-filled or filled in these cases, and therefore, the guest is stabilized without forming covalent bonds with the host, unlike the remaining cases. Nevertheless, note that life-times of atoms with semi-filled shells are much smaller, since they are able to form more stable surface-structures than Ag and Cd.
Finally, it should be pointed out that, in general, second-row transition-metal doped nanoclusters are thermodynamically more stable, so they have longer lifetimes, than first-row ones.
3.4. Silver-Doped Dimers
Transition-metal compounds are interesting, among other features, due to their magnetic properties. Therefore, endohedral nanoclusters with large enough lifetimes would lead to materials with combined magnetic and semiconducting properties. In this vein, the only magnetic endohedral structures with large enough lifetimes are those of silver, since Ag atoms have one unpaired electron. We have studied both the ferromagnetic and antiferromagnetic coupling on (Ag@ZnS) and (Ag@ZnS) dimers and calculated the exchange-magnetic coupling, J.
Both ZnS and ZnS nanoclusters can be linked together in different ways as they are made up of squares and hexagons. In a previous work with similar compounds [44], it was observed that the most stable dimers are those which are bonded via hexagon-to-hexagon. Accordingly, we have made the dimers linking the monomers through their hexagons. In this manner we have considered the magnetic exchange coupling of the two Ag centers. First, we have calculated the ferromagnetic state, where the two unpaired electrons of the silver atoms (one unpaired electron on each Ag atom) are spin parallel (triplet state), and the antiferromagnetic state, where the unpaired electron of one Ag atom is spin up and the other unpaired electron of the second Ag is spin down (singlet state).
In Table 4 the data corresponding to the characterized dimers are given. For both cases the dimerization energies are negative, specially for (Ag@ZnS), meaning that the formation of these dimers is thermodynamically allowed.

Table 4.
Symmetry of the dimers and the distance between the two Ag atoms, R, in Å. The dimerization energies, , are given in kcal/mol. J is the exchange coupling constant (cm) and and are the spin expectation values of high spin and broken symmetry states respectively.
| Dimer | Symm | R | J | |||
|---|---|---|---|---|---|---|
| (Ag@ZnS) | C | 6.65 | −5.81 | −133.93 | 2.0029 | 0.9670 |
| (Ag@ZnS) | C | 8.69 | −13.92 | 0.63 | 2.0028 | 1.0027 |
The exchange coupling constant, J, for (Ag@ZnS) reveals that the antiferromagnetic interaction is clearly favored. However, in the case of (Ag@ZnS), the value of J is very small indicating that there is a competition between ferromagnetic and antiferromagnetic states. Indeed, the distance between the two magnetic centers is much smaller in (Ag@ZnS) than in (Ag@ZnS) ( 6.65 and 8.69 Å respectively) due to the size of the clusters. Thus, we can conclude that silver atoms tend to couple between them antiferromagnetically in short distances, but the AF and F coupling are near-degenerate when increasing the distance, in agreement with previous calculations in related systems [17]. Hence, control of the TM-TM distance would lead to different magnetic properties. Regarding the assembly in 2D or 3D, the endohedral doping facilitates the control of the distance between guest metals, since the position of the TM at the center of the cage is well defined. Therefore, assemblies of small clusters would lead to AF materials, while assemblies of large clusters would lead to F materials, being the AF coupling close in energy. Moreover, considering the Ag-Ag distances in these dimers, along with related studies on other encapsulated X@ZnS and X@CdS assemblies [44,45], we suggest that the Ag-Ag distances would remain quite similar in the solid compared to the dimers.
In Figure 3, the spin density of the most stable states are depicted, i.e., the ferromagnetic (Ag@ZnS) and the antiferromagnetic (Ag@ZnS). Observe that in the former electron of Ag is spin up and electron of Ag is spin down, while in (Ag@ZnS) dimer, the unpaired electron of each Ag atom have the same sign. Finally, the spin expectation values show that, although there is spin contamination, it is small.
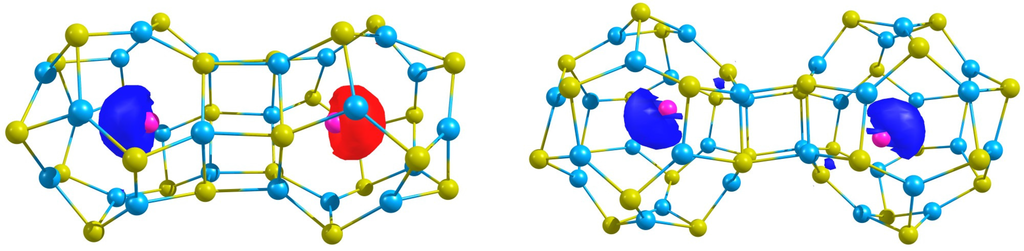
Figure 3.
The spin density of the the antiferromagnetic (Ag@ZnS) and the ferromagnetic (Ag@ZnS) structures.
4. Conclusions
The thermal stability of the second-row transition-metal-doped TM@ZnS nanoclusters (i = 12, 16) has been analyzed. On the basis of the calculated energy differences between the endohedral compounds and the TS compounds that connect the former with the surface-doped structures, we have estimated the lifetime of each endohedral structure. Although surface-doped structures are thermodynamically more stable than endohedral ones, large enough barriers would prevent endohedral compounds to rearrange into the surface-doped structures. As mentioned before, these techniques are approximate. Hence, the calculated data have not to be taken quantitatively, but qualitatively. In spite of that, the data obtained are very enlightening, as all the calculated lifetimes are very small, indicating that most of the endohedrally-doped nanoclusters are not thermally stable. However there are two exceptions: the lifetimes of Ag(S)@ZnS and Cd(S)@ZnS are extremely large. These compounds are predicted to be metastable. This metastability is associated to the electronic structure of Ag and Cd, where the 3d and 4s shells are almost or completely filled. As mentioned in the Introduction, no experiments have been carried out regarding endohedral II-VI compounds. Nevertheless, hollow bare II-VI structures have been characterized experimentally by Belbruno and coworkers [46,47]. They generated these structures by means of direct laser ablation, and then the generated compounds were analyzed in a time-of-flight mass spectrometer. We believe that this technique could also be used for the detection of endohedral compounds.
Since Cd does not have magnetic properties because it is a closed-shell transition metal, we have focused on silver doped nanoclusters, i.e., Ag@ZnS and Ag@ZnS. We have characterized (Ag@ZnS) and (Ag@ZnS) magnetic dimers and have calculated their exchange coupling constant, J. In the case of (Ag@ZnS), J reveals that the antiferromagnetic interaction is clearly favored. Conversely, in the case of (Ag@ZnS), the value of J is small but positive indicating a weak ferromagnetic coupling between the two encapsulated silver atoms. This difference is ascribed to the Ag-Ag distance. Short Ag-Ag distances lead to antiferromagnetic coupling, while long distances stabilize the ferromagnetic coupling. These results are in agreement with those obtained for related II-VI compounds.
Acknowledgments
This research was funded by Eusko Jaurlaritza (the Basque Government), and the Spanish Office for Scientific Research. The SGI/IZO-SGIker UPV/EHU (supported by Fondo Social Europeo and MCyT) is gratefully acknowledged for generous allocation of computational resources. JMM would like to thank Spanish Ministry of Science and Innovation for funding through a Ramon y Cajal fellow position (RYC 2008-03216). We thanks Elixabete Rezabal for cheerful discussion.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chuchev, K.; BelBruno, J. Small, nonstoichiometric zinc sulfide clusters. J. Phys. Chem. A. 2005, 109, 1564–1569. [Google Scholar] [CrossRef] [PubMed]
- Datta, S.; Kabir, M.; Saha-Dasgupta, T.; Sarma, D.D. First-principles study of structural stability and electronic structure of CdS nanoclusters. J. Phys. Chem. C 2008, 112, 8206–8214. [Google Scholar] [CrossRef]
- Mocatta, D.; Cohen, G.; Schattner, J.; Millo, O.; Rabani, E.; Banin, U. Heavily doped semiconductor nanocrystal quantum dots. Science 2011, 332, 77–81. [Google Scholar] [CrossRef] [PubMed]
- Wei, S.; Zhang, S.B. Chemical trends of defect formation and doping limit in II-VI semiconductors: The case of CdTe. Phys. Rev. B 2002, 66, 155211. [Google Scholar] [CrossRef]
- Markus, T.Z.; Itzhakov, S.; Alkotzer, Y.I.; Cahen, D.; Hodes, G.; Oron, D.; Naaman, R. Energetics of CdSe quantum dots adsorbed on TiO2. J. Phys. Chem. C 2011, 115, 13236–13241. [Google Scholar] [CrossRef]
- Matxain, J.M.; Piris, M.; Formoso, E.; Mercero, J.M.; Lopez, X.; Ugalde, J.M. Endohedral stannaspherenes: Mn@Sn12 and its dimer: Ferromagnetic or antiferromagnetic? ChemPhysChem 2007, 8, 2096–2099. [Google Scholar] [CrossRef] [PubMed]
- Archer, P.I.; Santangelo, S.A.; Gamelin, D.R. Inorganic cluster syntheses of TM2+-doped quantum dots (CdSe, CdS, CdSe/CdS): Physical property dependence on dopant locale. JACS 2007, 129, 9808–9818. [Google Scholar] [CrossRef] [PubMed]
- Jimenez-Izal, E.; Matxain, J.M.; Piris, M.; Ugalde, J.M. Thermal stability of endohedral first-row transition-metal TM@ZniSi structures, i = 12, 16. J. Phys. Chem. C 2011, 115, 7829–7835. [Google Scholar] [CrossRef]
- Liu, H.; Wang, S.; Zhou, G.; Wu, J.; Duan, W. Structural, electronic, and magnetic properties of manganese-doped Zn12O12 clusters: A first-principles study. J. Chem. Phys. 2006, 124, 174705. [Google Scholar] [CrossRef] [PubMed]
- Khanna, S.N.; Rao, B.K.; Jena, P. Magic numbers in metallo-inorganic clusters: Chromium encapsulated in silicon cages. Phys. Rev. Lett. 2002, 89, 016803. [Google Scholar] [CrossRef] [PubMed]
- Khanna, S.N.; Rao, B.K.; Jena, P. Electronic signature of the magicity and ionic bonding in Al13X (X = Li, Na, K) clusters. Phys. Rev. B 2002, 65, 125105. [Google Scholar] [CrossRef]
- Jimenez-Izal, E.; Matxain, J.M.; Piris, M.; Ugalde, J.M. Structure and stability of the endohedrally doped (X@CdiSi), X = Na, K, Cl, Br, nanoclusters. J. Phys. Chem. C 2010, 114, 2476–2483. [Google Scholar] [CrossRef]
- Matxain, J.M.; Mercero, J.M.; Fowler, J.E.; Ugalde, J.M. Small clusters of group-(II-VI) materials: ZniXi, X = Se, Te, i = 1–9. Phys. Rev. A 2001, 64, 053201. [Google Scholar] [CrossRef]
- Matxain, J.M.; Eriksson, L.A.; Formoso, E.; Piris, M.; Ugalde, J.M. Endohedral (X@ZniSi), Nanoclusters, X = Li, Na, K, Cl, Br. J. Phys. Chem. C 2007, 111, 3560–3565. [Google Scholar] [CrossRef]
- Yadav, M.K.; Sanyal, B.; Mookerjee, A. Structural, electronic and magnetic properties of Cr-doped (ZnTe)12. J. Magn. Magn. Mater. 2009, 321, 235–240. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, L.; Zhang, J.; Miao, X. Theoretical investigation of structural and magnetic properties of ZnnSen (n = 6–13) nanoclusters doped with manganese atoms. J. Am. Ceram. Soc. 2011, 94, 759–764. [Google Scholar] [CrossRef]
- Ganguli, N.; Dasgupta, I.; Sanyal, B. Electronic structure and magnetism of transition metal doped Zn12O12 clusters: Role of defects. J. Appl. Phys. 2010, 108, 123911. [Google Scholar] [CrossRef]
- Yong, Y.; Wang, Z.; Liu, K.; Song, B.; He, P. Structures, stabilities, and magnetic properties of Cu-doped ZnnOn (n = 3, 9, 12) clusters: A theoretical study. Comput. Theor. Chem. 2012, 989, 90–96. [Google Scholar] [CrossRef]
- Chen, H.; Shi, D.; Qi, J.; Wang, B. First-principles study on the structure, electronic, and magnetic properties of Mn-doped (ZnS)12 clusters. Phys. E 2010, 43, 117–124. [Google Scholar] [CrossRef]
- Chen, H.; Shi, D.; Qi, J.; Wang, B. Structure, electronic, and magnetic properties of Cr-doped (ZnS)12 clusters: A first-principles study. Phys. Lett. A 2010, 374, 4133–4139. [Google Scholar] [CrossRef]
- Matxain, J.M.; Formoso, E.; Mercero, J.M.; Piris, M.; Lopez, X.; Ugalde, J.M. Magnetic endohedral transition-metal-doped semiconduncting-nanoclusters. Chem. Eur. J. 2008, 14, 8547–8554. [Google Scholar] [CrossRef]
- Matxain, J.M.; Mercero, J.M.; Fowler, J.E.; Ugalde, J.M. Electronic excitation energies of ZniOi clusters. J. Am. Chem. Soc. 2003, 125, 9494–9499. [Google Scholar] [CrossRef] [PubMed]
- Hamad, S.; Catlow, C.R.A.; Spano, E.; Matxain, J.M.; Ugalde, J.M. Structure and properties of ZnS nanoclusters. J. Phys. Chem. B 2005, 109, 2703–2709. [Google Scholar] [CrossRef] [PubMed]
- Timmer, G.H.; Berry, J.F. Jahn-Teller distortion, ferromagnetic coupling, and electron delocalization in a high-spin Fe-Fe bonded dimer. C. R. Chemie 2012, 15, 192–201. [Google Scholar] [CrossRef]
- Herzberg, G.; Smith, V.H.; Schaefer, H.F.; Morokuma, K. Applied Quantum Chemistry; Smith, V.H., Schaefer, H.F., Morokuma, K., Eds.; D. Reidel: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Soda, T.; Kitagawa, Y.; Onishi, T.; Takano, Y.; Shigeta, Y.; Nagao, H.; Yoshioka, Y.; Yamaguchi, K. Ab initio computations of effective exchange integrals for H–H, H–He–H and Mn2O2 complex: Comparison of broken-symmetry 2. Chem. Phys. Lett. 2000, 319, 223–230. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, 864–871. [Google Scholar] [CrossRef]
- Stevens, W.J.; Krauss, M.; Basch, H.; Jasien, P.G. Relativistic compact effective potentials and efficient, shared exponent basis sets for the third, fourth and fifth row atoms. Can. J. Chem. 1992, 70, 612–630. [Google Scholar] [CrossRef]
- Matxain, J.M.; Fowler, J.E.; Ugalde, J.M. Small Clusters of II-VI materials: ZniSi, i = 1–9. Phys. Rev. A 2000, 61, 053201. [Google Scholar] [CrossRef]
- Dolg, M.; Wedig, U.; Stoll, H.; Preuss, H. Energy-adjusted ab initio pseudopotentials for the first row transition elements. J. Chem. Phys. 1987, 86, 866–872. [Google Scholar] [CrossRef]
- Martin, J.M.L.; Sundermann, A. Correlation consistent valence basis sets for use with the Stuttgart–Dresden–Bonn relativistic effective core potentials: The atoms Ga–Kr and In–Xe. J. Chem. Phys. 2001, 114, 3408–3420. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03, Revision C.02; Gaussian, Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Peng, C.; Ayala, P.Y.; Schlegel, H.B.; Frisch, M.J. Using redundant internal coordinates to optimize equilibrium geometries and transition states. J. Comp. Chem. 1996, 17, 49–56. [Google Scholar] [CrossRef]
- Gonzalez, C.; Schlegel, H.B. An improved algorithm for reaction path following. J. Chem. Phys. 1989, 90, 2154–2161. [Google Scholar] [CrossRef]
- Gonzalez, C.; Schlegel, H.B. Reaction path following in mass-weighted internal coordinates. J. Phys. Chem. 1990, 94, 5523–5527. [Google Scholar] [CrossRef]
- Ramachandran, K.I.; Deepa, G.; Namboori, K. Computational Chemistry and Molecular Modelling: Principles and Applications; Springer: Berlin, Germany, 2008. [Google Scholar]
- Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Schafer, A.; Horn, H.; Ahlrichs, E. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoin. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Jimenez-Izal, E.; Matxain, J.M.; Piris, M.; Ugalde, J.M. Self-assembling endohedrally doped CdS nanoclusters: New porous solid phases of CdS. Phys. Chem. Chem. Phys. 2012, 14, 9676–9682. [Google Scholar] [CrossRef] [PubMed]
- Matxain, J.M.; Piris, M.; Lopez, X.; Ugalde, J.M. Thermally stable solids based on endohedrally doped ZnS clusters. Chem. Eur. J 2009, 15, 5138–5144. [Google Scholar] [CrossRef] [PubMed]
- Burnin, A.; Sanville, E.; BelBruno, J.J. Experimental and computational study of the ZnnSn and ZnnSn+ clusters. J. Phys. Chem. A 2005, 109, 5026–5034. [Google Scholar] [CrossRef] [PubMed]
- Sanville, E.; Burnin, A.; BelBruno, J.J. Experimental and computational study of small (n = 1–16) stoichiometric Zinc and Cadmium chalcogenide clusters. J. Phys. Chem. A 2006, 110, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).