Modeling Thermal Energy Storage Capability of Organic PCMs Confined in a 2-D Cavity
Abstract
1. Introduction
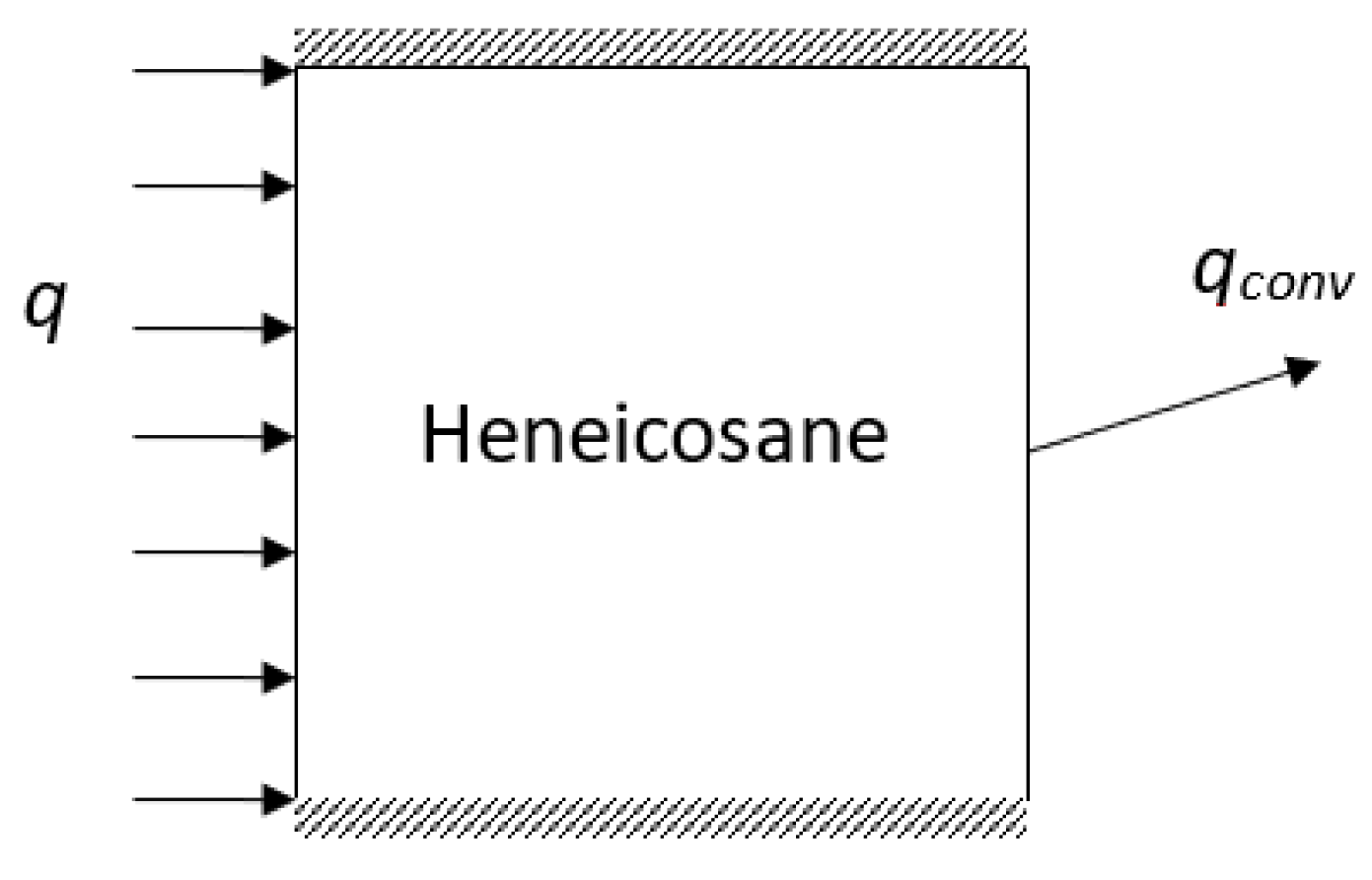
2. Mathematical Model
3. Solution Methodology
3.1. Grid Test
3.2. Time Step Selection
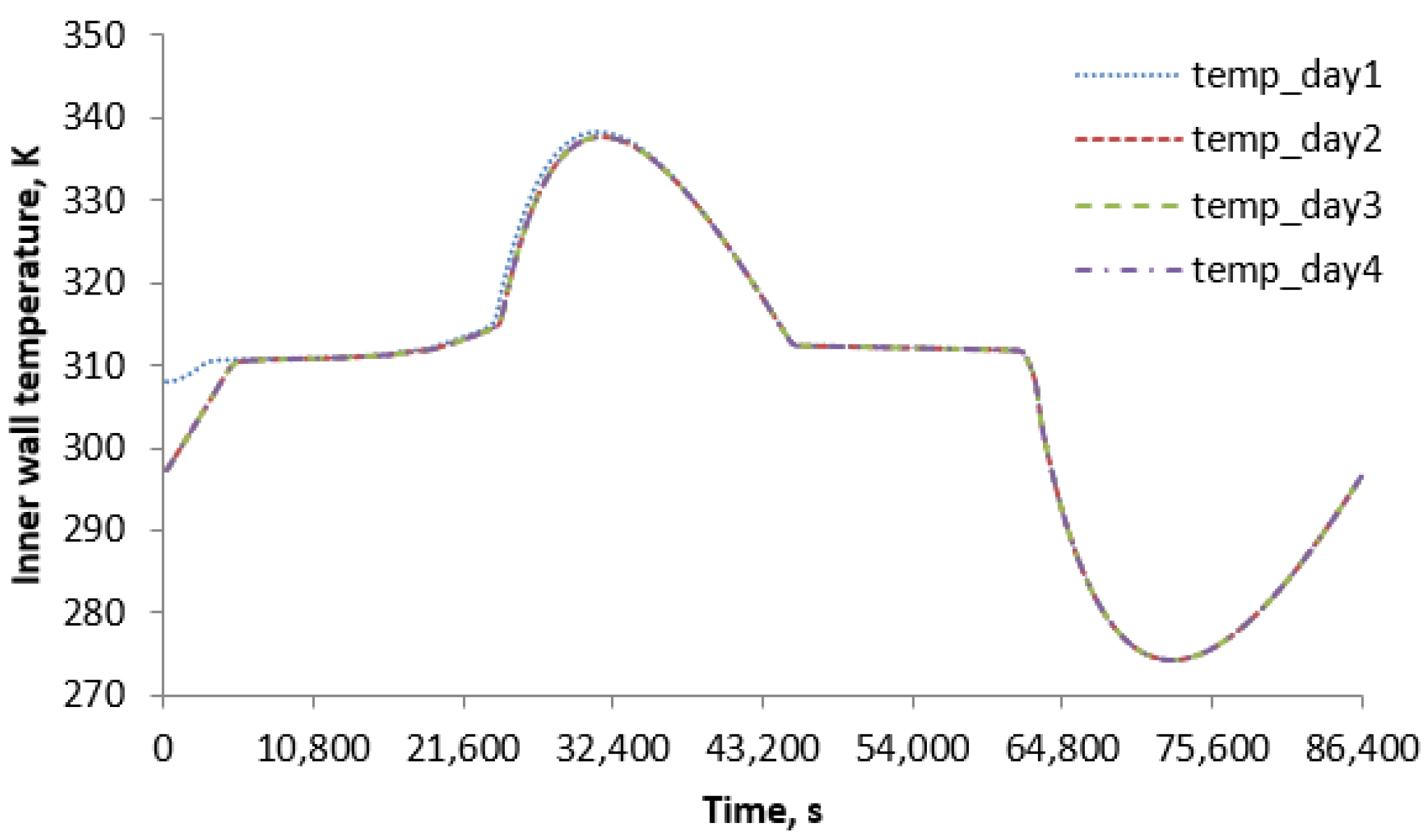
3.3. Initial Condition Effect
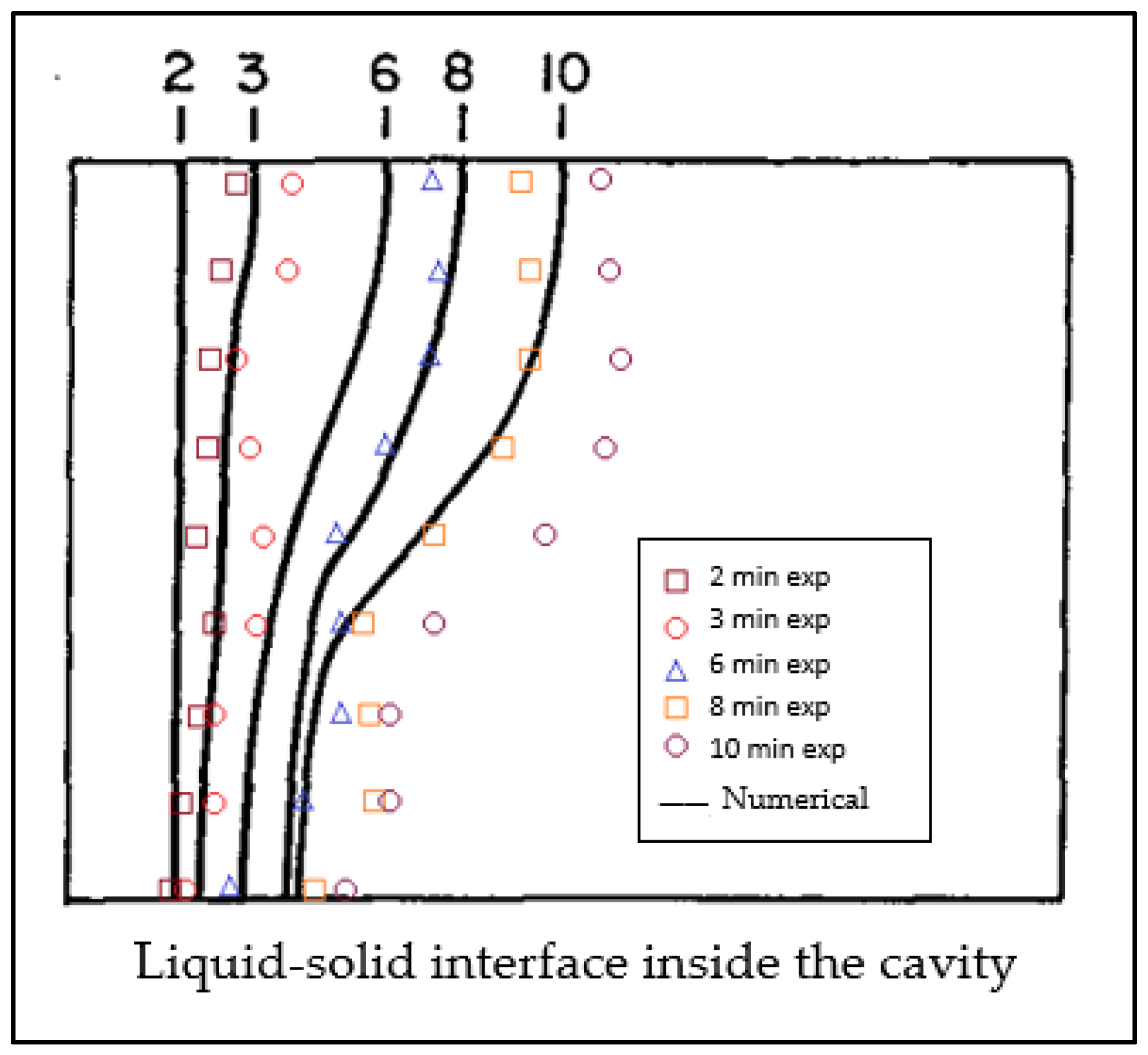
3.4. Numerical Model Validation
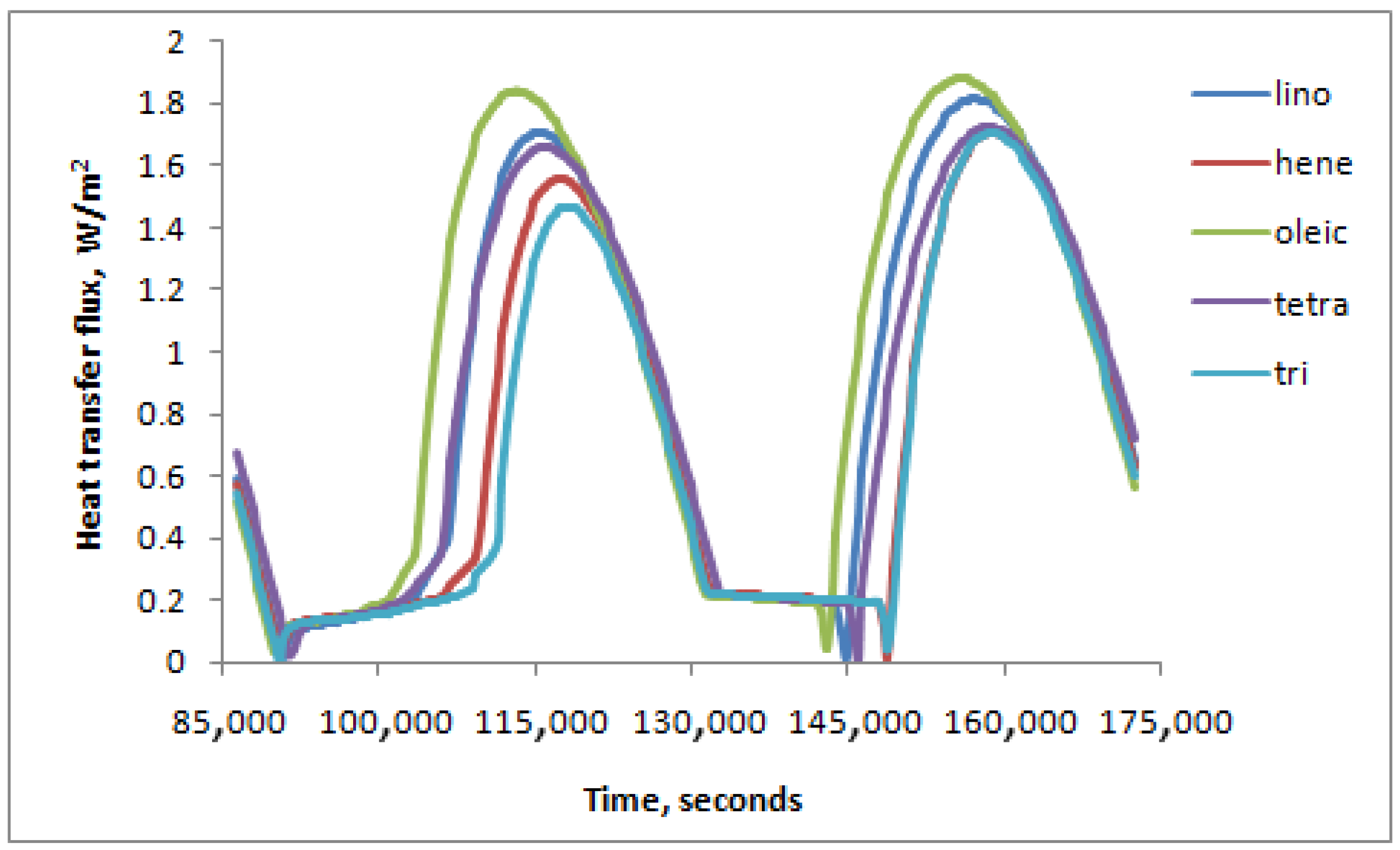
4. Results and Discussion
5. Conclusions
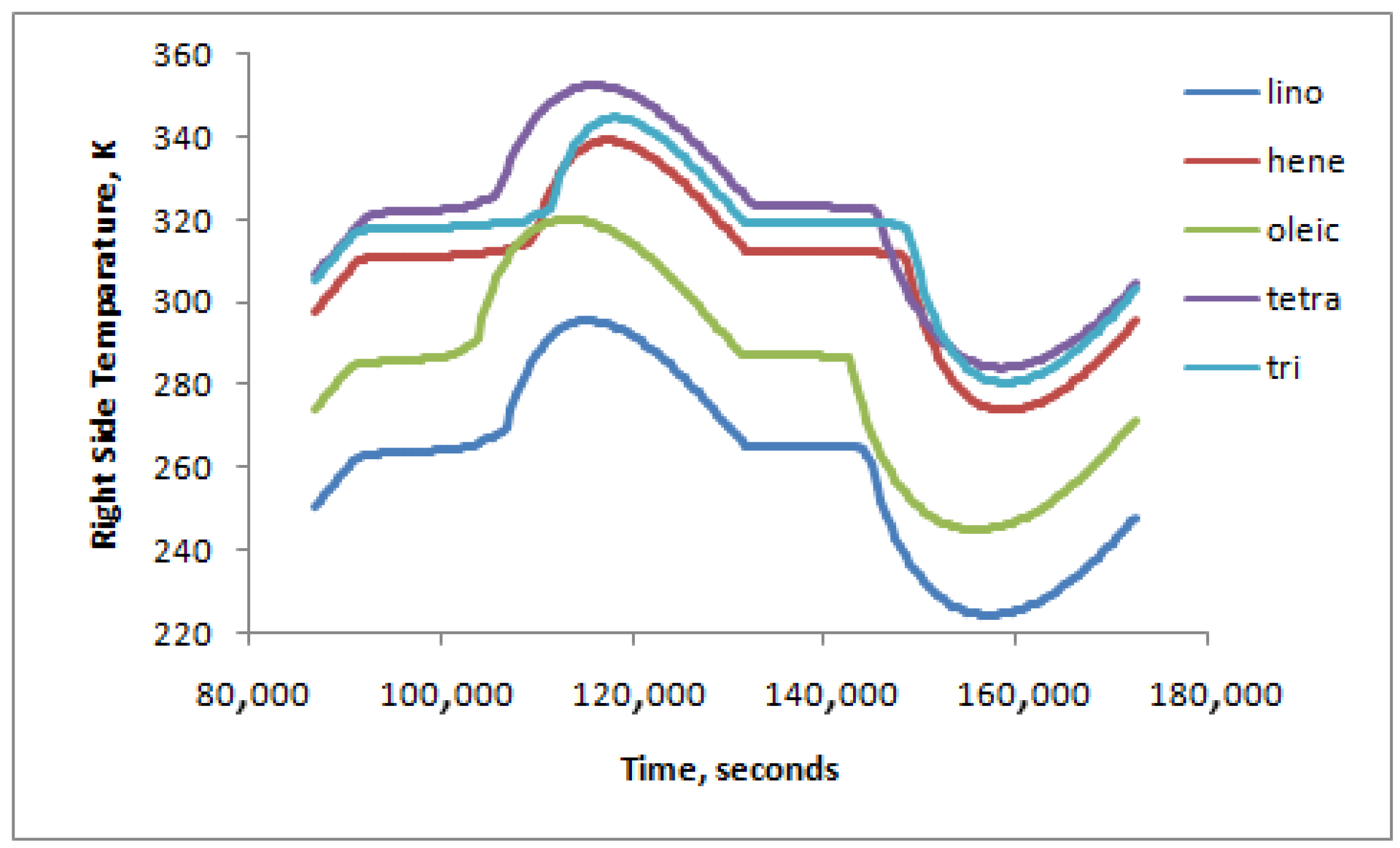
- Linoleic Acid provided the highest inner surface heat flux, while Tricosane provided the lowest.
- Higher outer wall heat flux gain resulted in higher inner surface heat flux on the right side.
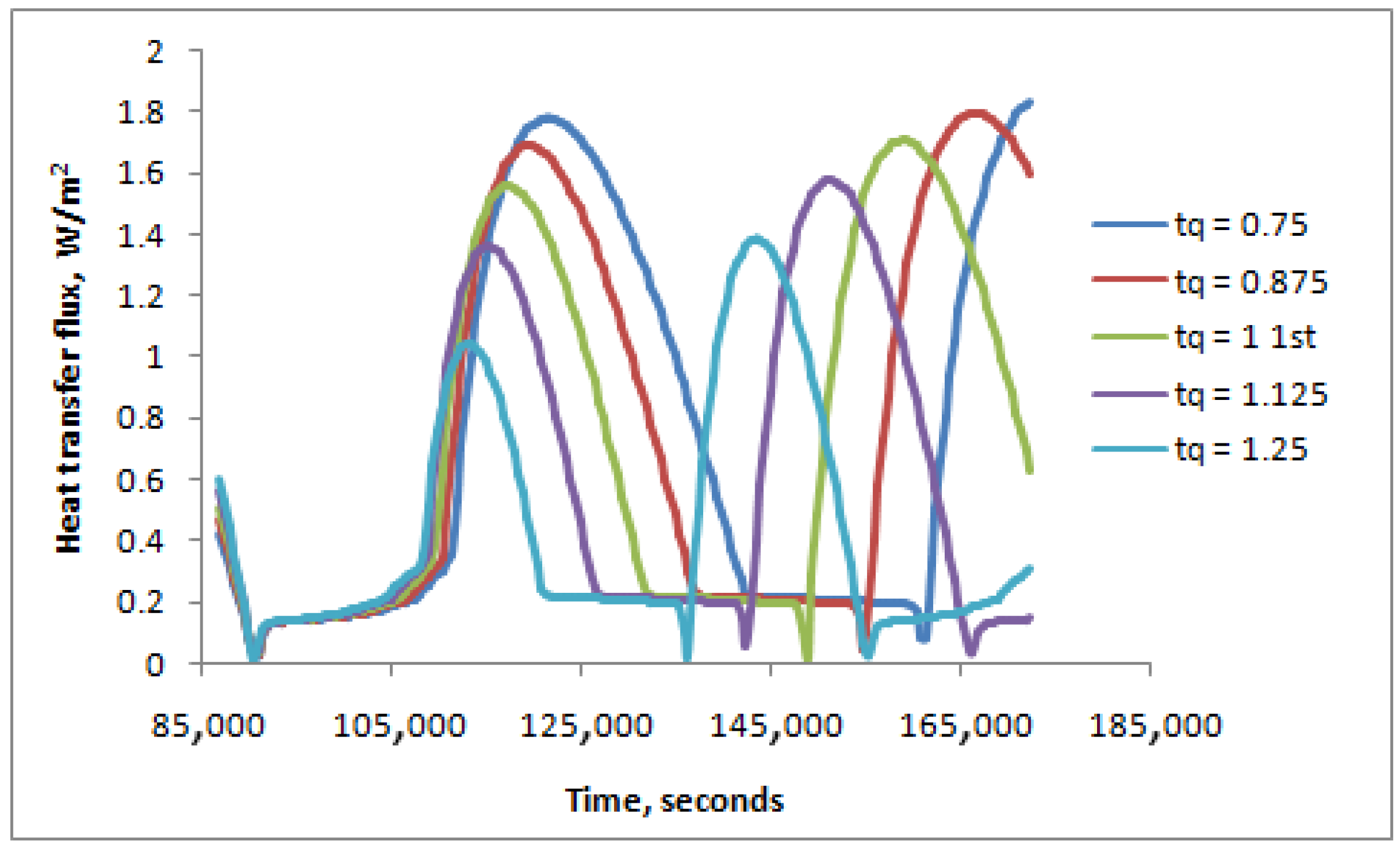
- For longer daytime hours (t/τq < 1), the PCM was in a liquid form for a longer time, while it was solid for a longer time for shorter daytime hours (t/τq > 1).
- Linoleic Acid and Tricosane have the highest melting heat gain, about 10% more than the energy released during the solidification period.
- Melting heat gain has a proportional relation with the outer wall heat flux gain (left side). It could go up to 13% when doubling the outer wall heat flux gain.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Nomenclature
| Cp | thermal specific heat | J/kg·K |
| Em | total energy gains during melting time | W/m2 |
| Es | total energy release during solidification time | W/m2 |
| ho | convective heat transfer coefficient | W/m2·K |
| h | daytime hours | h |
| G | gravity | m/s2 |
| k | thermal conductivity | W/m·K |
| P | pressure | Pa |
| q | outer wall heat flux | W/m2 |
| qo | constant component of outer wall heat transfer flux | W/m2 |
| qr″ | right-side heat flux | W/m2 |
| T | temperature | K |
| Tml | liquidus temperature | K |
| Tm | melting temperature | K |
| Tms | solidus temperature | K |
| T∞ | inner ambient temperature | K |
| u | x-component velocity | m/s |
| v | y-component velocity | m/s |
| x | axial direction | m |
| y | vertical direction | m |
| Greek symbols | ||
| thermal diffusivity | Kg/m·s | |
| β | thermal coefficient of expansion | K−1 |
| ΔHf | melting heat | J/K |
| μ | dynamic viscosity | Pa·s |
| ρ | density | Kg/m3 |
| τq | time period | s−1 |
References
- O’Connor, W.E.; Warzoha, R.; Weigand, R.; Fleischer, A.S.; Wemhoff, A.P. Thermal property prediction and measurement of organic phase change materials in the liquid phase near the melting point. Appl. Energy 2014, 132, 496–506. [Google Scholar] [CrossRef]
- O’Connor, W.E.; Wemhoff, A.P. Quantification of phase change material energy storage capability using multiphysics simulations. In International Electronic Packaging Technical Conference and Exhibition; American Society of Mechanical Engineers: San Francisco, CA, USA, 2015; Volume 56888, p. V001T09A065. [Google Scholar] [CrossRef]
- European Association for Storage of Energy. Available online: https://ease-storage.eu/wp-content/uploads/2023/09/2023.09.26-Thermal-Energy-Storage_for-distribution.pdf (accessed on 3 July 2025).
- Sarbu, I.; Sebarchievici, C. A comprehensive review of thermal energy storage. Sustainability 2018, 10, 191. [Google Scholar] [CrossRef]
- Tay, N.H.; Liu, M.; Belusko, M.; Bruno, F. Review on transportable phase change material in thermal energy storage systems. Renew. Sustain. Energy Rev. 2017, 75, 264–277. [Google Scholar] [CrossRef]
- Tehrmtest Instruments. Available online: https://thermtest.com/phase-change-material-pcm#:~:text=There%20are%203%20types%20of,paraffin%20compounds%20or%20fatty%20acids%20 (accessed on 3 July 2025).
- PCM Products. Available online: https://www.pcmproducts.net/Phase-Change-Material-Solutions.htm (accessed on 3 July 2025).
- Jian-you, L. Numerical and experimental investigation for heat transfer in triplex concentric tube with phase change material for thermal energy storage. Sol. Energy 2008, 82, 977–985. [Google Scholar] [CrossRef]
- Veerappan, M.; Kalaiselvam, S.; Iniyan, S.; Goic, R. Phase change characteristic study of spherical PCMs in solar energy storage. Sol. Energy 2009, 83, 1245–1252. [Google Scholar] [CrossRef]
- Hoshi, A.; Mills, D.R.; Bittar, A.; Saitoh, T.S. Screening of high melting point phase change materials (PCM) in solar thermal concentrating technology based on CLFR. Sol. Energy 2005, 79, 332–339. [Google Scholar] [CrossRef]
- Trp, A. An experimental and numerical investigation of heat transfer during technical grade paraffin melting and solidification in a shell-and-tube latent thermal energy storage unit. Sol. Energy 2005, 79, 648–660. [Google Scholar] [CrossRef]
- Medina, M.A.; King, J.B.; Zhang, M. On the heat transfer rate reduction of structural insulated panels (SIPs) outfitted with phase change materials (PCMs). Energy 2008, 33, 667–678. [Google Scholar] [CrossRef]
- Kenisarin, M.; Mahkamov, K. Solar energy storage using phase change materials. Renew. Sustain. Energy Rev. 2007, 11, 1913–1965. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, B.; Zhang, S. Organic, cross-linking, and shape-stabilized solar thermal energy storage materials: A reversible phase transition driven by broadband visible light. Appl. Energy 2014, 113, 59–66. [Google Scholar] [CrossRef]
- Neeper, D.A. Thermal dynamics of wallboard with latent heat storage. Sol. Energy 2000, 68, 393–403. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, Y.; Zhang, Q.; Lin, K.; Di, H. Performance of a hybrid heating system with thermal storage using shape-stabilized phase-change material plates. Appl. Energy 2007, 84, 1068–1077. [Google Scholar] [CrossRef]
- Athienitis, A.K.; Liu, C.; Hawes, D.; Banu, D.; Feldman, D. Investigation of the thermal performance of a passive solar test-room with wall latent heat storage. Build. Environ. 1997, 32, 405–410. [Google Scholar] [CrossRef]
- Zhu, N.; Ma, Z.; Wang, S. Dynamic characteristics and energy performance of buildings using phase change materials: A review. Energy Convers. Manag. 2009, 50, 3169–3181. [Google Scholar] [CrossRef]
- Diaconu, B.M.; Cruceru, M. Novel concept of composite phase change material wall system for year-round thermal energy savings. Energy Build. 2010, 42, 1759–1772. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Castellón, C.; Nogués, M.; Medrano, M.; Leppers, R.; Zubillaga, O. Use of microencapsulated PCM in concrete walls for energy savings. Energy Build. 2007, 39, 113–119. [Google Scholar] [CrossRef]
- Castellón, C.; Medrano, M.; Roca, J.; Cabeza, L.F.; Navarro, M.E.; Fernández, A.I.; Lázaro, A.; Zalba, B. Effect of microencapsulated phase change material in sandwich panels. Renew. Energy 2010, 35, 2370–2374. [Google Scholar] [CrossRef]
- Eddhahak-Ouni, A.; Drissi, S.; Colin, J.; Neji, J.; Care, S. Experimental and multi-scale analysis of the thermal properties of Portland cement concretes embedded with microencapsulated Phase Change Materials (PCMs). Appl. Therm. Eng. 2014, 64, 32–39. [Google Scholar] [CrossRef]
- Li, M.; Wu, Z.; Tan, J. Heat storage properties of the cement mortar incorporated with composite phase change material. Appl. Energy 2013, 103, 393–399. [Google Scholar] [CrossRef]
- Weinstein, R.D.; Kopec, T.C.; Fleischer, A.S.; D’Addio, E.; Bessel, C.A. The experimental exploration of embedding phase change materials with graphite nanofibers for the thermal management of electronics. J. Heat Transf. 2008, 130, 042405. [Google Scholar] [CrossRef]
- Garimella, S.V.; Fleischer, A.S.; Murthy, J.Y.; Keshavarzi, A.; Prasher, R.; Patel, C.; Bhavnani, S.H.; Venkatasubramanian, R.; Mahajan, R.; Joshi, Y.; et al. Thermal challenges in next-generation electronic systems. IEEE Trans. Compon. Packag. Technol. 2008, 31, 801–815. [Google Scholar] [CrossRef]
- Garimella, S.V. Advances in mesoscale thermal management technologies for microelectronics. Microelectron. J. 2006, 37, 1165–1185. [Google Scholar] [CrossRef]
- Bianco, V.; De Rosa, M.; Vafai, K. Phase-change materials for thermal management of electronic devices. Appl. Therm. Eng. 2022, 214, 118839. [Google Scholar] [CrossRef]
- Kandasamy, R.; Wang, X.Q.; Mujumdar, A.S. Application of phase change materials in thermal management of electronics. Appl. Therm. Eng. 2007, 27, 2822–2832. [Google Scholar] [CrossRef]
- Sikiru, S.; Oladosu, T.L.; Amosa, T.I.; Kolawole, S.Y.; Soleimani, H. Recent advances and impact of phase change materials on solar energy: A comprehensive review. J. Energy Storage 2022, 53, 105200. [Google Scholar] [CrossRef]
- Javadi, F.S.; Metselaar, H.S.; Ganesan, P.J. Performance improvement of solar thermal systems integrated with phase change materials (PCM), a review. Sol. Energy 2020, 206, 330–352. [Google Scholar] [CrossRef]
- Ismail, K.A.; Lino, F.A.; Machado, P.L.; Teggar, M.; Arıcı, M.; Alves, T.A.; Teles, M.P. New potential applications of phase change materials: A review. J. Energy Storage 2022, 53, 105202. [Google Scholar] [CrossRef]
- Faraj, K.; Khaled, M.; Faraj, J.; Hachem, F.; Castelain, C. Phase change material thermal energy storage systems for cooling applications in buildings: A review. Renew. Sustain. Energy Rev. 2020, 119, 109579. [Google Scholar] [CrossRef]
- Mahdaoui, M.; Hamdaoui, S.; Ait Msaad, A.; Kousksou, T.; El Rhafiki, T.; Jamil, A.; Ahachad, M. Building bricks with phase change material (PCM): Thermal performances. Constr. Build. Mater. 2021, 269, 121315. [Google Scholar] [CrossRef]
- Hawes, D.W.; Banu, D.; Feldman, D. Latent heat storage in concrete. Sol. Energy Mater. 1989, 19, 335–348. [Google Scholar] [CrossRef]
- Memon, S.A. Phase change materials integrated in building walls: A state of the art review. Renew. Sustain. Energy Rev. 2014, 31, 870–906. [Google Scholar] [CrossRef]
- Zhu, N.; Li, S.; Hu, P.; Wei, S.; Deng, R.; Lei, F. A review on applications of shape-stabilized phase change materials embedded in building enclosure in recent ten years. Sustain. Cities Soc. 2018, 43, 251–264. [Google Scholar] [CrossRef]
- Benyahia, I.; Abderrahmane, A.; Khetib, Y.; AAlazwari, M.; Younis, O.; Belazreg, A.; Laouedj, S. Enhancing Phase Change Material Efficiency in Wavy Trapezoidal Cavities: A Numerical Investigation of Nanoparticle Additives. Physics 2025, 7, 17. [Google Scholar] [CrossRef]
- Shaban, M.; Khan, T.I.; Anwar, M.; Alzaid, M.; Alanazi, R. Effect of asymmetric fins on thermal performance of phase change material-based thermal energy storage unit. Materials 2023, 16, 2567. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Q.; Wu, M.; Du, P.; Liu, C.; Rao, Z. Thermal properties optimization of lauric acid as phase change material with modified boron nitride nanosheets-sodium sulfate for thermal energy storage. J. Energy Storage 2023, 6, 106781. [Google Scholar] [CrossRef]
- Zhang, G.; Sun, Y.; Wu, C.; Yan, X.; Zhao, W.; Peng, C. Low-cost and highly thermally conductive lauric acid–paraffin–expanded graphite multifunctional composite phase change materials for quenching thermal runaway of lithium-ion battery. Energy Rep. 2023, 9, 2538–2547. [Google Scholar] [CrossRef]
- Ishak, S.; Mandal, S.; Lee, H.S.; Singh, J.K. pH-controlled synthesis of sustainable lauric acid/SiO2 phase change material for scalable thermal energy storage. Sci. Rep. 2021, 11, 15012. [Google Scholar]
- Jalghaf, H.K.; Kovács, E. Simulation of phase change materials in building walls using effective heat capacity model by recent numerical methods. J. Energy Storage 2024, 83, 110669. [Google Scholar] [CrossRef]
- Warzoha, R.J.; Weigand, R.M.; Fleischer, A.S. Temperature-dependent thermal properties of a paraffin phase change material embedded with herringbone style graphite nanofibers. Appl. Energy 2015, 137, 716–725. [Google Scholar] [CrossRef]
- Gau, C.; Viskanta, R.C. Melting and solidification of a pure metal on a vertical wall. J. Heat Transf. 1986, 108, 174–181. [Google Scholar] [CrossRef]
- O’Connor, W.E. Predictions of Phase Change Material Thermal Efficiency Using Multiscale Analysis. Master’s Thesis, Villanova University, Villanova, PA, USA, 2015. [Google Scholar]
- White, F.M.; Majdalani, J. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 2006; Volume 3, pp. 433–434. [Google Scholar]
- Nikitin, E.D.; Pavlov, P.A.; Bessonova, N.V. Critical constants of n-alkanes with from 17 to 24 carbon atoms. J. Chem. Thermodyn. 1994, 26, 177–182. [Google Scholar] [CrossRef]
- CAMEO Chemicals. Database of Hazardous Materials; National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 2013. [Google Scholar]
- National Institutes of Health. PubChem; National Institutes of Health: Bethesda, MD, USA, 2013. [Google Scholar]
- Weast, R.C.; Graselli, J.G. CRC Handbook of Data on Organic Compounds, 2nd ed.; CRC Press, Inc: Boca Raton, FL, USA, 1989. [Google Scholar]
- LookChem. LookChem; LookChem: Hangzhou, China, 2013. [Google Scholar]
- Domalski, E.S.; Hearing, E.D. Heat capacities and entropies of organic compounds in the condensed phase. Volume III. J. Phys. Chem. Ref. Data 1996, 25, 1–525. [Google Scholar] [CrossRef]
- Jalal, I.M.; Zografi, G.; Rakshit, A.K.; Gunstone, F.D. Thermal analysis of fatty acids. Chem. Phys. Lipids 1982, 31, 395–404. [Google Scholar] [CrossRef]
- Grodzka, P.G. Study of Phase-Change Materials for a Thermal Control System; Huntsville, A., Ed.; Lockheed Missiles & Space Company: Sunnyvale, CA, USA, 1970. [Google Scholar]




| Property | Symbol | Value | Units |
|---|---|---|---|
| Density | ρ | 772 | kg/m3 |
| Thermal Specific Heat | Cp | 2390 | J/kg·K |
| Thermal Conductivity | k | 0.145 | W/m·K |
| Dynamic Viscosity | μ | 0.008 | kg/m·s |
| Thermal Coefficient of Expansion | β | 0.0005 | K−1 |
| Melting Heat | ΔHf | 295,000 | J/kg |
| Solidus Temperature | Tms | 311.5 | K |
| Liquidus Temperature | Tml | 312.5 | K |
| First-Day Run | Second-Day Run | |||
|---|---|---|---|---|
| Average parameters on right side along edge | 50 × 50 | 100 × 100 | 50 × 50 | 100 × 100 |
| Temperature, average error % compared to 200 × 200 | 0.4684% | 0.2473% | 0.4877% | 0.2490% |
| Efficiency, average error % compared to 200 × 200 | 0.04651% | 0.02765% | 0.05795% | 0.03083% |
| First-Day Run | Second-Day Run | |||
|---|---|---|---|---|
| Average parameters on right side along edge | 10 s | 5 s | 10 s | 5 s |
| Temperature, average error % compared to 3 s | 0.3235% | 0.04177% | 0.3388% | 0.05028% |
| Efficiency, average error % compared to 3 s | 0.04130% | 0.005230% | 0.04372% | 0.006251% |
| Error Compared to 4th-Day Results | |||
|---|---|---|---|
| Average parameters on right-hand side along edge | First day | Second day | Third day |
| Temperature, average error % compared to 4th day | 0.1763% | 0.01080% | 0.001704% |
| Heat transfer rate, average error % compared to 4th day | 26.58% | 0.1007% | 0.003386% |
| Efficiency, average error % compared to 4th day | 0.0009194% | 0.00006136% | 0.00000181% |
| Property | Symbol | Value | Units |
|---|---|---|---|
| Liquid density | ρ | 6093 | Kg/m3 |
| Mass-based specific heat | Cp | 381.5 | J/kg·K |
| Thermal conductivity | k | 32.0 | W/m·K |
| Dynamic viscosity | μ | 1.81 × 10−3 | Pa.s |
| Thermal coefficient of expansion | β | 1.2 × 10−4 | K−1 |
| Latent heat of fusion | ΔHf | 80.16 | kJ/kg |
| Melting temperature | Tm | 302.93 | K |
| PCM | Tm (K) | ρ (kg/m3) | Cp (kJ/kg·K) | K (W/m·K) | ΔHf (kJ/kg) |
|---|---|---|---|---|---|
| Heneicosane | 312 | 772 | 2.39 | 0.145 | 295 |
| Tricosane | 319 | 778 | 2.18 | 0.124 | 303 |
| Tetracosane | 323 | 774 | 2.92 | 0.137 | 208 |
| Oleic Acid | 287 | 871 | 1.74 | 0.103 | 140 |
| Linoleic Acid | 265 | 902 | 1.92 | 0.087 | 170 |
| Energy W/m2 | Linoleic Acid | Heneicosane | Oleic Acid | Tetracosane | Tricosane |
|---|---|---|---|---|---|
| Em | 39,054.34 | 31,667.62 | 42,228.67 | 36,582.22 | 31,020.95 |
| Es | −35,404.06 | −31,253.53 | −404,73.03 | −36,508.74 | −28,189.34 |
| Difference | 3650.28 | 414.09 | 1755.64 | 73.48 | 2831.61 |
| % (Em − Es) × 100/Es | 10.31% | 1.32% | 4.34% | 0.20% | 10.04% |
| Energy W/m2 | qo = 200 | qo = 250 | qo = 300 | qo = 350 | qo = 400 |
|---|---|---|---|---|---|
| Em | 31,667.62 | 44,176.07 | 57,136 | 70,161.63 | 83,619.01 |
| Es | −31,253.5 | −41,708.4 | −52,170.2 | −62,864.6 | −73,635 |
| Difference | 414.09 | 2467.632 | 4965.755 | 7296.996 | 9983.967 |
| % (Em − Es) × 100/Es | 1.32% | 5.92% | 9.52% | 11.61% | 13.56% |
| Energy W/m2 | t/Tq = 0.75 | t/Tq = 0.875 | t/Tq = 1.0 | t/Tq = 1.125 | t/Tq = 1.25 |
|---|---|---|---|---|---|
| Em | 16,290.54 | 27,036.66 | 31,667.62 | 25,749.34 | 18,623.55 |
| Es | −46,114.85 | −38,710.06 | −31,253.53 | −24,570.23 | −19,233.81 |
| Difference | −29,824.30 | −11,673.40 | 414.09 | 1179.11 | −610.26 |
| % (Em − Es) × 100/Es | −64.67% | −30.16% | 1.32% | 4.80% | −3.17% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gari, A.A. Modeling Thermal Energy Storage Capability of Organic PCMs Confined in a 2-D Cavity. Computation 2025, 13, 209. https://doi.org/10.3390/computation13090209
Gari AA. Modeling Thermal Energy Storage Capability of Organic PCMs Confined in a 2-D Cavity. Computation. 2025; 13(9):209. https://doi.org/10.3390/computation13090209
Chicago/Turabian StyleGari, Abdullatif A. 2025. "Modeling Thermal Energy Storage Capability of Organic PCMs Confined in a 2-D Cavity" Computation 13, no. 9: 209. https://doi.org/10.3390/computation13090209
APA StyleGari, A. A. (2025). Modeling Thermal Energy Storage Capability of Organic PCMs Confined in a 2-D Cavity. Computation, 13(9), 209. https://doi.org/10.3390/computation13090209







