Constrained Nonlinear Control of Semi-Active Hydro-Pneumatic Suspension System
Abstract
1. Introduction
2. Vehicle Dynamics Modeling with Semi-Active Hydro-Pneumatic Suspension
2.1. Quarter Vehicle Dynamic Equations
2.2. Dynamic Equations Relative to Static Equilibrium Position
2.3. Static Stiffness and Equivalent Damping Coefficient
3. Nonlinear Control of Semi-Active Hydro-Pneumatic Suspension System
3.1. Dynamic Equation for Nonlinear Term Minimization
3.2. State Space Equations of the System with Road Random Inputs
3.3. Linear Quadratic Optimal Control Under Ride Comfort Indexes
3.4. Constrained Optimization Model for Optimal Control
- (1)
- Design variable: A03, which represents the effective acting area of the controllable damping valve at each moment.
- (2)
- Objective function:
- (3)
- Constraint condition: .
4. Simulation of Hydro-Pneumatic Suspension Control System
4.1. Dynamic Simulation Parameters of the Suspension System
4.2. Simulation Settings and Results of Four Control Systems
- (1)
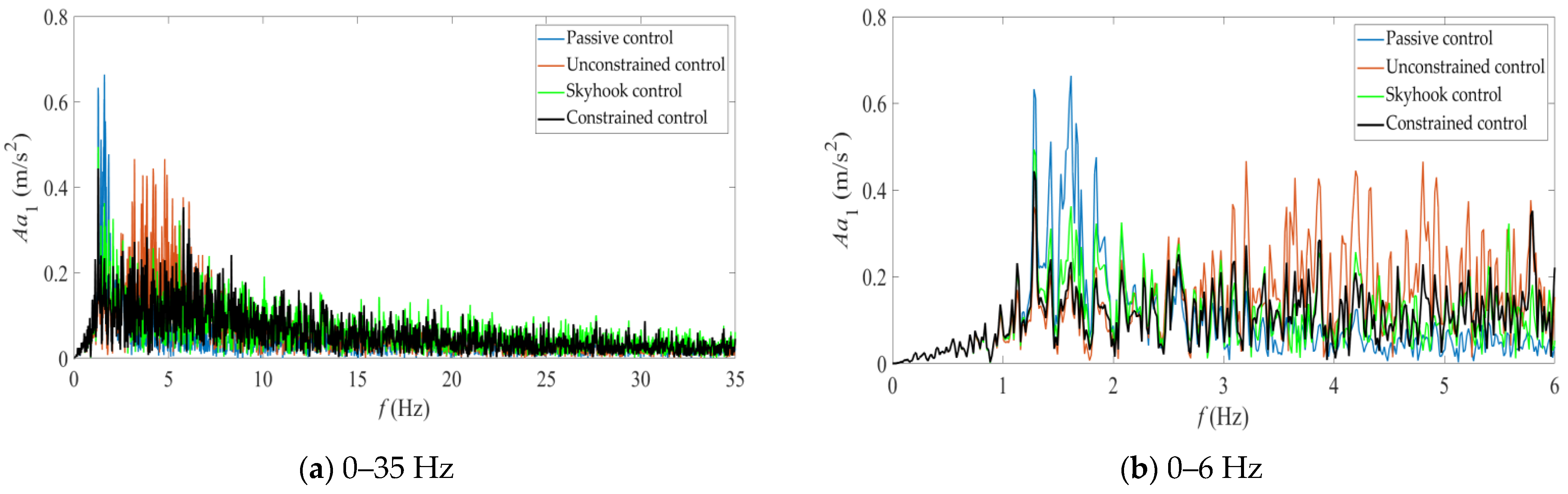
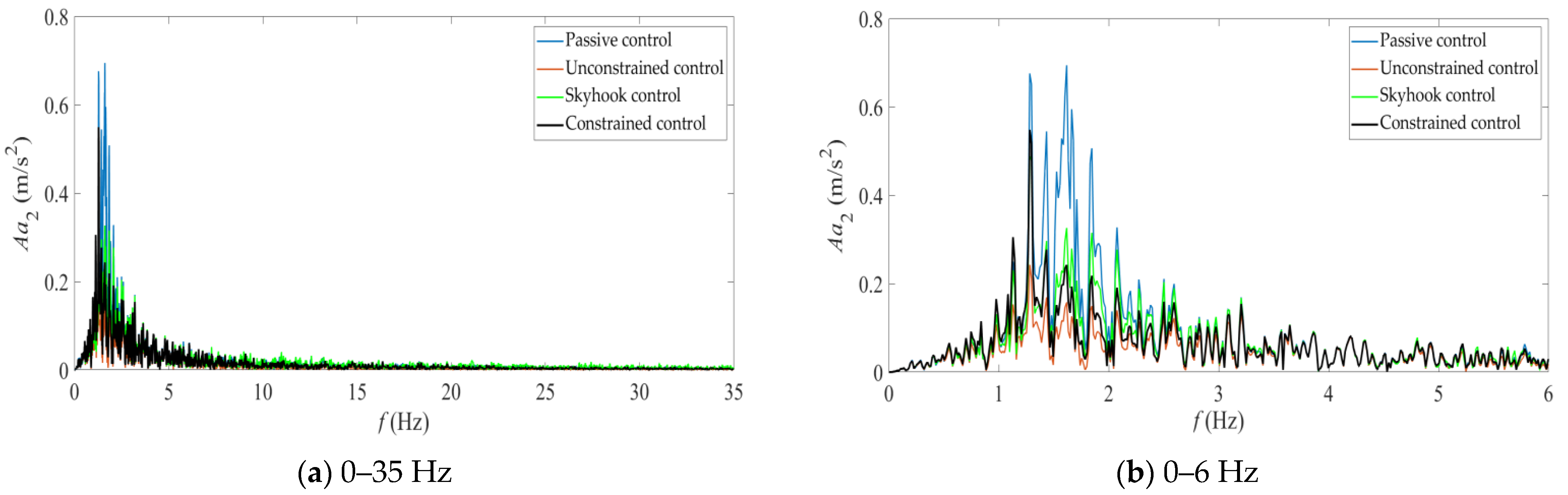
- Passive control. It refers to the situation when the controllable damping valve is closed, i.e., A03 is constantly equal to 0.
- (2)
- Unconstrained control. The difference between it and the constrained semi-active hydro-pneumatic suspension is that its actuation capability is not constrained (or its actuation capability is relatively large), which means that the system can provide an actuation force of any magnitude at each moment and can achieve the desired overall control force (i.e., u = uopt). In this case, such a controller degenerates into a linear quadratic optimal control. For the convenience of comparison, this paper presents the simulation results of the unconstrained semi-active hydro-pneumatic suspension nonlinear control.
- (3)
- Skyhook control. Skyhook damping control mainly realizes an “on-off” switch control mode through a two-state damping, and the control algorithm can be referred to in reference [30]. It has the advantages of simple control law and good effect, and is one of the most commonly used suspension control strategies in commercial vehicles at present.
- (4)
- Constrained control. The “constrained control” mentioned in this section is the abbreviation of the nonlinear control method proposed in this paper for the semi-active suspension system.
5. Analysis of Simulation Results for Hydro-Pneumatic Suspension Control
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wagh, R.R. A Review on Controlling Methods for Semi-Active Suspension Systems. Int. J. Res. Appl. Sci. Eng. 2024, 12, 3188–3193. [Google Scholar] [CrossRef]
- Ni, F.; Luo, Y.; Xu, J.; Liu, D.; Sun, Y.; Ji, W. Review of Fault-Tolerant Control Methods for Suspension Systems: From Road Vehicles to Maglev Trains. Mathematics 2024, 12, 2576. [Google Scholar] [CrossRef]
- Wang, X.; Huang, D.; Qin, N.; Chen, C.; Zhang, K. Modeling and Second-Order Sliding Mode Control for Lateral Vibration of High-Speed Train With MR Dampers. IEEE Trans. Intell. Transp. Syst. 2022, 23, 10299–10308. [Google Scholar] [CrossRef]
- Ab Talib, M.H.; Muhammad Afandi, M.A.D.; Mat Darus, I.Z.; Mohd Yatim, H.; Asus, Z.; Mohd Yamin, A.H.; Hadi, M.S. Magnetorheological Damper Control for Semi-Active Suspension System Using Skyhook-Differential Evolution. In Lecture Notes in Electrical Engineering; Springer: Singapore, 2021; pp. 161–171. [Google Scholar] [CrossRef]
- Kumar, S.; Chandramohan, S.; Sujatha, S. Geometric Optimization of Magnetorheological Damper for Prosthetic Ankles Using Artificial Neural Networks. Mechatronics 2024, 98, 103108. [Google Scholar] [CrossRef]
- Saglam, F.; Unlusoy, Y.S. Adaptive ride comfort and attitude control of vehicles equipped with active hydro-pneumatic suspension. Int. J. Veh. Des. 2016, 71, 31–51. [Google Scholar] [CrossRef]
- Soh, M.; Jang, H.; Park, J.; Sohn, Y.; Park, K. Development of Preview Active Suspension Control System and Performance Limit Analysis by Trajectory Optimization. Int. J. Automot. Technol. 2018, 19, 1001–1012. [Google Scholar] [CrossRef]
- Brezas, P.; Smith, M.C.; Hoult, W. A Clipped-Optimal Control Algorithm for Semi-Active Vehicle Suspensions: Theory and Experimental Evaluation. Automatica 2015, 53, 188–194. [Google Scholar] [CrossRef]
- Sun, Q.; Yin, C.; Wang, B. Experimental Validation of Truck Cab Suspension Model and Ride Comfort Improvement under Various Semi-Active Control Strategies. Processes 2024, 12, 1880. [Google Scholar] [CrossRef]
- Likaj, R.; Shala, A. Optimisation and Control of Vehicle Suspension Using Linear Quadratic Gaussian Control. Stroj. časopis-J. Mech. Eng. 2018, 68, 61–68. [Google Scholar] [CrossRef]
- Shehata Gad, A. Preview Model Predictive Control Controller for Magnetorheological Damper of Semi-Active Suspension to Improve Both Ride and Handling. SAE Int. J. Veh. Dyn. Stab. NVH 2020, 4, 305–326. [Google Scholar] [CrossRef]
- Yang, L.; Wang, R.; Ding, R.; Liu, W.; Zhu, Z. Investigation on the Dynamic Performance of a New Semi-Active Hydro-Pneumatic Inerter-Based Suspension System with MPC Control Strategy. Mech. Syst. Signal Process. 2021, 154, 107569. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, R.; Yang, L.; Sun, Z.; Meng, X. Modelling and Control of a Semi-Active Dual-Chamber Hydro-Pneumatic Inerter-Based Suspension System. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2355–2370. [Google Scholar] [CrossRef]
- Wang, G.; Deng, J.; Duan, D.; Zhou, T.; Liu, S. Constrained H∞ Optimal Control for Nonlinear Active Suspensions Via Data-Driven Reinforcement Learning Algorithm. J. Comput. Nonlinear Dyn. 2025, 20, 071007. [Google Scholar] [CrossRef]
- Jibril, M.; Tadese, M.; Hassen, N. Nonlinear Active Suspension System Based on Fuzzy Model Predictive Controller. J. Eng. Appl. Sci. 2021, 16, 289–295. [Google Scholar] [CrossRef]
- Shi, J.-W.; Li, X.-W.; Zhang, J.-W. Feedback Linearization and Sliding Mode Control for Active Hydropneumatic Suspension of a Special-Purpose Vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2009, 224, 41–53. [Google Scholar] [CrossRef]
- Hao, R.; Wang, H.; Liu, S.; Yang, M.; Tian, Z. Multi-Objective Command Filtered Adaptive Control for Nonlinear Hydraulic Active Suspension Systems. Nonlinear Dyn. 2021, 105, 1559–1579. [Google Scholar] [CrossRef]
- Hu, Y.M.; Li, Y.N.; Zheng, L. Hybrid control of electromagnetic active suspension based on nonlinear actuators. China Mech. Eng. 2022, 33, 134–142. [Google Scholar]
- Pan, H.; Sun, W.; Zhang, J.; Yan, S.; Lin, W. Adaptive Event-Triggered Control for Vehicle Active Suspension Systems With State Constraints. IFAC-Pap. 2018, 51, 955–960. [Google Scholar] [CrossRef]
- Yan, S.; Sun, W.; Xia, Y. A Joint Fault-Tolerant and Fault Diagnosis Strategy for Multiple Actuator Faults of Full-Vehicle Active Suspension Systems. IEEE Trans. Automat. Sci. Eng. 2025, 22, 1928–1940. [Google Scholar] [CrossRef]
- Feng, Z.; Li, R.-B.; Jing, X. Neuroadaptive Control for Active Suspension Systems With Time-Varying Motion Constraints: A Feasibility-Condition-Free Method. IEEE Trans. Cybern. 2024, 54, 287–297. [Google Scholar] [CrossRef] [PubMed]
- Yan, G.; Zou, H.-X.; Wang, S.; Zhao, L.-C.; Wu, Z.-Y.; Zhang, W.-M. Bio-Inspired Vibration Isolation: Methodology and Design. Appl. Mech. Rev. 2021, 73, 020801. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, M.; Huang, J.; Mohammed, S. Load-Transfer Suspended Backpack With Bioinspired Vibration Isolation for Shoulder Pressure Reduction Across Diverse Terrains. IEEE Trans. Robot. 2025, 41, 3059–3077. [Google Scholar] [CrossRef]
- Pan, H.; Jing, X.; Sun, W.; Gao, H. A Bioinspired Dynamics-Based Adaptive Tracking Control for Nonlinear Suspension Systems. IEEE Trans. Contr. Syst. Technol. 2018, 26, 903–914. [Google Scholar] [CrossRef]
- Bosso, N.; Zampieri, N.; Somà, A.; Mocera, F.; Conte, E. Simulation of a Hydropneumatic Suspension for Agricultural Working Vehicles. In Advances in Mechatronics and Mechanical Engineering; IGI Global: Hershey, PA, USA, 2021; pp. 268–287. [Google Scholar] [CrossRef]
- Yin, Y.; Rakheja, S.; Yang, J.; Boileau, P.-E. Characterization of a Hydro-Pneumatic Suspension Strut with Gas-Oil Emulsion. Mech. Syst. Signal Process. 2018, 106, 319–333. [Google Scholar] [CrossRef]
- Dong, M.M.; Bian, N. Military Vehicle Suspension Design; Beijing Institute of Technology Press: Beijing, China, 2016; pp. 76–99. [Google Scholar]
- Zhang, Y.; Li, M.; Zhang, Y.; Hu, Z.; Sun, Q.; Lu, B. An Enhanced Adaptive Unscented Kalman Filter for Vehicle State Estimation. IEEE Trans. Instrum. Meas. 2022, 71, 6502412. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. Lyapunov Exponent Sign Reversal: Stability and Instability by the First Approximation. In Nonlinear Systems and Complexity; Springer International Publishing: Cham, Switzerland, 2013; pp. 41–77. [Google Scholar] [CrossRef]
- Aljarbouh, A.; Fayaz, M.; Qureshi, M.S.; Boujoudar, Y. Hybrid Sliding Mode Control of Full-Car Semi-Active Suspension Systems. Symmetry 2021, 13, 2442. [Google Scholar] [CrossRef]




| Name | Symbol | Value | Unit | Name | Symbol | Value | Unit |
|---|---|---|---|---|---|---|---|
| Vehicle speed | v | 20 | km/h | Equivalent diameter of the controllable damping valve | d03 | 0~20.00 | mm |
| Unsprung mass | mw | 1780 | kg | Flow coefficient | Cd | 0.62 | - |
| Tire stiffness | kt | 1150 | kN/m | Polytropic exponent of gas | r | 1.444 | - |
| Tire damping | ct | 3 | kN·s/m | Pipe diameter | Dp | 0.012 | m |
| Sprung mass | mb | 8745 | kg | Pipe length | Lp | 0.180 | m |
| Road grade | - | Class D | - | Accumulator outlet area | Sa | 113.10 | mm2 |
| Oil density | ρ | 860 | kg/m3 | Local pressure loss coefficient | ζ | 0.960 | - |
| Cylinder inner diameter | D | 190 | mm | Coefficient of pressure loss along the way | λ | 0.049 | - |
| Piston rod outer diameter | d | 150 | mm | Weight of tire dynamic deflection | q1 | 200 | - |
| Gas pressure under static equilibrium | P1 | 4.85 | MPa | Weight of suspension dynamic travel | q2 | 200 | - |
| Gas volume under static equilibrium | V1 | 2.5 | L | Weight of sprung mass acceleration | q3 | 1 | - |
| Equivalent diameter of normally open damping orifice | d01 | 6.00 | mm | Weight of the overall control force u | q4 | 0 | - |
| Equivalent diameter of one-way valve | d02 | 6.00 | mm |
| Control Method | Unsprung Mass Acceleration (a1) | Sprung Mass Acceleration (a2) | Suspension Working Stroke (SWS) | Dynamic Tire Load (DTL) | |
|---|---|---|---|---|---|
| Root Mean Square value | Passive control | 2.104 | 1.434 | 5.716 | 15.918 |
| Unconstrained control | 2.613 | 0.620 | 7.899 | 8.379 | |
| Skyhook control | 2.508 | 1.023 | 5.965 | 11.653 | |
| Constrained control | 2.410 | 0.910 | 7.276 | 10.244 | |
| Minimum value | Passive control | −10.124 | −7.175 | −22.936 | −71.846 |
| Unconstrained control | −10.540 | −2.153 | −27.293 | −34.376 | |
| Skyhook control | −27.465 | −6.133 | −19.277 | −51.865 | |
| Constrained control | −13.702 | −3.577 | −20.572 | −39.111 | |
| Maximum value | Passive control | 9.137 | 6.516 | 6.916 | 77.253 |
| Unconstrained control | 10.595 | 2.135 | 28.104 | 32.421 | |
| Skyhook control | 24.136 | 4.380 | 21.927 | 53.162 | |
| Constrained control | 9.788 | 3.469 | 26.600 | 41.267 | |
| Unit | m/s2 | m/s2 | mm | kN | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, B.; Jettanasen, C. Constrained Nonlinear Control of Semi-Active Hydro-Pneumatic Suspension System. Computation 2025, 13, 206. https://doi.org/10.3390/computation13090206
Qiu B, Jettanasen C. Constrained Nonlinear Control of Semi-Active Hydro-Pneumatic Suspension System. Computation. 2025; 13(9):206. https://doi.org/10.3390/computation13090206
Chicago/Turabian StyleQiu, Biao, and Chaiyan Jettanasen. 2025. "Constrained Nonlinear Control of Semi-Active Hydro-Pneumatic Suspension System" Computation 13, no. 9: 206. https://doi.org/10.3390/computation13090206
APA StyleQiu, B., & Jettanasen, C. (2025). Constrained Nonlinear Control of Semi-Active Hydro-Pneumatic Suspension System. Computation, 13(9), 206. https://doi.org/10.3390/computation13090206






