A Method for the Solution of Certain Non-Linear Problems of Combined Seagoing Main Engine Performance and Fixed-Pitch Propeller Hydrodynamics with Imperative Assignment Statements and Streamlined Computational Sequences
Abstract
1. Introduction
1.1. Approximate Representation [1] of the Thermo-Fluid and Frictional Processes of the Main Engines in Terms of FOC and of the Hydrodynamic Performance in Terms of FPP’s Shaft Propulsive Power and Rotational Speed, Applicable to Standard Vessels Under Actual Seagoing Conditions
1.1.1. The Thermo-Fluid and Frictional Processes of the Main Engines of Standard Vessels Under Actual Seagoing Conditions (Also See Section 2.2)
- (1.1.1)
- The engine power, P;
- (1.1.2)
- The engine rotational speed, r;
- (1.1.3)
- The engine rotational acceleration, if any, dr/dt;
- (1.1.4)
1.1.2. The Hydrodynamic Performance of Standard Vessels Under Actual Seagoing Conditions (See Also Section 2.1)
- (1.2.1)
- The applicable reference (correction) parameters, specifically referring to the ambient, meteorological and oceanographic, environmental, reference, ideal, still air and water, conditions and ship-tracking data pursuant to Section 2.1.2, Correlation Scheme #2, and Section 2.3, “Big data” set, and the specific vessel’s hydrostatic conditions pursuant to Section 2.1.4, Correlation Scheme #4;
- (1.2.2)
- The vessel’s TTW (through-the-water) speed (or simply, the log-speed) in the vessel’s forward direction, TTWSFD;
- (1.2.3)
- Either of the following:
- (1.2.3.1)
- The FPP shaft’s rotational speed, r;
- (1.2.3.2)
- The actual ambient, meteorological, and oceanographic environmental conditions and ship-tracking data pursuant to Section 2.1.1, Correlation Scheme #1, and Section 2.3, “Big data” set, and the specific vessel’s service margin pursuant to Section 2.1.3, Correlation Scheme #3.
2. Materials and Methods
2.1. The Fixed-Pitch (Screw) Marine Propulsion Approximating Functional [1] System
2.1.1. Correlation Scheme #1
2.1.2. Correlation Scheme #2
2.1.3. Correlation Scheme #3
2.1.4. Correlation Scheme #4
2.1.5. Sea Margin, Speed Loss, Light Running Margin, Sea Running Margin, Apparent TTW Slip
- (a)
- The above shaft power ratio when considered to sustain the same “ideal” conditions, TTWSFD, decreased by one (or by 100% if calculated as a percentage), is defined as the sea margin.
- (b)
- The above shaft power ratio, when considered to sustain the same “ideal” conditions shaft rotational speed, r, decreased by one (or by 100% if calculated as a percentage), is defined as the sea running margin.
- (c)
- The light running margin is defined as the reduction percentage (%) of the shaft rotational speed, r, under “ideal conditions”, required to sustain the same “ideal” FPP’s shaft power; the light running margin is common for, and representative of, steady (fixed) sea margin and/or sea running margin values, for any given value of the FPP’s shaft power.
- (d)
- The speed loss is defined as the reduction (%) in the “ideal” conditions, TTWSFD, necessary to sustain the same “ideal” FPP’s shaft power. It is representative of steady (fixed) sea margin and/or sea running margin values for any given value of the FPP’s shaft power. Regarding the different meanings of the term speed loss in the marine industry [56,57,58,59,60,61,62,63,64,65,124,125], in conjunction with the relevant discussion on the steady rotational speed, r, of the main engine, the shaft and the FPP, more details are available in Appendix F.
- (e)
- The above dimensionless indexes (sea margin, sea running margin, light running margin, and speed loss) are all interrelated, meaning that when one of them is determined, the other three are determined as well. Furthermore, they may be, either individually or together, comprehensively defined based on the above actual, non-ideal, conditions. The above are not referred to in a trivial manner: instead, they are of particular value and significance as different researchers and different stakeholders report their relevant observations, conclusions, and data in terms of different indexes among those discussed in (a)–(d) above, (f) below, and in other contexts.
- (f)
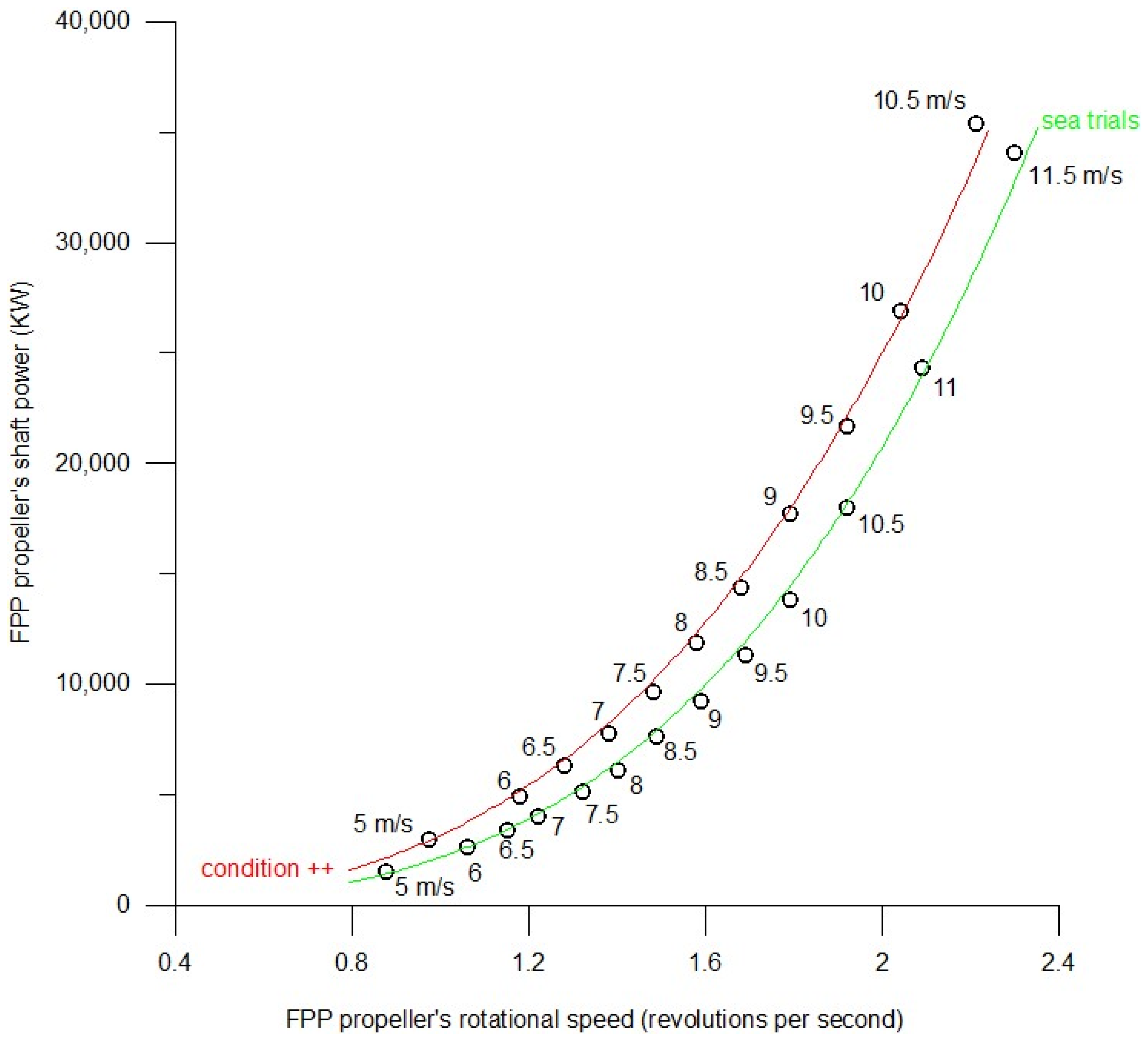
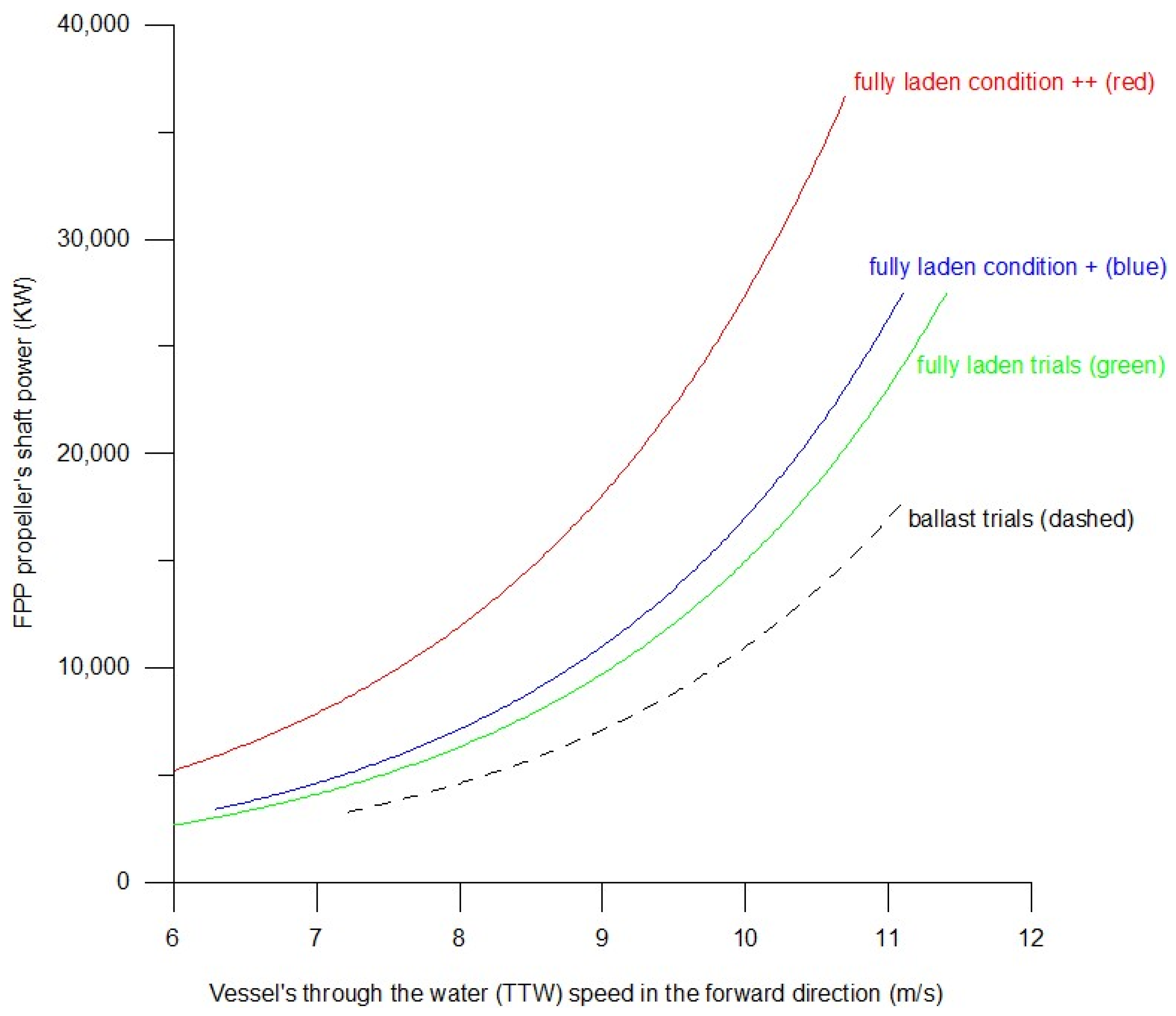
- One (1, unity) minus the dimensionless apparent TTW slip is a ship specific dimensionless ratio of, TTWSFD to the FPP rotational speed, r; as such, it is heavily dependent on any or all of the above dimensionless indexes (sea margin, sea running margin, light running margin, and speed loss), with a slight only additional dependence on a proper dimensionless form of the FPP rotational speed, r. The above “apparent” designation is not a trivial one. It clarifies that the apparent TTW slip is calculated based on the vessel’s TTWSFD which as far as the FPP is concerned, is the “apparent” and not the “evident” velocity at which the water enters the FPP. More relevant information and technical background regarding the above “apparent” designation is available in Appendix E, in conjunction with the relevant points of Appendix Z. Figure 1 depicts the system of axes of the FPP’s rotational speed, r vs. the FPP’s shaft power, P, and three sets of curves:

- (g)
- The set of curves representing the steady (fixed) TTWSFD are depicted in Figure 1 (e.g., 13, 16, 19 and 22 knots).
- (h)
- The set of curves representing the steady (fixed) apparent TTW slip are shown in Figure 1 (e.g., −2%, 2%, 6% and 10%).
- (i)
- The, effectively, steady (fixed) weather conditions are also shown in Figure 1 (e.g., A: extremely good weather; B: average weather; and C: extremely bad weather; these are depicted, in green, blue and red, respectively).
- (j)
- The set of purely deterministic ones;
- (k)
- The set of hybrid, stochastic and deterministic, ones.

| 6 | 7 | 8h | 8H | 8n | 9h | 9H | 9n | 10 | 11 | 12h | 12H | 12n | 13h | 13H | 13n | 14h | 14H | 14n | 15 | 16 | 17 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | X | X | X | X | X | X | ||||||||||||||||
| 2 | X | X | X | X | X | X | X | X | X | |||||||||||||
| 3 | X | X | X | X | X | X | X | X | X | |||||||||||||
| 4 | X | X | X | X | X | X | X | X | X | X | X | X | ||||||||||
| 5 | X | X | X | X | X | X | X | X | X | X | ||||||||||||
| 6 | X | X | X | X | X | X | X | X | X | X | X | X | X | |||||||||
| 7 | X | X | X | X | X | X | X | X | X(b) | X | ||||||||||||
| 8 | X | X | X | X | X | X | X | X | X | X | X | X(b) | X | |||||||||
| 9 | X | X | X | X | X | X | X | X | X | X | X | X | X | |||||||||
| 10 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | ||||||
| 11 | X | X | X | X | X | X | X | X | X | X | X | X(b) | X | |||||||||
| 12 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X(b) | X | ||||||
| 13 | X | X | X | X | X | X | X | X | X | X | X | X(b) | X | |||||||||
| 14 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X(b) | X | ||||||
| 15 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X(b) | X | ||||||
| 16 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X(b) | X | |||
| 17 | X | X | X | X | X | X | ||||||||||||||||
| 18 | X | X | X | X | X | X | ||||||||||||||||
| 19 | X | X | X | X | X(b) | X | ||||||||||||||||
| 20 | X | X | X | X | X | X | X | X | X | X | ||||||||||||
| 21 | X | X | X | X | X | X | X | X(b) | X | |||||||||||||
| 22 | X | X | X | X | X | X | X | X | X(b) | X | ||||||||||||
| 23 | X | X | X | X | X | X | X | X | X | X | X | X(b) | X | |||||||||
| 24 | X | X | X | X | X | X | ||||||||||||||||
| 25 | X | X | X | X | X | X | ||||||||||||||||
| 26 | X | X | X(a) | X | X | X | ||||||||||||||||
| 27 | X | X | X | X | X | X | X | X | X | |||||||||||||
| 28 | X | X | X | X | X(a) | X | X | X | ||||||||||||||
| 29 | X | X | X | X | X | X(a) | X | X | X | |||||||||||||
| 30 | X | X | X | X | X | X | X | X(a) | X | X | X |
| 8n | 9n | 12h | 12n | 13h | 13n | 14h | 14n | 15 | x, y, z, … iaw eq. 11, 17 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Iobs + Lobs | (1.2.1); TTWSFD; (1.2.3.2) | ||||||||
| 2 | Iobs + Lobs | Iobs + Lobs | (1.2.1); TTWSFD; (1.2.3.2) | |||||||
| 3 | Iobs + Lobs | Nrev | I-Nrev | (1.2.1); TTWSFD; (1.2.3.2) | ||||||
| 4 | Iobs + Lobs | Iobs + Lobs | Nrev | I-Nrev | (1.2.1); TTWSFD; (1.2.3.2) | |||||
| 5 | Iobs + Lobs | W | I-W | (1.2.1); TTWSFD; (1.2.3.2) | ||||||
| 6 | Iobs + Lobs | Iobs + Lobs | W | I-W | (1.2.1); TTWSFD; (1.2.3.2) | |||||
| 7 | Iobs + Lobs | FOC | I-FOC | (1.2.1); TTWSFD; (1.2.3.2) | ||||||
| 8 | Iobs + Lobs | Iobs + Lobs | FOC | I-FOC | (1.2.1); TTWSFD; (1.2.3.2) | |||||
| 9 | Iobs + Lobs | Nrev | I-Nrev | W | I-W | (1.2.1); TTWSFD; (1.2.3.2) | ||||
| 10 | Iobs + Lobs | Iobs + Lobs | Nrev | I-Nrev | W | I-W | (1.2.1); TTWSFD; (1.2.3.2) | |||
| 11 | Iobs + Lobs | Nrev | I-Nrev | FOC | I-FOC | (1.2.1); TTWSFD; (1.2.3.2) | ||||
| 12 | Iobs + Lobs | Iobs + Lobs | Nrev | I-Nrev | FOC | I-FOC | (1.2.1); TTWSFD; (1.2.3.2) | |||
| 13 | Iobs + Lobs | W | I-W | FOC | I-FOC | (1.2.1); TTWSFD; (1.2.3.2) | ||||
| 14 | Iobs + Lobs | Iobs + Lobs | W | I-W | FOC | I-FOC | (1.2.1); TTWSFD; (1.2.3.2) | |||
| 15 | Iobs + Lobs | Nrev | I-Nrev | W | I-W | FOC | I-FOC | (1.2.1); TTWSFD; (1.2.3.2) | ||
| 16 | Iobs + Lobs | Iobs + Lobs | Nrev | I-Nrev | W | I-W | FOC | I-FOC | (1.2.1); TTWSFD; (1.2.3.2) | |
| 17 | Nrev | I-Nrev | (1.2.1); TTWSFD; (1.2.3.2) | |||||||
| 18 | W | I-W | (1.2.1); TTWSFD; (1.2.3.2) | |||||||
| 19 | FOC | I-FOC | (1.2.1); TTWSFD; (1.2.3.2) | |||||||
| 20 | Nrev | I-Nrev | W | I-W | (1.2.1); TTWSFD; (1.2.3.2) | |||||
| 21 | W | I-W | FOC | I-FOC | (1.2.1); TTWSFD; (1.2.3.2) | |||||
| 22 | Nrev | I-Nrev | FOC | I-FOC | (1.2.1); TTWSFD; (1.2.3.2) | |||||
| 23 | Nrev | I-Nrev | W | I-W | FOC | I-FOC | (1.2.1); TTWSFD; (1.2.3.2) | |||
| 24 | Nrev | I-intervals | (1.2.1); TTWDFD;W; t | |||||||
| 25 | W | I-intervals | (1.2.1); TTWDFD;Nrev; t | |||||||
| 26 | FOC | I-intervals | (1.2.1); TTWDFD;Nrev; t | |||||||
| 27 | Nrev | W | I-intervals | (1.2.1); TTWDFD;Nrev; W; t | ||||||
| 28 | W | FOC | I-intervals | (1.2.1); TTWDFD;Nrev; t | ||||||
| 29 | Nrev | FOC | I-intervals | (1.2.1); TTWDFD;Nrev; W; t | ||||||
| 30 | Nrev | W | FOC | I-intervals | (1.2.1); TTWDFD;Nrev; W; t |
2.2. The Main Engine, Thermo-Fluid and Frictional, SFOC Approximating Functional [1] System
| Step | Applicable Equations Superset | Computational Content |
|---|---|---|
| A | Pursuant to Steps 1, 2, 7 & 8 below | Data acquisition pursuant to Appendix O and Appendix Q |
| B | Pursuant to Steps 1, 2, 7 & 8 below | Data pre-processing pursuant to Appendix Q |
| 1 | {(19h)/(19n) and/or (20h)/(20n),(22)} | Determination of applicable Equations |
| 2 | {(19h)/(19n) and/or (20h)/(20n),(22)} | Assignments as per applicable Equations |
| 3 | (21a) | Assignments as per Equation (21a) |
| 4 | {(18),(19H) and/or (20H)} | As per Appendix H & applicable equations |
| 5 | (21b) | Assignments as per Equation (21b) |
| 6 | {(18),(19H) and/or (20H)} | Finalization as per applicable equations |
| C | Pursuant to Steps 4, 5 & 6 above | Assessment of initial values assigned in Step 3 |
| 7 | (*) {(8n),(9n),(11),(12h),(12n),(13h), (13n),(14h),(14n),(15),(17)} (*) | Determination of Tables’ 1 and 2 applicable line |
| 8 | Assignments as per Table’s 2 applicable line | |
| 9 | (10a) or (16a) | Assignments as per Table’s 1 applicable line |
| 10 | {(6),(7),(8H),(9H),(12H),(13H),(14H)} | As per Appendix H & Table’s 1 applicable line |
| 11 | (10b) or (16b) | Assignments as per Table’s 1 applicable line |
| 12 | {(6),(7),(8H),(9H),(12H),(13H),(14H)} | Finalization as per Table’s 1 applicable line |
| D | Pursuant to Steps 10, 11 & 12 above | Assessment of initial values assigned in Step 9 |
2.3. “Big Data” Set
2.3.1. Ship-Tracking Data (AIS, LRIT, and Other)
2.3.2. Environmental, “Met-Ocean” (Meteorological and Oceanographic) Data
2.4. Reduced Uncertainty, Reasonable Degree of Certainty, Reasonable Assurance and Materiality
2.4.1. FOC Uncertainty Type 1.1 (Analysis Type 1, per Voyage)
2.4.2. FOC Uncertainty Type 1.2 (i) (Analysis Type 1, for a Specific Reporting Interval, i)
2.4.3. FOC Uncertainty Type 2.1 (Analysis Type 2, per Voyage)
2.4.4. FOC Uncertainty Type 2.2 (i) (Analysis Type 2, for a Specific Reporting Interval, i)
2.4.5. FOC Uncertainty Type 3.1 (Analysis Type 3, per Voyage)
2.4.6. FOC Uncertainty Type 3.2 (i) (Analysis Type 3, for a Specific Reporting Interval, i)
2.4.7. FOC Materiality Type 1 (Analysis Type 1)
2.4.8. FOC Materiality Type 2 (Analysis Type 2)
2.4.9. FOC Materiality Type 3 (Analysis Type 3)
2.4.10. FOC Standard Deviation Type 1 (Analysis Type 1)
2.4.11. FOC Standard Deviation Type 2 (Analysis Type 2)
3. Results
| Vessel Number | Power (MCR, KW) | RPM (MCR) | Number of Cylinders | Cylinder Bore (m) | Stroke (m) |
|---|---|---|---|---|---|
| 1 | 13,560 | 105 | 6 | 0.6 | 2.4 |
| 2 | 13,560 | 105 | 6 | 0.6 | 2.4 |
| 3 | 13,560 | 105 | 6 | 0.6 | 2.4 |
| 4 | 11,080 | 83 | 6 | 0.62 | 2.658 |
| 5 | 11,080 | 83 | 6 | 0.62 | 2.658 |
| 6 | 11,080 | 83 | 6 | 0.62 | 2.658 |
| 7 | 11,080 | 83 | 6 | 0.62 | 2.658 |
| 8 | 15,088 | 71.8 | 6 | 0.72 | 3.086 |
| 9 | 15,088 | 71.8 | 6 | 0.72 | 3.086 |
| 10 | 15,200 | 90 | 7 | 0.65 | 2.73 |
| Vessel Number | Type | DWT (MT) | GT (RT) | Draft (m) | LOA (m) | LBP (m) | Beam (m) | Speed (knots) |
|---|---|---|---|---|---|---|---|---|
| 1 | Tanker | 115,700 | 61,200 | 15 | 250 | 240 | 44 | 15 |
| 2 | Tanker | 115,700 | 61,300 | 15 | 250 | 240 | 44 | 15 |
| 3 | Tanker | 115,700 | 61,300 | 15 | 250 | 240 | 44 | 15 |
| 4 | Tanker | 114,300 | 62,900 | 15 | 250 | 240 | 45 | 14 |
| 5 | Tanker | 114,300 | 62,900 | 15 | 250 | 240 | 45 | 14 |
| 6 | Tanker | 114,300 | 62,900 | 15 | 250 | 240 | 45 | 14 |
| 7 | Tanker | 114,400 | 62,900 | 15 | 250 | 240 | 45 | 14 |
| 8 | Tanker | 157,500 | 81,600 | 17 | 275 | 265 | 48 | 14 |
| 9 | Tanker | 157,500 | 81,600 | 17 | 275 | 265 | 48 | 14 |
| 10 | Tanker | 159,200 | 82,600 | 17 | 275 | 265 | 48 | 14 |
| Vessel Number | Number of Legs | Analysis Type 1 | Analysis Type 2 | Analysis Type 3 | Reporting Intervals |
|---|---|---|---|---|---|
| 1 | 38 | 38 | 38 | 38 | 306 |
| 2 | 31 | 31 | 31 | 31 | 333 |
| 3 | 35 | 35 | 35 | 35 | 297 |
| 4 | 29 | 29 | 29 | 29 | 284 |
| 5 | 5 | 5 | 5 | 5 | 87 |
| 6 | 4 | 4 | 4 | 4 | 81 |
| 7 | 32 | 32 | 32 | 32 | 298 |
| 8 | 13 | 13 | 13 | 13 | 172 |
| 9 | 30 | 30 | 30 | 27 | 165 |
| 10 | 5 | 5 | 5 | 5 | 49 |
3.1. Analysis Type 1
| Vessel Number | Column 1 (%) | Column 2 (%) | Column 3 (%) | Column 4 (%) | Column 5 (%) | Column 6 (%) | Column 7 (%) |
|---|---|---|---|---|---|---|---|
| 1 | 1.38 | 0.00 | 4.33 | 5.79 | 50.1 | 92.1 | 46.2 |
| 2 | 0.89 | 0.00 | 9.40 | 6.99 | 50.1 | 91.8 | 46.0 |
| 3 | 0.01 | 0.00 | 4.76 | 4.92 | 47.6 | 89.5 | 42.6 |
| 4 | 0.06 | 0.00 | 1.71 | 3.74 | 52.8 | 91.6 | 48.4 |
| 5 | 0.05 | 3.74 | 2.62 | 3.82 | 50.9 | 92.1 | 46.9 |
| 6 | 0.10 | 0.00 | 5.21 | 6.65 | 48.3 | 92.4 | 44.6 |
| 7 | 0.02 | 0.00 | 0.88 | 2.62 | 53.2 | 91.6 | 48.7 |
| 8 | 4.17 | 0.00 | 0.98 | 4.38 | 56.2 | 91.7 | 51.5 |
| 9 | 0.06 | 4.30 | 5.70 | 5.68 | 55.8 | 90.2 | 50.4 |
| 10 | 4.89 | 0.00 | 0.06 | 5.20 | 57.8 | 91.5 | 52.8 |
3.2. Analysis Type 2
| Vessel Number | Column 1 (%) | Column 2 (%) | Column 3 (%) | Column 4 (%) | Column 5 (%) | Column 6 (%) | Column 7 (%) |
|---|---|---|---|---|---|---|---|
| 1 | 2.72 | 10.63 | 20.29 | 15.11 | 0.73 | 0.00 | 7.27 |
| 2 | 4.13 | 9.43 | 20.47 | 12.67 | 0.86 | 0.00 | 10.58 |
| 3 | 2.02 | 4.64 | 12.38 | 8.73 | 0.52 | 0.00 | 4.29 |
| 4 | 1.39 | 0.00 | 12.36 | 13.64 | 1.04 | 0.00 | 9.79 |
| 5 | 0.85 | 3.73 | 7.05 | 8.92 | 0.16 | 0.00 | 1.87 |
| 6 | 0.36 | 0.00 | 10.10 | 8.11 | 0.63 | 0.00 | 11.21 |
| 7 | 2.02 | 1.76 | 11.50 | 16.19 | 0.81 | 0.00 | 8.19 |
| 8 | 1.13 | 5.85 | 9.12 | 12.27 | 1.76 | 2.22 | 6.33 |
| 9 | 2.96 | 7.24 | 13.70 | 10.79 | 1.97 | 1.96 | 11.65 |
| 10 | 1.18 | 0.00 | 7.95 | 6.20 | 1.42 | 0.00 | 10.50 |
3.3. Analysis Type 3
4. Discussion
5. Conclusions
- (a)
- (b)
- the thermo-fluid and frictional functional system originally presented in this article that mathematically approximates the fuel oil consumption of vessels’ main engines under actual seagoing conditions;
- (c)
- the functional system originally presented in this article that mathematically approximates the hydrodynamic performance of the respective vessels in terms of the shaft propulsion power and the shaft rotational speed of the fixed-pitch propellers driven by the a/m engines, also under actual seagoing conditions.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| a/m | Aforementioned (abovementioned/mentioned above) |
| AIS | Automatic Identification (Tracking) System |
| ANN | Artificial Neural Network |
| BDN | Bunker Delivery Note |
| BIPM | Bureau International des Poids et Mesures, Sèvres, France |
| BMEP | Brake Mean Effective Pressure |
| BSR | Barred Speed Range |
| BSRA | British Shipbuilding Research Association |
| CII | Carbon Intensity Index |
| COG | Course Over Ground |
| CPP | Controllable Pitch Propeller |
| DGPS | Differential Global Positioning System |
| DI | Direct Injection |
| DLS | Damped Least Squares [1,2] |
| ECDIS | Electronic Chart Display and Information System |
| ECU | Engine Control Unit |
| EEXI | Energy Efficiency Index for Existing ships |
| EIAPPC | Engine International Air Pollution Prevention Certificate |
| ETA | Estimated Time of Arrival |
| FAT | Factory Acceptance Test |
| FOC | Fuel Oil Consumption |
| FPGA | Field Programmable Gate Array |
| FPP | Fixed-Pitch Propeller |
| GHG | Green House Gases |
| GPS | Global Positioning System |
| IAPPC | International Air Pollution Prevention Certificate |
| IDI | Indirect Injection |
| IMO | International Maritime Organization, London, UK |
| IMSL® | International Mathematics and Statistics Library® |
| ITTC | International Towing Tank Conference |
| LRIT | Long Range Identification Tracking (System) |
| MDO | Marine Diesel Oil |
| MEPC | Marine Environment Protection Committee (under a remit) of IMO |
| MGO | Marine Gas Oil |
| NGA | National Geospatial-Intelligence Agency, Fort Belvoir, Springfield, Virginia, USA |
| NTUA | National Technical University of Athens, Hellas (Greece) |
| NUC | Not Under Command |
| SFOC | Specific Fuel Oil Consumption |
| OEM | Original Equipment Manufacturer |
| OOW | Officer On Watch |
| OTG | Over The Ground |
| PTH | Power Take Home |
| PTI | Power Take In |
| PTO | Power Take Out |
| RIATM | Restricted In Ability To Maneuver (also known/referred to as: RAM) |
| ROT | Rate of Turn |
| SOG | Speed Over Ground |
| TTW | Through-The-Water |
| TTWDFD | TTW Distance (travelled/made good/sensed/measured in the) Forward Direction |
| TTWSFD | TTW (or, log) Speed (determined/sensed/measured in the) Forward Direction |
| UTC | Universal Coordinated Time |
| Nomenclature | |
| Cj | calibration constant of order j, j = 1, K (dimensionless) |
| cor | set of parameters applied for the correction, alignment and benchmarking of engines’ SFOC values pursuant to industry standards and experience |
| f1i | expression of sea margin in position/timestamp pair i |
| f2i | expression of sea running margin in position/timestamp pair i |
| f3i | expression of light running margin in position/timestamp pair i |
| f4i | expression of speed loss in position/timestamp pair i |
| f5i | expression of apparent TTW slip in position/timestamp pair i |
| fi | residuals, fi (α, β, γ, …), at points, (xi, yi, zi,…), i = 1, 2, …, n, in Equations (1)–(3) of Reference [1] |
| Fi | “…set of linear approximations to the residuals, fi (α, β, γ, …) …” [1], i = 1, 2, …, n, in Equations (3) and (4) of Reference [1] |
| FOC | fuel oil consumption, mass (kg) |
| FOCi | or, FOCi, value of, FOC, for period i, i = 1, 2, …, n, in Equations (1)–(4) of Reference [1]; i, and, n, hold the same meaning in this article |
| h | function to be approximated, h(xi, yi, zi,…), in Equation (1) of Reference [1] |
| h′ | occurrence of function to be approximated, h, right above, h′(xi, yi, zi,…; J), applicable for the numerical contributor, J, which may or may not be, equal to an Equation’s or Equation Set’s index, (J), or, (Jh), or, (JH), or (Jn), of this article |
| H | approximating function, H(xi, yi, zi,…; α, β, γ,…), in Equation (1) of Reference [1] |
| H′ | occurrence of approximating function, H, right above, H′(xi, yi, zi,…; α, β, γ,…; J), applicable for the numerical contributor, J, which may or may not be, equal to an Equation’s or Equation Set’s index, (J), or, (Jh), or, (JH), or (Jn), of this article |
| i | points, 1, 2, …, n, in Equations (1)–(4) of Reference [1], holding the same exact meaning in the context of the present article |
| I-FOC | number of periods during which FOC is reported for each such period |
| I-intervals | number of reporting intervals between daily, or other, reports |
| I-Nrev | number of periods during which Nrev is reported for each such period |
| Iobs | number of pairs of ship’s position and timestamp of steady rotational speed |
| Isfoc-obs | number of SFOC observations in Equation (19n) |
| I-voy | number of reporting intervals per voyage |
| Isfoc-voy | number of SFOC reporting intervals per voyage |
| I-W | number of periods during which W is reported for each such period |
| j | order j, j = 1, K, of calibration constant, Cj, or order j, j = 1, M, of calibration constant, Xj |
| J | numerical contributor, J, which may or may not be, equal to an Equation’s or Equation Set’s index, (J), or (Jh), or, (JH), or (Jn), of this article |
| K | number of calibration constants, Cj, j = 1, K |
| Lobs | number of pairs of ship’s position and timestamp of unsteady rotational speed |
| M | number of thermo-fluid/frictional SFOC calibration constants, Xj, j = 1, M |
| n | number of points, i, in Equations (2) and (4) of Reference [1], whereas in the context of, and throughout, the present article, is substituted in the form of occurrence of it, n′(J), “mutatis—mutandis” by, I-intervals, or, Iobs, or, Isfoc-obs, or, (Isfoc-obs)′, or, Lobs, or, Iobs + Lobs, or, I-Nrev, or, I-W, or, I-FOC, above |
| n′(J) | occurrence of, n, number of points, i, in Equations (2) and (4) of Reference [1], applicable for the numerical contributor, J, which may or may not be, equal to an Equation’s or Equation Set’s index, (J), or (Jn), of this article |
| Nrev | number of shaft’s/engine’s revolutions (dimensionless) |
| Nrevi | value of, Nrev, for period, i, i = 1, 2, …, n, in Equations (1)–(4) of Reference [1]; i, and, n, hold the same meaning in this article |
| P | shaft’s/engine’s power (W), also measured in the context of this article, in KW (1 KW = 1000 W), and in BHP (1 BHP = 0.7457 KW = 745.700 W) as well |
| Pi | or, Pi, value of, P, in point (position/timestamp pair), or for period, i, i = 1, 2, …, n, in Equations (1)–(4) of Reference [1]; i, and, n, hold the same meaning in this article |
| r | shaft’s/main engine’s rotational speed (revolutions per second), also measured in the context of this article and of the marine industry’s practice as well, in revolutions per minute, RPM (1 revolution per second = 60 RPM), and used interchangeably with (effectively, substituted by) the term, RPM, as well |
| ri | or, ri, shaft’s/main engine’s rotational speed, r, in point (position/timestamp pair), or for period, i, i = 1, 2, …, n, in Equations (1)–(4) of Reference [1]; i, and, n, hold the same meaning in this article |
| s | sum of squares of residuals, fi, to be minimized, in Equation (2) of Reference [1] |
| S | sum of squares of, Fi, the “… linear approximations to the residuals, fi (α, β, γ, …) …” [1], in Equation Set (4) and (5) of Reference [1] |
| SFOC | specific fuel oil consumption (kg/J), also measured in the context of this article and of the marine industry’s practice, in g/(KW h): 1 kg/J = 3,600,000,000 g/(KW h) |
| SFOCi | value of, SFOC, in point (position/timestamp pair), or for period, i, i = 1, 2, …, n, in Equations (1)–(4) of Reference [1]; i, and, n, hold the same meaning in this article |
| t | time (s); in the context of the present article, and of the marine industry’s practice as well, also main engine’s running hours (1 running hour = 3600 s) |
| TTWDFD | vessel’s TTW (through-the-water, or simply, log) distance travelled/made good/sensed/measured/determined in the vessel’s forward direction (m), in the context of the present article, and of the marine industry’s practice as well, also measured in, nautical miles (1 nautical mile = 1852 m, or, 1 nautical mile = 1.852 km); TTWDFD is also discussed in further detail and within relevant context in the Abbreviations list, as well as in Appendix H of this article, and in this regard the use of the, TTWDFD, abbreviation alone would suffice in terms of reference of it, in all other sections of this article |
| TTWSFD | vessel’s TTW (through-the-water) speed (or simply, log-speed) determined/sensed/measured in the vessel’s forward direction (m/s), in the context of the present article, and of the marine industry’s practice as well, also measured in, Knots (1 Knot = 1.852 km/h, or, 1 Knot = 0.51444 m/s); TTWSFD is also discussed in further detail and within relevant context in Section 1.1, in the Abbreviations list, as well as in Appendix E, Appendix G, Appendix H, Appendix I, Appendix Q, Appendix Y and Appendix Z of this article, and in this regard the use of the, TTWSFD, abbreviation alone would suffice in terms of reference of it, in all other sections of this article |
| U | symbol of data sets union |
| W | shaft’s/engine’s mechanical work (J) |
| Wi | or, Wi, value of, W, for period, i, i = 1, 2, …, n, in Equations (1)–(4) of Reference [1]; i, and, n, hold the same meaning in this article |
| x, y, z,… | variables of functions, h(xi, yi, zi,…), and, H(xi, yi, zi,…; α, β, γ,…), in Equation (1) of Reference [1] |
| xi, yi, zi, … | value set of variables, x, y, z,…, in Equations (1)–(4) of Reference [1], in point (position/timestamp pair), or for period, i, i = 1, 2, …, n, in Equations (1)–(4) of Reference [1]; i, and, n, hold the same meaning in this article |
| Xj | main engine’s thermo-fluid/frictional SFOC calibration constant of order j, j = 1, M (dimensionless) |
| α, β, γ,… | (initially only) unknown parameters, in Equations (1)–(5) of Reference [1], and in, H(xi, yi, zi,…; α, β, γ,…) [1], fi (α, β, γ, …) [1], Fi (α, β, γ, …) [1], s(α, β, γ, …) [1], and, S(α, β, γ, …) [1], in particular |
| (Cj, j = 1, K) | set of calibration constants, Cj, j = 1, K, applicable for cases (lines) in Table 1 and Table 2, 1 to 23, where an Equation Set to be resolved includes Equation (10) and does not include Equation (16) |
| (Cj, j = 1, K)′ | set of calibration constants, Cj, j = 1, K, applicable for cases (lines) in Table 1 and Table 2, 24 to 30, where an Equation Set to be resolved includes Equation (16) and does not include Equation (10) |
| (dr/dt)i | also, dr(xi, yi, zi, …)/dt, occurrence of function to be approximated [1], h′(xi, yi, zi,…; 8), of propeller’s and engine’s rotational acceleration, in point (position/timestamp pair), i, i = 1, 2, …, n, in Equations (1)–(4) of Reference [1]; i, and, n, hold the same meaning in this article |
| (d2r/dt2)i | also, d2r(xi, yi, zi, …)/dt2, occurrence of function to be approximated [1], h′(xi, yi, zi,…; 9), of, d2r/dt2, in point (position/timestamp pair), i, i = 1, 2, …, n, in Equations (1)–(4) of Reference [1]; i, and, n, hold the same meaning in this article |
| (Isfoc-obs)′ | number of, FOC to W ratio, observations in Equation (20n) |
| (SFOC)i | occurrence of function to be approximated [1], h′(xi, yi, zi,…; 19), of SFOC, in point (position/timestamp pair), or for period, i, i = 1, 2, …, n, in Equations (1)–(4) of Reference [1]; i, and, n, hold the same meaning in this article |
| (α,β,γ,…)′ | set of initially estimated values of unknown parameters, α, β, γ,…, before Equation Set (1)–(5) of Reference [1] is resolved |
| (α,β,γ,…)″ | set of values of (initially) unknown parameters, α, β, γ,…, attained by solving Equation Set (1)–(5) of Reference [1], pursuant to Reference [1]. |
Appendix A
Appendix A.1. Correlation Scheme #1
- (a)
- For ships propelled by a single FPP driven by one directly coupled low speed two-stroke main diesel engine (accounting for ~ +90% of ships in service), the following are applicable: The FPP shaft revolutions divided by the respective time spent at sea when the ship is making way by its own propulsion (“by engines”), t, (main engine running hours) would be equivalent to an average steady rotational speed of the FPP, r. The above are to be particularly considered in conjunction with the fact that such as above standard vessels are making way (“by engines”) by keeping a steady shaft rotational speed, r, which is increased or decreased by as smooth as necessary ramp up and down, and as near as possible linear over time, commands.
- (b)
- Distance through-the-water (TTW) data, when the ship is making way by its own propulsion (“by engines”), are calculated on the basis of the respective distance made over the ground (OTG) acquired by (Differential) Global Positioning System, (D)GPS, and/or Electronic Chart Display and Information System (ECDIS). These acquired data are then compared to available independent distance OTG tracking data, corrected by comparison to available speed-log (TTW) measurements, and finally verified by comparison to available independent data on speed and direction of water current, as well as, of vessel’s heading and actual course/tracking data. The above corrected and verified data values on distance made good through-the-water (TTW), divided by the respective time spent at sea during which the ship is making way by its own propulsion (“by engines”), t, (main engine running hours) equal the average TTW speed, calculated both in the forward and in the athwart ship directions.
- (c)
- The fuel consumption of the main diesel engine, per fuel type and Bunker Delivery Note (BDN), divided by the respective diesel engine running hours, t, and by the appropriate respectively applicable value of specific fuel consumption (SFOC) as well, is equivalent to an average engine power, P. For calculating or verifying SFOC, direct measurements of mechanical work, W, and average engine power, P, by torque meters are also possible. The main engine/shaft/propeller rotational acceleration and deceleration, dr/dt, may also be considered, or neglected, as applicable.
- (d)
- Hydrostatic conditions (draft/trim, displacement, water density) are measured at the start, and if possible at the end, of the voyage or leg.
- (e)
- Any given sea and wind state conditions in terms of waves and wind speed and direction, air humidity, density and temperature, rain, snow or hail, resulting to the composite environmental effect on the FPP’s shaft power.
- (f)
- The a/m fundamental principle of the Law of Similarity and Dimensional Analysis is to be always satisfied.
Appendix B
Appendix B.1. Correlation Scheme #2
- (a)
- Water density changes, which for voyages in sea waters with salinity ranging from~33 to 37 g/kg (~0.3% of density change) and temperature ranging from ~5 to 35 °C (~0.7% of density change), and/or entering/leaving inland fresh or low salinity waters from/to sea water and/or combinations thereof (within a maximum range of ~2.8% of density change for same temperature), may be considered for representing the actual density, salinity and temperature values.
- (b)
- Water density change has also a secondary effect as, for the same voyage, or leg of it, and/or for effectively the same loading and/or ballast hydrostatic conditions before vessel cast off, water density changes will consequently cause draft changes, and draft is also a factor related to the FPP’s shaft power.
- (c)
- Water kinematic viscosity also varies with salinity and temperature and relates to the dimensionless hull (waterline) and propeller Reynolds numbers which in turn have an effect on the FPP’s shaft power when the ship is making way (“by engines”), and on the frictional contributor to the shaft power in particular.
- (d)
- In a similar manner, acceleration of gravity as such varies with latitude, relates to the dimensionless hull (waterline) and propeller Froude numbers which in turn have an effect on the FPP’s shaft power when the ship is making way (“by engines”), and on the dynamic contributor to the shaft power in particular, as such is discussed above.
- (e)
- The distribution of the shaft power to a frictional and dynamic contributor is ship and voyage specific and mainly depends on the ship category, design and speed.
- (f)
- Air barometric pressure, as well as water density and water saturated vapour pressure, as the last two vary with water temperature and salinity, acceleration of gravity as such varies with latitude, and draft as well, relate to the propeller cavitation dimensionless number, σ. The propeller cavitation dimensionless number, σ, has an effect to the FPP’s shaft power, and on the propeller performance in particular.
- (g)
- Sufficiently deep, also otherwise unconstrained, non–icy, waters will not effect to the propulsion power calculation, however shallow, or otherwise constrained, or icy waters, will result to affecting the vessel’s attainable speed.
- (h)
- The ratio of the TTW speed in the athwart ship direction, to the TTW speed in the forward direction, is a direct indication of the rudder angle as such may be statically controlled for keeping a steady course against current, wind and waves of steady lateral direction and scale, and as such may have a significant speed loss effect on the vessel’s attainable TTW speed in the forward direction.
- (i)
- The Rate of Turn (ROT) is also a direct indication of the rudder angle as such may be dynamically controlled for turning the vessel, or for keeping a steady course against dynamically fluctuating current’s, wind’s and waves’ direction and scale, and as such may have a significant speed loss effect on the vessel’s attainable TTW speed in the forward direction.
- (j)
- The effect of the TTW acceleration/deceleration, including TTW acceleration/decele- ration in the forward and in the athwart ship direction, calculated on the basis of data availability, and analysis thereof, with regard to the TTW speed in the forward and in the athwart-ship direction, Rate of Turn (ROT) and Ship’s position, on the FPP’s shaft power, may also be considered, or neglected, as applicable.
- (k)
- The a/m fundamental principle of the Law of Similarity and Dimensional Analysis is to be always satisfied.
Appendix C
Appendix C.1. Correlation Scheme #3
- (a)
- The vessel/voyage specific “virtual” sea trials “ideal” condition is effectively equivalent to a certain operating condition (service margin) of the same ship when in “new vessel” condition upon the latest delivery of the vessel by a shipyard after her newbuilding or her major modification, and for the same draft and trim.
- (b)
- The reason for the above effective equivalence is the change of the geometry, wetted surface and roughness condition of the hull, the rudder, the propeller and the appendages of the vessel, due to sea-keeping, as well as the permanent, or not, effect of the loading distribution.
- (c)
- Same or similar are applicable for the shaft line and stern tube as well, and to this end, the level of deterioration of the shaft line and stern tube in terms of their, frictional and/or hydraulic, mechanical efficiency is also included in the so called service margin discussed in this article.
- (d)
- All the, across Correlation Scheme #3, alternative shaft power ratio forms/expressions (sea margin, speed loss, light running margin, sea running margin, apparent TTW slip) discussed in Section 2.1.5, shall be properly balanced to each other, on the basis of properly balanced mean effective values of particular characteristics of them.
Appendix D
Appendix D.1. Correlation Scheme #4
- (a)
- The ship’s sea trials corrected results to be determined for the ship’s actual draft and trim, and for the respective displacement as well, are the “virtual” sea trials corrected results at “ideal/newbuilding” conditions upon the latest delivery of the vessel by a shipyard after her newbuilding or her major modification.
- (b)
- The ship’s sea trials corrected results for the same as above (actual) draft and trim, and for the respective displacement as well, are attained on the basis of the ship’s official sea trials corrected results in either laden or ballast conditions (as well as, of the calculated official results for the remaining, not tried, one of the two, laden or ballast, loading conditions, as/if available).
- (c)
- All the, across Correlation Scheme #4, alternative shaft power ratio forms/expressions (sea margin, speed loss, light running margin, sea running margin, apparent TTW slip) discussed in this article, shall be properly balanced to each other, on the basis of properly balanced mean effective values of particular characteristics of them.
- (d)
- Such particular characteristics of the above conditions shall include draft, trim and displacement, as applicable.
Appendix E
Appendix E.1. FPP Apparent Through-the-Water (TTW) Slip and Alternative Shaft Power Ratio Forms/Expressions
Appendix F
Appendix F.1. Main Engine’s and FPP’s Rotational Speed Control in Standard Vessels
Appendix G
Appendix G.1. Analysis of Figure 1, Figure 2, Figure 3 and Figure 4 and Formulations (1) to (7), in Section 2.1.5 of This Article
- (g)
- The set of curves pursuant to point (g) in Section 2.1.5 is representing contours of steady/fixed vessel’s through-the-water (TTW) speed in the forward direction, TTWSFD, with the vessel’s through-the-water (TTW) speed in the forward direction, TTWSFD, values increasing from the left to the right.
- (h)
- The set of curves pursuant to point (h) in Section 2.1.5 is representing contours of steady/fixed FPP’s apparent TTW slip, with the FPP’s apparent TTW slip also increasing from the right to the left.
- (i)
- The set of curves pursuant to point (i) in Section 2.1.5 is representing contours of, effectively, steady/fixed weather conditions with the weather getting heavier from the right to the left of these sets of curves.
- (1)
- (2)
- (3)
Appendix H
Appendix H.1. Solution of Equation Sets in the Imperative Assignment Statement Ready Format of Reference [1]
- (1)
- Dell® Inspiron 3520 Touch i7-1255U/16 GB/1 TB: Intel® Core i7-1255U @ 4.7 GHz/Total Cores: 10; 16.0 GB RAM; Graphics Card: Intel® Iris Xe Graphics; HD: 1000 GB SSD/M.2 PCIe NVMe SSD; screen diagonal dimension: 15.6”/1920 X 1080 pixels;
- (2)
- Microsoft ® Windows 11 Pro; Version 24H2; OS Build 26100.4061; Windows Feature Experience Pack 1000.26100.84.0
- (3)
- Microsoft ® Visual Studio 2022 Community; Version 17.14.4
- (4)
- Intel® oneAPI Base Toolkit; Version 2025.1
- (5)
- Intel® oneAPI HPC Toolkit; Version 2025.1
- (6)
- Perforce® Rogue Wave® IMSL® Fortran Numerical Library (FNL); Version 2025.1.0 for Microsoft ® Windows 11 Pro, Intel® oneAPI and x86-64 system architecture; fnl-2025.1.0-win110ix250x64:
- a.
- IMSL® Fortran Numerical Library PC Development License
- b.
- IMSL® Fortran Numerical Library PC Deployment License
- (a)
- n, in the context of Equation (4) of Reference [1], equals the value calculated pursuant to the formulation referenced by the single respective column, 8n, or, 12n, or, 13n, or, 14n, or, 15, of Table 1 in Section 2.1.5, which is applicable for any one of the above cases (lines) of Table 1 and Table 2 in Section 2.1.5.
- (b)
- S, in the context of Equation Set (1)–(4) of Reference [1], is calculated pursuant to the formulations referenced by the single pair of respective columns, 8h and 8H, or, 12h and 12H, or, 13h and 13H, or, 14h and 14H, of Table 1 in Section 2.1.5, which is applicable for any one of the above cases (lines) of Table 1 and Table 2 in Section 2.1.5.
- (c)
- n, in the context of Equation (4) of Reference [1], equals the sum of the values calculated pursuant to the formulations referenced by those of the respective columns, 8n, 12n, 13n, 14n and 15 of Table 1 in Section 2.1.5, which are simultaneously applicable for each one of the above cases (lines).
- (d)
- S, in the context of Equation Set (1)–(4) of Reference [1], equals the total of the sums of squares of, Fi (α, β, γ, …) [1], calculated pursuant to the formulations referenced by those of the respective columns, 8h, 8H, 9h, 9H, 12h, 12H, 13h, 13H, 14h and 14H of Table 1 in Section 2.1.5, which are simultaneously applicable for each one of the above cases (lines).
- (e)
- (f)
- Such as the above similar and/or effectively equivalent considerations may, or not, be expressed in the form of Equation (3.1.5) of Reference [22] which is essential and instrumental as well for the solution of the set of Equations (3.1.8)–(3.1.17) of Reference [22] which are simply a particular occurrence of the set of Equation (5) of Reference [1] simultaneously resolved with more than one Equation Sets such as the above.
- (g)
- n, in the context of Equation (4) of Reference [1], equals either, Isfoc-obs, or, (Isfoc-obs)′, pursuant to Equations (19n) or (20n) in Section 2.2.
- (h)
- S, in the context of Equation Set (1)–(4) of Reference [1], is calculated pursuant to the single pair of Equation Sets, (19H) and (19h), or, (20H) and (20h), in Section 2.2.
- (i)
- n, in the context of Equation (4) of Reference [1], equals the sum of, Isfoc-obs + (Isfoc-obs)′ = n′(19) + n′(20), pursuant to Equations (19n) and (20n) in Section 2.2.
- (j)
- S, in the context of Equation Set (1)–(4) of Reference [1], equals the total of the sums of squares of, Fi (α, β, γ, …) [1], calculated pursuant to Equations (19H), (19h), (20H) and (20h) in Section 2.2, which are simultaneously applicable.
- (k)
- (l)
- Such as the above similar and/or effectively equivalent considerations may, or not, be expressed in the form of Equation (3.1.5) of Reference [22] which is essential and instrumental as well for the solution of the set of Equations (3.1.8)–(3.1.17) of Reference [22] which are simply a particular occurrence of the set of Equation (5) of Reference [1] simultaneously resolved with more than Equation Sets such as the above.
Appendix I
Appendix I.1. Main Engine’s and FPP’s Rotational Speed, Power and TTWSFD (log) Speed
Appendix J
Appendix J.1. “Big Data” Sets: AIS, or Other Ship-Tracking, Data
- (a)
- IMO Number and Type of ship.
- (b)
- Ship’s position (longitude and latitude in decimal degrees) with accuracy indication and integrity status: Automatically updated from the position sensor connected to AIS. The accuracy indication is approximately 10 m.
- (c)
- Position Timestamp in UTC (date; hour; minute; second; 24 h format YYYY/MM/DD HH:mm:ss: Automatically updated from ship’s main position sensor connected to AIS.
- (d)
- Course over ground (COG, ° −180 to 180 Northbound, 0 to 360 Southbound): Automatically updated from ship’s main position sensor connected to AIS, if that sensor calculates COG. This information might not be available.
- (e)
- Speed over ground (SOG, knots): Automatically updated from the position sensor connected to AIS. This information might not be available.
- (f)
- Heading (°−180 to 180 Northbound, °0 to 360 Southbound): Automatically updated from the ship’s heading sensor connected to AIS.
- (g)
- Navigational status: To be manually entered by the OOW and changed as necessary:
- (i)
- underway by engines;
- (ii)
- at anchor;
- (iii)
- not under command (NUC);
- (iv)
- restricted in ability to maneuver (RIATM);
- (v)
- moored;
- (vi)
- constrained by draught;
- (vii)
- aground;
- (viii)
- underway by sail.
- (h)
- Rate of turn, or (ROT, ° per minute): Automatically updated from the ship’s ROT sensor or derived from the gyro. This information might not be available.
- (i)
- Draft (Ship’s draught, m): To be manually entered at the start of the voyage using the maximum draft for the voyage and amended as required (e.g.,—result of de-ballasting prior to port entry).
- (j)
- Destination: To be manually entered at the start of the voyage and kept up to date as necessary.
- (k)
- ETA (Estimated Time of Arrival: date; hour; minute; second; UTC 24 h format): To be manually entered at the start of the voyage and kept up to date as necessary.
Appendix K
Appendix K.1. “Big Data” Sets: Meteorological and Oceanographic, “Hind-Cast” or Historical Data
- (a)
- Barometric Air Pressure (mbar): At AIS Ship’s position, AIS Position Timestamp in UTC and sea surface level.
- (b)
- Air Temperature (°C): At AIS Ship’s position, AIS Position Timestamp in UTC and sea surface level.
- (c)
- Air Relative Humidity (%): At AIS Ship’s position, AIS Position Timestamp in UTC and sea surface level.
- (d)
- Air Density (kg/m3): At AIS Ship’s position, AIS Position Timestamp in UTC and sea surface level.
- (e)
- Wind Speed (m/s): At AIS Ship’s position, AIS Position Timestamp in UTC and sea surface level.
- (f)
- Wind Direction (°): At AIS Ship’s position, AIS Position Timestamp in UTC and sea surface level.
- (g)
- Rain, Snow, or Hail Data: At AIS Ship’s position, AIS Position Timestamp in UTC and sea surface level.
- (h)
- Water Depth (m): At AIS Ship’s position (sufficiently deep unconstrained waters needed not be reported/tracked in detail, while the non-availability of depth data would denote an erroneous position ashore).
- (i)
- Water Salinity (g/kg): Average value between surface (zero depth) and depth equal to AIS Ship’s draught, at AIS Ship’s position and AIS Position Timestamp in UTC.
- (j)
- Water Temperature (°C): Average value between surface (zero depth) and depth equal to AIS Ship’s draught, at AIS Ship’s position and AIS Position Timestamp in UTC.
- (k)
- Water Density (kg/m3): Average value between surface (zero depth) and depth equal to AIS Ship’s draught, at AIS Ship’s position and AIS Position Timestamp in UTC.
- (l)
- Water Kinematic Viscosity (m2/s): Average value between surface (zero depth) and depth equal to AIS Ship’s draught, at AIS Ship’s position and AIS Position Timestamp in UTC.
- (m)
- Water Saturated Vapor Pressure (mbar): Average value between surface (zero depth) and depth equal to AIS Ship’s draught, at AIS Ship’s position and AIS Position Timestamp in UTC.
- (n)
- Ice in Water Data: Average value between surface (zero depth) and depth equal to AIS Ship’s draught, at AIS Ship’s position and AIS Position Timestamp in UTC:
- (o)
- Water Current Speed (m/s): Average value between surface (zero depth) and depth equal to AIS Ship’s draught, at AIS Ship’s position and AIS Position Timestamp in UTC.
- (p)
- Water Current Direction (°): Average value between surface (zero depth) and depth equal to AIS Ship’s draught, at AIS Ship’s position and AIS Position Timestamp in UTC.
- (q)
- Wave Data: At AIS Ship’s position, AIS Position Timestamp in UTC and sea surface level.
Appendix L
Appendix L.1. Closest Possible Approximate Representation of One Function by Another [1]
Appendix M
Appendix M.1. Approximation of Residuals in Reference [1]
Appendix N
Appendix N.1. Two Conditions for Attaining Remarkably Close Approximate Representations [1]
Appendix O
Appendix O.1. Components of the Functional Systems to Be Approximated, h(xi, yi, zi, …) [1]
Appendix P
Appendix P.1. Error Component of the Functional Systems to Be Approximated, h(xi, yi, zi, …) [1]
Appendix Q
Appendix Q.1. Contemporary, Shipboard and Universal, “Big Data” Sets Acquisition Systems
- (1.2.1)
- the applicable reference (correction) parameters, specifically referring to the ambient, meteorological and oceanographic, environmental, reference, ideal, still air and water, conditions and ship-tracking data pursuant to Section 2.1.2, Correlation Scheme #2, and Section 2.3, “Big data” set, and the vessel-specific hydrostatic conditions pursuant to Section 2.1.4, Correlation Scheme #4;
- (1.2.2)
- the vessel’s TTW (through-the-water) speed (or simply, log-speed) in the vessel’s forward direction, TTWSFD;
- (1.2.3.2)
- the ambient, meteorological and oceanographic, environmental, actual conditions and ship-tracking data pursuant to Section 2.1.1, Correlation Scheme #1, and, Section 2.3, “Big data” set, as well as, the specific vessel’s service margin pursuant to Section 2.1.3, Correlation Scheme #3.
- (1.2.1)
- the applicable reference (correction) parameters, specifically referring to, the ambient, meteorological and oceanographic, environmental, reference, ideal, still air and water, conditions and ship-tracking data pursuant to Section 2.1.2, Correlation Scheme #2, and Section 2.3, “Big data” set, and also, specific vessel’s hydrostatic conditions pursuant to Section 2.1.4, Correlation Scheme #4;
- (1.2.2)
- the vessel’s TTW (through-the-water) speed (or simply, log-speed) in the vessel’s forward direction, TTWSFD; and also,
- (1.2.3.1)
- the FPP shaft’s rotational speed, r.
Appendix R
Appendix R.1. Stochastic Nature of the Functional System to Be Approximated, h(xi, yi, zi, …) [1]
Appendix S
Appendix S.1. Hybrid Nature of the Approximating Function, H(xi, yi, zi,…; α, β, γ, …) [1]
Appendix T
Appendix T.1. Regulated Definition of Uncertainty by Stochastic Regulatory Context [79,81]
Appendix U
Appendix U.1. FOC Standard Deviation
Appendix V
Appendix V.1. Indicated and Mechanical (Frictional) Efficiencies of the Main Engines
Appendix W
Appendix W.1. Table 5 Details
Appendix X
Appendix X.1. Content of Columns of Table 7 and Table 8 in Section 3.1 and Section 3.2
Appendix Y
Appendix Y.1. Limitations and Conditions for the Application of the Methodology of This Article
- (a)
- the vessel is provided with a Fixed-Pitch Propeller (FPP), and not with a Controllable Pitch Propeller (CPP);
- (b)
- the FPP is directly coupled to the main engine by means of the FPP shaft;
- (c)
- in case the above assumption, (b), is not met, that the FPP is instead coupled to a reduction gearbox driven by the main engine;
- (d)
- in case the above assumption (c) is met, that the reduction gearbox is of fixed and known RPM reduction ratio (Input: Output) and mechanical efficiency;
- (e)
- in cases the determination of the engine power is not possible or evident because the above assumptions are not met, the methodology specified in this article is still applicable for the determination of the FPP shaft power (instead of the engine power);
Appendix Z
Appendix Z.1. Relevant to This Article Existing Engineering Context
- (1)
- The relevant to this article existing engineering context is mainly applied for vessels design, newbuilding, classification and regulatory compliance purposes, including in this regard: towing tank activities under scale, propellers testing and development by means of apparatus and (data acquisition or other) equipment resembling and controlling as far as possible the open waters conditions and the behind hull effect applicable for the propellers actual service conditions including cavitation avoidance, sea trials, as well as academic, industry standard and research contemporary activities such as CFD and FEA analyses pertaining to the above.
- (2)
- Although this truly excellent engineering context is considered by many to be one of the most demanding and challenging among all engineering disciplines, it is still neither easily transferable, nor easily applicable, to actual seagoing conditions, for the reasons discussed in this Appendix Z and in other parts of this article as well.
- (3)
- This context is actually based on the theory of added resistance where the towing resistance force is calculated pursuant to a number of assumptions inherent in the above context. These assumptions include the theoretical (“virtual”) concept that the vessel under consideration is towed by another vessel by means of a marine towing line (rope or cable) sufficiently long so that the towing vessel is not interfering in any other way with the vessel being towed.
- (4)
- In fact, this towing theoretical concept resembles far more the actual conditions experienced, and the (data acquisition or other) apparatus and equipment used, during the towing tank model trials under scale before the newbuilding of a vessel. Any conclusions to be drawn by these towing tank model (under scale) trials’ results, data acquisition and calculations, need to be very cautiously, diligently and vigilantly projected to the actual full scale calculations and considerations. These actual full scale calculations and considerations depend on different applicable similarity and dimensional analysis’ dimensionless blocks/numbers and correlation schemes between model scale and full scale pursuant to the applicable fundamental principle/theory of the Law of Similarity and Dimensional Analysis and the subject engineering context as well.
- (5)
- Considering the fact that an actual standard vessel is self-thrusted/self-propelled by means of her fixed-pitch propeller (FPP), and not towed by a towing vessel by means of a marine towing line, or towed by other means, the effective thrust force induced by her FPP needs to be higher than the respectively applicable calculated towing resistance force. This is so, because of the effect of the, behind the hull, interference of the vessel with her rotating FPP. The difference between the effective thrust force and the towing resistance force is referred to as the thrust loss force. An alternative dimensionless expression of this type of loss may also be the thrust deduction coefficient/factor calculated as a proper function of the towing resistance force and the effective thrust force.
- (6)
- The velocity relative to the vessel at which the water enters the FPP in the axial aft direction, is also referred to as the, arriving water velocity to the FPP, or as the, speed of advance of the FPP; this velocity is lower than the speed at which the vessel is making way relative to (through) the, sea or fresh or other (low salinity), water of bulk mass which in the medium term may be, either still over the ground (OTG) or not, also referred to as the vessel’s TTW (through-the-water) speed (or simply, log-speed) in the vessel’s forward direction, TTWSFD. Such cases of vessels making way relative to (through) the water (TTW) of bulk mass which in the medium term is not still over the ground (OTG), include vessels making way upstream or downstream, relative to: river flows, or ocean/sea currents, or oscillating currents produced by tides also known as tidal streams or tidal currents which may be particularly important in cases of sailing through constrained canals or seaways affected by such currents especially at times of slack water and turning tides.
- (7)
- This lower velocity loss may be expressed as the effective wake velocity standing for the difference between the vessel’s TTW (through-the-water) speed in the vessel’s forward direction, TTWSFD, and the velocity relative to the vessel at which the water actually enters the FPP in the axial aft direction, or, speed of advance of the FPP. An alternative form of expression of this loss may also be the dimensionless, wake fraction coefficient/factor calculated as a proper function of the, TTWSFD, and the speed of advance of the FPP. More relevant information and technical background is available in Appendix E.
- (8)
- In summary, and apart from the listed below dimensionless coefficient/factors (a) and (b) also discussed in points (5), (6) and (7) of this Appendix Z, the following hull and FFP related dimensionless efficiencies (coefficients/factors), (c), (d), (e) and (f), are also defined within the subject engineering context:
- (a)
- thrust deduction coefficient/factor;
- (b)
- wake fraction coefficient/factor;
- (c)
- hull efficiency calculated as a proper function of (a) and (b) above;
- (d)
- FPP open water efficiency;
- (e)
- FPP relative (behind hull effect) efficiency (correction coefficient/factor);
- (f)
- FPP shaft line and stern tube efficiency
- (9)
- The product of the main engine/shaft’s power, times, (f), times, (e), times, (d), times, (c), above, divided by the vessel’s TTW (through-the-water) speed in the vessel’s forward direction, TTWSFD, equals under (quasi-)steady-state conditions, the towing resistance force calculated pursuant to the a/m theory of added resistance.
- (10)
- The above verbal, analytical and computational correlation steps are applicable as far as the following two trial conditions are concerned, which as discussed above are also correlated to each other:
- (i)
- The towing tank model trials under scale before the newbuilding of a vessel, which may conveniently be performed (tried) for a number of different hydrostatic conditions of the model vessel.
- (ii)
- The sea (power and speed) full scale trials usually performed (tried) in one hydrostatic (loading) condition of the vessel only, laden (usually for tankers), or ballast (usually for other, dry cargo, types of vessels).
- (11)
- During these trial conditions, (i) and (ii) above, the data acquired from the respective systems are analyzed in terms of the content and context of the applicable international and/or industry standards which are embedded to the a/m subject engineering context. In fact, these data are acquired and analyzed in certain occasions, and apart from the attending key stakeholders (shipbuilder and ship owner), in the presence (attendance) of also other parties such as Classification Societies, Flag Administrations and/or Competent Regulatory Authorities.
- (12)
- With regard to the trial conditions (ii) above, and particularly during the sea (power and speed) trials of any vessel, the environmental and other reference conditions are never exactly same to the applicable, set as standard, ideal reference conditions. To this end, a set of corrective calculations are necessary for benchmarking purposes pursuant to the a/m applicable international and/or industry standards which are embedded to the subject engineering context.
- (13)
- Similar, although not exactly same, are also applicable with regard to the trial conditions (i) above, in the sense that different towing tank facilities around the world, usually members of the International Towing Tank Conference, ITTC, also provided with different apparatus and (data acquisition or other) equipment, have also different (unique, singular) experience based (effectively, correction) factors/coefficients.
- (14)
- These different (unique, singular) experience based (effectively, correction) factors/co- efficients are applicable for the a/m projection of the towing tank model (under scale) trials’ results, data acquisition and calculations, to the full scale calculations and considerations, based on different applicable similarity and dimensional analysis’ dimensionless blocks/numbers and correlation schemes between scale model and full scale, pursuant to the applicable fundamental principle/theory of the Law of Similarity and Dimensional Analysis and the subject engineering context as well.
- (15)
- As a result of the above considerations, as these are particularly related to conditions (i) and (ii) above, the shipbuilder may in the best case scenario issue more sets of power and speed curves and reports than the single set of power and speed curve and report pertaining to the condition actually tried (sea trials). In any case the above would be pursuant to the applicable international and/or industry standards which are embedded to the a/m subject engineering context.
- (16)
- In any of the above trial conditions (i) and (ii), as well as of their specific occurrences (in terms of sets of power and speed curves and reports), a set of dimensionless efficiencies/coefficients/factors, same or similar to, (a)–(f), above are expected to be evaluated, reported and analysed pursuant to the a/m applicable international and/or industry standards. These expectations however depend in practice on the diligence, professionalism and engineering merit of the shipbuilder, as well as on the contracted service level agreement (SLA) and also on the experience, vigilance and prejudice stance of the ship owner. Such as above expectations however may also be included, or not, in any tripartite or other agreement of the above two parties with the Classification Society attending the newbuilding, and/or with the Flag Administration, and/or or with any other interested party, in conjunction of course with the extent any relevant mandatory regulatory rules and provisions are applied, or not.
- (17)
- Other than the above trial conditions (i) and (ii), as well as their specific occurrences (in terms of different sets of power and speed curves and reports generated as an outcome of these trials, (i) and (ii), as well as of their combined consideration), the dimensionless efficiencies/coefficients/factors, same or similar to, (a)–(f), above, cannot any more be safely evaluated pursuant to the subject, added resistance oriented, engineering context.
- (18)
- Consequently, also the main engine/shaft’s power cannot any more be determined/predicted pursuant to point (9) of this Appendix Z, based on the following (as applied in the case of point (9) of this Appendix Z): the vessel’s TTW (through-the-water) speed in the vessel’s forward direction, TTWSFD, as well as, the towing resistance force calculated pursuant to the a/m theory of added resistance and with the a/m applicable international and/or industry standards and subject a/m engineering context.
- (19)
- The reason that such conditions, other than the trial conditions (i) and (ii) above and occurrences thereof, cannot any more be analyzed and evaluated in terms of the dimensionless efficiencies/coefficients/factors, same or similar to, (a)–(f), listed in point 8 in this Appendix Z, in the same manner that the trial conditions (i) and (ii) above and their occurrences as well can be, is the following: the above conditions are actual seagoing conditions, and not any more, sea trial conditions or towing tank trial conditions.
- (20)
- This is so because, although the added resistance theory may, safely or not, estimate or predict the towing resistance force under actual seagoing conditions, this does not any more hold true for the dimensionless efficiencies/coefficients/factors, same or similar to, (a)–(f), listed in point 8 in this Appendix Z.
- (21)
- In fact, the dimensionless efficiencies/coefficients/factors, same or similar to, (a)–(f), listed in point 8 in this Appendix Z, may only be calculated under ideal reference trial conditions such as (i) and (ii) above, by taking into account all the requisite systematic factors in terms of relevant data acquired under the controlled trial conditions (i) and (ii) above, and pursuant to the following: the a/m applicable international and/or industry standards which are specifically applicable only within a very close range of their ideal/reference conditions, and always subject to the a/m applicable corrective calculations for benchmarking purposes. In this regard, more relevant information and technical background on random and systematic factors is available in Appendix R, Appendix S and Appendix T.
- (22)
- For overcoming the above shortcomings, different possibilities of sensors and CFD analysis applications under actual seagoing conditions have been considered in the past, without however promising results. One reason among others for this lack of promising results is that the actual seagoing conditions are random and not systematic factors with regard to the above possibilities. For more relevant information and technical background on random and systematic factors, see Appendix R, Appendix S and Appendix T.
- (23)
- Another more promising attempt for coping with the above shortcomings is the semi-empirical/phenomenological approach introduced many decades ago [56,57,58,59,60,61,62,63,64,65], for designing experiments and acquiring, organizing, analyzing and classifying experimental data. This approach is similar in certain terms and ways, however significantly and essentially different in others, to the application of the methodology of the approximate representation of one function by another [1] presented in this article, and particularly in Section 1, Section 1.1.2, Section 2.1, Section 2.3, Section 2.4, Section 3, Section 3.2, Section 3.3 and Section 4, as well as in Appendix A, Appendix B, Appendix C, Appendix D, Appendix E, Appendix F, Appendix G, Appendix I, Appendix J, Appendix K and Appendix Y of it.
| Key Elements & Features of Different Approaches Outlined in Appendix Z | Existing Engineering Context | Semi-Empirical Phenomenological Approach | Approximate Representation of One Function by Another |
|---|---|---|---|
| Vessels design | X | ||
| Vessels newbuilding | X | ||
| Vessels classification | X | ||
| Regulatory compliance | X | ||
| Towing tank model trials | X | ||
| Vessel models under scale | X | ||
| Propellers testing apparatus | X | ||
| Data acquisition apparatus | X | X | Table 2 and Table 3 |
| CFD analysis | Optional | Optional | |
| Towing theoretical concept | X | ||
| Added resistance theory | X | ||
| Full scale calculations | X | ||
| Similarity | X | Section 2.1 and Section 2.1.5 (m) | |
| Dimensional Analysis | X | Section 2.1 and Section 2.1.5 (m) | |
| Thrust force loss | X | Point Z(26) | |
| Effective wake velocity loss | X | Point Z(26) | |
| Factors/Coefficients | Point Z(8) | ||
| Shaft power determination | Point Z(9) | X | Section 1.1, Section 2.1.5 and Section 2.2 |
| Full scale sea trials | X | ||
| Sea trials reports | Point Z(15) | Point Z(26) | |
| Sea trials curves | Point Z(15) | Point Z(26) | |
| Design of experiments | Points Z(23) & Z(24) | ||
| Additional data sensors | Point Z(10) | Points Z(22) & Z(23) | |
| Met/ocean data availability | X | X | Table 2 and Table 3 |
| Vessel data availability | X | X | Table 2 and Table 3 |
| Vessel-tracking/monitoring | Section 2.3, Section 2.3.1 and Section 2.3.2 | ||
| Data sets processing | X | X | Table 1 and Table 3, Appendix H |
| Actual seagoing conditions | Section 1.1, Section 2.1.5 and Section 2.2 | ||
| Section 6.3.1.3 Reference [36] | Point Z(30) | Section 1, Point Z(31) | |
| Section 6.4.3.4 Reference [36] | Point Z(30) | Section 1, Point Z(35) | |
| Section 6.4.3.4.2 Reference [36] | Point Z(30) | Section 1, Point Z(35) |
- (24)
- In fact, although the semi-empirical/phenomenological approach [56,57,58,59,60,61,62,63,64,65] referred to in point (23) of this Appendix Z is, in principle, not dissimilar to the application of the approximate representation of one function by another [1] under actual seagoing conditions presented in this article, the former is still extremely receptive of significant contributions in terms of: clarity, general applicability, endurance, robustness, versatility, physical/technical significance and insight on the basis of fundamental principles. Furthermore, this approach unlike the application of the approximate representation of one function by another [1] under actual seagoing conditions, requires the design of experiments.
- (25)
- Last but not least, the application of the methodology of the approximate representation of one function by another [1] presented in this article connects very effectively to both, the subject engineering context discussed in this Appendix Z, and the semi-empirical/phenomenological approach [56,57,58,59,60,61,62,63,64,65] discussed in points (23) and (24) of this Appendix Z. Considering all different approaches on the subject matter outlined in this Appendix Z, their key elements and features are summarized and compared in Table A1.
- (26)
- In the case of the subject engineering context discussed in this Appendix Z, this is related to the, “virtual” or actual, sea trials, and to their respective sets of power and speed curves and reports, discussed or referred to, under Section 2.1.3 and Section 2.1.4, as well as under the corresponding to these Appendix C and Appendix D, and also in points (10), (11), (12), (15) and (16) in this Appendix Z. This discussion is directly relevant and cross referring to Section 5, Conclusions, as far as the reference of it to Appendix Z in its entirety and to points of it (15), (16) and (26) in particular is concerned, as well as to Appendix E in its entirety, and also to the above points (1), (8)(d), (8)(e), (9), (17), (18), (19), (20), (21) and (25) of Appendix Z.
- (27)
- In the case of the semi-empirical/phenomenological approach [56,57,58,59,60,61,62,63,64,65], the common foundation between the two compared counterparts is that the knowledge, or estimation, and application of the dimensionless efficiencies/coefficients/factors, same or similar to, (a)–(f), listed in point 8 in this Appendix Z is not required, whereas the same also holds also true for the calculation of the main engine/shaft’s power pursuant to point (9) in this Appendix Z. This is so because in both compared counterparts the main engine/shaft’s power is not correlated to the dimensionless efficiencies/coefficients/factors, same or similar to, (a)–(f), listed in point 8 in this Appendix Z or to the towing resistance force calculated pursuant to the a/m theory of added resistance.
- (28)
- The above points (1) to (27) are laid out as background and context reference information only, and by no means are to be considered as an exact account of the subject of this Appendix Z. This is so, among other reasons, due to the fact that the relevant terminology and exact methods applied with regard to the above vary significantly between different stakeholders, organizations, Regulatory Authorities, States and Federations, as well as between different specific areas of application of the above. Or in other words, the standardization and alignment of the exact content of the subject engineering context, internationally and across different groups of entities interested in this content and context, are highly receptive of significant improvements. This reasoning is also directly relevant to the conditions similar to the above, implied in the opening paragraph and in the closing sentence of Reference [1] considering in this regard the affiliation of the author of it at the time of this reference’s first presentation (1943) and publication (1944).
- (29)
- With regard to the IAPP (International Air Pollution Prevention) and EIAPP (Engine IAPP) (re)certification pursuant to Reference [36], the “on-board Engine Parameter Check” method is not the only method (the only available option) for attaining the a/m (re)certification. In fact, Reference [36] offers two (2) additional/alternative, available in principle, methods (options) for the above recertification. Both the above additional/alternative, available in principle for the above (re)certification, methods (options) require the determination of engine power, either by direct measurement (engine shaft power measurement by means of torque meters or strain gauges), or when this is not possible or not feasible or not precise, by additional/alternative indirect methods for the determination of engine power.
- (30)
- These additional/alternative indirect methods for the determination of engine power are referred to (and not specified) in an abstract, vague and generic manner, merely as “last resort” options offered in the context of the “on-board Simplified Measurement” method for confirmation of compliance at renewal, annual and intermediate surveys or confirmation of pre-certified engines for initial certification surveys, pursuant to Section 6.3 of Reference [36], when required, and/or of the “on-board Direct Measurement and Monitoring” method for confirmation of compliance at renewal, annual and intermediate surveys only, pursuant to Section 6.4 of Reference [36].
- (31)
- Pursuant to Section 6.3.1.3 of Reference [36], “… If it is difficult to measure the torque directly, the brake power may be estimated by any other means recommended by the engine manufacturer and approved by the Administration …”
- (32)
- Pursuant to Section 6.3.1.4 of Reference [36], “… In practical cases, it is often impossible to measure the fuel oil consumption once an engine has been installed on board a ship. To simplify the procedure on board, the results of the measurement of the fuel oil consumption from an engine’s pre-certification test-bed testing may be accepted …” This quoted content outlines a very rough, raw, early, simplified and superseded/outdated version only, of the inverse solution to the problem outlined in Section 1.1.1 pursuant to Section 2.2, Section 2.4, Section 3, Section 3.1 and Section 4, as well as to Appendix F, Appendix I and Appendix V.
- (33)
- Pursuant to Section 6.3.3.1 of Reference [36], “… an engine, as may be presented on board, could in many applications, be arranged such that the measurements of torque (as obtained from a specially installed strain gauge) may not be possible due to the absence of a clear shaft …”
- (34)
- Pursuant to Section 6.3.3.2 of Reference [36], “… For propeller law governed equipment, a declared speed power curve may be applied together with ensured capability to measure engine speed, either from the free end or by ratio of, for example, the camshaft speed …” This quoted content outlines a very rough, raw, early, simplified and superseded/outdated version only, of the solution to the problem outlined in Section 1.1.2 pursuant to Section 2.1, Section 2.3, Section 2.4, Section 3, Section 3.2, Section 3.3 and Section 4, as well as to Appendix A, Appendix B, Appendix C, Appendix D, Appendix E, Appendix F, Appendix G, Appendix I, Appendix J, Appendix K and Appendix Y.
- (35)
- Pursuant to Section 6.4.3.4 of Reference [36], “… If it is difficult to measure power directly, uncorrected brake power may be estimated by any other means as approved by the Administration. Possible methods to determine brake power include, but are not limited to:
- 1.
- indirect measurement in accordance with 6.3.3; or
- 2.
- by estimation from nomographs …”
References
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Resolution 128; Council of the County of Hawaii: Hilo, HI, USA, 1973.
- Marquardt, D. An algorithm for least-squares estimation of nonlinear parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Brown, K.M.; Dennis, J.E. Derivative free analogues of the Levenberg-Marquardt and Gauss algorithms for nonlinear least squares approximation. Numer. Math. 1971, 18, 289–297. [Google Scholar] [CrossRef]
- Moré, J.; Garbow, B.; Hillstrom, K. User Guide for MINPACK-1; Argonne National Labs Report ANL-80-74; Argonne National Labs: Argonne, IL, USA, 1980. [Google Scholar]
- Dennis, J.E.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1983. [Google Scholar]
- Kouremenos, D.A.; Rakopoulos, C.D.; Andritsakis, E.C. A non-linear differential equations methodology for the determination of gas properties variation in diesel engines cylinders. In Proceedings of the “ECOS′92” International Conference, Zaragoza, Spain, 15–18 June 1992; pp. 653–664. [Google Scholar]
- Gelegenis, I.; Sokratidou, A.; Andritsakis, E.C.; Tsavdaris, A.; Koumoutsos, N.; Souter, X. Feasibility Study for the District and Greenhouses Heating in Hellas (Greece) via Geothermal Energy; Geothermal Energy Program, EU Program VALOREN 31204; Project Internal Report; Centre for Renewable Energy Sources (CRES): Athens, Greece, 1992. [Google Scholar]
- Trankle, T.L. Identification of ship steering dynamics using inertial sensors. IFAC Proc. Vol. 1985, 18, 179–182. [Google Scholar] [CrossRef]
- Su, H.; Liu, H.; Heyman, W.D. Automated derivation of bathymetric information from multi-spectral satellite imagery using a non-linear inversion model. Mar. Geod. 2008, 31, 281–298. [Google Scholar] [CrossRef]
- Naess, A.; Moan, T. Stochastic Dynamics of Marine Structures; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Yetkin, M.; Mentes, A. Optimization of spread mooring systems with artificial neural networks. In Proceedings of the 16th International Congress of IMAM: “Towards Green Marine Technology and Transport”, Pula, Croatia, 21–24 September 2015; pp. 233–238. [Google Scholar]
- Mohd Noor, C.W.; Mamat, R.; Najafi, G.; Mat Yasin, M.H.; Ihsan, C.K.; Noor, M.M. Prediction of marine diesel engine performance by using artificial neural network model. J. Mech. Eng. Sci. 2016, 10, 1917–1930. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Andritsakis, E.C. DI and IDI diesel engines combustion irreversibility analysis. In Proceedings of the American Society of Mechanical Engineers (ASME) Winter Annual Meeting (WAM), New Orleans, LA, USA, 29 November–3 December 1993; AES-Volume 30/HTD-Volume 266, pp. 17–32. [Google Scholar]
- Rakopoulos, C.D.; Andritsakis, E.C.; Kyritsis, D.C. Availability accumulation and destruction in a DI diesel engine with special reference to the limited cooled case. Int. J. Heat Recovery Syst. CHP Pergamon Press Great Br. 1993, 13, 261–276. [Google Scholar] [CrossRef]
- Giakoumis, E.G.; Andritsakis, E.C. Irreversibility production during transient operation of a turbocharged diesel engine, publication description. Int. J. Veh. Des. 2007, 45, 128–149. [Google Scholar] [CrossRef]
- Andritsakis, E.C. An IT solution for enhancing vessels performance by applying “big–data”/“AI”/“ML” approaches. In Proceedings of the 6th Ship IT Conference, Amaroussion, Athens, Greece, 28 September 2020. [Google Scholar]
- Rakopoulos, C.D.; Andritsakis, E.C.; Hountalas, D.T. Modeling the wave action in the exhaust system of reciprocating internal combustion engines. In Proceedings of the 8th IASTED-MIC International Conference, Grindelwald, Switzerland, 7–10 February 1989; ACTA Press: Calgary, AB, Canada, 1989; pp. 211–214. [Google Scholar]
- Rakopoulos, C.D.; Rakopoulos, D.C.; Kyritsis, D.C.; Andritsakis, E.C.; Mavropoulos, G.C. Exergy evaluation of equivalence ratio, compression ratio and residual gas effects in variable compression ratio spark-ignition engine using quasi-dimensional combustion modeling. Energy 2022, 244 Pt B, 123080. [Google Scholar] [CrossRef]
- Kouremenos, D.A.; Rakopoulos, C.D.; Andritsakis, E.C. A simulation analysis of the unsteady gas flow in the inlet and exhaust manifolds of a multi-cylinder piston internal combustion engine. In Proceedings of the American Society of Mechanical Engineers (ASME) Winter Annual Meeting (WAM), Anaheim, CA, USA, 8–13 November 1992; AES-Volume 27/HTD-Volume 228, pp. 253–270. [Google Scholar]
- Kouremenos, D.A.; Rakopoulos, C.D.; Andritsakis, E.C. Theoretical and experimental investigation of the wave action in the exhaust system of a multi-cylinder, turbocharged, marine, IDI diesel engine. In Proceedings of the American Society of Mechanical Engineers (ASME) Winter Annual Meeting (WAM), New Orleans, LA, USA, 29 November–3 December 1993; AES-Volume 30/HTD-Volume 266, pp. 337–354. [Google Scholar]
- Andritsakis, E.C. Study of the Alternation of Gases in Reciprocating Internal Combustion Engines. Ph.D. Thesis, Mechanical Engineering Department, National Technical University of Athens (NTUA), Athens, Greece, 5 July 1993. [Google Scholar]
- Rakopoulos, C.D.; Andritsakis, E.C.; Hountalas, D.T. The influence of the exhaust system unsteady gas flow and insulation on the performance of a turbocharged diesel engine. Int. J. Heat Recovery Syst. CHP Pergamon Press Great Br. 1995, 15, 51–72. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Antonopoulos, K.A.; Rakopoulos, D.C.; Hountalas, D.T.; Andritsakis, E.C. Study of the performance and emissions of a high-speed direct injection diesel engine operating on ethanol diesel fuel blends. Int. J. Altern. Propuls. 2007, 1, 309–324. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Rakopoulos, D.C.; Hountalas, D.T.; Giakoumis, E.G.; Andritsakis, E.C. Performance and emissions of bus engine using blends of diesel fuel with bio-diesel of sunflower or cottonseed oils derived from Greek feedstock. Fuel J. 2008, 87, 147–157. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Rakopoulos, D.C.; Kyritsis, D.C. Development and validation of a comprehensive two-zone model for combustion and emissions formation in a DI diesel engine. Int. J. Energy Res. 2003, 27, 1221–1249. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Rakopoulos, D.C.; Giakoumis, E.G.; Kyritsis, D.C. Validation and sensitivity analysis of a two zone diesel engine model for combustion and emissions prediction. Energy Convers. Manag. 2004, 45, 1471–1495. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Rakopoulos, D.C.; Mavropoulos, G.C.; Giakoumis, E.G. Experimental and theoretical study of the short term response temperature transients in the cylinder walls of a diesel engine at various operating conditions. Appl. Therm. Eng. 2004, 24, 679–702. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Giakoumis, E.G. Second-law analyses applied to internal combustion engines operation. Prog. Energy Combust. Sci. 2006, 32, 2–47. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Rakopoulos, D.C.; Mavropoulos, G.C.; Kosmadakis, G.M. Investigating the EGR rate and temperature impact on diesel engine combustion and emissions under various injection timings and loads by comprehensive two-zone modeling. Energy 2018, 157, 990–1014. [Google Scholar] [CrossRef]
- Hountalas, D.T.; Mavropoulos, G.C.; Binder, K.B. Effect of exhaust gas recirculation (EGR) temperature for various EGR rates on heavy duty DI diesel engine performance and emissions. Energy 2008, 33, 272–283. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Giakoumis, E.G. Diesel Engine Transient Operation: Principles of Operation and Simulation Analysis; Springer Science & Business Media: London, UK, 2009. [Google Scholar]
- Mavropoulos, G.C. Experimental study of the interactions between long and short-term unsteady heat transfer responses on the in-cylinder and exhaust manifold diesel engine surfaces. Appl. Energy 2011, 88, 867–881. [Google Scholar] [CrossRef]
- Mavropoulos, G.C. Unsteady heat conduction phenomena in internal combustion engine chamber and exhaust manifold surfaces. In Heat Transfer: Engineering Applications; InTech Open: Rijeka, Croatia, 2011. [Google Scholar]
- Mavropoulos, G.C.; Hountalas, D.T. Exhaust Phases in a DI Diesel Engine Based on Instantaneous Cyclic Heat Transfer Experimental Data; SAE Technical Paper 2013-01-1646; SAE International: Warrendale, PA, USA, 2013. [Google Scholar]
- Marine Environment Protection Committee (under a remit) of IMO. Technical Code on Control of Emission of Nitrogen Oxides from Marine Diesel Engines (NOx Technical Code); Marine Environment Protection Committee (MEPC), IMO: London, UK, 2008. [Google Scholar]
- ISO 15550-2002; Internal Combustion Engines—Determination and Method for the Measurement of Engine Power—General Requirements. ISO: Geneva, Switzerland, 2002.
- ISO 14396 First Edition 2002-06-01; Reciprocating Internal Combustion Engines—Determination and Method for the Measurement of Engine Power—Additional Requirements for Exhaust Emissions Tests Pursuant to ISO 8178. ISO: Geneva, Switzerland, 2002.
- ISO 3046-1.2002; Reciprocating Internal Combustion Engines—Performance—Part 1 (Incorporating corrigendum of April 30, 2008): Declarations of Power, Fuel and Lubricating Oil Consumptions, and Test Methods—Additional Requirements for Engines for General Use. ISO: Geneva, Switzerland, 2002.
- ISO 3046-3.2006; Reciprocating Internal Combustion Engines—Performance—Part 3: Test Measurements. ISO: Geneva, Switzerland, 2006.
- ISO 3046-4.2009; Reciprocating Internal Combustion Engines—Performance—Part 4: Speed Governing. ISO: Geneva, Switzerland, 2009.
- Rakopoulos, C.D. Reciprocating Internal Combustion Engines: Dynamics—Balancing—Vibrations; Plaisio Publications: Athens, Greece, 1986. [Google Scholar]
- MAN Diesel & Turbo. Basic Principles of Ship Propulsion; MAN Energy Solutions: Augsburg, Germany, 2011. [Google Scholar]
- MAN Diesel & Turbo. Market Update Note on Light Running Margin (LRM); MAN Energy Solutions: Augsburg, Germany, 2015. [Google Scholar]
- ISO 15016:2002; Ships and Marine Technology—Guidelines for the Assessment of Speed and Power Performance by Analysis of Speed Trial Data. ISO: Geneva, Switzerland, 2002.
- ISO 15016:2015; Ships and Marine Technology—Guidelines for the Assessment of Speed and Power Performance by Analysis of Speed Trial Data. ISO: Geneva, Switzerland, 2015.
- ITTC. Recommended Procedures and Guidelines 7.5-04-01-01.2: Full Scale Measurements Speed and Power Trials—Analysis of Speed/Power Trial Data; Revision 0; ITTC: Zürich, Switzerland, 2005. [Google Scholar]
- ISO/DIS 19030-1-2015; Ships and Marine Technology—Measurement of Changes in Hull and Propeller Performance—Part 1: General Principles. ISO: Geneva, Switzerland, 2015.
- ISO/DIS 19030-2-2015; Ships and Marine Technology—Measurement of Changes in Hull and Propeller Performance—Part 1: Default Method. ISO: Geneva, Switzerland, 2015.
- ISO/DIS 19030-3-2015; Ships and Marine Technology—Measurement of Changes in Hull and Propeller Performance—Part 1: Alternative Methods. ISO: Geneva, Switzerland, 2015.
- Schneekluth, H.; Bertram, V. Ship Design for Efficiency and Economy; Butterworth-Heinemann: Oxford, UK, 1998. [Google Scholar]
- Molland, A.F.; Turnock, S.R.; Hudson, D.A. Ship Resistance and Propulsion: Practical Estimation of Ship Propulsive Power; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Loukakis, T.A.; Dodoulas, A.; Politis, G.; Tzabiras, G.; Kouremenos, D.A.; Maliatsos, K. Ship Propulsion; Kallipos Open Academic Editions: Athens, Greece, 2016; Volumes A, B, C and D. [Google Scholar]
- Insel, M. Uncertainty in the analysis of speed and powering trials. Ocean Eng. 2008, 35, 1183–1193. [Google Scholar] [CrossRef]
- Dinham-Peren, T.A.; Dand, I.W. The need for full scale measurements. In Proceedings of the William Froude Conference: Advances in Theoretical and Applied Hydrodynamics—Past and Future, Portsmouth, UK, 24–25 November 2010. [Google Scholar]
- Lackenby, H. The effect of shallow water on ship speed. Shipbuild. Mar. Engine-Build. 1963, 70, 446–450. [Google Scholar]
- Lackenby, H. Note on the Effect of Shallow Water on Ship Resistance; BSRA Report No. 377; British Shipbuilding Research Association (BSRA): London, UK, 1961. [Google Scholar]
- Kwon, Y.J. The Effect of Weather, Particularly Short Sea Waves, on Ship Speed Performance. Ph.D. Thesis, Department of Naval Architecture and Shipbuilding, University of Newcastle upon Tyne, Newcastle upon Tyne, UK, 1981. [Google Scholar]
- Townsin, R.L.; Kwon, Y.J. Approximate formulae for the speed loss due to added resistance in wind and waves. Trans. R. Inst. Nav. Archit. 1983, 125, 199–207. [Google Scholar]
- Townsin, R.L.; Kwon, Y.J.; Baree, M.S.; Kim, D.Y. Estimating the influence of weather on ships performance. Trans. R. Inst. Nav. Archit. 1993, 135, 191–209. [Google Scholar]
- Kwon, Y.J. Speed loss due to added resistance in wind and waves. Nav. Archit. 2008, 3, 14–16. [Google Scholar]
- Lataire, E.; Vantorre, M.; Delefortrie, G. A prediction method for squat in restricted and unrestricted rectangular fairways. Ocean Eng. 2012, 55, 71–80. [Google Scholar] [CrossRef]
- Steen, S.; Chuang, Z. Measurement of speed loss due to waves. In Proceedings of the Third International Symposium on Marine Propulsion, Launceston, TAS, Australia, 5–8 May 2013. [Google Scholar]
- Lu, R.; Turan, O.; Boulougouris, E.; Banks, C.; Incecik, A. A semi-empirical ship operational performance prediction model for voyage optimization towards energy efficient shipping. Ocean Eng. 2015, 110, 18–28. [Google Scholar] [CrossRef]
- Bentin, M.; Zastrau, D.; Schlaak, M.; Freye, D.; Elsner, R.; Kotzur, S. A new routing optimization tool-influence of wind and waves on fuel consumption of ships with and without wind assisted ship propulsion systems. In Proceedings of the 6th Transport Research Arena, Warsaw, Poland, 18–21 April 2016. [Google Scholar]
- Journée, J.M.J. Prediction of speed and behavior of a ship in a seaway. ISP 1976, 23, 285–301. [Google Scholar] [CrossRef]
- Grigoropoulos, G.J.; Loukakis, T.A.; Perakis, A.N. Sea keeping standard series for oblique seas. Ocean Eng. 2000, 27, 111–126. [Google Scholar] [CrossRef]
- Wang, S.A.; Meng, Q. Sailing speed optimization for container ships in a liner shipping network. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 701–714. [Google Scholar] [CrossRef]
- Xiao, G.; Wang, Y.; Wu, R.; Li, J.; Cai, Z. Sustainable Maritime Transport: A Review of Intelligent Shipping Technology and Green Port Construction Applications. J. Mar. Sci. Eng. 2024, 12, 1728. [Google Scholar] [CrossRef]
- Chen, X.; Dou, S.; Song, T.; Wu, H.; Sun, Y.; Xian, J. Spatial-Temporal Ship Pollution Distribution Exploitation and Harbor Environmental Impact Analysis via Large-Scale AIS Data. J. Mar. Sci. Eng. 2024, 12, 960. [Google Scholar] [CrossRef]
- Mueller, N.; Westerby, M.; Nieuwenhuijsen, M. Health impact assessments of shipping and port-sourced air pollution on a global scale: A scoping literature review. Environ. Res. 2023, 216, 114460. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Fei, Y.; Wan, Z. The relationship between the development of global maritime fleets and GHG emission from shipping. J. Environ. Manag. 2019, 242, 31–39. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Y.; Zhou, Z.; Zhao, J.; Wang, S.; Chen, X. Multiship Speed Measurement Method Based on Machine Vision and Drone Images. IEEE Trans. Instrum. Meas. 2023, 72, 2513112. [Google Scholar] [CrossRef]
- Bilgili, L.; Ölçer, A.I. IMO 2023 strategy-Where are we and what’s next? Mar. Policy 2024, 160, 105953. [Google Scholar] [CrossRef]
- Huang, J.X.; Duan, X.L. A comprehensive review of emission reduction technologies for marine transportation. J. Renew. Sustain. Energy 2023, 15, 032702. [Google Scholar] [CrossRef]
- Wu, X.; Wu, J.; Xu, L. Advanced research on the sustainable maritime transportation. J. Mar. Sci. Eng. 2024, 12, 1104. [Google Scholar] [CrossRef]
- Lagemann, B.; Lindstad, E.; Fagerholt, K.; Rialland, A.; Erikstad, S.O. Optimal ship lifetime fuel and power system selection. Transp. Res. Part D Transp. Environ. 2022, 102, 103145. [Google Scholar] [CrossRef]
- Du, Y.Q.; Meng, Q.; Wang, S.A.; Kuang, H.B. Two-phase optimal solutions for ship speed and trim optimization over a voyage using voyage report data. Transp. Res. Part B Methodol. 2019, 122, 88–114. [Google Scholar] [CrossRef]
- Regulation (EU) 2015/757 of the European Parliament and of the Council of 29 April 2015 on the Monitoring, Reporting and Verification of Carbon Dioxide Emissions from Maritime Transport, and Amending Directive 2009/16/EC; European Union: Brussels, Belgium, 2015.
- Commission Delegated Regulation (EU) 2016/2071 of 22 September 2016 amending Regulation (EU) 2015/757 of the European Parliament and of the Council as Regards the Methods for Monitoring Carbon Dioxide Emissions and the Rules for Monitoring Other Relevant Information; European Union: Brussels, Belgium, 2016.
- Commission Delegated Regulation (EU) 2016/2072 of 22 September 2016 on the Verification Activities and Accreditation of Verifiers Pursuant to Regulation (EU) 2015/757 of the European Parliament and of the Council on the Monitoring, Reporting and Verification of Carbon Dioxide Emissions from Maritime Transport; European Union: Brussels, Belgium, 2016.
- Commission Implementing Regulation (EU) 2016/1927 of 4 November 2016 on Templates for Monitoring Plans, Emissions Reports and Documents of Compliance Pursuant to Regulation (EU) 2015/757 of the European Parliament and of the Council on Monitoring, Reporting and Verification of Carbon Dioxide Emissions from Maritime Transport; European Union: Brussels, Belgium, 2016.
- Commission Implementing Regulation (EU) 2016/1928 of 4 November 2016 on Determination of Cargo Carried for Categories of Ships Other Than Passenger, ro-ro and Container Ships Pursuant to Regulation (EU) 2015/757 of the European Parliament and of the Council on the Monitoring, Reporting and Verification of Carbon Dioxide Emissions from Maritime Transport; European Union: Brussels, Belgium, 2016.
- Resolution MEPC.278(70). Amendments to MARPOL Annex VI (Data Collection System for Fuel Oil Consumption of Ships); IMO: London, UK, 2016.
- Resolution MEPC.282(70). 2016 Guidelines for the Development of a Ship Energy Efficiency Management Plan (SEEMP); IMO: London, UK, 2016.
- Resolution MEPC.292(71). 2017 Guidelines for Administration Verification of Ship Fuel Oil Consumption Data; IMO: London, UK, 2017.
- Resolution MEPC.293(71). 2017 Guidelines for the Development and Management of the IMO Ship Fuel Oil Consumption Database; IMO: London, UK, 2017.
- Resolution MEPC.304(72). Initial IMO Strategy on Reduction of GHG Emissions from Ships; IMO: London, UK, 2018.
- Resolution MEPC.327(75). Encouragement of Member States to Develop and Submit Voluntary National Action Plans to Address GHG Emissions From Ships; IMO: London, UK, 2020.
- Resolution MEPC.333(76). 2021 Guidelines on the Method of Calculation of the Attained Energy Efficiency Existing Ship Index (EEXI); IMO: London, UK, 2021.
- Resolution MEPC.334(76). 2021 Guidelines on Survey and Certification of the Attained Energy Efficiency Existing Ship Index (EEXI); IMO: London, UK, 2021.
- Resolution MEPC.335(76). 2021 Guidelines on the Shaft/Engine Power Limitation System to Comply With the EEXI Requirements and Use of a Power Reserve; IMO: London, UK, 2021.
- Resolution MEPC.336(76). 2021 Guidelines on Operational Carbon Intensity Indicators and the Calculation Methods (CII Guidelines, G1); IMO: London, UK, 2021.
- Resolution MEPC.337(76). 2021 Guidelines on the Reference Lines for Use with Operational Carbon Intensity Indicators (CII Reference Lines Guidelines, G2); IMO: London, UK, 2021.
- Resolution MEPC.338(76). 2021 Guidelines on the Operational Carbon Intensity Reduction Factors Relative to Reference Lines (CII Reduction Factors Guidelines, G3); IMO: London, UK, 2021.
- Resolution MEPC.339(76). 2021 Guidelines on the Operational Carbon Intensity Rating of Ships (CII Rating Guidelines, G4); IMO: London, UK, 2021.
- Resolution MEPC.346(78). 2022 Guidelines for the Development of a Ship Energy Efficiency Management Plan (SEEMP); IMO: London, UK, 2022.
- Resolution MEPC.347(78). Guidelines for the Verification and Company Audits by the Administration of Part III of the Ship Energy Efficiency Management Plan (SEEMP); IMO: London, UK, 2022.
- Resolution MEPC.348(78). 2022 Guidelines for Administration Verification of Ship Fuel Oil Consumption Data and Operational Carbon Intensity; IMO: London, UK, 2022.
- Resolution MEPC.349(78). 2022 Guidelines for the Development and Management of the IMO Ship Fuel Oil Consumption Database; IMO: London, UK, 2022.
- Resolution MEPC.350(78). 2022 Guidelines on the Method of Calculation of the Attained Energy Efficiency Existing Ship Index (EEXI); IMO: London, UK, 2022.
- Resolution MEPC.351(78). 2022 Guidelines on Survey and Certification of the Attained Energy Efficiency Existing Ship Index (EEXI); IMO: London, UK, 2022.
- Resolution MEPC.352(78). 2022 Guidelines on Operational Carbon Intensity Indicators and the Calculation Methods (CII Guidelines, G1); IMO: London, UK, 2022.
- Resolution MEPC.353(78). 2022 Guidelines on the Reference Lines for Use with Operational Carbon Intensity Indicators (CII Reference Lines Guidelines, G2); IMO: London, UK, 2022.
- Resolution MEPC.354(78). 2022 Guidelines on the Operational Carbon Intensity Rating of Ships (CII Rating Guidelines, G4); IMO: London, UK, 2022.
- Resolution MEPC.355(78). 2022 Interim Guidelines on Correction Factors and Voyage Adjustments for CII Calculations (CII Guidelines, G5); IMO: London, UK, 2022.
- Resolution MEPC.375(80). Amendments to the 2021 Guidelines on the Shaft/Engine Power Limitation System to Comply with the EEXI Requirements and Use of a Power Reserve (Resolution MEPC.335(76)); IMO: London, UK, 2023.
- Resolution MEPC.376(80). Guidelines on Life Cycle GHG Intensity of Marine Fuels (LCA Guidelines); IMO: London, UK, 2023.
- Resolution MEPC.377(80). 2023 IMO Strategy on Reduction of GHG Emissions from Ships; IMO: London, UK, 2023.
- Resolution MEPC.388(81). Amendments to the 2022 Guidelines for the Development of a Ship Energy Efficiency Management Plan (SEEMP) (Resolution MEPC.346(78)); IMO: London, UK, 2024.
- Resolution MEPC.389(81). Amendments to the 2022 Guidelines for Administration Verification of Ship Fuel Oil Consumption Data and Operational Carbon Intensity (Resolution MEPC.348(78)); IMO: London, UK, 2024.
- Resolution MEPC.390(81). Amendments to the 2021 Guidelines on the Shaft/Engine Power Limitation System to Comply with the EEXI Requirements and Use of a Power Reserve (Resolution MEPC.335(76)), as Amended by Resolution MEPC.375(80)); IMO: London, UK, 2024.
- Resolution MEPC.391(81). 2024 Guidelines on Life Cycle GHG Intensity of Marine Fuels (2024 LCA Guidelines); IMO: London, UK, 2024.
- Fuel for Thought: Methanol; Expert Insights into the Future of Alternative Fuels; Lloyd’s Register Group Limited: London, UK, 2023.
- Goldberg, R.N.; Weir, R.D. Conversion of temperatures and thermodynamic properties to the basis of the international temperature scale of 1990 (Technical Report). Pure Appl. Chem. 1992, 64, 1545–1562. [Google Scholar] [CrossRef]
- Sharqawya, M.H.; Lienhard, J.H.; Zubair, S.M. Thermophysical properties of seawater: A review of existing correlations and data. Desalination Water Treat. 2010, 16, 354–380. [Google Scholar] [CrossRef]
- ITTC Recommended Procedures 7.5-02-01-03: Fresh Water and Seawater Properties; Revision 2; ITTC: Zürich, Switzerland, 2011.
- Fellmuth, B. Guide to the Realization of the ITS-90: Introduction; Consultative Committee for Thermometry Under the Auspices of the International Committee for Weights and Measures, Bureau International des Poids et Mesures (BIPM): Sèvres, France, 2015. [Google Scholar]
- Nayar, K.G.; Sharqawy, M.H.; Banchik, L.D.; Lienhard, J.H. Thermophysical properties of seawater: A review and new correlations that include pressure dependence. Desalination Water Treat. 2016, 390, 1–24. [Google Scholar] [CrossRef]
- Nayar, K.G.; Sharqawy, M.H.; Lienhard, J.H. Seawater Thermophysical Properties Library Tables; Massachusetts Institute of Technology: Cambridge, MA, USA, 2017. [Google Scholar]
- Aas-Hansen, M. Monitoring of Hull Condition of Ships. Master’s Thesis, Department of Marine Technology, Norwegian University of Science and Technology, Trondheim, Norway, 2010. [Google Scholar]
- Hansen, S.V. Performance Monitoring of Ships. Ph.D. Thesis, Technical University of Denmark (DTU), Kongens Lyngby, Denmark, 2012. [Google Scholar]
- Egill, E. Calculation of Service and Sea Margins. Master’s Thesis, Department of Marine Technology, Norwegian University of Science and Technology, Trondheim, Norway, 2015. [Google Scholar]
- Wiik, S. Voluntary Speed Loss of Ships. Master’s Thesis, Department of Marine Technology, Norwegian University of Science and Technology, Trondheim, Norway, 2017. [Google Scholar]
- Shigunov, V.; Papanikolaou, A. Criteria for minimum powering and maneuverability in adverse weather conditions. In Proceedings of the 14th International Ship Stability Workshop (ISSW), Kuala Lumpur, Malaysia, 29 September–1 October 2014. [Google Scholar]
- Clairaut, A.C. Solution de plusieurs problèmes où il s’agit de trouver des Courbes dont la propriété consiste dans une certaine relation entre leurs branches, exprimée par une Équation donnée. In Histoire de l’Académie Royale des Sciences; Académie Royale des Sciences: Paris, France, 1736; pp. 196–215. [Google Scholar]
- Inman, J. Navigation and Nautical Astronomy for the Use of British Seamen, 3rd ed.; Woodward, C.W., Rivington, J., Eds.; Science and Education Publishing: London, UK, 1835. [Google Scholar]
- Goodwin, H.B. The haversine in nautical astronomy. Nav. Inst. Proc. 1910, 36, 735–746. [Google Scholar]
- Moritz, H. Geodetic Reference System 1980. J. Geod. 2000, 74, 128–133. [Google Scholar] [CrossRef]
- Vincenty, T. Direct and inverse solutions of geodesics on the ellipsoid with application of nested equations. Surv. Rev. 1975, XXII, 88–93. [Google Scholar] [CrossRef]
- Decker, B.L. World Geodetic System 84 Ellipsoidal Gravity (WGS 84). In Proceedings of the 4th International Geodetic Symposium on Satellite Positioning, Austin, TX, USA, 28 April–2 May 1986. [Google Scholar]
- National Imagery and Mapping Agency (NIMA) Technical Report TR 8350.2, 3rd ed.; Amendment 1; Department of Defense World Geodetic System 1984, National Geospatial-Intelligence Agency (NGA), NGA Campus East (NCE), Fort Belvoir: Springfield, VA, USA, 2000.
- IMO. Resolution A.526(13): Performance Standards of Rate–Of–Turn Indicators; IMO: London, UK, 1983. [Google Scholar]
- IMO. Resolution A.601(15): Provision and Display of Maneuvering Information Onboard Ships; IMO: London, UK, 1987. [Google Scholar]
- IMO. Resolution MSC.137(76): Standards for Ship Maneuverability; IMO: London, UK, 2002. [Google Scholar]
- IMO. MSC/Circ.1053: Explanatory Notes to the Standards for Ship Maneuverability; IMO: London, UK, 2002. [Google Scholar]
- IMO. A.917(22): Guidelines for the Onboard Operational Use of Shipborne Automatic Identification Systems (AIS); IMO: London, UK, 2002. [Google Scholar]
- IMO. SN/Circ.227: Guidelines for the Installation off a Shipborne Automatic Identification System (AIS); IMO: London, UK, 2003. [Google Scholar]
- IMO. Resolution A.1106(29): Revised Guidelines for the Onboard Operational Use of Shipborne Automatic Identification Systems (AIS); IMO: London, UK, 2015. [Google Scholar]
- Aarsæther, K.G.; Moan, T. Combined Maneuvering Analysis, AIS and Full-Mission Simulation. Int. J. Mar. Navig. Saf. Sea Transp. 2007, 1, 31–36. [Google Scholar]
- Jalkanen, J.P.; Brink, A.; Kalli, J.; Stipa, T. State of the art—AIS based emission calculations for the Baltic Sea shipping. Croat. Meteorol. J. 2008, 43, 177–180. [Google Scholar]
- Androjna, A.; Perkovič, M.; Pavic, I.; Mišković, J. AIS Data Vulnerability Indicated by a Spoofing Case-Study. Appl. Sci. 2021, 11, 5015. [Google Scholar] [CrossRef]
- Li, H.H.; Jiao, H.; Yang, Z.L. AIS data-driven ship trajectory prediction modelling and analysis based on machine learning and deep learning methods. Transp. Res. Part E Logist. Transp. Rev. 2023, 175, 103152. [Google Scholar] [CrossRef]
- Rakopoulos, C.D. Principles of Reciprocating Internal Combustion Engines: Introduction—Operation—Thermodynamics; Foundas Publications: Athens, Greece, 1991. [Google Scholar]
- Aldous, L.G. Ship Operational Efficiency: Performance Models and Uncertainty Analysis. Ph.D. Thesis, University College London, London, UK, 2015. [Google Scholar]
- Bialystocki, N.; Konovessis, D. On the estimation of ship’s fuel consumption and speed curve: A statistical approach. J. Ocean Eng. Sci. 2016, 1, 157–166. [Google Scholar] [CrossRef]
- Rakopoulos, C.D. Heat and Mass Transfer II; Plaisio Publications: Athens, Greece, 1985. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andritsakis, E.C. A Method for the Solution of Certain Non-Linear Problems of Combined Seagoing Main Engine Performance and Fixed-Pitch Propeller Hydrodynamics with Imperative Assignment Statements and Streamlined Computational Sequences. Computation 2025, 13, 202. https://doi.org/10.3390/computation13080202
Andritsakis EC. A Method for the Solution of Certain Non-Linear Problems of Combined Seagoing Main Engine Performance and Fixed-Pitch Propeller Hydrodynamics with Imperative Assignment Statements and Streamlined Computational Sequences. Computation. 2025; 13(8):202. https://doi.org/10.3390/computation13080202
Chicago/Turabian StyleAndritsakis, Eleutherios Christos. 2025. "A Method for the Solution of Certain Non-Linear Problems of Combined Seagoing Main Engine Performance and Fixed-Pitch Propeller Hydrodynamics with Imperative Assignment Statements and Streamlined Computational Sequences" Computation 13, no. 8: 202. https://doi.org/10.3390/computation13080202
APA StyleAndritsakis, E. C. (2025). A Method for the Solution of Certain Non-Linear Problems of Combined Seagoing Main Engine Performance and Fixed-Pitch Propeller Hydrodynamics with Imperative Assignment Statements and Streamlined Computational Sequences. Computation, 13(8), 202. https://doi.org/10.3390/computation13080202





