Abstract
We propose a two-stage statistical learning framework to investigate how financial news headlines posted over weekends affect stock returns. In the first stage, Natural Language Processing (NLP) techniques are used to extract sentiment features from news headlines, including FinBERT sentiment scores and Impact Probabilities derived from Logistic Regression models (Binomial, Multinomial, and Bayesian). These Impact Probabilities estimate the likelihood that a given headline influences the stock’s opening price on the following trading day. In the second stage, we predict over-weekend log returns using various sets of covariates: sentiment-based features, traditional financial indicators (e.g., trading volumes, past returns), and headline counts. We evaluate multiple statistical learning algorithms—including Linear Regression, Polynomial Regression, Random Forests, and Support Vector Machines—using cross-validation and two performance metrics. Our framework is demonstrated using financial news from MarketWatch and stock data for Apple Inc. (AAPL) from 2014 to 2023. The results show that incorporating sentiment features, particularly Impact Probabilities, improves predictive accuracy. This approach offers a robust way to quantify and model the influence of qualitative financial information on stock performance, especially in contexts where markets are closed but news continues to develop.
1. Introduction
Due to the widespread use of the Internet and increasing interconnectedness, financial news headlines impact the market within seconds [1]. These headlines may carry positive, negative, or neutral sentiment and often influence investors’ decisions to buy or sell stocks. Recent advances in Natural Language Processing (NLP) and statistical learning methods have made the influence of financial news on the market an increasingly appealing and dynamic field of research.
Sentiment analysis, or opinion mining, is a method for extracting underlying sentiment from text [2]. It has been effectively applied in diverse fields, such as political analysis [3], online and product reviews [4,5], and fake news detection [6]. In finance, sentiment analysis has evolved from relying on predefined financial phrases to incorporating more advanced language models. For instance, the Financial PhraseBank, a structured collection of financial news, was first published in 2013 [7].
In recent years, natural language processing tools have significantly advanced, leading to the adoption of models such as FinBERT and VADER for financial sentiment analysis [8,9]. FinBERT (Financial Bidirectional Encoder Representations from Transformers) is a finance-specific adaptation of BERT, a natural language processing model developed by Google in 2019 [10]. FinBERT is pre-trained on financial texts and assigns probabilities to whether a sentence is positive, negative, or neutral in financial tone. VADER (Valence Aware Dictionary and Sentiment Reasoner) is a lexicon- and rule-based sentiment analysis tool available in the nltk Python library (version 3.8.1). More recently, Large Language Models (LLMs) have gained popularity for sentiment analysis, including BloombergGPT by Bloomberg [11], the open-source FinGPT by AI4Finance [12], Instruct-FinGPT by Zhang et al. [13], and other LLMs, including BERT, OPT, and FinBERT [14,15,16].
Statistical learning algorithms have proven useful for modelling, predicting, and classifying financial sentiment. For example, Prabhat et al. analyzed the sentiment of Twitter messages using supervised learning algorithms such as Naïve Bayes (NB) and Logistic Regression (LR), in combination with the Apache Mahout and Apache Hadoop frameworks [17]. Similarly, Hasanli and Rustamov examined the sentiment of Azerbaijani tweets using Logistic Regression, Naïve Bayes, and Support Vector Machines (SVMs) [18].
Using a news archive from FINET, a major Hong Kong-based financial news vendor, Li et al. investigated the impact of news sentiment on stock returns, focusing on SVM [19]. He et al. analyzed how financial news influences asset prices, specifically studying stocks such as Apple Inc. (AAPL) and the Dow Jones Index (DJIA). Their research examined the effects of news on daily returns and trading volume. Using Logistic Regression models, they classified news headlines as positively impactful, negatively impactful, or non-impactful [20].
The objectives of this study are multifold. First, we conduct a correlation analysis using two-sided t-tests to determine the statistical significance of FinBERT sentiment scores and the number of news articles mentioning Apple Inc. published on the MarketWatch website (https://www.marketwatch.com, accessed on 5 May 2024), applying correction criteria for multiple hypothesis testing. We then apply FinBERT as a sentiment analysis tool to each financial news headline and use various Natural Language Processing (NLP) techniques to create a Bag of Words representation. To estimate the probabilities of financial news headlines having a positive or negative impact, we implement various Logistic Regression models, including Binomial, Multinomial, and Bayesian approaches. Furthermore, we apply statistical learning methods at different stages of our study, incorporating Linear Regression, Polynomial Regression, Random Forests, and Support Vector Regression. These models integrate features beyond the Impact Probabilities obtained through Logistic Regression, such as trading volume metrics, FinBERT-generated sentiment scores, the number of news headlines published on MarketWatch, and weekday returns prior to each weekend, to better understand their influence on stock market returns. Finally, we evaluate these statistical learning methods using different sets of covariates to determine which approach yields the best predictive performance.
Weekends provide a unique setting in which information accumulates while trading is paused. This disconnect can cause price adjustments when the market opens on Monday. Unlike intraday or pre-market periods, weekend news cannot be immediately acted upon, which can increase sentiment spillovers. This aligns with the classic literature on the “weekend effect” in financial markets, where average Monday returns tend to be lower—often due to the buildup of information and sentiment during non-trading hours [21,22]. It contradicts the Efficient Market Hypothesis, which argues that stocks always trade at their fair value on exchanges, since it suggests that all available information is instantly and fully reflected in asset prices, leaving no room for predictable patterns or systematic anomalies like the weekend effect. Our focus on over-weekend returns is therefore both empirically and theoretically justified.
While pre- and post-market sessions allow limited trading via electronic communication networks or institutional platforms, the weekend represents a complete market closure. This fundamental difference increases the likelihood of delayed reactions and behavioural biases, making it a natural and less-studied period for examining how sentiment influences asset prices.
We focus on Apple Inc. (AAPL) because of its high media visibility, frequent news coverage, and importance in the technology sector, which makes it a representative and data-rich subject for examining the effects of weekend financial news on stock returns.
The paper is structured as follows. In Section 2, we review the related literature. In Section 3, we outline the data preparation process, including the selection and rationale for our time frame, define the trading volume metrics, and provide a brief overview of FinBERT and its sentiment scores. We also apply various NLP techniques—tokenization, lemmatization, synonym normalization, named entity recognition, and stopword removal—to determine which words should be included in the Bag of Words. In Section 4, we outline the Logistic Regression models used to compute the Impact Probabilities of news headlines over the weekends. Section 5 details our data engineering pipeline and final models, and Section 6 presents our results along with the assessment criteria. Finally, Section 7 summarizes our study and proposes potential directions for future research.
2. Related Literature and Contributions
A growing body of research has demonstrated that investor sentiment—whether extracted from textual sources, survey data, or behavioural proxies—can predict short-term movements in asset prices. Prior work has largely focused on weekday sentiment, particularly news published during trading hours or shortly before the market opens. In particular, Tetlock [23] showed that daily media pessimism, measured from news content in the Wall Street Journal, predicted short-term stock price declines followed by reversals. This work established that qualitative media sentiment can have systematic effects on prices, possibly due to overreaction or delayed information absorption.
Antweiler and Frank’s early research [24] documented that activity on Internet stock message boards can predict market volatility. They found that while this activity has a statistically significant impact on stock returns, the effect is generally small in economic terms. Additionally, they observed that disagreement among messages correlates with a higher trading volume. Similarly, Baker and Wurgler [25] provided an influential review and framework for understanding how investor sentiment can drive mispricings, especially in securities that are hard to arbitrage (e.g., small-cap, high-volatility stocks). Their work helped explain why sentiment effects may persist despite the presence of rational traders.
Other studies have extended this line of research by examining how mood (e.g., weather, sports results), attention (e.g., search volume), and media tone influence return predictability [26,27]. Building on the evolving methodological landscape, Kelly and Ahmad [28] emphasized the role of domain-specific dictionaries in extracting sentiment from financial news. They demonstrated that negative news sentiment could forecast the next-day returns of stocks and crude oil, thus improving trading strategies. More recently, with the rise of advanced natural language processing techniques, researchers have employed BERT-based models for sentiment analysis. Case and Clements [29] observed that sentiment in financial news released before trading hours can predict daily S&P 500 price movements, while longer-term economic sentiment shows a statistically significant negative correlation with monthly returns. Furthermore, Abudy et al. [30] documented how the sentiment around geopolitical events, such as a country’s independence day, influences market reactions across different countries and asset classes.
Social media-based studies such as Bollen et al. [31] and Ranco et al. [32] further demonstrated that real-time sentiment extracted from platforms, such as Twitter or financial news, combined with user engagement data, can predict short-term stock price movements. These approaches typically assume that markets can absorb and respond to sentiment signals with minimal delay. In contrast, our study focuses on weekend-only sentiment, where the absence of trading for a fixed period introduces a rigid information-to-action lag. This structural break offers a natural setting to examine the build-up and delayed incorporation of sentiment, potentially amplifying behavioural or informational effects that may be smoothed out during continuous trading periods.
Our paper fills this gap by analyzing how sentiment extracted from weekend news headlines predicts weekend returns, with particular attention to Impact Probabilities derived via Logistic Regression on a Bag of Words model. This approach offers a complementary angle to prior research. Also, it relates to the “weekend effect” in finance—a well-known anomaly where Monday returns tend to be lower, possibly reflecting post-weekend pessimism or delayed information flows.
3. Data Preparation
3.1. Data Sources
We consider two datasets, from which we develop our data engineering pipeline. The first dataset contains essential sentiment and financial information for each trading day. More precisely, it includes the trading date, the number of headlines (positive, neutral, or negative) posted each day, the average FinBERT sentiment scores (positive, neutral, or negative) of these headlines, and the average combined FinBERT sentiment scores derived from the individual sentiment scores. Additionally, it provides the stock’s opening, closing, high, low, and adjusted closing prices, as well as the trading volume. The dataset also includes trading volume-related metrics: On-Balance Volume (OBV), Average True Range (ATR), and Adjusted Trading Volume (ATV). Notably, the opening, closing, high, low, and adjusted closing prices were obtained via an API from Yahoo Finance using the ticker symbol (AAPL) referring to Apple Inc. stock.
The second dataset contains detailed information on individual financial news headlines posted on MarketWatch. It includes the date each headline was published; the exact text of the financial news headline; the corresponding positive, neutral, and negative FinBERT sentiment scores; the combined FinBERT sentiment scores derived from these individual sentiment scores; and the sentiment label categorizing the headline as positive, neutral, or negative.
We select Apple Inc. due to its media prominence, consistent data availability, and investor sensitivity to tech sector news. Headlines were filtered to include those that mention “Apple” or its products, posted on weekends between January 2014 and December 2023 on the MarketWatch website. Including both weekdays and weekends, there are 24,061 financial news headlines in total, out of which 7497 are classified by FinBERT as negative, 10,238 as neutral, and 6326 as positive. However, there are 2774 financial news headlines posted over weekends, out of which 785 are classified as negative, 1434 as neutral, and 555 as positive.
3.2. Variables
3.2.1. Response Variable
We define the over-weekend log return for the i-th weekend (, where ) as
where represents the opening price of the first trading day after the weekend and represents the closing price of the last trading day before the weekend. For instance, on a regular weekend consisting only of Saturday and Sunday, compares the opening price on Monday with the closing price on Friday. is defined this way to account for bank or federal holidays. That is, if Monday is a statutory holiday, then the opening price considered would be Tuesday’s opening price, while the closing price would still be Friday’s closing price. Note that the original dataset contained 483 weekends. However, for 22 weekends (approximately of observations), no Apple-related financial news headlines were posted on MarketWatch.
In this study, the log returns are standardized:
where the mean log return is
and the standard deviation of log returns is
The histogram of standardized log returns is provided in Figure 1. Note that is used throughout the study when referring to over-weekend log returns.
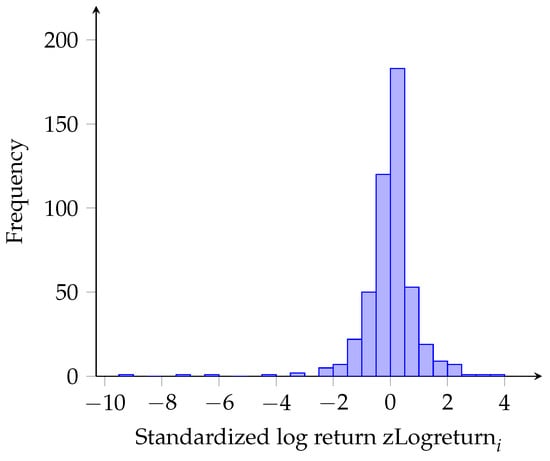
Figure 1.
Histogram of standardized log returns over weekends.
A key point to address is why the opening price of a stock differs from its previous day’s closing price. The closing price of a stock is the final trading price at the end of a trading day, representing the last available price until the next session begins. For equities, it is calculated as the weighted average price over the last 30 min of trading.
In contrast, the opening price is the first price at which a stock trades when the market opens for the day, typically at 9:15 a.m. Before this, from 9:00 a.m. to 9:06 a.m., orders are collected in a pre-market window, and these orders are matched to determine the stock’s opening price based on supply and demand.
Additionally, factors such as After-Market Orders (AMOs) placed after trading hours and news released when the market is closed can influence stock prices. Positive news generally raises prices, while negative news lowers them, leading to fluctuations between the closing and opening prices. Since the market remains closed over the weekend, news posted on Saturday and Sunday can impact the opening price on Monday.
This reasoning, supported by findings from [1], motivated our choice of time frame comparing the opening price on the first trading day after the weekend with the closing price on the last trading day before the weekend—given the nature of our data. If our dataset contained intraday news updates at an hourly or minute-by-minute frequency, alternative time frames might have been more suitable as response variables.
3.2.2. Trading Volume Metrics and Other Covariates
We include volume metrics to capture underlying trends, such as seasonality or bearish/bullish market patterns. To capture these within our final model, we decided, prior to developing the data engineering pipeline, which trading volume metrics had to be included in the final models. We expand our main dataset with three kinds of trading volume metrics, namely, On-Balance Volume, Average True Range, and Average Trading Volume. We use the values computed for those weekdays between the i-th and -st weekends to predict the open price after the i-th weekend.
The On-Balance Volume (OBV) measures the buying and selling pressure based on volumes. It helps identify the strength of price trends. A rising OBV indicates that there is a buying pressure, while a decreasing OBV indicates that there is a selling pressure. It is defined for the t-th day as follows:
where is the on-balance volume from the previous trading day, is the trading volume from the current trading day, and and are the closing prices on the current and previous trading days, respectively.
The Average True Range (ATR) measures the market volatility. It helps establish stop-loss levels and provides insights into market volatility. The True Range (TR) for the t-th trading day is defined as
where is the high price (the stock’s intraday highest trading price) and is the low price (the stock’s intraday lowest trading price).
The Average True Range (ATR) considers a 14-day period. It is defined for the t-th trading day as follows:
The Average Trading Volume (ATV) provides a more accurate reflection of the market activity, as it adjusts the raw volume data to account for certain market factors, such as seasonality. It is defined as follows for the t-th trading day:
where is the adjusted closing stock price.
We also include Intraday Returns for the weekdays prior to each weekend. More specifically, we define the intraday returns as follows:
where and are, respectively, the closing and opening stock prices on weekday t.
FinBERT was initially developed by Dogu Araci as part of their Master’s thesis [6]. FinBERT is a finance-oriented curated version of BERT, which is a natural language processing model developed by Google in 2019 [9].
The primary dataset on sentiment analysis intended for FinBERT is Financial PhraseBank. This dataset comprises 4845 randomly selected English sentences extracted from financial news articles in the LexisNexis database [7]. The FinBERT model, unlike general sentiment analysis models, is trained explicitly on financial text. It uses a multi-layer neural network to classify sentiment into three categories: positive, negative, and neutral. It then produces the corresponding scores we use in our modelling.
FinBERT is particularly well-suited for financial text because it underwent additional pre-training on a large corpus of finance-specific documents—including analyst reports, earnings call transcripts, and financial news—allowing it to internalize financial terminology and context far better than general-purpose models. This domain-specific adaptation helps FinBERT correctly interpret words like “short,” “margin,” or “beat” when they carry nuanced meanings in finance. Yang et al. showed that FinBERT substantially outperformed general BERT methods in financial sentiment classification tasks [33].
FinBERT sentiment scores typically range from 0 to 1 for each sentiment class probability (positive, neutral, and negative), or from to 1 if the output is a single sentiment polarity score, i.e., the combined FinBERT sentiment score. The combined FinBERT sentiment score is calculated by converting the model’s output probabilities for each sentiment class (positive, neutral, and negative) into a single sentiment value. In other words, FinBERT outputs three probabilities corresponding to each sentiment class: , , and . These probabilities satisfy the constraint The predicted sentiment is the class with the highest probability.
The combined sentiment score, denoted , is calculated as
This formulation assigns a weight of to positive sentiment and to negative sentiment, while neutral sentiment is assigned a weight of zero and therefore does not influence the score. Consequently, the score lies within the interval , where indicates fully negative sentiment, indicates fully positive sentiment, and values near zero represent neutral or balanced sentiment.
In Section 4, we also define Impact Probabilities. Section 3.4 discusses NLP techniques necessary to compute the Impact Probabilities prior to fitting Logistic Regression methods. We use three approaches, namely, the Binomial, Multinomial (Trinomial), and Bayesian Logistic Regression models.
3.3. Correlation Analysis of FinBERT Sentiment Scores
Our preliminary investigations show that correlations between over-weekend log returns and (i) the number of news headlines or (ii) the average FinBERT sentiment score of these headlines can be statistically significant () in most cases, based on a two-tailed t-test. In this test, the null hypothesis states that there is no correlation between the two variables (), while the alternative hypothesis asserts the presence of a correlation (). The t-test statistic is defined as
where r is the empirical correlation, n is the number of observations ( for our dataset), and the test statistic follows Student’s t-distribution with degrees of freedom: .
Even when accounting for multiple hypothesis tests using conservative significance levels, such as the Bonferroni or Šidák correction, we find that correlations exceeding 11.3% (Bonferroni) or 11.2% (Šidák) are statistically significant [34]. The statistical significance of correlations between Apple’s weekend stock returns and the number of headlines posted over the weekend motivated us to conduct further research. Refer to Table 1 for the results of our investigation.

Table 1.
Correlations were computed for various weekend-centred time frames between Apple’s stock log returns and (i) the number of positive or negative news headlines published in MarketWatch over the weekend or (ii) the average FinBERT sentiment scores of those headlines. Here, denotes the opening price on the first trading day after the weekend, the opening price on the last trading day before the weekend, the closing price on the first trading day after the weekend, and the closing price on the last trading day before the weekend.
3.4. Bag of Words
A Bag of Words is, in essence, a method of representing text data and describing the occurrence or frequency of words in the text. Bags of Words can be obtained through several NLP techniques. We include five techniques, namely, tokenization, lemmatization, synonym normalization, named entity recognition, and stopwords removal.
Tokenization breaks the given text into individual words or tokens while removing punctuation. It is the first step in NLP, enabling stopword removal, feature extraction, lemmatization, and synonym normalization. In our study, tokenization identifies common words in financial news headlines from MarketWatch.
Defining stopwords involves eliminating common words that add little meaning to the analysis, such as prepositions and auxiliary verbs. The nltk Python package automatically filters out 179 predefined English stopwords (e.g., “where”, “what”, “further”) to which we add others, such as “etc”.
Lemmatization reduces words to their base forms, ensuring consistency. While stemming also simplifies words, it produces less readable tokens. We use lemmatization to preserve context, making it more suitable for sentiment analysis.
Synonym normalization groups words with similar meanings to standardize analysis. We create a dictionary of 40 synonyms, such as firm for company, benefit for profit, and iphone, iphones, and ipad for Apple products.
Named Entity Recognition identifies key terms, ensuring multi-word entities like “Donald Trump” or “Dow Jones Index” remain intact. Other examples include “Apple Inc.,” “Warren Buffett,” “Berkshire Hathaway,” and “Tim Cook.”
Word Frequency Analysis counts word occurrences in texts. Our Bag of Words consists of 370 words, with stock appearing 485 times, the highest, and without 16 times, the lowest. See Figure 2 for an overview. The rationale for restricting the number of words is detailed in Section 4.
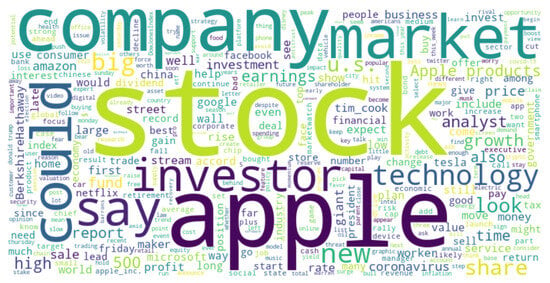
Figure 2.
Word Cloud sample of the Bag of Words. The counts range from 16 for without to 485 for stock.
Observe that the four highest words after stock are apple (381), company (367), market (285), and could (266). Other words of interest are S&P 500 (113); Dow Jones Index (21); Apple products (106); Berkshire Hathaway (72); Tim Cook (86); technology companies, e.g., Microsoft (58), Tesla (54), Facebook (49), Netflix (41); and market sentiments bull (36) and bear (20).
3.5. Temporal Drift Considerations
Recent literature highlights that financial sentiment is not necessarily stationary over time but can evolve in response to changing macroeconomic conditions and shifts in the editorial tone of information sources. For example, research from the Federal Reserve Bank of Cleveland indicates that the economic sentiment derived from the Beige Book aligns closely with the U.S. business cycle fluctuations and displays regional differences, suggesting that sentiment responds to the wider economic environment [35]. Similarly, in [36], Zhang constructed a global macro-news sentiment index using FinBERT-applied GDELT data and demonstrated that sentiment changed alongside structural shifts in global economic regimes, producing what the author called “macro alpha.” These results support the idea that sentiment drift can happen over time, whether due to cyclical macroeconomic changes or gradual editorial shifts. In light of this, we specifically investigate the possibility of temporal drift in our sentiment scores over the nine years. Our analysis, both visual and statistical, finds no significant trend or shift in sentiment over time, confirming the robustness of our sentiment inputs despite the potential for changing economic conditions. One reason for this is that we use news headlines rather than full news articles in our analysis. Headlines are typically crafted to convey the most salient or market-relevant aspect of a story in a concise and often standardized manner. Although the editorial tone may shift over time, headlines tend to be more stable in style and sentiment framing, as journalistic conventions and space constrain them.
To assess potential temporal drift in news sentiment, we conduct a time trend analysis using monthly average combined FinBERT sentiment scores throughout the nine years (see Figure 3). Linear regressions of FinBERT sentiment scores against time (in months) reveal no statistically significant trends for positive () or negative () sentiments. While the neutral category shows a marginally significant upward trend (), the estimated slope was near zero, indicating a practically negligible effect over time. These results support the assumption that news sentiment, as measured by our approach, remains stable over the sample period.
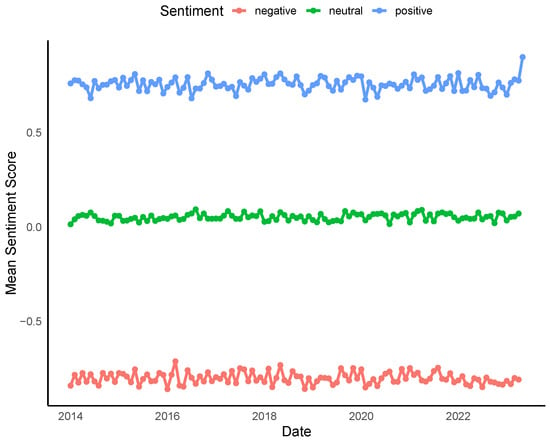
Figure 3.
Monthly average combined FinBERT sentiment scores for news headlines posted from 2014 to 2023 during both weekdays and weekends are shown. Each line indicates the mean combined FinBERT sentiment score for a specific category, namely, positive, neutral, or negative, as classified by FinBERT, aggregated on a monthly basis. The consistent shape of the curves over time suggests there is no significant change in sentiment scores, which confirms the reliability of the sentiment labelling method despite macroeconomic and editorial shifts.
4. Estimating and Aggregating Impact Probabilities
In this section, we introduce a key concept in our modelling framework: the Impact Probability. Intuitively, this refers to the estimated likelihood that a group of specific financial news headlines published over the weekend will significantly affect the stock’s opening price on the following trading day.
In addition to FinBERT sentiment scores, trading volume-related metrics, and weekday returns, we include Impact Probabilities as covariates of the models. To estimate these probabilities, we fit three types of Logistic Regression models, namely, Binomial, Multinomial, and Bayesian Logistic Regression models. For each method, we fit four variations: one for each impact category (news headlines having either a positive or negative effect on weekend returns) and one for each of the two approaches explained below. In these models, the covariates are the vectorized individual words from the Bag of Words.
We consider two approaches. The first approach assesses the total positive or negative impact of all financial news headlines posted over a given weekend. We aggregate these headlines into a single textual input (effectively forming one long headline) and apply the selected Logistic Regression model to estimate their collective effect on the corresponding weekend’s log return.
The second approach evaluates the average impact of individual headlines. Each headline is assessed separately using the Logistic Regression model to estimate its contribution to the weekend return. We then compute the mean positive or negative Impact Probability by averaging the individual headline-level predictions.
The mean Impact Probability is motivated by the law of total probability. The collection of K financial news headlines posted over a given weekend has a positive or negative impact on the log return with probability
where is the impact probability of news headline with , and all K headlines are assumed to be equiprobable.
After standardizing the weekend log returns (denoted as zLogreturn), we classify them as positive if they fall in the upper 75th percentile of the standardized distribution and negative if they fall in the lower 25th percentile. Specifically, weekend log returns above are considered positive, while those below are considered negative:
In summary, we use the following terms consistently throughout:
- Headline-level Impact Probability: Estimated probability that a single headline affects the stock weekend log return.
- Total Impact Probability: Estimated probability by treating all weekend headlines as a single aggregated headline that impacts the stock’s weekend log return.
- Mean Impact Probability: Average of headline-level probabilities across all headlines posted over the weekend affecting the stock weekend log return.
4.1. Logistic Regression Models for Impact Probabilities
We apply Logistic Regression to obtain four Impact Probabilities: the total probability of a positive or negative impact from all news headlines posted over a weekend and the mean probability of a positive or negative impact based on individual headlines.
Out of 461 observations, each representing a weekend, 370 observations, accounting for about 80% of the data, are used to fit the model for the total positive/negative Impact Probabilities. Similarly, out of 2775 observations, where each represents a single financial news headline, 1992 observations, representing about 70% of the data, are used to fit the model for the mean positive/negative Impact Probabilities. The cut-off weekend for all total and mean Impact Probabilities is 3 July 2021, as data after this date are reserved for testing. The Impact Probabilities obtained through Logistic Regression are derived by fitting the same Bag of Words as covariates, with corresponding binary indicator variables—indicating either a positive (negative) or non-positive (non-negative) over-weekend log return based on our thresholds—as response variables.
4.1.1. Approach 1: Total Impact Probability
The Logistic Regression models used to compute the total positive impact of all financial news headlines each weekend (first approach) are generalized as follows:
where denotes the probability that financial news headlines posted over the i-th weekend, considered together, have a positive impact on the corresponding log return. represents the 370 words from the Bag of Words corresponding to the i-th weekend used as independent covariates, and denotes their corresponding coefficients. The dependent variable is a binary indicator:
The probability is obtained by exponentiating and solving for the above equation, resulting in the following:
Similarly, the Logistic Regression models used to compute the total negative impact of all financial news headlines each weekend follow the same general form. The probability is defined using the dependent variable
Solve for the Impact Probability to obtain
4.1.2. Approach 2: Mean Impact Probability
We apply the Logistic Regression model to compute the probabilities and that the k-th headline posted over the i-th weekend has a positive impact on the corresponding log return:
where represents the combination of words in the headline. After that, the mean probability of positive (or negative) impact for the financial news headlines posted over the weekend is calculated as follows:
Note that the binary vector , which represents the aggregated headlines posted over the i-th weekend, can be obtained by applying an element-wise maximum function to the binary vectors since all vectors have the same length:
4.1.3. Example
This example helps build intuition for the formal models introduced in the previous subsection. Note that the same rationale as in this example is used for the Multinomial Logistic Regression and Bayesian Logistic Regression approaches.
Let us consider the fourth weekend of January 2014. We have one news headline posted on 25 January 2014 (Headline A: “Letters to Barron’s about income-producing investments, the market’s P/E multiple, a poverty cure, and the constitutionality of accrual accounting”) and three news headlines posted on 26 January 2014 (Headline B: “SEOUL– Samsung Electronics Co. and Google Inc. have signed a long-term cross-licensing deal on technology patents that cover a broad range of areas, the South Korean company said Monday in a statement”, Headline C: “After the worst week for stocks in over a year, investors face a Federal Reserve meeting, an earnings deluge including Apple Inc. and Facebook Inc., plus a host of economic data”, Headline D: “TAIPEI–Taiwanese contract manufacturer Hon Hai Precision Industry Co. aims to more than double its annual revenue to 10 trillion New Taiwan dollars over the next decade as the company steps up its effort to diversify.”) They are respectively considered neutral (neutral score of 0.88), positive (positive score of 0.93), negative (negative score of 0.92), and positive (positive score of 0.94) by FinBERT.
The value of zLogreturn for this weekend is 0.519, which, as mentioned in the previous subsection, is deemed positive. This intuitively makes sense since we see that there are two positive, one neutral, and one negative headlines posted over the weekend.
There are four words in Headline A (HA) appearing in the BOW: income, investment, letter, market. There are eight words in Headline B (HB) appearing in the BOW: company, deal, long, monday, say, sign, technology, and term. There are eleven words in Headline C (HC) appearing in the BOW: apple, data, earnings, economic, face, government, include, investor, plus, reserve, and stock. There are six words in Headline D (HD) appearing in the BOW: aim, annual, company, new, revenue, and step.
The total positive impact probability can be calculated as follows:
Thus, is nearly 1.
On the other hand, the mean positive impact probability is obtained as the average of the four headline-level Impact Probabilities calculated as follows:
The average of these is then:
4.2. Multinomial Logistic Regression
The standard (Binomial) Logistic Regression method is limited to a response variable with only two outcomes. In contrast, Multinomial Logistic Regression expands this capability, accommodating more than two possible outcomes [37]. This approach is often utilized as a classification algorithm for cases where the response variable contains multiple categories. In our scenario, we implement Trinomial Logistic Regression, which involves a response variable with three categories: weekend-associated log returns identified as positive, weekend-associated log returns labelled as negative, and those categorized as neutral, which includes weekend-associated log returns that fall in between.
The definition of binary indicator variables changes. For the positive impact probability models, we have
where the dependent variable is a binary indicator variable such that
For the negative impact probability models, we have
where the dependent variable is a binary indicator variable such that
Note that the main difference between Multinomial Logistic Regression and Binomial or Bayesian Logistic Regression is that, unlike the Binomial or Bayesian cases, in Multinomial Logistic Regression we work with two Logistic Regression models encompassing three classes. Specifically, the total and mean positive Impact Probabilities are modelled based on positive log returns in relation to neutral log returns, while the total and mean negative Impact Probabilities are modelled based on negative log returns in relation to neutral log returns.
In the Binomial or Bayesian cases, the total and mean positive Impact Probabilities are modelled using positive log returns relative to both neutral and negative log returns. Likewise, the total and mean negative Impact Probabilities are modelled using negative log returns relative to both neutral and positive log returns.
4.3. Bayesian Logistic Regression
The key concepts in Bayesian statistics are the prior probability, the likelihood, and the posterior probability. The prior probability represents what is known about the possible values of a parameter before observing the current data. The likelihood is the probability of observing the given data under different parameter values. The posterior probability is the updated probability of a parameter, denoted , after observing the data , thereby combining the prior with the likelihood. This is expressed as:
where is the posterior probability distribution, is the likelihood, is the prior probability distribution, and is the marginal likelihood (i.e., the evidence or normalizing constant that ensures that the posterior is a valid probability distribution). In other words, the posterior distribution represents our updated belief about after observing the data , the likelihood is the probability of the data given , the prior is the belief about before seeing the data, and the evidence is the normalizing constant.
In standard Logistic Regression models, the words in the Bag of Words are treated as independent covariates. Although these covariates are not binary per se, they resemble indicator variables because most financial news headlines do not contain every word in the Bag of Words. In other words, the covariate vectors contain many zeros. When applying Bayesian Logistic Regression, it is reasonable to assume that our regression coefficients follow standard Normal distributions. That is, the prior distributions for the regression coefficients are
More specifically, our data observations are modelled as follows:
and our prior distributions are . Note that represents the binary indicator variable for positive or negative impact (as defined in Section 4.1), and denotes an observation of .
The likelihood function is given by:
where . Here, represents the specific words from the Bag Of Words appearing in the news headlines posted over the i-th weekend. Similarly, the posterior distribution is:
Substituting the prior density and likelihood function, we obtain
In summary, our posterior distribution is:
4.4. Additional Logistic Regression Methods
We explored two additional Logistic Regression approaches because the coefficients estimated by the Binomial Logistic Regression appeared excessively large. These significant coefficients (e.g., exceeding 100 in absolute value) resulted in Impact Probabilities that are very close to 0 or very close to 1. This phenomenon particularly applies to the total weekend Impact Probabilities, where there are 370 observations alongside 370 covariates. We are encountering the curse of dimensionality, leading to overfitting in our Logistic Regression model, causing perfect separation. Although this would not pose a problem if we were concerned solely with the model’s predictive power, our goal is to derive Impact Probabilities that remain stable regardless of the covariates’ values.
4.4.1. Frequentist Algorithms Attempted: LASSO, Ridge Regression, and Firth’s Logistic Regression
Under the frequentist algorithms, the methods we have also considered include the Least Absolute Shrinkage Selection Operator (LASSO) [38], Ridge Regression [39], and Firth’s Logistic Regression [40]. LASSO and Ridge Regression are both techniques that perform variable selection and regularization to enhance the model’s prediction accuracy and interpretability by introducing penalty terms. LASSO adds a penalty term that is the sum of absolute values of the coefficients: . This penalty sparsifies the coefficients, tending to shrink some coefficients to exactly zero, effectively performing variable selection. Ridge Regression adds a penalty term that is the sum of squared values of the coefficients: . This penalty shrinks the coefficients towards zero but typically does not lead to exact zeros unless the regularization parameter is very large.
Although LASSO and Ridge Regression might have been good starting points to address our dimensionality issue, with optimal , in our data the regularization parameter that controls the strength of the penalty applied to the coefficients causes all coefficients to shrink to zero, implying that no variables appear to be relevant. This complicates our attempts to obtain Impact Probabilities through these methods more than expected.
On the other hand, Firth’s Logistic Regression is a bias-reduced regression method that handles separation in Logistic Regression settings. The formula for Firth’s Logistic Regression involves the penalized likelihood, which adjusts the standard maximum likelihood estimation. The formula for the objective function in Firth’s Logistic Regression is
where are the regression coefficients, is the binary outcome for the i-th observation, is the Fisher information matrix, and is the predicted probability for the i-th observation.
Similar to LASSO and Ridge Regression, Firth’s Logistic Regression has not produced desirable results, which prompts us to look into Bayesian versions of Logistic Regression.
Despite these frequentist approaches, we found that LASSO and Ridge Regression tended to shrink all coefficients toward zero in our high-dimensional Bag of Words setting, limiting variable selection and interpretability. Firth’s Logistic Regression, while effective at reducing bias due to separation, did not yield sufficiently stable estimates for our Impact Probability calculations. By contrast, Bayesian Logistic Regression with standard Normal priors provided greater stability in coefficient estimation and generated more reliable Impact Probability estimates. The Bayesian framework’s use of informative priors allows for effective regularization without overly penalizing coefficients, thus maintaining a balance between model complexity and interpretability. Consequently, we base our primary Impact Probability estimates on the Bayesian logistic models, as they offer a robust and consistent measure of the influence of financial news headlines on stock returns.
4.4.2. Bayesian Algorithms Attempted: Other Prior Distributions
Bayesian Logistic Regression is especially beneficial in situations where data are sparse or the number of predictors is large, providing strong inference in these cases. By incorporating priors, Bayesian Logistic Regression avoids the extreme coefficient shrinkage seen in frequentist regularization methods, thereby maintaining meaningful variable effects essential for interpreting Impact Probabilities. Since our covariates comprise the Bag of Words with 370 words, we determined that the standard Normal prior distribution is the most appropriate choice. Nevertheless, we also explored the Laplace and Horseshoe probability distributions.
For the Laplace prior distribution, we have for all j, with the probability density function . For the Horseshoe prior distribution, we have with , where is a local shrinkage parameter and is a hyperparameter acting as a global shrinkage parameter. Note that is a one-sided Cauchy distribution with a location parameter of 0 and a scale parameter of 1. The probability density function is given by .
Although initially the Horseshoe and Laplace distributions might be more suitable as prior distributions because they have slightly heavier tails than the Normal distribution, it turns out that the standard Normal distribution is more effective at conveying Impact Probabilities that are less sensitive to the covariates.
5. Final Models
5.1. Combined Data and Unified Models
Here, we present an overview of the project, the imputation methods used to handle missing data, and our final modelling approach. After collecting financial data including trading volume metrics and obtaining the total and mean Impact Probabilities, we fit four types of Statistical Learning algorithms with four different sets of covariates.
Since our original datasets include long weekends, some weekdays associated with these long weekends may be missing. Therefore, before applying the Statistical Learning models discussed later in this section, we perform imputation to handle missing data. Imputation is the process of replacing missing or incomplete data with appropriate values. In this study, we use a mixed approach combining Mean Imputation and K-Nearest Neighbour (KNN) methods, where missing values are imputed by averaging the suggested values from KNN and Median Imputation. The features subject to imputation are related to daily trading volume, including the daily OBV, ATR, and ATV, along with their corresponding average measures.
K-Nearest Neighbour imputes missing values by considering the k closest observations (neighbours) in the dataset and using their values to estimate the missing ones. For each missing value, we identify the k closest observations based on the Euclidean distance. In our case, we set k equal to 3, meaning the missing value is imputed using the values from the three nearest neighbours.
Median Imputation replaces missing values with the median of the corresponding feature. We use Median Imputation instead of Mean Imputation, as it is a more robust technique in the presence of outliers [41].
We fit four types of Statistical Learning algorithms: Linear Regression, Polynomial Regression (with varying degrees), Random Forest, and Support Vector Machines.
Polynomial Regression extends Linear Regression by modelling the relationship between the dependent variable and the features using an n-th degree polynomial. Unlike Linear Regression, which models a straight-line relationship, Polynomial Regression can capture curves. We experimented with polynomial degrees up to 10.
Random Forest is an ensemble-based statistical learning algorithm that enhances predictive performance by combining multiple decision trees. Instead of relying on a single decision tree, Random Forests aggregates the predictions of many trees to improve accuracy and reduce overfitting. We use the default parameters in R: 500 trees in the ensemble, with terminal nodes set to 5, and randomly sampled variables at each split, where p represents the total number of covariates.
Support Vector Machines (SVMs) are Statistical Learning algorithms designed to find an optimal hyperplane that maximizes the margin between data points of different categories. We focus on Support Vector Regressors (SVRs), the regression-oriented variant of SVM, specifically using a linear kernel.
To train these algorithms, we employ cross-validation. The training dataset consists of 370 observations, which we divide into 10 folds, each containing 37 observations. During each iteration, one fold is used as the validation set while the remaining folds form the training set. This process repeats ten times, ensuring each fold serves as the validation set once. The model’s performance is evaluated using the Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE), and the results are averaged to estimate the model’s effectiveness.
The first set of covariates does not include features related to Sentiment Analysis. This set, referred to as base, includes the following:
- intraday returns from Tuesday to Friday prior to each weekend,
- the average of intraday returns from Monday to Friday prior to each weekend,
- OBV, ATR, and ATV averages from the five trading days before each weekend.
We exclude Monday’s intraday returns to avoid collinearity with the average of intraday returns from Monday to Friday.
The second set of covariates includes the following:
- positive and negative FinBERT sentiment scores,
- the number of positive news headlines posted each weekend,
- the number of neutral news headlines posted each weekend,
- the number of negative news headlines posted each weekend.
The third set of covariates includes positive and negative total and mean Impact Probabilities derived from each Logistic Regression method.
5.2. Linear Regression
Let us discuss the eight Linear Regression models in detail. Model 1 is based on the Financial data only. Model 2 includes Financial data and FinBERT data. Model 3 includes Financial and FinBERT data plus Impact Probabilities. Model 4 includes Financial data and Impact Probabilities without FinBERT data. The four types of Linear Regression models are the following:
Here, we define the set of base variables as follows:
Similarly, we define the variables related to FinBERT as follows:
Lastly, we define the variables related to the Impact Probabilities as follows:
Note that in Model 3 and Model 4, IP stands for Impact Probability. Since we use three Logistic Regression methods—Binomial, Multinomial, and Bayesian—to model the Impact Probabilities, we fit a total of eight Linear Regression models, including three variations of Model 3 and Model 4.
In summary, we observe that the positive FinBERT sentiment scores is not statistically significant in any of the seven models in which FinBERT sentiment scores are included as covariates. The negative FinBERT sentiment scores, however, are statistically significant in all four models that include FinBERT sentiment scores as covariates. Likewise, the number of positive news headlines posted each weekend is not statistically significant in any of the four models that include FinBERT variables as covariates. In contrast, the number of negative news headlines posted each weekend is statistically significant in three of the four models where FinBERT variables are included as covariates.
The total positive and negative Impact Probabilities are statistically significant in all models where Impact Probabilities are included as covariates. However, the mean positive and negative Impact Probabilities are only statistically significant in four of the six models in which Impact Probabilities are included as covariates. When Impact Probabilities are obtained through Multinomial Logistic Regression, both the mean positive and negative Impact Probabilities are statistically significant .
Refer to Figure A1 and Figure A2 in Appendix A for a summary of the eight Linear Regression models. The summary output includes the Linear Regression coefficient estimates, the standard errors of the coefficient estimates, the corresponding t-values, p-values, and an indication of whether the covariate is significant at (*), (**), or (***).
5.3. Polynomial Regression
We fit eight Polynomial Regression models, each corresponding to a different set of covariates. To create orthogonal polynomials up to a chosen degree, we use the poly function in R. For example, when fitting
the resulting model is a linear combination of first- and second-degree orthogonal polynomial terms of the covariates . If the degree is higher, such as 8, the formula extends up to the eighth-degree term. The poly command relies on the Gram–Schmidt process for these orthogonal transformations [42].
Before applying the test data, we explore the polynomial degrees from 2nd to 10th on the training set. Using RMSE as the metric, a 2nd-degree polynomial yields the lowest RMSE in all models. However, using MAE, degree 2 is selected when no sentiment features are used, when only FinBERT sentiment scores are included, and when FinBERT sentiment scores are combined with Impact Probabilities from Bayesian Logistic Regression. Degree 8 is chosen when only financial data are used (no FinBERT or Impact Probabilities), and degree 6 is chosen when FinBERT sentiment scores are combined with Impact Probabilities from either Logistic Regression or Multinomial Logistic Regression. Refer to Figure A3 in Appendix A for a summary of each model, including coefficient estimates, standard errors, and the corresponding t- and p-values.
5.4. Random Forests
Since Random Forests are non-parametric methods, there is no explicit formula as in Linear or Polynomial Regression, nor can we identify statistically significant covariates in the same way. Therefore, we use the Mean Decrease in Impurity (MDI) to assess the importance of each covariate. MDI quantifies how much a feature reduces impurity in the decision trees, with the Mean Decrease Accuracy component reflecting its contribution to reducing variance in the response variable.
Note that the Mean Decrease in Impurity for regression can be expressed as:
where T is the total number of trees in the forest and is the variance reduction at node n in tree t from splitting on feature . The VarImp function from the caret library computes covariate importance.
In summary, covariate importance follows a consistent pattern across the eight models. Covariates are ranked (from most to least important) as total positive/negative Impact Probabilities, returns on Thursdays and Fridays, ATV/ATR, OBV, positive/negative FinBERT sentiment scores, and finally, the number of positive/negative news headlines posted each weekend. See Figure A4, Figure A5 and Figure A6 in Appendix B for permutation importance plots for each covariate across the eight models.
5.5. Support Vector Machines
Support Vector Regressors are SVMs applied in a regression context. Since SVM methods are non-parametric, there is no explicit formula as in Linear or Polynomial Regression, nor can we determine statistically significant covariates in the same way. Therefore, we use Permutation Importance to estimate the importance of each covariate in our models.
The VarImp function from the caret library computes the permutation importance of each covariate. In essence, we first measure the model’s baseline performance on a validation set. Then, for each covariate, we permute its values in the validation set, make predictions with the SVR model, and calculate the performance drop relative to the baseline.
In summary, the importance of covariates follows a consistent pattern across the eight models. Variables are ranked (from most to least important) as follows: total and mean Impact Probabilities, returns on Thursdays and Fridays, then OBV, ATR, ATV, positive and negative FinBERT sentiment scores, the number of positive and negative news headlines posted each weekend, and finally, returns on Wednesdays. Refer to Figure A7, Figure A8 and Figure A9 in the Appendix B for the Permutation Importance plots for each covariate across the eight models.
6. Results
Here, we examine the predictive performance of our final models and discuss the broader implications of incorporating sentiment-based variables into statistical learning algorithms for forecasting over-weekend stock returns. We focus on a comparative analysis between the base model and sentiment-enhanced models, highlighting their predictive improvements and economic significance.
6.1. Performance Metrics
We measure the performance of the Statistical Learning algorithms described in the previous section using the Root Mean Squared Error (RMSE) and the Mean Absolute Error (MAE). These metrics quantify the difference between predicted and actual values, thereby providing a measure of model performance. We define the RMSE and MAE as follows:
where is the actual value and is the value predicted by the respective model. In our case, represents the associated weekend’s standardized log return.
6.2. Evaluating the Performance of Models
In this subsection, we present the results of our computations. We observe that including Impact Probabilities improves out-of-sample MAE and RMSE performance, especially in nonlinear models such as Polynomial Regression and Support Vector Machines. Notably, the Logistic Regression-based Impact Probabilities perform best. This indicates that explicitly modelling news impact, rather than relying solely on sentiment polarity, provides predictive advantages (see Table 2 and Table 3).

Table 2.
Training and testing RMSEs for each algorithm and set of covariates. TR stands for the training set of data, while TE stands for the testing set of data. IP LR/MLR/BLR denotes Impact Probabilities computed using the Logistic Regression, Multinomial Logistic Regression, and Bayesian Logistic Regression, respectively.

Table 3.
Training and testing MAEs for each algorithm and set of covariates.TR stands for the training set of data, while TE stands for the testing set of data. IP LR/MLR/BLR denotes Impact Probabilities computed using the Logistic Regression, Multinomial Logistic Regression, and Bayesian Logistic Regression, respectively.
Table 2 shows the training and testing RMSEs for the four Statistical Learning algorithms and the eight sets of covariates. Table 3 displays the training and testing MAEs for the four Statistical Learning algorithms and the four sets of covariates. We designated 370 weekends as part of the training dataset and allocated the remaining 91 weekends to the testing dataset, following the standard 80/20 training/testing split [43]. That is, the cut-off weekend for splitting weekends into training or testing is the weekend starting 3 July 2021.
In Table 2, we consider Polynomial Regression of degree 2 for the four sets of covariates. In Table 3, we consider Polynomial Regression with degree 2 when no sentiment analysis features are applied, when only FinBERT sentiment scores are used, and when FinBERT sentiment scores are applied together with Impact Probabilities obtained through Bayesian Logistic Regression. Polynomial Regression with degree 8 is used when only financial data are applied, meaning there are no covariates related to FinBERT or Impact Probabilities. Meanwhile, Polynomial Regression with degree 6 is considered when FinBERT sentiment scores are combined with either Impact Probabilities obtained through Logistic Regression or Multinomial Logistic Regression. When training Polynomial Regression algorithms, we examine degrees from 2 to 10, inclusive. We select the Polynomial Regression algorithm with the lowest training error among the nine versions.
Overall, the MAE values are smaller than the RMSE values. RMSE is more sensitive to outliers because it squares the differences between actual and predicted values. Additionally, when the MAE or RMSE is lower than 1 with standardized variables, it implies that the model’s average prediction error is less than one standard deviation unit. This suggests that the predictions of the Statistical Learning models are relatively close to the actual values, indicating good predictive accuracy within the context of the standardized data. It is observed that considering MAE and the training set, Random Forests, regardless of Impact Probabilities, perform the best. However, when looking at MAE and the testing set, Random Forests with only Impact Probabilities calculated through Logistic Regression perform the best, followed by Polynomial Regression with only Impact Probabilities (with the best ones computed through Multinomial Logistic Regression, followed by Bayesian Logistic Regression and Binomial Logistic Regression). Next, Polynomial Regression with Impact Probabilities and FinBERT variables performs better than Polynomial Regression with only the base variables.
These outcomes remain consistent if we consider RMSE as our deciding assessment criterion. We note that models with FinBERT variables and Impact Probabilities do not necessarily outperform those with either of them alone. Instead, models with only Impact Probabilities perform better than models with only FinBERT variables.
6.3. Base Model Performance and Predictive Value of Sentiment-Enriched Models
Our benchmark model (Model 1, based on Linear Regression) includes only traditional financial covariates such as trading volume metrics (OBV, ATR, and ATV) and intraday returns from weekdays prior to each weekend. On the test dataset, this model yields a Root Mean Squared Error (RMSE) of 1.109 and a Mean Absolute Error (MAE) of 0.834. These values serve as our baseline for assessing the incremental value of sentiment-derived features.
When FinBERT sentiment scores and headline counts are added to the base model (Model 2), the test RMSE improves to 0.750, and the MAE to 0.821. This initial result suggests that textual tone, as captured by FinBERT, holds predictive power beyond traditional financial data indicators.
The inclusion of Impact Probabilities, calculated through Logistic Regression methods applied to the Bag of Words representations of headlines, also contributes to predictive performance.
Model 4, which combines FinBERT and Impact Probabilities, does not consistently outperform Model 3, suggesting that the more comprehensive probabilistic approach to headline impact captures much of the information contained in FinBERT tone scores. Across all models, the highest performance on the test set is seen in sentiment-enriched models, particularly those utilizing logistic-model-derived Impact Probabilities.
6.4. Variable Significance and Feature Importance
Examining statistical significance in the linear regression models indicates that negative FinBERT sentiment scores and the number of negative headlines are consistently significant predictors of over-weekend returns, whereas positive scores are not. This asymmetry suggests that markets respond more strongly to negative sentiment, aligning with behavioural finance theories such as negativity bias and loss aversion.
Furthermore, both total and mean Impact Probabilities are statistically significant in nearly all models where they are included, regardless of the Logistic Regression variant used to compute them. Notably, the Impact Probabilities derived from Multinomial Logistic Regression are the most robust, being significant across the board and associated with lower prediction errors.
In machine learning models such as Random Forests and Support Vector Machines, variable importance rankings confirm the central role of these Impact Probabilities. They consistently rank above both FinBERT sentiment scores and the number of news headlines in predictive value, and often even above core financial features such as OBV or ATR.
6.5. Economic Interpretation and Implications
The empirical improvements in predictive accuracy highlight the economic value of sentiment features. The finding that Impact Probabilities outperform sentiment polarity scores aligns with the idea that not all headlines with a negative tone are impactful—and that context, timing, and phrasing are important. By training classifiers to estimate the likelihood that a given headline actually influences Monday’s return, we provide a more refined market signal relevance.
These results support behavioural theories of financial markets. The significance of negative sentiment and its ability to predict weekend returns aligns with the idea that investors respond more strongly to negative information, especially when trading is delayed. The “weekend effect”, where Monday’s returns tend to be lower on average, may partly reflect the build-up of negative sentiment during the weekend when markets are closed.
Our findings also offer a novel methodological contribution: sentiment should not be regarded as a single score but rather broken down into estimated Impact Probabilities derived from headline content. This method enables us to measure how much weekend news influences return predictability, connecting qualitative textual data with quantitative financial analysis modelling.
6.6. Theoretical Interpretation of Weekend Sentiment Effects
While this study has focused primarily on empirical and statistical modelling, the improvements in predictive performance suggest an underlying mechanism that could be interpreted within established financial theory.
We propose three possible economic explanations:
- (i)
- Delayed Information Processing and Limited Attention. According to models of delayed reaction or limited investor attention [44,45], investors may not fully process news released during weekends until markets open. The improved predictive power of sentiment-based features on Monday’s opening returns could reflect the correction of mispricings caused by staggered information absorption.
- (ii)
- Weekend Risk Premia. Holding stocks over the weekend involves risk exposure when markets are closed. Investors might require a weekend risk premium, especially if news volume or tone suggests uncertainty. Negative sentiment could increase this premium, resulting in lower Monday opening prices. This relates to intertemporal asset pricing models where changes in risk aversion over time influence returns [46].
- (iii)
- Behavioural Sentiment Spillover. Following the work of Baker and Wurgler, investor sentiment may drive temporary mispricings [25]. The effect of weekend sentiment might arise from increased reflection time, decreased distraction, or media amplification influencing retail investor mood disproportionately. Since institutional trading is often paused, this could generate Monday price pressure that corrects during the day or week.
6.7. Summary of Insights
In summary, incorporating sentiment features—particularly Logistic Regression-derived Impact Probabilities—significantly enhances model performance in predicting over-weekend stock returns. These improvements are consistent across various statistical learning techniques, such as Linear Regression, Polynomial Regression, Random Forests, and Support Vector Machines. The findings indicate that sentiment-based variables contain economically meaningful information that traditional financial metrics do not capture alone.
Moreover, our analysis emphasizes the importance of breaking down sentiment into components of influence rather than just tone, allowing a more detailed understanding of how financial news impacts asset pricing. These findings add to an expanding body of literature that aims to model the relationship between textual sentiment and market behaviour, especially in situations where timing issues—like market closures—amplify the significance of qualitative news.
7. Conclusions and Future Work
7.1. Summary of Work
First, we merged the three datasets to create a comprehensive dataset on Apple stock that spans approximately nine years. We then explored NLP techniques to extract the underlying sentiment from financial news headlines by establishing a Bag of Words, which serves as a foundation for calculating the total and mean Impact Probabilities of news headlines on weekend Apple stock log returns. We computed trading volume metrics and incorporated FinBERT sentiment scores along with Impact Probabilities derived from various Logistic Regression methods into the final dataset. We introduced three Logistic Regression methods: Binomial, Multinomial, and Bayesian. Additionally, we examined various statistical machine learning techniques, including LASSO, Ridge Regression, and Firth’s Logistic Regression, while considering other prior distributions in Bayesian Logistic Regression. Furthermore, we fitted four types of Statistical Machine Learning (SML) algorithms—Linear Regression, Polynomial Regression, Random Forests, and Support Vector Machines—to each of the four sets of covariates: those unrelated to sentiment analysis, the latter plus FinBERT sentiment scores, and the latter with Impact Probabilities, trained through cross-validation. Lastly, we compared the performance of these SML algorithms using two assessment metrics: the Root Mean Squared Error (RMSE) and the Mean Absolute Error (MAE).
7.2. Future Work
While this study provides valuable insights using Apple Inc. as a case study, future research should broaden the scope to include multiple stocks from diverse sectors and market capitalizations to assess the robustness and general applicability of the proposed sentiment-driven modelling framework. Different industries and geographic markets may exhibit distinct relationships between news sentiment and stock returns, influenced by varying investor behaviours and information environments. Additionally, incorporating a wider range of data sources—such as social media platforms, analyst reports, and alternative financial news providers—would enrich the sentiment signals and potentially improve predictive performance. Expanding the dataset both in breadth (across assets and regions) and depth (varied data channels) represents a critical direction for future work to enhance the external validity and practical relevance of the models.
Our results indicate that negative sentiment variables tend to be more statistically significant and predictive of stock returns than positive sentiment variables, revealing an asymmetry in how sentiment affects market behaviour. This phenomenon aligns with established behavioural finance theories such as negativity bias, where investors disproportionately weigh negative information, and loss aversion, which suggests that potential losses impact decision-making more strongly than equivalent gains. However, the underlying mechanisms driving this asymmetry warrant further investigation. Future research could strengthen this discussion by conducting robustness checks and sensitivity analysis to confirm the stability of these findings across different time periods, stocks, and market conditions. Additionally, incorporating models that explicitly capture investor psychology and market sentiment asymmetry could provide deeper theoretical insights and improve predictive accuracy.
While our analysis using linear trend tests on monthly aggregated sentiment scores suggests relative stability in sentiment over the nine-year period, we acknowledge that this approach may not fully capture more complex temporal dynamics. Financial sentiment can exhibit nonlinear trends, seasonal patterns, or structural breaks related to macroeconomic events or shifts in media framing that simple linear models might overlook. Future research could apply advanced time series techniques—such as change point detection, regime-switching models, or state-space methods—to more effectively identify subtle shifts and regime changes in sentiment. Moreover, analyzing sentiment at finer temporal resolutions (e.g., weekly or daily) may uncover nuanced patterns that are obscured by monthly aggregation. Incorporating these methods would enhance the robustness and reliability of sentiment-driven models over extended periods.
Furthermore, while this study has focused on three Logistic Regression models to determine the positive and negative Impact Probabilities of financial news headlines over weekends, we believe it would be beneficial to explore other methods. For instance, researchers could build two-stage Logistic Regression models to compute the Impact Probabilities (see [20]).
Additionally, expanding the dataset size could yield valuable insights. Researchers might consider increasing the volume of weekend headlines or adding a more comprehensive news dataset that includes accurate timestamps, enabling analysis of intraday or weekday sentiment changes. Such an extension would also aid in comparing weekend and weekday effects.
Given the temporal nature of financial markets, researchers may also explore time series models, especially for studies that focus on weekdays. These models can capture time-dependent structures and volatility patterns, potentially enhancing predictive accuracy compared to static classification models.
Building based on the findings of this study, there is also potential to explore trading strategies that leverage sentiment-derived signals. For example, one could investigate options-based trading strategies using vanilla European or American call and put options, as suggested in He et al. [20].
Moreover, future research could explore the impact of demographic and contextual variables, such as gender-coded language or toxicity levels, on sentiment interpretation. Prior studies, such as those by Thakur et al. [47] and Kondakciu et al. [48], demonstrate that these factors can considerably influence how sentiment is perceived and how markets respond.
While our analysis focuses solely on Apple Inc., this choice was deliberate: as one of the most actively traded and widely followed stocks, Apple provides an ideal test case for studying sentiment effects, especially over non-trading periods like weekends. The framework and methodology are designed to be generalizable and replicable. Future work can extend this approach to other firms or sectors to explore cross-sectional robustness. Along with expanding our approach to other stocks, we plan to examine how incorporating sentiment-based features can improve the performance of statistical machine learning forecasting models for cryptocurrencies and commodities. Additionally, we can consider other time frames, specifically Open-to-Close, Open-to-Open, Close-to-Close, and Close-to-Open, over trading days. The main challenge is obtaining reliable and extensive datasets for each individual asset.
Lastly, one limitation of this study is that Bag of Words models do not capture semantic relationships between words or their contextual meaning. For example, words with similar financial implications, such as “gain” and “rise,” are treated as entirely distinct features. Future research could explore more advanced representations such as word embeddings (e.g., Word2Vec, GloVe) or contextualized vectors from transformer-based models (e.g., FinBERT), which are better suited to capture the nuances of financial language and sentiment. These techniques may help improve model generalization and interpretability across different financial contexts.
7.3. Conclusions
The primary objective of this paper is to utilize NLP-based techniques to analyze and model the relationship between the weekend log returns of Apple stock and variables related to sentiment analysis (FinBERT sentiment scores and Impact Probabilities), in addition to variables unrelated to sentiment analysis (trading volume metrics, previous weekdays’ returns, and the number of headlines posted over each weekend).
This study suggests that Bayesian Logistic Regression methods should be considered when a small pool of data is available for training Logistic Regression models to obtain Impact Probabilities, given a sufficiently large Bag of Words. With a larger dataset, this study offers the option of using Binomial Logistic Regression or Multinomial Logistic Regression for Impact Probabilities [49].
Furthermore, this study evaluates four different statistical learning algorithms with four distinct sets of covariates, based on two assessment metrics: the RMSE and the MAE. MAE is preferred over RMSE due to being less sensitive to outliers. Consequently, Polynomial Regression with sentiment analysis covariates, such as Impact Probabilities calculated through multinomial or Bayesian Logistic Regression, appears to be the more suitable algorithm.
Across the algorithms fitted, the total Impact Probabilities seem to be more important or statistically significant than the mean Impact Probabilities. While the mean Impact Probability approach offers a more conservative estimate by averaging the effects of individual headlines, it tends to exhibit slightly lower predictive performance compared to the total Impact Probability approach. This suggests that aggregating all headlines into a single combined input can capture stronger collective sentiment signals that enhance predictive accuracy, albeit at the cost of increased sensitivity to specific keywords. Therefore, there is a trade-off between stability and predictive power, with the total Impact Probability providing a more sensitive but potentially less robust measure, and the mean Impact Probability delivering greater robustness with somewhat reduced prediction effectiveness.
In each of the statistical learning algorithms trained, most RMSE or MAE values fall below 1, indicating the effectiveness of these statistical learning algorithms in modelling the relationship between weekend stock log returns and variables related to financial news headlines and, thus, sentiment analysis. Although FinBERT sentiment scores and Impact Probabilities computed through any Logistic Regression method do not significantly enhance the predictive performance of the statistical learning algorithms when they are combined, they do play a crucial role in building the algorithms independently, as demonstrated with statistical significance in the case of linear regression, through variable importance measured by the mean decrease in impurity in the case of Random Forests, and permutation importance in the case of support vector regression.
These predictive gains indicate more than just statistical artifacts. They point to an underlying economic mechanism. The findings are consistent with behavioural theories of sentiment-driven mispricing, models of delayed information processing over non-trading days, or weekend-specific risk premia. A detailed exploration of these mechanisms remains a promising avenue for future research. It would help clarify whether the effect aligns with rational pricing, behavioural biases, or structural frictions in financial markets.
Author Contributions
Conceptualization, R.N.M.; methodology, R.N.M. and P.K.K.; software, P.K.K.; investigation, P.K.K.; analysis, R.N.M. and P.K.K.; writing—original draft preparation, P.K.K.; writing—review and editing, R.N.M.; resources, R.N.M.; supervision, R.N.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was supported by the discovery grant RGPIN-2020-04782 from the Natural Sciences and Engineering Research Council of Canada (NSERC).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been updated to include a Data Availability Statement. This change does not affect the scientific content of the article.
Abbreviations
For the reader’s benefit, we provide a list of abbreviations and their meanings used throughout this paper.
| AMO | After Market Order |
| API | Application Programming Interface |
| ATR | Average True Range |
| ATRAvg | ATR averaged from the five trading days before each weekend |
| ATV | Adjusted Trading Volume |
| ATVAvg | ATV averaged from the five trading days before each weekend |
| BERT | Bidirectional Encoder Representations from Transformers |
| BLR | Bayesian Logistic Regression |
| BOW | Bag of Words |
| FINET | Financial Information Network |
| FinBERT | Financial Bidirectional Encoder Representations from Transformers |
| GPT | Generative Pre-trained Transformer |
| IP | Impact Probability |
| IPPos | (total) Positive Impact Probability |
| IPNeg | (total) Negative Impact Probability |
| IPPos_mean | (mean) Positive Impact Probability |
| IPNeg_mean | (mean) Negative Impact Probability |
| KNN | K-Nearest Neighbours |
| LASSO | Least Absolute Shrinkage Selection Operator |
| LLM | Large Language Model |
| LR | Logistic Regression |
| MAE | Mean Absolute Error |
| MDI | Mean Decrease in Impurity |
| MLR | Multinomial Logistic Regression |
| NB | Naïve Bayes |
| NLP | Natural Language Processing |
| OBV | On-Balance Volume |
| OBVAvg | OBV averaged from the five trading days before each weekend |
| ReturnsAvg | Average of the weekly Returns prior to each weekend |
| ReturnsTu | Intraday Return on Tuesday prior to each weekend |
| ReturnsWd | Intraday Return on Wednesday prior to each weekend |
| ReturnsTh | Intraday Return on Thursday prior to each weekend |
| ReturnsFr | Intraday Return on Friday prior to each weekend |
| RMSE | Root Mean Squared Error |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| VADER | Valence Aware Dictionary and sEntiment Reasoner |
| Glossary of Terms | |
| ATV | Adjusted Trading Volume: A trading volume metric that normalizes raw volume by adjusting for stock splits and dividends, offering a more accurate picture of market activity. |
| BoW | Bag of Words: A text representation method that converts text into a vector of word counts, ignoring grammar and word order but capturing word frequency. |
| BLR | Bayesian Logistic Regression: A probabilistic version of Logistic Regression that incorporates prior beliefs about model parameters and updates these beliefs using observed data. |
| BERT | Bidirectional Encoder Representations from Transformers: A general-purpose pretrained language model developed by Google, forming the base architecture for FinBERT. |
| Cross-val. | Cross-validation: A resampling technique used to evaluate model performance by partitioning data into training and validation sets multiple times. |
| Err. Metrics | Error Metrics: Quantitative indicators (e.g., MAE, RMSE) that measure predictive performance of regression models. |
| Feat. Imp. | Feature Importance: A score indicating how much each variable contributes to a model’s predictive accuracy, often derived from Random Forests or permutation analysis. |
| FinBERT | A domain-specific adaptation of BERT pretrained on financial corpora for sentiment analysis of financial text. |
| IP | Impact Probability: A probability estimated via Logistic Regression that quantifies the likelihood that a news headline will significantly affect the corresponding stock return. |
| IP-Mean | Mean Impact Probability: The average of headline-level Impact Probabilities for a given weekend. |
| IP-Total | Total Impact Probability: The probability that the full set of weekend headlines collectively impacts the stock return. |
| IntradayRet | Intraday Return: The log return from a stock’s opening price to its closing price on the same trading day. |
| LogRet | Log Return: The natural logarithm of the ratio between two stock prices, often used in financial modelling for return calculation. |
| MAE | Mean Absolute Error: A common regression performance metric representing the average absolute difference between predicted and observed values. |
| MDI | Mean Decrease in Impurity: A Random Forest metric that ranks variables based on their ability to reduce classification or regression error. |
| MLR | Multinomial Logistic Regression: A classification algorithm that generalizes Logistic Regression to cases with more than two discrete outcomes. |
| NLP | Natural Language Processing: A field of artificial intelligence focused on enabling computers to process and analyze human language. |
| OBV | On-Balance Volume: A cumulative volume-based indicator used to detect shifts in buying or selling pressure. |
| PermImp | Permutation Importance: A model interpretation technique where feature values are randomly shuffled to test the resulting drop in predictive accuracy. |
| PolyReg | Polynomial Regression: A type of regression that models nonlinear relationships using polynomial terms of the predictors. |
| RF | Random Forests: An ensemble learning algorithm that combines many decision trees to improve predictive power and reduce overfitting. |
| RMSE | Root Mean Squared Error: A regression metric representing the square root of the average of squared prediction errors, penalizing larger errors more heavily. |
| SentSpill | Sentiment Spillover: The phenomenon by which news sentiment released outside of trading hours affects subsequent price movements. |
| zLogRet | Standardized Log Return: A z-score normalized version of log returns, used to compare values across different scales or time periods. |
| SVM | Support Vector Machine: A supervised learning model that separates data classes by finding the optimal boundary (hyperplane) in feature space. |
| SVR | Support Vector Regressor: The regression counterpart to SVM, which fits a function that stays within an epsilon-tube around the data points. |
| VADER | Valence Aware Dictionary and Sentiment Reasoner: A rule-based sentiment tool effective on short, informal text such as social media or headlines. |
Appendix A. Summary of Output for Regression Models
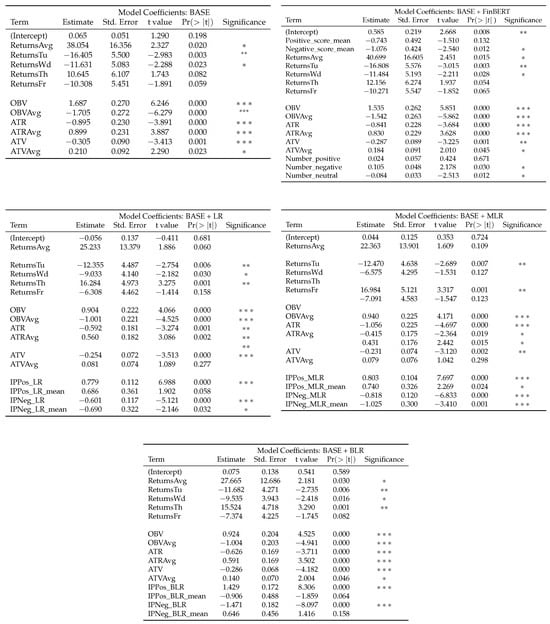
Figure A1.
Summary output for five Linear Regression Models: the model without any Sentiment Analysis covariates, the model with FinBERT positive and negative scores included as covariates, and the three models with total and mean Impact Probabilities included as covariates (Binomial, Multinomial, and Bayesian Logistic Regression methods). For the meaning of the acronyms used here and below, see Abbreviations.
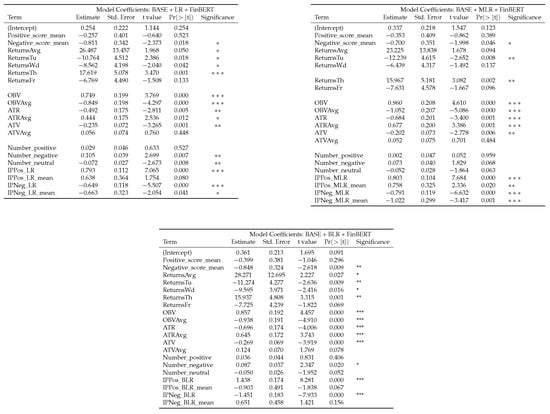
Figure A2.
Summary output for three Linear Regression models where the base variables, FinBERT variables, and total and mean positive and negative Impact Probabilities are included as covariates.
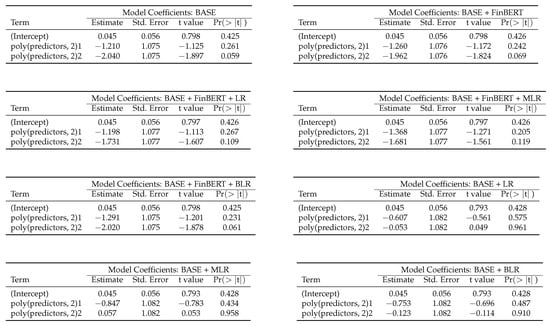
Figure A3.
Summary of RMSE output for the eight Polynomial Regression models. Polynomial Regression with degree 2 is considered when no sentiment analysis features are applied, only FinBERT sentiment scores are used, and when FinBERT sentiment scores are combined with Impact Probabilities obtained through Bayesian Logistic Regression. Polynomial Regression with degree 8 is considered when only financial data is used, i.e., no covariates related to FinBERT and no covariates related to Impact Probabilities. Polynomial Regression with degree 6 is considered when FinBERT sentiment scores are combined with either Impact Probabilities obtained through Logistic Regression or Multinomial Logistic Regression. When training Polynomial Regression algorithms, we consider degrees from 2 to 10, both inclusive.
Appendix B. Summary of Output for Random Forests and SVM Models
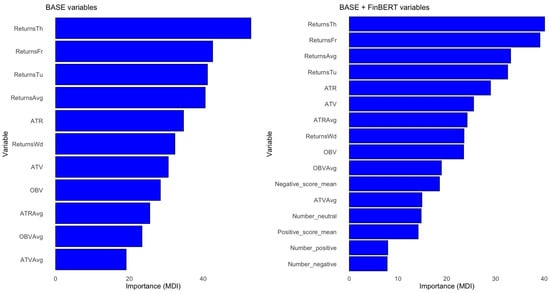
Figure A4.
Variable Importance according to the Mean Decrease in Impurity for the Random Forests models, both without Sentiment Analysis covariates and with Base variables plus FinBERT variables included covariates.
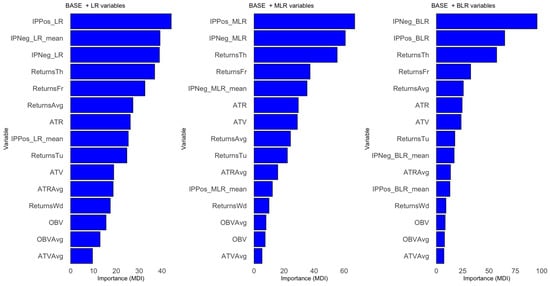
Figure A5.
Variable Importance according to the Mean Decrease in Impurity for the Random Forests models when the base variables, along with the total and mean positive and negative Impact Probabilities, are included as covariates.
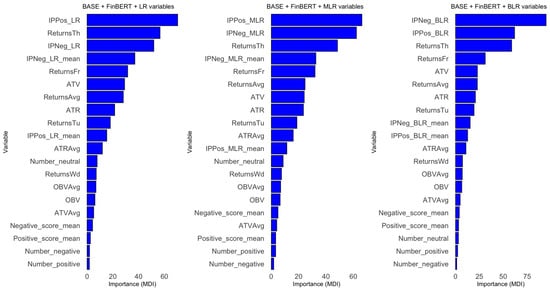
Figure A6.
Variable Importance according to the Mean Decrease in Impurity for the Random Forests models when including the Base variables, FinBERT variables, and the total and mean positive and negative Impact Probabilities are added as covariates.
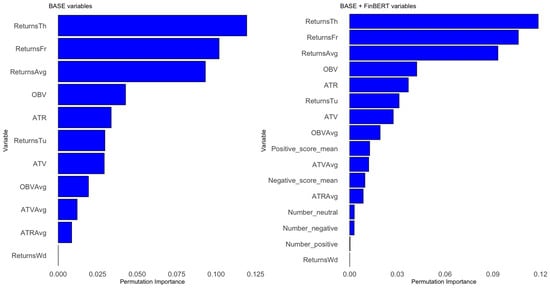
Figure A7.
Permutation Importance according to the Mean Decrease in Impurity for the SVM models, excluding Sentiment Analysis covariates and considering only FinBERT positive and negative scores as well as the count of positive, neutral, and negative news headlines published each weekend covariates.
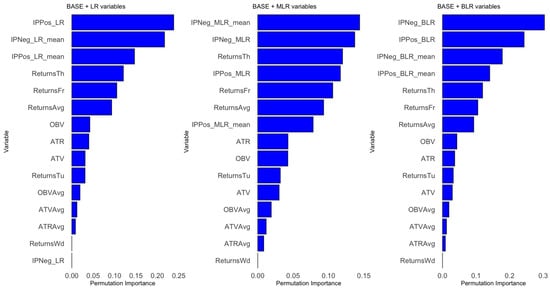
Figure A8.
Permutation Importance according to the Mean Decrease in Impurity for the SVM models when the Base variables plus the total and mean positive and negative Impact Probabilities are included as covariates.
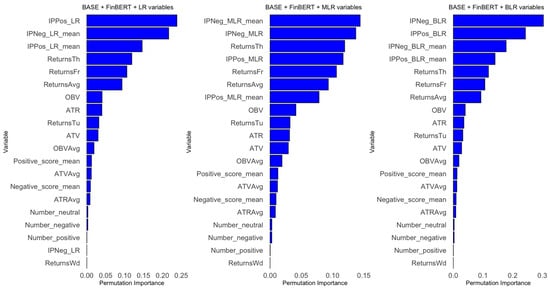
Figure A9.
Permutation Importance according to the Mean Decrease in Impurity for the SVM models when the Base variables, the FinBERT variables plus the total and mean positive and negative Impact Probabilities are included as covariates.
References
- Busse, J.A.; Green, T.C. Market efficiency in real time. J. Financ. Econ. 2002, 65, 415–437. [Google Scholar] [CrossRef]
- Pang, B.; Lee, L. Opinion mining and sentiment analysis. Found. Trends Inf. Retr. 2008, 2, 1–135. [Google Scholar] [CrossRef]
- Ansari, M.Z.; Aziz, M.B.; Siddiqui, M.O.; Mehra, H.; Singh, K.P. Analysis of political sentiment orientations on Twitter. Procedia Comput. Sci. 2020, 167, 1821–1828. [Google Scholar] [CrossRef]
- Abbasi Moghaddam, S. Aspect-Based Opinion Mining in Online Reviews. Master’s Thesis, Simon Fraser University, Burnaby, BC, Canada, 2013. [Google Scholar]
- Hu, M.; Liu, B. Mining and summarizing customer reviews. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle WA USA, 22–25 August 2004; pp. 168–177. [Google Scholar] [CrossRef]
- Alonso, M.A.; Vilares, D.; Gómez-Rodríguez, C.; Vilares, J. Sentiment analysis for fake news detection. Electronics 2021, 10, 1348. [Google Scholar] [CrossRef]
- Malo, P.; Sinha, A.; Takala, P.; Korhonen, P.; Wallenius, J. Good debt or bad debt: Detecting semantic orientations in economic texts. J. Am. Soc. Inf. Sci. Technol. 2014, 66, 723–742. [Google Scholar] [CrossRef]
- Araci, D. FinBERT: Financial sentiment analysis with pre-trained language models. arXiv 2019, arXiv:1908.10063. [Google Scholar] [CrossRef]
- Hutto, C.; Gilbert, E. VADER: A parsimonious rule-based model for sentiment analysis of social media text. In Proceedings of the International AAAI Conference on Web and Social Media, Ann Arbor, MI, USA, 1–4 June 2014; Volume 8, pp. 216–225. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar] [CrossRef]
- Wu, S.; Irsoy, O.; Lu, S.; Dabravolski, V.; Dredze, M.; Gehrmann, S.; Kambadur, P.; Rosenberg, D.; Mann, G. BloombergGPT: A large language model for finance. arXiv 2023, arXiv:2303.17564. [Google Scholar] [CrossRef]
- Yang, H.; Liu, X.Y.; Wang, C.D. FinGPT: Open-source financial large language models. arXiv 2023, arXiv:2306.06031. [Google Scholar] [CrossRef]
- Zhang, B.; Yang, H.; Liu, X.Y. Instruct-FinGPT: Financial sentiment analysis by instruction tuning of general-purpose large language models. In Proceedings of the FinLLM Symposium at IJCAI 2023, Macao, China, 19–25 August 2023. [Google Scholar]
- Jiang, T.; Zeng, A. Financial sentiment analysis using FinBERT with application in predicting stock movement. arXiv 2023, arXiv:2306.02136. [Google Scholar] [CrossRef]
- Gu, W.; Zhong, Y.; Li, S.; Wei, C.; Dong, L.; Wang, Z.; Yan, C. Predicting stock prices with FinBERT-lstm: Integrating news sentiment analysis. In Proceedings of the 2024 8th International Conference on Cloud and Big Data Computing, Oxford, UK, 15–17 August 2024; pp. 67–72. [Google Scholar]
- Kirtac, K.; Germano, G. Sentiment trading with large language models. Financ. Res. Lett. 2024, 62, 105227. [Google Scholar] [CrossRef]
- Prabhat, A.; Khullar, V. Sentiment classification on big data using naïve Bayes and logistic regression. In Proceedings of the 2017 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 5–7 January 2017; pp. 1–5. [Google Scholar]
- Hasanli, H.; Rustamov, S. Sentiment analysis of Azerbaijani twits using logistic regression, Naïve Bayes and SVM. In Proceedings of the 2019 IEEE 13th International Conference on Application of Information and Communication Technologies (AICT), Baku, Azerbaijan, 23–25 October 2019; pp. 1–7. [Google Scholar]
- Li, X.; Xie, H.; Chen, L.; Wang, J.; Deng, X. News impact on stock price return via sentiment analysis. Knowl.-Based Syst. 2014, 69, 14–23. [Google Scholar] [CrossRef]
- He, J.; Makarov, R.N.; Tuero, J.; Wang, Z. Performance Evaluation Metric for Statistical Learning Trading Strategies. Data Sci. Financ. Econ. 2024, 4, 570–600. [Google Scholar] [CrossRef]
- Cross, F. The Behavior of Stock Prices on Fridays and Mondays. Financ. Anal. J. 1973, 29, 67–69. [Google Scholar] [CrossRef]
- French, K.R. Stock Returns and the Weekend Effect. J. Financ. Econ. 1980, 8, 55–69. [Google Scholar] [CrossRef]
- Tetlock, P.C. Giving content to investor sentiment: The role of media in the stock market. J. Financ. 2007, 62, 1139–1168. [Google Scholar] [CrossRef]
- Antweiler, W.; Frank, M.Z. Is All That Talk Just Noise? The Information Content of Internet Stock Message Boards. J. Financ. 2004, 59, 1259–1294. [Google Scholar] [CrossRef]
- Baker, M.; Wurgler, J. Investor sentiment in the stock market. J. Econ. Perspect. 2007, 21, 129–152. [Google Scholar] [CrossRef]
- Engelberg, J.E.; Parsons, C.A. The causal impact of media in financial markets. J. Financ. 2011, 66, 67–97. [Google Scholar] [CrossRef]
- Da, Z.; Engelberg, J.; Gao, P. In search of attention. J. Financ. 2011, 66, 1461–1499. [Google Scholar] [CrossRef]
- Kelly, S.; Ahmad, K. Estimating the impact of domain-specific news sentiment on financial assets. Knowl.-Based Syst. 2018, 150, 116–126. [Google Scholar] [CrossRef]
- Case, J.; Clements, A. The impact of sentiment in the news media on daily and monthly stock market returns. In Proceedings of the Data Mining: 19th Australasian Conference on Data Mining, AusDM 2021, Brisbane, QLD, Australia, 14–15 December 2021; Proceedings 19. Springer: Singapore, 2021; pp. 180–195. [Google Scholar]
- Abudy, M.M.; Mugerman, Y.; Shust, E. National Pride, Investor Sentiment, and Stock Markets. J. Int. Financ. Mark. Inst. Money 2023, 89, 101879. [Google Scholar] [CrossRef]
- Bollen, J.; Mao, H.; Zeng, X.J. Twitter mood predicts the stock market. J. Comput. Sci. 2011, 2, 1–8. [Google Scholar] [CrossRef]
- Ranco, G.; Bordino, I.; Bormetti, G.; Caldarelli, G.; Lillo, M. Coupling news sentiment with web browsing data improves prediction of intra-day price dynamics. EPJ Data Sci. 2014, 3, e0146576. [Google Scholar]
- Yang, Y.; UY, M.C.S.; Huang, A. FinBERT: A Pretrained Language Model for Financial Communications. arXiv 2020, arXiv:2006.08097. [Google Scholar] [CrossRef]
- Sidak, Z. Rectangular confidence regions for the means of multivariate normal distributions. J. Am. Stat. Assoc. 1967, 62, 626–633. [Google Scholar] [CrossRef]
- Filippou, I.; Garciga, C.; Mitchell, J.; Nguyen, M.T. Regional Economic Sentiment: Constructing Quantitative Estimates from the Beige Book and Testing Their Ability to Forecast Recessions; Economic Commentary 2024-08; Federal Reserve Bank of Cleveland: Cleveland, OH, USA, 2024. [Google Scholar]
- Zhang, Z. Macro Alpha from Macro News: A Sentiment-Based Global Asset Pricing Perspective. arXiv 2025, arXiv:2505.16136. [Google Scholar]
- Agresti, A. Foundations of Linear and Generalized Linear Models; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Firth, D. Bias Reduction of Maximum Likelihood Estimates. Biometrika 1993, 80, 27–38. [Google Scholar] [CrossRef]
- Little, R.; Rubin, D. Statistical Analysis with Missing Data, 2nd ed.; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- What Does the R Function poly Really Do? 2013. Available online: https://stackoverflow.com/questions/19484053/what-does-the-r-function-poly-really-do (accessed on 3 August 2024).
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Hong, H.; Stein, J.C. A unified theory of underreaction, momentum trading, and overreaction in asset markets. J. Financ. 1999, 54, 2143–2184. [Google Scholar] [CrossRef]
- Barber, B.M.; Odean, T. All that glitters: The effect of attention and news on the buying behavior of individual and institutional investors. Rev. Financ. Stud. 2008, 21, 785–818. [Google Scholar] [CrossRef]
- Campbell, J.Y.; Cochrane, J.H. By force of habit: A consumption-based explanation of aggregate stock market behavior. J. Polit. Econ. 1999, 107, 205–251. [Google Scholar] [CrossRef]
- Thakur, N.; Cui, S.; Khanna, K.; Knieling, V.; Duggal, Y.N.; Shao, M. Investigation of the Gender-Specific Discourse about Online Learning during COVID-19 on Twitter Using Sentiment Analysis, Subjectivity Analysis, and Toxicity Analysis. Computers 2023, 12, 221. [Google Scholar] [CrossRef]
- Kondakciu, K.; Souto, M.; Zayer, L.T. Self-presentation and gender on social media: An exploration of the expression of “authentic selves”. Qual. Mark. Res. Int. J. 2022, 25, 80–99. [Google Scholar] [CrossRef]
- Sias, R.W.; Starks, L.T.; Turtle, H.J. The negativity bias and perceived return distributions: Evidence from a pandemic. J. Financ. Econ. 2023, 147, 627–657. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).