Adaptive Working Set Model for Memory Management and Epidemic Control: A Unified Approach
Abstract
1. Introduction
2. Methods
2.1. Working Set in Virtual Memory Systems
2.2. Adaptive Working Set in Epidemiological Modeling
2.3. Model States and Equations
3. Modeling and Results
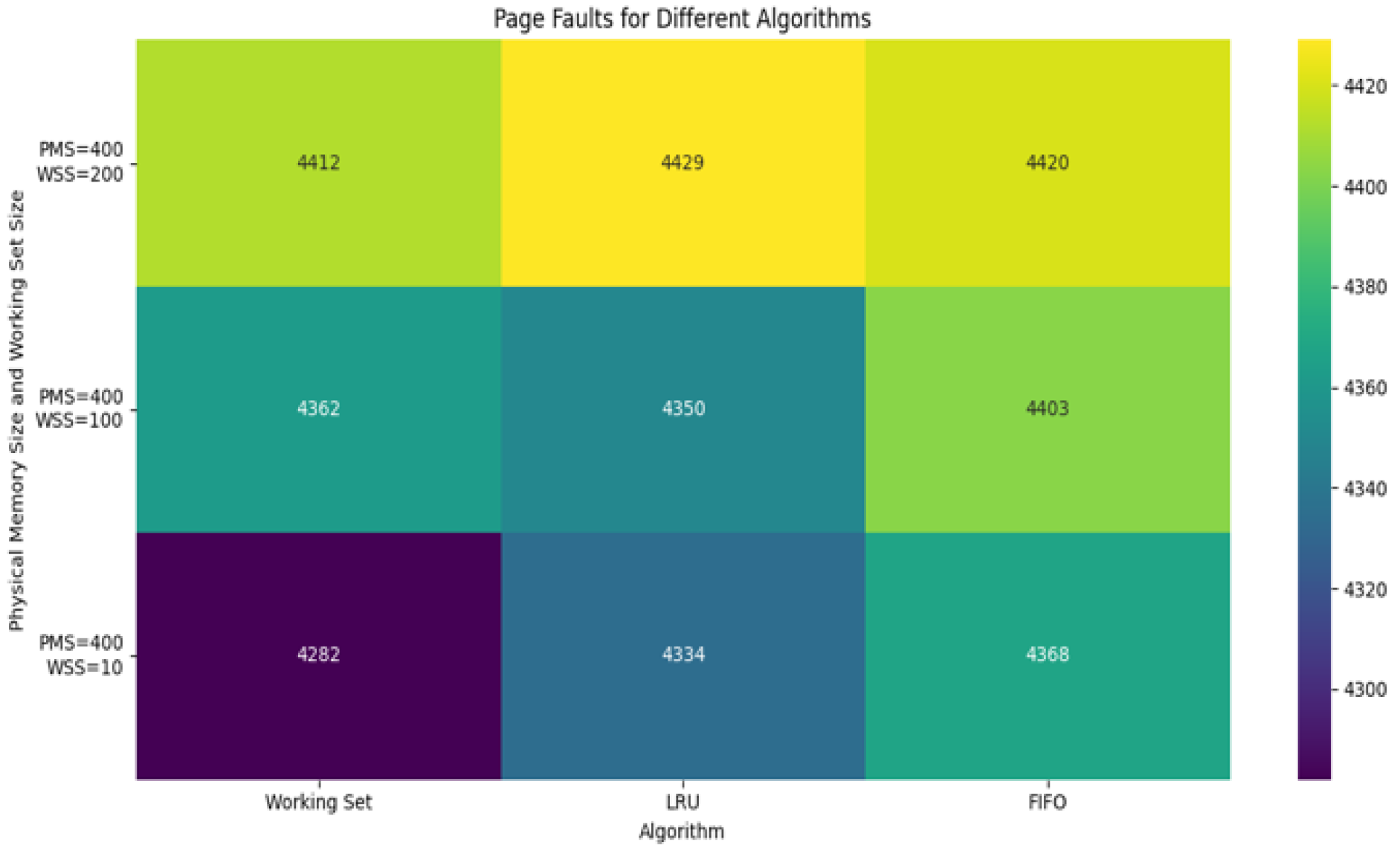
3.1. Simulation Results for Virtual Memory Page Management
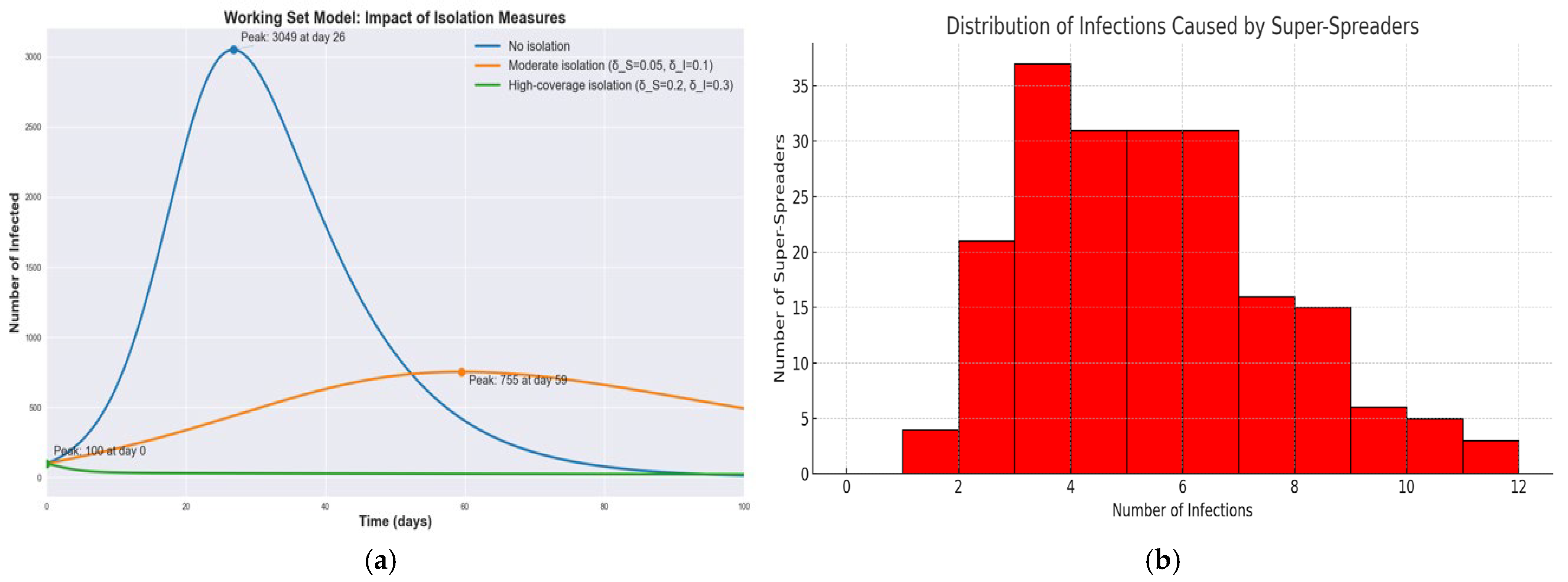
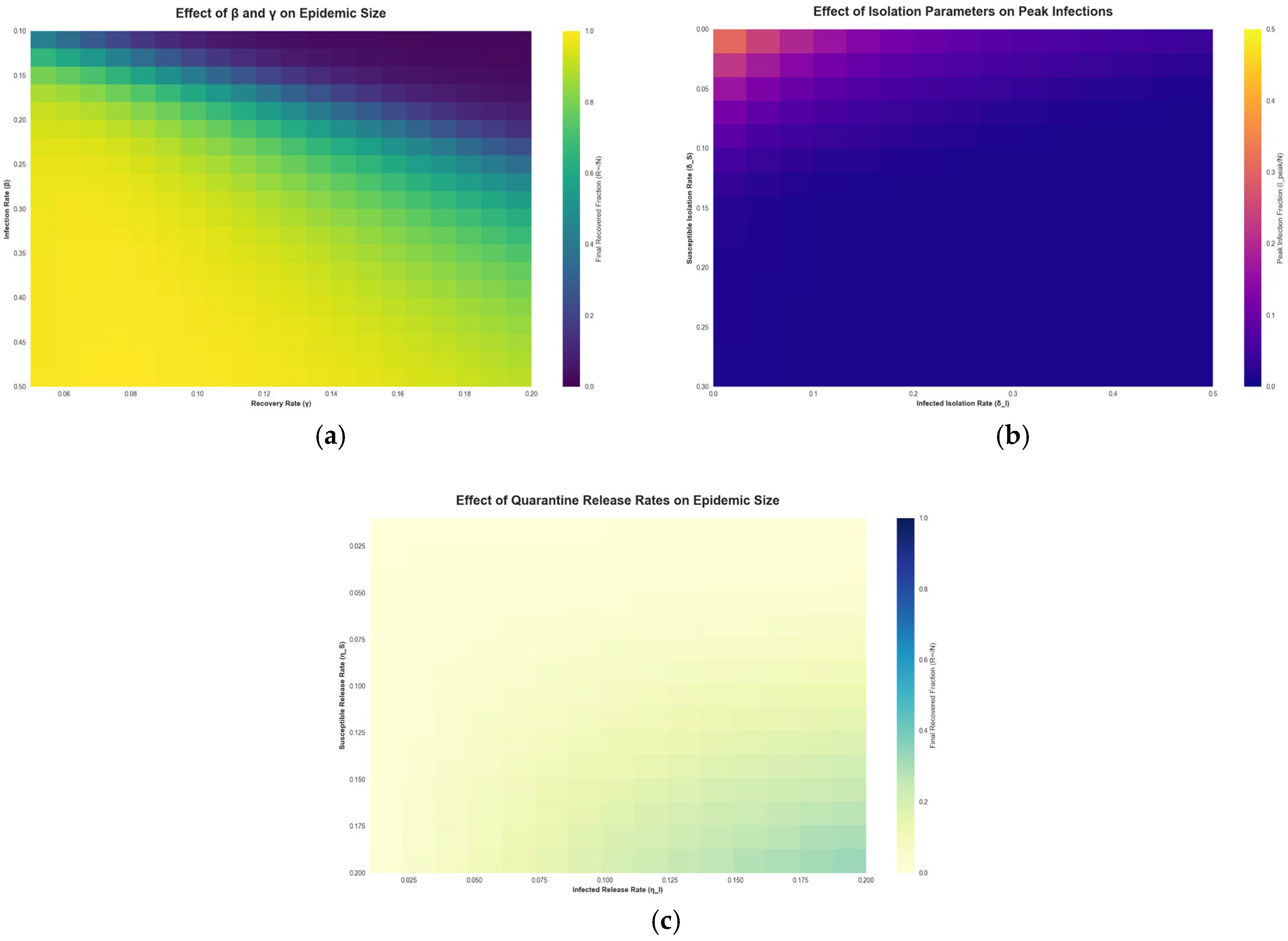
3.2. Results from Epidemiological Modeling with Working Set
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Denning, P.J. The working set model for program behavior. In Proceedings of the ACM Symposium on Operating System Principles—SOSP ’67, Gatlinburg, TN, USA, 1–4 October 1967; ACM Press: New York, NY, USA, 1967; pp. 15.1–15.12. [Google Scholar] [CrossRef]
- Denning, P.J. Working Set Analytics. ACM Comput. Surv. 2021, 53, 1–36. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Wu, C.-F.; Chang, Y.-H.; Kuo, T.-W. Exploring Synchronous Page Fault Handling. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2022, 41, 3791–3802. [Google Scholar] [CrossRef]
- Doron-Arad, I.; Naor, J.S. Non-Linear Paging. LIPIcs ICALP 2024, 297, 57.1–57.19. [Google Scholar] [CrossRef]
- Wood, C.; Fernandez, E.B.; Lang, T. Minimization of Demand Paging for the LRU Stack Model of Program Behavior. Inf. Process. Lett. 1983, 16, 99–104. [Google Scholar] [CrossRef]
- Arasteh, B.; Ghanbarzadeh, R.; Gharehchopogh, F.S.; Hosseinalipour, A. Generating the Structural Graph-based Model from a Program Source-code Using Chaotic Forrest Optimization Algorithm. Expert Syst. 2023, 40, e13228. [Google Scholar] [CrossRef]
- Arasteh, B.; Abdi, M.; Bouyer, A. Program Source Code Comprehension by Module Clustering Using Combination of Discretized Gray Wolf and Genetic Algorithms. Adv. Eng. Softw. 2022, 173, 103252. [Google Scholar] [CrossRef]
- Park, Y.; Bahn, H. A Working-Set Sensitive Page Replacement Policy for PCM-Based Swap Systems. JSTS J. Semicond. Technol. Sci. 2017, 17, 7–14. [Google Scholar] [CrossRef]
- Sha, S.; Hu, J.-Y.; Luo, Y.-W.; Wang, X.-L.; Wang, Z. Huge Page Friendly Virtualized Memory Management. J. Comput. Sci. Technol. 2020, 35, 433–452. [Google Scholar] [CrossRef]
- Hu, J.; Bai, X.; Sha, S.; Luo, Y.; Wang, X.; Wang, Z. Working Set Size Estimation with Hugepages in Virtualization. In Proceedings of the 2018 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Ubiquitous Computing & Communications, Big Data & Cloud Computing, Social Computing & Networking, Sustainable Computing & Communications (ISPA/IUCC/BDCloud/SocialCom/SustainCom), Melbourne, Australia, 13 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 501–508. [Google Scholar]
- Nitu, V.; Kocharyan, A.; Yaya, H.; Tchana, A.; Hagimont, D.; Astsatryan, H. Working Set Size Estimation Techniques in Virtualized Environments: One Size Does Not Fit All. In Proceedings of the Abstracts of the 2018 ACM International Conference on Measurement and Modeling of Computer Systems, Irvine, CA, USA, 12 June 2018; ACM: New York, NY, USA, 2018; pp. 62–63. [Google Scholar]
- Verbart, A.; Stolpe, M. A Working-Set Approach for Sizing Optimization of Frame-Structures Subjected to Time-Dependent Constraints. Struct. Multidisc. Optim. 2018, 58, 1367–1382. [Google Scholar] [CrossRef]
- Billah, M.A.; Miah, M.M.; Khan, M.N. Reproductive Number of Coronavirus: A Systematic Review and Meta-Analysis Based on Global Level Evidence. PLoS ONE 2020, 15, e0242128. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic Processes in Complex Networks. Rev. Mod. Phys. 2015, 87, 925–979. [Google Scholar] [CrossRef]
- Hethcote, H.W. The Mathematics of Infectious Diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Siegenfeld, A.F.; Kollepara, P.K.; Bar-Yam, Y. Modeling Complex Systems: A Case Study of Compartmental Models in Epidemiology. Complexity 2022, 2022, 3007864. [Google Scholar] [CrossRef]
- Kermak, W.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. Lond. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Sun, R. Global Stability of the Endemic Equilibrium of Multigroup SIR Models with Nonlinear Incidence. Comput. Math. Appl. 2010, 60, 2286–2291. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. A Highly Accurate Peak Time Formula of Epidemic Outbreak from the SIR Model. Chin. J. Phys. 2023, 84, 39–50. [Google Scholar] [CrossRef]
- KhudaBukhsh, W.R.; Rempała, G.A. How to Correctly Fit an SIR Model to Data from an SEIR Model? Math. Biosci. 2024, 375, 109265. [Google Scholar] [CrossRef]
- Korobeinikov, A. Global Properties of SIR and SEIR Epidemic Models with Multiple Parallel Infectious Stages. Bull. Math. Biol. 2009, 71, 75–83. [Google Scholar] [CrossRef]
- Džiugys, A.; Bieliūnas, M.; Skarbalius, G.; Misiulis, E.; Navakas, R. Simplified Model of COVID-19 Epidemic Prognosis under Quarantine and Estimation of Quarantine Effectiveness. Chaos Solitons Fractals 2020, 140, 110162. [Google Scholar] [CrossRef]
- Gumel, A.B.; Iboi, E.A.; Ngonghala, C.N.; Elbasha, E.H. A Primer on Using Mathematics to Understand COVID-19 Dynamics: Modeling, Analysis and Simulations. Infect. Dis. Model. 2021, 6, 148–168. [Google Scholar] [CrossRef]
- Yan, P.; Chowell, G. Beyond the Initial Phase: Compartment Models for Disease Transmission. In Quantitative Methods for Investigating Infectious Disease Outbreaks; Springer International Publishing: Cham, Switzerland, 2019; Volume 70, pp. 135–182. ISBN 9783030219222. [Google Scholar]
- Marques, J.A.L.; Gois, F.N.B.; Xavier-Neto, J.; Fong, S.J. Epidemiology Compartmental Models—SIR, SEIR, and SEIR with Intervention. In Predictive Models for Decision Support in the COVID-19 Crisis; Springer International Publishing: Cham, Switzerland, 2021; pp. 15–39. ISBN 9783030619121. [Google Scholar]
- Meng, X.; Cai, Z.; Si, S.; Duan, D. Analysis of Epidemic Vaccination Strategies on Heterogeneous Networks: Based on SEIRV Model and Evolutionary Game. Appl. Math. Comput. 2021, 403, 126172. [Google Scholar] [CrossRef] [PubMed]
- Safarishahrbijari, A.; Lawrence, T.; Lomotey, R.; Liu, J.; Waldner, C.; Osgood, N. Particle Filtering in a SEIRV Simulation Model of H1N1 Influenza. In Proceedings of the 2015 Winter Simulation Conference (WSC), Huntington Beach, CA, USA, 6–9 December 2015; pp. 1240–1251. [Google Scholar]
- Bissett, K.R.; Cadena, J.; Khan, M.; Kuhlman, C.J. Agent-Based Computational Epidemiological Modeling. J. Indian Inst. Sci. 2021, 101, 303–327. [Google Scholar] [CrossRef] [PubMed]
- Salem, F.A.; Moreno, U.F. A Multi-Agent-Based Simulation Model for the Spreading of Diseases Through Social Interactions During Pandemics. J. Control Autom. Electr. Syst. 2022, 33, 1161–1176. [Google Scholar] [CrossRef]
- Tolles, J.; Luong, T. Modeling Epidemics With Compartmental Models. JAMA 2020, 323, 2515. [Google Scholar] [CrossRef]
- Roberts, M.; Andreasen, V.; Lloyd, A.; Pellis, L. Nine Challenges for Deterministic Epidemic Models. Epidemics 2015, 10, 49–53. [Google Scholar] [CrossRef]
- Givan, O.; Schwartz, N.; Cygelberg, A.; Stone, L. Predicting Epidemic Thresholds on Complex Networks: Limitations of Mean-Field Approaches. J. Theor. Biol. 2011, 288, 21–28. [Google Scholar] [CrossRef]
- Dhar, A. What One Can Learn from the SIR Model. Iascs 2020, 3, 213–215. [Google Scholar] [CrossRef]
- Lloyd-Smith, J.O.; Schreiber, S.J.; Kopp, P.E.; Getz, W.M. Superspreading and the Effect of Individual Variation on Disease Emergence. Nature 2005, 438, 355–359. [Google Scholar] [CrossRef]
- Adam, D.C.; Wu, P.; Wong, J.Y.; Lau, E.H.Y.; Tsang, T.K.; Cauchemez, S.; Leung, G.M.; Cowling, B.J. Clustering and Superspreading Potential of SARS-CoV-2 Infections in Hong Kong. Nat. Med. 2020, 26, 1714–1719. [Google Scholar] [CrossRef]
- Poonia, R.C.; Saudagar, A.K.J.; Altameem, A.; Alkhathami, M.; Khan, M.B.; Hasanat, M.H.A. An Enhanced SEIR Model for Prediction of COVID-19 with Vaccination Effect. Life 2022, 12, 647. [Google Scholar] [CrossRef]
- Ramalingam, R.; Gnanaprakasam, A.J.; Boulaaras, S. Stability and Control Analysis of COVID-19 Spread in India Using SEIR Model. Sci. Rep. 2025, 15, 9095. [Google Scholar] [CrossRef]
- James, A.; Plank, M.J.; Hendy, S.; Binny, R.; Lustig, A.; Steyn, N.; Nesdale, A.; Verrall, A. Successful Contact Tracing Systems for COVID-19 Rely on Effective Quarantine and Isolation. PLoS ONE 2021, 16, e0252499. [Google Scholar] [CrossRef] [PubMed]
- Kabanikhin, S.I.; Krivorotko, O.I. Mathematical Modeling of the Wuhan COVID-2019 Epidemic and Inverse Problems. Comput. Math. Math. Phys. 2020, 60, 1889–1899. [Google Scholar] [CrossRef]
- Lieberthal, B.; Gardner, A.M. Connectivity, Reproduction Number, and Mobility Interact to Determine Communities’ Epidemiological Superspreader Potential in a Metapopulation Network. PLOS Comput. Biol. 2021, 17, e1008674. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhang, Y.; Xu, Y.; Xia, C.; Tanimoto, J. An Epidemic Spread Model with Nonlinear Recovery Rates on Meta-Population Networks. Nonlinear Dyn. 2025, 113, 3943–3957. [Google Scholar] [CrossRef]
- Horii, M.; Gould, A.; Yun, Z.; Ray, J.; Safta, C.; Zohdi, T. Calibration Verification for Stochastic Agent-Based Disease Spread Models. PLoS ONE 2024, 19, e0315429. [Google Scholar] [CrossRef]
- Taghizadeh, E.; Mohammad-Djafari, A. SEIR Modeling, Simulation, Parameter Estimation, and Their Application for COVID-19 Epidemic Prediction. Phys. Sci. Forum 2022, 5, 18. [Google Scholar] [CrossRef]
- Chen, K.; Jiang, X.; Li, Y.; Zhou, R. A Stochastic Agent-Based Model to Evaluate COVID-19 Transmission Influenced by Human Mobility. Nonlinear Dyn. 2023, 111, 12639–12655. [Google Scholar] [CrossRef]
- Fan, Q.; Li, Q.; Chen, Y.; Tang, J. Modeling COVID-19 Spread Using Multi-Agent Simulation with Small-World Network Approach. BMC Public Health 2024, 24, 672. [Google Scholar] [CrossRef]
- Wood, A.D.; Berry, K. COVID-19 Transmission in a Resource Dependent Community with Heterogeneous Populations: An Agent-Based Modeling Approach. Econ. Hum. Biol. 2024, 52, 101314. [Google Scholar] [CrossRef]
- Gallagher, K.; Bouros, I.; Fan, N.; Hayman, E.; Heirene, L.; Lamirande, P.; Lemenuel-Diot, A.; Lambert, B.; Gavaghan, D.; Creswell, R. Epidemiological Agent-Based Modelling Software (Epiabm). J. Open Res. Softw. 2024, 12, 3. [Google Scholar] [CrossRef]
- Nitzsche, C.; Simm, S. Agent-Based Modeling to Estimate the Impact of Lockdown Scenarios and Events on a Pandemic Exemplified on SARS-CoV-2. Sci. Rep. 2024, 14, 13391. [Google Scholar] [CrossRef]
- Schluter, P.J.; Généreux, M.; Landaverde, E.; Chan, E.Y.Y.; Hung, K.K.C.; Law, R.; Mok, C.P.Y.; Murray, V.; O’Sullivan, T.; Qadar, Z.; et al. An Eight Country Cross-Sectional Study of the Psychosocial Effects of COVID-19 Induced Quarantine and/or Isolation during the Pandemic. Sci. Rep. 2022, 12, 13175. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Wu, L.; Ouyang, H.; Zhan, J.; Wang, J.; Liu, W.; Jia, Y. Behavioral Intentions and Perceived Stress under Isolated Environment. Brain Behav. 2024, 14, e3347. [Google Scholar] [CrossRef]
- Yamaka, W.; Lomwanawong, S.; Magel, D.; Maneejuk, P. Analysis of the Lockdown Effects on the Economy, Environment, and COVID-19 Spread: Lesson Learnt from a Global Pandemic in 2020. Int. J. Environ. Res. Public Health 2022, 19, 12868. [Google Scholar] [CrossRef]
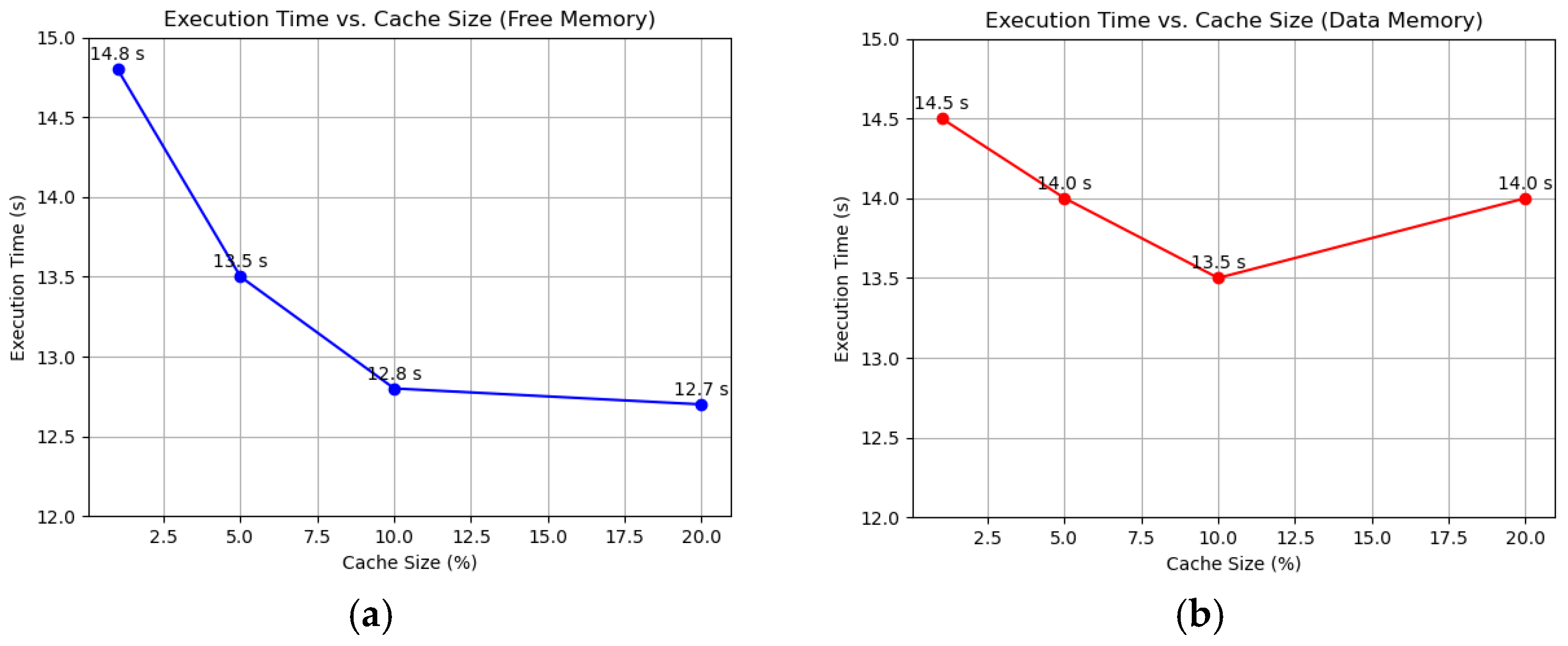
| Algorithm | Av. Page Fault Time (µs) | Page Fault Frequency (%) | Total Execution Time (s) |
|---|---|---|---|
| WS | 6 | 35 | 13 |
| LRU | 7 | 38 | 14.5 |
| FIFO | 7 | 38 | 14.5 |
| Variable | Default Value | Explanation |
|---|---|---|
| 10,000 | total number of agents in the population | |
| 9970 | initial number of susceptible agents | |
| 30 | initial number of infected agents | |
| 0 | initial number of recovered agents | |
| 0 | initial number of exposed agents (for SEIR model) | |
| 0 | initial number of isolated susceptible agents | |
| 0 | initial number of isolated infected agents | |
| 0 | initial number of isolated recovered agents | |
| 0.3 | infection rate | |
| 0.2 | incubation rate; rate at which exposed agents become infectious (for SEIR model) | |
| 0.1 | recovery rate; proportion of infected agents recovering per unit time | |
| 0.1 | isolation release rate for susceptible agents | |
| 0.1 | isolation release rate for infected agents |
| Aspect | SIR/SEIR | WS |
|---|---|---|
| Isolation | Not directly accounted, expansion required | Included as centerpiece, dynamic adjustment |
| Transmission speed | Fixed or dependent on S and I | Dynamically adjusted based on active set |
| Contact heterogeneity | Requires extensions (e.g., network) | Accounting through groups and subsets |
| Behavioral solutions | Not modeled | May be enabled via agent rules |
| Applicability for interventions | Limited without modifications | Easy to model isolation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borankulova, G.; Murzakhmetov, A.; Tungatarova, A.; Taszhurekova, Z. Adaptive Working Set Model for Memory Management and Epidemic Control: A Unified Approach. Computation 2025, 13, 190. https://doi.org/10.3390/computation13080190
Borankulova G, Murzakhmetov A, Tungatarova A, Taszhurekova Z. Adaptive Working Set Model for Memory Management and Epidemic Control: A Unified Approach. Computation. 2025; 13(8):190. https://doi.org/10.3390/computation13080190
Chicago/Turabian StyleBorankulova, Gaukhar, Aslanbek Murzakhmetov, Aigul Tungatarova, and Zhazira Taszhurekova. 2025. "Adaptive Working Set Model for Memory Management and Epidemic Control: A Unified Approach" Computation 13, no. 8: 190. https://doi.org/10.3390/computation13080190
APA StyleBorankulova, G., Murzakhmetov, A., Tungatarova, A., & Taszhurekova, Z. (2025). Adaptive Working Set Model for Memory Management and Epidemic Control: A Unified Approach. Computation, 13(8), 190. https://doi.org/10.3390/computation13080190






