A Hybrid Quantum–Classical Architecture with Data Re-Uploading and Genetic Algorithm Optimization for Enhanced Image Classification
Abstract
1. Introduction
2. Materials and Methods
2.1. Quantum Computing Preliminaries
2.1.1. Qubit Representation and Quantum States
2.1.2. Quantum Gate Operations
2.1.3. Quantum Measurement and Expectation Values
2.2. Parameterized Quantum Circuits (PQCs)
2.2.1. Variational Quantum Circuits
2.2.2. Data Re-Uploading Strategy
- encodes data x into rotation angles for qubit q at layer l
- applies entangling gates at layer l
- n is the number of qubits and L is the number of layers
2.2.3. Expressibility and Entanglement Measures
3. Proposed Quantum–Classical Hybrid Architecture
3.1. Overall Framework Architecture
- Data Preprocessing Layer: Classical image preprocessing and augmentation
- Quantum Convolutional Layer (QConv2D): Quantum feature extraction using sliding windows
- Re-uploading Quantum Circuit (ReUploadingPQC): Enhanced feature processing through iterative encoding
- Classical Dense Layers: Final classification using traditional neural network layers
3.2. Quantum Convolutional Layer (QConv2D)
3.2.1. Quantum Convolution Operation
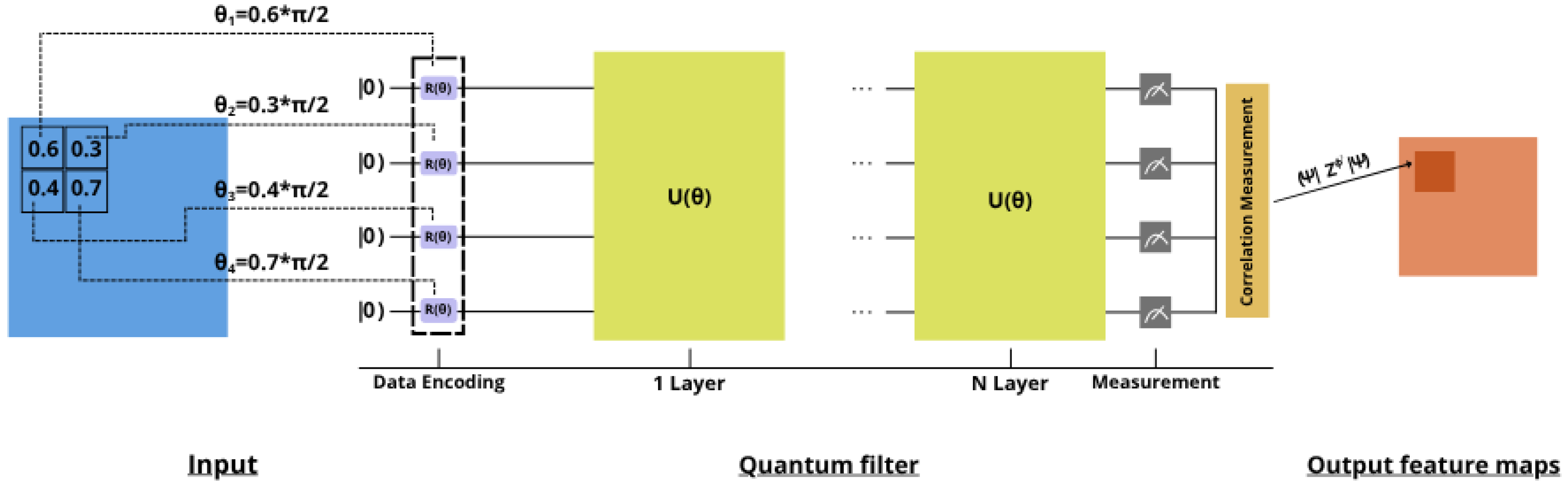
3.2.2. Quantum Filter Implementation
- Data Encoding: The K_h × K_w patch is flattened and padded to ensure divisibility by 3:
- Layer-wise Processing: For L layers and n qubits:
- Parameter Mapping: Input data is mapped to rotation angles:
- Measurement: Expectation values are computed:
- Figure 3 illustrates in more detail the operation of a quantum convolutional kernel.
3.2.3. Multi-Channel Processing
3.3. Re-Uploading Parameterized Quantum Circuit
3.3.1. Circuit Architecture
- Data Re-uploading:
- Entangling Layer:
3.3.2. Parameter Optimization
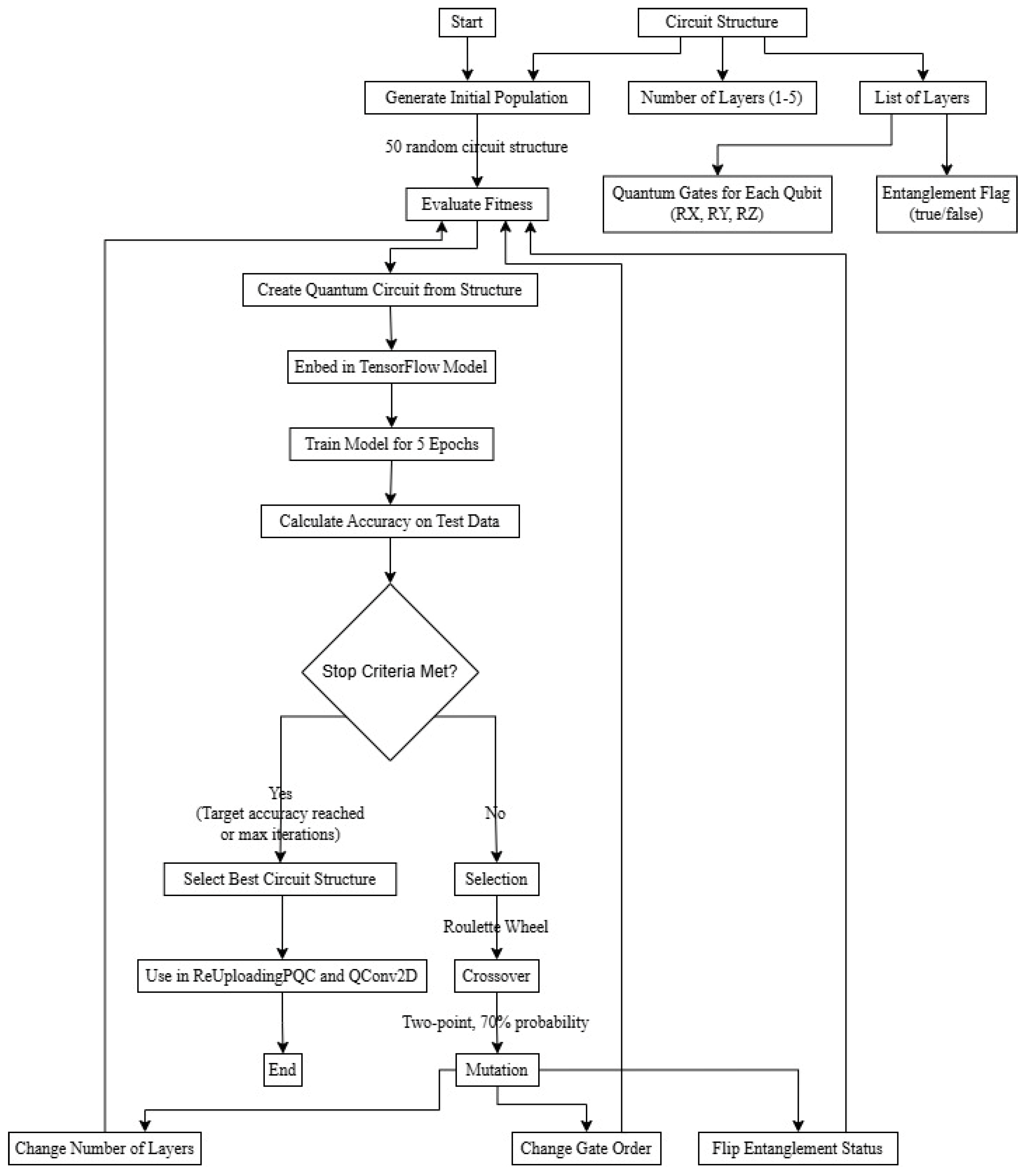
3.4. Genetic Algorithm for Circuit Optimization
3.4.1. Individual Representation
- L: number of layers
- : gate sequence for layer l
- entanglement configuration for layer l
3.4.2. Fitness Function
3.4.3. Genetic Operators
- Layer Addition/Removal:
- Gate Modification:
- Entanglement Toggle:
3.4.4. Evolution Strategy
- Initialization: Generate random population P0 of size
- Evaluation: Compute fitness for each individual
- Selection: Tournament selection with size
- Reproduction: Apply crossover with probability
- Mutation: Apply mutations with respective probabilities
- Replacement: Generate new population
| Algorithm 1 Genetic Algorithm for Quantum Circuit Optimization |
| Require: Population size s_pop = 20, generations g = 20, crossover probability pc = 0.8, retention rate rr = 0.1, layer mutation prob. pm_layer = 0.02, gate modification prob. pm_gate = 0.05, entanglement toggle prob. pm_ent = 0.05, tournament size k_tour = 3, circuit search space csp, training data D_train, validation data D_val |
| 1: pop_configs = InitializePopulation(s_pop, csp) 2: pop_fitness = [EvaluateFitness(config, D_train, D_val) for config in pop_configs] 3: for generation = 1 to g do 4: SortPopulationByFitness(pop_configs, pop_fitness, descending = True) 5: next_pop_configs = [] 7: num_retained = floor(rr * s_pop) 8: next_pop_configs.extend(pop_configs[:num_retained] 9: next_pop_fitness.extend(pop_fitness[:num_retained]) 10: parent_pool_configs = pop_configs 11: parent_pool_fitness = pop_fitness 12: for i = 1 to s_pop − num_retained do 13: p1_config = TournamentSelect(parent_pool_configs, parent_pool_fitness, k_tour) 14: p2_config = TournamentSelect(parent_pool_configs, parent_pool_fitness, k_tour) 15: if random() < pc then 16: child_config = CrossoverCircuits(p1_config, p2_config, csp) 17: else 18: child_config = copy(p1_config) 19: end if 20: mutated_child_config = MutateCircuit(child_config, pm_layer, pm_gate, pm_ent, csp) 21: next_pop_configs.append(mutated_child_config) 22: next_pop_fitness.append(EvaluateFitness(mutated_child_config, D_train, D_val)) 23: end for 24: pop_configs = next_pop_configs 25: pop_fitness = next_pop_fitness 26: end for 27: SortPopulationByFitness(pop_configs, pop_fitness, descending = True) 28: return pop_configs [0] |
4. Experiments and Results Analysis
4.1. Dataset and Experimental Setup
Dataset Specifications
- Random horizontal flips (50% probability, CIFAR-100 only)
- Random rotations ± 15° (30% probability, both datasets)
- Random brightness adjustments ±0.2 (25% probability, both datasets)
- Random zoom 0.9–1.1 scale (20% probability, CIFAR-100 only)
4.2. Results of Genetic Algorithm for Quantum Circuit Optimization
4.2.1. Mutation Impact Evaluation
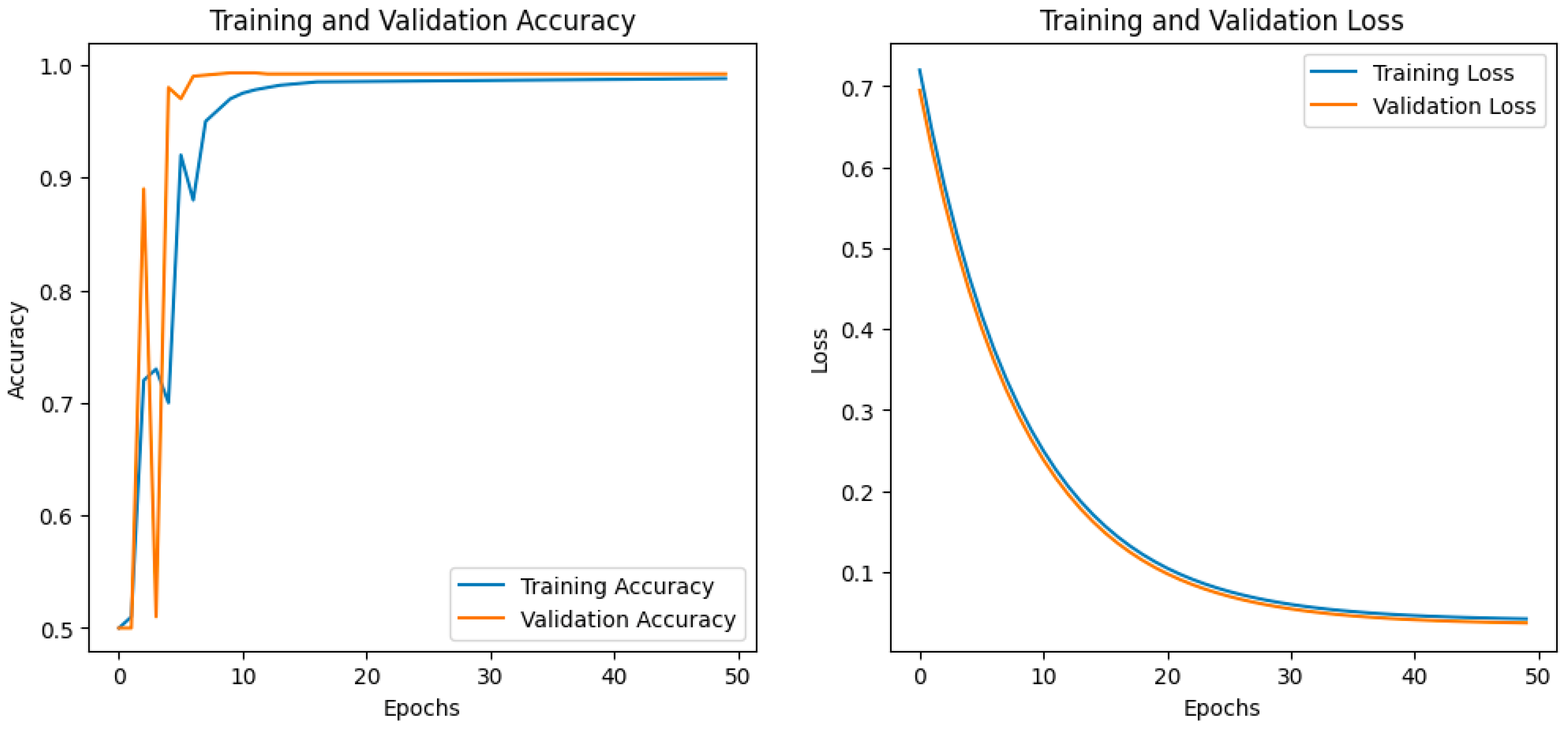
4.2.2. Experiment on MNIST
- Validation accuracy increased to 99.2%, with similar results on the training set.
- Loss function decreased to 0.0393.
- GA helped automatically determine efficient configurations of quantum circuits, including optimizing network depth and the number of qubits.
- More compact architectures have also been found that maintain or even improve accuracy compared to previous models.
- When including regularization techniques in the search space, the genetic algorithm successfully selected efficient regularization schemes, which had a positive effect on overall performance by preventing overfitting and improving generalization.
4.2.3. Experiment on CIFAR100
- HQCNN–REGA: The best results were obtained by combining QCNN with the data re-uploading technique and using genetic algorithm for optimization.
- The accuracy on the validation set was 97.4%, and on the training set it was more than 97.2%.
- The loss function was reduced compared to previous models, and the learning curves showed fast and stable convergence.
- GA allowed us to find optimal architectural parameters, including the number of layers, the number of qubits, the obfuscation strategy, and the data reloading schemes.
- Additionally, a reduction in the number of parameters was achieved without a loss of accuracy, which increased the efficiency of the model in terms of computational resources.
4.3. Final Model Performance
Complete Architecture Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; Technical Report; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Aaronson, S. Quantum Machine Learning Algorithms: Read the Fine Print. Nat. Phys. 2015, 11, 291–293. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ Era and Beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Bharti, K.; Cervera-Lierta, A.; Kyaw, T.H.; Haug, T.; Alperin-Lea, S.; Anand, A.; Degroote, M.; Lau, H.K.; Simonetto, A.; Kwek, L.C. Noisy Intermediate-Scale Quantum Algorithms. Rev. Mod. Phys. 2022, 94, 015004. [Google Scholar] [CrossRef]
- Harrow, A.W.; Hassidim, A.; Lloyd, S. Quantum Algorithm for Linear Systems of Equations. Phys. Rev. Lett. 2009, 103, 150502. [Google Scholar] [CrossRef]
- Lloyd, S.; Mohseni, M.; Rebentrost, P. Quantum Principal Component Analysis. Nat. Phys. 2014, 10, 631–633. [Google Scholar] [CrossRef]
- Mari, A.; Bromley, T.R.; Izaac, J.; Schuld, M.; Killoran, N. Transfer Learning in Hybrid Classical–Quantum Neural Networks. Quantum 2020, 4, 340. [Google Scholar] [CrossRef]
- Grant, E.; Benedetti, M.; Cao, S.; Hallam, A.; Lockhart, J.; Stojevic, V.; Carleo, G.; Severini, S. Hierarchical Quantum Classifiers. npj Quantum Inf. 2018, 4, 65. [Google Scholar] [CrossRef]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum Machine Learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef]
- Dunjko, V.; Briegel, H.J. Machine Learning and Artificial Intelligence in the Quantum Domain. Rep. Prog. Phys. 2018, 81, 074001. [Google Scholar] [CrossRef]
- Daribayev, B.; Mukhanbet, A.; Imankulov, T. Implementation of the HHL Algorithm for Solving the Poisson Equation on Quantum Simulators. Appl. Sci. 2023, 13, 11491. [Google Scholar] [CrossRef]
- Schuld, M.; Fingerhuth, M.; Petruccione, F. Implementing a Distance-Based Classifier with a Quantum Interference Circuit. EPL 2017, 119, 60002. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Approximate Optimization Algorithm. arXiv 2014, arXiv:1411.4028. [Google Scholar] [CrossRef]
- Benedetti, M.; Lloyd, E.; Sack, S.; Fiorentini, M. Parameterized Quantum Circuits as Machine Learning Models. Quantum Sci. Technol. 2019, 4, 043001. [Google Scholar] [CrossRef]
- Cong, I.; Choi, S.; Lukin, M.D. Quantum Convolutional Neural Networks. Nat. Phys. 2019, 15, 1273–1278. [Google Scholar] [CrossRef]
- Henderson, M.; Shakya, S.; Pradhan, S.; Cook, T. Quanvolutional Neural Networks: Powering Image Recognition with Quantum Circuits. Quantum Mach. Intell. 2020, 2, 2. [Google Scholar] [CrossRef]
- Liu, Y.; Arunachalam, S.; Gheorghiu, V.; Dunjko, V. Variational Quantum Circuits for Deep Reinforcement Learning. IEEE Access 2021, 9, 78269–78282. [Google Scholar]
- Pérez-Salinas, A.; Cervera-Lierta, A.; Gil-Fuster, E.; Latorre, J.I. Data Re-Uploading for a Universal Quantum Classifier. Quantum 2020, 4, 226. [Google Scholar] [CrossRef]
- Griol-Barres, I.; Milla, S.; Cebrián, A.; Mansoori, Y.; Millet, J. Variational Quantum Circuits for Machine Learning. An Application for the Detection of Weak Signals. Appl. Sci. 2021, 11, 6427. [Google Scholar] [CrossRef]
- Schuld, M.; Sweke, R. Effect of Data Encoding on the Expressive Power of Variational Quantum-Machine-Learning Models. Phys. Rev. A 2021, 103, 032430. [Google Scholar] [CrossRef]
- Spector, L.; Barnum, H.; Bernstein, H.J.; Swamy, N. Finding a Better-than-Classical Quantum AND/OR Algorithm Using Genetic Programming. In Proceedings of the 1999 Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 2239–2246. [Google Scholar]
- Malossini, A.; Blanzieri, E.; Calarco, T. Quantum Genetic Optimization. IEEE Trans. Evol. Comput. 2008, 12, 231–241. [Google Scholar] [CrossRef]
- Cincio, L.; Rudinger, K.; Sarovar, M.; Coles, P.J. Machine Learning of Noise-Resilient Quantum Circuits. PRX Quantum 2021, 2, 010324. [Google Scholar] [CrossRef]
- McClean, J.R.; Boixo, S.; Smelyanskiy, V.N.; Babbush, R.; Neven, H. Barren Plateaus in Quantum Neural Network Training Landscapes. Nat. Commun. 2018, 9, 4812. [Google Scholar] [CrossRef]
- Mitarai, K.; Negoro, M.; Kitagawa, M.; Fujii, K. Quantum Circuit Learning. Phys. Rev. A 2018, 98, 032309. [Google Scholar] [CrossRef]
- Cerezo, M.; Arrasmith, A.; Babbush, R.; Benjamin, S.C.; Endo, S.; Fujii, K.; McClean, J.R.; Mitarai, K.; Yuan, X.; Cincio, L.; et al. Variational Quantum Algorithms. Nat. Rev. Phys. 2021, 3, 625–644. [Google Scholar] [CrossRef]
- Huang, H.Y.; Kueng, R.; Preskill, J. Power of Data in Quantum Machine Learning. Nat. Commun. 2021, 12, 2631. [Google Scholar] [CrossRef] [PubMed]
- Ramzan, F.; Khan, M.U.G.; Rehmat, A.; Iqbal, S.; Saba, T.; Rehman, A.; Mehmood, Z. A Deep Learning Approach for Automated Diagnosis and Multi-Class Classification of Alzheimer’s Disease Stages Using Resting-State fMRI and Residual Neural Networks. J. Med. Syst. 2020, 44, 37. [Google Scholar] [CrossRef]
- Schuld, M. Supervised Quantum Machine Learning Models Are Kernel Methods. arXiv 2021, arXiv:2101.11020. [Google Scholar] [CrossRef]
- Lloyd, S.; Schuld, M.; Ijaz, A.; Izaac, J.; Killoran, N. Quantum Embeddings for Machine Learning. arXiv 2020, arXiv:2001.03622. [Google Scholar] [CrossRef]
- Thumwanit, N.; Lortaraprasert, C.; Raymond, R. Invited: Trainable Discrete Feature Embeddings for Quantum Machine Learning. In Proceedings of the 2021 58th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 5–9 December 2021; pp. 1352–1355. [Google Scholar]
- Phalak, K.; Ghosh, A.; Ghosh, S. Optimizing Quantum Embedding Using Genetic Algorithm for QML Applications. arXiv 2024, arXiv:2412.00286. [Google Scholar] [CrossRef]







| Parameter | Meaning | Impact on the Result |
|---|---|---|
| Population size | 50 | Basic for search |
| Number of generations | 20 | Enough for convergence |
| Probability of crossing | 0.7 (70%) | High recombination |
| Probability of mutation | 0.2 (20%) | Moderate research |
| Selection size | 3 | Balanced selection |
| Maximum number of layers | 5 | Difficulty Limit |
| Gate types | RX, RY, RZ | Full set of rotations |
| Generation | Number of Ratings (Nevals) | Percentage of Population | Search Activity | Crossbreeding | Mutations |
|---|---|---|---|---|---|
| 0 | 50 | 100% | Maximum | 0 | 0 |
| 1 | 42 | 84% | High | ~35 | ~10 |
| 2 | 30 | 60% | Moderate | ~25 | ~7 |
| 3 | 35 | 70% | Average | ~29 | ~8 |
| 4 | 39 | 78% | High | ~32 | ~9 |
| 5 | 35 | 70% | Average | ~29 | ~8 |
| 6 | 38 | 76% | High | ~31 | ~9 |
| 7 | 38 | 76% | High | ~31 | ~9 |
| 8 | 33 | 66% | Moderate | ~27 | ~8 |
| 9 | 36 | 72% | Average | ~30 | ~8 |
| 10 | 42 | 84% | High | ~35 | ~10 |
| 11 | 41 | 82% | High | ~34 | ~10 |
| 12 | 36 | 72% | Average | ~30 | ~8 |
| 13 | 46 | 92% | Very high | ~38 | ~11 |
| 14 | 45 | 90% | Very high | ~37 | ~11 |
| 15 | 27 | 54% | Low | ~22 | ~6 |
| 16 | 40 | 80% | High | ~33 | ~9 |
| 17 | 39 | 78% | High | ~32 | ~9 |
| 18 | 44 | 88% | Very high | ~36 | ~10 |
| 19 | 45 | 90% | Very high | ~37 | ~11 |
| 20 | 38 | 76% | High | ~31 | ~9 |
| Mutation Type | Frequency | Success Rate | Avg. Improvement |
|---|---|---|---|
| Layer Number | 20% | 34% | +2.1% |
| Gate Order | 35% | 67% | +1.8% |
| Entanglement State | 25% | 78% | +8.3% |
| Gate-Type Substitution | 20% | 45% | +1.2% |
| Dataset | Re-Uploading | Accuracy (%) | Number of Parameters | Epochs to Convergence |
|---|---|---|---|---|
| MNIST | No | 97.9 | 14,000 | 35 |
| MNIST | Yes | 99.0 | 18,000 | 26 |
| CIFAR-100 | No | 85.0 | 22,000 | 50 |
| CIFAR-100 | Yes | 96.9 | 28,000 | 35 |
| Model | MNIST | CIFAR-100 |
|---|---|---|
| ResNet-18 | 99.2% | 97.1% |
| Basic QCNN | 98.0% | 85% |
| QCNN with Data Re-uploading | 99.0% | 96.90% |
| QCNN with Data Re-uploading and GA (optimization) | 99.2% | 97.40% |
| Number of Qubits | Best Model | Accuracy | Time Step |
|---|---|---|---|
| 1 | -Rx(theta0)-Ry(theta1)-Rz(theta2)-@ | 98.35% | 1 min 38 s |
| 2 | -Rx(theta0)-Ry(theta1)-Rz(theta2- -Rx(theta3)-Ry(theta4)-Rz(theta5)-@ | 98.37% | 1 min 46 s |
| 3 | -Rx(theta0)-Ry(theta1)-Rz(theta2)- -Rx(theta3)-Ry(theta4)-Rz(theta5)- -Rx(theta6)-Ry(theta7)-Rz(theta8)-@-@- | 99.19% | 2 min 13 s |
| Parameter | Meaning | Impact on the Result | Combined Score = (A + B)/2 |
|---|---|---|---|
| GA [33] | 98.0 | 96.0 | 97.0 |
| QEK [30] | 97.37 | 96.0 | 96.68 |
| QAOA Emb. [31] | 92.88 | 94.5 | 93.69 |
| QRAC [32] | 90.3 | 91.2 | 90.75 |
| HQCNN–REGA (proposed) | 98.7 | 99.2 | 98.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukhanbet, A.; Daribayev, B. A Hybrid Quantum–Classical Architecture with Data Re-Uploading and Genetic Algorithm Optimization for Enhanced Image Classification. Computation 2025, 13, 185. https://doi.org/10.3390/computation13080185
Mukhanbet A, Daribayev B. A Hybrid Quantum–Classical Architecture with Data Re-Uploading and Genetic Algorithm Optimization for Enhanced Image Classification. Computation. 2025; 13(8):185. https://doi.org/10.3390/computation13080185
Chicago/Turabian StyleMukhanbet, Aksultan, and Beimbet Daribayev. 2025. "A Hybrid Quantum–Classical Architecture with Data Re-Uploading and Genetic Algorithm Optimization for Enhanced Image Classification" Computation 13, no. 8: 185. https://doi.org/10.3390/computation13080185
APA StyleMukhanbet, A., & Daribayev, B. (2025). A Hybrid Quantum–Classical Architecture with Data Re-Uploading and Genetic Algorithm Optimization for Enhanced Image Classification. Computation, 13(8), 185. https://doi.org/10.3390/computation13080185







