Research on the Branch Road Traffic Flow Estimation and Main Road Traffic Flow Monitoring Optimization Problem
Abstract
1. Introduction
2. Materials and Methods
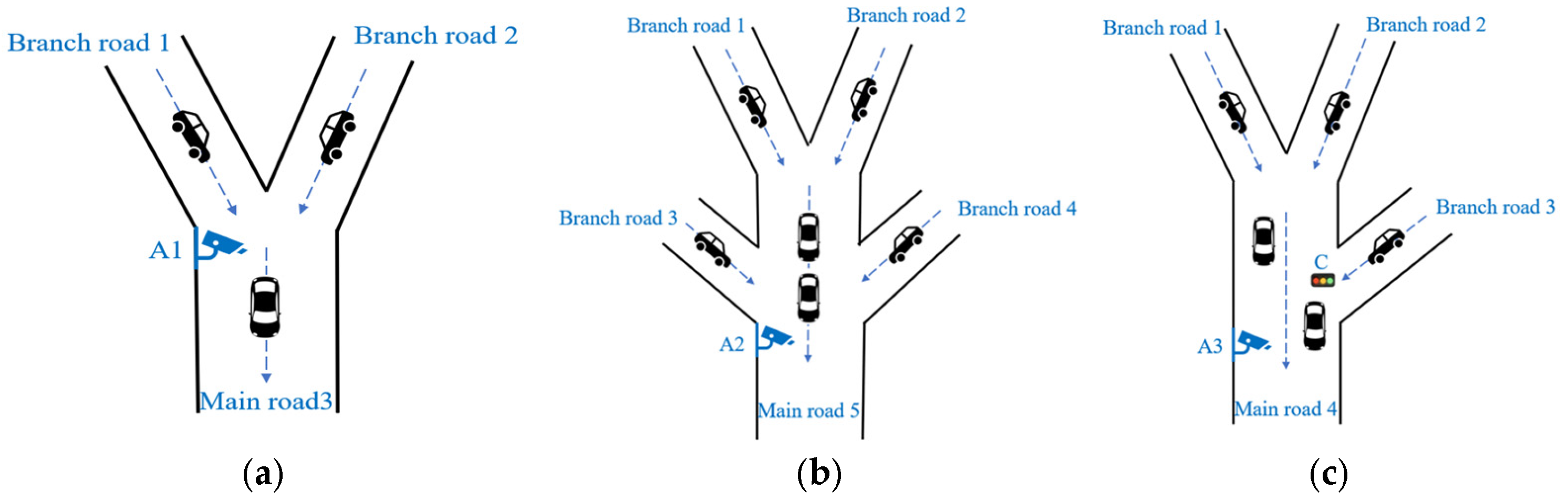
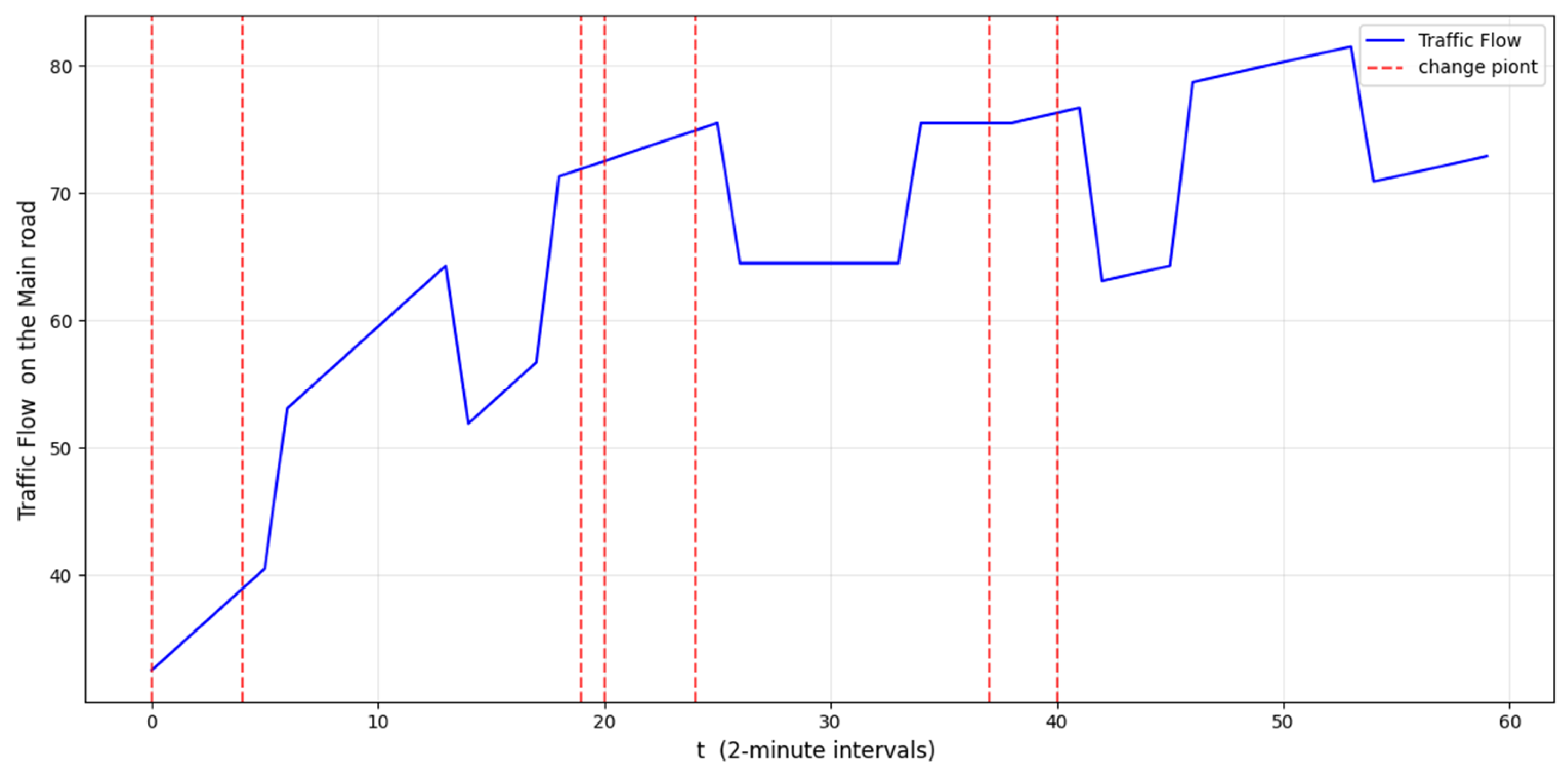
2.1. Scene Overviews
2.2. Model Hypothesis
2.3. Model Analysis and Establishment
2.3.1. Mathematical Model I
2.3.2. Mathematical Model II
2.3.3. Mathematical Model III
2.3.4. Mathematical Model IV
3. Results
4. Discussion
- (1)
- Rapid identification of incident locations;
- (2)
- Dynamic generation of optimal rerouting strategies.
5. Conclusions
- (1)
- The strict monotonicity of traffic flow assumed in Assumption 3 may not hold in actual road conditions;
- (2)
- The fixed signal timing in Model III/IV reduces adaptability to adaptive signal systems;
- (3)
- The computational complexity of the GA–SA hybrid limits real-time deployment (>2 s/iteration);
- (4)
- The validation datasets lack extreme weather conditions. Future work will integrate reinforcement learning for dynamic signal optimization.
- (1)
- Periodic fluctuation modeling through the Fourier spectral method.
- (2)
- Constrained optimization for enforcing continuity in piecewise functions.
- (3)
- Hybrid global optimization combining genetic algorithms with simulated annealing.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Moment | Time | Traffic Flow on Main Road 3 in Figure 1a | Traffic Flow on Main Road 5 in Figure 1b | Traffic Flow on Main Road 4 in Figure 1c | Traffic Flow on Main Road 4 in Figure 1c |
|---|---|---|---|---|---|
| 07:00 | 0 | 7.00 | 32.5 | 0.8 | 20.1178 |
| 07:02 | 1 | 8.50 | 34.1 | 2 | 21.6463 |
| 07:04 | 2 | 10.00 | 35.7 | 3.2 | 31.0159 |
| 07:06 | 3 | 11.50 | 37.3 | 4.4 | 40.5070 |
| 07:08 | 4 | 13.00 | 38.9 | 34.6 | 41.4589 |
| 07:10 | 5 | 14.50 | 40.5 | 37.3 | 40.3803 |
| 07:12 | 6 | 16.00 | 53.1 | 40 | 45.0280 |
| 07:14 | 7 | 17.50 | 54.7 | 42.7 | 23.5751 |
| 07:16 | 8 | 19.00 | 56.3 | 45.4 | 27.6601 |
| 07:18 | 9 | 20.50 | 57.9 | 20.625 | 28.5191 |
| 07:20 | 10 | 22.00 | 59.5 | 30.31 | 22.8609 |
| 07:22 | 11 | 23.50 | 61.1 | 39.395 | 54.4147 |
| 07:24 | 12 | 25.00 | 62.7 | 47.82 | 56.3573 |
| 07:26 | 13 | 26.50 | 64.3 | 81.075 | 54.6330 |
| 07:28 | 14 | 28.00 | 51.9 | 87.35 | 59.2022 |
| 07:30 | 15 | 29.50 | 53.5 | 92.785 | 55.9851 |
| 07:32 | 16 | 31.00 | 55.1 | 97.32 | 37.2741 |
| 07:34 | 17 | 32.50 | 56.7 | 100.895 | 43.2759 |
| 07:36 | 18 | 34.00 | 71.3 | 81.15 | 44.3377 |
| 07:38 | 19 | 35.50 | 71.9 | 83.275 | 46.9259 |
| 07:40 | 20 | 37.00 | 72.5 | 84.26 | 74.7459 |
| 07:42 | 21 | 38.50 | 73.1 | 84.045 | 69.1357 |
| 07:44 | 22 | 40.00 | 73.7 | 109.97 | 74.9930 |
| 07:46 | 23 | 41.50 | 74.3 | 106.375 | 75.0219 |
| 07:48 | 24 | 43.00 | 74.9 | 101.4 | 72.3299 |
| 07:50 | 25 | 44.50 | 75.5 | 101.8 | 52.8119 |
| 07:52 | 26 | 46.00 | 64.5 | 102.2 | 53.9451 |
| 07:54 | 27 | 47.50 | 64.5 | 79.2 | 52.3878 |
| 07:56 | 28 | 49.00 | 64.5 | 80.4 | 55.7438 |
| 07:58 | 29 | 50.50 | 64.5 | 81.6 | 81.1195 |
| 08:00 | 30 | 52.00 | 64.5 | 82.8 | 86.6484 |
| 08:02 | 31 | 51.50 | 64.5 | 108.8 | 81.2547 |
| 08:04 | 32 | 51.00 | 64.5 | 110.8 | 83.2154 |
| 08:06 | 33 | 50.50 | 64.5 | 112.8 | 81.3694 |
| 08:08 | 34 | 50.00 | 75.5 | 110.2 | 53.7771 |
| 08:10 | 35 | 49.50 | 75.5 | 107.6 | 59.5877 |
| 08:12 | 36 | 49.00 | 75.5 | 76.2 | 58.5586 |
| 08:14 | 37 | 48.50 | 75.5 | 71.6 | 54.5368 |
| 08:16 | 38 | 48.00 | 75.5 | 67 | 80.8018 |
| 08:18 | 39 | 47.50 | 75.9 | 62.4 | 71.8756 |
| 08:20 | 40 | 47.00 | 76.3 | 76.8 | 73.5100 |
| 08:22 | 41 | 46.50 | 76.7 | 72.2 | 68.9525 |
| 08:24 | 42 | 46.00 | 63.1 | 67.6 | 67.9241 |
| 08:26 | 43 | 45.50 | 63.5 | 63 | 44.8616 |
| 08:28 | 44 | 45.00 | 63.9 | 63 | 36.4950 |
| 08:30 | 45 | 44.50 | 64.3 | 44 | 35.4181 |
| 08:32 | 46 | 44.00 | 78.7 | 44 | 31.5647 |
| 08:34 | 47 | 43.50 | 79.1 | 44 | 71.6705 |
| 08:36 | 48 | 43.00 | 79.5 | 44 | 68.6749 |
| 08:38 | 49 | 42.50 | 79.9 | 82.15 | 65.5375 |
| 08:40 | 50 | 42.00 | 80.3 | 82.3 | 58.2082 |
| 08:42 | 51 | 41.50 | 80.7 | 82.45 | 60.4376 |
| 08:44 | 52 | 41.00 | 81.1 | 82.6 | 17.2408 |
| 08:46 | 53 | 40.50 | 81.5 | 82.75 | 12.3009 |
| 08:48 | 54 | 40.00 | 70.9 | 38.9 | 10.9520 |
| 08:50 | 55 | 39.50 | 71.3 | 38.05 | 12.9869 |
| 08:52 | 56 | 39.00 | 71.7 | 37.2 | 36.8780 |
| 08:54 | 57 | 38.50 | 72.1 | 36.35 | 31.1231 |
| 08:56 | 58 | 38.00 | 72.5 | 52.5 | 32.2821 |
| 08:58 | 59 | 37.50 | 72.9 | 51.65 | 28.5905 |
Appendix B
| Model | II | III | IV | ||
|---|---|---|---|---|---|
| Method | LS-FSM | SA-NLS | NLS | GA–SA | RPCA |
| Software implementation details | NumPy pandas SciPy scikit-learn (1.6.1) | NumPy pandas SciPy | NumPy pandas SciPy scikit-learn | NumPy pandas SciPy scikit-learn | NumPy pandas scikit-learn CVXPY (1.6.6) |
| RMSE | 3.6526 | 11.9175 | 10.7004 | 3.6733 | 5.8200 |
| MAE | 3.0606 | 9.4187 | 8.0558 | 2.8329 | 3.6315 |
| MAPE | 5.0600% | 32.2188% | 20.6800% | 7.4200% | 10.5100% |
| PSI | 0.0861 | 0.4094 | 0.1284 | 0.0184 | 0.0200 |
| SSS | 99.68% | 99.76% | 99.44% | 99.89% | 97.96% |
| RMSE without time delay compensation | 3.8152 | 12.4331 | 10.9357 | 4.6824 | 7.6431 |
References
- Li, A.R.; Xu, Z.L.; Li, W.H.; Chen, Y.Y.; Pan, Y.Y. Urban Signalized Intersection Traffic State Prediction: A Spatial-Temporal Graph Model Integrating the Cell Transmission Model and Transformer. Appl. Sci. 2025, 15, 2377. [Google Scholar] [CrossRef]
- Shintani, M. Nonlinear forecasting analysis using diffusion indexes: An application to Japan. J. Money Credit. Bank. 2005, 37, 517–538. [Google Scholar] [CrossRef]
- Smalter Hall, A.; Cook, T.R. Macroeconomic Indicator Forecasting with Deep Neural Networks; Technical Report 17–11; Federal Reserve Bank of Kansas City: Kansas City, MO, USA, 2017. [Google Scholar]
- Yan, B.; Cao, L.J.; Zhao, C.X. Analysis Method of Transmission Line Parameter Estimation Based on Linear Least Squares Regression and PMU Data. Chin. J. Electron Devices 2024, 47, 1362–1367. (In Chinese) [Google Scholar]
- Zamani, V.; Abtahi, S.; Chen, Y.X.; Li, Y. Parameter-input estimation of RC thermal models of buildings using unscented Kalman filter and nonlinear least square method. Indoor Built Environ. 2025, 34, 41–75. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.D.; Jawad, M.; Ramanuja, M.; Ghodhbani, R.; Yook, S.J.; Abdallah, S.A.O. Forecasting heat and mass transfer enhancement in magnetized non-Newtonian nanofluids using Levenberg-Marquardt algorithm: Influence of activation energy and bioconvection. Mech. Time Depend. Mater. 2024, 29, 14. [Google Scholar] [CrossRef]
- Lovett, N.; Bhatt, H.P. Efficiently and accurately simulating multi-dimensional M-coupled nonlinear Schrödinger equations with fourth-order time integrators and Fourier pseudo-spectral method. Int. J. Comput. Math. 2025, 102, 653–677. [Google Scholar] [CrossRef]
- Zhang, J.; Dong, L.X.; Zhang, Z.R. Second-order scalar auxiliary variable Fourier-spectral method for a liquid thin film coarsening model. Math. Methods Appl. Sci. 2023, 46, 18815–18836. [Google Scholar] [CrossRef]
- Venkataraman, S.; Rumpler, R. Urban traffic flow estimation with noise measurements using log-linear regression. Appl. Acoust. 2025, 236, 110745. [Google Scholar] [CrossRef]
- Graffelman, J.; Bruce, S.W.; Goudet, J. Estimation of Jacquard’s genetic identity coefficients with bi-allelic variants by constrained least-squares. Heredity 2024, 134, 10–20. [Google Scholar] [CrossRef]
- Ma, B.; Li, H.P. Optimal flexible power allocation energy management strategy for hybrid energy storage system with genetic algorithm based model predictive control. Energy 2025, 324, 135958. [Google Scholar] [CrossRef]
- Altaha, M.A.; Jarraya, I.; Haddad, L.; Hamdani, T.M.; Chabchoub, H.; Alim, A.M. RLGA-FER: Reinforcement learning based on genetic algorithm for facial expression recognition enhancing. Int. J. Mach. Learn. Cybern. 2024. preprint. [Google Scholar] [CrossRef]
- Wang, Y.X.; Huang, Y.; Chen, F. Optimisation of Spare Parts Quality Inspection Cost Based on Simulated Annealing and Genetic Algorithm. Front. Comput. Intell. Syst. 2024, 10, 48–53. [Google Scholar] [CrossRef]
- Arellano, M.T.; Vergara, A.B.; Gonzalez, S.P.; Hernández, E.C.H.; Edgar, A.; Franco Ur quiza, E.A. Optimal design of laminates orientation in a composite material by genetics algorithm and simulated annealing. Mech. Adv. Mater. Struct. 2024, 31, 10592–10600. [Google Scholar] [CrossRef]
- Wu, B.H.; Xie, R.H.; Xiao, L.Z.; Guo, J.F.; Jin, G.W.; Fu, J.W. Integrated classification method of tight sandstone reservoir based on principal component analysis simulated annealing genetic algorithm—fuzzy cluster means. Pet. Sci. 2023, 20, 2747–2758. [Google Scholar] [CrossRef]
- Zhang, D.W.; Li, W.L.; Wang, C.G.; Li, J.H. Simulation research on breakdown diagnosis based on least squares support vector machine optimized by simulated annealing genetic algorithm. Int. J. Model. Simul. Sci. Comput. 2024, 15, 2350046. [Google Scholar] [CrossRef]
- Li, S.Z.; Zhou, X.H.; Zhang, X.S.; Wang, Y.H.; Jiang, L.M. Optimization of Tuned Mass Damper for Steel–Concrete Hybrid Wind Turbine Tower Using Genetic Algorithm. Int. J. Struct. Stab. Dyn. 2024. preprint. [Google Scholar] [CrossRef]
- Li, H.Z.; Zhang, Z.Y.; Huang, Y.H.; Lin, Z.H.; Lei, Z. Analysis of Tourism Management Based on Genetic Algorithm and Simulated Annealing Algorithm. World Sci. Res. J. 2025, 11, 133–141. [Google Scholar]
- Zhang, Y.H.; Zhang, H.F.; Liu, Z.Y.; Zhu, J.; Gu, J.Y.; Wang, X.B.; Zhu, Z.Y.; Tang, Y.J.; Wang, J. Glow and hot pixels removal using improved robust principal component analysis. J. Electron. Imaging 2023, 32, 043012. [Google Scholar] [CrossRef]
- Wan, G.H.; He, B.; Schweitzer, H. The art of centering without centering for robust principal component analysis. Data Min. Knowl. Discov. 2023, 38, 699–724. [Google Scholar] [CrossRef]
- Likassa, H.T.; Chen, D.-G.; Chen, K.; Wang, Y.; Zhu, W. Robust PCA with Lw,∗ and L2,1 Norms: A Novel Method for Low-Quality Retinal Image Enhancement. J. Imaging 2024, 10, 151. [Google Scholar] [CrossRef]
- Kou, A.Q.; Cheng, Y.; Huang, X.Y.; Jin, J. Dynamic replenishment policy for perishable goods using change point detection-based soft actor-critic reinforcement learning. Expert Syst. Appl. 2025, 270, 126556. [Google Scholar] [CrossRef]
- Bouman, R.; Schmeitz, L.; Buise, L.; Heres, J.; Shapovalova, Y.; Heskes, T. Acquiring better load estimates by combining anomaly and change point detection in power grid time-series measurements. Sustain. Energy Grids Netw. 2024, 40, 101540. [Google Scholar] [CrossRef]
- Wang, X.L.; Lv, M.H. Research on the Initial Arrival Recognition and Judgment Method of Microseismic Signals Based on PELT. Pure Appl. Geophys. 2024, 182, 1263–1278. [Google Scholar] [CrossRef]
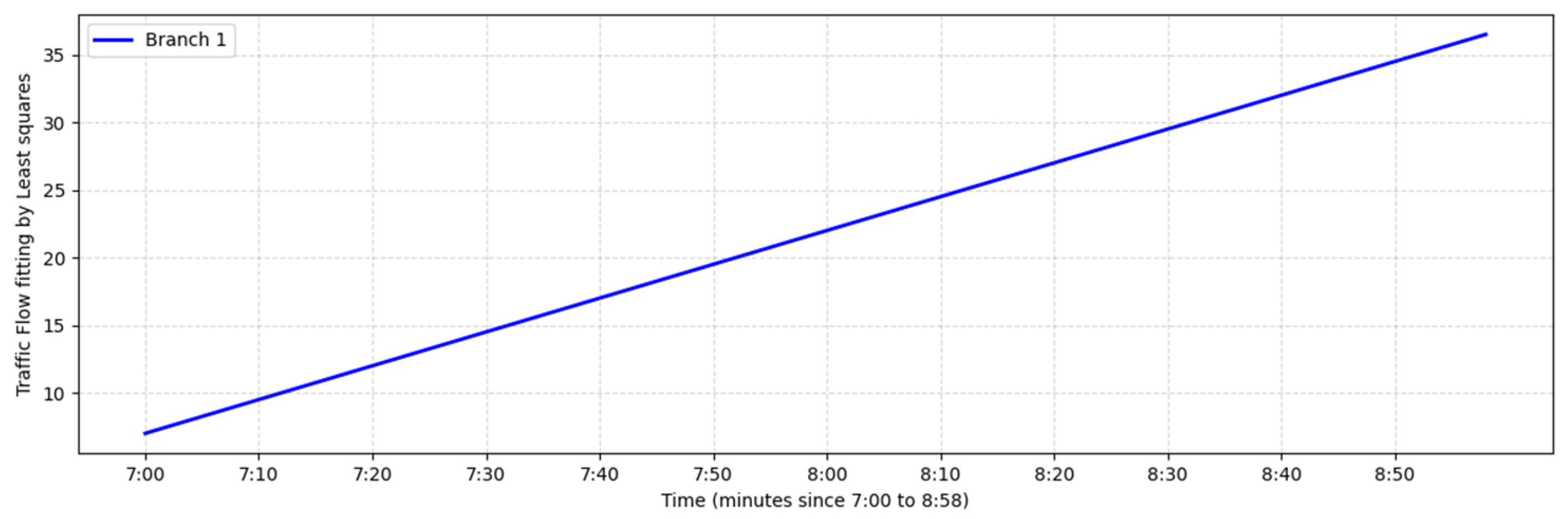
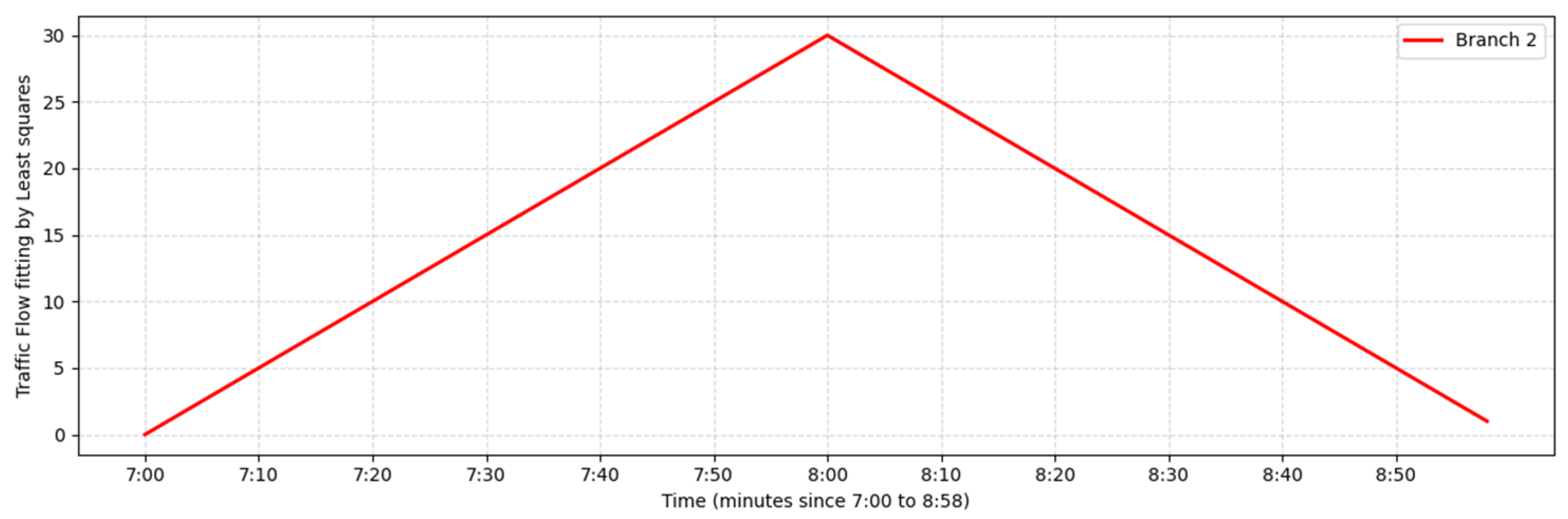
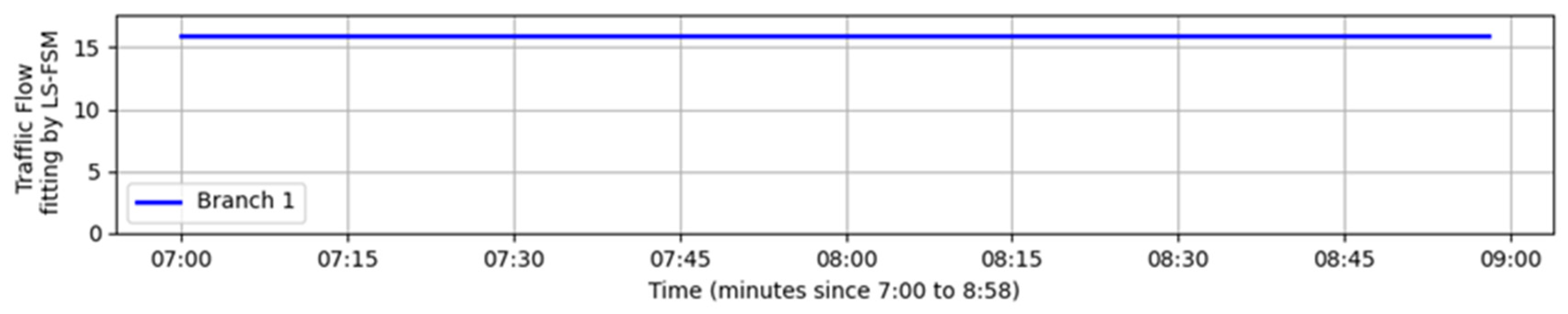



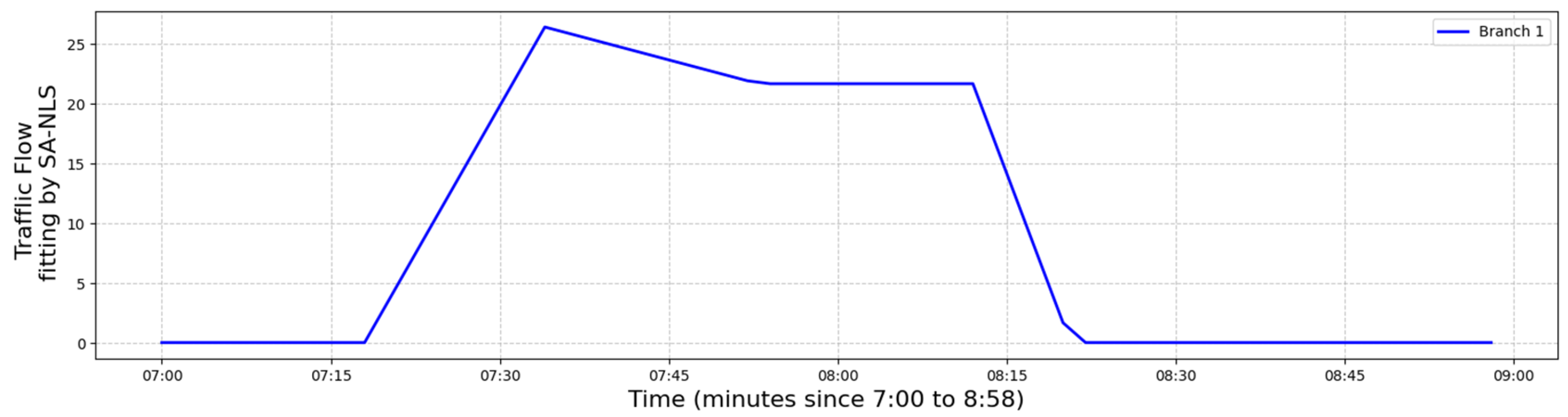
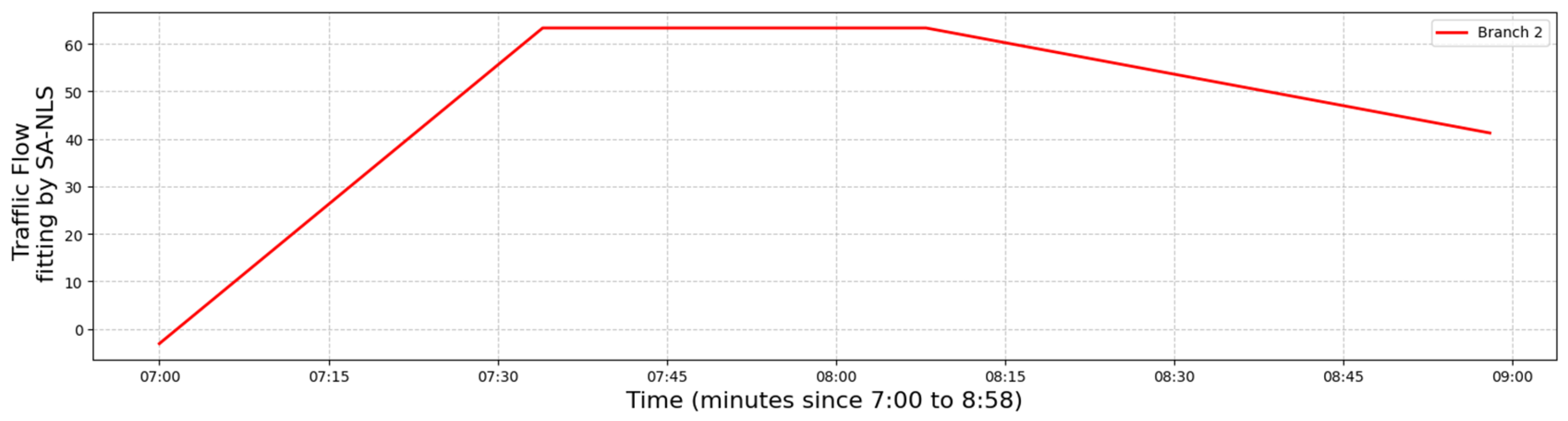


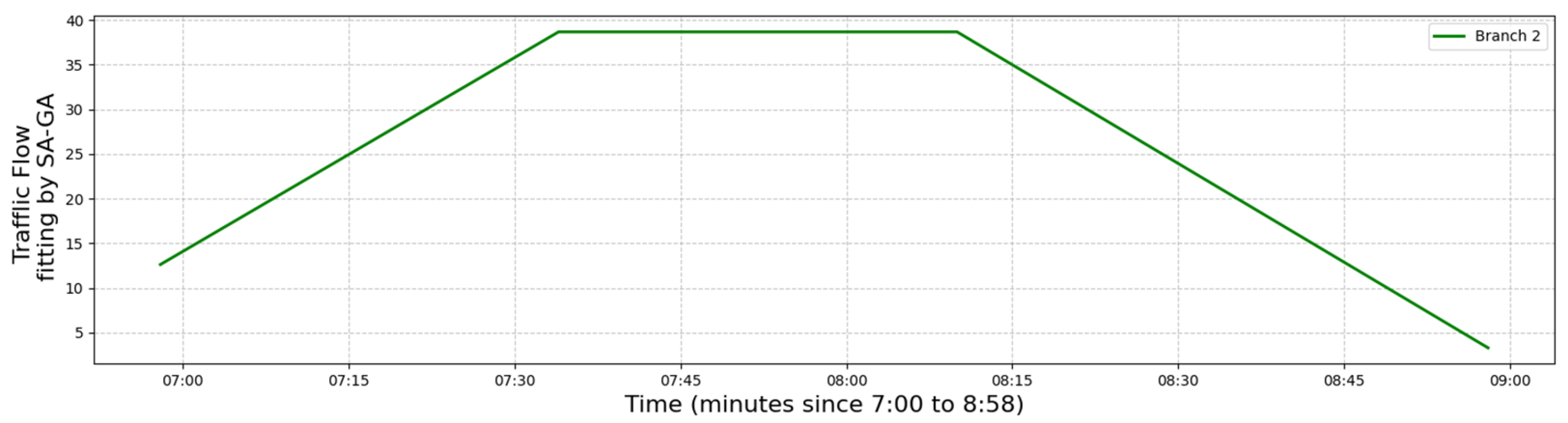
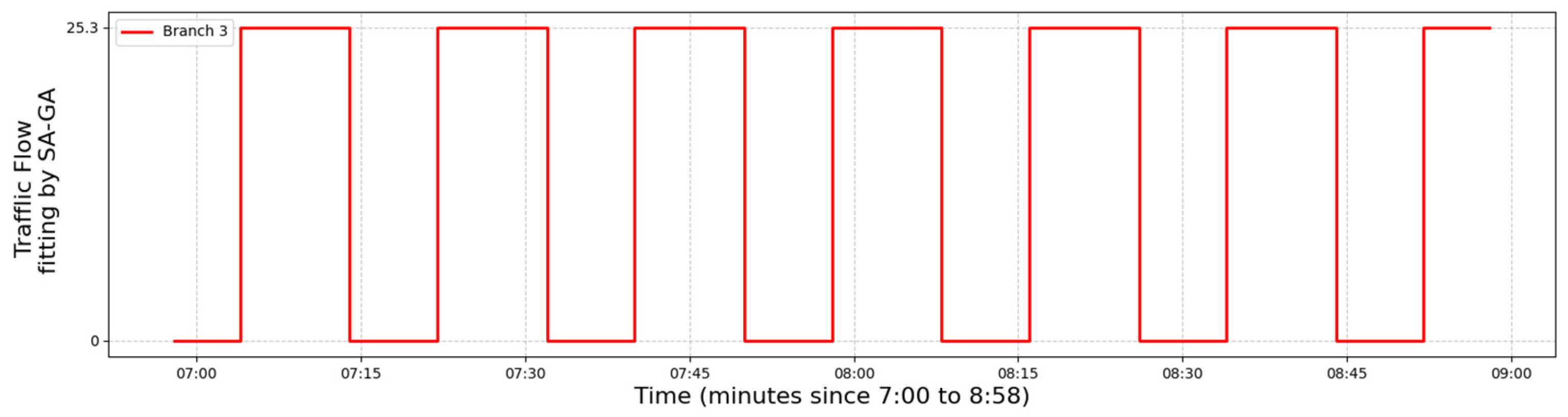


| Moment | Branch Road 1 | Branch Road 2 |
|---|---|---|
| 7:30 | 14.5 | 15 |
| 8:30 | 29.5 | 7.5 |
| Moment | Branch Road 1 | Branch Road 2 | Branch Road 3 | Branch Road 4 |
|---|---|---|---|---|
| 7:30 | 16.5204 | 18.776 | 17.561 | 3.58 |
| 8:30 | 16.5204 | 25.4979 | 24.161 | 5.54 |
| Moment | Branch Road 1 | Branch Road 2 | Branch Road 3 |
|---|---|---|---|
| 7:30 | 23.1 | 59.435 | 15.218 |
| 8:30 | 0 | 52.738 | 0 |
| Moment | Branch Road 1 | Branch Road 2 | Branch Road 3 |
|---|---|---|---|
| 7:30 | 1.68 | 36.6185 | 24.67 |
| 8:30 | 16.34 | 39.61 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Zhu, S. Research on the Branch Road Traffic Flow Estimation and Main Road Traffic Flow Monitoring Optimization Problem. Computation 2025, 13, 183. https://doi.org/10.3390/computation13080183
Wang B, Zhu S. Research on the Branch Road Traffic Flow Estimation and Main Road Traffic Flow Monitoring Optimization Problem. Computation. 2025; 13(8):183. https://doi.org/10.3390/computation13080183
Chicago/Turabian StyleWang, Bingxian, and Sunxiang Zhu. 2025. "Research on the Branch Road Traffic Flow Estimation and Main Road Traffic Flow Monitoring Optimization Problem" Computation 13, no. 8: 183. https://doi.org/10.3390/computation13080183
APA StyleWang, B., & Zhu, S. (2025). Research on the Branch Road Traffic Flow Estimation and Main Road Traffic Flow Monitoring Optimization Problem. Computation, 13(8), 183. https://doi.org/10.3390/computation13080183






