Solution of Coupled Systems of Reaction–Diffusion Equations Using Explicit Numerical Methods with Outstanding Stability Properties
Abstract
1. Introduction
2. The Equations and the Analytical Solutions
2.1. Coupled Diffusion Equations
2.2. The Modified Equations and Their Solution for Simple Coupling
2.3. The Time-Decaying Isomerization
3. The Numerical Methods and Their Properties
3.1. The Spatial and Temporal Discretization
3.2. The Algorithms
3.3. Properties of the Algorithms
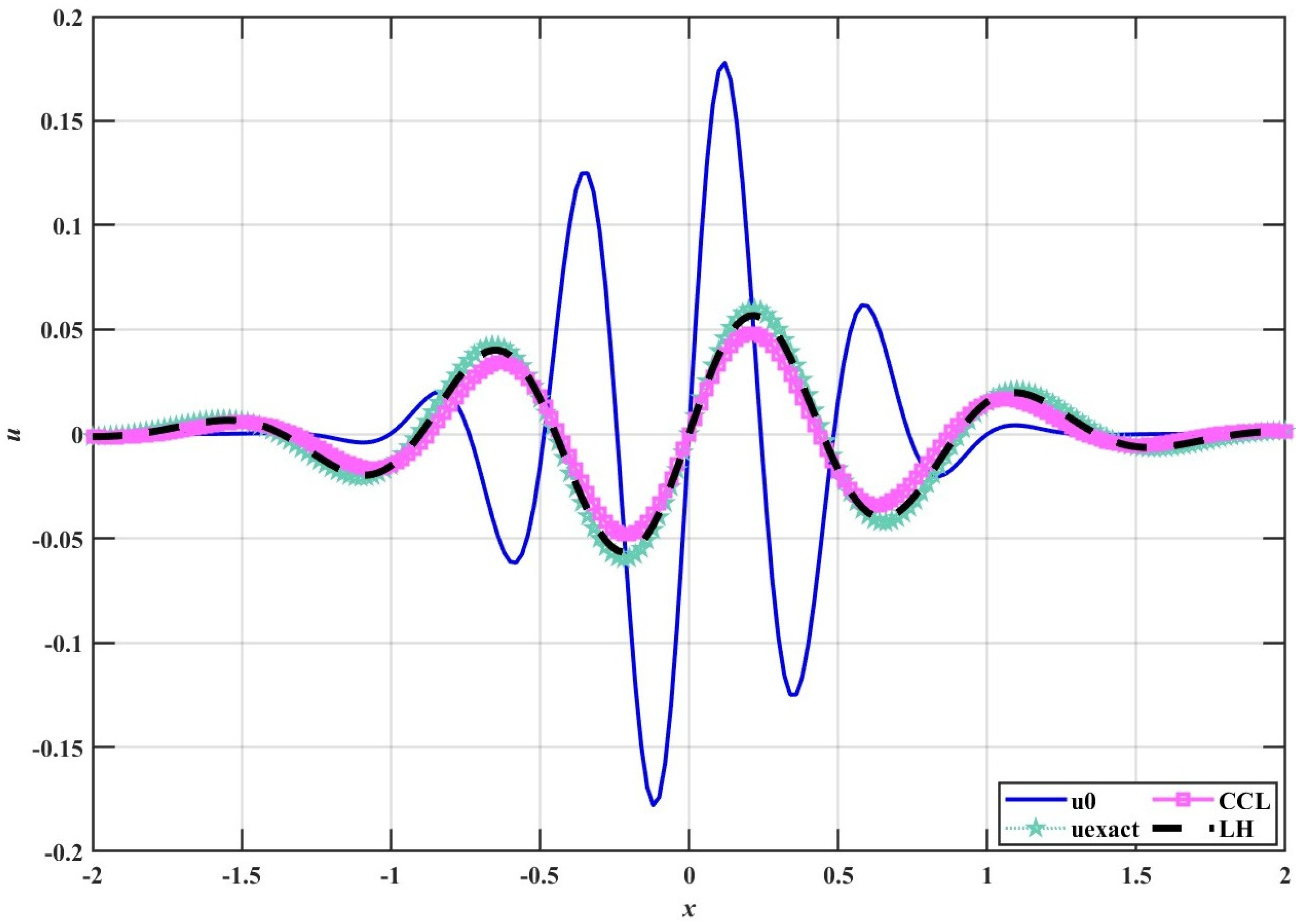
4. Verification in 1D
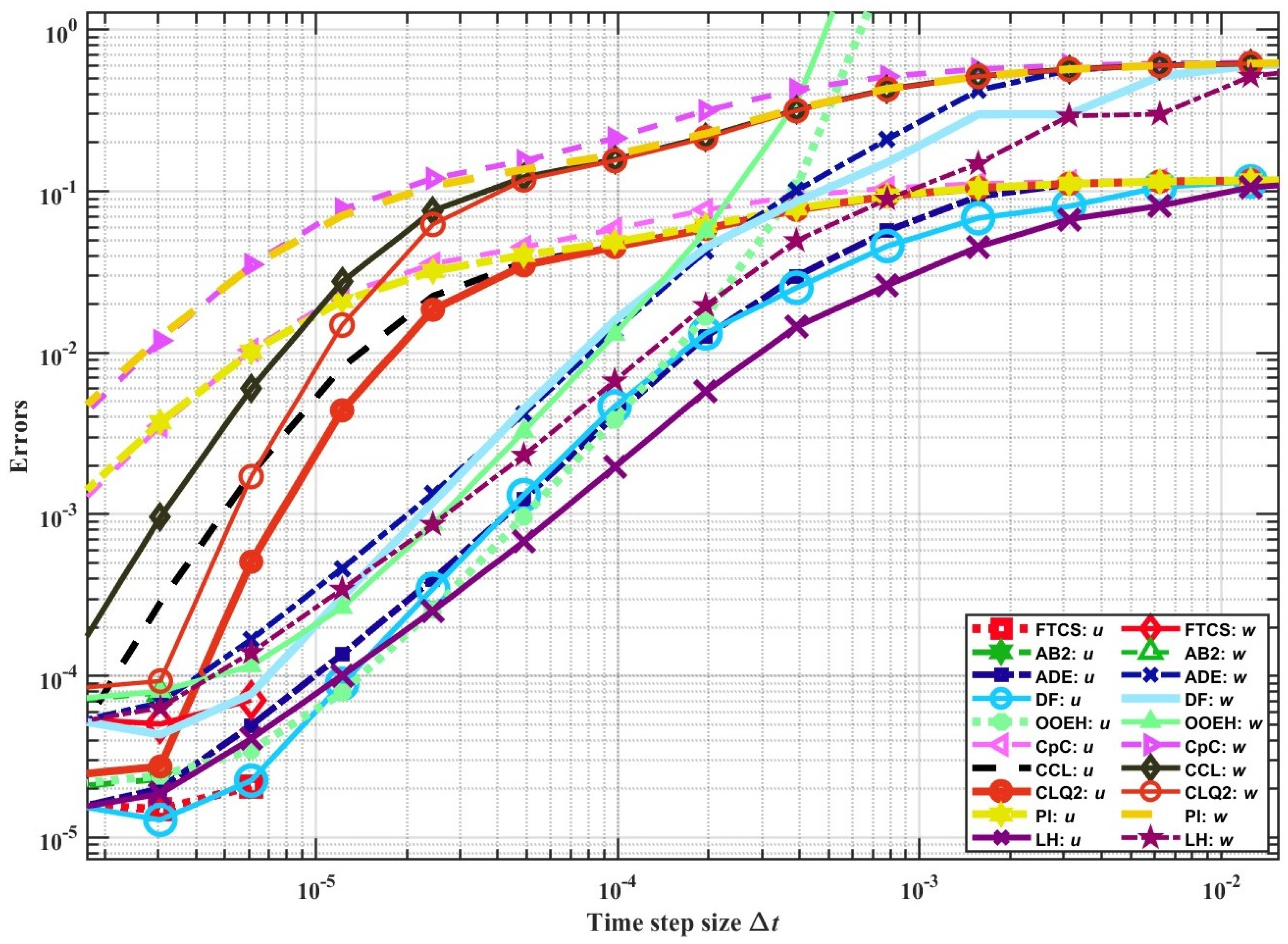
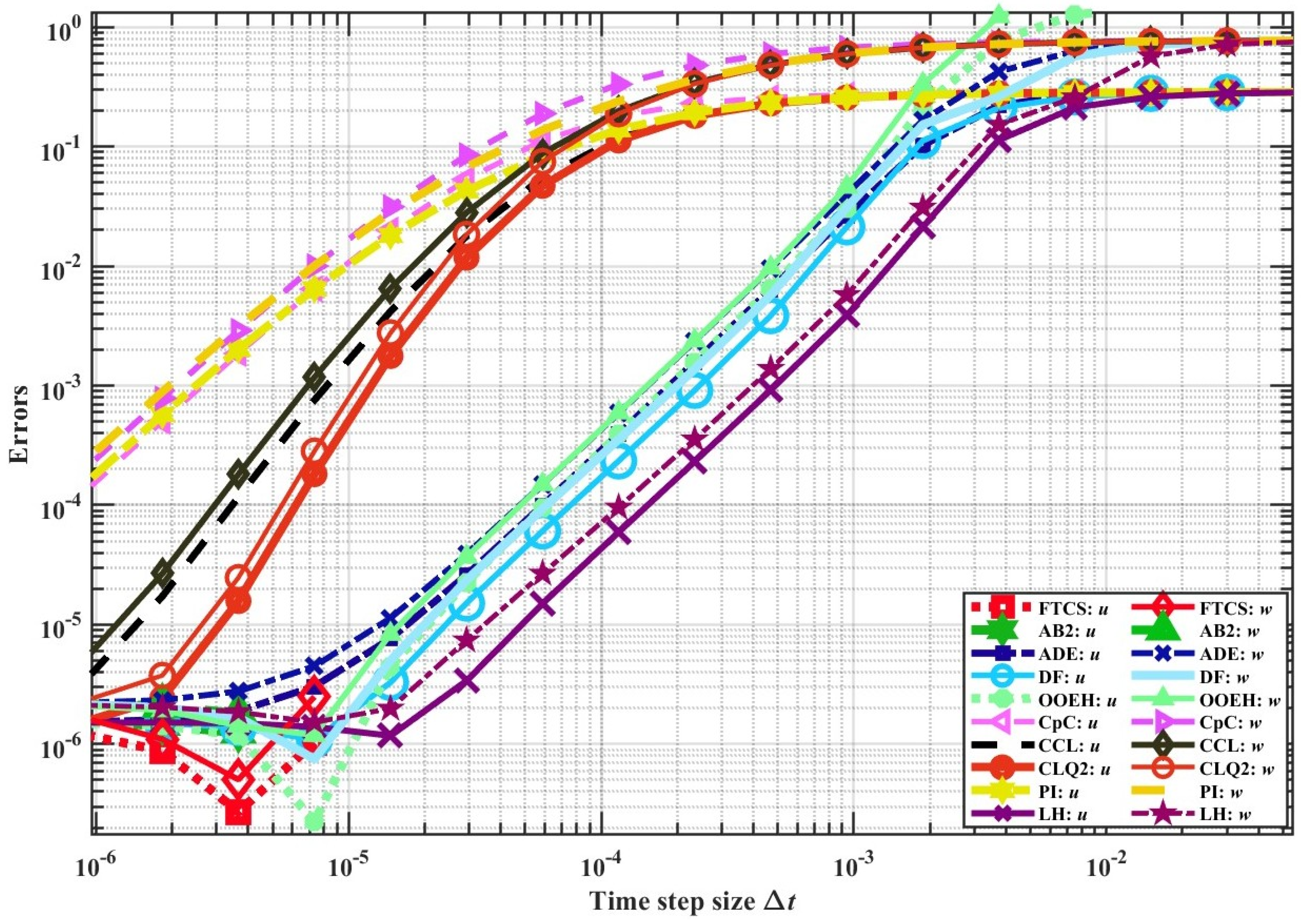
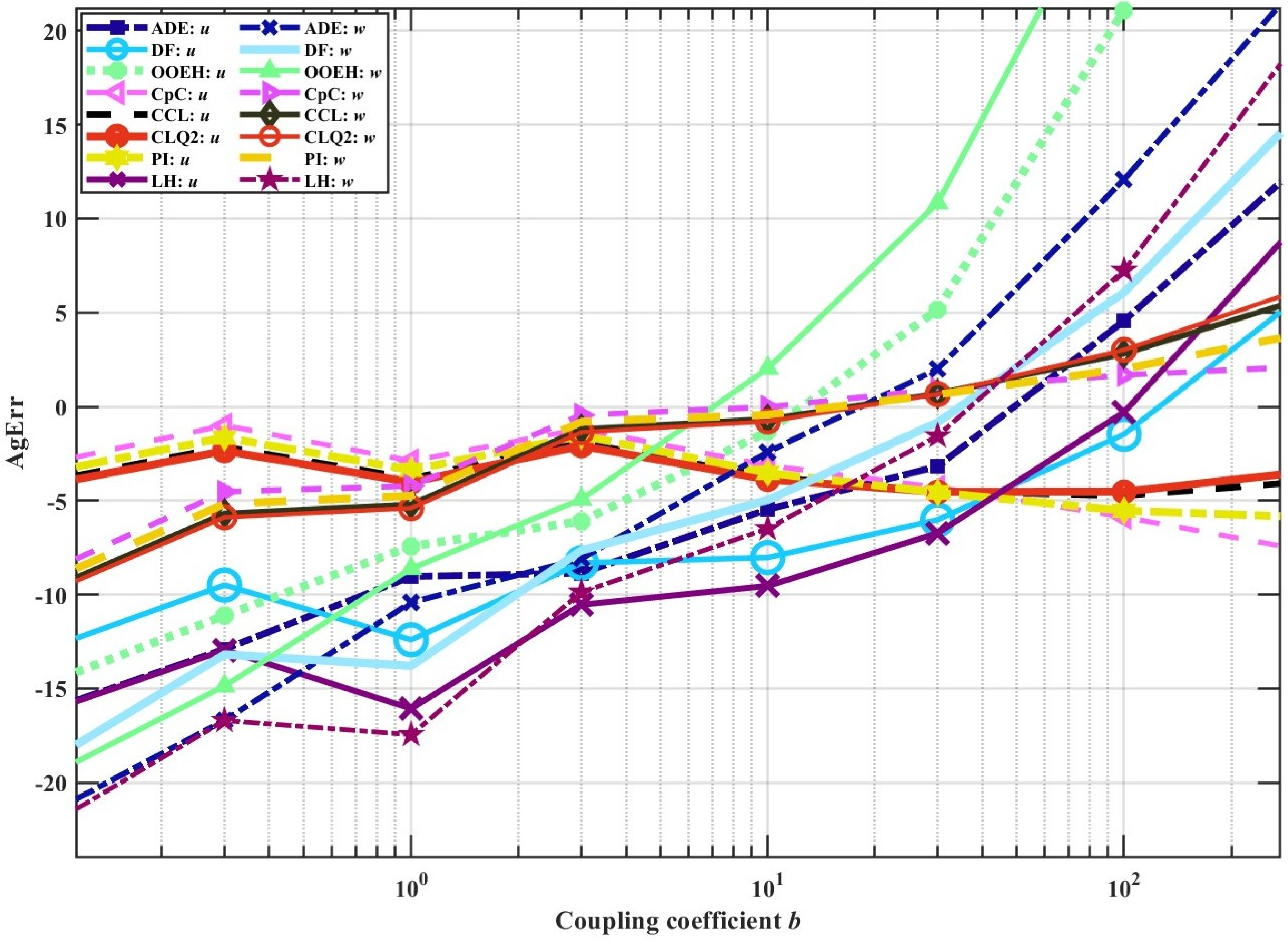
5. Parameter Sweeps for Further Testing of the Methods
6. Conclusions and Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jacobs, M.H. Diffusion Processes; Springer: Berlin/Heidelberg, Germany, 1935; ISBN 978-3-642-86414-8. [Google Scholar]
- Lienhard, J.H., IV; Lienhard, J.H., V. A Heat Transfer Textbook, 4th ed.; Phlogiston Press: Cambridge, MA, USA, 2017; ISBN 978-0-9713835-2-4. [Google Scholar]
- Simpson, M.J.; Sharp, J.A.; Morrow, L.C.; Baker, R.E. Exact Solutions of Coupled Multispecies Linear Reaction–Diffusion Equations on a Uniformly Growing Domain. PLoS ONE 2015, 10, e0138894. [Google Scholar] [CrossRef]
- Escorcia, J.M.; Suazo, E. On explicit solutions for coupled reaction-diffusion and Burgers-type equations with variable coefficients through a Riccati system. Discret. Contin. Dyn. Syst. S 2025. [Google Scholar] [CrossRef]
- Covei, D.-P. A nonlinear diffusion equation of the Gurtin-MacCamy type: Existence, uniqueness, and numerical simulations. arXiv 2025. [Google Scholar] [CrossRef]
- Mátyás, L.; Barna, I.F. General Self-Similar Solutions of Diffusion Equation and Related Constructions. Rom. J. Phys. 2022, 67, 101. [Google Scholar]
- Barna, I.F.; Mátyás, L. Diffusion Cascades and Mutually Coupled Diffusion Processes. Mathematics 2024, 12, 3298. [Google Scholar] [CrossRef]
- Jejeniwa, O.A.; Gidey, H.H.; Appadu, A.R. Numerical Modeling of Pollutant Transport: Results and Optimal Parameters. Symmetry 2022, 14, 2616. [Google Scholar] [CrossRef]
- Köroğlu, C.; Aydin, A. Exact and nonstandard finite difference schemes for the Burgers equation B(2,2). Turk. J. Math. 2021, 45, 647–660. [Google Scholar] [CrossRef]
- Agbavon, K.M.; Appadu, A.R. Construction and analysis of some nonstandard finite difference methods for the FitzHugh–Nagumo equation. Numer. Methods Partial. Differ. Equ. 2020, 36, 1145–1169. [Google Scholar] [CrossRef]
- Agbavon, K.M.; Appadu, A.R.; Khumalo, M. On the numerical solution of Fisher’s equation with coefficient of diffusion term much smaller than coefficient of reaction term. Adv. Differ. Equ. 2019, 2019, 146. [Google Scholar] [CrossRef]
- Appadu, A.R.; Inan, B.; Tijani, Y.O. Comparative study of some numerical methods for the Burgers-Huxley equation. Symmetry 2019, 11, 1333. [Google Scholar] [CrossRef]
- Marc, E. Songolo a Positivity-Preserving Nonstandard Finite Difference Scheme for Parabolic System with Cross-Diffusion Equations and Nonlocal Initial Conditions. Am. Sci. Res. J. Eng. Technol. Sci. 2016, 18, 252–258. [Google Scholar]
- Chapwanya, M.; Lubuma, J.M.S.; Mickens, R.E. Positivity-Preserving nonstandard finite difference schemes for Cross-Diffusion equations in biosciences. Comput. Math. Appl. 2014, 68, 1071–1082. [Google Scholar] [CrossRef]
- Bansal, S.; Natesan, S. A novel Higher-Order efficient computational method for pricing European and Asian options. Numer. Algorithms 2024. [Google Scholar] [CrossRef]
- Rieth, Á.; Kovács, R.; Fülöp, T. Implicit numerical schemes for generalized heat conduction equations. Int. J. Heat. Mass. Transf. 2018, 126, 1177–1182. [Google Scholar] [CrossRef]
- Britz, D.; Baronas, R.; Gaidamauskaitė, E.; Ivanauskas, F. Further comparisons of finite difference schemes for computational modelling of biosensors. Nonlinear Anal. Model. Control 2009, 14, 419–433. [Google Scholar] [CrossRef]
- Mbroh, N.A.; Munyakazi, J.B. A robust numerical scheme for singularly perturbed parabolic Reaction-Diffusion problems via the method of lines. Int. J. Comput. Math. 2021, 99, 1139–1158. [Google Scholar] [CrossRef]
- Manaa, S.; Sabawi, M. Numerical Solution and Stability Analysis of Huxley Equation. AL-Rafidain J. Comput. Sci. Math. 2005, 2, 85–97. [Google Scholar] [CrossRef]
- Pargaei, M.; Kumar, B.V.R. A 3D Haar wavelet method for a coupled degenerate system of parabolic equations with nonlinear source coupled with Non-Linear ODEs. Appl. Numer. Math. 2023, 185, 141–164. [Google Scholar] [CrossRef]
- Anjuman; Leung, A.Y.T.; Das, S. Two-Dimensional Time-Fractional Nonlinear Drift Reaction–Diffusion Equation Arising in Electrical Field. Fractal Fract. 2024, 8, 456. [Google Scholar] [CrossRef]
- Rufai, M.A.; Kosti, A.A.; Anastassi, Z.A.; Carpentieri, B. A New Two-Step Hybrid Block Method for the FitzHugh–Nagumo Model Equation. Mathematics 2024, 12, 51. [Google Scholar] [CrossRef]
- Ndou, N.; Dlamini, P.; Jacobs, B.A. Enhanced Unconditionally Positive Finite Difference Method for Advection–Diffusion–Reaction Equations. Mathematics 2022, 10, 2639. [Google Scholar] [CrossRef]
- Heidari, M.; Ghovatmand, M.; Skandari, M.H.N.; Baleanu, D. Numerical Solution of Reaction–Diffusion Equations with Convergence Analysis. J. Nonlinear Math. Phys. 2023, 30, 384–399. [Google Scholar] [CrossRef]
- Kolev, M.K.; Koleva, M.N.; Vulkov, L.G. An Unconditional Positivity-Preserving Difference Scheme for Models of Cancer Migration and Invasion. Mathematics 2022, 10, 131. [Google Scholar] [CrossRef]
- Ascher, U.M.; Ruuth, S.J.; Wetton, B.T.R. Implicit-Explicit Methods for Time-Dependent Partial Differential Equations. SIAM J. Numer. Anal. 1995, 32, 797–823. [Google Scholar] [CrossRef]
- Calvo, M.P.; de Frutos, J.; Novo, J. Linearly implicit Runge–Kutta methods for Advection–Reaction–Diffusion equations. Appl. Numer. Math. 2001, 37, 535–549. [Google Scholar] [CrossRef]
- Settanni, G.; Sgura, I. Devising efficient numerical methods for oscillating patterns in Reaction-Diffusion systems. J. Comput. Appl. Math. 2016, 292, 674–693. [Google Scholar] [CrossRef]
- Yadav, V.S.; Singh, A.; Maurya, V.; Rajpoot, M.K. New RK type Time-Integration methods for stiff Convection–Diffusion–Reaction systems. Comput. Fluids 2023, 257, 105865. [Google Scholar] [CrossRef]
- Beuken, L.; Cheffert, O.; Tutueva, A.; Butusov, D.; Legat, V. Numerical Stability and Performance of Semi-Explicit and Semi-Implicit Predictor–Corrector Methods. Mathematics 2022, 10, 2015. [Google Scholar] [CrossRef]
- Fedoseev, P.; Pesterev, D.; Karimov, A.; Butusov, D. New Step Size Control Algorithm for Semi-Implicit Composition ODE Solvers. Algorithms 2022, 15, 275. [Google Scholar] [CrossRef]
- Ji, Y.; Xing, Y. Highly Accurate and Efficient Time Integration Methods with Unconditional Stability and Flexible Numerical Dissipation. Mathematics 2023, 11, 593. [Google Scholar] [CrossRef]
- Chou, C.S.; Zhang, Y.T.; Zhao, R.; Nie, Q. Numerical methods for stiff Reaction-Diffusion systems. Discret. Contin. Dyn. Syst.-Ser. B 2007, 7, 515–525. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, Y.T. Krylov implicit integration factor WENO methods for semilinear and fully nonlinear Advection-Diffusion-Reaction equations. J. Comput. Phys. 2013, 253, 368–388. [Google Scholar] [CrossRef]
- Essongue, S.; Ledoux, Y.; Ballu, A. Speeding up mesoscale thermal simulations of powder bed additive manufacturing thanks to the forward Euler Time-Integration scheme: A critical assessment. Finite Elem. Anal. Des. 2022, 211, 103825. [Google Scholar] [CrossRef]
- Chen-Charpentier, B.M.; Kojouharov, H.V. An unconditionally positivity preserving scheme for Advection-Diffusion reaction equations. Math. Comput. Model. 2013, 57, 2177–2185. [Google Scholar] [CrossRef]
- Appadu, A.R. Performance of UPFD scheme under some different regimes of advection, diffusion and reaction. Int. J. Numer. Methods Heat. Fluid. Flow. 2017, 27, 1412–1429. [Google Scholar] [CrossRef]
- Savović, S.; Drljača, B.; Djordjevich, A. A comparative study of two different finite difference methods for solving Advection–Diffusion reaction equation for modeling exponential traveling wave in heat and mass transfer processes. Ric. Mat. 2022, 71, 245–252. [Google Scholar] [CrossRef]
- Al-Bayati, A.; Manaa, S.; Al-Rozbayani, A. Comparison of Finite Difference Solution Methods for Reaction Diffusion System in Two Dimensions. AL-Rafidain J. Comput. Sci. Math. 2011, 8, 21–36. [Google Scholar] [CrossRef][Green Version]
- Pourghanbar, S.; Manafian, J.; Ranjbar, M.; Aliyeva, A.; Gasimov, Y.S. An efficient alternating direction explicit method for solving a nonlinear partial differential equation. Math. Probl. Eng. 2020, 2020, 47416. [Google Scholar] [CrossRef]
- Nagy, Á.; Majár, J.; Kovács, E. Consistency and Convergence Properties of 20 Recent and Old Numerical Schemes for the Diffusion Equation. Algorithms 2022, 15, 425. [Google Scholar] [CrossRef]
- Nagy, Á.; Omle, I.; Kareem, H.; Kovács, E.; Barna, I.F.; Bognar, G. Stable, Explicit, Leapfrog-Hopscotch Algorithms for the Diffusion Equation. Computation 2021, 9, 92. [Google Scholar] [CrossRef]
- Saleh, M.; Kovács, E.; Barna, I.F.; Mátyás, L. New Analytical Results and Comparison of 14 Numerical Schemes for the Diffusion Equation with Space-Dependent Diffusion Coefficient. Mathematics 2022, 10, 2813. [Google Scholar] [CrossRef]
- Saleh, M.; Kovács, E.; Barna, I.F. Analytical and Numerical Results for the Transient Diffusion Equation with Diffusion Coefficient Depending on Both Space and Time. Algorithms 2023, 16, 184. [Google Scholar] [CrossRef]
- Askar, A.H.; Nagy, Á.; Barna, I.F.; Kovács, E. Analytical and Numerical Results for the Diffusion-Reaction Equation When the Reaction Coefficient Depends on Simultaneously the Space and Time Coordinates. Compututation 2023, 11, 127. [Google Scholar] [CrossRef]
- Barakat, H.Z.; Clark, J.A. On the solution of the diffusion equations by numerical methods. J. Heat. Transf. 1966, 88, 421–427. [Google Scholar] [CrossRef]
- Liu, H.; Leung, S. An Alternating Direction Explicit Method for Time Evolution Equations with Applications to Fractional Differential Equations. Methods Appl. Anal. 2020, 26, 249–268. [Google Scholar] [CrossRef]
- Hirsch, C. Numerical Computation of Internal and External Flows, Volume 1: Fundamentals of Numerical Discretization; John Wiley & Sons: Hoboken, NJ, USA, 1988. [Google Scholar]
- Gourlay, A.R.; McGuire, G.R. General Hopscotch Algorithm for the Numerical Solution of Partial Differential Equations. IMA J. Appl. Math. 1971, 7, 216–227. [Google Scholar] [CrossRef]
- Kovács, E.; Nagy, Á.; Saleh, M. A set of new stable, explicit, second order schemes for the Non-Stationary heat conduction equation. Mathematics 2021, 9, 2284. [Google Scholar] [CrossRef]
- Kovács, E.; Nagy, Á. A new stable, explicit, and generic Third-Order method for simulating conductive heat transfer. Numer. Methods Partial. Differ. Equ. 2023, 39, 1504–1528. [Google Scholar] [CrossRef]
- Kovács, E.; Majár, J.; Saleh, M. Unconditionally Positive, Explicit, Fourth Order Method for the Diffusion- and Nagumo-Type Diffusion–Reaction Equations. J. Sci. Comput. 2024, 98, 39. [Google Scholar] [CrossRef]
- Jalghaf, H.K.; Kovács, E.; Majár, J.; Nagy, Á.; Askar, A.H. Explicit stable finite difference methods for Diffusion-Reaction type equations. Mathematics 2021, 9, 3308. [Google Scholar] [CrossRef]







| Numerical Methods | 0.1 | 0.3 | 1 | 3 | 6 | 10 | 20 | 30 | 100 | 300 |
|---|---|---|---|---|---|---|---|---|---|---|
| ADEu | −20.45 | −18.70 | −12.14 | −8.56 | −2.21 | 4.33 | 24.69 | 38.61 | 166.61 | 420.26 |
| ADEw | −16.91 | −16.05 | −10.02 | −6.51 | −0.16 | 6.36 | 26.69 | 40.61 | 168.60 | 422.25 |
| DFu | −20.29 | −16.63 | −13.09 | −11.74 | −5.26 | −0.79 | 13.52 | 23.05 | 87.91 | 215.24 |
| DFw | −16.92 | −14.68 | −10.84 | −9.73 | −3.22 | 1.22 | 15.56 | 25.08 | 89.93 | 217.23 |
| OOEHu | −18.71 | −17.06 | −10.68 | −4.49 | 6.10 | 18.11 | 50.65 | 75.71 | 267.83 | 676.56 |
| OOEHw | −15.08 | −14.04 | −8.44 | −2.19 | 8.58 | 20.86 | 53.98 | 79.51 | 273.61 | 684.90 |
| CpCu | −9.40 | −6.12 | −4.96 | −2.95 | −1.26 | −1.36 | 0.29 | 3.41 | 33.03 | 123.56 |
| CpCw | −6.54 | −3.79 | −2.69 | −0.84 | 0.80 | 0.69 | 2.31 | 5.44 | 35.03 | 125.56 |
| CCLu | −10.27 | −7.05 | −6.38 | −4.30 | −1.89 | −1.14 | 3.81 | 9.31 | 60.57 | 208.27 |
| CCLw | −7.42 | −4.71 | −4.17 | −2.22 | 0.16 | 0.90 | 5.82 | 11.33 | 62.57 | 210.27 |
| CLQ2u | −10.46 | −7.23 | −6.61 | −4.51 | −1.96 | −1.05 | 4.33 | 10.23 | 65.33 | 228.88 |
| CLQ2w | −7.61 | −4.90 | −4.41 | −2.43 | 0.09 | 0.98 | 6.33 | 12.25 | 67.33 | 230.88 |
| PIu | −9.80 | −6.58 | −5.78 | −3.67 | −1.68 | −1.38 | 1.97 | 6.32 | 47.37 | 165.17 |
| PIw | −6.95 | −4.24 | −3.57 | −1.57 | 0.37 | 0.66 | 3.98 | 8.34 | 49.37 | 167.16 |
| LHu | −23.69 | −19.97 | −17.01 | −15.08 | −6.31 | −0.86 | 17.25 | 29.56 | 113.61 | 278.26 |
| LHw | −20.43 | −18.05 | −14.78 | −12.98 | −4.29 | 1.14 | 19.28 | 31.58 | 115.61 | 280.25 |
| Numerical Methods | 0.1 | 0.3 | 1 | 3 | 10 | 30 | 100 | 300 |
|---|---|---|---|---|---|---|---|---|
| ADEu | −16.03 | −12.90 | −9.03 | −8.85 | −5.46 | −3.17 | 4.56 | 12.58 |
| ADEw | −21.48 | −16.69 | −10.41 | −8.08 | −2.41 | 2.00 | 12.07 | 22.22 |
| DFu | −12.74 | −9.49 | −12.40 | −8.31 | −8.02 | −6.01 | −1.46 | 5.60 |
| DFw | −18.70 | −13.19 | −13.79 | −7.64 | −4.96 | −0.83 | 6.06 | 15.30 |
| OOEHu | −14.57 | −11.11 | −7.42 | −6.09 | −1.32 | 5.14 | 21.09 | 42.46 |
| OOEHw | −19.50 | −14.86 | −8.60 | −4.92 | 2.02 | 10.82 | 29.48 | 53.50 |
| CpCu | −2.93 | −0.99 | −2.88 | −1.18 | −3.12 | −4.28 | −5.87 | −7.54 |
| CpCw | −8.62 | −4.53 | −4.21 | −0.44 | −0.02 | 0.92 | 1.67 | 2.09 |
| CCLu | −3.89 | −2.15 | −3.82 | −1.92 | −3.74 | −4.51 | −4.72 | −4.03 |
| CCLw | −9.59 | −5.68 | −5.20 | −1.19 | −0.65 | 0.68 | 2.80 | 5.59 |
| CLQ2u | −4.08 | −2.35 | −4.01 | −2.08 | −3.87 | −4.53 | −4.52 | −3.52 |
| CLQ2w | −9.77 | −5.88 | −5.40 | −1.35 | −0.78 | 0.66 | 3.01 | 6.10 |
| PIu | −3.42 | −1.64 | −3.36 | −1.53 | −3.51 | −4.56 | −5.53 | −5.84 |
| PIw | −9.11 | −5.17 | −4.73 | −0.80 | −0.42 | 0.64 | 2.00 | 3.78 |
| LHu | −16.09 | −12.95 | −16.06 | −10.53 | −9.53 | −6.72 | −0.28 | 9.53 |
| LHw | −22.09 | −16.70 | −17.45 | −9.87 | −6.48 | −1.55 | 7.23 | 19.21 |
| Numerical Methods | −10 | −3 | −1 | 0 | 1 | 3 | 10 |
|---|---|---|---|---|---|---|---|
| ADEu | −8.43 | −10.59 | −8.10 | −13.86 | −22.27 | −38.65 | −88.89 |
| ADEw | −67.24 | −23.25 | −6.75 | −5.48 | −6.57 | −8.04 | −9.96 |
| DFu | −8.09 | −7.60 | −10.85 | −18.43 | −26.66 | −43.72 | −97.15 |
| DFw | −65.49 | −19.45 | −9.50 | −9.45 | −10.23 | −12.91 | −14.55 |
| OOEHu | −9.87 | −6.78 | −4.01 | −9.94 | −17.95 | −32.74 | −80.60 |
| OOEHw | −67.03 | −18.38 | −2.38 | −1.55 | −2.83 | −4.04 | −5.52 |
| CpCu | −2.64 | −0.58 | −2.25 | −9.92 | −19.80 | −37.71 | −92.86 |
| CpCw | −60.87 | −13.13 | −0.90 | −0.85 | −2.57 | −4.43 | −6.22 |
| CCLu | −3.47 | −1.45 | −3.59 | −10.94 | −20.54 | −37.94 | −92.41 |
| CCLw | −61.37 | −13.91 | −2.24 | −2.05 | −3.74 | −5.56 | −7.96 |
| CLQ2u | −3.64 | −1.62 | −3.84 | −11.10 | −20.69 | −38.05 | −92.39 |
| CLQ2w | −61.51 | −14.06 | −2.49 | −2.22 | −3.90 | −5.73 | −8.15 |
| PIu | −3.11 | −1.02 | −2.96 | −10.54 | −20.24 | −37.70 | −91.99 |
| PIw | −61.07 | −13.50 | −1.60 | −1.62 | −3.36 | −5.17 | −7.40 |
| LHu | −10.00 | −10.08 | −14.72 | −19.77 | −27.89 | −44.40 | −100.32 |
| LHw | −67.32 | −21.82 | −13.37 | −11.13 | −12.03 | −14.53 | −20.20 |
| Numerical Methods | 0.0001 | 0.0003 | 0.001 | 0.003 | 0.01 | 0.03 | 0.1 | 0.3 | 1 | 3 | 10 | 30 | 100 | 300 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ADEu | −52.56 | −47.12 | −40.45 | −32.62 | −22.69 | −13.64 | −8.56 | −7.20 | −9.39 | −9.53 | −8.55 | −7.80 | −6.43 | −5.91 |
| ADEw | −50.28 | −44.85 | −38.18 | −30.35 | −20.43 | −11.45 | −6.51 | −5.31 | −7.30 | −7.54 | −6.51 | −5.48 | −4.14 | −3.61 |
| DFu | −48.82 | −42.92 | −36.21 | −29.69 | −22.20 | −15.01 | −11.74 | −6.28 | −4.83 | −4.69 | −2.64 | −2.06 | −2.67 | −3.25 |
| DFw | −46.49 | −40.58 | −33.91 | −27.42 | −19.95 | −12.82 | −9.73 | −4.41 | −3.13 | −3.20 | −0.91 | −0.11 | −0.96 | −1.54 |
| OOEHu | −53.20 | −48.50 | −41.81 | −34.40 | −24.77 | −14.54 | −4.49 | 6.83 | 18.73 | 34.10 | 52.17 | 63.97 | 73.20 | 79.25 |
| OOEHw | −51.96 | −46.83 | −39.85 | −32.11 | −22.22 | −11.89 | −2.19 | 8.97 | 20.59 | 35.56 | 53.21 | 64.58 | 73.34 | 78.96 |
| CpCu | −47.82 | −39.68 | −30.37 | −21.53 | −12.55 | −5.79 | −2.95 | −0.40 | −8.05 | −4.40 | −5.53 | −4.64 | −4.50 | −4.52 |
| CpCw | −45.48 | −37.32 | −27.99 | −19.24 | −10.27 | −3.56 | −0.84 | 1.52 | −5.94 | −3.30 | −2.81 | −2.26 | −2.21 | −2.23 |
| CCLu | −51.52 | −44.14 | −35.15 | −26.33 | −16.16 | −7.85 | −4.30 | −0.74 | −8.23 | −4.99 | −6.37 | −5.54 | −5.59 | −5.73 |
| CCLw | −49.20 | −41.80 | −32.78 | −24.04 | −13.90 | −5.63 | −2.22 | 1.15 | −6.20 | −4.01 | −3.75 | −3.27 | −3.37 | −3.49 |
| CLQ2u | −52.89 | −45.88 | −36.93 | −28.14 | −17.98 | −8.68 | −4.51 | −0.77 | −8.43 | −5.01 | −6.37 | −5.54 | −5.59 | −5.73 |
| CLQ2w | −50.56 | −43.52 | −34.56 | −25.83 | −15.70 | −6.46 | −2.43 | 1.12 | −6.21 | −4.02 | −3.75 | −3.27 | −3.37 | −3.50 |
| PIu | −47.69 | −39.67 | −30.54 | −21.83 | −13.03 | −6.41 | −3.67 | −0.66 | −7.59 | −4.95 | −6.24 | −5.41 | −5.41 | −5.43 |
| PIw | −45.35 | −37.31 | −28.15 | −19.55 | −10.76 | −4.18 | −1.57 | 1.23 | −5.98 | −3.93 | −3.65 | −3.15 | −3.20 | −3.21 |
| LHu | −50.12 | −44.52 | −38.13 | −31.76 | −24.23 | −17.10 | −15.08 | −9.11 | −8.07 | −8.73 | −6.69 | −4.02 | −3.19 | −3.73 |
| LHw | −47.79 | −42.19 | −35.85 | −29.50 | −22.01 | −14.92 | −12.98 | −7.29 | −6.41 | −7.14 | −5.11 | −2.26 | −1.40 | −1.85 |
| Numerical Method | 0.0001 | 0.0003 | 0.001 | 0.003 | 0.01 | 0.03 | 0.1 | 0.3 | 1 | 3 | 10 | 30 | 100 | 300 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ADEu | −68.44 | −62.54 | −55.36 | −47.34 | −37.54 | −28.60 | −20.34 | −17.65 | −15.43 | −14.64 | −12.99 | −11.14 | −9.63 | −9.00 |
| ADEw | −81.73 | −76.07 | −68.39 | −60.20 | −50.42 | −41.13 | −31.54 | −26.54 | −24.12 | −22.05 | −21.29 | −20.08 | −19.59 | −19.58 |
| DFu | −62.42 | −55.65 | −47.85 | −40.71 | −32.86 | −25.84 | −19.77 | −14.45 | −9.78 | −7.44 | −3.44 | −1.75 | −0.93 | −0.64 |
| DFw | −71.05 | −63.66 | −55.17 | −47.40 | −39.11 | −32.38 | −29.13 | −21.52 | −19.26 | −17.15 | −12.74 | −11.96 | −11.40 | −11.55 |
| OOEHu | −69.91 | −64.44 | −57.03 | −49.07 | −39.32 | −29.95 | −19.48 | −15.66 | −9.79 | −5.81 | 0.64 | 5.71 | 10.40 | 14.62 |
| OOEHw | −82.76 | −76.75 | −68.90 | −60.71 | −50.28 | −40.29 | −29.67 | −22.47 | −16.36 | −8.60 | 1.33 | 10.16 | 19.05 | 27.14 |
| CpCu | −61.06 | −51.54 | −40.12 | −30.35 | −21.57 | −14.87 | −8.71 | −4.57 | −2.22 | −1.46 | −1.23 | −1.19 | −1.19 | −1.19 |
| CpCw | −69.20 | −58.62 | −46.87 | −37.18 | −28.23 | −21.67 | −16.29 | −13.01 | −11.39 | −11.62 | −12.87 | −14.84 | −16.25 | −17.81 |
| CCLu | −66.24 | −57.47 | −46.83 | −36.66 | −25.40 | −17.05 | −9.91 | −5.33 | −2.84 | −2.13 | −2.01 | −2.02 | −2.05 | −2.06 |
| CCLw | −76.31 | −66.46 | −54.48 | −43.21 | −31.79 | −23.54 | −17.17 | −13.63 | −12.20 | −12.97 | −14.14 | −15.73 | −16.92 | −18.29 |
| CLQ2u | −67.91 | −59.61 | −49.04 | −38.79 | −27.70 | −17.91 | −10.12 | −5.39 | −2.86 | −2.14 | −2.01 | −2.03 | −2.05 | −2.07 |
| CLQ2w | −78.83 | −69.35 | −57.48 | −46.18 | −33.82 | −24.36 | −17.36 | −13.67 | −12.22 | −13.00 | −14.15 | −15.74 | −16.92 | −18.29 |
| PIu | −60.84 | −51.36 | −40.12 | −30.60 | −22.03 | −15.48 | −9.38 | −5.17 | −2.78 | −2.10 | −1.98 | −2.00 | −2.03 | −2.04 |
| PIw | −68.88 | −58.42 | −46.89 | −37.36 | −28.55 | −22.06 | −16.69 | −13.46 | −12.12 | −12.90 | −14.13 | −15.70 | −16.85 | −18.04 |
| LHu | −63.78 | −57.23 | −49.73 | −42.79 | −35.23 | −28.59 | −22.32 | −17.01 | −13.13 | −11.22 | −7.89 | −3.91 | −1.63 | −0.94 |
| LHw | −73.22 | −66.26 | −58.30 | −50.91 | −42.77 | −35.93 | −30.48 | −24.46 | −22.75 | −20.90 | −16.49 | −13.42 | −11.13 | −10.88 |
| Numerical Method | 0.01 | 0.03 | 0.1 | 0,3 | 1 | 3 | 10 | 30 | 60 | 100 | 170 | 300 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ADEu | −18.3 | −18.5 | −19.1 | −20.34 | −22.07 | −22.84 | −22.48 | −18.89 | −5.39 | 21.37 | 79.39 | 198.79 |
| ADEw | −42.81 | −38.67 | −34.48 | −31.54 | −29.95 | −29.51 | −28.8 | −24.59 | −10.66 | 16.07 | 74.48 | 193.67 |
| DFu | −19.43 | −19.80 | −20.07 | −19.77 | −18.52 | −16.88 | −11.14 | 18.85 | 57.48 | 101.26 | 165.45 | 262.00 |
| DFw | −38.57 | −34.60 | −31.13 | −29.13 | −25.89 | −25.22 | −18.42 | 12.13 | 51.26 | 95.02 | 159.50 | 256.10 |
| OOEHu | −16.86 | −17.07 | −17.77 | −19.48 | −23.34 | −24.15 | −22.45 | −12.48 | 3.91 | 23.42 | 63.60 | 142.68 |
| OOEHw | −41.34 | −37.16 | −32.86 | −29.67 | −27.69 | −27.19 | −25.72 | −16.33 | −0.23 | 19.04 | 59.13 | 137.85 |
| CpCu | −10.17 | −10.88 | −12.10 | −8.71 | −6.85 | −6.71 | −7.56 | −8.790 | −9.56 | −7.14 | 6.08 | 48.02 |
| CpCw | −27.72 | −23.57 | −19.35 | −16.29 | −14.62 | −14.63 | −15.94 | −17.71 | −18.17 | −15.27 | −1.55 | 40.72 |
| CCLu | −11.09 | −11.82 | −13.69 | −9.91 | −7.99 | −8.02 | −9.14 | −10.56 | −11.43 | −3.54 | 16.33 | 65.85 |
| CCLw | −28.57 | −24.42 | −20.20 | −17.17 | −15.63 | −15.94 | −17.77 | −19.58 | −20.00 | −11.37 | 8.91 | 58.87 |
| CLQ2u | −11.28 | −12.02 | −13.93 | −10.12 | −8.20 | −8.24 | −9.37 | −10.79 | −11.69 | −12.30 | −12.20 | 3.89 |
| CLQ2w | −28.75 | −24.60 | −20.38 | −17.36 | −15.83 | −16.17 | −18.03 | −19.80 | −20.28 | −20.57 | −19.75 | −2.89 |
| PIu | −10.59 | −11.32 | −13.07 | −9.38 | −7.45 | −7.42 | −8.51 | −9.97 | −10.91 | −11.57 | −11.88 | −1.10 |
| PIw | −28.11 | −23.96 | −19.70 | −16.69 | −15.10 | −15.31 | −17.04 | −19.04 | −19.61 | −19.90 | −19.58 | −7.98 |
| LHu | −22.80 | −23.13 | −23.41 | −22.32 | −20.46 | −18.91 | −19.46 | −19.56 | −19.67 | −19.20 | −16.47 | −6.27 |
| LHw | −41.86 | −37.82 | −33.82 | −30.48 | −27.98 | −27.00 | −27.90 | −27.81 | −26.83 | −25.96 | −22.92 | −12.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khayrullaev, H.; Zain, A.; Kovács, E. Solution of Coupled Systems of Reaction–Diffusion Equations Using Explicit Numerical Methods with Outstanding Stability Properties. Computation 2025, 13, 129. https://doi.org/10.3390/computation13060129
Khayrullaev H, Zain A, Kovács E. Solution of Coupled Systems of Reaction–Diffusion Equations Using Explicit Numerical Methods with Outstanding Stability Properties. Computation. 2025; 13(6):129. https://doi.org/10.3390/computation13060129
Chicago/Turabian StyleKhayrullaev, Husniddin, Andicha Zain, and Endre Kovács. 2025. "Solution of Coupled Systems of Reaction–Diffusion Equations Using Explicit Numerical Methods with Outstanding Stability Properties" Computation 13, no. 6: 129. https://doi.org/10.3390/computation13060129
APA StyleKhayrullaev, H., Zain, A., & Kovács, E. (2025). Solution of Coupled Systems of Reaction–Diffusion Equations Using Explicit Numerical Methods with Outstanding Stability Properties. Computation, 13(6), 129. https://doi.org/10.3390/computation13060129





