Hybrid Machine Learning-Driven Automated Quality Prediction and Classification of Silicon Solar Modules in Production Lines
Abstract
1. Introduction
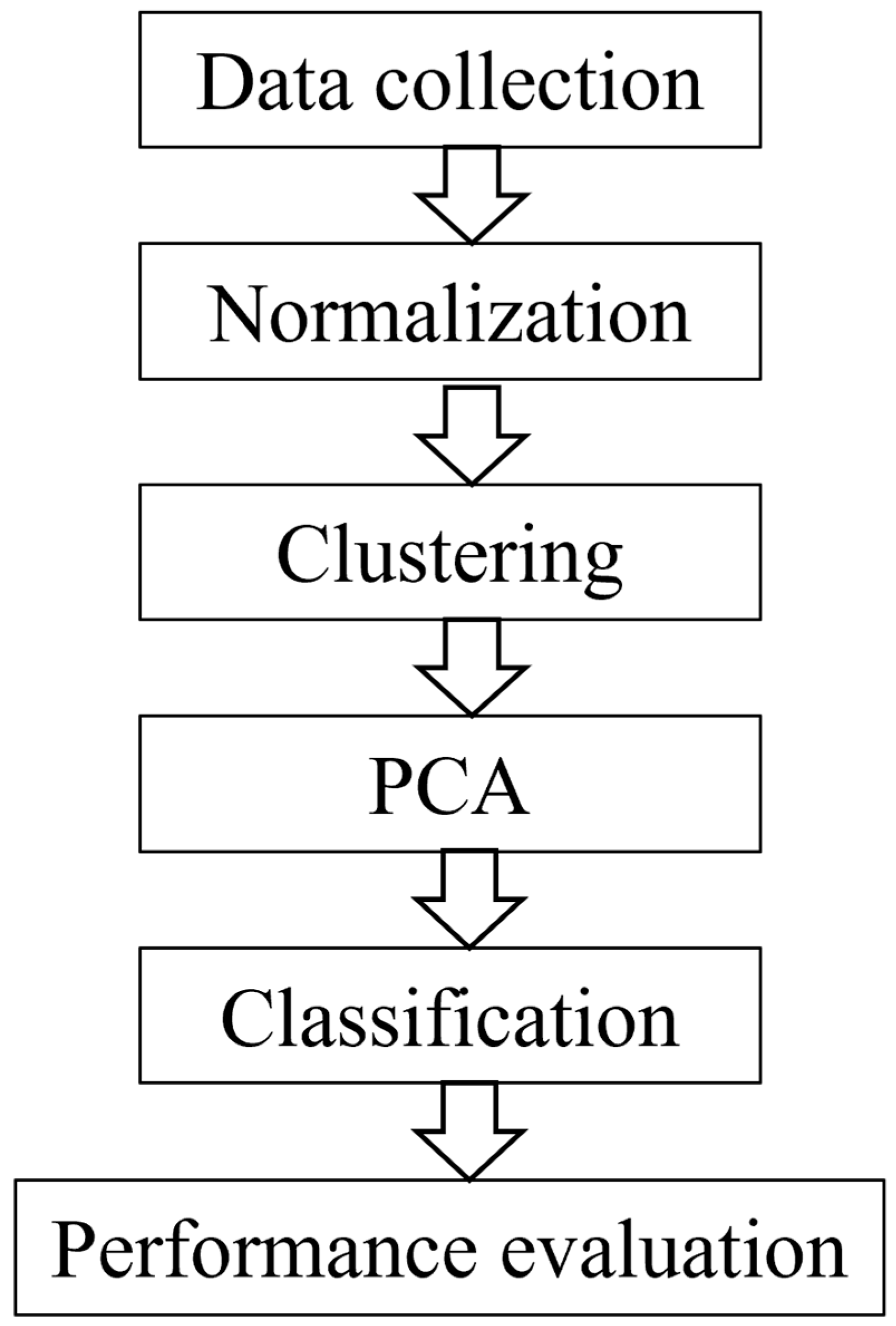
2. Data Processing and Theoretical Foundations
2.1. Data Processing
2.2. Monocrystalline Silicon Photovoltaic Module Performance Analysis Methods
2.2.1. Performance Parameters
- (1)
- Photoelectric conversion efficiency. Photoelectric conversion efficiency is an important parameter that measures the ability of a solar cell or photoelectric conversion material to convert light energy into electricity, usually expressed as a percentage and calculated by the formula [25]:where is the maximum output power of the monocrystalline silicon module, denotes the solar irradiance per unit area (W/m2), and is the total area of the monocrystalline silicon module.
- (2)
- Encapsulation loss rate. refers to the difference between the actual power and the theoretical power of PV cells after they are encapsulated in series into a module, usually expressed as a percentage and calculated by the formula [26]:wherein denotes the encapsulation loss rate from cell to module, and is used to measure the efficiency loss brought about by the encapsulation of the cell into the module, which is expressed by the ratio of the actual maximum output power of the module to the theoretical sum of the power of the cell, P, so as to calculate the encapsulation loss rate from the cell to the module, and the higher the value of , the lower the degree of loss of encapsulated power of the module is indicated.
- (3)
- Short circuit current. reflects the maximum current generated by a solar cell when its external circuit is shorted (i.e., load resistance is zero). It is primarily determined by the photogenerated carrier density and collection efficiency. Specifically, the short-circuit current increases with enhancing light intensity, as expressed by the following relationship:
- (4)
- Open circuit voltage. VOC of a solar cell represents the maximum output voltage under no external load (i.e., an open circuit condition). It reflects the ultimate potential difference generated by photogenerated carrier separation, which is determined by both the intrinsic properties of the semiconductor material (e.g., bandgap) and device parameters (e.g., diode characteristics, series resistance). Notably, exhibits significant temperature dependence: as the operating temperature increases, lattice thermal expansion and enhanced electron–phonon interactions reduce the semiconductor bandgap, thereby directly suppressing . This relationship is quantitatively described by the following:
- (5)
- Filling factor. FF reflects to a certain extent the effective filling degree of photogenerated charge carriers inside the cell and is an important parameter for measuring the output characteristics of solar cells. The closer its value is to 100%, the better the performance of the cell. The formula [27] is as follows:where FF denotes the fill factor, and VPM and IPM denote the maximum output power point voltage and maximum output power point current, respectively.
2.2.2. Performance Evaluation Indicators
2.3. Machine Learning Methods
2.3.1. Clustering and Dimensionality Reduction Algorithms
2.3.2. Classification Algorithm
3. Results and Discussion
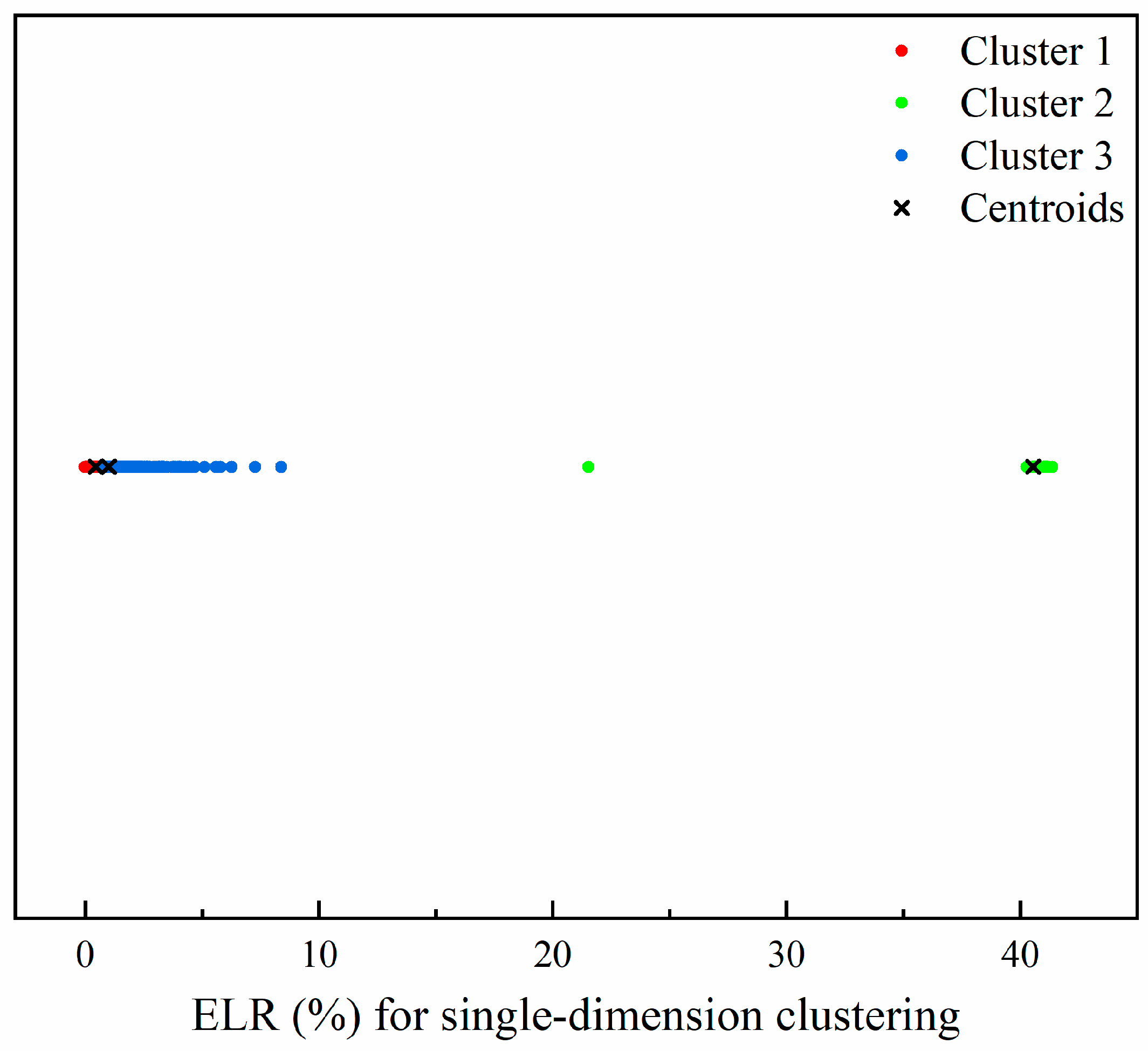
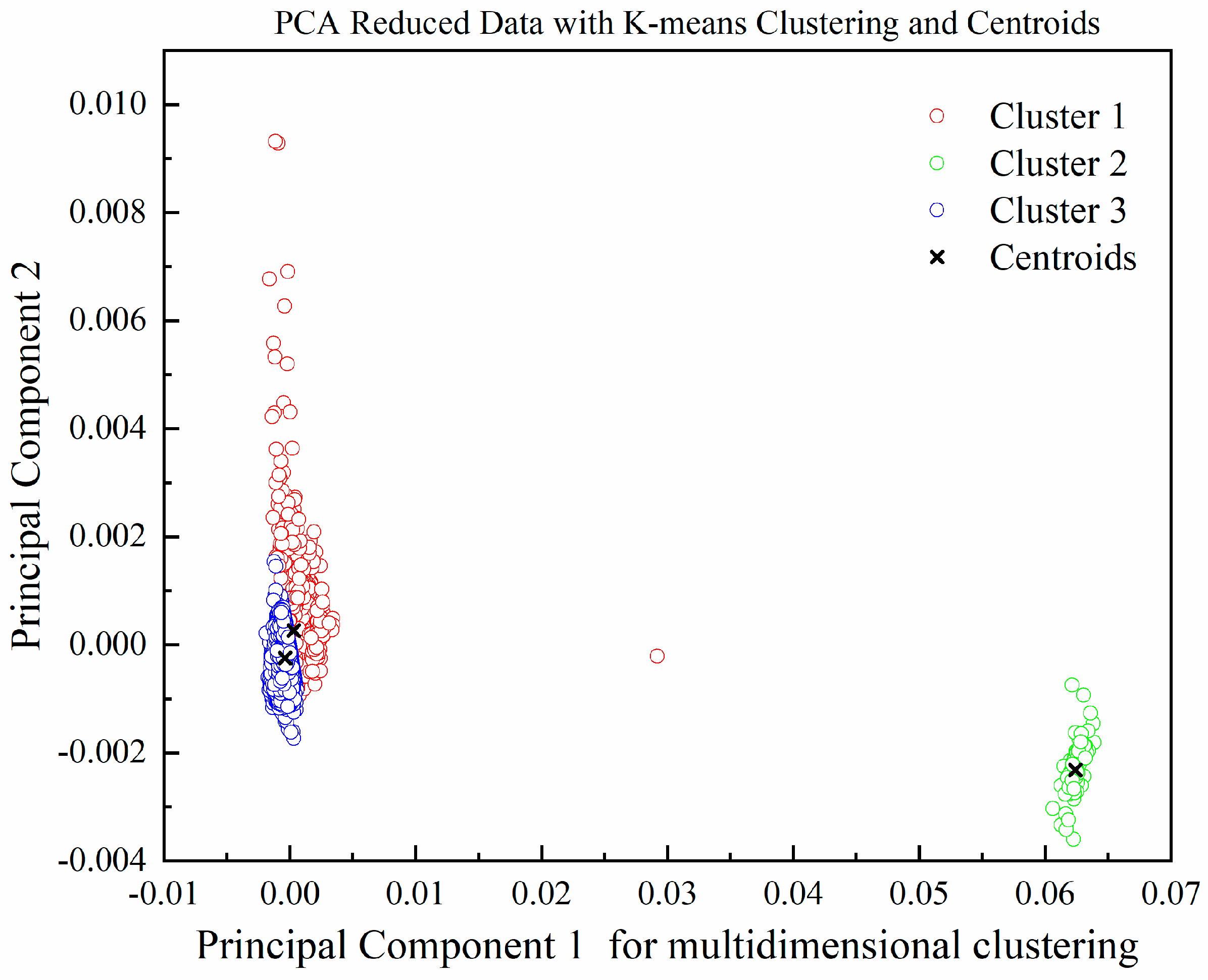
3.1. Cluster Analysis
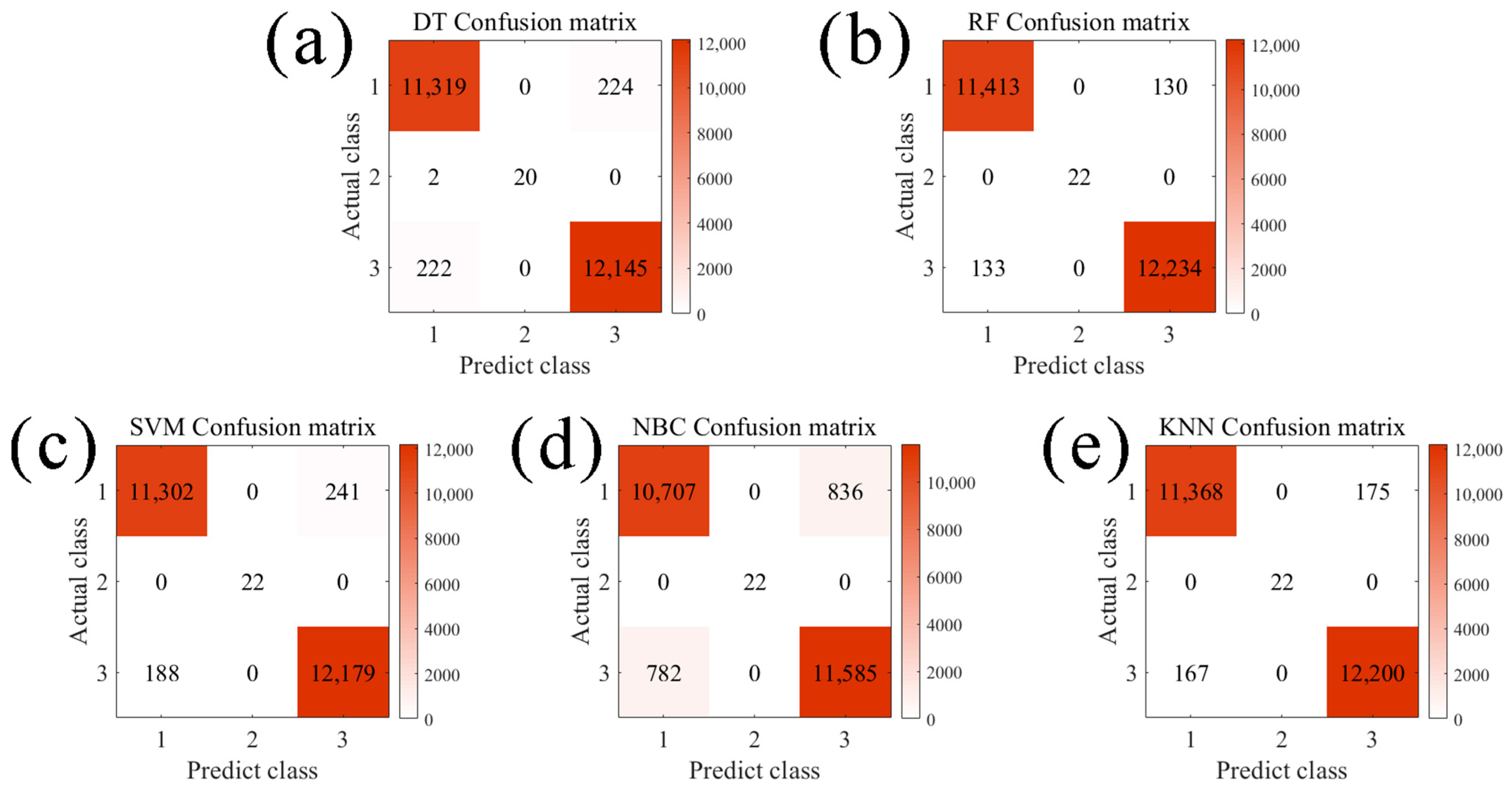
3.2. Classification Algorithm Predicts Overall Performance of Monocrystalline Silicon Modules
- (1)
- Class 1 modules (64.17% of production) can be prioritized for high-efficiency product lines.
- (2)
- Class 3 modules (0.07% of production) are automatically flagged for rework.
4. Innovations, Limitations, and Scalability of the Hybrid Machine Learning Framework
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Depauw, V.; Trompoukis, C.; Massiot, I.; Chen, W.; Dmitriev, A.; Cabarrocas, P.; Gordon, I.; Poortmans, J. Sunlight-thin nanophotonic monocrystalline silicon solar cells. Nano Futures 2017, 1, 021001. [Google Scholar] [CrossRef]
- Han, K.; Lee, H.; Cho, J.; Park, S.; Yun, J.; Yoon, K.; Yoo, J. Fabrication and characterization of monocrystalline-like silicon solar cells. J. Korean Phys. Soc. 2012, 61, 1279–1282. [Google Scholar] [CrossRef]
- Sun, J.; Zuo, Y.; Sun, R.; Zhou, L. Research on the conversion efficiency and preparation technology of monocrystalline silicon cells based on statistical distribution. Sustain. Energy Technol. Assess. 2021, 47, 101482. [Google Scholar] [CrossRef]
- Bock, F.E.; Aydin, R.C.; Cyron, C.J.; Huber, N.; Kalidindi, S.; Klusemann, B. A Review of the Application of Machine Learning and Data Mining Approaches in Continuum Materials. Mech. Front. Mater. 2019, 6, 110. [Google Scholar] [CrossRef]
- Cai, J.; Chu, X.; Xu, K.; Li, H.; Wei, J. Machine learning-driven new material discovery. Nanoscale Adv. 2020, 2, 3115–3130. [Google Scholar] [CrossRef]
- Gao, C.; Min, X.; Fang, M.; Tao, T.; Zheng, X.; Liu, Y.; Wu, X.; Huang, Z. Innovative Materials Science via Machine Learning. Adv. Funct. Mater. 2021, 32, 2108044. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, T.; Ju, W.; Shi, S. Materials discovery and design using machine learning. J. Mater. 2017, 3, 159–177. [Google Scholar] [CrossRef]
- Zhang, Y.; Ling, C. A strategy to apply machine learning to small datasets in materials science. NPJ Comput. Mater. 2018, 4, 25. [Google Scholar] [CrossRef]
- Forootan, M.M.; Larki, I.; Zahedi, R.; Ahmadi, A. Machine Learning and Deep Learning in Energy Systems: A Review. Sustainability 2022, 14, 4832. [Google Scholar] [CrossRef]
- Gao, T.; Lu, W. Machine learning toward advanced energy storage devices and systems. Iscience 2021, 24, 101936. [Google Scholar] [CrossRef]
- Shen, Z.H.; Liu, H.X.; Shen, Y.; Hu, J.M.; Chen, L.Q.; Nan, C.W. Machine learning in energy storage materials. Interdiscip. Mater. 2022, 1, 175–195. [Google Scholar] [CrossRef]
- Almanei, M.; Oleghe, O.; Jagtap, S.; Salonitis, K. Machine Learning Algorithms Comparison for Manufacturing Applications. In Advances in Manufacturing Technology XXXIV; IOS Press: Amsterdam, The Netherlands, 2021; Volume 15, pp. 377–382. [Google Scholar]
- Rai, R.; Tiwari, M.K.; Ivanov, D.; Dolgui, A. Machine learning in manufacturing and industry 4.0 applications. Int. J. Prod. Res. 2021, 59, 4773–4778. [Google Scholar] [CrossRef]
- Wang, C.; Tan, X.P.; Tor, S.B.; Lim, C.S. Machine learning in additive manufacturing: State-of-the-art and perspectives. Addit. Manuf. 2020, 36, 101538. [Google Scholar] [CrossRef]
- Mahmood, A.; Wang, J.L. Machine learning for high performance organic solar cells: Current scenario and future prospects. Energy Environ. Sci. 2021, 14, 90–105. [Google Scholar] [CrossRef]
- Fu, Y.; Li, X.; Ma, X. Deep-Learning-Based Defect Evaluation of Mono-Like Cast Silicon Wafers. Photonics 2021, 8, 426. [Google Scholar] [CrossRef]
- Buratti, Y.; Dick, J.; Gia, Q.L.; Hameiri, Z. Deep Learning Extraction of the Temperature-Dependent Parameters of Bulk Defects. ACS Appl. Mater. Interfaces 2022, 14, 48647–48657. [Google Scholar] [CrossRef]
- Jaiswal, R.; Martinez-Ramon, M.; Busani, T. Recent Advances in Silicon Solar Cell Research Using Data Science-Based Learning. IEEE J. Photovolt. 2023, 13, 2–15. [Google Scholar] [CrossRef]
- Kamath, R.S.; Kamat, R.K. Modelling of Random Textured Tandem Silicon Solar Cells Characteristics: Decision Tree Approach. J. Nano-Electron. Phys. 2016, 8, 04021. [Google Scholar] [CrossRef]
- Biau, G. Analysis of a Random Forests Model. J. Mach. Learn. Res. 2012, 13, 1063–1095. [Google Scholar]
- Nagy, G.I.; Barta, G.; Kazi, S.; Borbély, G.; Simon, G. GEFCom2014: Probabilistic solar and wind power forecasting using a generalized additive tree ensemble approach. Int. J. Forecast. 2016, 32, 1087–1093. [Google Scholar] [CrossRef]
- Scornet, E.; Biau, G.; Vert, J.P. Consistency of random forests. Ann. Stat. 2015, 43, 1716–1741. [Google Scholar] [CrossRef]
- Ding, S.; Xu, L.; Su, C.; Zhu, H. Using Genetic Algorithms to Optimize Artificial Neural Networks. J. Converg. Inf. Technol. 2010, 5, 54–62. [Google Scholar]
- Ding, S.; Xu, X.; Zhu, H. Studies on Optimization Algorithms for Some Artificial Neural Networks Based on Genetic Algorithm (GA). J. Comput. 2011, 6, 939–946. [Google Scholar] [CrossRef]
- Park, N. High Efficiency Perovskite Solar Cells: Materials and Devices Engineering. Trans. Electr. Electron. Mater. 2020, 21, 1–15. [Google Scholar] [CrossRef]
- Roy, J. Comprehensive analysis and modeling of cell to module (CTM) conversion loss during c-Si Solar Photovoltaic (SPV) module manufacturing. Sol. Energy 2016, 130, 184–192. [Google Scholar] [CrossRef]
- Gupta, D.; Mukhopadhyay, S.; Narayan, K. Fill factor in organic solar cells. Sol. Energy Mater. Sol. Cells 2010, 94, 1309–1313. [Google Scholar] [CrossRef]


| Methods | Cluster1 | Cluster2 | Cluster3 | Accuracy | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| TPR | PPV | F1 | TPR | PPV | F1 | TPR | PPV | F1 | ||
| DT | 98.06% | 98.06% | 98.06% | 90.91% | 100.00% | 95.24% | 98.20% | 98.19% | 98.20% | 98.13% |
| RF | 98.87% | 98.85% | 98.86% | 100.00% | 100.00% | 100.00% | 98.92% | 98.95% | 98.94% | 98.90% |
| SVM | 97.91% | 98.36% | 98.14% | 100.00% | 100.00% | 100.00% | 98.48% | 98.06% | 98.27% | 98.21% |
| NBC | 92.76% | 93.19% | 92.97% | 100.00% | 100.00% | 100.00% | 93.68% | 93.27% | 93.47% | 93.24% |
| KNN | 98.48% | 98.55% | 98.52% | 100.00% | 100.00% | 100.00% | 98.65% | 98.59% | 98.62% | 98.57% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Xia, X.; Zhang, J.; Wang, K.; Yu, B.; Wu, M.; Shi, J.; Ma, C.; Liu, Y.; Hu, B.; et al. Hybrid Machine Learning-Driven Automated Quality Prediction and Classification of Silicon Solar Modules in Production Lines. Computation 2025, 13, 125. https://doi.org/10.3390/computation13050125
Liu Y, Xia X, Zhang J, Wang K, Yu B, Wu M, Shi J, Ma C, Liu Y, Hu B, et al. Hybrid Machine Learning-Driven Automated Quality Prediction and Classification of Silicon Solar Modules in Production Lines. Computation. 2025; 13(5):125. https://doi.org/10.3390/computation13050125
Chicago/Turabian StyleLiu, Yuxiang, Xinzhong Xia, Jingyang Zhang, Kun Wang, Bo Yu, Mengmeng Wu, Jinchao Shi, Chao Ma, Ying Liu, Boyang Hu, and et al. 2025. "Hybrid Machine Learning-Driven Automated Quality Prediction and Classification of Silicon Solar Modules in Production Lines" Computation 13, no. 5: 125. https://doi.org/10.3390/computation13050125
APA StyleLiu, Y., Xia, X., Zhang, J., Wang, K., Yu, B., Wu, M., Shi, J., Ma, C., Liu, Y., Hu, B., Wang, X., Wang, B., Wang, R., & Wang, B. (2025). Hybrid Machine Learning-Driven Automated Quality Prediction and Classification of Silicon Solar Modules in Production Lines. Computation, 13(5), 125. https://doi.org/10.3390/computation13050125








