MultiGNN: A Graph Neural Network Framework for Inferring Gene Regulatory Networks from Single-Cell Multi-Omics Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Data Preprocessing
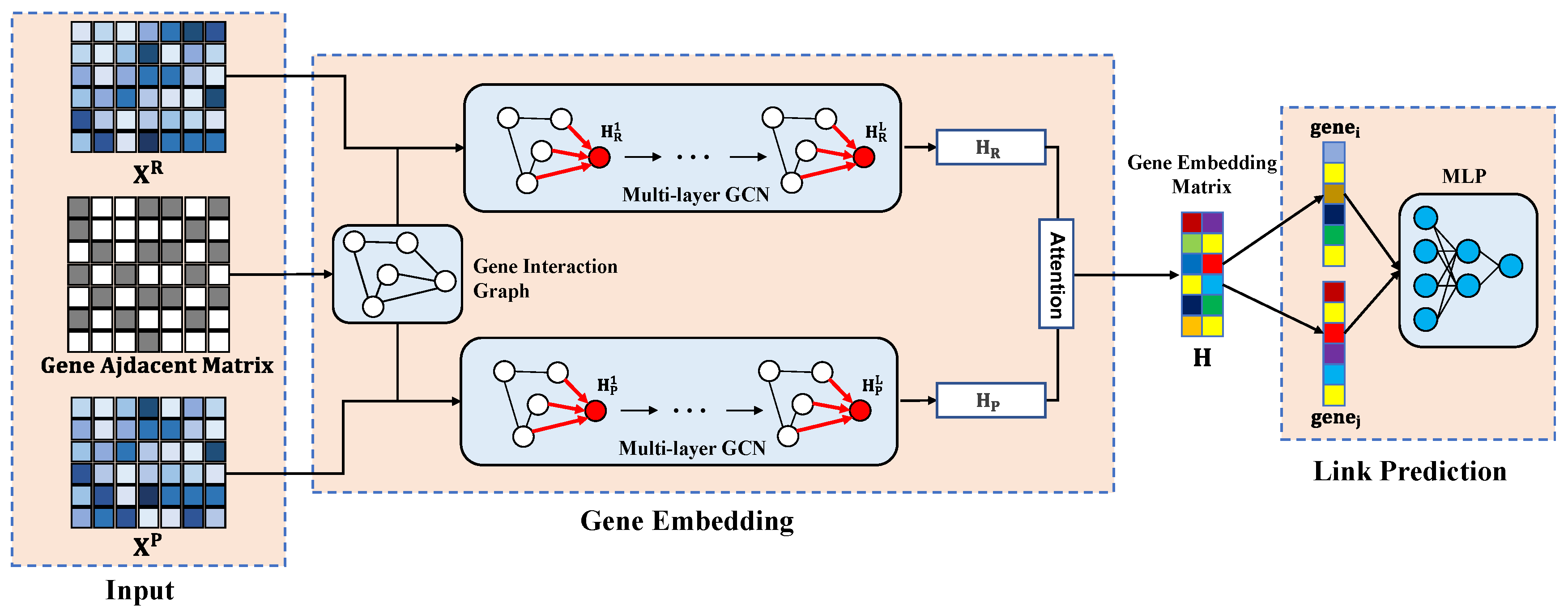
2.3. The MultiGNN Framework
2.4. Experimental Setting and Hyperparameter Optimization
- GNNLink [33]: uses MGCN to predict potential gene dependencies from scRNA-seq data and gene network topologies.
- GENELink [31]: proposes a graph attention network approach to infer potential GRNs.
- GNE [20]: predicts gene relationships by learning transcriptomics data and genomics network topology via MLP.
- CNNC [19]: predicts GRNs using deep convolutional neural networks.
- STGRNS [34]: a supervised learning method based on Transformer architecture.
- GENIE3 [35]: an unsupervised learning method based on random forests that constructs GRNs using regression coefficient weights.
3. Results
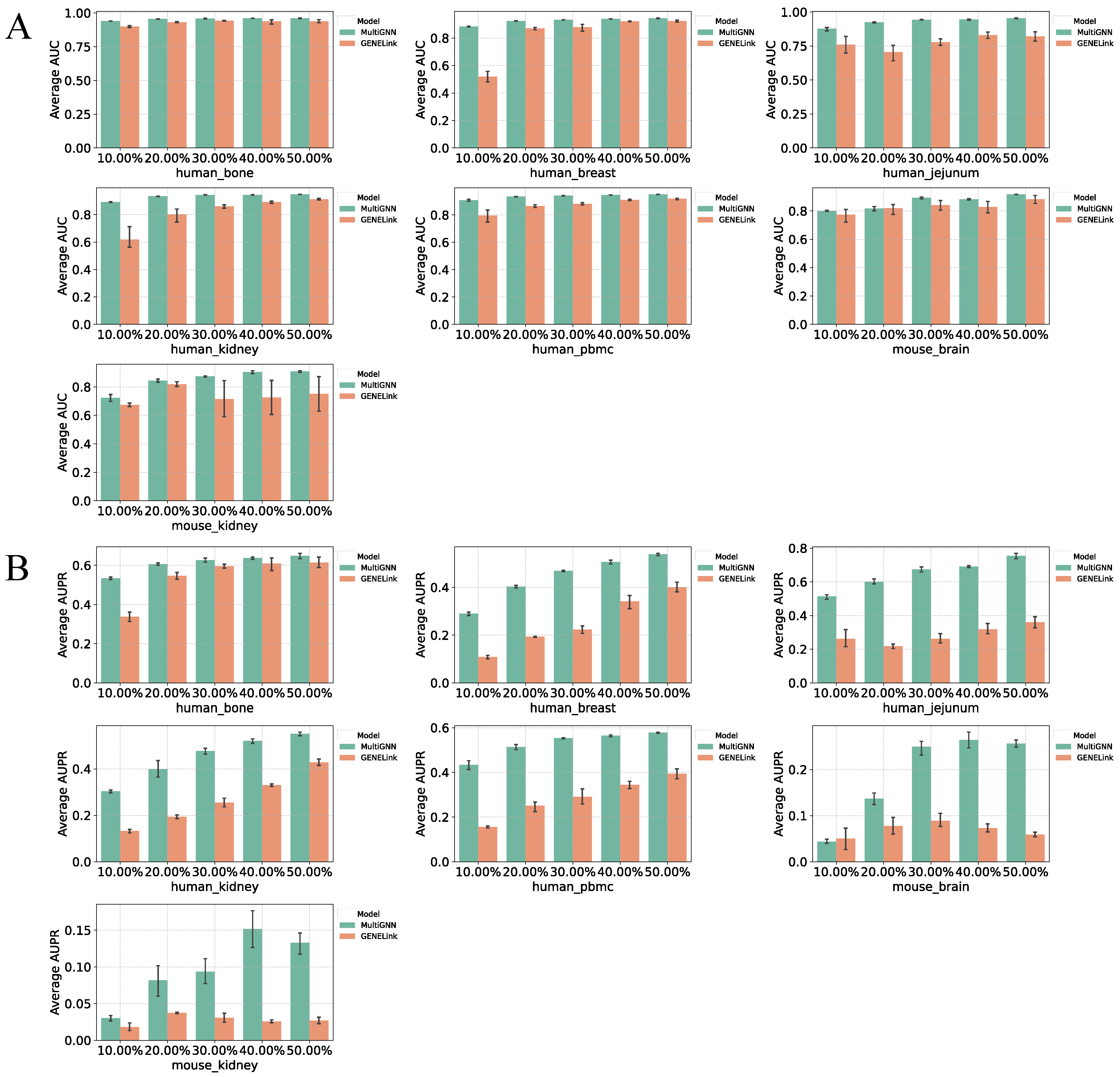
3.1. Performance on Benchmark Datasets
3.2. Multi-Omics Data Enhances Prediction Accuracy
3.3. Effectiveness of Feature Fusion in MultiGNN
3.4. Robustness of MultiGNN
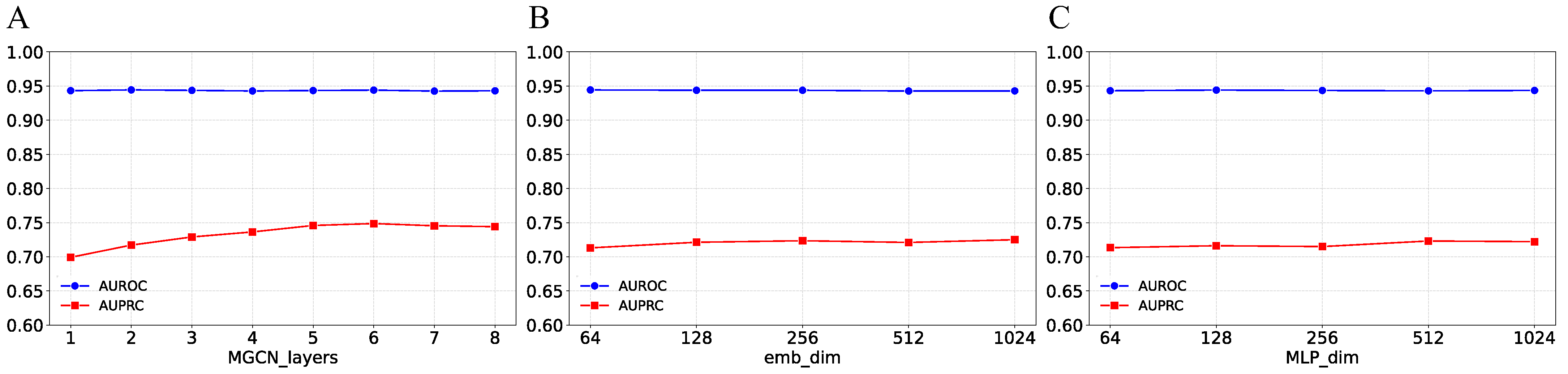
3.5. Parameter Analysis
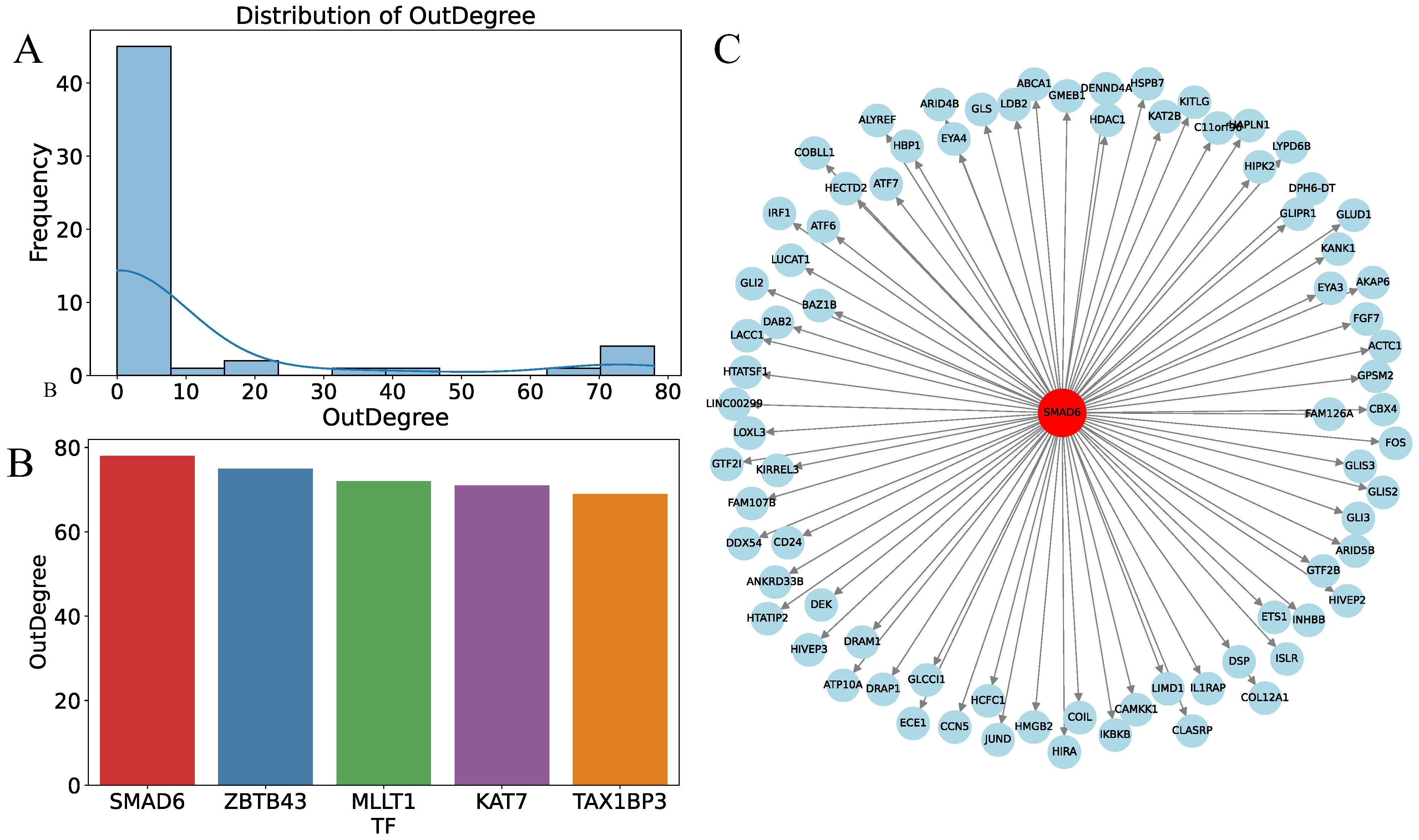
3.6. Prediction of Key Regulatory Factors Using MultiGNN
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, J.; Choi, M.; Kim, J.R.; Jin, H.; Kim, V.N.; Cho, K.H. The co-regulation mechanism of transcription factors in the human gene regulatory network. Nucleic Acids Res. 2012, 40, 8849–8861. [Google Scholar] [CrossRef] [PubMed]
- Karlebach, G.; Shamir, R. Modelling and analysis of gene regulatory networks. Nat. Rev. Mol. Cell Biol. 2008, 9, 770–780. [Google Scholar] [CrossRef]
- Pratapa, A.; Jalihal, A.P.; Law, J.N.; Bharadwaj, A.; Murali, T.M. Benchmarking algorithms for gene regulatory network inference from single-cell transcriptomic data. Nat. Methods 2020, 17, 147–154. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lee, H.; Fear, J.M.; Berger, I.; Oliver, B.; Przytycka, T.M. NetREX-CF integrates incomplete transcription factor data with gene expression to reconstruct gene regulatory networks. Commun. Biol. 2022, 5, 1282. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Zou, Q. Inferring gene regulatory network from single-cell transcriptomes with graph autoencoder model. PLoS Genet. 2023, 19, e1010942. [Google Scholar] [CrossRef]
- Fiers, M.W.E.J.; Minnoye, L.; Aibar, S.; González-Blas, C.B.; Atak, Z.K.; Aerts, S. Mapping gene regulatory networks from single-cell omics data. Brief. Funct. Genom. 2018, 17, 246–254. [Google Scholar] [CrossRef]
- Crow, M.; Paul, A.; Ballouz, S.; Huang, Z.J.; Gillis, J. Exploiting single-cell expression to characterize co-expression replicability. Genome Biol. 2016, 17, 101. [Google Scholar] [CrossRef]
- Li, H.; Sun, Y.; Hong, H.; Huang, X.; Tao, H.; Huang, Q.; Wang, L.; Xu, K.; Gan, J.; Chen, H.; et al. Inferring transcription factor regulatory networks from single-cell ATAC-seq data based on graph neural networks. Nat. Mach. Intell. 2022, 4, 389–400. [Google Scholar] [CrossRef]
- Grandi, F.C.; Modi, H.; Kampman, L.; Corces, M.R. Chromatin accessibility profiling by ATAC-seq. Nat. Protoc. 2022, 17, 1518–1552. [Google Scholar] [CrossRef]
- Kim, D.; Tran, A.; Kim, H.J.; Lin, Y.; Yang, J.Y.H.; Yang, P. Gene regulatory network reconstruction: Harnessing the power of single-cell multi-omic data. NPJ Syst. Biol. Appl. 2023, 9, 51. [Google Scholar] [CrossRef]
- Badia-I-Mompel, P.; Wessels, L.; Müller-Dott, S.; Trimbour, R.; Flores, R.O.R.; Argelaguet, R.; Saez-Rodriguez, J. Gene regulatory network inference in the era of single-cell multi-omics. Nat. Rev. Genet. 2023, 24, 739–754. [Google Scholar] [CrossRef]
- Ma, A.; Wang, X.; Li, J.; Wang, C.; Xiao, T.; Liu, Y.; Cheng, H.; Wang, J.; Li, Y.; Chang, Y.; et al. Single-cell biological network inference using a heterogeneous graph transformer. Nat. Commun. 2023, 14, 964. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Tian, T.; Wei, Z.; Hakonarson, H. Clustering of single-cell multi-omics data with a multimodal deep learning method. Nat. Commun. 2022, 13, 7705. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Pyne, S.; Pietrzak, S.; Halberg, S.; McCalla, S.G.; Siahpirani, A.F.; Sridharan, R.; Roy, S. Inference of cell type-specific gene regulatory networks on cell lineages from single cell omic datasets. Nat. Commun. 2023, 14, 3064. [Google Scholar] [CrossRef]
- González-Blas, C.B.; De Winter, S.; Hulselmans, G.; Hecker, N.; Matetovici, I.; Christiaens, V.; Poovathingal, S.; Wouters, J.; Aibar, S.; Aerts, S. SCENIC+: Single-cell multiomic inference of enhancers and gene regulatory networks. Nat. Methods 2023, 20, 1355–1367. [Google Scholar] [CrossRef]
- Bailey, T.L.; Williams, N.; Misleh, C.; Li, W.W. MEME: Discovering and analyzing DNA and protein sequence motifs. Nucleic Acids Res. 2006, 34, W369–W373. [Google Scholar] [CrossRef]
- Song, Q.; Ruffalo, M.; Bar-Joseph, Z. Using single cell atlas data to reconstruct regulatory networks. Nucleic Acids Res. 2023, 51, e38. [Google Scholar] [CrossRef]
- La Manno, G.; Soldatov, R.; Zeisel, A.; Braun, E.; Hochgerner, H.; Petukhov, V.; Lidschreiber, K.; Kastriti, M.E.; Lönnerberg, P.; Furlan, A.; et al. RNA velocity of single cells. Nature 2018, 560, 494–498. [Google Scholar] [CrossRef]
- Yuan, Y.; Bar-Joseph, Z. Deep learning for inferring gene relationships from single-cell expression data. Proc. Natl. Acad. Sci. USA 2019, 116, 27151–27158. [Google Scholar] [CrossRef]
- Kc, K.; Li, R.; Cui, F.; Yu, Q.; Haake, A.R. GNE: A deep learning framework for gene network inference by aggregating biological information. BMC Syst. Biol. 2019, 13, 38. [Google Scholar] [CrossRef]
- Chen, J.; Cheong, C.; Lan, L.; Zhou, X.; Liu, J.; Lyu, A.; Cheung, W.K.; Zhang, L. DeepDRIM: A deep neural network to reconstruct cell-type-specific gene regulatory network using single-cell RNA-seq data. Brief. Bioinform. 2021, 22, bbab325. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; He, W.; Tang, J.; Zou, Q.; Guo, F. A hybrid deep learning framework for gene regulatory network inference from single-cell transcriptomic data. Brief. Bioinform. 2022, 23, bbab568. [Google Scholar] [CrossRef]
- Binder, M.; Szalat, R.E.; Talluri, S.; Fulciniti, M.; Avet-Loiseau, H.; Parmigiani, G.; Samur, M.K.; Munshi, N.C. Bone marrow stromal cells induce chromatin remodeling in multiple myeloma cells leading to transcriptional changes. Nat. Commun. 2024, 15, 4139. [Google Scholar] [CrossRef]
- Bhat-Nakshatri, P.; Gao, H.; Khatpe, A.S.; Adebayo, A.K.; McGuire, P.C.; Erdogan, C.; Chen, D.; Jiang, G.; New, F.; German, R.; et al. Single-nucleus chromatin accessibility and transcriptomic map of breast tissues of women of diverse genetic ancestry. Nat. Med. 2024, 30, 3482–3494. [Google Scholar] [CrossRef]
- 10k Human PBMCs, Single Cell Multiome ATAC Gene Expression Demonstration Data by Cell Ranger ARC 1.0.0, 10x Genomics. 2021. Available online: https://www.10xgenomics.com/datasets/10-k-human-pbm-cs-multiome-v-1-0-chromium-x-1-standard-2-0-0 (accessed on 9 April 2024).
- Szklarczyk, D.; Kirsch, R.; Koutrouli, M.; Nastou, K.; Mehryary, F.; Hachilif, R.; Gable, A.L.; Fang, T.; Doncheva, N.T.; Pyysalo, S.; et al. The STRING database in 2023, protein-protein association networks and functional enrichment analyses for any sequenced genome of interest. Nucleic Acids Res. 2023, 51, D638–D646. [Google Scholar] [CrossRef]
- Wang, C.; Sun, D.; Huang, X.; Wan, C.; Li, Z.; Han, Y.; Qin, Q.; Fan, J.; Qiu, X.; Xie, Y.; et al. Integrative analyses of single-cell transcriptome and regulome using MAESTRO. Genome Biol. 2020, 21, 198. [Google Scholar] [CrossRef]
- Mou, L.; Lu, X.; Li, X.; Zhu, X.X. Nonlocal Graph Convolutional Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8246–8257. [Google Scholar] [CrossRef]
- Cui, Z.; Henrickson, K.; Ke, R.; Wang, Y. Traffic Graph Convolutional Recurrent Neural Network: A Deep Learning Framework for Network-Scale Traffic Learning and Forecasting. IEEE Trans. Intell. Transp. Syst. 2020, 21, 4883–4894. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, S.; Xu, Y.; Miao, C.; Wu, M.; Zhang, J. Contextualized Graph Attention Network for Recommendation with Item Knowledge Graph. IEEE Trans. Knowl. Data Eng. 2023, 35, 181–195. [Google Scholar] [CrossRef]
- Chen, G.; Liu, Z. Graph attention network for link prediction of gene regulations from single-cell RNA-sequencing data. Bioinformatics 2022, 38, 4522–4529. [Google Scholar] [CrossRef]
- Yuan, Y.; Bar-Joseph, Z. GCNG: Graph convolutional networks for inferring gene interaction from spatial transcriptomics data. Genome Biol. 2020, 21, 300. [Google Scholar] [CrossRef] [PubMed]
- Mao, G.; Pang, Z.; Zuo, K.; Wang, Q.; Pei, X.; Chen, X.; Liu, J. Predicting gene regulatory links from single-cell RNA-seq data using graph neural networks. Brief. Bioinform. 2023, 24, bbad414. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Zhang, A.; Liu, F.; Zhang, X. STGRNS: An interpretable transformer-based method for inferring gene regulatory networks from single-cell transcriptomic data. Bioinformatics 2023, 39, btad165. [Google Scholar] [CrossRef]
- Huynh-Thu, V.A.; Irrthum, A.; Wehenkel, L.; Geurts, P. Inferring regulatory networks from expression data using tree-based methods. PLoS ONE 2010, 5, e12776. [Google Scholar] [CrossRef]
- Moerman, T.; Santos, S.A.; González-Blas, C.B.; Simm, J.; Moreau, Y.; Aerts, J.; Aerts, S. GRNBoost2 and Arboreto: Efficient and scalable inference of gene regulatory networks. Bioinformatics 2019, 35, 2159–2161. [Google Scholar] [CrossRef]
- Luyckx, I.; Verstraeten, A.; Goumans, M.-J.; Loeys, B. SMAD6-deficiency in human genetic disorders. NPJ Genom. Med. 2022, 7, 68. [Google Scholar] [CrossRef]
- Kabra, A.; Bushweller, J. The Intrinsically Disordered Proteins MLLT3 (AF9) and MLLT1 (ENL)—Multimodal Transcriptional Switches With Roles in Normal Hematopoiesis, MLL Fusion Leukemia, and Kidney Cancer. J. Mol. Biol. 2022, 434, 167117. [Google Scholar] [CrossRef]
- Wang, W.; Zheng, Y.; Sun, S.; Li, W.; Song, M.; Ji, Q.; Wu, Z.; Liu, Z.; Fan, Y.; Liu, F.; et al. A genome-wide CRISPR-based screen identifies KAT7 as a driver of cellular senescence. Sci. Transl. Med. 2021, 13, eabd2655. [Google Scholar] [CrossRef]
- Reinstein, E.; Orvin, K.; Tayeb-Fligelman, E.; Stiebel-Kalish, H.; Tzur, S.; Pimienta, A.L.; Bazak, L.; Bengal, T.; Cohen, L.; Gaton, D.D.; et al. Mutations in TAX1BP3 cause dilated cardiomyopathy with septo-optic dysplasia. Hum. Mutat. 2015, 36, 439–442. [Google Scholar] [CrossRef]
- Ogbeide, S.; Giannese, F.; Mincarelli, L.; Macaulay, I.C. Into the multiverse: Advances in single-cell multiomic profiling. Trends Genet. 2022, 38, 831–843. [Google Scholar] [CrossRef]
- Pickett, S.J.; Hudson, G.; Greaves, L.C. Single-cell multiomic analyses sheds light on mitochondrial mutational selection. Nat. Genet. 2023, 55, 1083–1085. [Google Scholar] [CrossRef] [PubMed]
- Ledru, N.; Wilson, P.C.; Muto, Y.; Yoshimura, Y.; Wu, H.; Li, D.; Asthana, A.; Tullius, S.G.; Waikar, S.S.; Orlando, G.; et al. Predicting proximal tubule failed repair drivers through regularized regression analysis of single cell multiomic sequencing. Nat. Commun. 2024, 15, 1291. [Google Scholar] [CrossRef] [PubMed]
- Weng, C.; Gu, A.; Zhang, S.; Lu, L.; Ke, L.; Gao, P.; Liu, X.; Wang, Y.; Hu, P.; Plummer, D.; et al. Single cell multiomic analysis reveals diabetes-associated β-cell heterogeneity driven by HNF1A. Nat. Commun. 2023, 14, 5400. [Google Scholar] [CrossRef]
- Xu, J.; Lu, C.; Jin, S.; Meng, Y.; Fu, X.; Zeng, X.; Nussinov, R.; Cheng, F. Deep learning-based cell-specific gene regulatory networks inferred from single-cell multiome data. Nucleic Acids Res. 2025, 53, gkaf138. [Google Scholar] [CrossRef]
- Jiang, J.; Ge, W.; Wang, Y.; Cheng, Y.; Xu, Y. Soft-label recover based label-specific features learning. Sci. Rep. 2024, 14, 23099. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Sowmya, A.; Chen, F. Soft Hough Forest-ERTs: Generalized Hough Transform based object detection from soft-labelled training data. Pattern Recognit. 2016, 60, 145–156. [Google Scholar] [CrossRef]


| Dataset | Cells | Non-Specific ChIP-Seq | STRING | |||||
|---|---|---|---|---|---|---|---|---|
| TFs | Genes | Density | TFs | Genes | Density | |||
| human | bone | 6742 | 717 (722) | 1217 (1566) | 0.032 (0.029) | 792 (796) | 937 (1113) | 0.051 (0.045) |
| breast | 1446 | 186 (190) | 447 (693) | 0.052 (0.043) | 223 (231) | 300 (435) | 0.070 (0.055) | |
| jejunum | 5368 | 57 (59) | 124 (166) | 0.134 (0.117) | 81 (84) | 87 (105) | 0.133 (0.116) | |
| kidney | 13,666 | 175 (176) | 407 (583) | 0.060 (0.053) | 226 (230) | 277 (344) | 0.065 (0.057) | |
| pbmc | 6984 | 186 (196) | 551 (869) | 0.055 (0.046) | 230 (235) | 375 (562) | 0.061 (0.051) | |
| mouse | brain | 4362 | 100 (109) | 137 (167) | 0.028 (0.025) | |||
| kidney | 12,355 | 72 (81) | 122 (155) | 0.036 (0.034) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Chen, H.; Wang, J.; Wang, Y. MultiGNN: A Graph Neural Network Framework for Inferring Gene Regulatory Networks from Single-Cell Multi-Omics Data. Computation 2025, 13, 124. https://doi.org/10.3390/computation13050124
Liu D, Chen H, Wang J, Wang Y. MultiGNN: A Graph Neural Network Framework for Inferring Gene Regulatory Networks from Single-Cell Multi-Omics Data. Computation. 2025; 13(5):124. https://doi.org/10.3390/computation13050124
Chicago/Turabian StyleLiu, Dongbo, Hao Chen, Jianxin Wang, and Yeru Wang. 2025. "MultiGNN: A Graph Neural Network Framework for Inferring Gene Regulatory Networks from Single-Cell Multi-Omics Data" Computation 13, no. 5: 124. https://doi.org/10.3390/computation13050124
APA StyleLiu, D., Chen, H., Wang, J., & Wang, Y. (2025). MultiGNN: A Graph Neural Network Framework for Inferring Gene Regulatory Networks from Single-Cell Multi-Omics Data. Computation, 13(5), 124. https://doi.org/10.3390/computation13050124








