Fractional Order Mathematical Model for Predicting and Controlling Dengue Fever Spread Based on Awareness Dynamics
Abstract
1. Introduction
2. Mathematical Model Formulation of Dengue Fever
3. The Adomian Decomposition Method
4. Results and Discussion
5. Conclusions
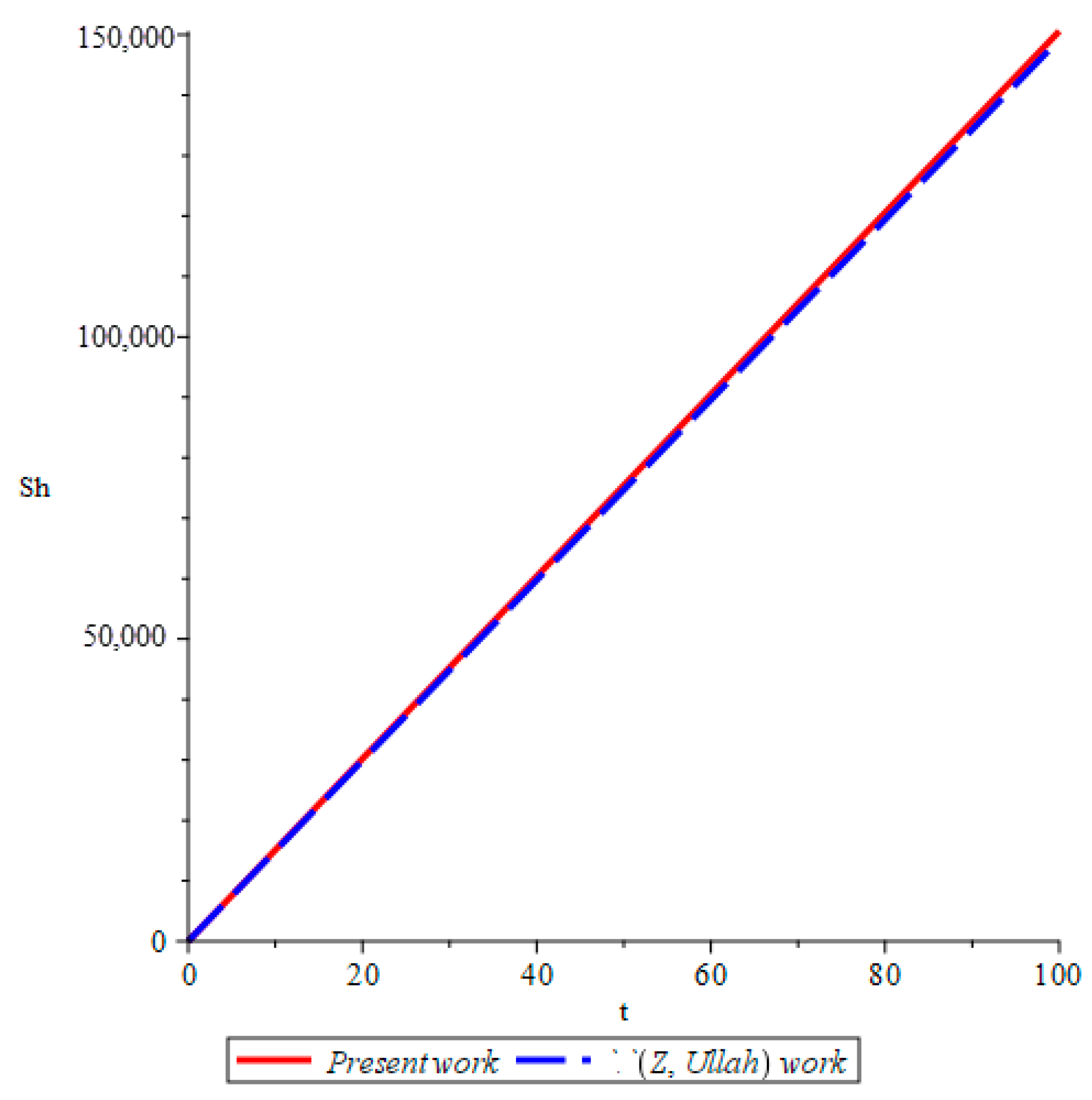
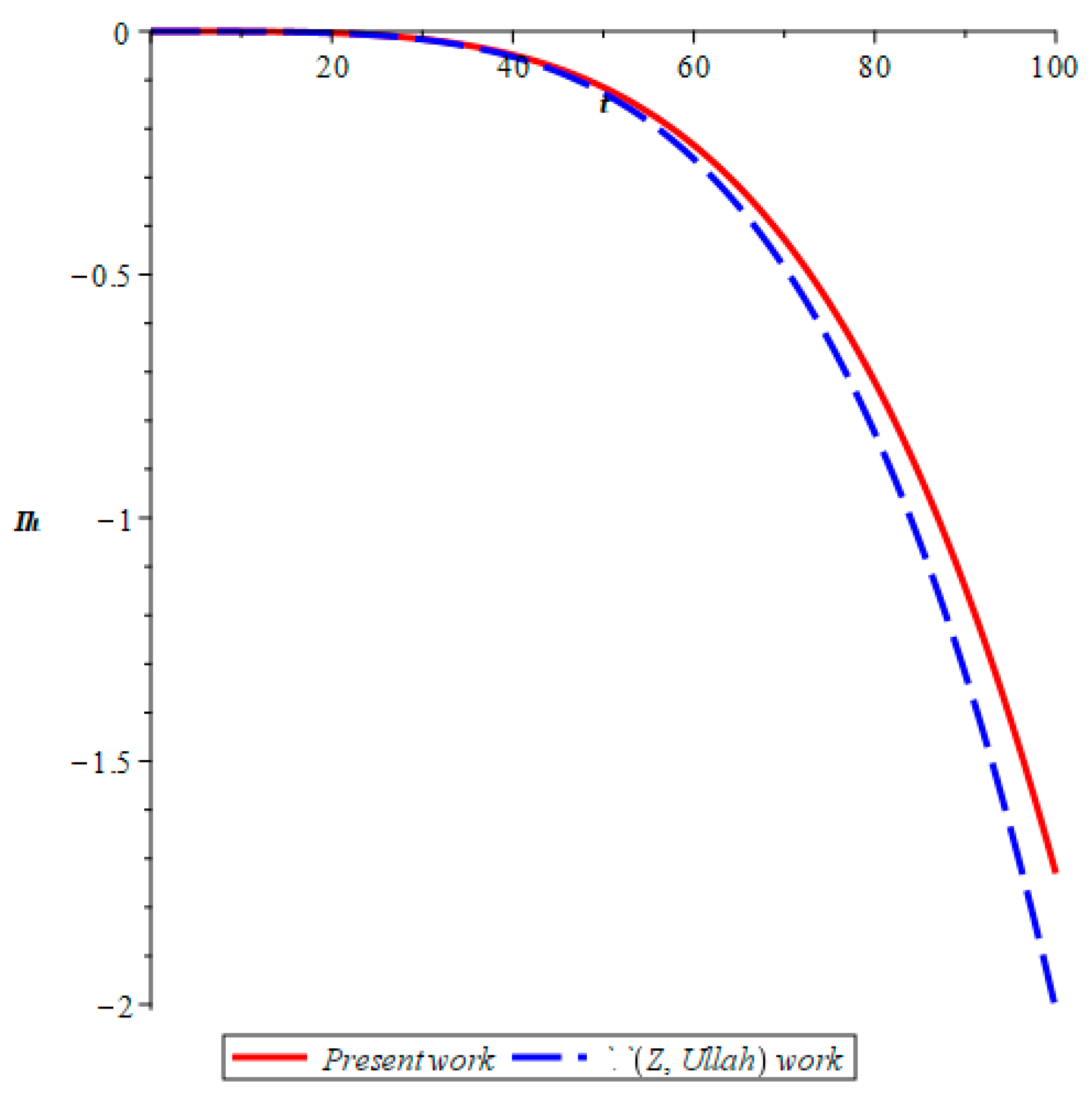
- The study verifies that the use of a fractional-order differential model offers a more realistic representation of dengue fever transmission dynamics than integer-order models. The inclusion of memory effects and hereditary properties enhances prediction accuracy and supports improved control strategies.
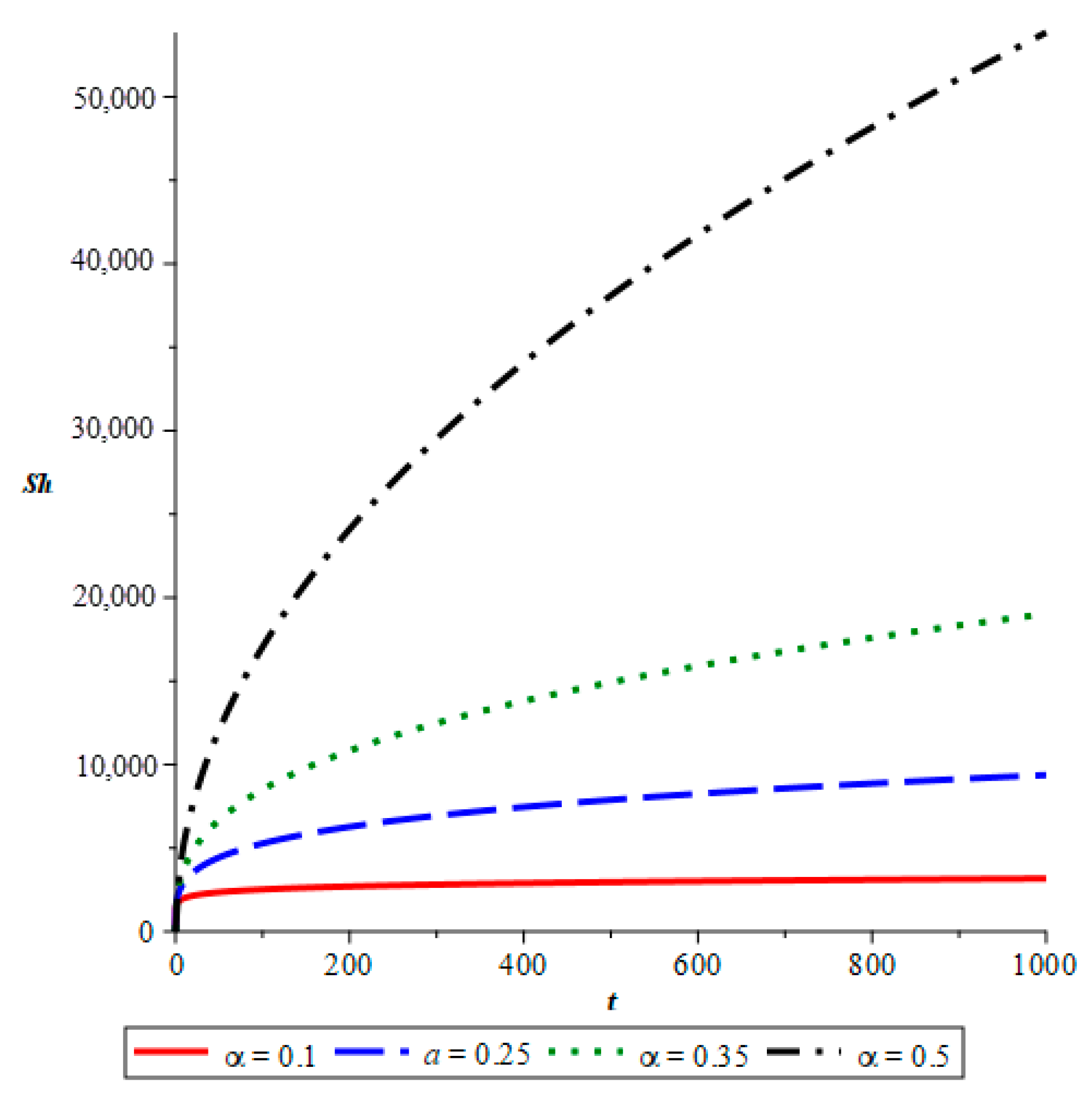
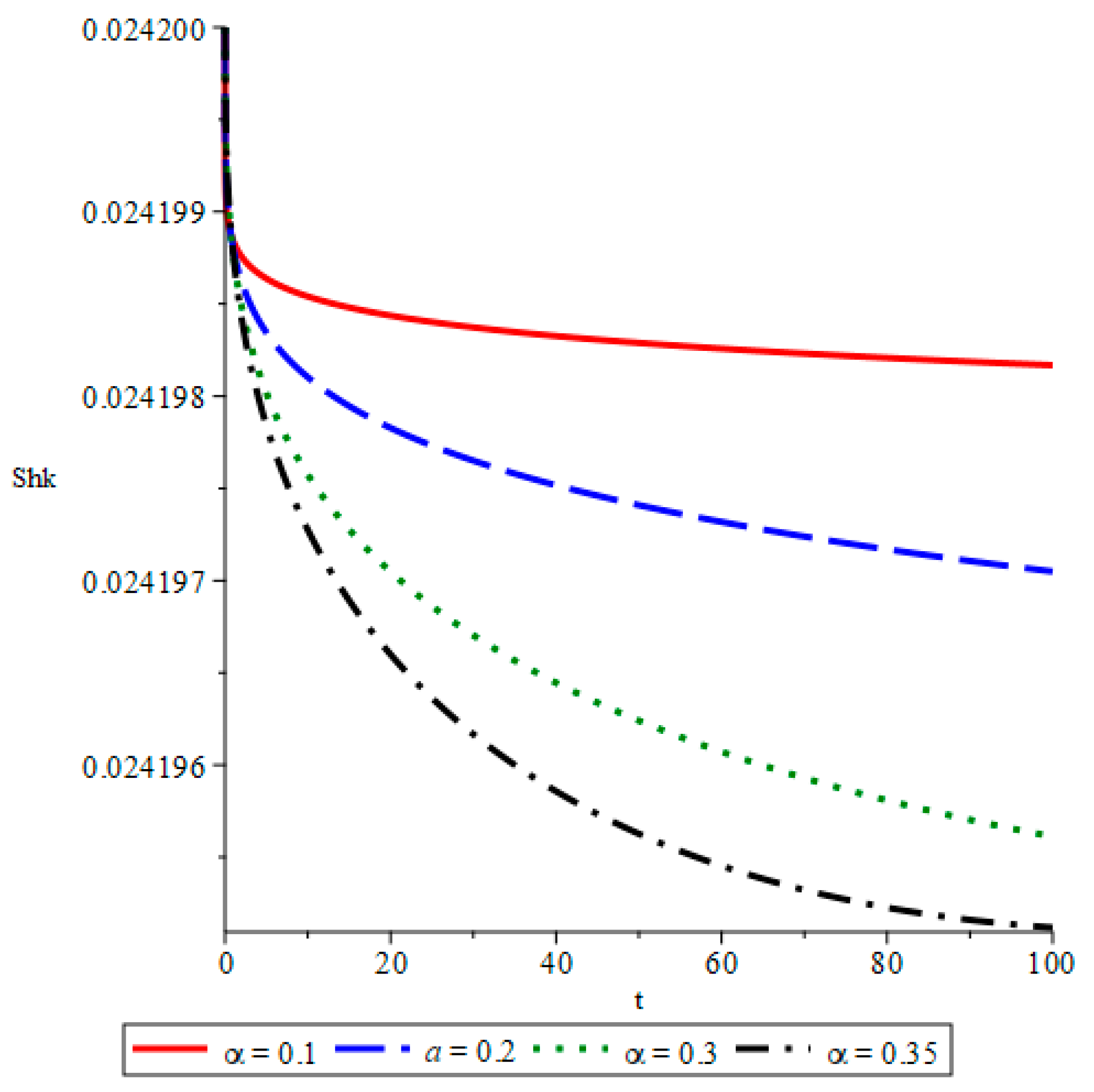
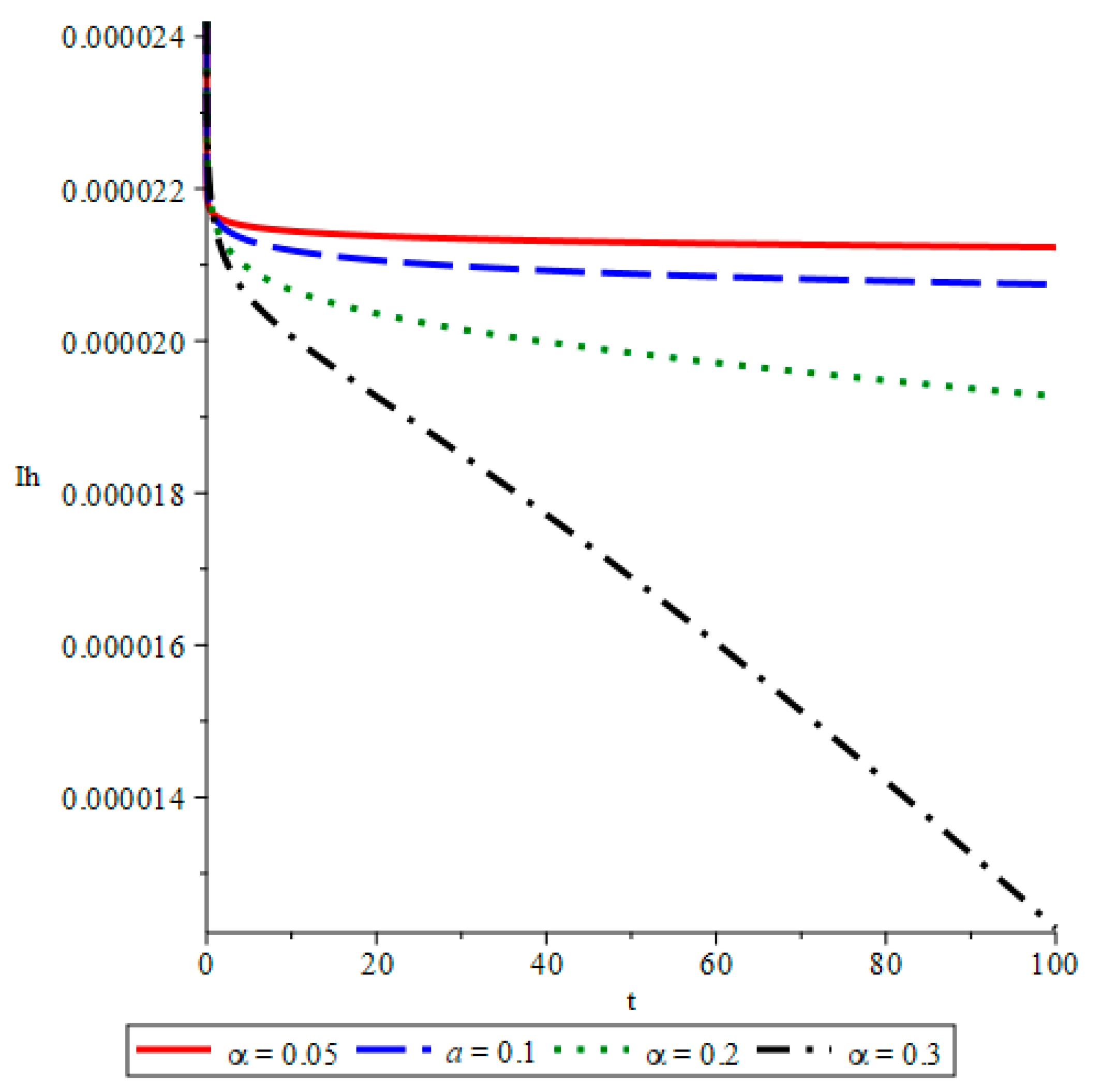
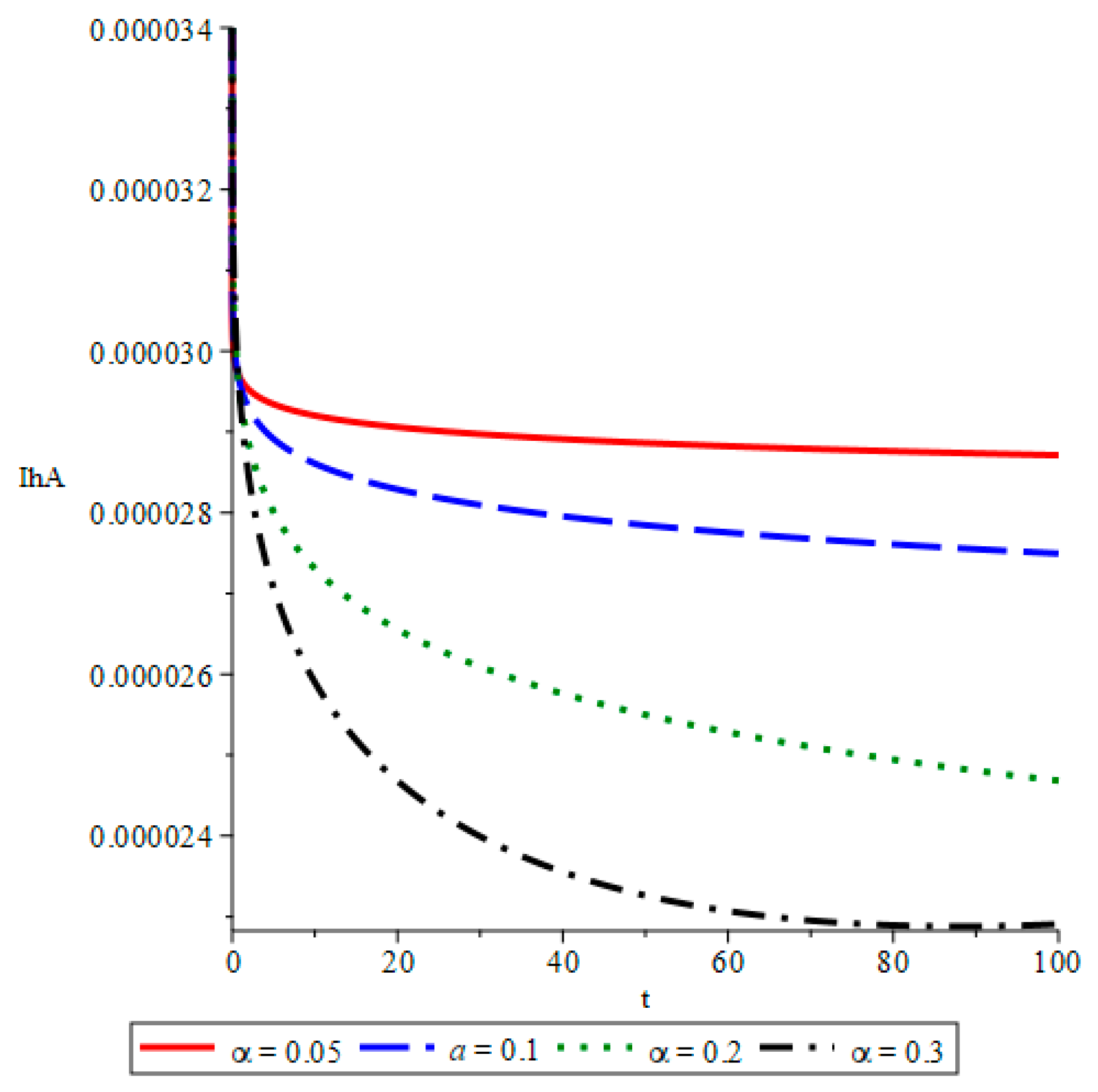
- The simulations reveal that smaller fractional orders (α) lead to longer disease persistence due to stronger memory effects, while larger α values result in faster infection reduction. This demonstrates that interventions altering the transmission rate significantly influence disease development.
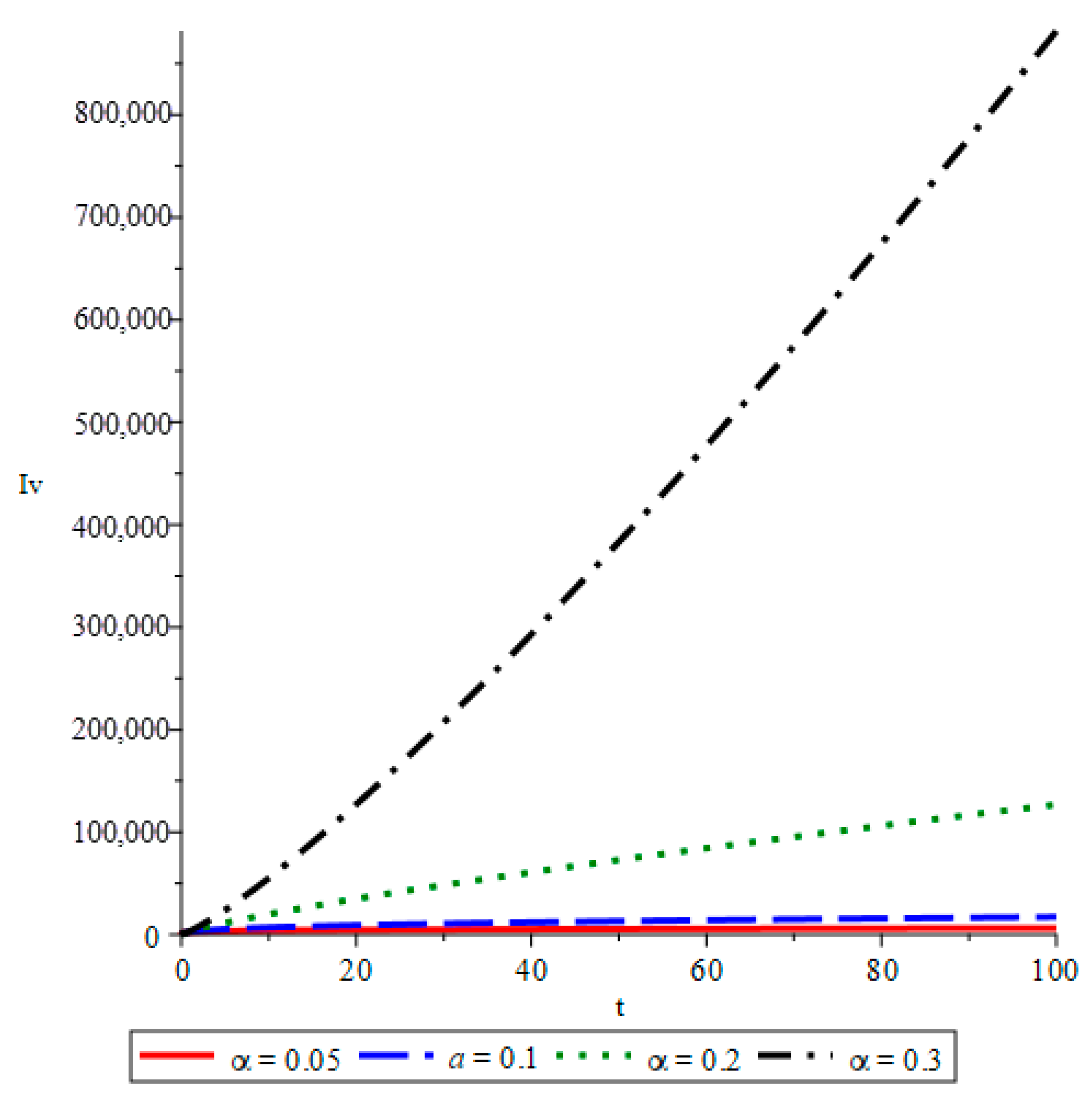
- The study confirms that infected mosquito populations closely follow the patterns of human infections. High values of α lead to explosive vector transmission, validating the need for mosquito control measures, such as the use of insecticides and the elimination of breeding sites.
- The outcomes show that an increase in recovery corresponds to a decline in both symptomatic and asymptomatic infections.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nh | constant host (human) population size |
| Sh | number of susceptible in host population |
| Shk | number of susceptible with partial immunity in host population |
| Ih | number of symptomatic infected in host population |
| IhA | number of asymptomatic infected in host population |
| Rh | number of recovered in host population |
| Nv | vector (mosquito) population size |
| Sv | number of susceptible in the vector population |
| Iv | number of infectives in the vector population |
References
- Eegunjobi, A.S.; Anyanwu, M.C.; Neossi-Nguetchue, S.N. Modelling the super-infection of two strains of dengue virus. J. Egypt. Math. Soc. 2023, 31, 1. [Google Scholar] [CrossRef]
- Ogunlade, S.T.; Meehan, M.T.; Adekunle, A.I.; McBryde, E.S. A systematic review of mathematical models of dengue transmission and vector control: 2010–2020. Viruses 2023, 15, 254. [Google Scholar] [CrossRef] [PubMed]
- Aguiar, M.; Anam, V.; Blyuss, K.B.; Estadilla, C.D.S.; Guerrero, B.V.; Knopoff, D.; Kooi, B.W.; Srivastav, A.K.; Steindorf, V.; Stollenwerk, N. Mathematical models for dengue fever epidemiology: A 10-year systematic review. Phys. Life Rev. 2022, 40, 65–92. [Google Scholar] [CrossRef] [PubMed]
- Naaly, B.Z.; Marijani, T.; Isdory, A.; Ndendya, J.Z. Mathematical modeling of the effects of vector control, treatment and mass awareness on the transmission dynamics of dengue fever. Comput. Methods Programs Biomed. Update 2024, 6, 100159. [Google Scholar] [CrossRef]
- El-Sayed, A.M.; Arafa, A.A.; Hanafy, I.M.; Gouda, M.I. A Fractional-Order Model of Dengue Fever with Awareness Effect: Numerical Solutions and Asymptotic Stability Analysis. Progr. Fract. Differ. Appl. 2022, 8, 267–274. [Google Scholar]
- Dwivedi, A.; Keval, R. Analysis for transmission of dengue disease with different class of human population. Epidemiol. Methods 2021, 10, 20200046. [Google Scholar] [CrossRef]
- Lin, S.; Cao, X.; Zheng, H.; Li, Y.; Li, W. An improved meshless numerical manifold method for simulating complex boundary seepage problems. Comput. Geotech. 2023, 155, 105211. [Google Scholar] [CrossRef]
- Fendzi-Donfack, E.; Kumar, D.; Tala-Tebue, E.; Nana, L.; Nguenang, J.P.; Kenfack-Jiotsa, A. Construction of exotical soliton-like for a fractional nonlinear electrical circuit equation using differential-difference Jacobi elliptic functions sub-equation method. Results Phys. 2022, 32, 105086. [Google Scholar] [CrossRef]
- Abdulazeez, S.T.; Modanli, M. Solutions of fractional order pseudo-hyperbolic telegraph partial differential equations using finite difference method. Alex. Eng. J. 2022, 61, 12443–12451. [Google Scholar] [CrossRef]
- Ali, K.K.; Wazwaz, A.-M.; Osman, M. Optical soliton solutions to the generalized nonautonomous nonlinear Schrödinger equations in optical fibers via the sine-Gordon expansion method. Optik 2020, 208, 164132. [Google Scholar] [CrossRef]
- Ouahid, L.; Owyed, S.; Abdou, M.; Alshehri, N.A.; Elagan, S. New optical soliton solutions via generalized Kudryashov’s scheme for Ginzburg–Landau equation in fractal order. Alex. Eng. J. 2021, 60, 5495–5510. [Google Scholar] [CrossRef]
- Fendzi-Donfack, E.; Temgoua, G.W.K.; Djoufack, Z.I.; Kenfack-Jiotsa, A.; Nguenang, J.P.; Nana, L. Exotical solitons for an intrinsic fractional circuit using the sine-cosine method. Chaos Solitons Fractals 2022, 160, 112253. [Google Scholar] [CrossRef]
- Mohamed, N.A.; Rashed, A.S.; Melaibari, A.; Sedighi, H.M.; Eltaher, M.A. Effective numerical technique applied for Burgers’ equation of (1+1)-, (2+1)-dimensional, and coupled forms. Math. Methods Appl. Sci. 2021, 44, 10135–10153. [Google Scholar] [CrossRef]
- Rashed, A.S.; Inc, M.; Saleh, R. Extensive novel waves evolution of three-dimensional Yu–Toda–Sasa–Fukuyama equation compatible with plasma and electromagnetic applications. Mod. Phys. Lett. B 2023, 37, 2250195. [Google Scholar] [CrossRef]
- Mohamed, M.; Mabrouk, S.M.; Rashed, A.S. Mathematical Investigation of the Infection Dynamics of COVID-19 Using the Fractional Differential Quadrature Method. Computation 2023, 11, 198. [Google Scholar] [CrossRef]
- Rashed, A.S.; Mostafa, A.N.M.; Mabrouk, S.M. Abundant families of solutions for (4+1)-dimensional Fokas fractional differential equation using New sub-equation method. Sci. Afr. 2024, 23, e02107. [Google Scholar] [CrossRef]
- Eguda, F.; Andrawus, J.; Babuba, S. The Solution of a Mathematical Model for Dengue Fever Transmission Using Differential Transformation Method. J. Niger. Soc. Phys. Sci. 2019, 1, 82–87. [Google Scholar] [CrossRef]
- Agarwal, P.; Singh, R.; Ul Rehman, A. Numerical solution of hybrid mathematical model of dengue transmission with relapse and memory via Adam–Bashforth–Moulton predictor-corrector scheme. Chaos Solitons Fractals 2021, 143, 110564. [Google Scholar] [CrossRef]
- Eguda, A.J.; Yakubu, F. Analysis of a mathematical model to investigate the dynamics of dengue fever. J. Appl. Sci. Environ. Manag. 2017, 21, 626–638. [Google Scholar] [CrossRef][Green Version]
- Wan, H.; Xu, J. How Does the Enhanced Mortality of Wolbachia-Infected Immature Mosquitoes Affect Dengue Transmission? Int. J. Biomath. 2024, 2450045. [Google Scholar] [CrossRef]
- Wang, Z.; Cai, S.; Chen, G.; Zheng, K.; Wei, F.; Jin, Z.; Mao, X.; Xie, J. Dynamics of a Dengue Transmission Model with Multiple Stages and Fluctuations. Mathematics 2024, 12, 2491. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, S.; Cheke, R.A.; Zhu, H. Modeling the Effects of Augmentation Strategies on the Control of Dengue Fever with an Impulsive Differential Equation. Bull. Math. Biol. 2016, 78, 1968–2010. [Google Scholar] [CrossRef] [PubMed]
- Jan, R.; Khan, M.A.; Kumam, P.; Thounthong, P. Modeling the transmission of dengue infection through fractional derivatives. Chaos Solitons Fractals 2019, 127, 189–216. [Google Scholar] [CrossRef]
- Jajarmi, A.; Arshad, S.; Baleanu, D. A new fractional modelling and control strategy for the outbreak of dengue fever. Phys. A Stat. Mech. Its Appl. 2019, 535, 122524. [Google Scholar] [CrossRef]
- Jan, R.; Khan, M.A.; Khan, Y.; Ullah, S. A new model of dengue fever in terms of fractional derivative. Math. Biosci. Eng. 2020, 17, 5267–5287. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Jan, R.; Jan, A.; Deebani, W.; Shutaywi, M. Fractional-calculus analysis of the transmission dynamics of the dengue infection. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 053130. [Google Scholar] [CrossRef]
- Boulaaras, S.; Jan, R.; Khan, A.; Ahsan, M. Dynamical analysis of the transmission of dengue fever via Caputo-Fabrizio fractional derivative. Chaos Solitons Fractals X 2022, 8, 100072. [Google Scholar] [CrossRef]
- Gurung, D. Mathematical Model of Dengue Fever with and without awareness in Host Population. Int. J. Adv. Eng. Res. Appl. (IJAERA) 2015, 1, 239. [Google Scholar]
- Andraud, M.; Hens, N.; Marais, C.; Beutels, P. Dynamic epidemiological models for dengue transmission: A systematic review of structural approaches. PLoS ONE 2012, 7, e49085. [Google Scholar] [CrossRef]
- Garba, S.M.; Gumel, A.B.; Abu Bakar, M.R. Backward bifurcations in dengue transmission dynamics. Math. Biosci. 2008, 215, 11–25. [Google Scholar] [CrossRef]
- Tatari, M.; Dehghan, M.; Razzaghi, M. Application of the Adomian decomposition method for the Fokker–Planck equation. Math. Comput. Model. 2007, 45, 639–650. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. A reliable modification of Adomian decomposition method. Appl. Math. Comput. 1999, 102, 77–86. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alex. Eng. J. 2020, 59, 2379–2389. [Google Scholar] [CrossRef]
- Nazir, G.; Zeb, A.; Shah, K.; Saeed, T.; Khan, R.A.; Ullah Khan, S.I. Study of COVID-19 mathematical model of fractional order via modified Euler method. Alex. Eng. J. 2021, 60, 5287–5296. [Google Scholar] [CrossRef]
- Ullah, Z. Analytical Solution of the Mathematical Model of Dengue Fever by the Laplace Adomian Decomposition Method. Commun. Nonlinear Anal. 2023, 2, 1–17. [Google Scholar]
- National Center for Vector Borne Diseases Control-India. National Guidelines for Clinical Management of Dengue Fever. 2023. Available online: https://ncvbdc.mohfw.gov.in (accessed on 15 May 2025).

| Symbol | Physical Meaning | Value | References |
|---|---|---|---|
| Constant host population size | 8,266,000 | [33] | |
| Susceptible people | 8,065,518 | [33] | |
| Susceptible people with partial immunity | 200,000 | [33] | |
| Symptomatic infected people | 200 | [33] | |
| Asymptomatic infected people | 282 | [33] | |
| Recovered people | 0 | [33] | |
| Vector (mosquito) population size | 50,000 | Assumed | |
| Susceptible mosquitoes | 49,000 | Assumed | |
| Infected mosquitoes | 1000 | Assumed | |
| Death rates of humans per capita | 0.0000457/day | [3,28,29,30] | |
| Death rates of mosquitoes per capita | 0.03/day | [3,28,29,30] | |
| The transmission probability from vector to human (effective contact rate) | 0.75 | [3,28,29,30] | |
| The transmission probability from vector to human with partial immunity (effective contact rate) | 1 | Assumed | |
| The transmission probability from human to vector (effective contact rate) | 0.75 | [3,28,29,30] | |
| b | Average bite per mosquito per day | 0.3/day | [3,28,29,30] |
| Effective contact rate, human to vector | 0.3750000 | [28] | |
| Effective contact rate, vector to human | 0.75 | [28] | |
| Recovery rate in the host population, time −1 | 0.14286/day | [3,28,29,30] | |
| Proportion of asymptomatic infection rate of people | 0.009 | [34] | |
| 0.9757 | |||
| 0.0242 | |||
| 0.0000242 | |||
| 0.000034 | |||
| 0 | |||
| 0.98 | |||
| 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashed, A.S.; Mahdy, M.M.; Mabrouk, S.M.; Saleh, R. Fractional Order Mathematical Model for Predicting and Controlling Dengue Fever Spread Based on Awareness Dynamics. Computation 2025, 13, 122. https://doi.org/10.3390/computation13050122
Rashed AS, Mahdy MM, Mabrouk SM, Saleh R. Fractional Order Mathematical Model for Predicting and Controlling Dengue Fever Spread Based on Awareness Dynamics. Computation. 2025; 13(5):122. https://doi.org/10.3390/computation13050122
Chicago/Turabian StyleRashed, Ahmed S., Mahy M. Mahdy, Samah M. Mabrouk, and Rasha Saleh. 2025. "Fractional Order Mathematical Model for Predicting and Controlling Dengue Fever Spread Based on Awareness Dynamics" Computation 13, no. 5: 122. https://doi.org/10.3390/computation13050122
APA StyleRashed, A. S., Mahdy, M. M., Mabrouk, S. M., & Saleh, R. (2025). Fractional Order Mathematical Model for Predicting and Controlling Dengue Fever Spread Based on Awareness Dynamics. Computation, 13(5), 122. https://doi.org/10.3390/computation13050122