Parallel Simulation Using Reactive Streams: Graph-Based Approach for Dynamic Modeling and Optimization

Abstract

Modern computational models tend to become more and more complex, especially in fields like computational biology, physical modeling, social simulation, and others. With the increasing complexity of simulations, modern computational architectures demand efficient parallel execution strategies. This paper proposes a novel approach leveraging the reactive stream paradigm as a general-purpose synchronization protocol for parallel simulation. We introduce a method to construct simulation graphs from predefined transition functions, ensuring modularity and reusability. Additionally, we outline strategies for graph optimization and interactive simulation through push and pull patterns. The resulting computational graph, implemented using reactive streams, offers a scalable framework for parallel computation. Through theoretical analysis and practical implementation, we demonstrate the feasibility of this approach, highlighting its advantages over traditional parallel simulation methods. Finally, we discuss future challenges, including automatic graph construction, fault tolerance, and optimization strategies, as key areas for further research.

1. Introduction

As simulations become increasingly complex, more and more computational resources are required to execute them. Computing power continues to grow per Moore’s law, but this growth shifts to the horizontal plane, i.e., it happens due to an increase in the number of parallel processors and their cores. Thus, there is a need to develop parallel simulation algorithms capable of utilizing the computing resources of multiple CPUs.

Today, several approaches exist for parallelizing simulations. In particular, we can consider the Time Warp algorithm [1] described in detail in [2]. This algorithm has been studied for many years and has several implementations in the code [3,4,5]. However, Time Warp uses its own synchronization protocol, which is complex and low level [6]. The RxHLA software framework (based on the reactive adaptation of IEEE 1516 standard) [7] is similar to Time Warp in terms of complexity and low levelness. Another approach, based on the CQRS + ES architecture, is described in [8]. However, the authors of that work concentrate more on the practical aspects of implementation without providing much theoretical background. The HPC simulation platform [9] is also a more practical implementation of parallel simulation; it is based on actors and the AKKA library and constitutes a more conservative approach than reactive streams.

The key concept of this paper is to use a general-purpose synchronization protocol to parallelize simulations, namely, the reactive-streams protocol [10,11,12], particularly the version implemented in the AKKA library [13,14,15,16]. Thus, on the one hand, we have a classical mathematical model. On the other hand, we have a general-purpose synchronization protocol. The goal of this work is to unite them.

The rest of this manuscript is organized as follows:

• Section 2 explains the basic modeling concepts and entities that we will use in this paper.
• Section 3 extends basic modeling to be represented in the form of a transition graph and shows how a simulation can be performed on this graph.
• Section 4 shows how the transition graph can be implemented with reactive streams and how simulations can be executed.

2. Substates

Before we start developing a parallel simulation algorithm with reactive streams, we define substate concepts and some objects for later use in this paper. Before reading this section, we suggest you check Supplementary S1, which describes the notation, and Supplementary S2, which gives a common basic definition used in this article. Also, in Section 5 and Supplementary S6, you can find real word examples that illustrate the described approach.

2.1. Substates ${{\mathfrak{S}}^{\mathfrak{K}}}_{\mathit{q}}$ as a Decomposition of the State $\mathfrak{V}$

Each state $\mathfrak{V}$ can be represented as a set of substates, each of which contains only a part of the values of ${\mathfrak{v}}_i\in \mathfrak{V}$. There must be a way to determine which of the substates belongs to a certain $\mathfrak{V}$. One option to achieve this is to use a unique key to mark all substates belonging to a certain $\mathfrak{V}$.

Definition 1. 

Let us define a substate ${{\mathfrak{S}}^{\mathfrak{K}}}_q$, where $\mathfrak{S}\subseteq \mathfrak{V}$ is part or all of the set of values, ${\mathfrak{v}}_i\in \mathfrak{V}$, $\mathfrak{K}$ is some key unique to the state $\mathfrak{V}\in {\mathbb{V}}^n$;, and $q\in \mathbb{N}$ is the index of the substate with the same key, $\mathfrak{K}$.

One or more ${\mathfrak{v}}_i\in \mathfrak{V}$ values can be used as key $\mathfrak{K}$. In this case, it makes no sense to include them in any of the substates since they will be presented in the key.

For some state $\mathfrak{V}$, we have the set of substates $\left\{{{\mathfrak{S}}^{\mathfrak{K}}}_q\right\}$ with the same key $\mathfrak{K}$. We will denote this set by a bold ${\mathfrak{S}}^{\mathfrak{K}}$. With such representation of the state $\mathfrak{V}$, it is necessary to ensure that all ${{\mathfrak{S}}^{\mathfrak{K}}}_q$ marked by the same $\mathfrak{K}$ are not contradictory. The pair of ${{\mathfrak{S}}^{\mathfrak{K}}}_q$ with the same key $\mathfrak{K}$ can be contradictory if one or more values ${\mathfrak{v}}_i\in \mathfrak{S},\mathfrak{V}$ differ under the same index.

Definition 2. 

Let us define the set of substates

$${\mathfrak{S}}^{\mathfrak{K}}≔\left\{{{\mathfrak{S}}^{\mathfrak{K}}}_q,{{\mathfrak{S}}^{{\mathfrak{K}}^{\prime }}}_{q^{\prime }}|\mathfrak{K}={\mathfrak{K}}^{\prime } \wedge q\ne q^{\prime }\right\}$$

where for all ${{\mathfrak{S}}^{\mathfrak{K}}}_q\in {\mathfrak{S}}^{\mathfrak{K}},$  the consistency criterion

$$\nexists {{\mathfrak{S}}^{\mathfrak{K}}}_i,{{\mathfrak{S}}^{\mathfrak{K}}}_j\in {\mathfrak{S}}^{\mathfrak{K}}\left(\exists {\mathfrak{v}}_l\in {{\mathfrak{S}}^{\mathfrak{K}}}_i\ne {\mathfrak{v}}_l\in {{\mathfrak{S}}^{\mathfrak{K}}}_j\forall l\right)$$

is true.

In this paper, we will talk about arbitrary sets of substates ${{\mathfrak{S}}^{\mathfrak{K}}}_q$, whose only requirement is to meet the consistency criterion.

Definition 3. 

Let us define an arbitrary set of substates

$${\mathfrak{S}}^K≔\left\{{\mathfrak{S}}^{\mathfrak{K}}\cup {\mathfrak{S}}^{{\mathfrak{K}}^{\prime }}|\mathfrak{K}\ne {\mathfrak{K}}^{\prime } \right\}$$

as the union of the sets ${\mathfrak{S}}^{\mathfrak{K}}$ with different $\mathfrak{K}$.

Notice that these definitions do not require the presence in the set ${\mathfrak{S}}^{\mathfrak{K}}$ (and consequently, in ${\mathfrak{S}}^K$) of a sufficient number of substates ${{\mathfrak{S}}^{\mathfrak{K}}}_q$ to cover all values ${\mathfrak{v}}_i\in \mathfrak{V}$.

Let us also note that, by definition, the set ${\mathfrak{S}}^K$ can contain more than one substate ${{\mathfrak{S}}^{\mathfrak{K}}}_q$ with the same key $\mathfrak{K}$. However, on an arbitrary set ${\mathfrak{S}}^K$ that contains duplicate keys $\mathfrak{K}$, we can construct a set ${\mathfrak{S}}^K$ that does not contain them. For this, we need to combine all substates with the same key into one substate:

$${{\mathfrak{S}}^K}_d\stackrel{\forall {\mathfrak{S}}^{\mathfrak{K}}\subseteq {{\mathfrak{S}}^K}_d\left({{\mathfrak{S}}^{\mathfrak{K}}}_1\in {{\mathfrak{S}}^K}_u={\displaystyle \bigcup _{\mathfrak{K}}}{\mathfrak{S}}^{\mathfrak{K}}\right)}{\Rightarrow }{{\mathfrak{S}}^K}_u$$

where ${{\mathfrak{S}}^K}_d$ is a set with duplicate keys and ${{\mathfrak{S}}^K}_u$ is a set with unique $\mathfrak{K}$. Thus, we can say that an arbitrary set of substates ${\mathfrak{S}}^K$ can be considered as a key–value structure or as the surjective function

$$f:\left\{\mathfrak{K}\right\}\to \left\{\mathfrak{S}\right\}$$

As follows from the definition, the set ${\mathfrak{S}}^K$ can only be constructed from a set of states $\mathfrak{V}\subseteq {\mathbb{V}}^n$ in which a unique key $\mathfrak{K}$ can be associated with each state $\mathfrak{V}\in \mathfrak{V}$. Otherwise, this will lead to the appearance of substates ${{\mathfrak{S}}^{\mathfrak{K}}}_q$ in conflict.

The inverse transformation, i.e., the construction of $\mathfrak{V}\subseteq {\mathbb{V}}^n$ from an arbitrary ${\mathfrak{S}}^K$

$${\mathfrak{S}}^K\stackrel{\forall {\mathfrak{S}}^{\mathfrak{K}}\subseteq {\mathfrak{S}}^K\left(\mathfrak{V}\in \mathfrak{V}={\displaystyle \bigcup _{\mathfrak{K}}}{\mathfrak{S}}^{\mathfrak{K}}\right)}{\Rightarrow }\mathfrak{V}$$

is possible only if ${\mathfrak{S}}^K$ contains enough substates ${{\mathfrak{S}}^{\mathfrak{K}}}_j$ to construct each state $\mathfrak{V}\in \mathfrak{V}$ completely.

The set of substates ${\mathfrak{S}}^K$ can be equivalent to the state space ${\mathbb{V}}^n$ if this state-space contains enough substates to construct each state $\mathfrak{V}\in {\mathbb{V}}^n$. We will denote such a set by ${\mathbb{S}}^K$.

2.2. Representation of the Dependence of Y on X as a Set of Substates: $Y={\mathfrak{S}}^{X|\mathfrak{G}}$

The dependence of the variables $Y$ upon $X$ can be represented as a set of states ${\mathfrak{S}}^K$. This representation is an alternative to a set of functions $F\left(X|\mathfrak{G}\right)$. In this case, it is convenient to choose the values $\mathfrak{X}\in {\mathbb{X}}^n$ as the key $\mathfrak{K}$ and the subset of the values $\mathfrak{Y}\in {\mathbb{Y}}^n$ as the values of $\mathfrak{S}$ (including $\mathfrak{S}=\mathfrak{\varnothing }$).

Definition 4. 

Let us define the substate ${{\mathfrak{S}}^{\mathfrak{X}}}_q$, where the key is $\mathfrak{K}=\mathfrak{X}$,$\mathfrak{X}\in {\mathbb{X}}^n$, the value$\mathfrak{S}\subseteq \mathfrak{Y}$,$\mathfrak{Y}\in {\mathbb{Y}}^n$, and the index$q\in \mathbb{N}$ is such that

$$\forall {{\mathfrak{S}}^{\mathfrak{X}}}_q, {{{\mathfrak{S}}^{\mathfrak{X}}}_q}^{\prime }\left(\mathfrak{X}={\mathfrak{X}}^{\prime },q\ne q^{\prime }\right)$$

also, $\mathfrak{X}\subseteq {{\mathfrak{S}}^{\mathfrak{X}}}_q$ and $\left({{\mathfrak{S}}^{\mathfrak{X}}}_q\backslash \mathfrak{X}\right)\subseteq \mathfrak{Y}.$

Since the values of the parameters $\mathfrak{G}\in {\mathbb{G}}^n$ are constant for any possible values of $\mathfrak{X}$ and $\mathfrak{Y}$, they are also constant for any possible substates ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ composed of the values of $\mathfrak{X}$ and $\mathfrak{Y}$. Thus, the definition of ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ does not include values $\mathfrak{G}$. Being joined into a set, the substates ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ will have the same parameters $\mathfrak{G}$, but may have different values of the key $\mathfrak{X}$.

Definition 5. 

Let us define the dependence

$$Y={\mathfrak{S}}^{X|\mathfrak{G}}≔\left\{{{\mathfrak{S}}^{\mathfrak{X}}}_q\right\}|\mathfrak{G}$$

which represents the dependence of the variables $Y$  upon $X$  for given parameters $\mathfrak{G}$  that are the same for all substates included in the set ${\mathfrak{S}}^{X|\mathfrak{G}}$. At the same time, substates should not be contradictory:

$$\nexists {{\mathfrak{S}}^{\mathfrak{X}}}_i,{{\mathfrak{S}}^{\mathfrak{X}}}_j\in {\mathfrak{S}}^{X|\mathfrak{G}}\left(\exists {\mathfrak{v}}_l\in {{\mathfrak{S}}^{\mathfrak{X}}}_i\ne {\mathfrak{v}}_l\in {{\mathfrak{S}}^{\mathfrak{X}}}_j \forall l\right),$$

(1)

The set ${\mathfrak{S}}^{X|\mathfrak{G}}$ with all substates having the same key $\mathfrak{X}$ will be denoted ${\mathfrak{S}}^{\mathfrak{X}|\mathfrak{G}}$.

Let us note that we do not impose a completeness restriction upon the set ${\mathfrak{S}}^{X|\mathfrak{G}}$—i.e., ${\mathfrak{S}}^{X|\mathfrak{G}}$ may not contain all of the keys $\mathfrak{X}\in {\mathbb{X}}^n$ or may even be empty: ${\mathfrak{S}}^{X|\mathfrak{G}}=\mathrm{\varnothing }$. ${\mathfrak{S}}^{X|\mathfrak{G}}$ may also not contain all $\mathfrak{Y}\in {\mathbb{Y}}^n$ and/or it may not contain enough ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ to build one or more complete $\mathfrak{Y}$.

The representation $Y={\mathfrak{S}}^{X|\mathfrak{G}}$ is equivalent to the representation $Y=F\left(X|\mathfrak{G}\right)$ if and only if, for each $\mathfrak{X}\in {\mathbb{X}}^n$ at a given $\mathfrak{G}\in {\mathbb{G}}^n$, the representations are equal:

$$\begin{gathered} Y={\mathfrak{S}}^{X|\mathfrak{G}}\iff Y= \\ =F\left(X|\mathfrak{G}\right)\Rightarrow \forall \mathfrak{X}\in {\mathbb{X}}^n\left(F\left(\mathfrak{X}|\mathfrak{G}\right)={\mathfrak{S}}^{\mathfrak{X}|\mathfrak{G}}\right) \end{gathered}$$

For each key $\mathfrak{X}$, there exists a set of substates ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ that cover all possible values $\mathfrak{Y}\in {\mathbb{Y}}^n$. We will denote this set by ${\mathbb{S}}^{\mathfrak{X}|\mathfrak{G}}$. This set may not satisfy the consistency criterion (Formula (1)) and will have cardinality

$$\left|{\mathbb{S}}^{\mathfrak{X}|\mathfrak{G}}\right|={\prod }_{i=1}^n\left|{\mathbb{y}}_i\right|$$

If we join the sets ${\mathbb{S}}^{\mathfrak{X}|\mathfrak{G}}$ for all possible keys $\mathfrak{X}\in {\mathbb{X}}^n$, we obtain the set of all possible substates. We will denote it by

$${\mathbb{S}}^{\mathbb{X}|\mathfrak{G}}={\bigcup }_{\mathfrak{X}\in {\mathbb{X}}^n}{\mathbb{S}}^{\mathfrak{X}|\mathfrak{G}},$$

(2)

The cardinality of this set when $\mathfrak{S}=\mathfrak{Y}$ will be

$$\left|{\mathbb{S}}^{\mathbb{X}|\mathfrak{G}}\right|={\displaystyle \sum _{\mathfrak{X}\in {\mathbb{X}}^n}}\left|{\mathbb{S}}^{\mathfrak{X}|\mathfrak{G}}\right|$$

Moreover, $\left|{\mathbb{S}}^{\mathbb{X}|\mathfrak{G}}\right|\le \left|{\mathbb{V}}^n\right|$ since, from the set ${\mathbb{G}}^n$ only, one set of values $\mathfrak{G}$ is used (note, the cardinalities will be equal in case $\left|{\mathbb{G}}^n\right|=1$).

In practice, we will more often see sparse ${\mathfrak{S}}^{X|\mathfrak{G}}$, where it is impossible to completely construct $\mathfrak{Y}$ for every $\mathfrak{X}\in {\mathbb{X}}^n$. The use of sparse ${\mathfrak{S}}^{X|\mathfrak{G}}$ will reduce the modeling accuracy. In general, this is not a problem from an engineering standpoint since increasing or decreasing the cardinality ${\mathfrak{S}}^{X|\mathfrak{G}}$ allows us to choose an acceptable accuracy level for solving a specific simulation problem.

2.3. Reflection $\check{\mathit{Y}}\left(\overline{\mathit{X}}|\mathfrak{G}\right)$ as a Record of Changes in the Values of Variables

We can reflect the behavior of a modeled object by measuring its properties and recording the corresponding values of the variables $X$, $Y,$ and $G$. By abstracting from a specific implementation, we will call such a record a reflection of the modeled object.

Definition 6. 

Let us define the reflection $\check{Y}\left(\overline{X}|\mathfrak{G}\right)$  as an arbitrary representation of the dependence of the dependent variables $\check{Y}$  upon the independent variables $\overline{X}$  and the values of the parameters $\mathfrak{G}$. Moreover, this dependence is constructed by studying and measuring the modeled object’s properties.

We can graphically represent the building of the reflection $\check{Y}\left(\overline{X}|\mathfrak{G}\right)$ by adding the points

$$\mathfrak{V}=\overline{\mathfrak{X}}\cup \check{\mathfrak{Y}}\cup \mathfrak{G}$$

into the state space ${\mathbb{V}}^n$ at the coordinates $\overline{X},\check{Y},\mathfrak{G}$, where $\overline{\mathfrak{X}}\in \overline{{\mathbb{X}}^n}$, $\check{\mathfrak{Y}}\in \check{{\mathbb{Y}}^n}$, and $\mathfrak{G}\in {\mathbb{G}}^n$. The added points will form a geometric figure that reflects the behavior of the modeled object.

A reflection can be represented as a set of functions

$${\check{Y}\left(\overline{X}|\mathfrak{G}\right)}^F=F\left(\overline{X}|\mathfrak{G}\right)=\check{Y}$$

or as a set of states

$${\check{Y}\left(\overline{X}|\mathfrak{G}\right)}^S={\mathfrak{S}}^{\overline{X}|\mathfrak{G}}=\check{Y}$$

In the first case, a set of functions can be constructed by recording the obtained or measured values of the variables $X$, $Y,$ and $G$ [17]. In the second case, from the values of $\check{\mathfrak{Y}}$ obtained or measured with respect to $\overline{\mathfrak{X}}$ and $\mathfrak{G}$, the substate ${{\mathfrak{S}}^{\overline{\mathfrak{X}}}}_{q=1}$ can be directly built and added to the set of substates ${\mathfrak{S}}^{\overline{X}|\mathfrak{G}}$.

In this case, writing down the values of the stopwatch (which reflects the variable $t$) and the level gauge (which reflects $v_{water}$), we obtain the function $v_{water}\left(t\right)$, which reflects the dependence of $v_{water}$ on $t$. In practice, this function will be defined only on a certain interval or several intervals of the time $t_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}}$, during which the measurement was performed.

2.4. Model $\widehat{\mathit{Y}}\left(\overline{\mathit{X}}\right|\mathfrak{G})$ as an Imitation of Changes in the Variables V

In one of several ways, we can define the dependencies of the variables $Y$ on $X$ and $G$ without directly measuring the properties of the modeled object [18,19,20]. We will call the dependence defined in this way the model of the modeled object.

Definition 7. 

The model of the modeled object $\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)$ is an arbitrary representation or implementation of the dependence of the dependent variables $\widehat{Y}$ upon the independent variables $\overline{X}$ and the values of the parameters $\mathfrak{G}$. Moreover, this dependence is constructed without the direct participation of the modeled object.

We can graphically represent the model $\widehat{Y}\left(\overline{X}\right|\mathfrak{G})$ as a geometrical figure in the state space ${\mathbb{V}}^n$ consisting of the points

$$\mathfrak{V}=\overline{\mathfrak{X}}\cup \widehat{\mathfrak{Y}}\cup \mathfrak{G}$$

that define the relationship between the variables $\widehat{Y}$ and $\overline{X}$ and the parameters $\mathfrak{G}$, where $\overline{\mathfrak{X}}\in \overline{{\mathbb{X}}^n}$, $\widehat{\mathfrak{Y}}\in \widehat{{\mathbb{Y}}^n}$ and $\mathfrak{G}\in {\mathbb{G}}^n$.

The model can be implemented as a set of possibly partial functions

$${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^F=F\left(\overline{X}|\mathfrak{G}\right)=\widehat{Y},$$

(3)

or as a set of states

$${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^S={\mathfrak{S}}^{\overline{X}|\mathfrak{G}}=\widehat{Y},$$

(4)

In the first case, the set of functions can be determined analytically or in another way. In the second case, many substates must be pre-built in one way or another.

We can define the model $\widehat{Y}\left(\overline{X}\right|\mathfrak{G})$ such that it completely coincides with certain reflection $\check{Y}\left(\overline{X}|\mathfrak{G}\right)$; however, it is much more reasonable and useful to construct $\widehat{Y}\left(\overline{X}\right|\mathfrak{G})$ to predict changes in the modeled object.

From a practical point of view, we are interested in how accurately the constructed model $\widehat{Y}\left(\overline{X}\right|\mathfrak{G})$ corresponds to the modeled object. One way to determine compliance is to compare the model and reflection $\check{Y}\left(\overline{X}|\mathfrak{G}\right)$ (i.e., to calculate the magnitude of their inconsistency in one way or another). Let us denote the inconsistency value by $\epsilon$.

For example, for the case in which all variables $V$ have domain $\mathbb{R}$, we can define $\mathsf{\epsilon }\in \mathbb{R}$ as the integral sum of the difference of the values $\check{Y}$ and $\widehat{Y}$ for each $\overline{\mathfrak{X}}\in \overline{{\mathbb{X}}^n}$:

$$\mathsf{\epsilon }={\displaystyle \sum _{\overline{\mathfrak{X}}\in \overline{{\mathbb{X}}^n}}}\sum _{i=1}^{\left|Y\right|}\left({\check{Y}\left(\overline{\mathfrak{X}}\right|\mathfrak{G})}_i-{\widehat{Y}\left(\overline{\mathfrak{X}}\right|\mathfrak{G})}_i\right)$$

where $\mathfrak{G}\in {\mathbb{G}}^n$.

2.5. Simulation of the Model $\widehat{\mathit{Y}}\left(\overline{\mathit{X}}\right|\mathfrak{G})$ as a Calculation of a Subset of $\widehat{\mathfrak{Y}}\subseteq \widehat{{\mathbb{Y}}^{\mathit{n}}}$ from the Subset $\overline{\mathfrak{X}}\subseteq \overline{{\mathbb{X}}^n}$ and the Parameters $\mathfrak{G}$

The simulation task can be reduced to obtaining or calculating the subset of the unknown values of the dependent variables $\widehat{Y}$ from the subset of the known values of the independent variables $\overline{X}$ and the values of the parameters $\mathfrak{G}$ using a certain model $\widehat{Y}\left(\overline{X}\right|\mathfrak{G})$.

Definition 8. 

Let us define the simulation as the operator

$$\overline{\mathfrak{X}}\stackrel{\widehat{Y}\left(\overline{X}\right|\mathfrak{G})}{\Rightarrow }\widehat{\mathfrak{Y}},$$

(5)

where $\overline{\mathfrak{X}}\subseteq \overline{{\mathbb{X}}^n}$ is a possibly ordered set of unique known values of independent variables, $\widehat{\mathfrak{Y}}\subseteq \widehat{{\mathbb{Y}}^n}$ is the desired set of possibly not unique values of the dependent variables, and $\widehat{Y}\left(\overline{X}\right|\mathfrak{G})$ is a certain model used to obtain the desired $\widehat{\mathfrak{Y}}\in \widehat{{\mathbb{Y}}^n}$ for a given $\overline{\mathfrak{X}}\in \widehat{{\mathbb{X}}^n}$.

For the case where the model is implemented as a set of functions (Formula (3)), the simulation

$$\overline{\mathfrak{X}}\stackrel{{\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^F}{\Rightarrow }\widehat{\mathfrak{Y}}$$

is simply a calculation of the result $\widehat{\mathfrak{Y}}\in \widehat{\mathfrak{Y}}$ for each argument $\overline{\mathfrak{X}}\in \overline{\mathfrak{X}}$:

$$\overline{\mathfrak{X}}\stackrel{\forall \overline{\mathfrak{X}}\in \overline{\mathfrak{X}}\left(\widehat{\mathfrak{Y}}\in \widehat{\mathfrak{Y}}=F\left(\overline{X}|\mathfrak{G}\right)\left(\overline{\mathfrak{X}}\right)\right)}{\Rightarrow }\widehat{\mathfrak{Y}}$$

where

$$\widehat{\mathfrak{Y}}=F\left(\overline{X}|\mathfrak{G}\right)\left(\overline{\mathfrak{X}}\right)$$

which is the operation for calculating $\widehat{\mathfrak{Y}}\in \widehat{{\mathbb{Y}}^n}$ for a given $\overline{\mathfrak{X}}\in \widehat{{\mathbb{X}}^n}$. For a model implemented as a set of substates (Formula (4)), the simulation is a matter of finding all substates for each key $\overline{\mathfrak{X}}\in \overline{\mathfrak{X}}$ and then building the values of $\widehat{\mathfrak{Y}}\in \widehat{\mathfrak{Y}}$ from the found substates

$$\overline{\mathfrak{X}}\stackrel{\forall \overline{\mathfrak{X}}\in \overline{\mathit{X}}\left(\widehat{\mathfrak{Y}}\in \widehat{\mathit{Y}}=\bigcup {\mathfrak{S}}^{\overline{X}|\mathfrak{G}}\left(\overline{\mathfrak{X}}\right)\right)}{\Rightarrow }\widehat{\mathfrak{Y}},$$

(6)

where

$${\mathfrak{S}}^{\overline{X}|\mathfrak{G}}\left(\overline{\mathfrak{X}}\right)={\mathfrak{S}}^{\overline{\mathfrak{X}}|\mathfrak{G}}$$

is the operation for selecting a subset ${\mathfrak{S}}^{\overline{\mathfrak{X}}|\mathfrak{G}}\subseteq {\mathfrak{S}}^{\overline{X}|\mathfrak{G}}$ of substates ${{\mathfrak{S}}^{\mathfrak{X}|\mathfrak{G}}}_j$ with the same key $\mathfrak{X}$.

A simulation can be interactive, i.e., it can react with external events and produce the results to the outside right during the calculation. In the simplest case, an interactive simulation can be represented as a series of simulations

$$\left\{{\overline{\mathfrak{X}}}_i\stackrel{{\widehat{Y}\left(\overline{X}\right|\mathfrak{G})}_i}{\Rightarrow }{\widehat{\mathfrak{Y}}}_i\right\},$$

(7)

of the set of models

$$\left\{{\widehat{Y}\left(\overline{X}\right|\mathfrak{G})}_i\right\}$$

for the corresponding sets of subsets of values of independent variables $\left\{{\overline{\mathfrak{X}}}_i\right\}$ sequentially received during the interaction and the sets of dependent $\left\{{\widehat{\mathfrak{Y}}}_i\right\}$ sequentially returned as simulation results.

3. Graph Modeling

We show how the model $\widehat{Y}\left(\overline{X}\right|\mathfrak{G})$ can be represented as a transition graph and how a simulation can be performed for this representation. We define and prove the rules for constructing a consistent transition graph. Before reading this section, we recommend to check Supplementary S3, which describes transition function concepts. In Section 5 and Supplementary S7, we present a simple example of the construction and simulation of a transition graph.

3.1. The Transition Graph ${\mathit{\Gamma }}^{|\mathfrak{G}}$ and the Simulation Graph ${\gamma }^{|\mathfrak{G}}$

We can join the function ${{\mathsf{\Theta }}^{|\mathfrak{P}}}_j\in {\mathsf{\Theta }}^{|\mathfrak{G}}$ and a set of functions ${{\mathsf{\Theta }}^{|\mathfrak{O}}}_{i,k=1},\dots ,{{\mathsf{\Theta }}^{|\mathfrak{O}}}_{i,k=n}\in {\mathsf{\Theta }}^{|\mathfrak{G}}$ represented as graphs by combining the result nodes

$$\stackrel{{{\mathsf{\Theta }}^{|\mathfrak{O}}}_{i,k=1}}{\to }\grave{\mathrm{S}}:{\grave{\mathbb{S}}}_{i,k=1},\dots ,\stackrel{{{\mathsf{\Theta }}^{|\mathfrak{O}}}_{i,k=n}}{\to }\grave{\mathrm{S}}:{\grave{\mathbb{S}}}_{i,k=n}$$

and the argument nodes

$${\mathrm{S}:\mathbb{S}}_{k=1,j},\dots ,S:{\mathbb{S}}_{k=n,j}\stackrel{{{\mathsf{\Theta }}^{|\mathfrak{O}}}_j}{\to }$$

with intermediate-variable nodes

$$\left(\stackrel{{{\mathsf{\Theta }}^{|\mathfrak{O}}}_{i,k=1}}{\to }{\mathrm{S}}_{k=1}:{\grave{\mathbb{S}}}_{i,k=1},\dots ,\stackrel{{{\mathsf{\Theta }}^{|\mathfrak{O}}}_{i,k=n}}{\to }{\mathrm{S}}_{k=n}:{\grave{\mathbb{S}}}_{i,k=n}\right)\stackrel{{{\mathsf{\Theta }}^{|\mathfrak{O}}}_j}{\to }$$

(see Figure 1).

We continue in the same way to sequentially join the functions included in the same set ${\mathsf{\Theta }}^{|\mathfrak{G}}$ (possibly using the same function more than once); we obtain some DAG (see Figure 2). We call such DAG a transition graph. Also, as an option, we can combine two or more root variables $S_{k,i=1},\dots ,S_{k,i=n}$ that do not have incoming edges, thereby reducing the total number of nodes.

Definition 9. 

We define the transition graph ${\Gamma }^{|\mathfrak{G}}$as a DAG constructed on the set of transition functions ${\mathit{\Theta }}^{|\mathfrak{G}}$ by sequentially joining arbitrary subsets of functions

$${{\Theta }^{|\mathfrak{O}}}_i,{{\Theta }^{|\mathfrak{O}}}_{j,k=1},\dots ,{{\Theta }^{|\mathfrak{O}}}_{j,k=n}\in {\mathit{\Theta }}^{|\mathfrak{G}}$$

and by combining the result node

$${\grave{S}}_i:{\grave{\mathbb{S}}}_i\stackrel{{{\Theta }^{|\mathfrak{O}}}_i}{\leftarrow }$$

and the argument nodes

$$\begin{gathered} S_{k,j,k=1}:{\mathbb{S}}_{k,j,k=1}\stackrel{{{\Theta }^{|\mathfrak{O}}}_{j,k=1}}{\to },\dots \\ \dots ,S_{k,j,k=n}:{\mathbb{S}}_{k,j,k=n}\stackrel{{{\Theta }^{|\mathfrak{O}}}_{j,k=n}}{\to } \end{gathered}$$

such that

$$\begin{gathered} {\grave{\mathbb{S}}}_i\subseteq {\mathbb{S}}_{k,j,k=1},\dots ,{\mathbb{S}}_{k,j,k=n} \\ {\grave{\mathbb{S}}}_i\cap {\mathbb{S}}_{k,j,k=1},\dots ,{\mathbb{S}}_{k,j,k=n}\ne \varnothing \end{gathered}$$

into intermediate variable nodes

$$\stackrel{{{\Theta }^{|\mathfrak{O}}}_i}{\to }S:{\grave{\mathbb{S}}}_i\stackrel{{{\Theta }^{|\mathfrak{O}}}_{j,k=1},\dots ,{{\Theta }^{|\mathfrak{O}}}_{j,k=n}}{\to }$$

Additionally, the root nodes

$$S_{k,i=1}\cup \dots \cup S_{k,i=n}$$

and their domains

$${\mathbb{S}}_{k,i=1}\cap \dots \cap {\mathbb{S}}_{k,i=1}$$

may also be combined.

We note that this definition imposes no restrictions on the graph structure except for its acyclicity (the result of the next joined ${\mathsf{\Theta }}^{|\mathfrak{O}}$ cannot be connected with the argument of any already joined ${\mathsf{\Theta }}^{|\mathfrak{O}}$) and continuity (all nodes of the graph ${\Gamma }^{|\mathfrak{G}}$ are connected by at least one edge).

When we join the transition functions ${\mathsf{\Theta }}^{|\mathfrak{O}}$, we also join the transitions ${\theta }^{|\mathfrak{O}}$ from the equivalent set ${\mathit{\theta }}^{|\mathfrak{O}}\iff {\mathsf{\Theta }}^{|\mathfrak{O}}$, forming a set of more complex DAGs with the same structure as the graph ${\Gamma }^{|\mathfrak{G}}$, but which consist of the substates ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ and transitions ${\theta }^{|\mathfrak{O}}$ (see Figure 3). We call such DAGs simulation graphs.

Definition 10. 

A simulation graph ${\gamma }^{|\mathfrak{G}}$ is defined as the DAG obtained by constructing a transition graph ${\Gamma }^{|\mathfrak{G}}$; it has the same structure as ${\Gamma }^{|\mathfrak{G}}$. The graph ${\gamma }^{|\mathfrak{G}}$consists of constructions of the form

$$\stackrel{{{\theta }^{|\mathfrak{O}}}_i}{\to }{{\mathfrak{S}}^{\mathfrak{X}}}_{q,i}\stackrel{{{\theta }^{|\mathfrak{O}}}_{j,k=1},\dots ,{{\theta }^{|\mathfrak{O}}}_{j,k=n}}{\to }$$

which results from joining the transitions

$${{\theta }^{|\mathfrak{O}}}_i\in {{\mathit{\theta }}^{|\mathfrak{O}}}_i\iff {{\Theta }^{|\mathfrak{O}}}_i$$

and

$$\begin{gathered} {{\theta }^{|\mathfrak{O}}}_{j,k=1}\in {{\mathit{\theta }}^{|\mathfrak{O}}}_{j,k=1}\iff \\ \iff {{\Theta }^{|\mathfrak{O}}}_{j,k=1},\dots ,{{\theta }^{|\mathfrak{O}}}_{j,k=n}\in {{\mathit{\theta }}^{|\mathfrak{O}}}_{j,k=n}\iff \\ \iff {{\Theta }^{|\mathfrak{O}}}_{j,k=n} \end{gathered}$$

belonging to the set of joined functions

$${{\Theta }^{|\mathfrak{O}}}_i,{{\Theta }^{|\mathfrak{O}}}_{j,k=1},\dots ,{{\Theta }^{|\mathfrak{O}}}_{j,k=n}\in {\mathit{\Theta }}^{|\mathfrak{G}}$$

such that

$$\begin{gathered} {{\grave{\mathfrak{S}}}^{\mathfrak{X}}}_{q,i}\stackrel{{{\theta }^{|\mathfrak{O}}}_i}{\leftarrow }={{\mathfrak{S}}^{\mathfrak{X}}}_{q,j,k=1}\stackrel{{{\theta }^{|\mathfrak{O}}}_{j,k=1}}{\to }=,\dots \\ \dots ,={{\mathfrak{S}}^{\mathfrak{X}}}_{q,j,k=n}\stackrel{{{\theta }^{|\mathfrak{O}}}_{j,k=n}}{\to } \end{gathered}$$

We note that all ${\mathsf{\gamma }}^{|\mathfrak{G}}$ will have a structure exactly matching ${\Gamma }^{|\mathfrak{G}}$. According to the definition of ${\mathsf{\gamma }}^{|\mathfrak{G}}$, during the construction of ${\Gamma }^{|\mathfrak{G}}$, incomplete graphs of ${\mathsf{\gamma }}^{|\mathfrak{G}}$ with structures not coinciding with that of ${\Gamma }^{|\mathfrak{G}}$ will be discarded. Thus, the substates ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ included in the discarded graphs ${\mathsf{\gamma }}^{|\mathfrak{G}}$ will also be removed from the domains $\mathbb{S}$ of the variables $S$ included in the constructed ${\Gamma }^{|\mathfrak{G}}$.

Let us denote some arbitrary set of graphs $\left\{{\mathsf{\gamma }}^{|\mathfrak{G}}\right\}$ by ${\mathsf{\gamma }}^{|\mathfrak{G}}$. According to the definitions of the graphs ${\Gamma }^{|\mathfrak{G}}$ and ${\mathsf{\gamma }}^{|\mathfrak{G}}$, each of the substates ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ from the domains $\mathbb{S}$ of the variable nodes $\mathrm{S}$ will belong to one of the simulation graphs ${\mathsf{\gamma }}^{|\mathfrak{G}}$. All ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ terms that do not belong to any ${\mathsf{\gamma }}^{|\mathfrak{G}}$ will be discarded during the construction of ${\Gamma }^{|\mathfrak{G}}$, along with the incomplete ${\mathsf{\gamma }}^{|\mathfrak{G}}$.

Thus, we can represent the graph ${\Gamma }^{|\mathfrak{G}}$ as an equivalent set of graphs ${\mathsf{\gamma }}^{|\mathfrak{G}}$. We will denote such a set as ${\mathsf{\gamma }}^{|\mathfrak{G}}\iff {\Gamma }^{|\mathfrak{G}}$; this set will include all ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ from all domains $\mathbb{S}$:

$$\bigcup \mathbb{S}\left({\Gamma }^{|\mathfrak{G}}\right)={\displaystyle \bigcup _{{\mathsf{\gamma }}^{|\mathfrak{G}}\in {\mathsf{\gamma }}^{|\mathfrak{G}}\iff {\Gamma }^{|\mathfrak{G}}}}{\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)$$

where $\mathbb{S}\left({\Gamma }^{|\mathfrak{G}}\right)$ is the set of domains $\mathbb{S}$ of the variable nodes $\mathrm{S}$ from the graph ${\Gamma }^{|\mathfrak{G}}$ and ${\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)$ is the set of all ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ belonging to ${\mathsf{\gamma }}^{|\mathfrak{G}}$, which is consistent:

$$\exists {\mathfrak{S}}^{X|\mathfrak{G}}\left({\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)={\mathfrak{S}}^{X|\mathfrak{G}}\right)$$

Moreover, all simulation graphs ${\mathsf{\gamma }}^{|\mathfrak{G}}$ will share the same set of parameters $\mathfrak{G}$ split into parts $\mathfrak{O}$.

Let us index each node from the set $S\left({\Gamma }^{|\mathfrak{G}}\right)$ with the depth index

$$d=\mathit{max}\left(len\left(\left\{{\mathbf{S}}_{root}\dots S_d\right\}\right)\right),$$

where $d\in \mathbb{N}$, $\left\{{\mathbf{S}}_{root}\dots S_d\right\}$ is the set of all possible paths from any root node $S_{root}\in {\mathbf{S}}_{root}$ (i.e., the node that has no incoming edges) to the indexed node $S_d$ and $len\left(\right)$ is the length of the path (the number of edges in the path). Let us also index all transition functions ${\mathsf{\Theta }}^{|\mathfrak{O}}$ with the same index $d$ same as the index of the result node

$$\dots \stackrel{{{\mathsf{\Theta }}^{|\mathfrak{O}}}_d}{\to }{S}_d$$

Thus, each root node of $S_{root}$ will have $d=0,$ and each leaf node $S_{leaf}$ (i.e., such that it has no outgoing edges) will have $d=n$, where $n$ is the minimum number of edges to the nearest root node $S_{d=0}$.

3.2. Construction of a Consistent Transition Graph ${\Gamma }^{|\mathfrak{G}}$

From a practical viewpoint, we want to be able to construct transitions ${\Gamma }^{|\mathfrak{G}}$ from a set of predefined transition functions ${\mathsf{\Theta }}^{|\mathfrak{G}}$—in other words, to build models from a set of ready-made functional blocks, similar to the Simulink software (Version R2024b). It is necessary to guarantee the consistency of ${\Gamma }^{|\mathfrak{G}}$ at the local level, i.e., at the level of individual functions ${\mathsf{\Theta }}^{|\mathfrak{P}}$, to implement this approach successfully.

We can represent some simulation graph ${\mathsf{\gamma }}^{|\mathfrak{G}}$ as the set of directional paths (dipaths) covering all substates ${{\mathfrak{S}}^{\mathfrak{X}}}_q\in {\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)$ and transitions ${\theta }^{|\mathfrak{O}}\in \theta \left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)$.

Definition 11. 

Let us define a dipath

$${\mathfrak{p}}^{|\mathfrak{G}}≔{{\mathfrak{S}}^{\mathfrak{X}}}_{q,l=0}\stackrel{{{\theta }^{|\mathfrak{O}}}_{l=1}}{\to }\dots \stackrel{{{\theta }^{|\mathfrak{O}}}_{l=n}}{\to }{{\mathfrak{S}}^{\mathfrak{X}}}_{q,l=n}$$

in the simulation graph ${\gamma }^{|\mathfrak{G}}\in {\mathit{\gamma }}^{|\mathfrak{G}}\iff {\Gamma }^{|\mathfrak{G}}$, where ${{\mathfrak{S}}^{\mathfrak{X}}}_{q,l=0}\in {\mathbb{S}}_{l=0}$, ${{\mathfrak{S}}^{\mathfrak{X}}}_{q, l=n}\in {\mathbb{S}}_{l=n}$, $l\in \mathbb{N}$ is the index of the node, which is in the dipath, such that $l=0$ corresponds to some root node ${{\mathfrak{S}}^{\mathfrak{X}}}_{q,root}$, and $l=n$ corresponds to some leaf node ${{\mathfrak{S}}^{\mathfrak{X}}}_{q,leaf}$ in the graph ${\gamma }^{|\mathfrak{G}}$, ${{\mathfrak{S}}^{\mathfrak{X}}}_{q,l=0},\dots ,{{\mathfrak{S}}^{\mathfrak{X}}}_{q,l=n}\in {\mathfrak{S}}^{\mathfrak{X}}\left({\gamma }^{|\mathfrak{G}}\right)$, ${{\theta }^{|\mathfrak{O}}}_{l=1},\dots ,{{\theta }^{|\mathfrak{O}}}_{l=n}\in \theta \left({\gamma }^{|\mathfrak{G}}\right)$, ${\mathbb{S}}_{l=0},\dots ,{\mathbb{S}}_{l=n}\in \mathbb{S}\left({\Gamma }^{|\mathfrak{G}}\right)$ , with ${\mathfrak{S}}^{\mathfrak{X}}\left({\mathfrak{p}}^{|\mathfrak{G}}\right)\subseteq {\mathfrak{S}}^{\mathfrak{X}}\left({\gamma }^{|\mathfrak{G}}\right)$.

We denote some arbitrary set of paths by ${\mathfrak{p}}^{|\mathfrak{G}}$, which is not necessarily related to the same graph ${\mathsf{\gamma }}^{|\mathfrak{G}}$.

The set of paths ${\mathfrak{p}}^{|\mathfrak{G}}$ can be equivalent to the graph ${\mathsf{\gamma }}^{|\mathfrak{G}}$ if the paths in this set contain all substates ${{\mathfrak{S}}^{\mathfrak{X}}}_q\in {\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)$ and transitions ${\theta }^{|\mathfrak{O}}\in \theta \left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)$:

$$\begin{gathered} {\mathfrak{p}}^{|\mathfrak{G}}\iff {\mathsf{\gamma }}^{|\mathfrak{G}}\Rightarrow {\displaystyle \bigcup _{{\mathfrak{p}}^{|\mathfrak{G}}\ni {\mathfrak{p}}^{|\mathfrak{G}}}}{\mathfrak{S}}^{\mathfrak{X}}\left({\mathfrak{p}}^{|\mathfrak{G}}\right)= \\ ={\mathfrak{S}}^{\mathfrak{X}}\left({{\mathsf{\gamma }}^{|\mathfrak{G}}}_j\right)\bigwedge {\displaystyle \bigcup _{{\mathfrak{p}}^{|\mathfrak{G}}\ni {\mathfrak{p}}^{|\mathfrak{G}}}}\theta \left(\mathfrak{p}\left({{\mathsf{\gamma }}^{|\mathfrak{G}}}_j\right)\right)=\theta \left({{\mathsf{\gamma }}^{|\mathfrak{G}}}_j\right) \end{gathered}$$

In order to guarantee the consistency condition

$$\forall {\mathsf{\gamma }}^{|\mathfrak{G}}\in {\mathsf{\gamma }}^{|\mathfrak{G}}\iff {\Gamma }^{|\mathfrak{G}}\left({\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)\subseteq {\mathfrak{S}}^{X|\mathfrak{G}}\right)$$

for the graph ${\Gamma }^{|\mathfrak{G}}$ (i.e., to guarantee that each of the simulation graphs ${\mathsf{\gamma }}^{|\mathfrak{G}}$ described by ${\Gamma }^{|\mathfrak{G}}$ will not contain any inconsistent substates), the graph ${\Gamma }^{|\mathfrak{G}}$ must meet the following two restrictions:

• For each graph ${{\mathsf{\gamma }}^{|\mathfrak{G}}}_{\mathrm{j}}\in {\mathsf{\gamma }}^{|\mathfrak{G}}\iff {\mathsf{\Gamma }}^{|\mathfrak{G}}$, each substate ${{\mathfrak{S}}^{\mathfrak{X}}}_{\mathrm{q},\mathrm{j}}\in {\mathfrak{S}}^{\mathfrak{X}}\left({{\mathsf{\gamma }}^{|\mathfrak{G}}}_{\mathrm{j}}\right),{\mathfrak{S}}^{\mathfrak{X}}\left({{\mathfrak{p}}^{|\mathfrak{G}}}_{\mathrm{j}}\right)$ (i.e., located on one of all possible paths ${{\mathfrak{p}}^{|\mathfrak{G}}}_{\mathrm{j}}$) must have a unique key $\mathfrak{X}\subseteq {{\mathfrak{S}}^{\mathfrak{X}}}_{\mathrm{q},\mathrm{j}}$ regarding the ${{\mathfrak{p}}^{|\mathfrak{G}}}_{\mathrm{j}}$.
• For each graph ${\mathsf{\gamma }}^{|\mathfrak{G}}\in {\mathsf{\gamma }}^{|\mathfrak{G}}\iff {\mathsf{\Gamma }}^{|\mathfrak{G}}$, the values $\mathfrak{y}\in \mathbb{y}$ of some variable $\mathrm{y}:\mathbb{y}\in \mathrm{Y}$ should only belong to the set of substates ${{\mathfrak{S}}^{\mathfrak{X}}}_{\mathrm{q},\mathrm{j}}\in {\mathfrak{S}}^{\mathfrak{X}}\left({{\mathsf{\gamma }}^{|\mathfrak{G}}}_{\mathrm{j}}\right)$ such that there exists in ${\mathsf{\gamma }}^{|\mathfrak{G}}$ at least one path ${\mathfrak{p}}^{|\mathfrak{G}}\in {\mathfrak{p}}^{|\mathfrak{G}}\iff {\mathsf{\gamma }}^{|\mathfrak{G}}$, including all of these substates.

At the local level (i.e., without studying the entire graph ${\Gamma }^{|\mathfrak{G}}$), the above restrictions can be met by applying the following construction principles (Supplementary S4):

I.

The set of keys ${\mathbb{X}}^{\mathrm{n}}$ must be linearly ordered.

II.

Each transition function

$$\left({S:\mathbb{S}}_{k=1},\dots ,{S:\mathbb{S}}_{k=n}\right)\stackrel{{\Theta }^{|\mathfrak{O}}}{\to }\grave{S}:\grave{\mathbb{S}}$$

(where ${\Theta }^{|\mathfrak{O}}\in \Theta \left({\Gamma }^{|\mathfrak{G}}\right)$) for each transition

$$\left({{\mathfrak{S}}^{\mathfrak{X}}}_{q,j,k=1},\dots ,{{\mathfrak{S}}^{\mathfrak{X}}}_{q,j,k=n}\right)\stackrel{{{\theta }^{|\mathfrak{O}}}_j}{\to }{{\grave{\mathfrak{S}}}^{\mathfrak{X}}}_{q,j}$$

(where ${{\theta }^{|\mathfrak{O}}}_j\in \theta \left({{\mathfrak{p}}^{|\mathfrak{G}}}_j\right),{\mathit{\theta }}^{|\mathfrak{O}}\iff {\Theta }^{|\mathfrak{O}}$) in some graph ${{\gamma }^{|\mathfrak{G}}}_j\in {\mathit{\gamma }}^{|\mathfrak{G}}\iff {\Gamma }^{|\mathfrak{G}}$ must generate the resulting substate ${{\grave{\mathfrak{S}}}^{\mathfrak{X}}}_{q,j}\in \grave{\mathbb{S}},{\mathfrak{S}}^{\mathfrak{X}}\left({{\gamma }^{|\mathfrak{G}}}_j\right)$ such that its key ${\mathfrak{X}}_{q,j}\subseteq {{\grave{\mathfrak{S}}}^{\mathfrak{X}}}_{q,j}$ will always satisfy the conditions

$${\mathfrak{X}}_{q,j}>\mathit{max}\left({\mathfrak{X}}_{q,j,k=1},\dots ,{\mathfrak{X}}_{q,j,k=n}\right)$$

or

$${\mathfrak{X}}_{q,j}<\mathit{min}\left({\mathfrak{X}}_{q,j,k=1},\dots ,{\mathfrak{X}}_{q,j,k=n}\right)$$

where

$${\mathfrak{X}}_{q,j,k}\subseteq {{\mathfrak{S}}^{\mathfrak{X}}}_{q,j,k}\in {\mathbb{S}}_k,{\mathfrak{S}}^{\mathfrak{X}}\left({{\gamma }^{|\mathfrak{G}}}_j\right)$$

III.

For each variable $y:\mathbb{y}\in Y$, its values $\mathfrak{y}\in \mathbb{y}$ must belong to no more than one root node ${S:\mathbb{S}}_{l=0}$:

$$\forall y:\mathbb{y}\in Y\left(\left|\left\{{S:\mathbb{S}}_{l=0}\in S\left({\Gamma }^{|\mathfrak{G}}\right)|\exists \mathfrak{y}\in \mathbb{y},\mathfrak{y}\left({\mathbb{S}}_{l=0}\right)\right\}\right|\le 1\right)$$

where

$$\begin{gathered} \mathfrak{y}\left(\mathbb{S}\right)≔\bigcup \mathfrak{S}\left(\mathbb{S}\right) \\ \mathfrak{S}\left(\mathbb{S}\right)≔\left\{{\mathfrak{S}}_q|{\mathfrak{S}}_q\subset {{\mathfrak{S}}^{\mathfrak{X}}}_q\in \mathbb{S}\right\} \end{gathered}$$

(i.e., the set of all $\mathfrak{y}$ values in all substates ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ form the domain of the variable $\mathbb{S}$).

IV.

If, for some node ${S:\mathbb{S}}_i\in S\left({\Gamma }^{|\mathfrak{G}}\right)$ and some variable $y:\mathbb{y}\in Y$ the condition $\exists \mathfrak{y}\in \mathbb{y},\mathfrak{y}\left({\mathbb{S}}_i\right)$ is true, then either the node $S_i$ must be a root, or there must be a transition function

$$\left(\dots ,{S:\mathbb{S}}_{i,k=0},\dots ,{S:\mathbb{S}}_{i,k=n},\dots \right)\stackrel{{{\Theta }^{|\mathfrak{O}}}_i}{\to }{\grave{S}}_i$$

with one or more arguments ${S:\mathbb{S}}_{i,k}$ for which the condition $\exists \mathfrak{y}\in \mathbb{y},\mathfrak{y}\left({\mathbb{S}}_i\right)$ is true and in the graph ${\Gamma }^{|\mathfrak{G}}$ there exists a chain

$$S_{i,k=0}\stackrel{{{\Theta }^{|\mathfrak{O}}}_{i,k=1}}{\to },\dots ,\stackrel{{{\Theta }^{|\mathfrak{O}}}_{i,k=n}}{\to }{S}_{i,k=n}$$

that includes all $S_{i,k}$. Moreover, for the last argument $S_{i,k=n}$ in the chain, there should not be another function

$$\left(\dots ,S_{i,k=n},\dots \right)\stackrel{{{{\Theta }^{|\mathfrak{O}}}_i}^{\prime }}{\to }{{\grave{S}}_i}^{\prime }$$

for which the condition $\exists \mathfrak{y}\in \mathbb{y},\mathfrak{y}\left({{\grave{S}}_i}^{\prime }\right)$ is true.

In practice, principle (I) can be easily implemented since linearly ordered sets are common. For example, time, speed, etc., can be represented using variables with ℝ. Next, if the domains of all independent variables are in linear order, then the set of keys ${\mathbb{X}}^n$ will also be in linear order.

Principle (II) says that the key–value constantly increases or decreases as the simulation graph ${\mathsf{\gamma }}^{|\mathfrak{G}}$ is calculated. This approach can be applied, for example, to physical models, where independent variables are usually rational numbers that increase or decrease over the simulation.

Principle (III) holds if the graph ${\Gamma }^{|\mathfrak{G}}$ has a single root node ${S:\mathbb{S}}_{l=0}\in S\left({\Gamma }^{|\mathfrak{G}}\right)$ such that in each graph ${{\mathsf{\gamma }}^{|\mathfrak{G}}}_j$ there will be only one substate ${{\mathfrak{S}}^{\mathfrak{X}}}_{q,j,l=0}\in {\mathbb{S}}_{l=0},$ thereby excluding the possibility that the values $\mathfrak{y}\in \mathbb{y}$ of the same variable $y:\mathbb{y}\in Y$ are in different substates ${{\mathfrak{S}}^{\mathfrak{X}}}_{q,j,l=0}$.

Another approach to implementing (III) is for each root node ${\mathrm{S}:\mathbb{S}}_{l=0}$ to include $\mathfrak{y}\in \mathbb{y}$ values only from its own unique set of variables ${\mathit{y}}_1,\dots ,{\mathit{y}}_n\subset Y$, such that

$$\forall {\mathit{y}}_i,{\mathit{y}}_j\left(i\ne j,{\mathit{y}}_i\bigcap {\mathit{y}}_j=\mathrm{\varnothing }\right)$$

This approach, for example, is convenient in the graphs ${\Gamma }^{|\mathfrak{G}}$ used for interactive simulation, where each next node $S_{l=0}$ reflects the next input of data from outside the simulation.

In practice, a simple way to implement principle (IV) is to check whether adding the next function ${\mathsf{\Theta }}^{|\mathfrak{O}}$ to form $\grave{S}$ does not include variables that are already in the results of the functions that have joint arguments $S$ with ${\mathsf{\Theta }}^{|\mathfrak{O}}$. For example, if there are nodes $S_{k=1}$ and $S_{k=2}$ for which $y\left(S_{k=1}\right)=\left[a,b\right]$ and $y\left(S_{k=2}\right)=\left[x,y\right]$, where

$$y\left(S:\mathbb{S}\right)≔\left\{y:\mathbb{y}\in Y|\exists \mathfrak{y}\in \mathbb{y},\mathfrak{y}\left(\mathbb{S}\right)\right\}$$

and these nodes are the arguments of some function

$$\left(S_{k=1},S_{k=2}\right)\stackrel{{{\mathsf{\Theta }}^{|\mathfrak{O}}}_{j=1}}{\to }{\grave{S}}_{j=1}$$

for which the result is $y\left({\grave{S}}_{j=1}\right)=\left[a,x\right]$, then we can add only a function

$$\left(S_{k=1},S_{k=2}\right)\stackrel{{{\mathsf{\Theta }}^{|\mathfrak{O}}}_{j=1}}{\to }{\grave{S}}_{j=1}$$

for which $y\left({\grave{S}}_{j=2}\right)=\left[b,y\right]$ and either $y\left({\grave{S}}_{j=2}\right)=\left[y\right]$ or $y\left({\grave{S}}_{j=2}\right)=\left[b\right]$, but not $y\left({\grave{S}}_{j=2}\right)=\left[a,b,y\right]$.

3.3. Computability of the Simulation Graph ${\mathit{\gamma }}^{|\mathfrak{G}}$ and the Initial Set of Substates ${\mathfrak{S}}^{\prime }$

In practice, we will need to find some specific simulation graph ${\mathsf{\gamma }}^{|\mathfrak{G}}\in {\mathsf{\gamma }}^{|\mathfrak{G}}\iff {\Gamma }^{|\mathfrak{G}}$ from some known set of consistent substates ${\mathfrak{S}}^{X|\mathfrak{G}}\subseteq {\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)$ associated with the nodes $S$ of the graph ${\Gamma }^{|\mathfrak{G}}$. We will call ${\mathfrak{S}}^{X|\mathfrak{G}}$ the initial set of substates.

Definition 12. 

Let us define the initial set of substates

$${\mathfrak{S}}^{\prime }≔\left\{S={{\mathfrak{S}}^{\mathfrak{X}}}_q\right\}$$

associated with the specific nodes $S$  of the graph ${\Gamma }^{|\mathfrak{G}}$  such that

$$\exists !{\gamma }^{|\mathfrak{G}}\left({\mathfrak{S}}^{\prime }\subseteq {\mathfrak{S}}^{\mathfrak{X}}\left({\gamma }^{|\mathfrak{G}}\right)\right),$$

(8)

where $S:\mathbb{S}\in S\left({\Gamma }^{|\mathfrak{G}}\right)$, ${{\mathfrak{S}}^{\mathfrak{X}}}_q\in \mathbb{S},{\mathfrak{S}}^{\mathfrak{X}}\left({\gamma }^{|\mathfrak{G}}\right)$, ${\gamma }^{|\mathfrak{G}}\in {\mathit{\gamma }}^{|\mathfrak{G}}\iff {\Gamma }^{|\mathfrak{G}}$.

The search for a specific graph ${\mathsf{\gamma }}^{|\mathfrak{G}}$ with some set ${\mathfrak{S}}^{\prime }$ can be imperatively represented as a calculation of all functions ${\mathsf{\Theta }}^{|\mathfrak{O}}\in \mathsf{\Theta }\left({\Gamma }^{|\mathfrak{G}}\right),$ using $\mathfrak{S}\prime$ as the initial arguments for these functions.

Note that the definition requires that $\mathfrak{S}\prime$ be a subset of the one and only one set ${\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)$. However, in the general case, some ${\mathfrak{S}}^{X|\mathfrak{G}}$ can be a subset of more than one ${\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)$. In this case, in the imperative representation of the search, a single graph ${\mathsf{\gamma }}^{|\mathfrak{G}}$ cannot be calculated from such ${\mathfrak{S}}^{X|\mathfrak{G}}$ since for some or all functions ${\mathsf{\Theta }}^{|\mathfrak{O}}\in \mathsf{\Theta }\left({\Gamma }^{|\mathfrak{G}}\right)$, not all arguments can be defined.

By representing the search for a specific ${\mathsf{\gamma }}^{|\mathfrak{G}}$ in the form of a calculation of the functions ${\mathsf{\Theta }}^{|\mathfrak{O}}\in \mathsf{\Theta }\left({\Gamma }^{|\mathfrak{G}}\right)$, we notice that all ${\mathsf{\Theta }}^{|\mathfrak{O}}$ will be calculated only if the values of all root nodes $S_{root}\in S\left({\Gamma }^{|\mathfrak{G}}\right)$ are known or can be obtained in some way. Thus, $\mathfrak{S}\prime$ is a subset of the unique set ${\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)$ (Formula (8)) if and only if, for each initial node $S_{root}\in S\left({\Gamma }^{|\mathfrak{G}}\right)$, there exists a path

$$S_{root}\stackrel{{{\mathsf{\Theta }}^{|\mathfrak{O}}}_1}{\to }\dots \stackrel{{{\mathsf{\Theta }}^{|\mathfrak{O}}}_n}{\to }{S}_{def}$$

where $S_{def}\in S\left({\Gamma }^{|\mathfrak{G}}\right),S\left(\mathfrak{S}\prime \right)$ is a node whose value is defined in $\mathfrak{S}\prime$, and all functions ${{\mathsf{\Theta }}^{|\mathfrak{O}}}_i$ are this reversible (Supplementary S5).

Another important property of this approach is the glitching freedom described in [21,22]. Since only one graph ${\mathsf{\gamma }}^{|\mathfrak{G}}$ is to be found, there never exist inconsistent substates ${{\mathfrak{S}}^{\mathfrak{X}}}_q$.

3.4. Representation of the Dependence of Y on X in the Form of a Simulation Graph ${\mathit{Y}=⟨{\mathit{\Gamma }}^{|\mathfrak{G}},\mathfrak{S}\prime ⟩}^{\mathit{X}}$ and a Graph Model ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^{\Gamma }$

The dependence of the dependent variables $Y$ upon the independent variables $X$ can be represented as a tuple of the transition graph ${\Gamma }^{|\mathfrak{G}}$, and the set of initial substates $\mathfrak{S}\prime$ with given values of the parameters $\mathfrak{G}$.

Definition 13. 

Let us define a pair

$$\begin{gathered} Y={⟨{\Gamma }^{|\mathfrak{G}},{\mathfrak{S}}^{\prime }⟩}^X≔ \\ ≔{\bigcup }_{\mathfrak{X}\in {\mathbb{X}}^n}{\mathfrak{S}}^{\mathfrak{X}}\left(\gamma \left({\Gamma }^{|\mathfrak{G}}|{\mathfrak{S}}^{\prime }\right)\right)\left(X\right) \end{gathered}$$

representing the dependence of the variables $Y$  on the variables $X$, as parametrized by the values of $\mathfrak{G}$, where

$${\gamma }^{|\mathfrak{G}}=\gamma \left({\Gamma }^{|\mathfrak{G}}|{\mathfrak{S}}^{\prime }\right)$$

is a simulation graph ${\gamma }^{|\mathfrak{G}}\in {\mathit{\gamma }}^{|\mathfrak{G}}\iff {\Gamma }^{|\mathfrak{G}}$  found for a given ${\Gamma }^{|\mathfrak{G}}$, ${\mathfrak{S}}^{\prime }$  and $\mathfrak{G}$, and

$$\mathfrak{Y}={\bigcup }_{\mathfrak{X}\in X}{\mathfrak{S}}^{X|\mathfrak{G}}\left(\mathfrak{X}\right)$$

is the merging operation of the substates ${{\mathfrak{S}}^{\mathfrak{X}}}_q\in {\mathfrak{S}}^{X|\mathfrak{G}}$ with the same key $\mathfrak{X}\in {\mathbb{X}}^n$ into the set of values $\mathfrak{Y}\in {\mathbb{Y}}^n$.

The representation $Y={⟨{\Gamma }^{|\mathfrak{G}},\mathfrak{S}\prime ⟩}^X$ can be used to implement the model $\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)$; we call this implementation a graph model and denote it as

$${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^{\mathsf{\Gamma }}={⟨{\Gamma }^{|\mathfrak{G}},\mathfrak{S}\prime ⟩}^{\overline{X}}=\widehat{Y},$$

(9)

This implementation is similar to a representation in the form of a set of substates (Formula (4)), except that the set ${\mathfrak{S}}^{\overline{X}|\mathfrak{G}}$ must first be found as

$${\mathfrak{S}}^{\overline{X}|\mathfrak{G}}={\mathfrak{S}}^{\mathfrak{X}}\left(\mathsf{\gamma }\left({\Gamma }^{|\mathfrak{G}}|{\mathfrak{S}}^{\prime }\right)\right)$$

3.5. Simulation of the Graph Model ${\widehat{\mathit{Y}}\left(\overline{\mathit{X}}|\mathfrak{G}\right)}^{\mathit{\Gamma }}$ as a Calculation of a Subset of the Values $\widehat{\mathfrak{Y}}\subseteq \widehat{{\mathbb{Y}}^{\mathit{n}}}$ on the Subset $\overline{\mathfrak{X}}\subseteq \overline{{\mathbb{X}}^{\mathit{n}}}$ and the Parameters G

For the graph model ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^{\mathsf{\Gamma }}$, we can define the simulation as the operator

$$\overline{\mathfrak{X}}\stackrel{{\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^{\mathsf{\Gamma }}}{\Rightarrow }\widehat{\mathfrak{Y}},$$

(10)

where $\overline{\mathfrak{X}}\subseteq \overline{{\mathbb{X}}^n}$ is the subset of known values of the set of independent variables $\overline{X}\subset V$ and $\widehat{\mathfrak{Y}}\subseteq \widehat{{\mathbb{Y}}^n}$ is the subset of unknown values of dependent variables $\widehat{Y}\subset V$.

The simulation can be implemented as a search for the simulation graph ${\mathsf{\gamma }}^{|\mathfrak{G}}\in {\mathsf{\gamma }}^{|\mathfrak{G}}\iff {\Gamma }^{|\mathfrak{G}}$ for a given initial set ${\mathfrak{S}}^{\prime }$ and a set $\mathfrak{G}$. Then, from the set ${\mathfrak{S}}^{\overline{X}|\mathfrak{G}},$ $\widehat{\mathfrak{Y}}\in \widehat{\mathfrak{Y}}$ is constructed for each $\overline{\mathfrak{X}}\in \overline{\mathfrak{X}}$ as follows:

$$\overline{\mathfrak{X}}\stackrel{\forall \overline{\mathfrak{X}}\in \overline{\mathfrak{X}}\left(\widehat{\mathfrak{Y}}\in \widehat{\mathfrak{Y}}=\bigcup {\mathfrak{S}}^{\mathfrak{X}}\left(\mathsf{\gamma }\left({\Gamma }^{|\mathfrak{G}}|{\mathfrak{S}}^{\prime }\right)\right)\left(\overline{\mathfrak{X}}\right)\right)}{\Rightarrow }\widehat{\mathfrak{Y}}$$

In the simulation problem, we can significantly optimize the search for the graph ${\mathsf{\gamma }}^{|\mathfrak{G}}$. Since the set $\overline{\mathfrak{X}}$ is usually much smaller than $\overline{{\mathbb{X}}^n}$, we can search or calculate only a part of the substates from ${\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)$, which contain all the required keys $\overline{\mathfrak{X}}\in \overline{\mathfrak{X}}$:

$${\mathfrak{S}}^{\overline{\mathfrak{X}}}=\left\{{{\mathfrak{S}}^{\mathfrak{X}}}_q\in {\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)|\mathfrak{X}\left({{\mathfrak{S}}^{\mathfrak{X}}}_q\right)\in \overline{\mathfrak{X}}\right\},$$

(11)

We can also optimize $\mathfrak{S}\prime$ by including substates that are as close as possible (from the point of view of the distance in the graph ${\Gamma }^{|\mathfrak{G}}$) to substates from the desired ${\mathfrak{S}}^{\overline{\mathfrak{X}}}$ or even equivalent to these substates. This will reduce the number of calculations not related to the search for ${\mathfrak{S}}^{\overline{\mathfrak{X}}}$ (see Figure 4).

For the graphical model ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^{\mathsf{\Gamma }}$, an interactive simulation can also be performed. In the simplest case, this requires many models $\left\{{{\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^{\mathsf{\Gamma }}}_i\right\}$; however, a more interesting and optimal approach is to undertake interactive manipulation of the values of the nodes $\mathrm{S}\in S\left({\Gamma }^{|\mathfrak{G}}\right)$ when imperative representations (sequential calculation of the functions ${\mathsf{\Theta }}^{|\mathfrak{P}}$) of the operation $\mathsf{\gamma }\left({\Gamma }^{|\mathfrak{G}}|{\mathfrak{S}}^{\prime }\right)$ are used. This approach was explored briefly in [23].

Two patterns are possible here:

• Push pattern:
  This pattern can help synchronize the simulation with some external processes (for example, to synchronize with real-time). The essence of the pattern is that some function ${\Theta }^{|\mathfrak{O}}$ cannot be calculated until all its arguments $S$ are defined; thus, we can locally pause the simulation, leaving some of the root nodes $S_{root}\in S\left({\Gamma }^{|\mathfrak{G}}\right)$ uninitialized. We can then continue it by defining these nodes.
• Pool pattern:
  This pattern can be used to implement an asynchronous simulation reaction to some external events—for example, to respond to user input. As in the previous case, some $S_{root}\in S\left({\Gamma }^{|\mathfrak{G}}\right)$ remain uninitialized. However, the simulation does not stop there. Their values are constructed as needed to calculate the next ${\Theta }^{|\mathfrak{O}}$. Using this approach, it is figuratively possible to imagine that undefined $S_{root}$ is computed by some set of unknown transition functions, possibly also combined into a transition graph. In other words, there is some “shadow” or “unknown” part of the graph ${\Gamma }^{|\mathfrak{G}}$ and, as a result of its calculation, the $S_{root}$ is initialized (see Figure 5).

4. Logical Processors

We show how the graph model ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^{\mathsf{\Gamma }}$ can be implemented using the reactive-stream paradigm in the form of a computational graph. We also show how the simulation can be evaluated on this graph and offer ways to optimize it. Additionally, in Supplementary S8, we implement a simple computational graph and perform a simulation with it.

4.1. Reactive Streams and Graph Model ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^{\Gamma }$

The concept of reactive streams was formulated in 2014 in manifest [10,11,12] and extended by AKKA library developers with tools for composing reactive streams into computational graphs [13,24], which are already widely used in practice [9,25,26,27]. The graph nodes are logical processors, and the edges are the channels representing the stream of messages that transmit data; each of the processors transforms the messages in some way. Generally, reactive streams are an implementation of the well-known dataflow-programming paradigm [25].

This chapter will follow the approach described in (i.e., we will compose a computational system from small blocks that process data streams) [22,28,29]. However, we will use reactive streams to do all the hard work for us to distribute computation and load balancing.

We will denote messages (values) by $M$, logical processors (reactors) by $LP$, channels connecting the processors by $D$, and the numeral graph by $C$.

We can transform an arbitrary graphical model ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^{\mathsf{\Gamma }}$ (Formula (9)) into a computational graph $C$:

• To represent each substate ${{\mathfrak{S}}^{\mathfrak{X}}}_q\in {\mathfrak{S}}^{\mathfrak{X}}\left({\Gamma }^{|\mathfrak{G}}\right)$ with the message $M=\left[{{\mathfrak{S}}^{\mathfrak{X}}}_q\right]$.
• To replace all ${\Theta }^{|\mathfrak{P}}\in \Theta \left({\Gamma }^{|\mathfrak{G}}\right)$ for which ${S\prime }_{k=1},\dots ,{S\prime }_{k=n}\in S\left(\mathfrak{S}\prime \right)$ with equivalent processors ${LP}^{eval}$:

  $$\begin{gathered} {S^{\prime }}_{k=1}\Rightarrow D_{k=1},\dots ,{S^{\prime }}_{k=n}\Rightarrow \\ \Rightarrow D_{k=n}\stackrel{{\Theta }^{|\mathfrak{P}}\Rightarrow {LP}^{eval}}{\to }\grave{S}\Rightarrow D \end{gathered}$$

  and all ${\Theta }^{|\mathfrak{P}}$ (for which $\grave{S}\in S\left(\mathfrak{S}\prime \right)$) with processors ${LP}^{eval}$ equivalent to the inverse functions ${{\Theta }^{-1}}^{|\mathfrak{P}}$:

  $$\begin{gathered} \grave{S^{\prime }}\Rightarrow D\stackrel{{\Theta }^{|\mathfrak{P}}\Rightarrow {{\Theta }^{-1}}^{|\mathfrak{P}}\Rightarrow {LP}^{eval}}{\to }{S}_{k=1}\Rightarrow \\ \Rightarrow D_{k=1},\dots ,S_{k=n}\Rightarrow D_{k=n} \end{gathered}$$
• To successively replace all functions ${\Theta }^{|\mathfrak{P}}\in \Theta \left({\Gamma }^{|\mathfrak{G}}\right)$ and all arguments $S_{k=1},\dots ,S_{k=n}$ that are already replaced by the channels $D_{k=1},\dots ,D_{k=n}$, which are equivalent to ${LP}^{eval}$:

  $$D_{k=1},\dots ,D_{k=n}\stackrel{{\Theta }^{|\mathfrak{P}}\Rightarrow {LP}^{eval}}{\to }\grave{S}\Rightarrow D$$
• And to successively replace all ${\Theta }^{|\mathfrak{P}}$, with the result $\grave{S}$ having already been replaced by channel $D$, by ${LP}^{eval}$, which is equivalent to the inverse functions ${{\Theta }^{-1}}^{|\mathfrak{P}}$, consider the following:

  $$\begin{gathered} D\stackrel{{\Theta }^{|\mathfrak{P}}\Rightarrow {{\Theta }^{-1}}^{|\mathfrak{P}}\Rightarrow {LP}^{eval}}{\to }{S}_{k=1}\Rightarrow \\ \Rightarrow D_{k=1},\dots ,S_{k=n}\Rightarrow D_{k=n} \end{gathered}$$

As a result, we obtain a graph $C$ containing the equivalent ${LP}^{eval}$ for each ${\mathsf{\Theta }}^{|\mathfrak{P}}\in \mathsf{\Theta }\left({\Gamma }^{|\mathfrak{G}}\right)$ but possibly differing structures compared to ${\Gamma }^{|\mathfrak{G}}$, since its construction was carried out starting from $\mathrm{S}\prime \in \mathrm{S}\left(\mathfrak{S}\prime \right)$ rather than from the root nodes $S_{root}\in S\left({\Gamma }^{|\mathfrak{G}}\right)$ (see Figure 6).

Next, each root channel $D_{root}\in D\left(C\right)$ must be connected to a logical processor ${LP}^{init}$, whose task is to send the corresponding $M^{\prime }=\left[{{{\mathfrak{S}}^{\prime }}^{\mathfrak{X}}}_q\right]$ (where ${{{\mathfrak{S}}^{\prime }}^{\mathfrak{X}}}_q\in {\mathfrak{S}}^{\mathfrak{X}}\left({\mathfrak{S}}^{\prime }\right))$, which starts the computational process (see Figure 7).

Moreover, all or part of the channels $D\in D\left(C\right)$ must be connected with one or more ${LP}^{collect}$, which will collect part or all of the calculated substates ${{\mathfrak{S}}^{\mathfrak{X}}}_q\in {\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)$ belonging to the graph ${\mathsf{\gamma }}^{|\mathfrak{G}}\in {\mathsf{\gamma }}^{|\mathfrak{G}}\iff {\Gamma }^{|\mathfrak{G}},$ given by the set of initial states $\mathfrak{S}\prime$ (see Figure 7).

4.2. Graph $C$ Optimization

Simply replacing ${\mathsf{\Theta }}^{|\mathfrak{P}}$ functions with processors ${LP}^{eval}$ yields an extremely suboptimal and potentially infinite processing graph $C$, which is not good from the viewpoint of minimizing computing resources. To solve this problem, we can optimize graph $C$. For example, consider two optimization methods:

• Folding of cyclic sequences in the graph ${\Gamma }^{|\mathfrak{G}}$:
  Consider a chain with an arbitrary length of the same functions ${\theta }^{|\mathfrak{P}}$, as in Figure 8a. This can be transformed into a chain of logical processors ${LP}^{eval}$ of equal length, as in Figure 8b. We can fold this chain into a single ${LP}^{eval}$ by adding a message-return loop as in Figure 8c. Thus, more than one message $M$ will go through one ${LP}^{eval}$, so that if ${\theta }^{|\mathfrak{P}}$ has more than one argument, it can lead to collisions. To resolve collisions and also to implement breakage of the loop, we need to determine the loop-iteration number of messages $M$. The simple way to do this is to add an iteration counter for each loop in $C$. Another approach is to use history-sensitive values [21]. As a more complex example, we consider the graph ${\Gamma }^{|\mathfrak{G}}$ in Figure 9a, which can be converted and collapsed into a compact graph $C$ as in Figure 9b.
• Folding of graph $C$:
  Inside each ${LP}^{eval}$, we can implement more than one function ${\Theta }^{|\mathfrak{P}}\in \Theta \left({\Gamma }^{|\mathfrak{G}}\right)$, thus reducing the number of nodes in the graph $C$. This folding can be performed over a wide range, up to the realization of all ${\Gamma }^{|\mathfrak{G}}$ in one ${LP}^{eval}$. For example, graph $C$ from Figure 9b can be folded into a single ${LP}^{eval}$ and will look like Figure 9c.

In general, the optimization problem for graph $C$ is rather complex and goes beyond the scope of this article.

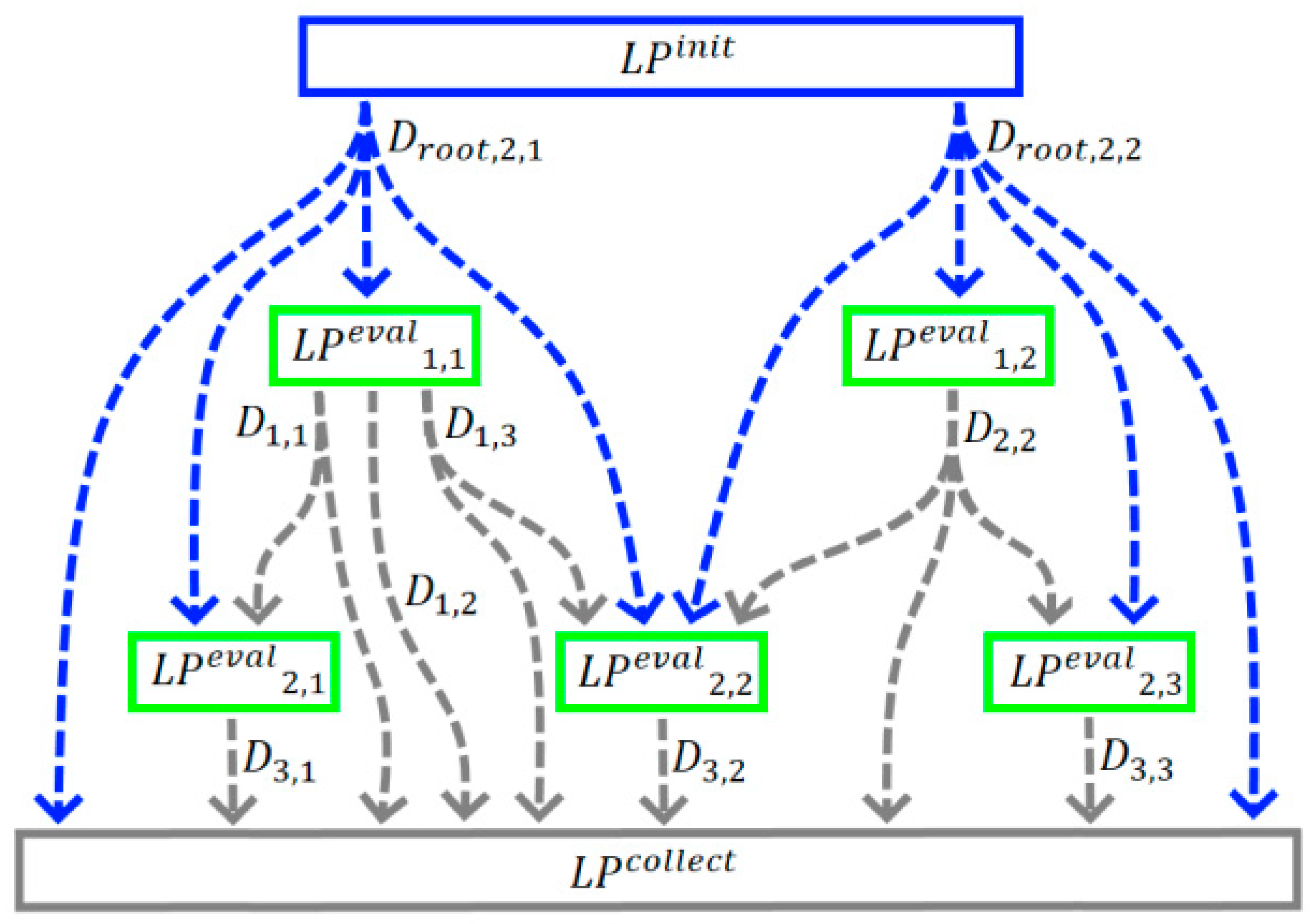
4.3. Simulation of the Graph Model ${\widehat{\mathit{Y}}\left(\overline{\mathit{X}}|\mathfrak{G}\right)}^{\Gamma }$ Using the Computational Graph $C$

In the simplest case, we can simulate the model ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^{\mathsf{\Gamma }}$ (Formula (10)) using the graph $C$ constructed on it in two stages:

• Calculate the set of substates

  $${\mathfrak{S}}^{\overline{X}|\mathfrak{G}}={\mathfrak{S}}^{\mathfrak{X}}\left(\gamma \left({\Gamma }^{|\mathfrak{G}}|{\mathfrak{S}}^{\prime }\right)\right)$$
  For this, we initialize the calculation by sending $M\prime$ messages using the processors ${LP}^{init}$. Using the processors ${LP}^{collect}$, we collect all the calculated messages, $M=\left[{{\mathfrak{S}}^{\mathfrak{X}}}_q\right]$.
• Find all substates for each key $\overline{\mathfrak{X}}\in \overline{\mathfrak{X}}$, and then collect the values $\widehat{\mathfrak{Y}}\in \widehat{\mathfrak{Y}}$ from the found substates (Formula (6)).

In most cases, this approach will be computationally expensive since, in practice, $\left|\mathfrak{X}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)\right|>\left|\overline{\mathfrak{X}}\right|$ usually occurs.

Generally, simulation optimization is the minimization of the number of calculated substates ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ such that $\mathfrak{X}\left({{\mathfrak{S}}^{\mathfrak{X}}}_q\right)\notin \overline{\mathfrak{X}}$. Several approaches are possible here—for example, constructing a minimalistic ${\Gamma }^{|\mathfrak{G}}$ with a certain well-known collection $\overline{\mathfrak{X}}$. Alternatively, lazy algorithms that cut off the calculations ${\mathsf{\Theta }}^{|\mathfrak{P}}$, whose result is not required to cover $\overline{\mathfrak{X}}$, could be used. However, this topic is beyond the scope of the present article.

5. Practice

In this chapter, we show our approach in practice. First, we describe a modeled object, then define its mathematical model and the analytical solution. In the next step, we explain the procedure of the construction of the graph and parallelization scheme and present the results. This chapter contains a shortened description; please check Supplementary S6–S8 for the full one.

5.1. Description of the Modeled Object and the Construction of Model $\widehat{\mathit{Y}}\left(\overline{\mathit{X}}\right|\mathfrak{G})$

As an example, consider the classic model of saline mixing. Here, the simulated object is a system of two connected tanks of volumes $v_1=4 L$ and $v_2=8 L$. Over time $t$, a saline solution circulates from the first tank to the second with a speed $q_3=5 L/m$ and in the opposite direction with a speed of $q_2=2 L/m$. In addition, the saline solution is poured into the first tank at a speed of $q_1=3 L/m$ and drains from the second tank at the same speed $q_4=3 L/m$, i.e., the volume of the saline solution in the tanks does not change. Initially, the first and second tanks are entirely filled with solutions with initial salt concentrations of ${\omega }_1=0 g/L$ and ${\omega }_2=20 g/L$, respectively. A saline solution with a concentration of ${\omega }_3=10 g/L$ is supplied to the first tank constantly. Thus, the set of variables reflecting the properties of interest will look like the following:

$$V=\left[\begin{array}{c}t\\ \begin{array}{c}{\mathsf{\omega }}_1\\ \begin{array}{c}{\mathsf{\omega }}_2\\ \begin{array}{c}{\mathsf{\omega }}_3\\ \begin{array}{c}{v}_1\\ \begin{array}{c}{v}_2\\ \begin{array}{c}{q}_1\\ \begin{array}{c}{q}_2\\ \begin{array}{c}{q}_3\\ q_4\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]$$

The modeling task is to predict the change in the salt concentrations ${\omega }_1=0 g/L$ and ${\omega }_2=20 g/L$ over time $t$.

As part of the modeling problem to be solved, we represent the simulated object in the form of the model ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^F$ (Formula (3)), breaking the variables $V$ as

$$\begin{gathered} \overline{X}=\left[t\right], \\ \widehat{Y}=\left[\begin{array}{c}{\mathsf{\omega }}_1\\ {\mathsf{\omega }}_2\end{array}\right], \\ \mathfrak{G}=\left[\begin{array}{c}{v}_1=4\\ \begin{array}{c}{v}_2=8\\ \begin{array}{c}{q}_1=3\\ \begin{array}{c}{q}_2=2\\ \begin{array}{c}{q}_3=5\\ \begin{array}{c}{q}_4=3\\ {\mathsf{\omega }}_3=10\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right] \end{gathered}$$

and specifying their dependence as a set of functions:

$$\widehat{Y}=F\left(\overline{X}|\mathfrak{G}\right)=\left[\begin{array}{c}{\widehat{\mathsf{\omega }}}_1\left(\overline{t}\right)={\displaystyle \frac{13e^{\frac{\left(\sqrt{105}-15\right)\overline{t}}{16}}\sqrt{105}}{21}}-{\displaystyle \frac{13e^{-\frac{\left(15+\sqrt{105}\right)\overline{t}}{16}}\sqrt{105}}{21}}-5e^{{\displaystyle \frac{\left(\sqrt{105}-15\right)\overline{t}}{16}}}-5e^{-{\displaystyle \frac{\left(15+\sqrt{105}\right)\overline{t}}{16}}}+10\\ {\widehat{\mathsf{\omega }}}_2\left(\overline{t}\right)={\displaystyle \frac{5e^{-\frac{\left(15+\sqrt{105}\right)\overline{t}}{16}}\sqrt{105}}{21}}-{\displaystyle \frac{5e^{\frac{\left(\sqrt{105}-15\right)\overline{t}}{16}}\sqrt{105}}{21}}+5e^{{\displaystyle \frac{\left(\sqrt{105}-15\right)\overline{t}}{16}}}+5e^{-{\displaystyle \frac{\left(15+\sqrt{105}\right)\overline{t}}{16}}}+10\end{array}\right],$$

(12)

which are obtained by solving the Cauchy problem

$$\left\{\begin{array}{c}{\displaystyle \frac{d{\widehat{\omega }}_1}{d\overline{t}}}={\displaystyle \frac{3\ast 10+2\ast {\widehat{\omega }}_2-5\ast {\widehat{\omega }}_1}{4}}\\ {\widehat{\omega }}_1\left(0\right)=0 \\ {\displaystyle \frac{d{\widehat{\mathsf{\omega }}}_2}{d\overline{t}}}={\displaystyle \frac{5\ast {\widehat{\mathsf{\omega }}}_1-2\ast {\widehat{\mathsf{\omega }}}_2-3\ast {\widehat{\mathsf{\omega }}}_2}{8}}\\ {\widehat{\mathsf{\omega }}}_2\left(0\right)=20 \end{array}. \right.$$

(13)

We can also represent the simulated object in the form of model ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^S$ (Formula (4)). In this case, the values of the variable $t$ will be used as keys, and those of the variables ${\omega }_1$ and ${\omega }_2$ can be separated by different substates in such a way that we obtain two types of substates ${{{\mathfrak{S}}^{\mathfrak{X}}}_{q=1}={\left[{\omega }_1\right]}^{\left[t\right]}}_{q=1}$ and ${{\mathfrak{S}}^{\mathfrak{X}}}_{q=2}={{\left[{\omega }_2\right]}^{\left[t\right]}}_{q=2}$. In the code, we can represent the values $\overline{\mathfrak{X}}$, $\widehat{\mathfrak{Y}}$ and the substate ${{\mathfrak{S}}^{\mathfrak{X}}}_q$ as OOP classes (source code B.1.L27).

One simple, but impractical, way to construct a set of substates ${\mathfrak{S}}^{\overline{X}|\mathfrak{G}}$ is to generate ${{\mathfrak{S}}^{\mathfrak{X}}}_{q=1},{{\mathfrak{S}}^{\mathfrak{X}}}_{q=2}\in {\mathfrak{S}}^{\overline{X}|\mathfrak{G}}$ using a set of functions (Formula (12)) with some step of key $∆t$ (source code B.2.L60).

Using the model $\widehat{Y}\left(\overline{X}|\mathfrak{G}\right),$ we can perform the simulation (Formula (5)) for some segment $\overline{\mathfrak{X}}=\left[t_{begin},t_{end}\right]$ and obtain the corresponding set of values $\widehat{\mathfrak{Y}}$ (source code B.1.L71 is an implementation of $\widehat{Y}=F\left(\overline{X}|\mathfrak{G}\right)$, and source code B.2.L70 is an implementation of ${\mathfrak{S}}^{\overline{X}|\mathfrak{G}}=\widehat{Y}$). Looking at the output plots, we can see that they are similar (see Figure 10).

We can compare the results of executing the models ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^F$ and ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^S$ just by accumulating different overall output values:

$$\mathsf{\epsilon }={\displaystyle \sum _{\overline{\mathfrak{X}}\in \overline{{\mathbb{X}}^n}}}{\displaystyle \sum _{i=1}^{\left|Y\right|}}\left({{\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^F}_i-{{\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^S}_i\right).$$

Evaluating this algorithm (source B.3.L24), we obtain $\mathsf{\epsilon }={1.1546319456101628}^{\mathrm{e}-14}$.

5.2. Building and Simulating a Graphical Model ${\widehat{\mathit{Y}}\left(\overline{\mathit{X}}|\mathfrak{G}\right)}^{\Gamma }$

The graph ${\Gamma }^{|\mathfrak{G}}$ for this example will represent an infinite chain of pairs of nodes $\mathrm{S}$ connected by edges ${\mathsf{\Theta }}^{|\mathfrak{O}}$. For convenience, in addition to the index of depth $d$, we index the nodes $\mathrm{S}$ with indices of width $w\in N$ so that the nodes $S_d,$ with the same index $d,$ will have different values of $w$. Moreover, we set $\mathrm{w}=\mathrm{k}=\mathrm{q}$, where $\mathrm{k}$ is the index of the argument (edges) ${{\mathsf{\Theta }}^{|\mathfrak{O}}}_d$ and q is the index of the substate assigned to $S_{d,w}$. Each pair $S_{d,w=1}$ and $S_{d,w=2}$ corresponds to a certain moment of discrete time $\overline{t}$. For simplicity, we will use a fixed time step $∆t=d\ast \gamma$, where $d$ is the depth index, and $\gamma$ is the time-step coefficient. Also, we restrict model time to a small interval $\left[t_{begin},t_{end}\right]\supset \overline{t}$. In this case, the graph ${\Gamma }^{|\mathfrak{G}}$ will contain

$$\mathrm{n}={\displaystyle \frac{t_{end}-t_{begin}}{∆t}}+1$$

pairs of nodes $S_{d,w}$.

The simplest way to implement the transition functions ${{\mathsf{\Theta }}^{|\mathfrak{O}}}_{d,w=1}$ and ${{\mathsf{\Theta }}^{|\mathfrak{O}}}_{d,w=2}$ is to use the functions ${\widehat{\omega }}_1\left(\overline{t}\right)$ and ${\widehat{\omega }}_2\left(\overline{t}\right)$ from the set $F\left(\overline{X}|\mathfrak{G}\right)$ (Formula (12)). In this case,

$$\begin{gathered} {{\mathsf{\Theta }}^{|\mathfrak{O}}}_{d,w=1}\left({{\left[{\widehat{\omega }}_1\right]}^{\left[\overline{t}\right]}}_{k=1},{{\left[{\widehat{\omega }}_2\right]}^{\left[\overline{t}\right]}}_{k=2}\right)= \\ ={{\left[{\widehat{\omega }}_1\left(\overline{t}+∆t\right)\right]}^{\left[\overline{t}+∆t\right]}}_{q=1}; \\ {{\mathsf{\Theta }}^{|\mathfrak{O}}}_{d,w=2}\left({{\left[{\widehat{\omega }}_1\right]}^{\left[\overline{t}\right]}}_{k=1},{{\left[{\widehat{\omega }}_2\right]}^{\left[\overline{t}\right]}}_{k=2}\right)= \\ ={{\left[{\widehat{\omega }}_2\left(\overline{t}+∆t\right)\right]}^{\left[\overline{t}+∆t\right]}}_{q=2}. \end{gathered}$$

A slightly more complicated implementation is to rewrite the system of differential equations (Formula (13)) to be solved by the Euler method

$$\left\{\begin{array}{c}{\widehat{\mathsf{\omega }}}_{1,i}={\widehat{\mathsf{\omega }}}_{1,i-1}+∆t\ast {\displaystyle \frac{q_1\ast {\mathsf{\omega }}_3+q_2\ast {\widehat{\omega }}_{2,i-1}-q_3\ast {\widehat{\omega }}_{1,i-1}}{v_1}} \\ {\widehat{\mathsf{\omega }}}_{2,i}={\widehat{\mathsf{\omega }}}_{2,i-1}+∆t\ast {\displaystyle \frac{q_3\ast {\widehat{\mathsf{\omega }}}_{1,i-1}-q_2\ast {\widehat{\mathsf{\omega }}}_{2,i-1}-q_4\ast {\widehat{\mathsf{\omega }}}_{2,i-1}}{v_2}}\end{array}\right.$$

as iterated by $∆t$:

$${\widehat{\omega }}_{\mathrm{1,0}}=0;{\widehat{\mathsf{\omega }}}_{\mathrm{2,0}}=20;i=\mathrm{1,2},3,\dots$$

In this case,

$${{\mathsf{\Theta }}^{|\mathfrak{O}}}_{d,w=1}\left({{\left[{\widehat{\omega }}_1\right]}^{\left[\overline{t}\right]}}_{k=1},{{\left[{\widehat{\omega }}_2\right]}^{\left[\overline{t}\right]}}_{k=2}\right)={{\left[{\widehat{\omega }}_1+∆t\ast {\displaystyle \frac{\mathfrak{O}.q_1\ast \mathfrak{O}.{\omega }_3+\mathfrak{O}.q_2\ast {\widehat{\omega }}_2-{\mathfrak{O}.q}_3\ast {\widehat{\omega }}_1}{{\mathfrak{O}.v}_1}}\right]}^{\left[\overline{t}+∆t\right]}}_{q=1};$$

$${{\mathsf{\Theta }}^{|\mathfrak{O}}}_{d,w=2}\left({{\left[{\widehat{\omega }}_1\right]}^{\left[\overline{t}\right]}}_{k=1},{{\left[{\widehat{\omega }}_2\right]}^{\left[\overline{t}\right]}}_{k=2}\right)={{\left[{\widehat{\omega }}_2+∆t\ast {\displaystyle \frac{\mathfrak{O}.q_3\ast {\widehat{\omega }}_1-\mathfrak{O}.q_2\ast {\widehat{\omega }}_2-\mathfrak{O}.q_4\ast {\widehat{\omega }}_2}{\mathfrak{O}.v_2}}\right]}^{\left[\overline{t}+∆t\right]}}_{q=2}.$$

We implement the nodes $\mathrm{S}$ and the sets of edges ${\mathsf{\Theta }}^{|\mathfrak{P}}$ as OOP classes (source code C.1.L89). $\mathrm{S}$ nodes are essentially variables that are not initially defined. The transition graph ${\Gamma }^{|\mathfrak{G}}$ and the simulation graph ${\mathsf{\gamma }}^{|\mathfrak{G}}$ can be represented as classes containing collections of nodes $\mathrm{S}$ of sets of edges ${\mathsf{\Theta }}^{|\mathfrak{P}}$ (source code C.1.L149). Moreover, the graph ${\mathsf{\gamma }}^{|\mathfrak{G}}$ is the same as graph ${\Gamma }^{|\mathfrak{G}}$, but with all variables $\mathrm{S}$ defined.

Due to the simplicity of the transition graph ${\Gamma }^{|\mathfrak{G}}$, we can implement the function build_Γ($n$, $∆t$), which automatically constructs ${\Gamma }^{|\mathfrak{G}}$ based on the given number of steps and the time step (source code C.1.L190).

The search for the simulation graph $\mathsf{\gamma }\left({\Gamma }^{|\mathfrak{G}}|{\mathfrak{S}}^{\prime }\right)$ is a calculation of the values of all nodes $\mathrm{S}$ from the initial set of substates

$${\mathfrak{S}}^{\prime }=\left\{{\mathrm{S}}_{d=0,w=1}={{\mathfrak{S}}^{\mathfrak{X}}}_{j=1},{\mathrm{S}}_{d=0,w=1}={{\mathfrak{S}}^{\mathfrak{X}}}_{j=2}\right\}.$$

We implement the search as method $\mathsf{\Gamma }$.γ(${\mathfrak{S}}^{\prime }$), using the indices $d$ and $w$ as the key in the set ${\mathfrak{S}}^{\prime }$ (source code C.1.L156). The method first initializes the nodes ${\mathrm{S}}_{d=0,w=1}$ and ${\mathrm{S}}_{d=0,w=2}$ with the initial substates ${{{\mathfrak{S}}^{\prime }}^{\mathfrak{X}}}_{j=1}$ and ${{{\mathfrak{S}}^{\prime }}^{\mathfrak{X}}}_{j=2}$ and then calculates the values of the rest nodes ${\mathrm{S}}_{d,w}$ by calling each method ${{\mathsf{\Theta }}^{|\mathfrak{O}}}_{d,w}$.eval() until all ${\mathrm{S}}_{d,w}$ are defined. The method ${{\mathsf{\Theta }}^{|\mathfrak{O}}}_{d,w}$.eval() checks whether the arguments

$${\mathrm{S}}_{d-1,w=1},{\mathrm{S}}_{d-1,w=2}\stackrel{{{\mathsf{\Theta }}^{|\mathfrak{O}}}_{d,w}}{\to }\dots$$

are defined and, if so, evaluates the result

$$\dots \stackrel{{{\mathsf{\Theta }}^{|\mathfrak{O}}}_{d,w}}{\to }{\mathrm{S}}_{d,w}.$$

The set of substates ${\mathfrak{S}}^{\mathfrak{X}}\left({\mathsf{\gamma }}^{|\mathfrak{G}}\right)$ can be obtained from the simulation graph $\mathsf{\gamma }\left({\Gamma }^{|\mathfrak{G}}|{\mathfrak{S}}^{\prime }\right)$ by simply extracting the values from the nodes $\mathrm{S}$ and combining them into the set ${\mathfrak{S}}^{\overline{X}|\mathfrak{G}}$. We implement this in the form of the method ${\mathsf{\gamma }}^{|\mathfrak{G}}$.$\mathfrak{S}$() (source code C.1.L179); next, ${\mathfrak{S}}^{\overline{X}|\mathfrak{G}}$ can be used to obtain the values of $\widehat{\mathfrak{Y}}\in \widehat{\mathfrak{Y}}$ from the values of $\overline{\mathfrak{X}}\in \overline{\mathfrak{X}}$.

5.3. Constructing and Calculating Graph $C$ Using the Graphical Model ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^{\Gamma }$

As an example, we construct graph $C$ using the model ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^{\mathsf{\Gamma }}$ for mixing salt solutions. To implement it, we use the AKKA Streams library. There was a similar approach for implementing the SwiftVis tool.

We can build an unoptimized version of graph $C$ by simply replacing the functions ${{\mathsf{\Theta }}^{|\mathfrak{P}}}_{d,w=1}$ and ${{\mathsf{\Theta }}^{|\mathfrak{P}}}_{d,w=2}$ with logical processors ${{LP}^{eval}}_{d,w=1}$ and ${{LP}^{eval}}_{d,w=2}$ and adding ${LP}^{collect}$, ${{LP}^{init}}_{d=0,w=1}$, and ${{LP}^{init}}_{d=0,w=2}$.

We represent the substates in the form of the messages $M_{d,w}=\left[{{\mathfrak{S}}^{\mathfrak{X}}}_{q,d,w}\right]$ produced by the corresponding ${{LP}^{eval}}_{d,w}$, where $q=w$. In particular, the substates from the set $\mathfrak{S}\prime$ can be represented as $M_{d=0,w=1}=\left[{\mathrm{S}}_{d=0,w=1}={{{\mathfrak{S}}^{\prime }}^{\mathfrak{X}}}_{q=1}\right]$ and $M_{d=0,w=2}=\left[{\mathrm{S}}_{d=0,w=2}={{{\mathfrak{S}}^{\prime }}^{\mathfrak{X}}}_{q=2}\right]$.

This will work as follows (see source code D.1): the initial messages $M_{d=0,w=1}$ and $M_{d=0,w=2}$ are sent by logical processors ${{LP}^{init}}_{d=0,w=1}$ and ${{LP}^{init}}_{d=0,w=2}$ to the processors ${{LP}^{eval}}_{d=1,w=1}$, ${{LP}^{eval}}_{d=1,w=2}$. Then, the messages will distribute throughout the graph, where a copy of each substate is fed into the processor ${LP}^{collect}$, which builds the resulting set of substates ${\mathfrak{S}}^{\overline{X}|\mathfrak{G}}$.

Since the standard blocks Zip, Flow.map, Broadcast, and Merge from the AKKA Streams library were used to construct graph $C$, the implementation of each ${{LP}^{eval}}_{d,w}$ will be a nested graph.

Since the obtained graph $C$ consists of recurring pairs ${{LP}^{eval}}_{d,w=1}$ and ${{LP}^{eval}}_{d,w=2}$, it can be optimized by implementing two cycles using two logical processors, ${{LP}^{eval}}_{w=1}$ and ${{LP}^{eval}}_{w=2}$.

Since it is necessary in this case to determine which incoming messages refer to particular iterations of the cycle, we add the iteration (depth) counter $d$ to them, $M_{d,w}=\left[{d,{\mathfrak{S}}^{\mathfrak{X}}}_q\right]$, and modify the grouping function Zip so that it selects pairs of incoming $M_{d,w}$ with the same value $d$ (source code D.2). When we execute this code, we obtain the simulation result (see Figure 11), which was the same as our findings from the implementation of the ${\widehat{Y}\left(\overline{X}|\mathfrak{G}\right)}^S$ model (see Figure 10).

6. Discussion

One of the primary contributions of this research is the synthesis of classical mathematical modeling techniques with the practical, high-performance synchronization mechanisms provided by reactive streams. Similar to earlier approaches, such as the Time Warp algorithm [1,2] and actor-based frameworks used in HPC simulation platforms [9], our method decomposes the complete object state into substates with unique keys. This modular representation not only supports reuse and flexibility but also enables the direct mapping of transition functions to logical processors. The resulting computational graph is reminiscent of systems such as RxHLA [7] and CQRS + ES architectures [8], which emphasize decoupling and distributed processing.

Representing the model as a transition graph ${\Gamma }^{|\mathfrak{G}}$ and initial set of sates $\mathfrak{S}\prime$ offers several benefits:

• Modularity and Reusability: By encapsulating transition rules as independent functional blocks, the approach supports reuse and flexibility. This modular structure is similar in spirit to block-diagram environments like Simulink [30,31,32] and has parallels in dataflow programming models discussed by Kuraj and Solar-Lezama [21].
• Scalability: Our implementation leverages the inherent parallelism of modern multi-core and distributed architectures. This approach aligns with the findings of actor-based models [9,25,26] and contemporary research on reactive programming in distributed systems [10,24].
• Interactive Simulation: The push and pool patterns introduced in our model are analogous to techniques used in recent studies on interactive and fault-tolerant reactive systems [23,33]. This design allows the simulation to respond in real time to external events or user inputs.

In summary, the proposed method of using reactive streams as a synchronization protocol for parallel simulation provides a compelling framework that unites rigorous mathematical modeling with practical, scalable implementation techniques. While challenges remain—particularly in optimization, continuous simulation, and fault tolerance, the initial results and conceptual clarity offer a solid foundation for further research and development. The integration of our approach with similar studies in the field [1,2,3,4,5,6,7,8,9,10,13,21,22,23,24,25,26,27,28,33,34] highlights its potential and provides clear directions for future work.

7. Future Work

Many unanswered questions remain, some of which we present for future research:

• Effective optimization of computational graph $C$ and simulation on it:
  Section 4.2 and Section 4.3 dealt with this topic. However, due to its complexity and vastness, it did not fit into this article. In general, this is a very important issue from a practical point of view. Solving it will significantly reduce the number of resources required to perform simulations. Another interesting question is the automation of the optimization of graph $C$. Say that, initially, we have non-optimal $C$, for example, obtained by the method described in Section 4.1. We want to automatically make C compact and computationally easy without loss of accuracy and consistency.
  The ML technique can be used to resolve the optimization task. For example, reinforcement rearming agents can be trained to explore various graph configurations (i.e., different ways to fold or collapse the computational graph) and learn which configurations yield the best performance in terms of latency, throughput, or resource consumption [35,36,37,38,39]. Also, techniques like neural architecture search (NAS) can be adapted to optimize the layout and parameters of the computational graph. This includes automatically deciding how to fold cyclic sequences, balancing load among logical processors, and minimizing redundant computations [38,39,40].
• Accurate simulation of continuous-valued models:
  Many properties of modeled objects can be represented in continuous quantities, for example, values from the set ℝ. However, the simulation (the calculation of which is based on message forwarding) is inherently discrete. An open question remains as to how accurately continuous quantities can be calculated. The question is how to increase the accuracy of calculating such quantities without increasing the requirements for computer resources.
• Fault-tolerance of reactive streams:
  We did not touch on fault tolerance of simulation in this work, but in most real/practical applications, fault tolerance is very important. This question was partially explored in [23], but we also suggest this for future work.
• Manual and automatic graph construction $C$:
  From a practical viewpoint, it is interesting to be able to use some IDE to manually construct a computational graph $C$ and to do this in such a way that the corresponding graph ${\Gamma }^{|\mathfrak{G}}$ will be consistent and optimal. For example, this might be performed similarly to the Simulink package [30,41], SwiftVis tool [25,42], or XFRP language (Version 2.9.644) [24,43]. It is also interesting to find ways to automate the construction of $C$. For example, the model can initially be defined as a certain set of rules by which graph $C$ can be automatically and even dynamically constructed. Specialized programming languages are also an interesting area to explore. For example, the EdgeC [33] language can be considered a tool to describe computational graphs.
  Also, the ML technique can be applied wildly here. For example, graph learning techniques from graph neural networks (GNNs) can be applied to learn the structure of the optimal computational graph from historical data. The learned model can then suggest or automatically construct a more efficient graph based on current simulation requirements. Adaptive scheduling ML algorithms can dynamically adjust the scheduling of tasks across logical processors, optimizing the execution order and balancing the load [44,45]. This is particularly useful in interactive or real-time simulations where conditions may change frequently.
• Testing with complex models and comparing with other parallelizing approaches:
  This work provides a small, simple example of parallel simulation to show how the described approach can be implemented in practice. However, the questions of checking this approach with large and complex models and comparing its effectiveness with other parallelizing approaches remain open.

8. Conclusions

The proposed method effectively integrates the reactive stream paradigm with classical mathematical modeling techniques to create a scalable framework for parallel simulation. By using a graph-based representation of object states and transition functions, this approach enhances modularity and reusability while supporting efficient computation through logical processors. The implementation using AKKA reactive streams demonstrates its scalability and practical feasibility for distributed systems. Despite its promise, the work highlights challenges such as graph optimization, continuous model simulation, fault tolerance, and automation of graph construction, which offer significant areas for future research and development. The study lays a strong foundation for advancing parallel simulation techniques, emphasizing both theoretical robustness and practical scalability.