Abstract
Numerical modeling was conducted to study the capture of particles diffusing in porous media with traps. The pores are cylindrical in shape, and the traps are randomly distributed along the cylindrical surfaces of the pores. The dynamics of particle capture by the traps, as well as the filling of the traps, were investigated. In general, the decrease in the number of particles follows an exponential trend, with a characteristic time determined by the trap concentration. However, at longer times, extended plateaus emerge in the particle distribution function. Additionally, the dynamics of the interface boundary corresponding to the median trap filling (M = 0.5) were examined. This interface separates regions where traps are filled with a probability greater than 0.5 from regions where traps are filled with a probability less than 0.5. The motion of the interface over time was found to follow a logarithmic dependence. The influence of the radius of the pore on the capture on traps, which are placed on the internal surface of the cylinders, was investigated. The different dependencies of the extinction time on the number of traps were found at different radii of pores the first time.
1. Introduction
The problem of particle diffusion in media with absorbing traps has been studied in many works [1,2,3,4,5,6]. Interest is also driven by the expected new features in particle transport [7,8,9,10,11], as well as various applications. One of the most relevant applications is the study of the processes of diffusion and capture of active particles into traps in porous dielectric low-k materials, which are used in modern electronics [11,12,13,14,15]. As is well known, one of these materials is a porous SiOC, which is exposed to radicals such as active oxygen atoms. These radicals diffuse in the pores of the material. Due to diffusion and capture n traps, the interface separating a rich (pristine) carbon phase from a damaged (oxygen-rich) layer appeared. It is important to understand the motion of this interface and its dependence on diffusion and reaction parameters, which can further be related to the properties of the material.
Additionally, the problem of diffusion in complex heterogeneous media and trapping also appeared in emerging bioengineering fields, e.g., in bone nanostructure [16,17,18], cartilage [19], or brain extracellular space [20]. This problem is studied by different methods, including numerical simulation [21,22,23].
In this paper, we investigate diffusion processes in porous media with traps, in particular, we study the decrease in the number of active particles over time as they are captured by traps. Also, we establish the characteristic time dependence of particle capture on trap concentration. As is known, in various physical phenomena, characteristic parameters usually arise that describe these phenomena. In the problem of diffusion processes in media with traps, a characteristic length arises—the distance between the traps and, accordingly, in dynamics, the diffusion time for a distance, equal to the length between the traps. In the one-dimensional case, this time is given by:
D is the diffusion coefficient, is the trap concentration. In the one-dimensional case, the average distance between traps is inversely proportional to the trap concentration. Accordingly, different behaviors are possible at short and long times , as described in the article.
The motion of the interface, which is divided into the region with fulfilling traps and the region with free traps, was studied in detail. The motion of this interface is important, and it is directly connected with the damage and mechanical properties of porous low-k materials, used in modern nanoelectronics.
The influence of the radius of the pore and the number of traps on the extinction time was studied in the paper firstly as far as we know. It is important to study the diffusion and capture of traps in real porous systems because these real systems have branched structures of pores with different sizes and different topologies.
The article is organized as follows. The Section 2 formulates the problem, briefly describes the algorithms and methods of numerical modeling, and provides characteristics of the trap seeds. The Section 3 presents the main results of the numerical experiment. The Section 4 discusses the features of the long-term asymptotic behavior of the active particles’ survival probability. The Conclusion summarizes the results and discusses their implications.
2. Problem Statement and Simulation Algorithms
We consider the active particle diffusion in a cylindrical pore; the cylinder radius R and height H are specified during the simulation. The traps are located randomly on the pore surface at different trap concentration degrees. Since the diffusion equation is a first-order equation in time, the diffusion process dynamics is determined by the initial condition at the zero moment of time N(x,t = 0) = N0, when there are only N-particles with a uniform density and boundary condition at the top of the cylinder in the plane Z = 0. This formulation corresponds to the propagation of free oxygen, which we call O-particles, in the pores of the material in which traps—C particles—are randomly located. A similar problem was considered in [24,25], but a one-dimensional approximation with three types of particles was used (bound oxygen was additionally taken into account). The simulation of diffusion was made in [26,27].
In the present work, a three-dimensional geometry is used—the pores of the material in the form of a cylinder, which is more consistent with the geometry of low-k materials.
2.1. Algorithm of Simulations. Diffusion Processes in Media with Traps
Let us briefly describe the modeling particle diffusion algorithm in cylindrical pores with traps on the surfaces of cylinders. A random number generator chooses the direction of particle movement arbitrarily at every step, it simulates the random motion of particles. In this case, there are a number of conditions: (a) after choosing the direction of movement, the algorithm checks whether there is a particle in the new coordinate, if the coordinate is “free” the particle moves to it, otherwise, it remains in its place. (b) Upon reaching the lower or upper boundary of the cylinder, the particles are “reflected”, that is, they return to their original position. (c) The cylindrical surface is reached when the distance from the center of the circle on the cut along the z coordinate exceeds the radius of the cylinder. In this case, “reflection” occurs.
The C++ programming language (ISO C++17) and the Visual Studio 2022 development environment were used for numerical calculations. To ensure the stability and correctness of the results, a series of experiments—20 for each trap configuration—were conducted. The obtained results were averaged, and statistical estimates (provided in Appendix A) demonstrate that the results are generally stable.
We used the “Mersenne Twister (mt19937)” algorithm to generate random numbers.
2.2. Placing of Traps
During diffusion, particles are captured on traps, which are placed on the surface of cylinder pores. Coordinates of traps are determined randomly, namely: the Z coordinate is selected randomly—the height of the location on the axis of the cylinder, then it randomly selects angle and calculates the X and Y coordinates. The obtained coordinates are rounded to an integer value by discarding the fractional part. Thus, the traps form a “belt” around the working area.
3. Modeling Process and Results of Numerical Simulation
To simulate diffusion, we generate various trap configurations, with the number of traps varying from 1000 to 10,000 in 1000 increments. Data of the active particle number were recorded for every 1000 iterations for all generated trap configurations. The resulting data on the configurations were averaged, and a graph of the change in the active particle number from the number of iterations was constructed, see Figure 1.
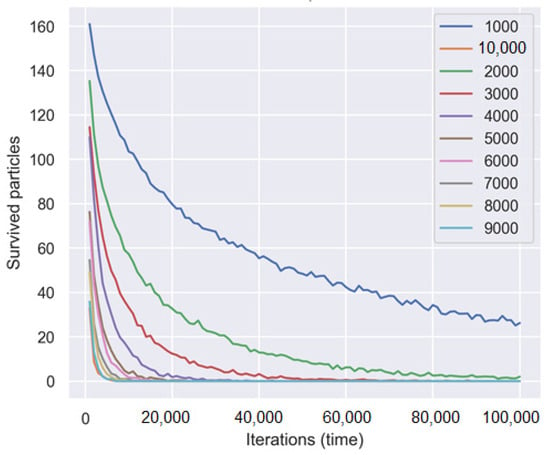
Figure 1.
Dependence of number of survived particles on the time (iterations) at different numbers of traps.
It is obvious that there is a sharp decrease in the number of survived particles with an increasing number of traps. So, let us use the logarithm scale for the number of survived particles at different concentrations of traps at the insert in Figure 2.
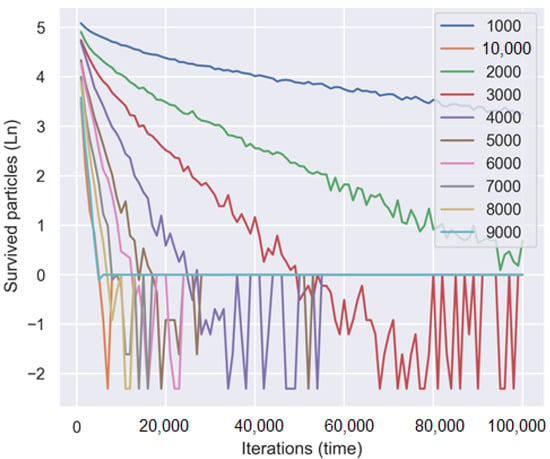
Figure 2.
Dependence of logarithm of number of active particles on time at different concentrations of traps.
For a more complete description of the processes of capture of diffusing particles on traps, we will calculate some characteristics of these processes.
3.1. Motion of the Interface of the Region with Median Filling of Traps
In addition to the surviving particles, the coordinates of the closed traps are recorded during the numerical simulation. Let us consider the moduli of the Z coordinate for each of the closed traps.
First, let us consider the distribution of closed traps along the Z axis. For each time step (each iteration), we obtain an array of pairs (Z value and number of closed traps). We can describe these data as a map object where the key is Z coordinate, and the value is the number of traps. The mean and median values can be used as characteristics of this array. Table 1 presents examples of medians and means for closed traps data of numerical simulation with traps Nt = 1000.

Table 1.
The average and median value of the z coordinate for closed traps (configuration with the number of traps 1000).
The results have a clear sense: as the more time steps (iterations), then the more traps are «closed» and, as a result, the «shift» of the median and average coordinate value occurs. It is necessary to clear the number of traps that were used in the modeling. It is obvious that in the case of the small number of traps, there are long times that will be required to obtain the temporal dependencies of the survival probability of particles, so the low bound of a number of traps begins from 1000 traps. The upper bound of traps is 10,000. This number corresponds to the total number of places for traps on the cylindrical surface: At R = 3a and H = 1000, the number of possible places for traps is equal to .
Let us consider how the median and average value of the boundary separating the areas with trap filling greater than 50% from the area with less filling changes over time (number of iterations) for different trap concentrations. For each trap concentration, the average and median values for the Z coordinates of closed traps, as well as the total number of closed traps, were calculated. Thus, for each numerical experiment, the average by coordinates, the median by coordinates, and the number of closed (knocked out) traps were obtained.
The general graph of the change in the average value of the interface position from the number of iterations is shown in Figure 3.
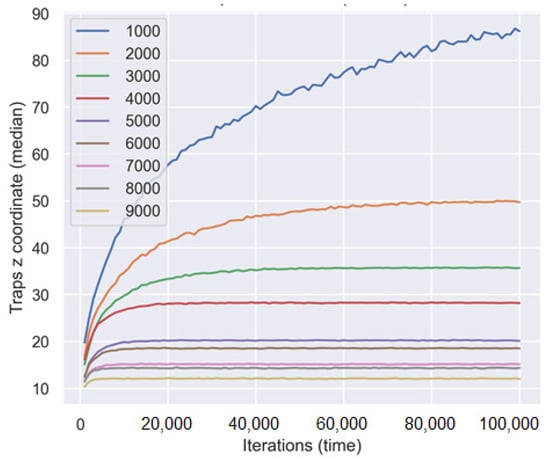
Figure 3.
Dynamics of interface, separating the areas with trap filling greater than 50% from the area with less filling, on time (number of iterations) for different trap concentrations.
One of the features of the obtained dependences of the interface displacement at different trap concentrations is different. At a small number of traps, this dependence is slow to change on time and may be described as log (t). But at a number of traps, Nt > 3000, one can observe the asymptotic exit to a plateau at large times. It is possible to explain this behavior due to the random placing of traps on the surface of pores these traps are fulfilled enough rapidly and as a result the observed plateau.
3.2. The Influence of Pore Size on the Time of Capture by Traps (Extinction Time)
In this section, we will consider the change in trap capture time–extinction time in pores with different pore radii. To describe the effect of the pore radius, two trap-filling options were considered.
Option 1: The seeding of traps for different pores was carried out independently. In this case, the general trends described below persist. However, it is quite difficult to compare the results for a specific number of traps. Upon detailed assessment of the configurations, it was found that the concentration of traps along the Z axis significantly affects trapping. The more traps are placed near the buffer zone, the faster trapping occurs. This fact can be logically explained: the probability of a change in the Z coordinate is two times lower than that of a change in the X or Y coordinate.
Option 2: After selecting the trap coordinates for a pore with a radius of 3a, traps with similar coordinates are generated for pores with radii 9a, 27a, and 81a. The traps share the same Z coordinates, while the X and Y coordinates are calculated using the polar coordinate formula for the corresponding radius. These configurations were used for the simulations described below.
Table 2 presents the results of modeling the processes of capture of diffusing particles into traps, namely, determining the extinction time.

Table 2.
Results of determining the time of capture by traps (extinction time) with different radii of pores, a is minimal size of problem.
Table 2 presents the results of modeling the capture of particles by traps in pores of various radii to determine the time of capture by traps (extinction time).
One of the features of results is that with a sufficiently small number of traps Nt < 140 for pores with radii R = 3, 9, 27, even at a larger number of steps (iterations) of the order of t = 1,000,000, it is not possible to achieve a reduction in the number of diffusing particles by 2.7 times and therefore it is impossible to determine the characteristic decrease time when approximating the time dependence of capture by traps with an exponentially decreasing function.
It should be noted that an increase in the number of traps Nt > 210 leads to achievements of the extinction time for all sizes according to R = 3, 9, 27, 81, which were used in numerical experiments. Moreover, due to the randomness of the location of traps on the surface and the random movement of particles inside, sometimes there is an exponential decrease in the number of particles immediately upon the first start (first configuration), sometimes later, but on average 20 starts are required, i.e., 20 numerical experiments are required with a given distribution of traps on the surface of the pores. Therefore, the median value of the extinction time across runs was used as the characteristic extinction time at which an exponential decrease in the number of diffusing particles occurs. The results are presented in Figure 4.
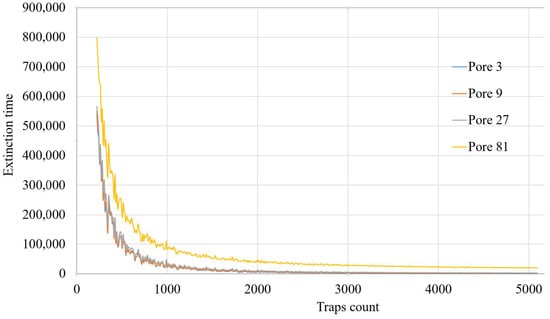
Figure 4.
Dependence of the median capture time on traps (extinction time) on the concentration of traps in pores of radius R = 3a, 9a, 27a and R=81a. In the figure, the x axis is the number of traps in the experiment, and the y axis is the extinction time (median value).
A feature of the presented functional dependencies is the general behavior of the capture time on the concentration of traps for pores with radii R = 3a, 9a, 27a, and significantly different behavior for a pore with a radius R = 81a. For a more complete and thorough analysis of the functional nature of the change in capture time, we will divide the intervals with a small number of traps Nt < 1000 and with a large number of traps Nt > 1000, see Figure 5a.
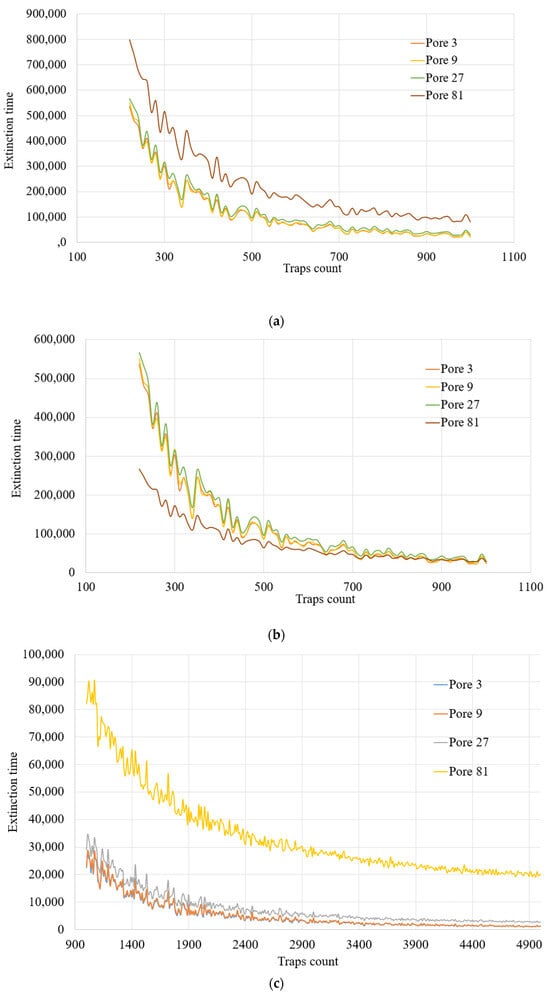
Figure 5.
(a). Dependence of capture time on traps (extinction time) on the number of traps inside pores with different radii and a small number of traps Nt < 1000. (b). Dependence of capture time on traps (extinction time) on the number of traps inside pores with different radii and a small number of traps Nt < 1000. The value for a pore with radius R = 81a is reduced by 3 times. (c). Dependence of capture time on traps (extinction time) on the number of traps inside pores with different radii with a large number of traps Nt > 1000.
For small numbers of traps, the functional dependences of the decrease are of a similar nature: for pores with a radius R = 3a, 9a, 27a they actually coincide, but for a pore with a radius R = 81a the decrease is slower. This can be easily verified by renormalizing the coordinates for a pore with a radius of R = 81a, see Figure 5b.
A feature of the obtained functional dependencies is a slower decrease for the case of a pore with a radius R = 81a, which is due to the need for particles to diffuse over much greater distances to get into traps. Another unexpected feature is the apparently different functional dependence on the number of traps. Further research is required to establish this relationship.
Here we can also see a different functional dependence of the time of capture by traps (extinction time) for pores with a radius of 81 a, in contrast to the behavior for pores with a radius of R = 3a, R = 9a, R = 27a.
Thus, the capture by traps in pores turns out to be significantly different depending on both the size of the pore radius and the number of traps. We will discuss the physical reasons for this in the Conclusion.
In addition, to check the reliability of the data obtained, an estimate of the normality of the distribution of standard deviations for the values of extinction times was obtained, see Appendix A.
4. Conclusions
Numerical modeling of particle capture by traps in cylindrical pores of a material was carried out. Different behaviors of the time depending on the number of active particles at small times and at large times have been established; the characteristic time is the time of capture by traps. Over the interval up to these times , a rapid exponential decrease in the number of active particles due to capture by traps has been established, as expected. The dependence of the characteristic time of decreasing survival particle probability on concentration was established.
The dynamics of the boundary separating regions with trap filling greater than 50% from the region with less filling over time (number of iterations) for different trap concentrations were studied in detail. It has been established that at longer times, the movement of the boundary slows down and reaches a plateau. In our opinion, the possible emergence of a plateau at large times is connected with the fast filling of 50% of the traps and further slow filling because the free traps are placed at large distances from the edge of the pore structure, and there are long times required to reach these free traps. As was written above, the motion of this interface is very important for understanding the damage of porous low-k materials due to diffusion and capture by traps. According to our results, the motion may be described as log(t) with the asymptotic approach to a plateau at large times, which depends on the number of traps. From our point of view, this behavior occurs due to the rapid filling of traps, which are randomly placed on the surface of the pores. If the number of traps is large enough (Nt > 3000Nt > 3000), then most of the diffusing particles are captured, and the motion of the interface is slowed, resulting in the observation of a plateau at long times. Before our theoretical work, by solving the diffusion equation for cylindrical coordinates with boundary absorbing conditions, the logarithmic dependence for the motion of diffusing particles, which is responsible for the motion of the studied interface, was obtained [26]. The reason is the cylindrical symmetry of the diffusion problem. The analogous logarithmic law for the motion of the interface was obtained in the paper [25] in a one-dimensional case. So, the simulation results of our paper are in correspondence with theoretical predictions.
Another factor that influences the capture by traps placed on the internal surface of the pore is the radius of the pore. The process of capture by traps was studied for pores with different radii. According to our results, the capture by traps placed on the internal surface of the pores is similar for pores with radii R = 3a, R = 9a, and R = 27a, but differs for pores with R = 81a. This can be explained by the fact that the space for diffusing particles in pores with small radii is confined, and the capture of particles occurs more frequently. However, in the case of pores with large radii, particles reach the surface less frequently, and the process of capture is slower due to this fact.
Additionally, the processes of capture differ for different numbers of traps. In the case of a small number of traps (less than 1000, Figure 5a), the value of the trap capture time changes by a factor of 10 for pores with R = 3a to R = 27a but changes only by a factor of 5 for R = 81a. However, for a larger number of traps (more than 1000, Figure 5c), the value of the extinction time for pores with R = 81a changes by approximately 5 times, while for pores with radii R = 3a to R = 27a, it decreases to a small value at Nt = 5000. These results show that the capture by traps inside pores depends on the radius of the pores in the material.
These results are important for understanding the influence of pore geometry on the process of particle penetration and capture by traps in pores with random shapes. For example, if the pores have different radii along the axis of the cylindrical pores, as shown in Figure 6, the process of capture by traps in pores with variable radii and the temporal asymptotic of the survival probability of particles will be determined by the “narrow neck”. In the case of a consecutive connection of pores, the effective time will be determined by the characteristic time of this “narrow neck”. According to our results, the difference in extinction time appears when the difference between the values of the radii becomes large enough.
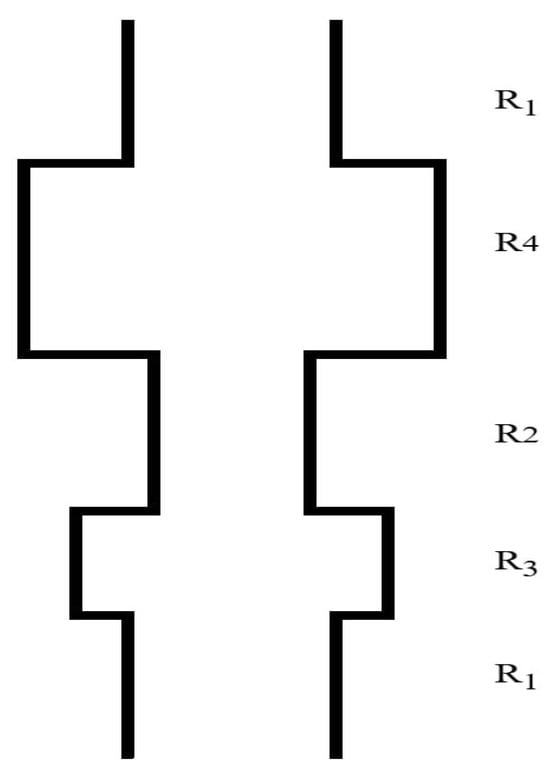
Figure 6.
Pore with variable radius.
Real materials, such as low-k materials or bone nanostructures and cartilage, have a branched system of pores with different radii. As a result, there is a possibility of escaping the “narrow neck”, and the percolation approach must be used to determine the effective extinction time for pores with a complex branched structure. Thus, the obtained results are considered as one of the steps toward studying complex systems with branched pore structures.
One of the important issues in using low-k dielectric materials is the effect of the penetration of active diffusing particles due to porosity on the reliability of microcircuits and the mechanical strength of these materials. From this point of view, our results on diffusion inside pores and capture are also useful for reliability problems.
The investigation of diffusion processes and capture by traps is also important for cell metabolism and protein activity [26]. The processes of water transfer are responsible for the diffusion of nutrients, metabolic exchange, and ion transport within bone structures. They contribute to the mechanism of bone adaptation, the stabilization of the mineral structure, and the interaction between minerals and collagen [27, 28, 29,30,31].
Briefly, we want to discuss the limitations of our paper. It is connected with the simple geometry of the studied object—the single pore in the form of a cylinder. Of course, the real porous low-k materials have a branched structure with different pores of different radii with intersections. Another issue is connected with using the random number counter as the “Mersenne Twister (mt19937)” algorithm to generate random numbers.
Author Contributions
Conceptualization, V.E.A. and B.V.K.; methodology, V.E.A. and B.V.K.; software, B.V.K.; validation, B.V.K. and S.P.M.; formal analysis, V.E.A. and B.V.K.; investigation, V.E.A.; resources, B.V.K. and S.P.M.; data curation, S.P.M.; writing—original draft preparation, V.E.A. and B.V.K.; writing—review and editing, V.E.A. and B.V.K.; visualization, S.P.M.; supervision, V.E.A.; project administration, V.E.A.; funding acquisition, V.E.A. All authors have read and agreed to the published version of the manuscript.
Funding
The research was funded by the Russian Science Foundation № 24-21-00356, https://rscf.ru/project/24-21-00356/ (1 March 2025).
Data Availability Statement
The original materials presented in this study are hosted on the github repository: https://github.com/bairinc0/MDPI_Diffustion_3_D_pores (19 March 2025). Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. The Estimation of Standard Deviation for Extinction Times
To check the data, the normality of the distribution of standard deviations for extinction times for different pore radii was assessed. The results of estimations are presented in Figure A1a,b.
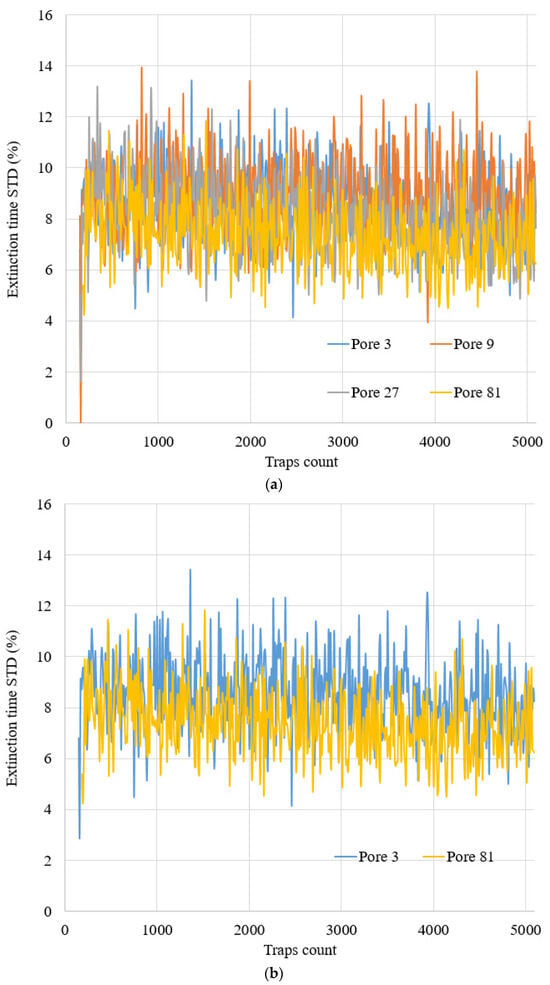
Figure A1.
(a). The standard deviation for pores with different radii, which are presented with different colors. (b). The standard deviation for a case with radius pore R = 3a and R = 81a.
Because the time of capture for all starts is reached for configurations with a number of traps Nt > 200, the graph begins from this value. The value of the mean standard deviation changes from 4% to 14% with the same random dependency for all pores.
After checking, this standard deviation corresponded to a normal distribution of errors.
References
- Montrol, E.W.; Weiss, G.H. Random Walks on Lattices. J. Math. Phys. 1965, 6, 167–175. [Google Scholar]
- Kozlov, S.V.; Ovchinnikov, A.A.; Yenikolopyan, N.S. Diffusion control in reactions between macromolecules. Polym. Sci. U.S.S.R. 1970, 12, 1115–1123. [Google Scholar]
- Ryazanov, G.V. Random walks on a flat lattice with traps. Theor. Math. Phys. 1972, 10, 271–277. [Google Scholar]
- Balagurov, B.Y.; Vaks, V.G. Theory of diffuse phase transitions. J. Exp. Theor. Phys. 1973, 65, 1600–1604. [Google Scholar]
- Balagurov, B.Y.; Vaks, V.G. Random walks of particles on lattices with traps. J. Exp. Theor. Phys. 1973, 65, 1939–1943. [Google Scholar]
- Torquato, S. Diffusion and Reaction Among Traps: Some Theoretical and Simulation Results. J. Stat. Phys. 1991, 65, 1173. [Google Scholar]
- Skolnick, M.; Torquato, S. Simulated diffusion spreadability for characterizing the structure and transport properties of two-phase materials. Acta Mater. 2023, 250, 118857. [Google Scholar] [CrossRef]
- Donsker, M.; Varadhan, S. Asymptotics for the Wiener sausage. Commun. Pure Appl. Math. 1975, 28, 525–565. [Google Scholar]
- Benitez, F.; Duclut, C.; Chaté, H.; Delamotte, B.; Dornic, I.; Muñoz, M.A. Langevin Equations for Reaction-Diffusion Processes. Phys. Rev. Lett. 2016, 117, 100601. [Google Scholar] [CrossRef]
- Ioffe, D.; Velenik, Y. Self-Attractive Random Walks: The Case of Critical Drifts. Commun. Math. Phys. 2012, 313, 209–235. [Google Scholar]
- Agliari, E.; Burioni, R.; Uguzzoni, G. The true reinforced random walk with bias. New J. Phys. 2012, 14, 063027. [Google Scholar]
- Arkhincheev, V.E. Effect of drift on the temporal asymptotic form of the particle survival probability in media with absorbing traps. J. Exp. Theor. Phys. 2017, 124, 275–278. [Google Scholar]
- Maex, K.; Baklanov, M.R.; Shamiryan, D.; Iacopi, F.; Brongersma, S.H.; Yanovitskaya, Z.S. Low Dielectric Constant Materials for Micro Electronics. J. Appl. Phys. 2003, 93, 8793–8841. [Google Scholar]
- Kunnen, E.; Barkema, G.T.; Maes, C.; Shamiryan, D.; Urbanowicz, A.; Struyf, A.; Baklanov, M.R. Integrated diffusion–recombination model for describing the logarithmic time dependence of plasma damage in porous low-k materials. Microelectron. Eng. 2011, 88, 631–634. [Google Scholar]
- Rasadujjaman, M.; Wang, X.; Wang, Y.; Zhang, J.; Arkhincheev, V.E.; Baklanov, M.R. Analytical Study of Porous Organosilicate Glass Films Prepared from Mixtures of 1,3,5- and 1,3-Alkoxysilylbenzenes. Materials 2021, 14, 1881. [Google Scholar] [CrossRef]
- Baklanov, M.R.; Mogilnikov, K.P.; Vishnevskiy, A.S. Challenges in porosity characterization of thin films:cross-evaluation of different techniques. J. Vac. Sci. Technol. A Vac. Surf. Film. 2021, 41, 050802. [Google Scholar]
- Nicholson, C. Diffusion and Related Transport Mechanisms in Brain Tissue. Rep. Prog. Phys. 2001, 64, 815–884. [Google Scholar]
- Bini, F.; Pica, A.; Novelli, S.; Pecci, R.; Bedini, R.; Marinozzi, A.; Marinozzi, F. 3D FEM Model to Simulate Brownian Motion inside Trabecular Tissue from Human Femoral Head. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2022, 10, 500–507. [Google Scholar] [CrossRef]
- Bini, F.; Pica, A.; Marinozzi, A.; Marinozzi, F. 3D random walk model of diffusion in human Hypo- and Hyper- mineralized collagen fibrils. J. Biomech. 2021, 125, 110586. [Google Scholar] [CrossRef]
- Bini, F.; Pica, A.; Marinozzi, A.; Marinozzi, F. A 3D model of the effect of tortuosity and constrictivity on the diffusion in mineralized collagen fibril. Sci. Rep. 2019, 9, 2658. [Google Scholar] [CrossRef]
- Momot, K.I. Diffusion tensor of water in articular cartilage. Eur. Biophys. J. 2011, 40, 81–91. [Google Scholar] [CrossRef] [PubMed]
- Jin, S.; Zador, Z.; Verkman, A. Random-Walk model of diffusion in three dimensions in brain extracellular space: Comparison with microfiberoptic photobleaching measurements. Biophys. J. 2008, 95, 1785–1794. [Google Scholar] [CrossRef] [PubMed]
- Maghsoudi-Ganjeh, M.; Wang, X.; Zeng, X. Computational investigation of the effect of water on the nanomechanical behavior of bone. J. Mech. Behav. Biomed. Mater. V 2020, 101, 103454. [Google Scholar]
- Vilinski-Mazur, K.; Kirillov, B.; Rogozin, O.; Kolomenskiy, D. Numerical modeling of oxygen diffusion in tissue spheroids undergoing fusion using function representation and finite volumes. Sci. Rep. 2025, 15, 5054. [Google Scholar]
- Safaverdi, S.; Barkema, G.T.; Kunnen, E.; Urbanowicz, A.M.; Maes, C. Saturation of front propagation in a reaction-diffusion process describing plasma damage in porous low-k materials. Phys. Rev. B 2011, 83, 245320. [Google Scholar]
- Arkhincheev, V.E.; Kunnen, E.; Baklanov, M.R. Active species in porous media: Random walk and capture in traps. J. Microelectron. 2011, 88, 686–689. [Google Scholar]
- Sycheva, A.A.; Voronina, E.N.; Rakhimova, T.V.; Rakhimov, A.T. Influence of porosity and pore size on sputtering of nanoporous structures by low-energy Ar ions: Molecular dynamics study. Appl. Surf. Sci. 2019, 475, 1021–1032. [Google Scholar]
- Sycheva, A.A.; Voronina, E.N.; Palov, A.P. Analysis of results of silicon sputtering simulation with various Ar–Si potentials. J. Surf. Investig. X-Ray Synchrotron Neutron Tech. 2019, 13, 1272–1279. [Google Scholar]
- Surowiec, R.K.; Allen, M.R.; Wallace, J.M. Bone Hydration: How We Can Evaluate It, What Can It Tell Us, and Is It an Effective Therapeutic Target? Bone Rep. 2022, 16, 101161. [Google Scholar]
- Wang, Y.; Von Euw, S.; Fernandes, F.M.; Cassaignon, S.; Selmane, M.; Laurent, G.; Pehau-Arnaudet, G.; Coelho, C.; Bonhomme-Coury, L.; Giraud-Guille, M.M.; et al. Water-Mediated Structuring of Bone Apatite. Nat. Mater. 2013, 12, 1144–1153. [Google Scholar]
- Rai, R.K.; Sinha, N. Dehydration-Induced Structural Changes in the Collagen-Hydroxyapatite Interface in Bone by High-Resolution Solid-State NMR Spectroscopy. J. Phys. Chem. C 2011, 115, 14219–14227. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).