Numerical Study and Model Validation of Low-Pressure Hydrogen–Air Combustion in a Closed Vessel
Abstract
1. Introduction
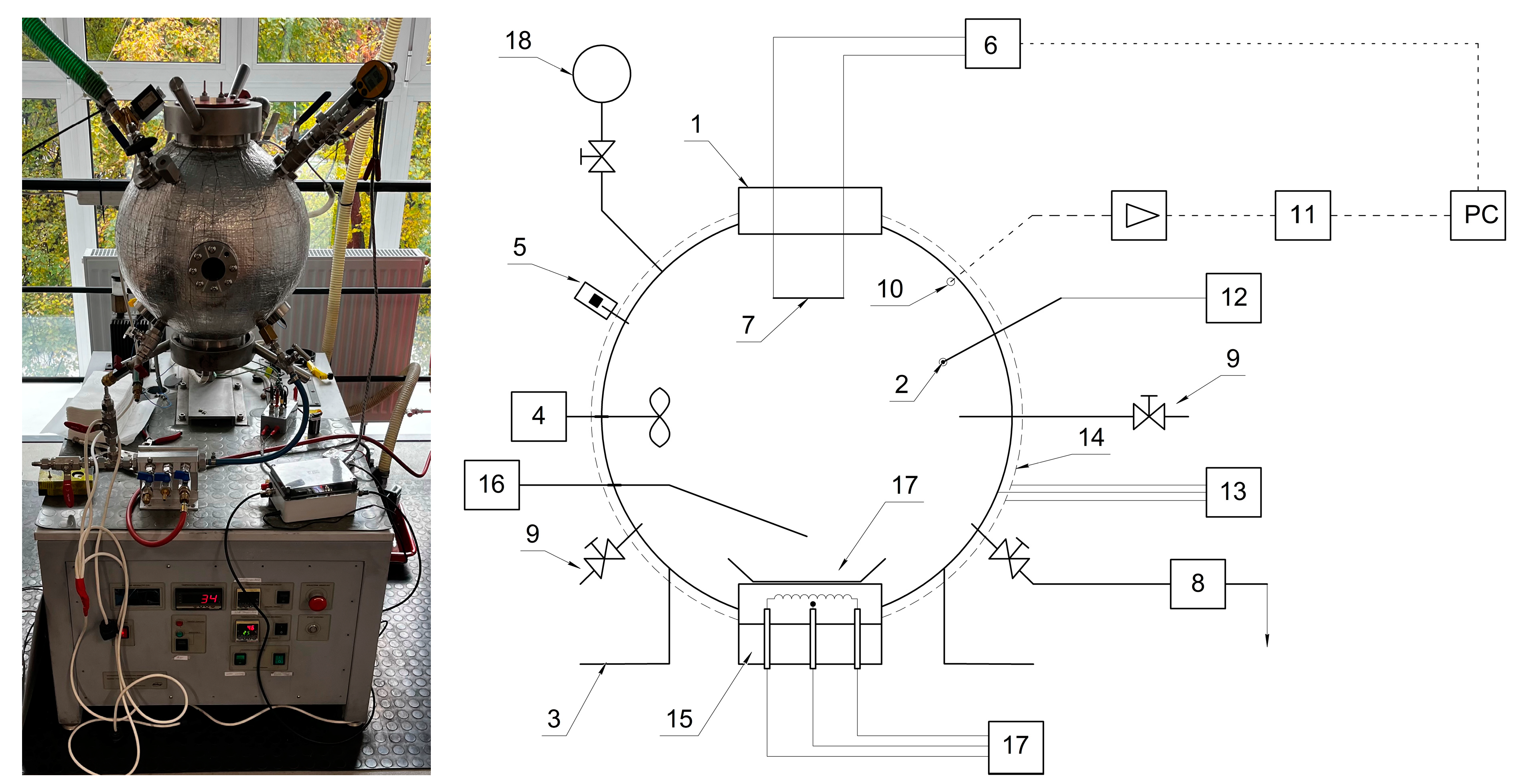
2. Materials and Methods
2.1. Governing Equations
2.2. Solver Settings
3. Results and Discussion
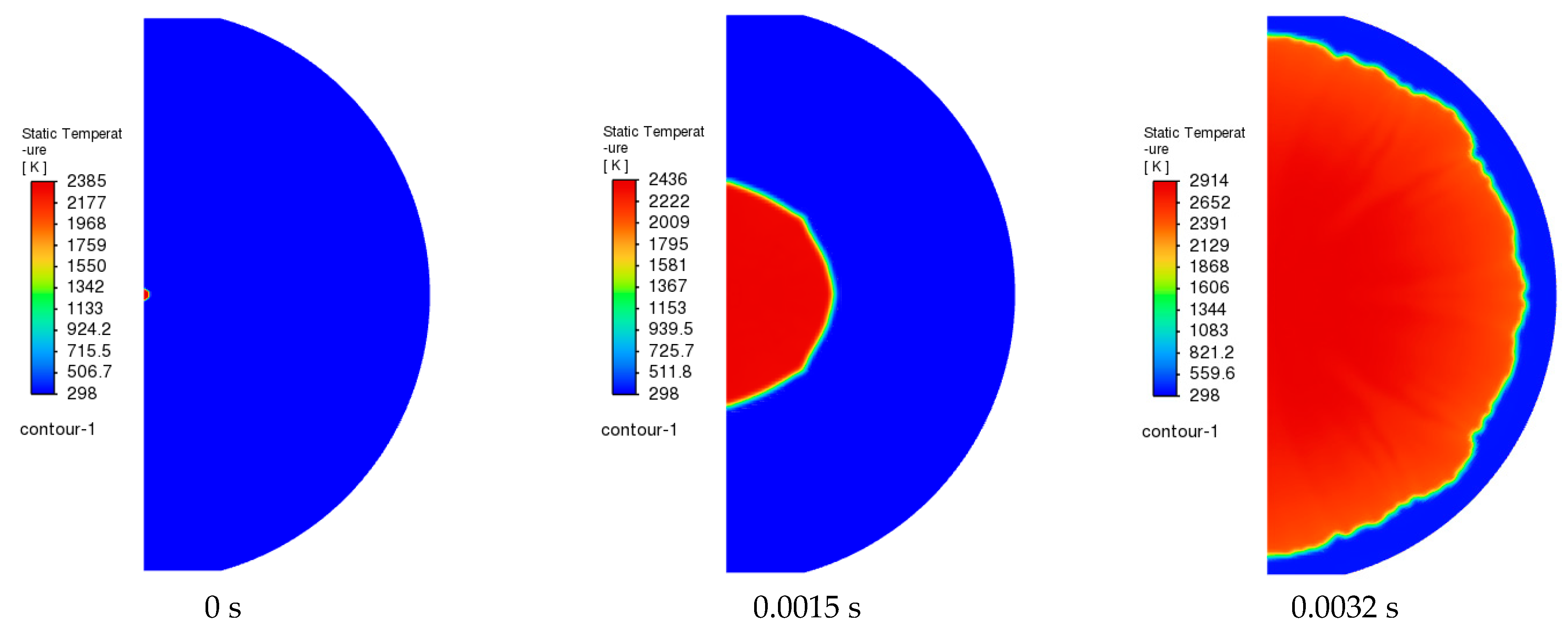
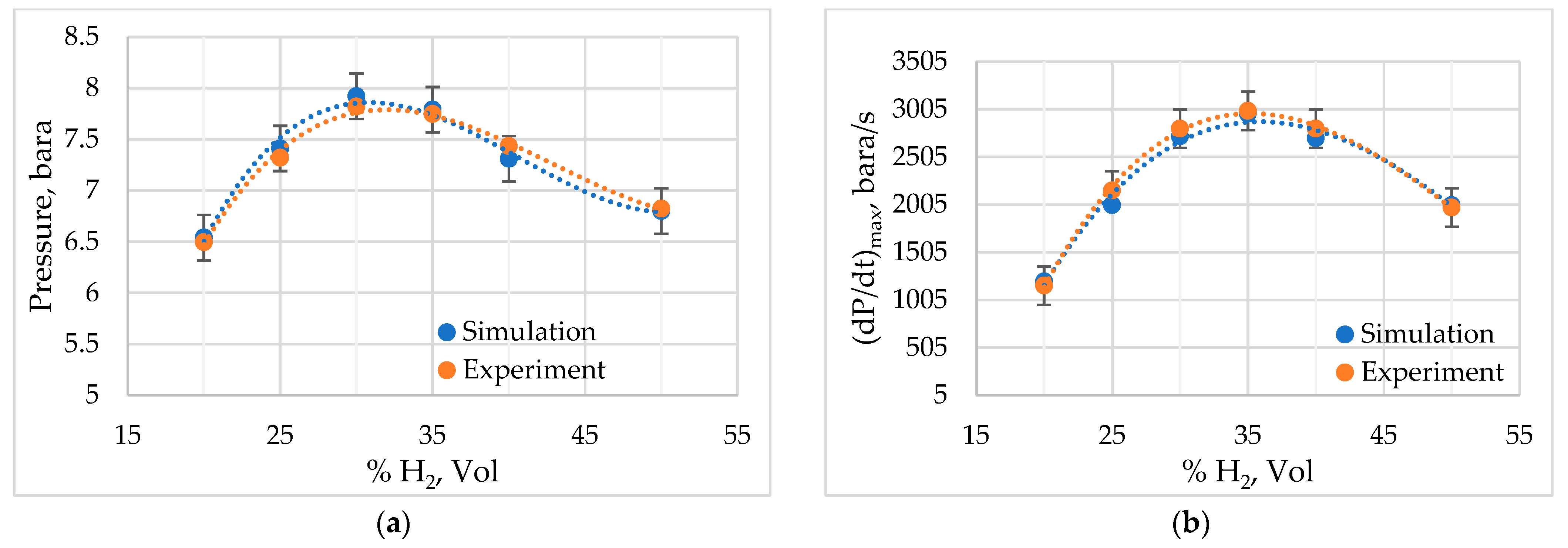
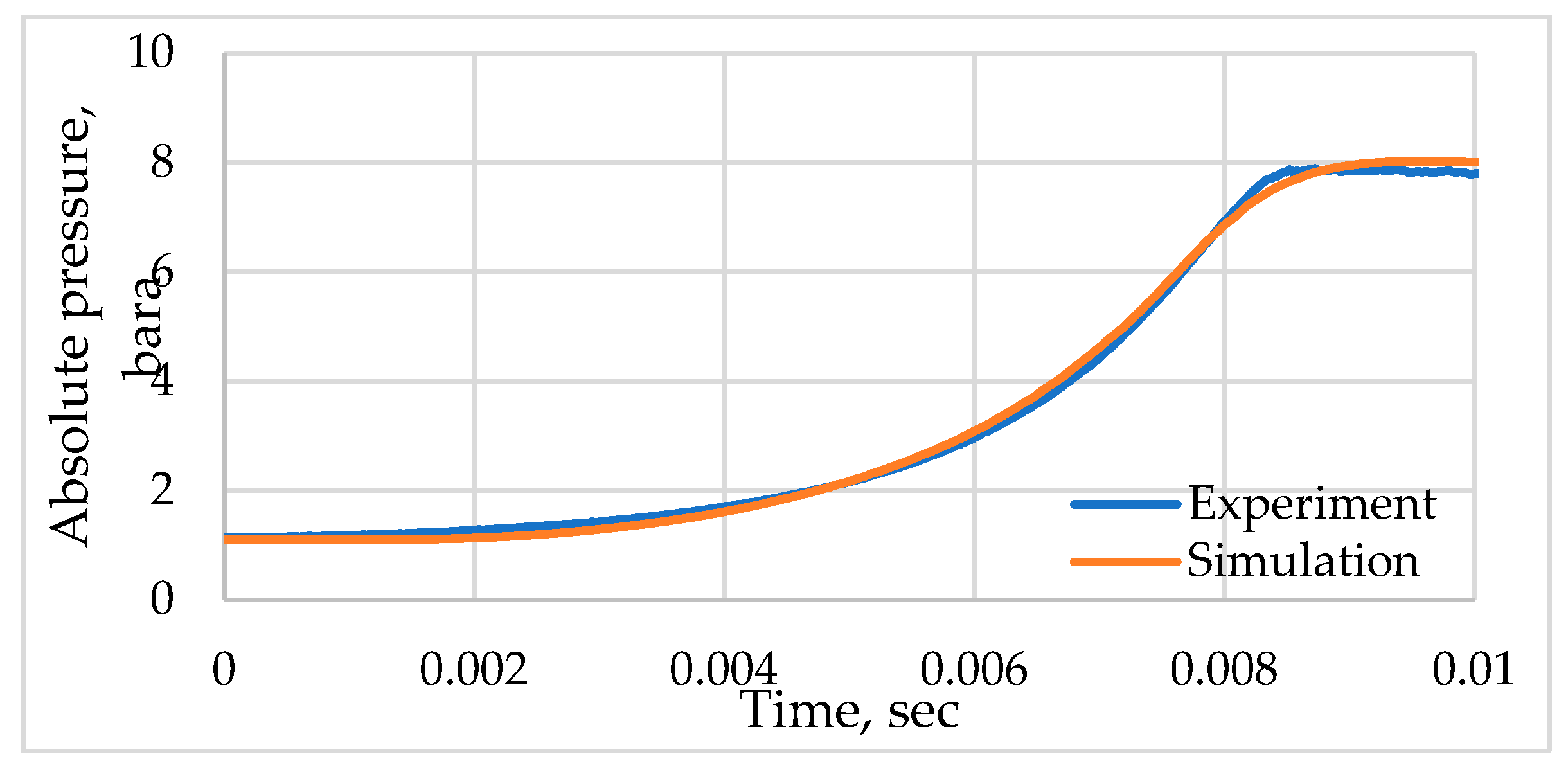
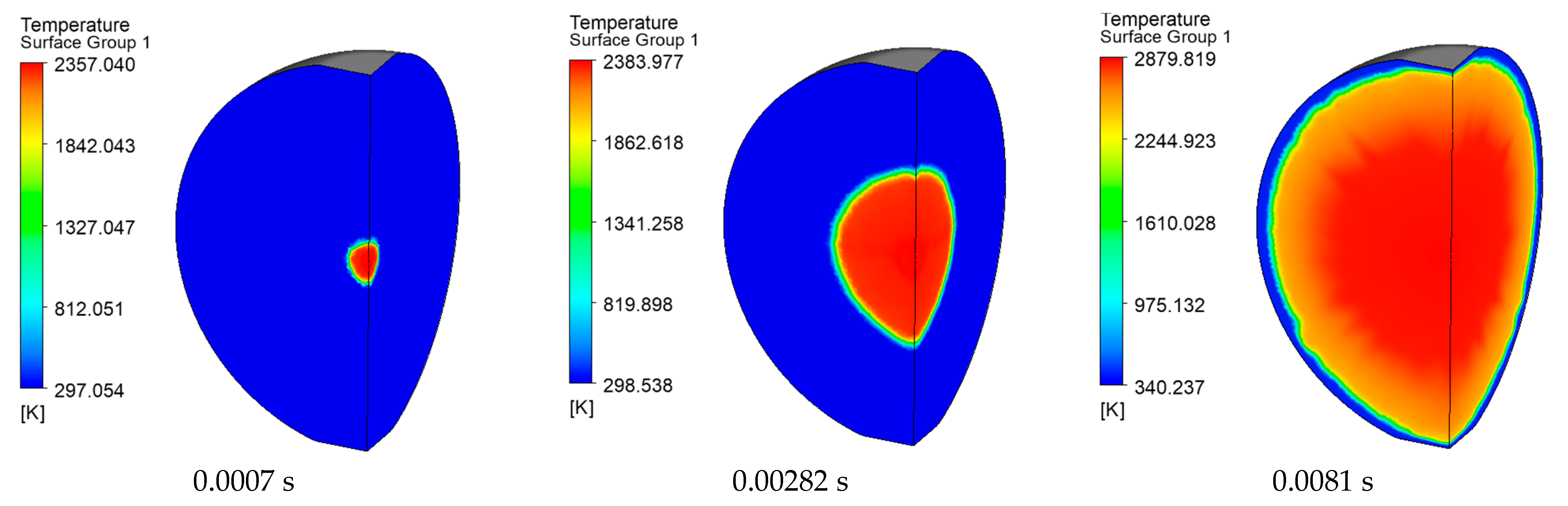
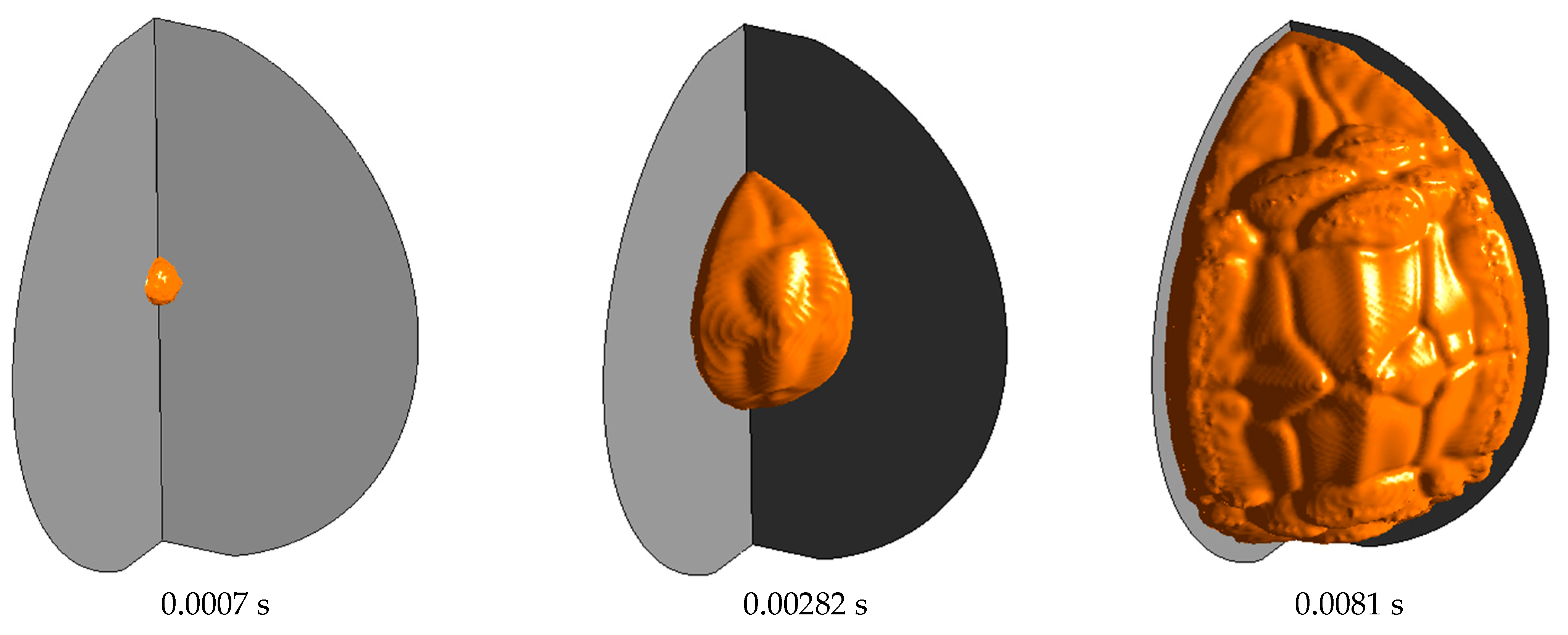
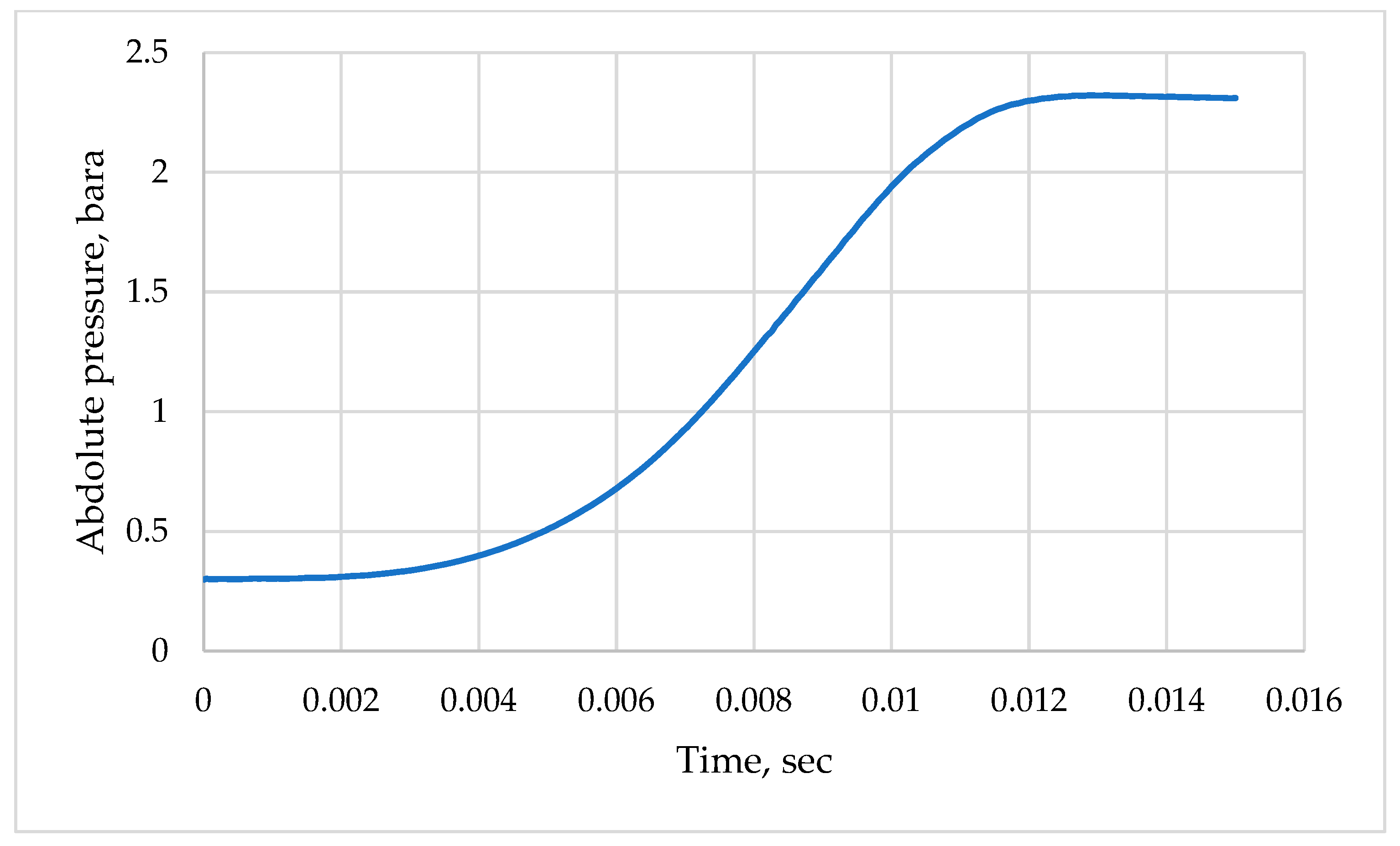
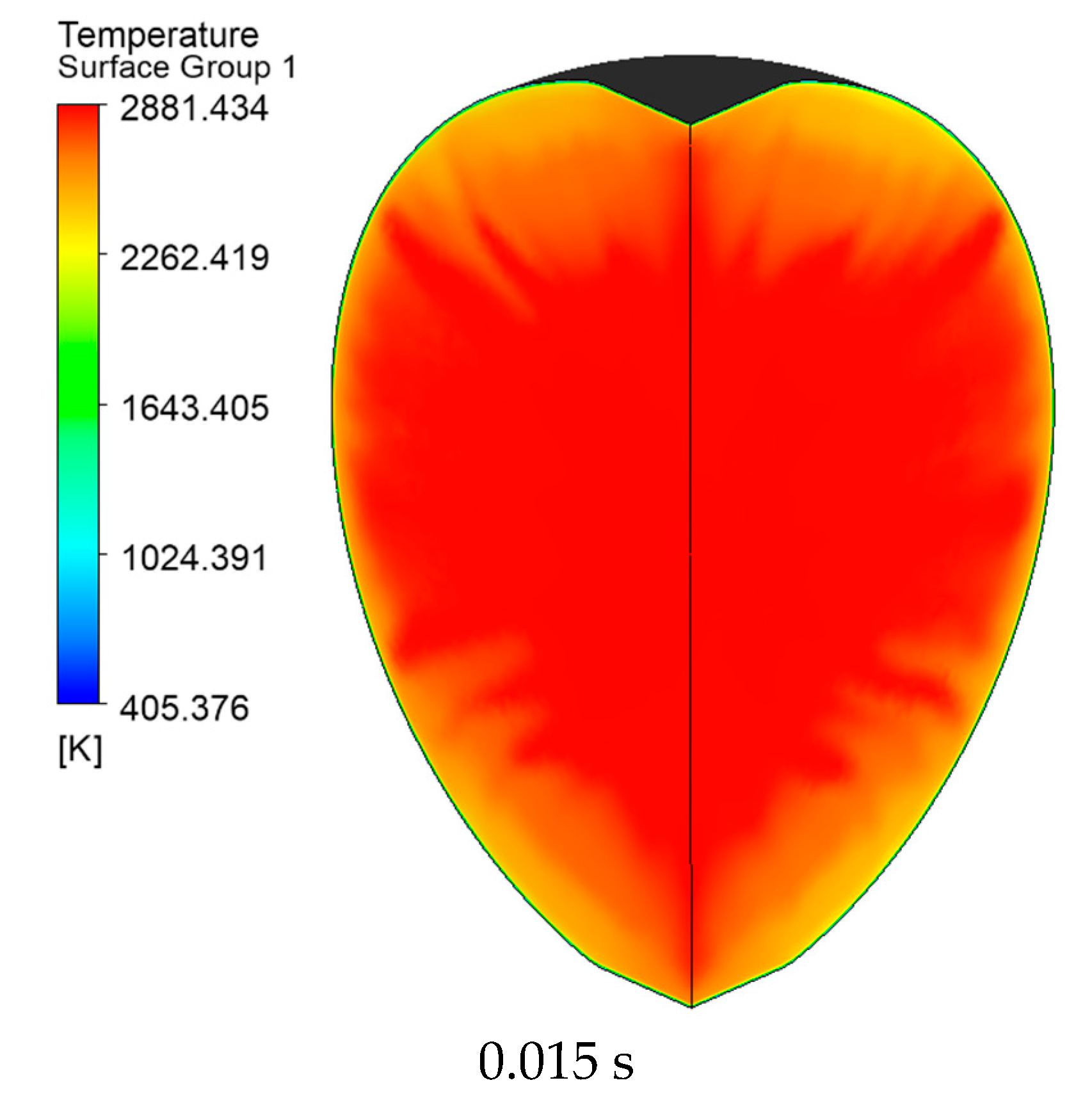
3.1. Model Verification
3.2. Simulation of the Stoichiometric Hydrogen–Air Mixture Combustion at Low Initial Pressure
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, S.; Li, X.; Jin, H.; Liu, Y.; Wu, Y. A Numerical Simulation Study on the Combustion of Natural Gas Mixed with Hydrogen in a Partially Premixed Gas Water Heater. Energies 2024, 17, 4069. [Google Scholar] [CrossRef]
- Ma, X.; Nie, B.; Wang, W.; Zhao, D.; Zhang, Y.; Yang, Y.; Ma, C.; Hu, B.; Chang, L.; Yang, L. Effect of hydrogen concentration, initial pressure and temperature on mechanisms of hydrogen explosion in confined spaces. Combust. Flame 2024, 269, 113696. [Google Scholar] [CrossRef]
- Han, H.; Ma, Q.; Qin, Z.; Li, Y.; Kong, Y. Experimental study on combustion and explosion characteristics of hydrogen-air premixed gas in rectangular channels with large aspect ratio. Int. J. Hydrogen Energy 2024, 57, 1041–1050. [Google Scholar] [CrossRef]
- Swaminathan, S.; Spijker, C.; Gruber, M.; Kofler, I.; Raupenstrauch, H. Numerical Simulation and Performance Evaluation of Hydrogen-Enriched Natural Gas for an Industrial Burner in a Testing Chamber. Energies 2023, 16, 6380. [Google Scholar] [CrossRef]
- Giacomazzi, E.; Troiani, G.; Di Nardo, A.; Calchetti, G.; Cecere, D.; Messina, G.; Carpenella, S. Hydrogen Combustion: Features and Barriers to Its Exploitation in the Energy Transition. Energies 2023, 16, 7174. [Google Scholar] [CrossRef]
- Ricci, F.; Zembi, J.; Avana, M.; Grimaldi, C.N.; Battistoni, M.; Papi, S. Analysis of Hydrogen Combustion in a Spark Ignition Research Engine with a Barrier Discharge Igniter. Energies 2024, 17, 1739. [Google Scholar] [CrossRef]
- Chijioke, E.G.; Teodorczyk, A. CFD simulation of a vortex-controlled diffuser for a jet engine burner. Combust. Engines 2023, 195, 71–82. [Google Scholar] [CrossRef]
- Rudy, W.; Pekalski, A.; Makarov, D.; Teodorczyk, A.; Molkov, V. Prediction of Deflagrative Explosions in Variety of Closed Vessels. Energies 2021, 14, 2138. [Google Scholar] [CrossRef]
- Reyes, M.; Tinaut, F.V.; Horrillo, A.; Lafuente, A. Experimental characterization of burning velocities of premixed methane-air and hydrogen-air mixtures in a constant volume combustion bomb at moderate pressure and temperature. Appl. Therm. Eng. 2018, 130, 684–697. [Google Scholar] [CrossRef]
- Kamran, M.; Turzynski, M. Exploring hydrogen energy systems: A comprehensive review of technologies, applications, prevailing trends, and associated challenges. J. Energy Storage 2024, 96, 112601. [Google Scholar] [CrossRef]
- Amzin, S.; Mohd Yasin, M.F. Modelling of a Bluff-Body Stabilised Premixed Flames Close to Blow-Off. Computation 2021, 9, 43. [Google Scholar] [CrossRef]
- Di Nardo, A.; Calabrese, M.; Venezia, V.; Portarapillo, M.; Turco, M.; Di Benedetto, A.; Luciani, G. Addressing Environmental Challenges: The Role of Hydrogen Technologies in a Sustainable Future. Energies 2023, 16, 7908. [Google Scholar] [CrossRef]
- Shen, H.; Crespo del Granado, P.; Jorge, R.S.; Loffler, K. Environmental and climate impacts of a large-scale deployment of green hydrogen in Europe. Energy Clim. Change 2024, 5, 100133. [Google Scholar] [CrossRef]
- Freitag, P.; Stolle, D.; Kullmann, F.; Linssen, J.; Stolten, D. A techno-economic analysis of future hydrogen reconversion technologies. Int. J. Hydrogen Energy 2024, 77, 1254–1267. [Google Scholar] [CrossRef]
- Plankovskyy, S.; Popov, V.; Shypul, O.; Tsegelnyk, Y.; Tryfonov, O.; Brega, D. Advanced thermal energy method for finishing precision parts. In Advanced Machining and Finishing; Gupta, K., Pramanik, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 527–575. [Google Scholar] [CrossRef]
- Plankovskyy, S.; Shypul, O.; Tsegelnyk, Y.; Brega, D.; Tryfonov, O.; Malashenko, V. Basic Principles for Thermoplastic Parts Finishing With Impulse Thermal Energy Method. In Handbook of Research on Advancements in the Processing, Characterization, and Application of Lightweight Materials; Kumar, K., Babu, B., Davim, J., Eds.; IGI Global: Hershey, PA, USA, 2022; pp. 49–87. [Google Scholar] [CrossRef]
- Galliková, J.; Grenčík, J.; Barta, D.; Barlok, M. FMECA analysis of thermal deburring machine EXTRUDE HONE TEM P-350. Sci. J. Marit. Univ. Szczec. 2020, 63, 9–16. [Google Scholar] [CrossRef]
- Kulik, P. Thermal Deburring Machine and Method of Thermal Deburring. WO Patent 2019/054886, 21 March 2019. [Google Scholar]
- Shypul, O.; Garyn, V.; Tryfonov, O.; Myntiuk, V.; Egedy, A. Study of the green hydrogen-air mixture formation in closed chamber with given composition. Hung. J. Ind. Chem. 2024, 52, 57–62. [Google Scholar] [CrossRef]
- Fluent Theory Guide. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v242/en/flu_th/flu_th.html (accessed on 29 October 2024).
- Nguyen, P.; Vervisch, L.; Subramanian, V.; Domingo, P. Multi-Dimensional Flamelet-Generated Manifolds for Partially Premixed Combustion. Combust. Flame 2010, 157, 43–61. [Google Scholar] [CrossRef]
- Lodier, G.; Vervisch, L.; Moureau, V.; Domingo, P. Composition-Space Premixed Flamelet Solution with Differential Diffusion for In Situ Flamelet-Generated Manifolds. Combust. Flame 2011, 158, 2009–2016. [Google Scholar] [CrossRef]
- Available online: http://combustion.berkeley.edu/gri-mech/version30/text30.html (accessed on 10 November 2024).
- Grabarczyk, M.; Żbikowski, M.; Mężyk, Ł.; Teodorczyk, A. Temperature effect on explosion parameters of hydrogen-air deflagrations in presence of water vapor. Chall. Mod. Technol. 2016, 7, 39–44. [Google Scholar] [CrossRef]
- BS EN 15967:2011; Determination of Maximum Explosion Pressure and the Maximum Rate of Pressure Rise of Gases and Vapors. BSI: London, UK, 2012.
- Tryfonov, O.; Sastela, O. Simulaiton of Gas Mixtures Combustion in a Closed Combustion Chamber of Thermal Pulse Equipment. Open Information and Computer Integration Technologies No 72. 2016, pp. 141–149. Available online: https://dspace.library.khai.edu/xmlui/bitstream/handle/123456789/5330/p141-149.pdf?sequence=1&isAllowed=y (accessed on 12 January 2025).

| Parameter | Value |
|---|---|
| Solver | Pressure-based (segregated) |
| Pressure–Velocity coupling | COUPLED |
| Spatial discretization | Second-order/second-order UPWIND |
| Temporal discretization | Second-order implicit |
| Gradient discretization | Least-squares cell-based |
| Case # | H2 Volume Fraction | Initial Pressure | Initial Mixture Temperature |
|---|---|---|---|
| Case # 1 | 20% | 0.1 MPa | 25 °C |
| Case # 2 | 25% | 0.1 MPa | 25 °C |
| Case # 3 | 30% | 0.1 MPa | 25 °C |
| Case # 4 | 35% | 0.1 MPa | 25 °C |
| Case # 5 | 40% | 0.1 MPa | 25 °C |
| Case # 6 | 50% | 0.1 MPa | 25 °C |
| Case # | Initial Pressure | Initial Mixture Temperature |
|---|---|---|
| Case # 1 | 0.3 bara | 297 K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tryfonov, O.; Teodorczyk, A.; Shypul, O.; Rudy, W.; Garin, V.; Myntiuk, V.; Tkachenko, D. Numerical Study and Model Validation of Low-Pressure Hydrogen–Air Combustion in a Closed Vessel. Computation 2025, 13, 54. https://doi.org/10.3390/computation13020054
Tryfonov O, Teodorczyk A, Shypul O, Rudy W, Garin V, Myntiuk V, Tkachenko D. Numerical Study and Model Validation of Low-Pressure Hydrogen–Air Combustion in a Closed Vessel. Computation. 2025; 13(2):54. https://doi.org/10.3390/computation13020054
Chicago/Turabian StyleTryfonov, Oleh, Andrzej Teodorczyk, Olga Shypul, Wojciech Rudy, Vadym Garin, Vitalii Myntiuk, and Denys Tkachenko. 2025. "Numerical Study and Model Validation of Low-Pressure Hydrogen–Air Combustion in a Closed Vessel" Computation 13, no. 2: 54. https://doi.org/10.3390/computation13020054
APA StyleTryfonov, O., Teodorczyk, A., Shypul, O., Rudy, W., Garin, V., Myntiuk, V., & Tkachenko, D. (2025). Numerical Study and Model Validation of Low-Pressure Hydrogen–Air Combustion in a Closed Vessel. Computation, 13(2), 54. https://doi.org/10.3390/computation13020054







