Increasing the Number of Material Recognition Classes in Cargo Inspection Using the X-Ray Dual High-Energy Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Classification of Materials by the Dual-Energy Method
3. Mathematical Model of Material Recognition by the Dual High-Energy Method
3.1. Mathematical Model of Material Recognition by Dual-Energy Method by Level Lines
- -
- Mathematical model of material recognition by Dual-Energy Method by Level Lines
- -
- Mathematical Model for Estimating the TO Thickness in Free Run Lengths
- -
- Material Recognition Criteria by Level Line Method
- -
- Recognition Parameter in the DEM Implementation by the Level Lines Method
- -
- Recognition Calibration in the DEM Implementation by the Level Lines Method
- -
- Material Recognition Criteria by Level Line Method
- -
- Estimation of the Effective Atomic Number by the Dual High-Energy Method
- -
- Monoenergetic Implementations of DEMs
- -
- Non-monoenergetic DEM Implementation.
3.1.1. Mathematical Model for Estimating the TO Thickness in Free Run Lengths
- -
- maximum energies of the bremsstrahlung EL, EH, MeV (EL < EH);
- -
- numerical energy spectra of the bremsstrahlung source for maximum energies EL and EH − f(E, EL), f(E, EH);
- -
- pulse repetition rate ν, Hz;
- -
- the average number of photons emitted by the source in one pulse (subscript “1”) and falling on the front surface of the radiation-sensitive element (RSE) of the detector, for maximum energies EL and EH − N1L, N1H;
- -
- number of bremsstrahlung pulses for generating digital signals for maximum energies EL and EH − nL, nH;
- -
- density, material atomic number, and pre-filter thickness—ρf, Zf, hf.
- -
- chemical formula of the RSE detector substance Chemd
- -
- RSE detector thickness and density of its material hd, cm, ρd, g/cm3;
- -
- ADC bit depth kADC, bits;
- -
- degree of filling of the digital signal range CADC;
- -
- maximum TO thickness in mean free paths P(Emax), MFP;
- -
- minimum digital signal level M.
- -
- the set of points V of the three-dimensional space occupied by the TO, ;
- -
- distribution of vectors , , and the density ρ of the material over the volume V.
3.1.2. Material Recognition Criteria by Level Lines Method
Recognition Parameter in the DEM Implementation by the Level Lines Method
Recognition Calibration in the DEM Implementation by the Level Lines Method
Material Recognition Criteria by Level Line Method
3.2. Estimation of the Effective Atomic Number by the Dual High-Energy Method
3.2.1. Monoenergetic Implementations of DEMs
3.2.2. Non-Monoenergetic DEM Implementation
4. Results
4.1. A Hypothetical Monoenergetic Realization of the Dual-Energy Method
- -
- energy spectra of radiation f(E, EL), f(E, EH) are described by δ-functions;
- -
- the detectors are total absorption detectors, i.e., ε(EL,H) ≈ 1 and Eab(EL,H) = E;
- -
- the number of photons incident on the detector surface for the maximum energies EL and EH is large; i.e., N1L → ∞ and N1H → ∞;
- -
- the ADC bit depth is high, i.e., kADC → ∞.
4.2. Material Recognition Using the High-Energy Dual-Energy Method
4.2.1. An Example of Calculating the Material Recognition Parameter by the Level Lines Method
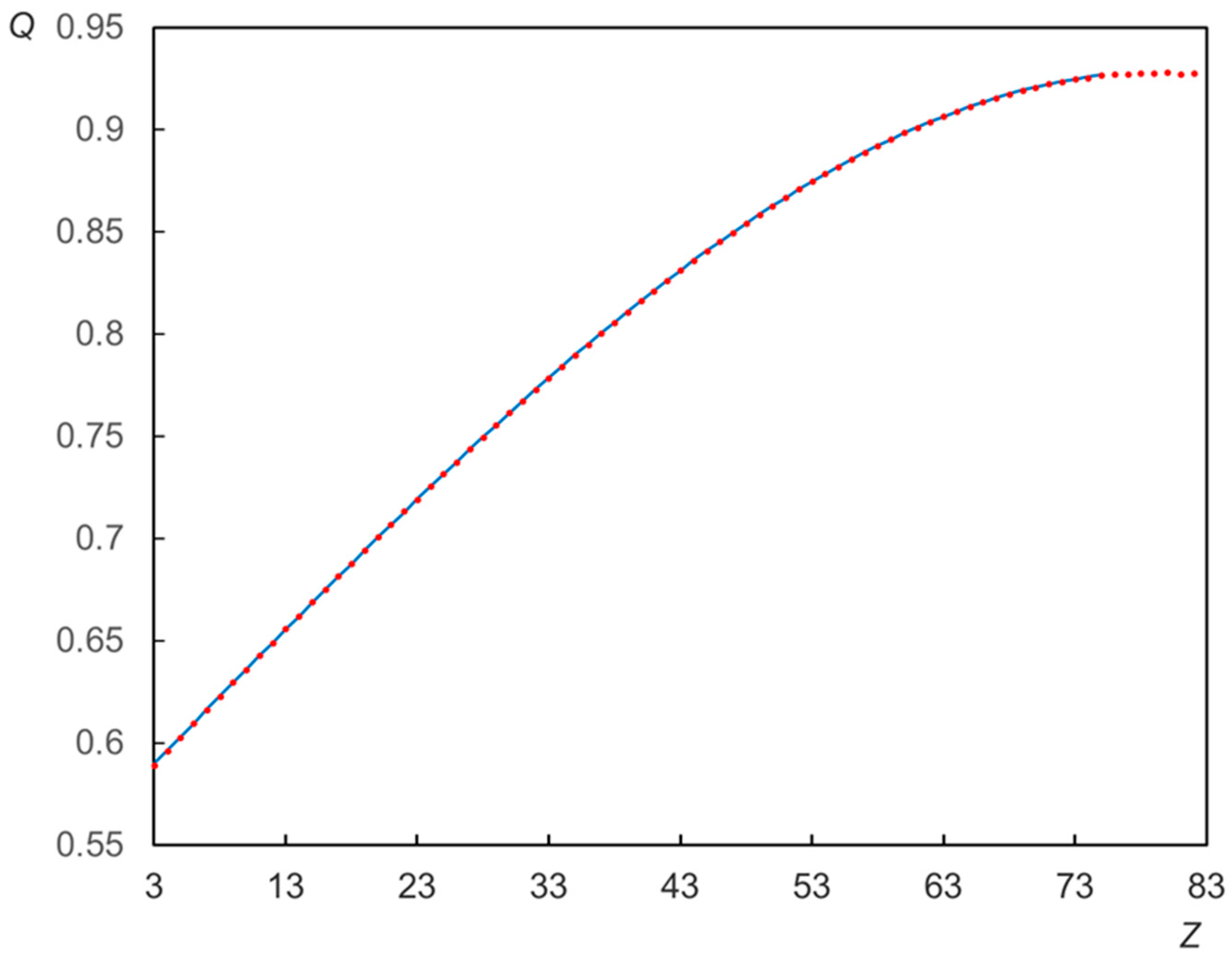
4.2.2. An Example of Calculating the Effective Atomic Number
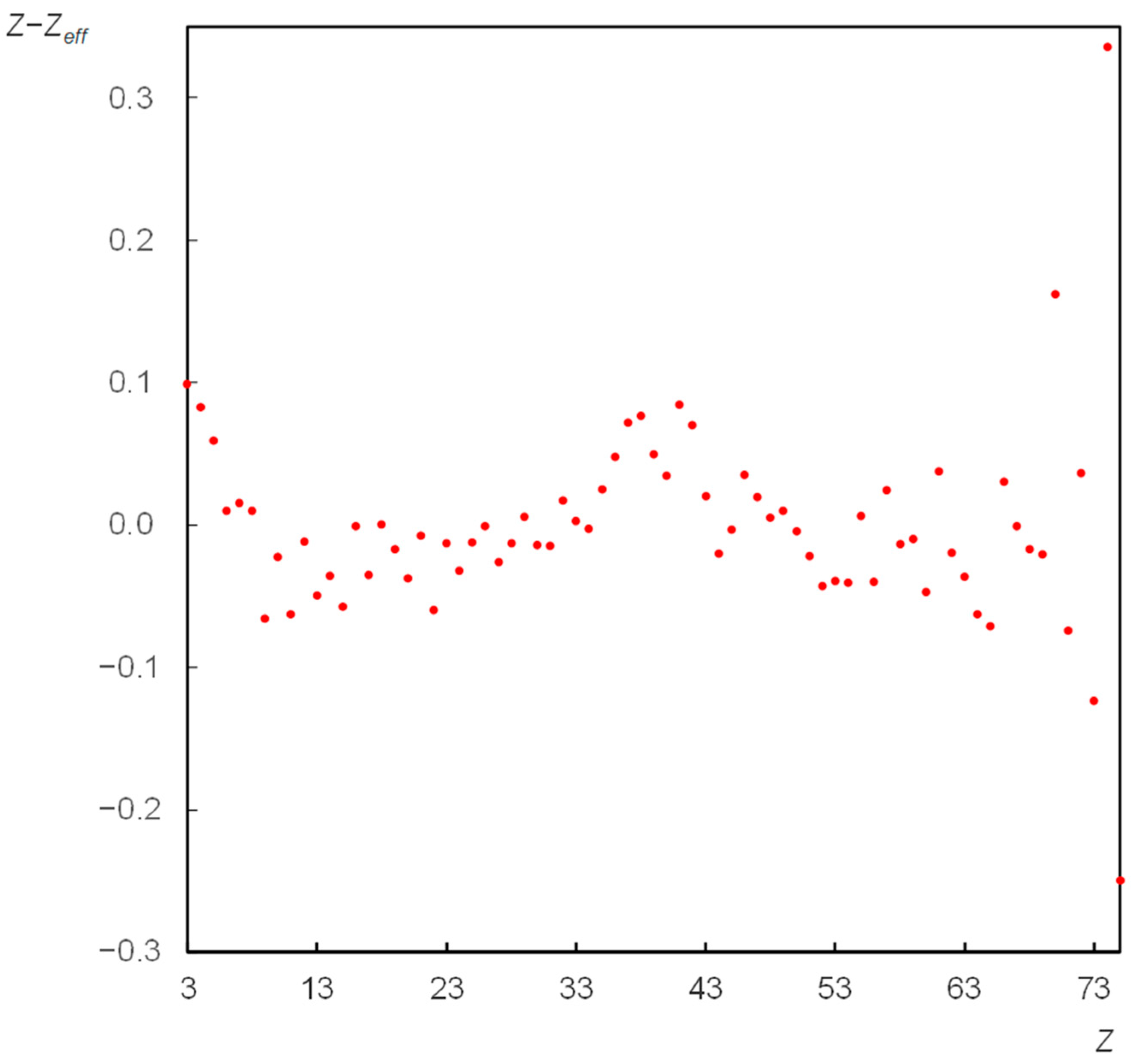
5. Simulation
6. Discussion
6.1. General Recommendations
6.2. Increasing the Accuracy of Effective Atomic Number Estimation
6.3. Comparison with Related Works
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ghaebi, M.; Tajik, M.; Azimirad, R. Studying the effect of the scanned objects’ location on material discrimination in a dual-energy cargo inspection system. Nucl. Instrum. Methods Phys. Res. B 2022, 510, 9–48. [Google Scholar] [CrossRef]
- Kayalvizhi, R.; Kumar, A.; Malarvizhi, S.; Topkar, A.; Vijayakumar, P. Raw data processing techniques for material classification of objects in dual energy X-ray baggage inspection systems. Radiat. Phys. Chem. 2022, 193, 109512. [Google Scholar] [CrossRef]
- Benedykciuk, E.; Denkowski, M.; Dmitruk, K. Material classification in X-ray images based on multi-scale CNN. Signal Image Video Process. 2021, 15, 1285–1293. [Google Scholar] [CrossRef]
- Fang, W.; Li, L. Attenuation image referenced (AIR) effective atom number image calculation for MeV dual-energy container CT using image-domain deep learning framework. Results Phys. 2022, 35, 105406. [Google Scholar] [CrossRef]
- Osipov, S.P.; Usachev, E.Y.; Chakhlov, S.V.; Shchetinkin, S.A.; Song, S.; Zhang, G.; Batranin, A.V.; Osipov, O.S. Limit capabilities of identifying materials by high dual- and multi-energy methods. Russ. J. Nondestruct. Test. 2019, 55, 687–699. [Google Scholar] [CrossRef]
- Saverskiy, A.Y.; Dinca, D.C.; Rommel, J.M. Cargo and container X-ray inspection with intra-pulse multi-energy method for material discrimination. Phys. Procedia 2015, 66, 232–241. [Google Scholar] [CrossRef][Green Version]
- Arodzero, A.; Boucher, S.; Kutsaev, S.V.; Lanza, R.C.; Palermo, V.; O’Shea, F.; Ziskin, V. MEBCIS: Multi-energy betatron-based cargo inspection system. In Proceedings of the 2016 IEEE Nuclear Science Symposium, Medical Imaging Conference and Room-Temperature Semiconductor Detector Workshop (NSS/MIC/RTSD), Strasbourg, France, 29 October–6 November 2016; IEEE: Strasbourg, France, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Osipov, S.P.; Usachev, E.J.; Chakhlov, S.V.; Schetinkin, S.A.; Osipov, O.S. Inspection of bulk cargoes and liquids by the dual energy method. Radiat. Phys. Chem. 2020, 177, 109133. [Google Scholar] [CrossRef]
- Mery, D.; Pieringer, C. X-Ray Testing. Computer Vision for X-Ray Testing; Springer: Cham, Switzerland, 2021; pp. 1–41. [Google Scholar] [CrossRef]
- Osipov, S.; Chakhlov, S.; Osipov, O.; Shtein, A.; Van, J. Adequacy criteria of models of the cargo inspection system with material discrimination option. J. Phys. Conf. Ser. 2016, 671, 012010. [Google Scholar] [CrossRef]
- Moshkbar-Bakhshayesh, K.; Afarideh, H.; Mohtashami, S.; Azimirad, R. Inspection of Cargo Using Dual-Energy X-Ray Radiography: A Review. Radiat. Phys. Chem. 2023, 212, 111180. [Google Scholar] [CrossRef]
- Lee, T.B.; Kang, H.S. Material Estimation Method Using Dual-Energy X-Ray Image for Cargo Inspection System. J. Korea Ind. Inf. Syst. Res. 2018, 1, 1–12. [Google Scholar] [CrossRef]
- Turturica, G.V.; Iancu, V.; Ur, C.A. A neural-network based approach to cargo inspections using photon spectroscopy. Nucl. Instrum. Methods Phys. Res. A Accel. Spectrom. Detect. Assoc. Equip. 2021, 1010, 165553. [Google Scholar] [CrossRef]
- Ogorodnikov, S.; Petrunin, V. Processing of interlaced images in 4–10 MeV dual energy customs system for material recognition. Phys. Rev. Accel. Beams 2002, 5, 104701. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Zhao, T.; Li, L. A curve-based material recognition method in MeV dual-energy X-ray imaging system. JNST 2016, 27, 25. [Google Scholar] [CrossRef]
- Rapiscan Systems. Cargo & Vehicle Inspection. Available online: https://www.rapiscansystems.com/en/products/category/cargo-and-vehicle-inspection (accessed on 25 November 2024).
- NUCTECH. Europe. Cargo Inspection & Vehicle Scanners. Available online: https://nuctecheurope.com/products/cargo-container (accessed on 27 November 2024).
- LINEV Systems US, Inc. DTP 7500/200UV. Available online: https://linevsystems.us/product/dtp-7500-200uv/ (accessed on 26 November 2024).
- Smiths Detections. Cargo & Vehicle Inspection. Available online: https://www.smithsdetection.com/product-finder/cargo-vehicle-inspection (accessed on 25 November 2024).
- Diagnostika-M LLC. Digital Systems and Installations. Available online: https://en.tsnk.ru/equip/equip/digital-systems-and-installations/ (accessed on 27 November 2024).
- Scantronic Systems. Available online: https://scantronicsystems.com/en/catalog/ (accessed on 27 November 2024).
- Duvillier, J.; Dierick, M.; Dhaene, J.; Van Loo, D.; Masschaele, B.; Geurts, R.; Van Hoorebeke, L.; Boone, M.N. Inline multi-material identification via dual energy radiographic measurements. NDT&E Int. 2018, 94, 120–125. [Google Scholar] [CrossRef]
- Yalçın, O.; Reyhancan, İ.A. Detection of explosive materials in dual-energy X-Ray security systems. Nucl. Instrum. Methods Phys. Res. A Accel. Spectrom. Detect. Assoc. Equip. 2022, 1040, 167265. [Google Scholar] [CrossRef]
- Çığla, C.; Küçükateş, B.; Yalçın, O.; Ak, D.S.; Işıkoğlu, Ş.T. Robust material classification on dual-energy x-ray imaging devices. Anomaly Detection and Imaging with X-Rays (ADIX) VII. SPIE 2022, 12104, 18–34. [Google Scholar] [CrossRef]
- Hubbell, J.H. Photon Cross Sections, Attenuation Coefficients, and Energy Absorption Coefficients from 10 keV to 100 GeV; U.S. Department of Commerce, The National Standard Reference Data System: Washington, DC, USA, 1969.
- Hubbell, J.H. Electron-positron pair production by photons: A historical overview. Radiat. Phys. Chem. 2006, 75, 614–623. [Google Scholar] [CrossRef]
- Rogers, T.W.; Jaccard, N.; Morton, E.J.; Griffin, L.D. Automated X-ray image analysis for cargo security: Critical review and future promise. J. X-Ray Sci. Technol. 2017, 25, 33–56. [Google Scholar] [CrossRef]
- Zhvyrblia, V.Y.; Osipov, S.P.; Sednev, D.A. Increasing penetrating power of digital radiography systems based on analysis of low-intensity signals. Russ. J. Nondestuct. Test. 2022, 58, 583–597. [Google Scholar] [CrossRef]
- Osipov, S.P.; Chakhlov, S.V.; Osipov, O.S.; Li, S.; Sun, X.; Zheng, J.; Hu, X.; Zhang, G. Physical and technical restrictions of materials recognition by the dual high energy X-ray imaging. Int. J. Appl. Eng. Res. 2017, 12, 13127–13136. [Google Scholar]
- Barnes, S.; Georgadze, A.; Giammanco, A.; Kiisk, M.; Kudryavtsev, V.A.; Lagrange, M.; Pinto, O.L. Cosmic-Ray Tomography for Border Security. Instruments 2023, 7, 13. [Google Scholar] [CrossRef]
- Kahani, M. Dose Evaluation of a Car Occupant in Dual Energy X-Ray Automobile Inspection System. Medicon Med. Sci. 2022, 2, 33–41. [Google Scholar] [CrossRef]
- Park, J.Y.; Mun, J.; Lee, J.H.; Yeon, Y.-H.; Chae, M.; Lee, M.; Lee, N.-H. Development of a Dual-Modality Gamma-ray/Fast Neutron Imaging System for Air Cargo Inspection. Appl. Sci. 2022, 12, 9775. [Google Scholar] [CrossRef]
- Alves, H.; Lima, I.; de Assis, J.T.; Neves, A.A.; Lopes, R.T. Mineralogy evaluation and segmentation using dual energy microtomography. X-Ray Spectrom. 2015, 44, 99–104. [Google Scholar] [CrossRef]
- Bonnin, A.; Duvauchelle, P.; Kaftandjian, V.; Ponard, P. Concept of effective atomic number and effective mass density in dual-energy X-ray computed tomography. Nucl. Instrum. Methods Phys. Res. B 2014, 22, 223–231. [Google Scholar] [CrossRef]
- Osipov, S.; Chakhlov, S.; Udod, V.; Usachev, E.; Schetinkin, S.; Kamysheva, E. Estimation of the effective mass thickness and effective atomic number of the test object material by the dual energy method. Radiat. Phys. Chem. 2020, 168, 108543. [Google Scholar] [CrossRef]
- Bauer, C.; Wagner, R.; Leisner, J. Foreign body detection in frozen food by dual energy X-ray transmission. Sens. Transducers 2021, 253, 23–30. [Google Scholar]
- Heckert, M.; Enghardt, S.; Bauch, J. Novel multi-energy X-ray imaging methods: Experimental results of new image processing techniques to improve material separation in computed tomography and direct radiography. PLoS ONE 2020, 15, e0232403. [Google Scholar] [CrossRef]
- Haase, V.; Noo, F.; Stierstorfer, K.; Maier, A.; McNitt-Gray, M. Reproducibility in dual energy CT: The impact of a projection domain material decomposition method. 7th International Conference on Image Formation in X-Ray Computed Tomography. SPIE 2022, 12304, 101–106. [Google Scholar] [CrossRef]
- Ilkukhin, N.J.; Moskvin, S.V. Simulators of explosives to test the performance of technical means of security based on the methods of X-ray and neutron radiation analysis. Probl. Def. Technol. Ser. 16 Tech. Means Countering Terror. 2016, 3–4, 76–81. (In Russian) [Google Scholar]
- Berger, M.J.; Hubbell, J.H.; Seltzer, S.M.; Chang, J.; Coursey, J.S.; Sukumar, R.; Zucker, D.S.; Olsen, K. XCOM: Photon Cross Sections Database, NIST Standard Reference Database 8 (XGAM); (Version 1.5); The U.S. Secretary of Commerce: Washington, DC, USA, 2010. [CrossRef]
- Cao, W.; Sun, T.; Kerckhofs, G.; Fardell, G.; Price, B.; Dewulf, W. A simulation-based study on the influence of the X-ray spectrum on the performance of multi-material beam hardening correction algorithms. Meas. Sci. Technol. 2018, 29, 095002. [Google Scholar] [CrossRef]
- Martini, M.; Francus, P.; Trotta, D.S.L.; Despres, P. Identification of Common Minerals Using Stoichiometric Calibration Method for Dual-Energy CT. Geochem. Geophys. Geosyst. 2021, 22, e2021GC009885. [Google Scholar] [CrossRef]
- Osipov, S.P.; Usachev, E.Y.; Chakhlov, S.V.; Shchetinkin, S.A.; Osipov, O.S. Specific features of material recognition by the multi-energy X-Ray method. Russ. J. Nondestruct. Test. 2019, 55, 308–321. [Google Scholar] [CrossRef]
- Zentai, G. X-ray imaging for homeland security. IEEE Int. Workshop Imaging Syst. Tech. 2008, 3, 13. [Google Scholar] [CrossRef]
- Lehnert, A.L.; Kearfott, K.J. The Detection of Explosive Materials: Review of Considerations and Methods. Nucl. Technol. 2010, 172, 325–334. [Google Scholar] [CrossRef]
- Scientific Educational Cargo Vehicle Inspection System. Available online: https://rkd.tpu.ru/en/developments/inspection/ (accessed on 27 November 2024).
- Kutsaev, S.; Agustsson, R.; Arodzero, A.; Berry, R.; Bezhanov, A.; Boucher, S.; Chimalpopoca, O.; Diego, A.; Faillace, L.; Gavryushkin, D.; et al. Compact X-Band electron linac for radiotherapy and security applications. Radiat. Phys. Chem. 2021, 185, 109494. [Google Scholar] [CrossRef]
- Chang, C.H.; Ni, Y.C.; Tseng, S.P. Calculation of effective atomic numbers using a rational polynomial approximation method with a dual-energy X-ray imaging system. J. X-Ray Sci. Technol. 2021, 29, 317–330. [Google Scholar] [CrossRef]
- Nabiev, S.S.; Palkina, L.A. Modern technologies for detection and identification of explosive agents and devices. Russ. J. Phys. Chem. B 2017, 11, 729–776. [Google Scholar] [CrossRef]
- Lalor, P.; Danagoulian, A. Atomic number estimation of dual energy cargo radiographs using a semiempirical transparency model. Nucl. Instrum. Methods Phys. Res. A Accel. Spectrom. Detect. Assoc. Equip. 2024, 1064, 169343. [Google Scholar] [CrossRef]


| Material and Chemical Substance | Chemical Formula | Theoretical Estimates Zeff | Experimental Values Zeff |
|---|---|---|---|
| Polyethylene | (CH2)n | 5.4 | |
| Carbon (graphite) | C | 6 | 6 |
| Sugar | C12H22O11 | 6.92 [23] | |
| Water | H2O | 7.49 [34] | |
| Trinitrotoluene | C7H5N3O6 | 7.27 [34], 7.09 [35] | |
| RDX | C6H6O6N6 | 7.41 [34], 7.11 [35] | |
| C-4 | C3H6O6N6 | 7.34 [33], 7.26 [35] | |
| Pentrite | C5H8O12N4 | 7.58 [33], 7.43 [35] | |
| Borax | Na2B4O7·10H2O | 8.06 [23] | |
| Fluoropolymer | (C2F4)n | 10.0 [36], 8.5 [37] | |
| Albite | NaAlSi3O8 | 11.62 [33], 11.44 [35] | 11.22 [33] |
| Quartz | SiO2 | 11.85 [33], 11.24 [34], 11.67 [35] | |
| Aluminum | Al | 13 | 13 |
| Dolomite | CaMg(CO3)2 | 13.94 [33], 13.33 [35] | 13.61 [33] |
| Calcite | CaCO3 | 15.88 [33], 15.26 [35] | |
| Fluorite | CaF2 | 16.98 [33], 16.76 [35] | |
| Rutile | TiO2 | 19.3 [33], 18.6 [35] | 19.4 [33] |
| Pyrite | FeS2 | 22.21 [33], 21.59 [35] | |
| Iron | Fe | 26 | 26 |
| Tin | Sn | 50 | 50 |
| Lead | Pb | 82 | 82 |
| Zeff | Class of Materials |
|---|---|
| 1–8 | Organic materials |
| 8–10 | Light inorganic materials |
| 10–12 | Heavy inorganic materials |
| 12–17 | Light metals |
| 17–29 | Heavy metals |
| 29+ | Superdense metals |
| – | Non-transparent materials |
| Z | ρH, g/cm2 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 17 | 24 | 31 | 38 | 45 | 52 | 59 | 66 | 73 | 80 | 87 | 94 | 101 | 108 | 115 | |
| 4 | 3.9 | 3.9 | 3.9 | 3.9 | 3.9 | 3.9 | 3.9 | 3.9 | 3.9 | 3.9 | 3.9 | 3.9 | 3.9 | 3.9 | 3.9 | 3.9 |
| 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8.1 | 8.1 | 8.1 | 8.1 | 8.1 | 8.1 | 8.1 |
| 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
| 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 |
| 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 |
| 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 | 32 |
| 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 |
| 40 | 40 | 40.1 | 40.1 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 | 40 |
| 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 |
| 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 |
| 52 | 52 | 52 | 52 | 52 | 52 | 52 | 52 | 52 | 52 | 52 | 52 | 52 | 52 | 52 | 52 | 52 |
| 56 | 68.8 | 55.9 | 56 | 56 | 56 | 56 | 56 | 56 | 56 | 56 | 56 | 56 | 56 | 56 | 56 | 56 |
| 60 | 68.8 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 |
| 64 | 68.8 | 64 | 64 | 64 | 64 | 64 | 64 | 64 | 64 | 64 | 64 | 64 | 64 | 64 | 64 | 64 |
| Material | EL = 1 MeV, EH = 4 MeV | EL = 2 MeV, EH = 5 MeV | EL = 2 MeV, EH = 6 MeV | EL =3 MeV, EH = 6 MeV | EL = 4 MeV, EH = 7 MeV | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Q | Zeff | Q | Zeff | Q | Zeff | Q | Zeff | Q | Zeff | |
| Polyethylene | 0.474 | 4.397 | 0.601 | 4.71 | 0.545 | 4.607 | 0.683 | 4.57 | 0.747 | 4.394 |
| Carbon (graphite) | 0.479 | 5.741 | 0.61 | 5.99 | 0.556 | 5.9 | 0.693 | 5.86 | 0.759 | 5.726 |
| Sugar | 0.48 | 6.099 | 0.612 | 6.34 | 0.559 | 6.245 | 0.696 | 6.208 | 0.762 | 6.091 |
| Water | 0.481 | 6.333 | 0.613 | 6.57 | 0.561 | 6.47 | 0.698 | 6.435 | 0.764 | 6.329 |
| Trinitrotoluene | 0.482 | 6.563 | 0.615 | 6.78 | 0.562 | 6.692 | 0.7 | 6.656 | 0.766 | 6.553 |
| RDX | 0.482 | 6.593 | 0.615 | 6.8 | 0.563 | 6.72 | 0.7 | 6.684 | 0.766 | 6.583 |
| C-4 | 0.483 | 6.728 | 0.616 | 6.93 | 0.564 | 6.849 | 0.701 | 6.814 | 0.767 | 6.718 |
| Pentrite | 0.483 | 6.892 | 0.617 | 7.1 | 0.565 | 7.009 | 0.702 | 6.973 | 0.769 | 6.882 |
| Borax | 0.484 | 7.096 | 0.618 | 7.31 | 0.567 | 7.215 | 0.704 | 7.175 | 0.771 | 7.096 |
| Polyvinylchloride | 0.499 | 11.28 | 0.645 | 11.38 | 0.6 | 11.32 | 0.737 | 11.29 | 0.806 | 11.27 |
| Polyvinylidene fluoride | 0.484 | 7.167 | 0.619 | 7.4 | 0.567 | 7.307 | 0.705 | 7.263 | 0.771 | 7.175 |
| Fluoropolymer | 0.487 | 8.084 | 0.625 | 8.3 | 0.575 | 8.204 | 0.712 | 8.158 | 0.779 | 8.096 |
| Albite | 0.497 | 10.63 | 0.641 | 10.71 | 0.595 | 10.64 | 0.732 | 10.62 | 0.8 | 10.6 |
| Quartz | 0.497 | 10.75 | 0.641 | 10.81 | 0.596 | 10.75 | 0.732 | 10.74 | 0.801 | 10.7 |
| Aluminum | 0.505 | 12.99 | 0.656 | 13.05 | 0.614 | 12.99 | 0.75 | 12.95 | 0.82 | 13.01 |
| Dolomite | 0.497 | 10.79 | 0.642 | 10.87 | 0.596 | 10.81 | 0.733 | 10.78 | 0.801 | 10.75 |
| Calcite | 0.504 | 12.52 | 0.653 | 12.56 | 0.61 | 12.52 | 0.746 | 12.48 | 0.815 | 12.47 |
| Fluorite | 0.512 | 14.81 | 0.667 | 14.83 | 0.629 | 14.79 | 0.764 | 14.76 | 0.833 | 14.77 |
| Rutile | 0.517 | 16.12 | 0.676 | 16.11 | 0.639 | 16.04 | 0.773 | 16.01 | 0.843 | 16.04 |
| Pyrite | 0.533 | 20.57 | 0.703 | 20.45 | 0.674 | 20.45 | 0.806 | 20.46 | 0.876 | 20.52 |
| Iron | 0.552 | 26.21 | 0.738 | 26 | 0.717 | 26.02 | 0.844 | 26.07 | 0.913 | 26.13 |
| Tin | 0.614 | 49.74 | 0.863 | 50 | 0.871 | 50.08 | 0.972 | 50.21 | 1.026 | 50.39 |
| Tantalum | 0.612 | 48.41 | 0.925 | 73.06 | 0.949 | 72.17 | 1.032 | 71.83 | 1.074 | 70.76 |
| Material | ρH, g/cm2 | ||||
|---|---|---|---|---|---|
| 16.5 | 24.75 | 33 | 41.25 | 49.5 | |
| Polyethylene | 0.7772 | 0.7753 | 0.7737 | 0.7723 | 0.7712 |
| Graphite | 0.7818 | 0.7803 | 0.7789 | 0.7783 | 0.7772 |
| Sugar | 0.7829 | 0.7813 | 0.7802 | 0.779 | 0.7785 |
| Water | 0.7834 | 0.782 | 0.7811 | 0.7798 | 0.7794 |
| Trinitrotoluene | 0.7844 | 0.7829 | 0.782 | 0.781 | 0.7805 |
| RDX | 0.7846 | 0.7831 | 0.7821 | 0.7812 | 0.7803 |
| C-4 | 0.7847 | 0.7835 | 0.7827 | 0.7819 | 0.7812 |
| Pentrite | 0.7854 | 0.784 | 0.7832 | 0.7825 | 0.7818 |
| Borax | 0.7859 | 0.7848 | 0.7839 | 0.783 | 0.7824 |
| Polyvinylchloride | 0.7986 | 0.7985 | 0.7982 | 0.7985 | 0.7988 |
| Polyvinylidene fluoride | 0.7865 | 0.7852 | 0.7843 | 0.7834 | 0.7828 |
| Fluoropolymer | 0.789 | 0.7884 | 0.7877 | 0.787 | 0.7868 |
| Albite | 0.7967 | 0.7964 | 0.796 | 0.796 | 0.7961 |
| Quartz | 0.797 | 0.7966 | 0.7963 | 0.7966 | 0.7963 |
| Aluminum | 0.8039 | 0.8041 | 0.8039 | 0.8046 | 0.8048 |
| Dolomite | 0.7973 | 0.7968 | 0.7965 | 0.7965 | 0.7968 |
| Calcite | 0.8021 | 0.8021 | 0.8024 | 0.8025 | 0.8032 |
| Fluorite | 0.809 | 0.8095 | 0.8099 | 0.8108 | 0.8112 |
| Rutile | 0.8126 | 0.8133 | 0.8143 | 0.8152 | 0.8158 |
| Pyrite | 0.8251 | 0.8266 | 0.8281 | 0.8296 | 0.831 |
| Iron | 0.8395 | 0.842 | 0.8445 | 0.8466 | 0.8485 |
| Tin | 0.881 | 0.8882 | 0.8942 | 0.8989 | 0.903 |
| Tantalum | 0.8877 | 0.9015 | 0.9114 | 0.9193 | 0.9257 |
| Material | ρH, g/cm2 | ||||
|---|---|---|---|---|---|
| 16.5 | 24.75 | 33 | 41.25 | 49.5 | |
| Polyethylene | 4.715 | 4.89 | 4.75 | 4.68 | 4.715 |
| Graphite | 5.87 | 5.94 | 6.01 | 6.01 | 5.94 |
| Sugar | 6.395 | 6.29 | 6.325 | 6.22 | 6.36 |
| Water | 6.535 | 6.605 | 6.5 | 6.5 | 6.57 |
| Trinitrotoluene | 6.745 | 6.71 | 6.78 | 6.815 | 6.78 |
| RDX | 6.815 | 6.78 | 6.745 | 6.815 | 6.78 |
| C-4 | 6.92 | 6.955 | 6.99 | 6.99 | 6.99 |
| Pentrite | 7.27 | 7.235 | 7.235 | 7.06 | 7.06 |
| Borax | 7.41 | 7.34 | 7.305 | 7.27 | 7.235 |
| Polyvinylchloride | 11.4 | 11.23 | 11.26 | 11.3 | 11.33 |
| Polyvinylidene fluoride | 7.375 | 7.41 | 7.34 | 7.375 | 7.34 |
| Fluoropolymer | 8.25 | 8.15 | 8.18 | 8.285 | 8.25 |
| Albite | 10.67 | 10.67 | 10.67 | 10.77 | 10.63 |
| Quartz | 10.95 | 10.74 | 10.74 | 10.84 | 10.7 |
| Aluminum | 12.94 | 12.94 | 12.98 | 12.98 | 12.98 |
| Dolomite | 10.91 | 10.88 | 10.84 | 10.81 | 10.81 |
| Calcite | 12.73 | 12.59 | 12.52 | 12.45 | 12.42 |
| Fluorite | 14.87 | 14.8 | 14.73 | 14.66 | 14.87 |
| Rutile | 15.99 | 15.85 | 16.02 | 15.92 | 16.02 |
| Pyrite | 20.4 | 20.4 | 20.33 | 20.47 | 20.36 |
| Iron | 26.17 | 26.03 | 26. | 25.93 | 26.07 |
| Tin | 49.83 | 50.01 | 50.11 | 49.9 | 49.97 |
| Tantalum | 72.93 | 68.70 | 72.65 | 72.97 | 72.76 |
| Zeff | Class of Materials | Material | Color | RGB |
|---|---|---|---|---|
| 2.1–6.1 | Light organic materials | Polyethylene | ██ | (0, 255, 255) |
| 6.1–7.8 | Heavy organic materials | Explosives | ██ | (255, 0, 0) |
| 7.8–10.5 | Heavy plastics, light metal oxides, and salts | Fluoropolymer | ██ | (255, 0, 255) |
| 10.5–15 | Light metals | Aluminum | ██ | (0, 255, 0) |
| 15–22 | Heavy inorganic materials | Calcium oxide | ██ | (255, 255, 0) |
| 22–30 | Heavy metals | Steel | ██ | (0, 0, 255) |
| 30–57 | Metals with a high atomic number | Tin | ██ | (255, 0, 255) |
| 57+ | Non-transparent materials | Tantalum | ██ | (128, 128, 128) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osipov, S.; Chakhlov, S.; Usachev, E. Increasing the Number of Material Recognition Classes in Cargo Inspection Using the X-Ray Dual High-Energy Method. Computation 2025, 13, 41. https://doi.org/10.3390/computation13020041
Osipov S, Chakhlov S, Usachev E. Increasing the Number of Material Recognition Classes in Cargo Inspection Using the X-Ray Dual High-Energy Method. Computation. 2025; 13(2):41. https://doi.org/10.3390/computation13020041
Chicago/Turabian StyleOsipov, Sergey, Sergei Chakhlov, and Eugeny Usachev. 2025. "Increasing the Number of Material Recognition Classes in Cargo Inspection Using the X-Ray Dual High-Energy Method" Computation 13, no. 2: 41. https://doi.org/10.3390/computation13020041
APA StyleOsipov, S., Chakhlov, S., & Usachev, E. (2025). Increasing the Number of Material Recognition Classes in Cargo Inspection Using the X-Ray Dual High-Energy Method. Computation, 13(2), 41. https://doi.org/10.3390/computation13020041






