Blind Source Separation Using Time-Delayed Dynamic Mode Decomposition
Abstract
1. Introduction
1.1. The BSS Framework
- The number of observations is greater than the number of sources () and the mixing matrix Q is of full column rank.
- Each row-vector of S is a stationary stochastic process with zero mean.
- The unknown sources are statistically independent (at each instant t, the components of are mutually statistically independent).
1.2. The DMD Framework
Reduced Order DMD Operator
1.3. BSS in Context of DMD
2. Time-Delayed DMD
2.1. Hankel DMD
2.2. Higher Order DMD
2.2.1. Cost Effective Calculation of Higher-Order DMD Operator
2.2.2. Reduced Order Aproximation of Higher-Order DMD Operator
3. BSS by Time-Delayed DMD
- When the sources have different frequency characteristics that can be dynamically separated.
- The system has a pronounced linear behavior.
- Mixed observations contain temporal or spatial information.
| Algorithm 1 BSS using Time-delayed DMD |
| Input: Data matrix X, delay embedding parameter s |
| and rank reduction parameter r. |
| Output: Mixing matrix and sources |
| 1: Procedure BSS by TD-DMD(X, s, r) |
| 2: and (Define as in (22) and (23)) |
| 3: (Reduced, r-rank, SVD of ) |
| 4: (Define matrices as in (30)) |
| 5: (Reduced DMD operator) |
| 6: (Eigen-decomposition of ) |
| 7: (DMD modes matrix) |
| 8: (Estimated mixing matrix) |
| 9: (Latent sources S) |
| 10: End Procedure |
Some Essential Remarks
- The algorithm is also applicable to overdetermined cases (). In Step 3, the parameter r is set to be equal to p (the number of sources), then the estimated mixing matrix is of dimension .
- In the case of , i.e., when the number of observed signals is equal to the number of sources, for and , the proposed algorithm reduces to the exact DMD algorithm.
- At Step 6 of Algorithm 1, is an diagonal matrix , where are the possibly complex eigenvalues of and they are ordered such thatThe columns of the matrix W are the corresponding, ordered, generally non-orthogonal, eigenvectors of .
4. Numerical Examples
4.1. Example 1: Three-Dimensional Oscillatory Signals
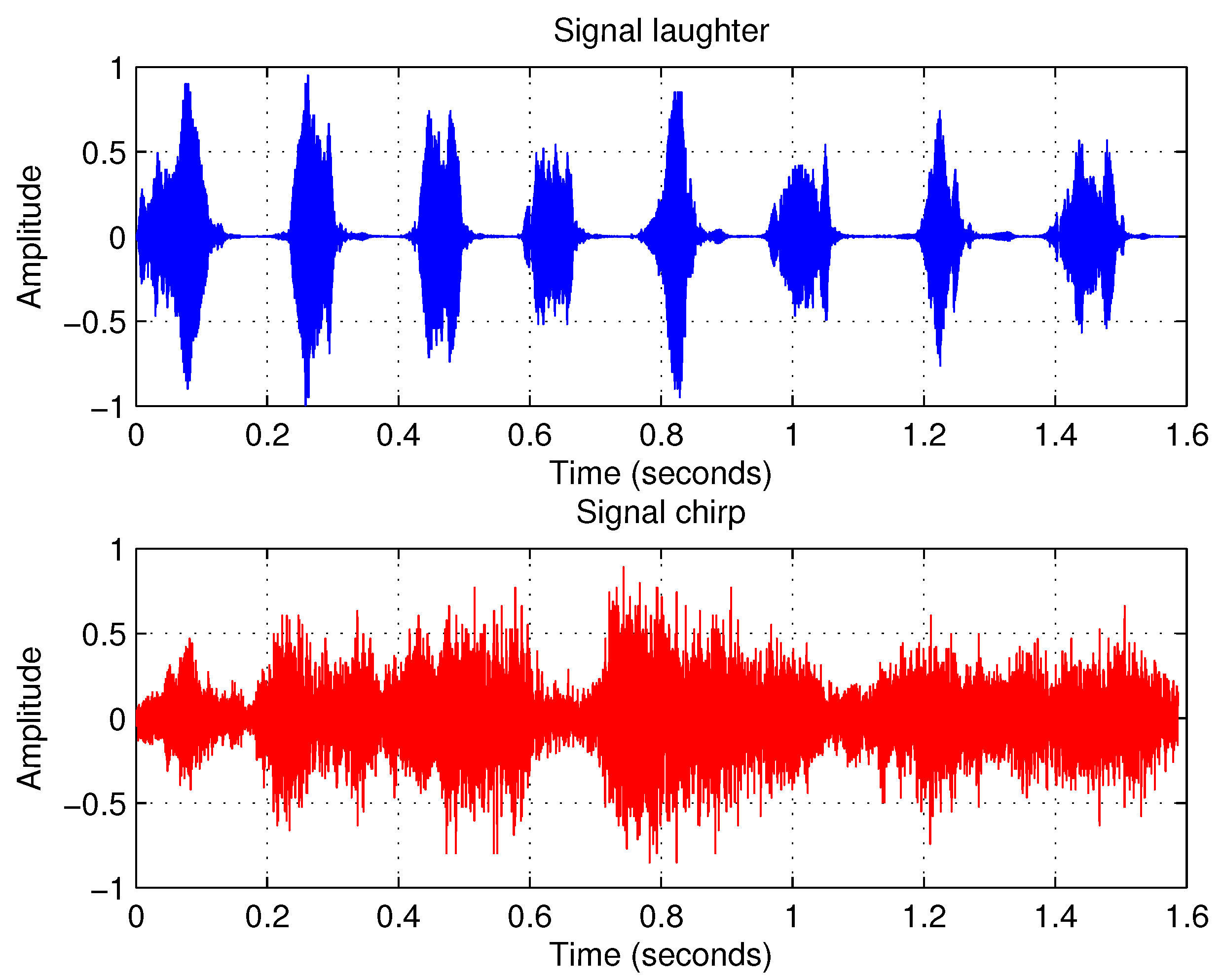
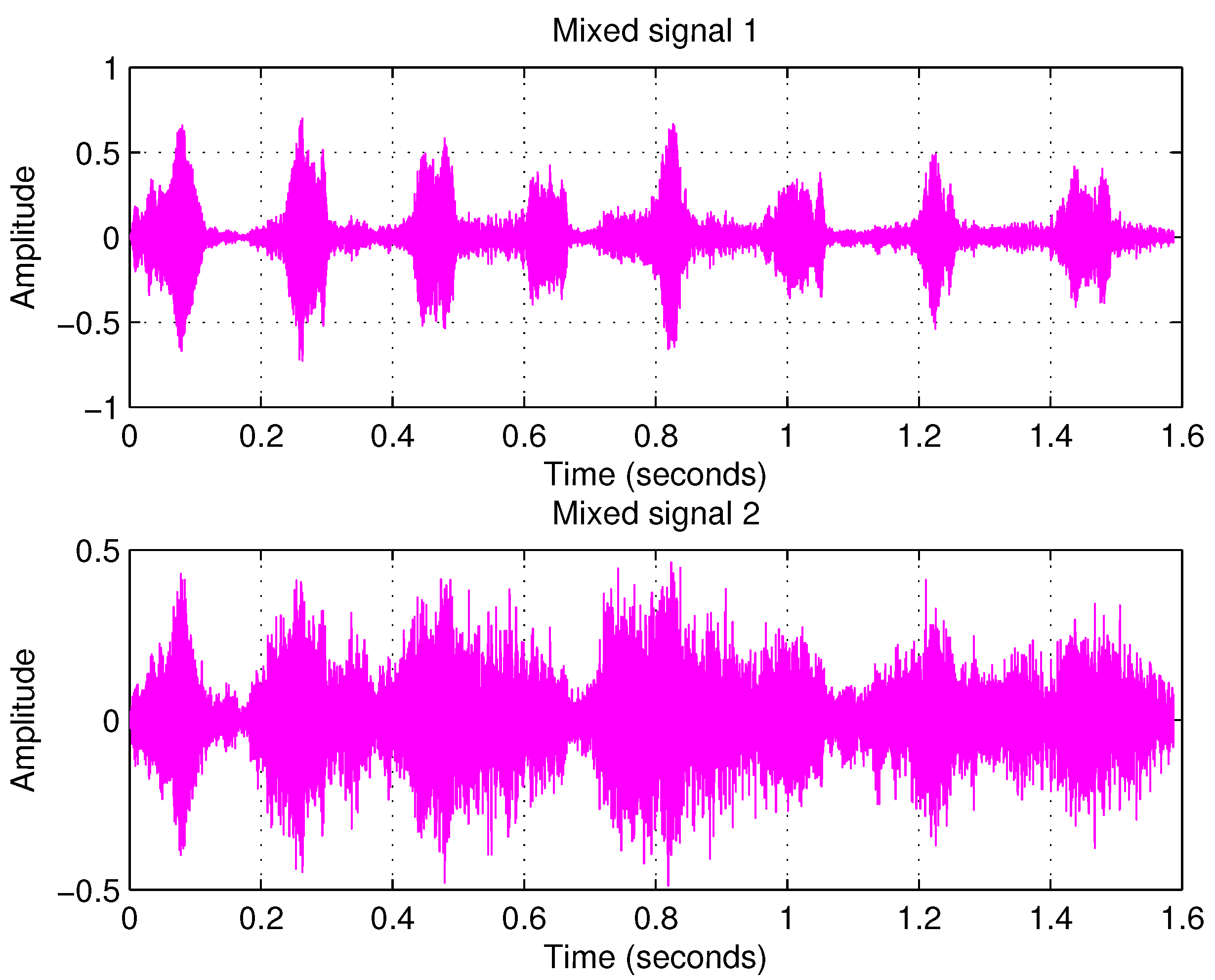
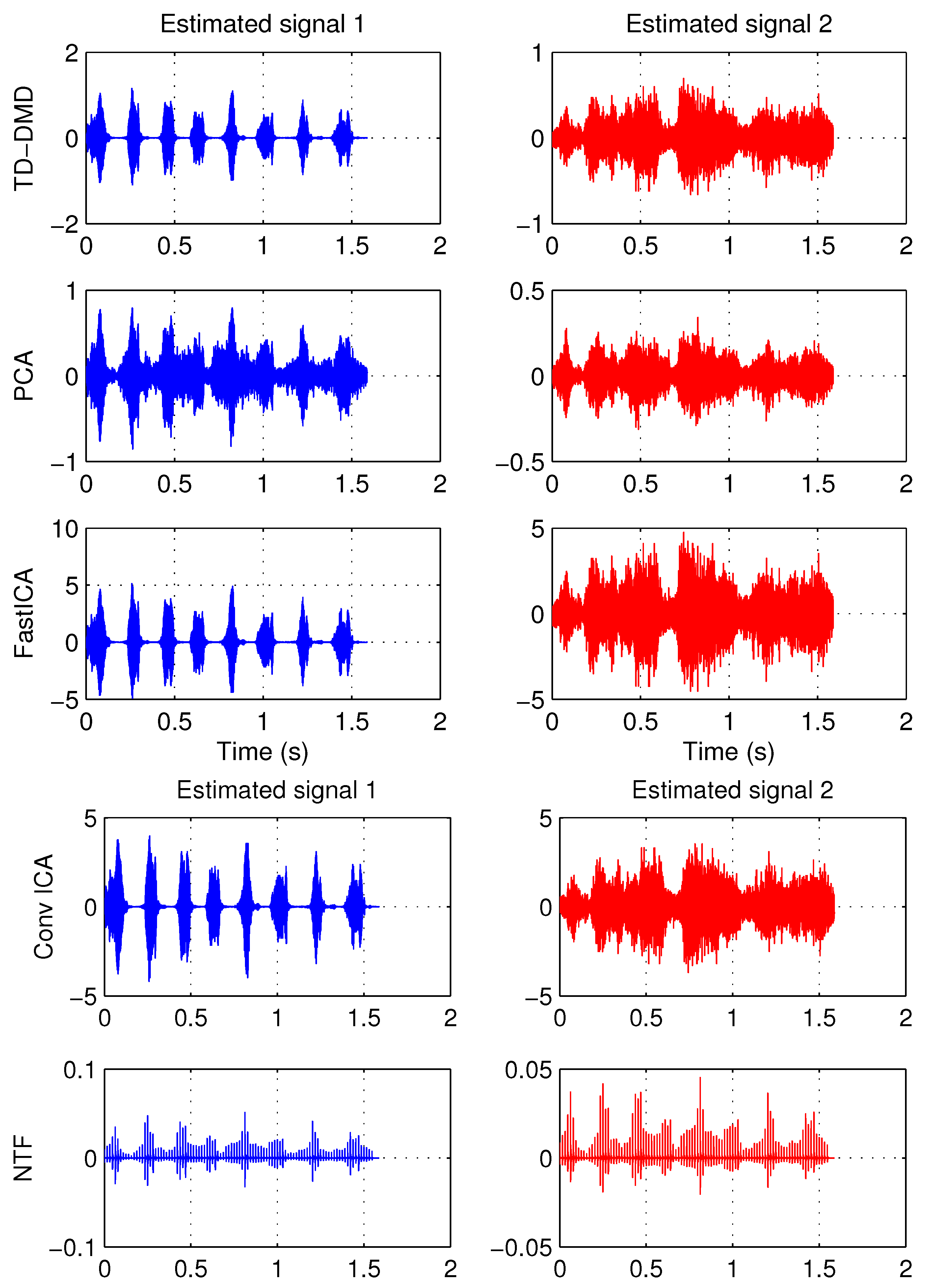
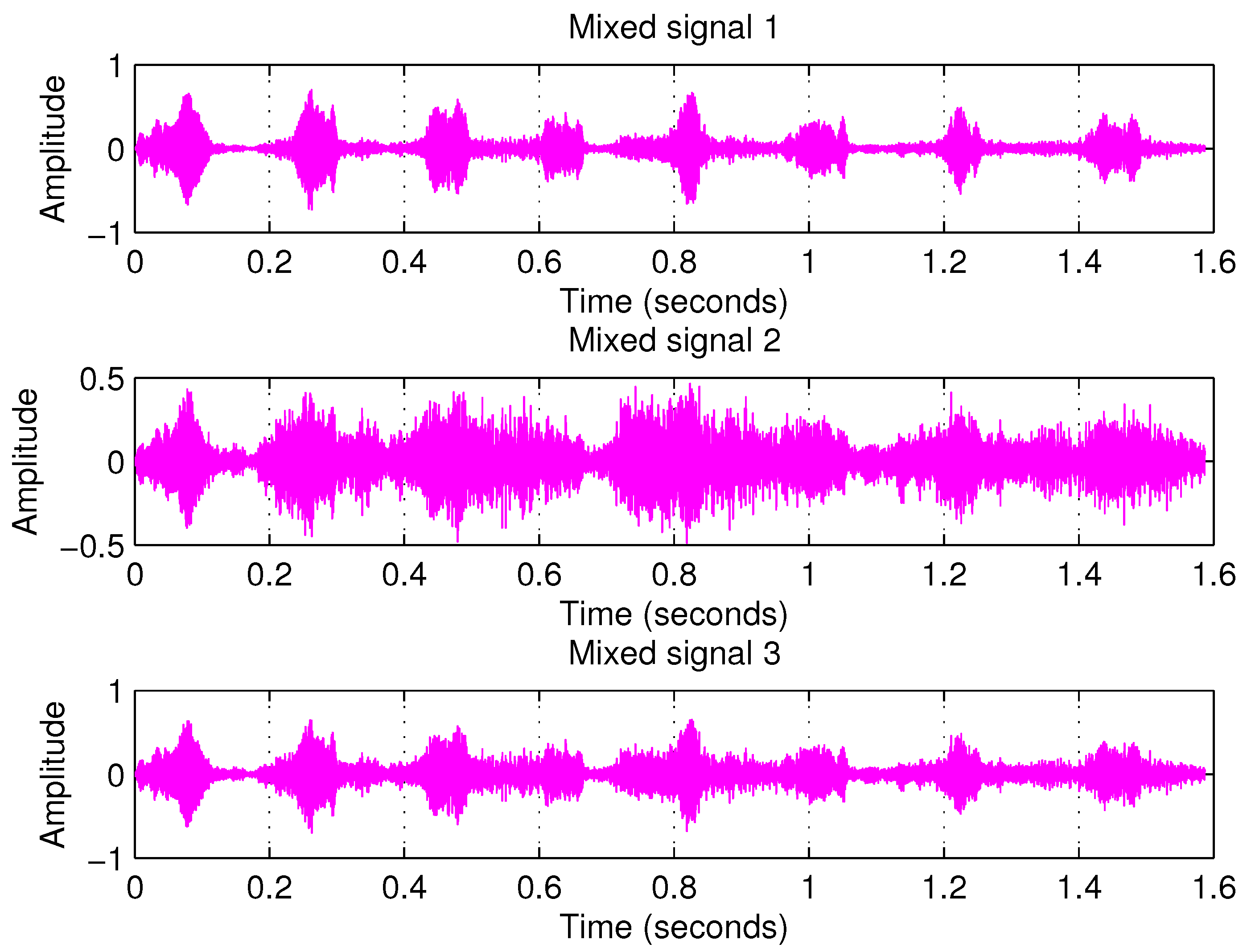
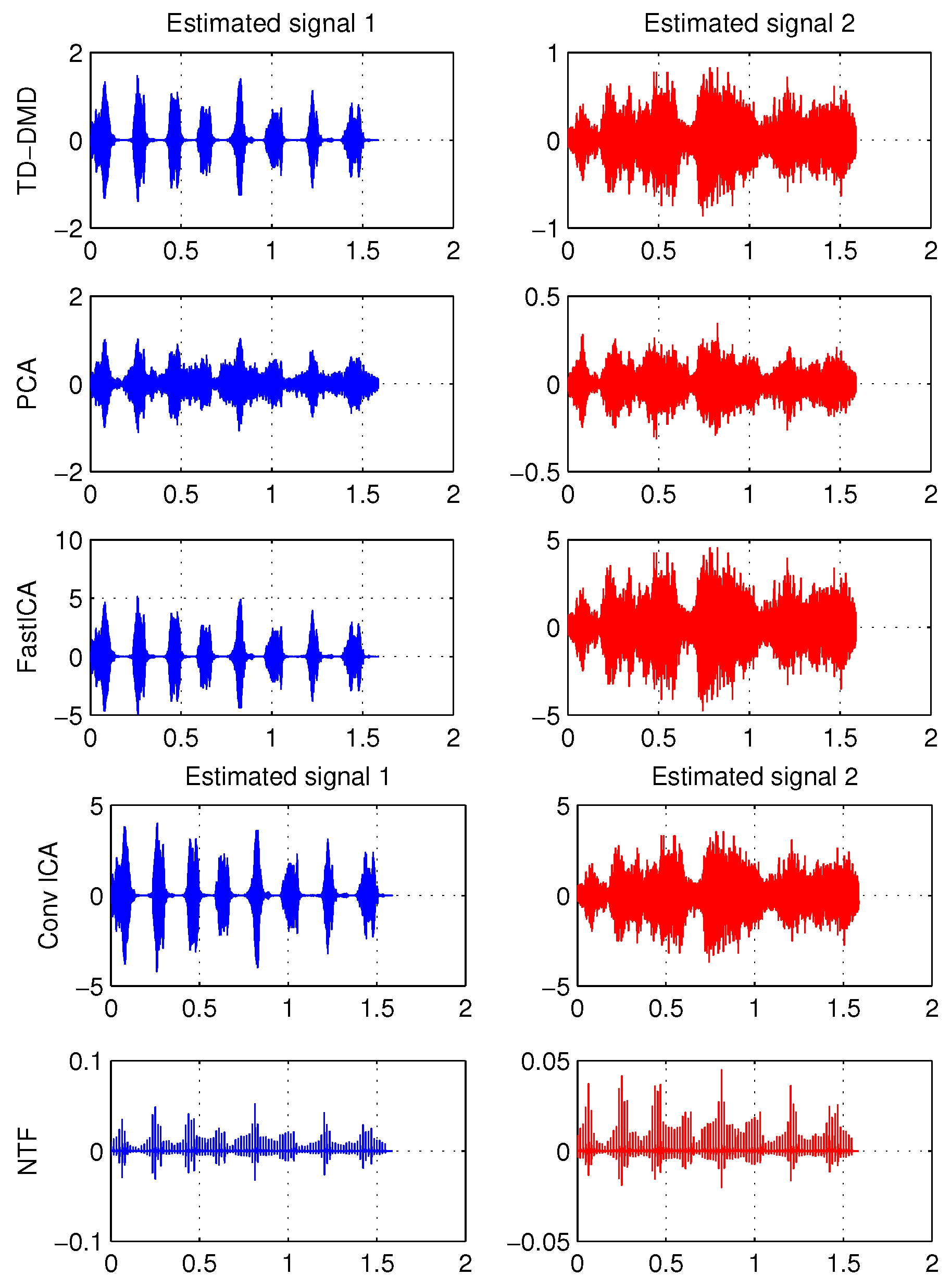
4.2. Example 2: Separating Audio Signals
Overdetermined Case
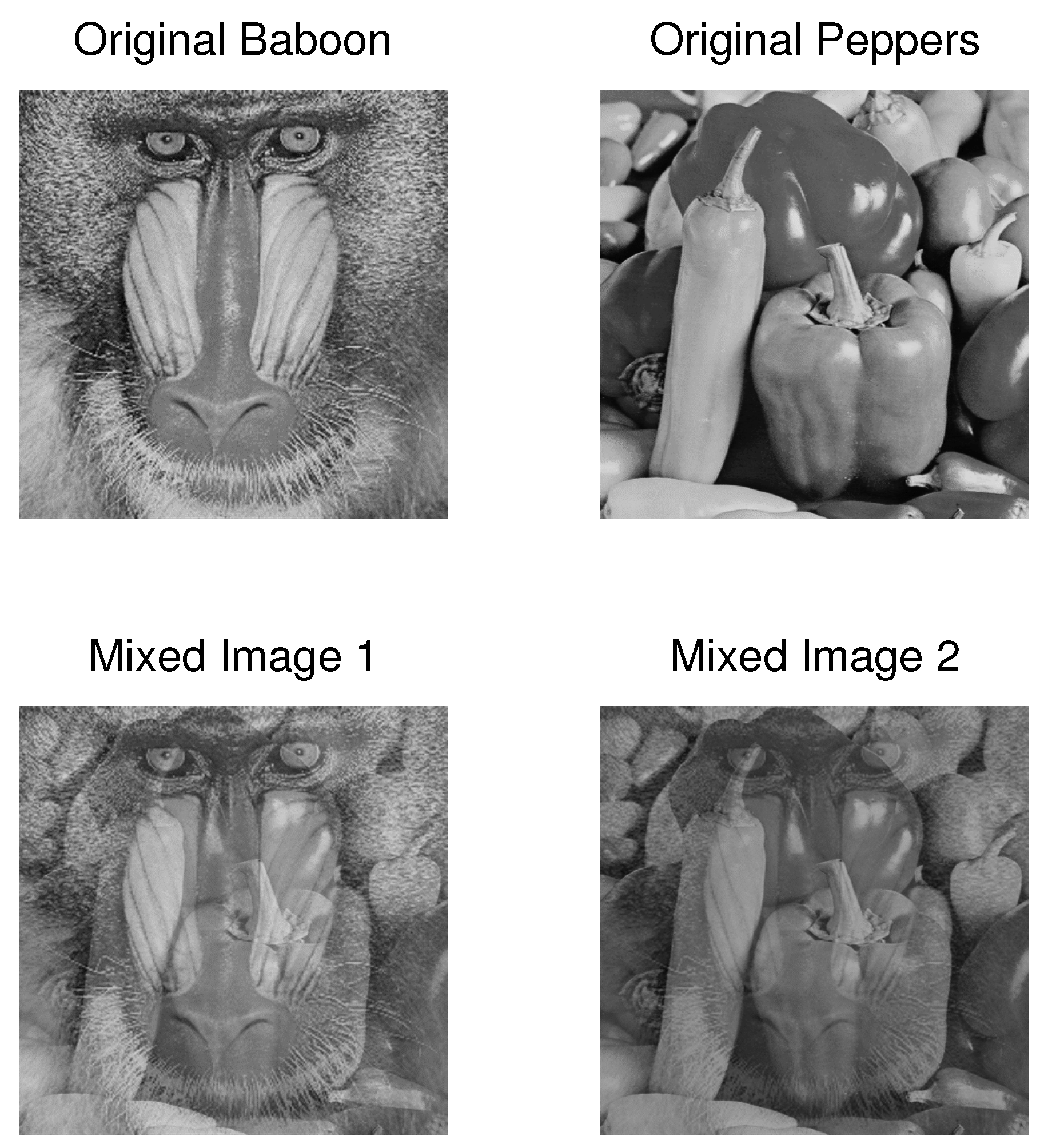
4.3. Example 3: Separation of Mixed Images
Overdetermined Case
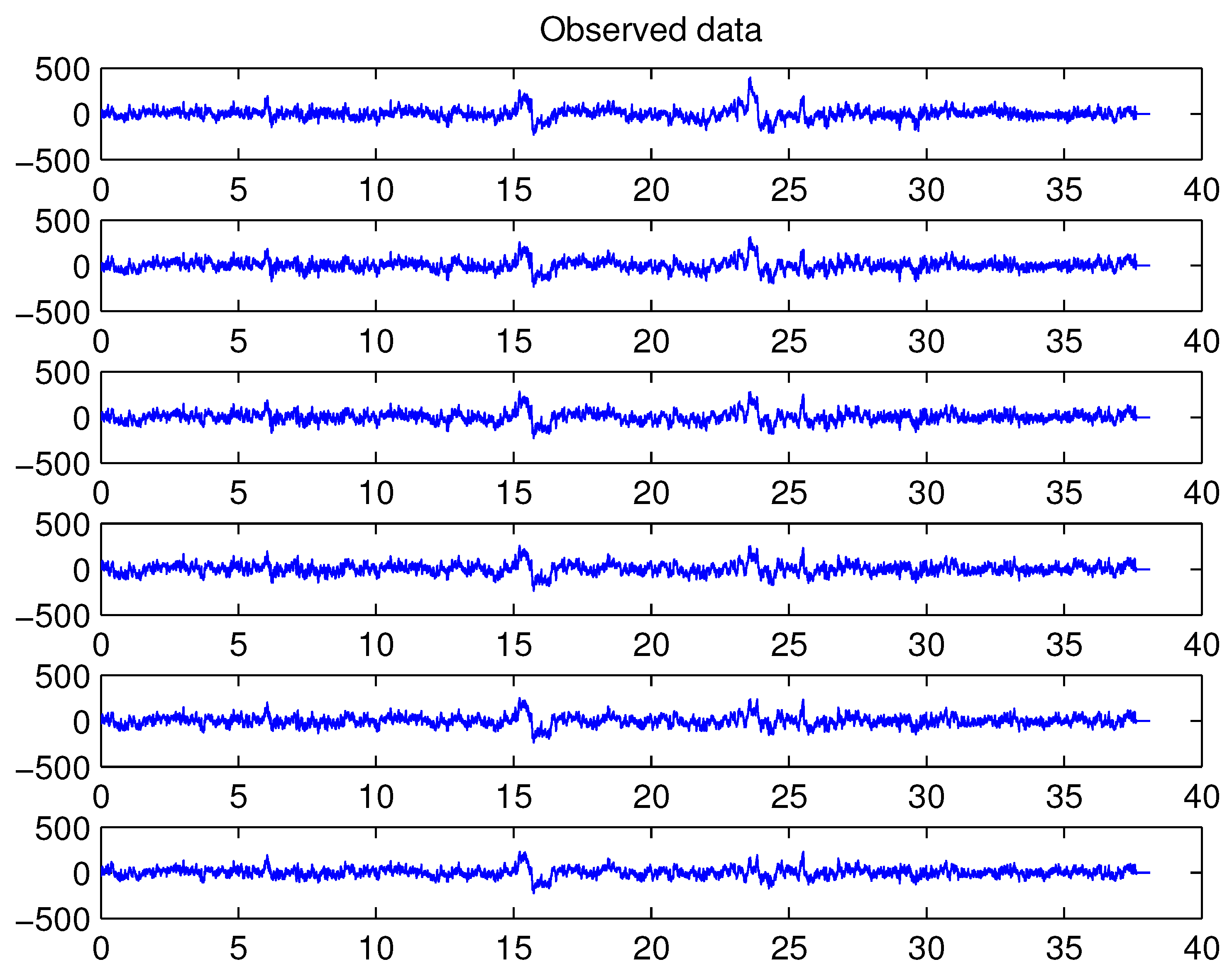
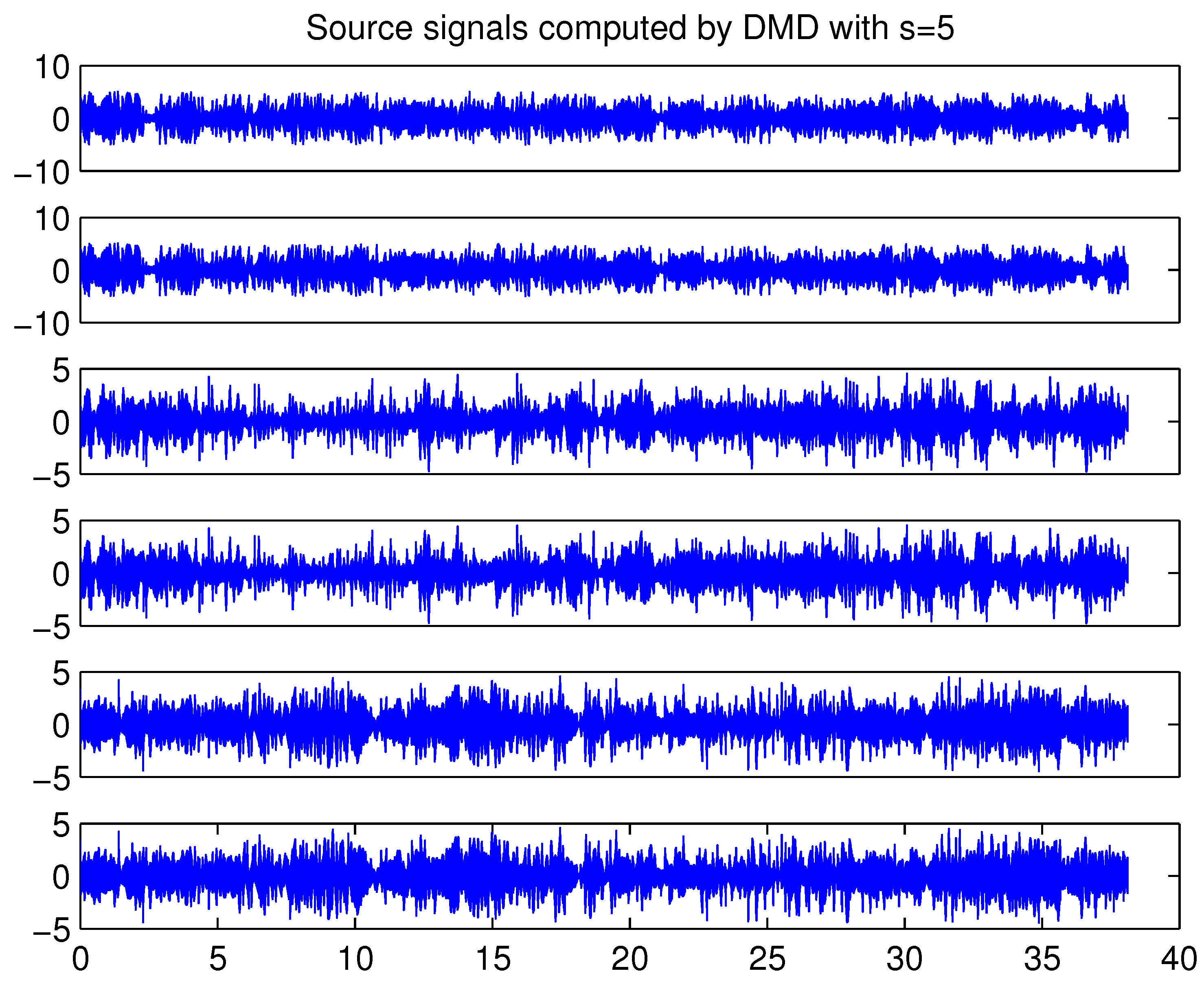
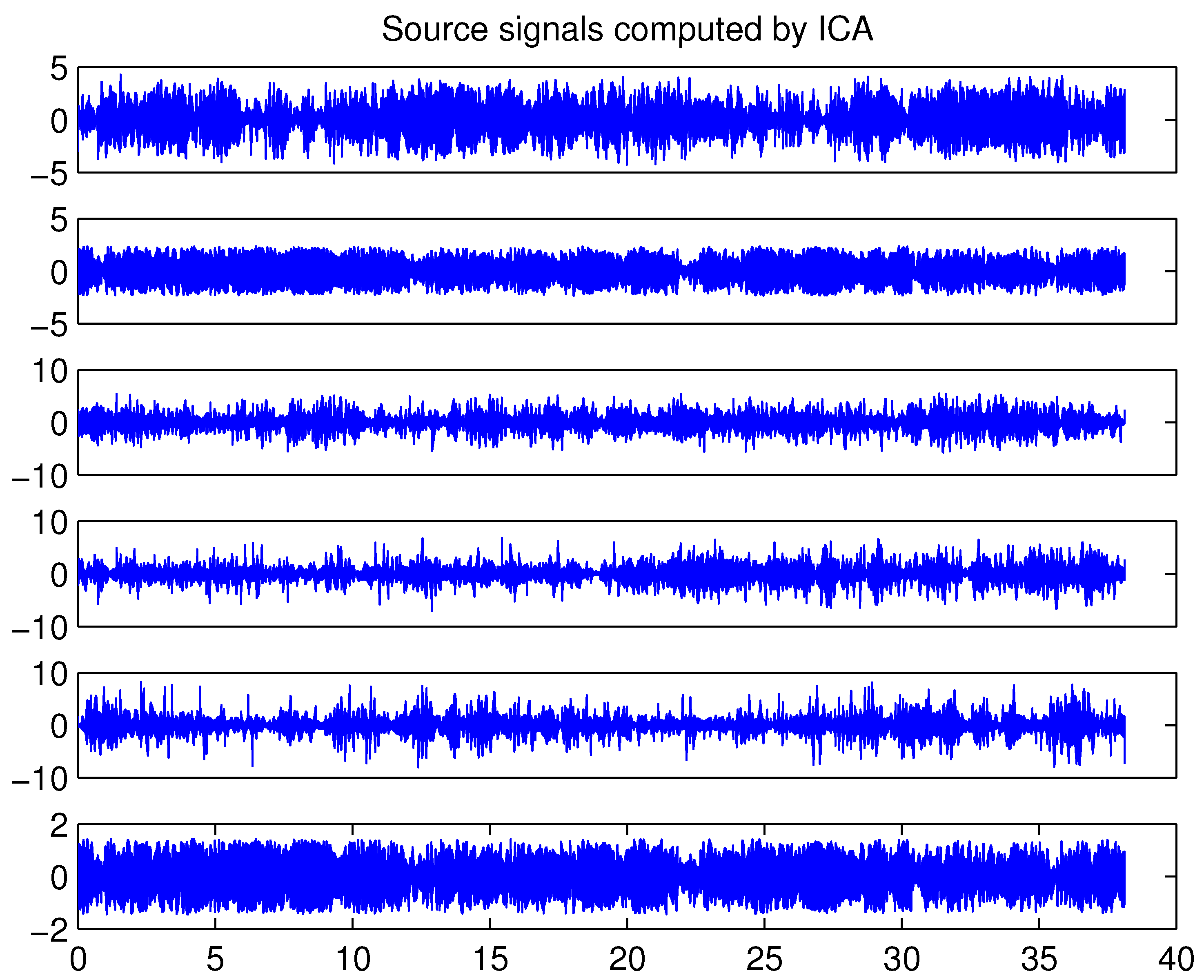
4.4. Example 4: Analysis of EEG-Data
5. Conclusions
- Extension to Nonlinear Dynamics: While our current approach primarily addresses linear dynamics, we aim to investigate the extension of DMD-based BSS to handle nonlinear systems through methods such as kernel DMD or deep learning-enhanced DMD.
- Real-Time and Online Implementations: Another direction is to develop real-time or online implementations of DMD-based BSS for applications in robotics, communications, and biomedical signal processing, where real-time performance is critical.
- Parallel Implementation: One of the key areas for future research will involve implementing the DMD-based BSS method in a parallel computing environment. This would allow us to efficiently process larger datasets and reduce computational times, making the method more suitable for real-time applications.
- Integration with Deep Learning Techniques: Combining DMD approach with machine learning and deep learning methods is another promising area of research. This could involve using neural networks to improve the performance and robustness of the DMD-based BSS in complex or noisy environments.
Funding
Data Availability Statement
Conflicts of Interest
References
- Hérault, J.; Ans, B. Circuits neuronaux à synapses modifiables: Décodage de messages composites par apprentissage non supervisé. Comptes Rendus Acad. Sci. 1984, 299, 525–528. [Google Scholar]
- Hérault, J.; Jutten, C. Space or time adaptive signal processing by neural networks models. In Proceedings of the International Conference on Neural Networks for Computing, Snowbird, UT, USA, 13–16 April 1986; pp. 206–211. [Google Scholar]
- Comon, P.; Jutten, C.; Hérault, J. Blind separation of sources, Part II: Problem statement. Signal Process. 1991, 24, 11–20. [Google Scholar] [CrossRef]
- Sorouchyari, E. Blind separation of sources, Part III: Stability analysis. Signal Process. 1991, 24, 21–29. [Google Scholar] [CrossRef]
- Makino, S.; Lee, T.-W.; Sawada, H. Blind Speech Separation. In Signals and Communication Technology; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Falk, R.H. Medical progress: Atrial fibrillation. N. Engl. J. Med. 2001, 344, 1067–1078. [Google Scholar] [CrossRef] [PubMed]
- Rieta, J.J.; Castells, F.; Snchez, C.; Zarzoso, V.; Millet, J. Atrial activity extraction for atrial fibrillation analysis using blind source separation. IEEE Trans. Biomed. Eng. 2004, 51, 1176–1186. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Karhunen, J.; Oja, E. Independent Component Analysis; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Yu, H.; Deng, X.; Tang, J.; Yue, F. Patterns Identification Using Blind Source Separation with Application to Neural Activities Associated with Anticipated Falls. Inf. Sci. 2025, 689, 121410. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, L.; Bertinetto, L.; Hu, W.; Torr, P.H. Fast online object tracking and segmentation: A unifying approach. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1328–1338. [Google Scholar]
- Wang, X.; Huang, D.-S. A novel multi-layer level set method for image segmentation. J. Univers. Comput. Sci. 2008, 14, 2427–2452. [Google Scholar]
- Zhao, Y.; Huang, D.-S.; Jia, W. Completed local binary count for rotation invariant texture classification. IEEE Trans. Image Process. 2012, 21, 4492–4497. [Google Scholar] [CrossRef]
- Wang, X.-F.; Huang, D.-S.; Du, J.-X.; Xu, H.; Heutte, L. Classification of plant leaf images with complicated background. Appl. Math. Comput. 2008, 205, 916–926. [Google Scholar] [CrossRef]
- Man, L.; Zhu, C. Research on Signal Separation Method for Moving Group Target Based on Blind Source Separation. In Proceedings of the ICCIP ’23: 2023 9th International Conference on Communication and Information Processing, Lingshui, China, 14–16 December 2023; pp. 256–260. [Google Scholar]
- Chang, S.; Deng, Y.; Zhang, Y.; Zhao, Q.; Wang, R.; Zhang, K. An Advanced Scheme for Range Ambiguity Suppression of Spaceborne SAR Based on Blind Source Separation. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 5230112. [Google Scholar] [CrossRef]
- Badaracco, F.; Banerjee, B.; Branchesi, M.; Chincarini, A. Blind source separation in 3rd generation gravitational-wave detectors. New Astron. Rev. 2024, 99, 101707. [Google Scholar] [CrossRef]
- Tolmachev, D.; Chertovskih, R.; Jeyabalan, S.R.; Zheligovsky, V. Predictability of Magnetic Field Reversals. Mathematics 2024, 12, 490. [Google Scholar] [CrossRef]
- Lee, T.-W. Independent component analysis. In Independent Component Analysis: Theory and Applications; Springer: New York, NY, USA, 1998; pp. 27–66. [Google Scholar]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Lee, D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Advances in Neural Information Processing Systems; Leen, T.K., Dietterich, T.G., Tresp, V., Eds.; MIT Press: Cambridge, MA, USA, 2000; pp. 535–541. [Google Scholar]
- Hyvärinen, A.; Hoyer, P.O. Emergence of phase-and shift-invariant features by decomposition of natural images into independent feature subspaces. Neural Comput. 2000, 12, 1705–1720. [Google Scholar] [CrossRef]
- Prasadan, A.; Nadakuditi, R. The finite sample performance of Dynamic Mode Decomposition. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–29 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Creager, E.; Stein, N.D.; Badeau, R.; Depalle, P. Nonnegative tensor factorization with frequency modulation cues for blind audio source separation. arXiv 2016, arXiv:1606.00037. [Google Scholar]
- Belouchrani, A.; Meraim, K.A.; Cardoso, J.F. A blind source separation technique based on second order statistics. IEEE Trans. Signal Process. 2002, 45, 434–444. [Google Scholar] [CrossRef]
- Webster, M.B.; Lee, J. Blind Source Separation of Single-Channel Mixtures via Multi-Encoder Autoencoders. arXiv 2024, arXiv:2309.07138. [Google Scholar]
- Erdogan, A.T.; Pehlevan, C. Blind Bounded Source Separation Using Neural Networks with Local Learning Rules. In Proceedings of the ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 3812–3816. [Google Scholar]
- Bando, Y.; Masuyama, Y.; Nugraha, A.A.; Yoshii, K. Neural Fast Full-Rank Spatial Covariance Analysis for Blind Source Separation. arXiv 2023, arXiv:2306.10240. [Google Scholar]
- Yu, X.; Hu, D.; Xu, J. Blind Source Separation—Theory and Applications; John Wiley and Sons: New York, NY, USA, 2014. [Google Scholar]
- Hassan, N.; Ramli, D.A. A comparative study of blind source separation for bioacoustics sounds based on FastICA, PCA and NMF. Procedia Comput. Sci. 2018, 126, 363–372. [Google Scholar] [CrossRef]
- Tharwat, A. Independent component analysis: An introduction. Appl. Comput. Inform. 2021, 17, 222–249. [Google Scholar] [CrossRef]
- Baysal, B.; Efe, M. A comparative study of blind source separation methods. Turk. J. Electr. Eng. Comput. Sci. 2023, 31, 9. [Google Scholar] [CrossRef]
- Schmid, P.J.; Sesterhenn, J. Dynamic mode decomposition of numerical and experimental data. In Proceedings of the 61st Annual Meeting of the APS Division of Fluid Dynamics, San Antonio, TX, USA, 23–25 November 2008; American Physical Society: College Park, MD, USA, 2008. [Google Scholar]
- Prasadan, A.; Lodhia, A.; Nadakuditi, R.R. Phase transitions in the dynamic mode decomposition algorithm. In Proceedings of the Computational Advances in Multi-Sensor Adaptive Processing, Le Gosier, Guadeloupe, 15–18 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Prasadan, A.; Nadakuditi, R. Time Series Source Separation Using Dynamic Mode Decomposition. Siam J. Appl. Dyn. 2020, 19, 1160–1199. [Google Scholar] [CrossRef]
- Chen, C.; Peng, H. Dynamic mode decomposition for blindly separating mixed signals and decrypting encrypted images. Big Data And Inf. Anal. 2024, 8, 1–25. [Google Scholar] [CrossRef]
- Nedzhibov, G.H. On Alternative Algorithms for Computing Dynamic Mode Decomposition. Computation 2022, 10, 210. [Google Scholar] [CrossRef]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. J. Comput. Dyn. 2014, 1, 391–421. [Google Scholar] [CrossRef]
- Hirsh, S.M.; Brunton, B.W.; Kutz, J.N. Data-driven Spatiotemporal Modal Decomposition for Time Frequency Analysis. Appl. Comput. Harmon. Anal. 2020, 49, 771–790. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence, in Dynamical Systems and Turbulence; Lecture Notes in Math; Springer: Berlin/Heidelberg, Germany, 1981; Volume 898. [Google Scholar]
- Clainche, S.L.; Vega, J.M. Higher order dynamic mode decomposition. SIAM J. Appl. Dyn. Syst. 2017, 16, 882–925. [Google Scholar] [CrossRef]
- Vega, J.M.; Clainche, S.L. Higher Order Dynamic Mode Decomposition and Its Applications; Academic Press: London, UK, 2021; ISBN 9780128227664. [Google Scholar]
- Nedzhibov, G.H. On Higher Order Dynamic Mode Decomposition. Ann. Acad. Rom. Sci. Ser. Math. Appl. 2024, 16, 5–16. [Google Scholar] [CrossRef]
- Williams, M.O.; Hemati, M.S.; Dawson, S.T.M.; Kevrekidis, I.G.; Rowley, C.W. Extending Data-Driven Koopman Analysis to Actuated Systems. IFAC-PapersOnLine 2016, 49, 704–709. [Google Scholar] [CrossRef]
- Anantharamu, S.; Mahesh, K. A parallel and streaming Dynamic Mode Decomposition algorithm with finite precision error analysis for large data. J. Comput. Phys. 2019, 380, 355–377. [Google Scholar] [CrossRef]
- Li, B.; Garicano-Menaab, J.; Valero, E. A dynamic mode decomposition technique for the analysis of nonuniformly sampled flow data. J. Comput. Phys. 2022, 468, 111495. [Google Scholar] [CrossRef]
- Mezić, I. On Numerical Approximations of the Koopman Operator. Mathematics 2022, 10, 1180. [Google Scholar] [CrossRef]
- Nedzhibov, G. Dynamic Mode Decomposition: A new approach for computing the DMD modes and eigenvalues. Ann. Acad. Rom. Sci. Ser. Math. Appl. 2022, 14, 5–16. [Google Scholar] [CrossRef]
- Nedzhibov, G. An Improved Approach for Implementing Dynamic Mode Decomposition with Control. Computation 2023, 11, 201. [Google Scholar] [CrossRef]
- Nedzhibov, G. Online Dynamic Mode Decomposition: An alternative approach for low rank datasets. Ann. Acad. Rom. Sci. Ser. Math. Appl. 2023, 15, 229–249. [Google Scholar] [CrossRef]
- Nedzhibov, G. Delay-Embedding Spatio-Temporal Dynamic Mode Decomposition. Mathematics 2024, 12, 762. [Google Scholar] [CrossRef]
- Arbabi, H.; Mezic, I. Ergodic Theory, Dynamic Mode Decomposition, and Computation of Spectral Properties of the Koopman Operator. SIAM J. Appl. Dyn. Syst. 2017, 16, 2096–2126. [Google Scholar] [CrossRef]
- Kamb, M.; Kaiser, E.; Brunton, S.L.; Kutz, J.N. Time-delay observables for Koopman: Theory and applications. SIAM J. Appl. Dyn. Syst. 2020, 19, 886–917. [Google Scholar] [CrossRef]
- Kutz, J.N.; Brunton, S.L.; Brunton, B.W.; Proctor, J. Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems; SIAM: Philadelphia, PA, USA, 2016; ISBN 978-1-611-97449-2. [Google Scholar]
- Wu, Z.; Brunton, S.L.; Revzen, S. Challenges in dynamic mode decomposition. arXiv 2021, arXiv:2109.01710. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Zhou, K.; Zhou, W.; Wen, X.; Liu, Y. Flow prediction using dynamic mode decomposition with time-delay embedding based on local measurement. Phys. Fluids 2021, 33, 095109. [Google Scholar] [CrossRef]
- Massar, H.; Nsiri, B.; Drissi, T.B. DWT-BSS: Blind Source Separation applied to EEG signals by extracting wavelet transform’s approximation coefficients. J. Phys. Conf. Ser. 2023, 2550, 012031. [Google Scholar] [CrossRef]
- EEG (Electroencephalogram). Mayo Clinic. Mayo Foundation for Medical Education and Research. 2022. Available online: https://www.mayoclinic.org/tests-procedures/eeg/about/pac-20393875 (accessed on 17 November 2022).
- Judith, A.M.; Priya, S.B.; Mahendran, R.K. Artifact Removal from EEG signals using Regenerative Multi-Dimensional Singular Value Decomposition and Independent Component Analysis. Biomed. Signal Process. Control. 2022, 74, 103452. [Google Scholar]
- Kachenoura, A.; Albera, L.; Senhadji, L. Séparation aveugle de sources en ingénierie biomédicale. IRBM 2007, 28, 20–34. [Google Scholar] [CrossRef][Green Version]
- Mannan, M.M.N.; Kamran, M.A.; Jeong, M.Y. Identification and removal of physiological artifacts from electroencephalogram signals: A review. IEEE Access 2018, 6, 30630–30652. [Google Scholar] [CrossRef]
- Rashmi, C.R.; Shantala, C.P. EEG artifacts detection and removal techniques for braincomputer interface applications: A systematic review. Int. J. Adv. Technol. Eng. Explor. 2022, 9, 354. [Google Scholar]
- Zhou, W.; Chelidze, D. Blind source separation based vibration mode identification. Mech. Syst. Signal Process. 2007, 21, 3072–3087. [Google Scholar] [CrossRef]
- Schalk, G.; McFarland, D.J.; Hinterberger, T.; Birbaumer, N.; Wolpaw, J.R. BCI2000: A General-Purpose Brain-Computer Interface (BCI) System. IEEE Trans. Biomed. Eng. 2004, 51, 1034–1043. [Google Scholar] [CrossRef] [PubMed]
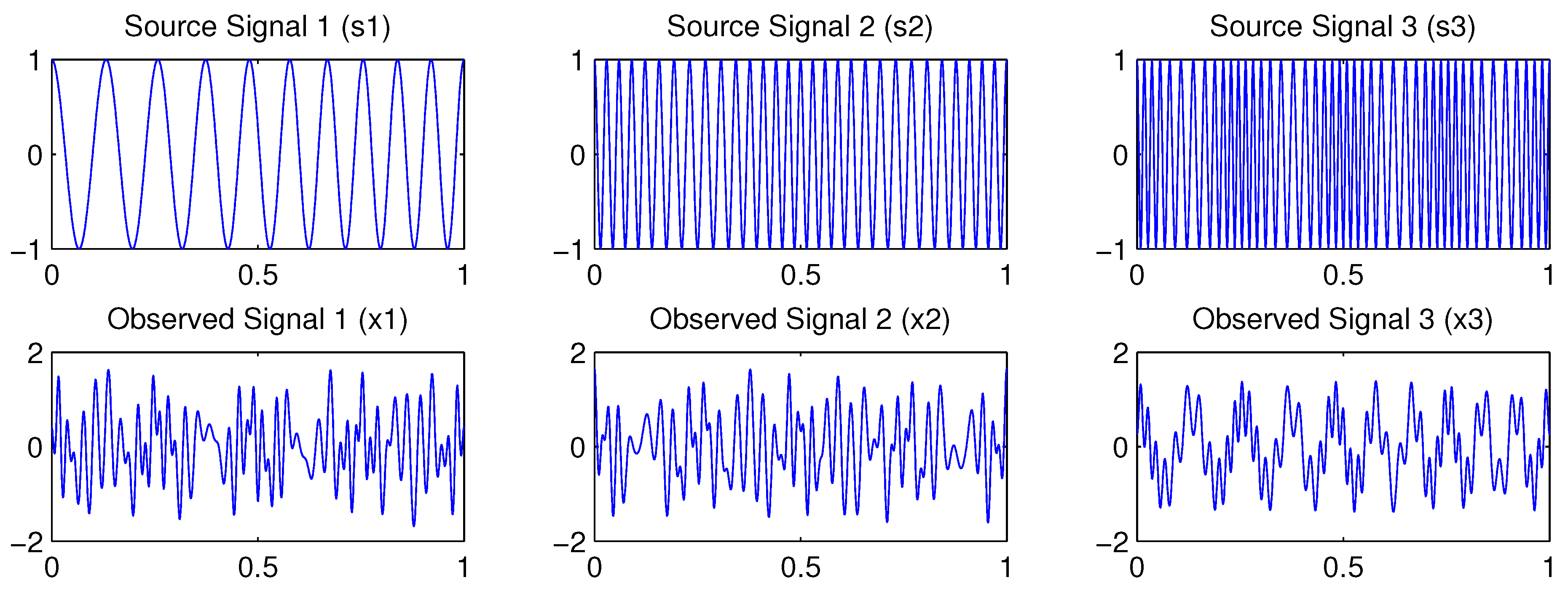

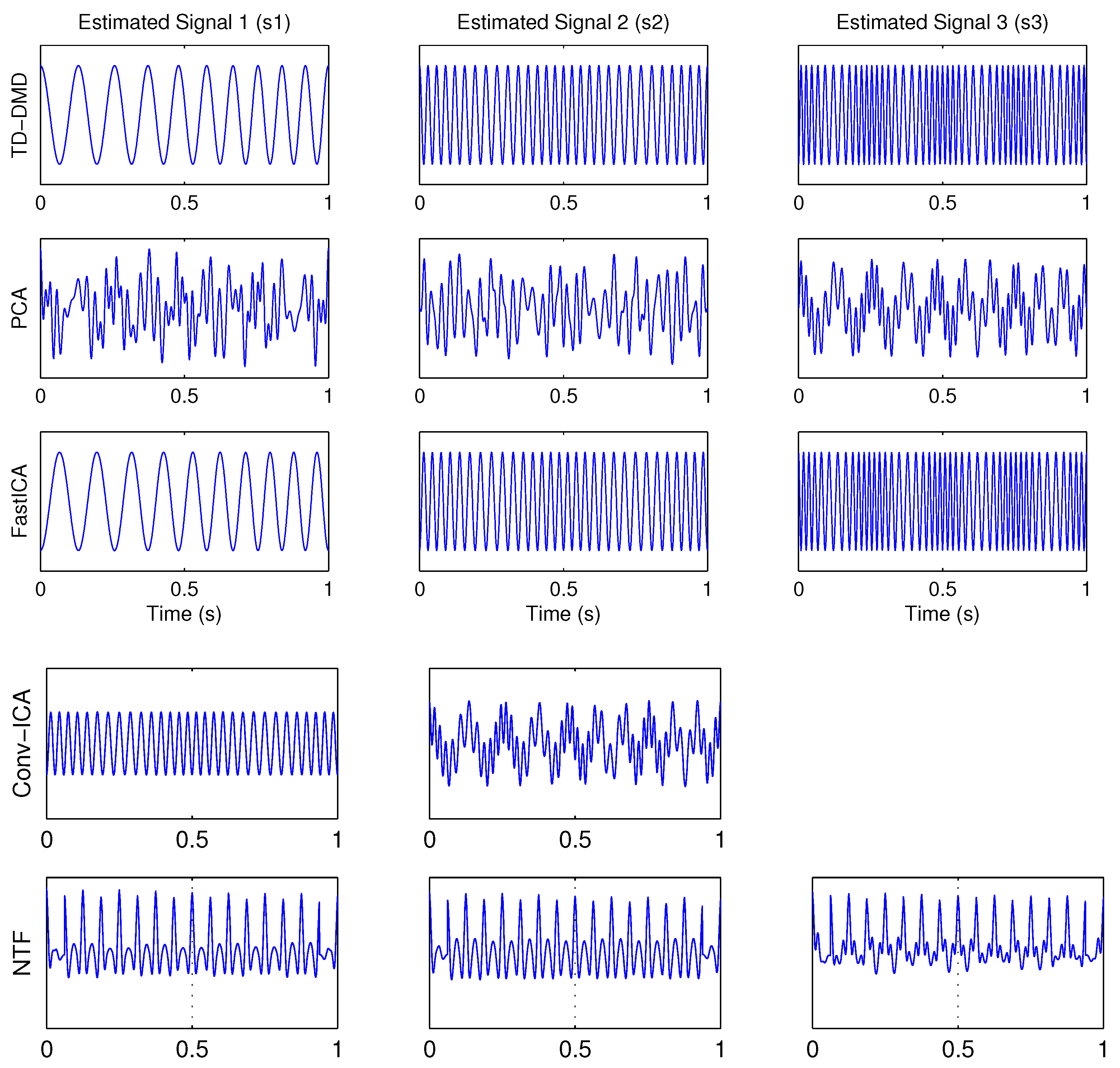
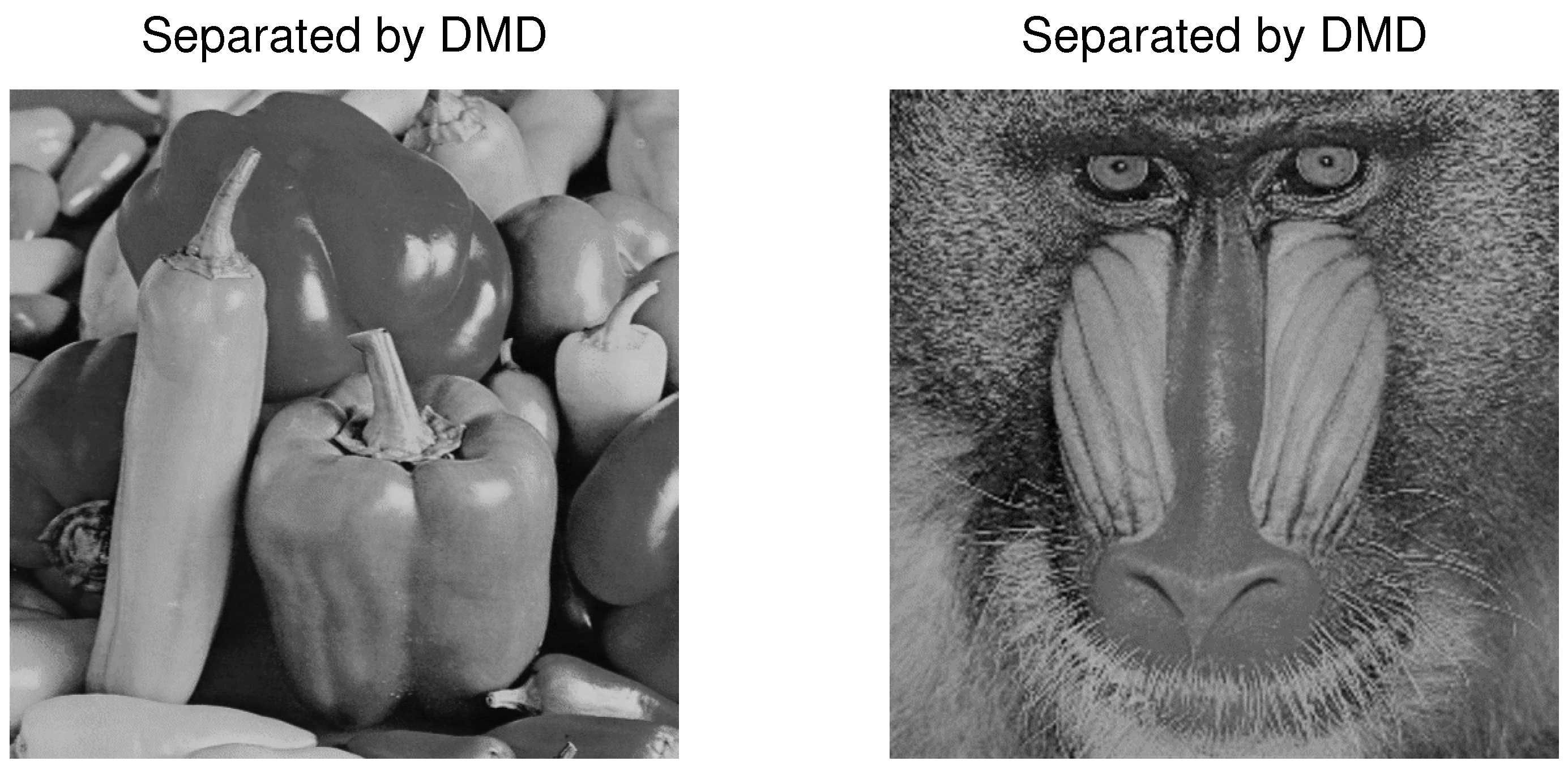
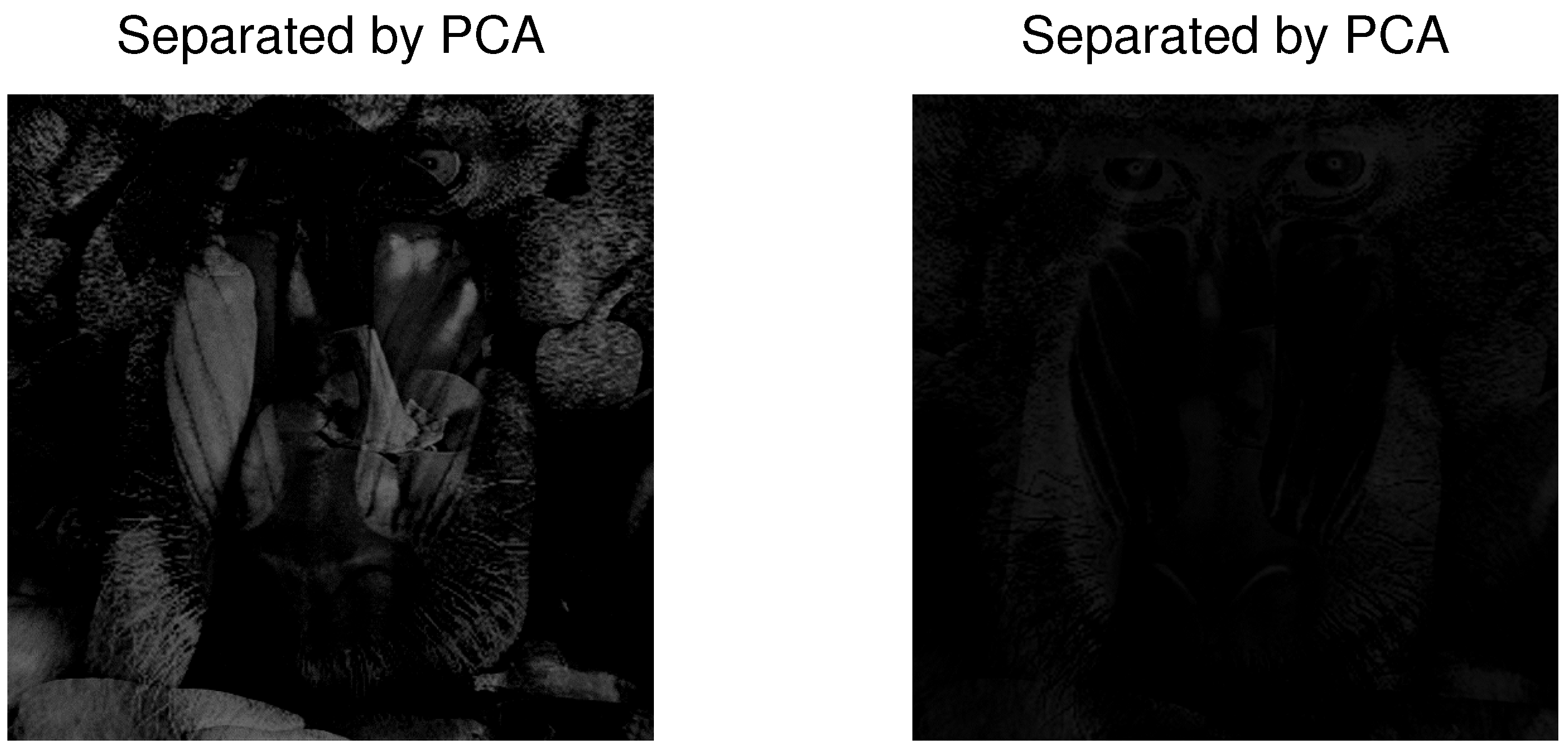


| PCA | FastICA | TD-DMD | Conv-ICA | NTF | |
|---|---|---|---|---|---|
| 0.58045 | 0.99893 | 1 | - | 0.02403 | |
| −0.81851 | −0.99914 | −1 | 0.7095 | 0.4763 | |
| −0.70819 | −0.99975 | −1 | 0.9994 | −0.0052 |
| PCA | FastICA | TD-DMD () | TD-DMD () | Conv-ICA | NTF | |
|---|---|---|---|---|---|---|
| 5.85 | −12.37 | 12.42 | −6.66 | −10.09 | −0.002 | |
| 0.51 | −14.68 | −3.73 | 13.04 | 12.4 | 20.33 |
| PCA | FastICA | TD-DMD () | TD-DMD () | Conv-ICA | NTF | |
|---|---|---|---|---|---|---|
| 4.59 | −15.78 | 29.92 | −7.85 | −10.04 | −0.002 | |
| −0.52 | −14.66 | 9.58 | −5.88 | 12.4 | 20.3 |
| TD-DMD with | MSE | ||
|---|---|---|---|
| 0.0595 | |||
| 0.0048 | |||
| Picture | PCA | FastICA | Conv-ICA | NTF | TD-DMD (s = 1) | TD-DMD (s = 2) | TD-DMD (s = 3) |
|---|---|---|---|---|---|---|---|
| Baboon | 0.081 | 0.15171 | −0.1881 | 0.0001 | 5.609 | 6.398 | 5.76 |
| Peppers | 0.131 | 0.17745 | 21.349 | 20.259 | 5.343 | 6.000 | 5.683 |
| Picture | PCA | FastICA | Conv-ICA | NTF | TD-DMD (s = 1) | TD-DMD (s = 2) | TD-DMD (s = 3) |
|---|---|---|---|---|---|---|---|
| Baboon | −0.0598 | 0.151 | −0.1881 | 0.0001 | 6.4812 | 5.2694 | 3.0961 |
| Peppers | 0.130 | 0.177 | 21.349 | 20.259 | 5.9691 | 5.4217 | 3.8431 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nedzhibov, G. Blind Source Separation Using Time-Delayed Dynamic Mode Decomposition. Computation 2025, 13, 31. https://doi.org/10.3390/computation13020031
Nedzhibov G. Blind Source Separation Using Time-Delayed Dynamic Mode Decomposition. Computation. 2025; 13(2):31. https://doi.org/10.3390/computation13020031
Chicago/Turabian StyleNedzhibov, Gyurhan. 2025. "Blind Source Separation Using Time-Delayed Dynamic Mode Decomposition" Computation 13, no. 2: 31. https://doi.org/10.3390/computation13020031
APA StyleNedzhibov, G. (2025). Blind Source Separation Using Time-Delayed Dynamic Mode Decomposition. Computation, 13(2), 31. https://doi.org/10.3390/computation13020031






