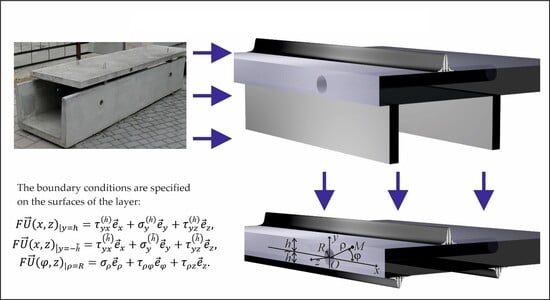
Consideration of Spatially Infinite Loads in the Problem for a Layer with a Cylindrical Cavity and Continuous Supports

Abstract

An analytical method is proposed for determining the stress-strain state in an elastic layer with a cylindrical cavity supported by linear continuous supports perpendicular to the cavity. The need for such a development is due to the fact that in aerospace and mechanical engineering, structural elements are often affected by loads and supports described by infinite functions. This complicates the calculation for spatial bodies with complex geometry and stress concentrators. The methodology is based on the generalized Fourier method within the spatial problem of elasticity theory. The model is considered as a layer with specified stresses at the outer boundaries, where the reactions of the supports are represented as applied loads. A combined approach is used to describe the geometry using a Cartesian coordinate system for the layer and a cylindrical coordinate system for the cavity. The key idea is to decompose the original problem into two simpler ones using the principle of superposition. Auxiliary problem: the stresses in a solid layer (without a cavity) are calculated to determine the stress fields at its nominal location. Main problem: a layer with a cavity is considered, on the surface of which the stresses calculated in the first step are acting but taken with the opposite sign. The complete solution is the sum of the solutions of these two problems. Each of them is reduced to an infinite system of linear algebraic equations, which is solved by the method of reduction. This approach makes it possible to calculate the stress-strain state at any point of the body with high accuracy. Numerical analysis confirmed the correctness of satisfying the boundary conditions and showed the dependence of stresses on the nature of the distributed loads. The cylindrical cavity acts as a stress concentrator, which leads to a local increase in stresses σ_x and σ_z at the upper and lower boundaries of the layer to values that exceed both the applied load by and the calculated resistance of concrete of class C25/30.

1. Introduction

The modern development of aerospace technology, mechanical engineering, and the construction industry places increased demands on the reliability and strength of structural elements. Such elements often have a complex geometric shape, in particular, are weakened by holes or cavities, which act as stress concentrators and significantly affect the overall bearing capacity. In the construction industry, these are floor slabs in civil construction that rest on walls and have technological openings. In the aerospace industry, these are elements of the aircraft wing’s power set, weakened by openings for communications. Additional analytical difficulties arise when structures are subjected to localized or infinitely distributed loads. In this regard, the problem of determining the stress-strain state of elastic bodies with cavities under such loads remains an urgent problem in the mechanics of deformable solids. The object of this study is an elastic layer with a cylindrical cavity resting on two infinite supports perpendicular to the cavity, a model that is often encountered in engineering practice and requires accurate calculation methods.

One of the options for determining the stress-strain state of structures is an experimental study of the physical and mechanical properties of their elements, followed by an analysis of the stress state of the entire structure. Such elements may have multiple boundary surfaces. To do this, a series of standardized mechanical tests are performed, including tension, compression, and shear. Thus, in [1], the elastic characteristics of a steel-cord rubber transportation belt are calculated, in particular, the tensile modulus (E) and the shear modulus (G). The E modulus was determined analytically by the rule of mixing components, and the G modulus was determined using variational principles with subsequent experimental verification. The study was performed using modified tensile testing techniques, including tensile testing of short specimens and two torsional methods. The results are used to accurately model the behavior of the belt under extreme conditions. The procedure for such tests is regulated, for example, by the standard [2] for polymers. The methods and results of testing composite materials are presented in [3]. Based on the test results, diagrams of physical and mechanical properties are constructed [4]. The obtained reliable data serve as mandatory input parameters for further mathematical modeling and are the basis for verifying analytical and numerical calculations. The disadvantages of this approach include high cost, labor-intensive testing procedures, physical nonlinearity of complex elements, and the need for new tests when geometric parameters change.

Experimental studies can be replaced by numerical methods. The finite element method [5,6] is the most common approach for determining the stress-strain state of complex structures, which is implemented in various software packages [7]. For example, in [8], a mathematical model of the dynamics of an elastic half-space with a cylindrical cavity reinforced by a shell and a plate under asymmetric surface loads, which are given as a step function of the Heaviside. The authors model the unsteady dynamic stress-strain state by solving an arbitrary static problem using the finite element method and then apply the Wilson-θ method for the dynamics, which transforms the differential matrix system into an iterative sequence of quasi-static problems. The results obtained by the finite element method often serve as a benchmark for assessing the reliability of the proposed analytical approach [9,10]. However, numerical methods provide approximate values of the stress-strain state, which reduces confidence when highly accurate results are required. Thus, despite the availability of numerous methods, there is a need for a precise analytical tool that allows modeling the effect of infinitely distributed loads (e.g., fluid pressure or reactions of continuous supports) on structures with cavities, which is the main gap that this work fills.

In the mechanics of deformable solids [11], classical analytical methods are known to obtain accurate solutions to problems of the stress-strain state of a layer with a cylindrical cavity or inclusion [12,13]. Paper [12] considers a dynamic problem for an infinite elastic layer with a cylindrical cavity. To solve it, they apply the Fourier and Laplace integral transforms, which reduces the problem to a one-dimensional boundary value vector problem, and then solve this problem, obtaining accurate formulas for displacements and stresses. Paper [13] investigates the problem of stress concentration around holes in perforated plates, which can lead to material failure. To solve this problem, the authors apply three different metaheuristic optimization algorithms: the Whale Optimization Algorithm (WOA), the Sine-Cosine Algorithm (SCA), and the Genetic Algorithm (GA). They optimize parameters such as hole orientation, composite layer sequence, shape, and hole “bluntness” to achieve a minimum thermal stress field.

However, their application has certain limitations, in particular, they are usually suitable only for a plane problem formulation and are effective when considering no more than three boundary surfaces. Modern research develops the concepts laid down in the classic works, expanding their functionality. Currently, there are approaches that use an integral transformation. Paper [14] considers the problem of torsion of an elastic half-space with a vertical cylindrical cavity. To solve this contact problem of elasticity theory, Weber-Orr integral transforms are used. The authors propose two new methods that reduce the problem to regular integral equations of the second kind, which enables obtaining highly accurate approximate solutions for all values of geometric parameters.

Also, this method can be used to analyze cases with several cylindrical inclusions [9,15]. For example, in [9], a general analytical solution was developed for the problem of the stress state around circular holes in plates with functional-gradient properties under the action of various in-plane loads. The methodology is based on the expansion of functions into series and takes into account changes in mechanical properties along the thickness according to a power law. Also, a set of cylindrical inclusions located in an inhomogeneous elastic half-space is analytically studied in [15], where the authors use the method of wave function expansion to solve the problem, which allows obtaining an accurate solution. The study shows how the stress distribution is affected by inclusion depth.

Despite the expansion of the toolkit, this approach still has limitations: it allows considering only a single or cylindrical inhomogeneity located perpendicular to the layer surface. Thus, it cannot be used to analyze cases with multiple or parallel cylindrical inclusions, which are relevant for many engineering applications. These limitations emphasize the need for further development of more versatile analytical and numerical methods for modeling complex geometries and configurations.

The classical Fourier method was developed in [16]. The authors substantiate an analytical and numerical method that allows solving spatial problems of elasticity theory and constructing exact solutions of the Lamé equations for multi-connected domains bounded by several canonical surfaces. This is a generalized Fourier method.

This method is also used in solving problems for transversally isotropic multi-coupled bodies and thermoelasticity problems. Thus, in [17], the problem of the action of an axial concentrated force on an elastic transversally isotropic half-space with a fixed inclusion in the form of a paraboloid of rotation is studied. Paper [18] investigates the stress state of a transversally isotropic space with periodic systems of planar circular cracks, the centers of which are on the anisotropy axis of the space and their planes are perpendicular to it. In [19], a stationary axisymmetric problem of thermoelasticity was considered for a half-space with a spherical inclusion and a cavity. Papers [20,21,22] considered boundary value problems of elasticity theory for multi-connected bodies in the form of an infinite circular cylinder with four and N cylindrical cavities, as well as for a cylinder with cylindrical cavities forming a hexagonal structure.

Using the generalized Fourier method, mixed problems of elasticity theory for a half-space with a cylindrical cavity located parallel to its boundary were studied in [23,24]. The authors of [25] studied a similar geometry by considering a half-space with several cavities, but for contact-type boundary conditions, which allowed them to model the interaction with other bodies. However, the proposed method [23,24,25] does not allow solving problems for a layer.

Several studies have applied the generalized Fourier method has been applied to solve spatial problems of elasticity theory for a layer with a cylindrical cavity. For example, in [26], the three-dimensional stress-strain state of an elastic layer containing a cylindrical cavity and resting on an absolutely rigid base was investigated. A numerical analysis was performed to determine the stress concentration coefficient near the cavity and its dependence on key geometric parameters of the problem, such as the relative layer thickness and cavity radius, was investigated. Paper [27] is devoted to solving the first basic problem of elasticity theory for a three-dimensional elastic layer weakened by a cylindrical cavity. It is assumed that the boundaries of the layer are subjected to specified displacements. A numerical analysis of the stress distribution is performed and the influence of geometric parameters, in particular, the cavity radius, on the stress concentration factor is investigated.

The second basic spatial problem of the theory of elasticity for a layer with a longitudinal cylindrical cavity under periodic displacements on the layer surface was solved in [28]. The stress-strain state of the layer on the surface of the cavity and the isthmuses from the cavity to the boundaries of the layer were investigated. Works [29,30] analyzed the stress state of a layer with a longitudinal cavity and given non-proprietary mixed boundary conditions, as well as a layer with a cylindrical cavity under the given conditions of smooth contact at the boundaries of the layer and displacements on the surface of the cavity. However, the proposed solution methods cannot take into account loads in the form of constant functions.

Developing this direction, the authors in [31] solved the problem for a layer with a system of N embedded cylindrical supports, taking into account the conditions of ideal contact at the boundaries, and analyzed the effect of the number of supports and their location on the overall stiffness of the structure and the distribution of stresses in it.

A separate example is the solution of the problem of rotation of a layer with a cylindrical pipe around a rigid cylinder [32]. The stress-strain state arising from the action of centrifugal forces and contact interaction is modeled. This work is an example of solving a complex contact problem of dynamics for bodies of revolution and demonstrates the flexibility of the method for analyzing complex engineering problems.

The generalized Fourier method has been successfully used to solve spatial problems of elasticity theory for multi-connected bodies when setting contact-type boundary conditions. For example, in [33], the bearing connection is presented as a layer with a cylindrical pipe, for which contact-type conditions are considered on the inner surface of the pipe. The authors investigated the stress state of the bearing layer connection with the support shaft and analyzed the stress state of the bearing layer and ring under the action of counteracting moments. The analysis of the stress state of a layer with two cylindrical tubes is presented in [34], and of a layer with a cylindrical cavity and a tube in [35]. The stress state of a layer with two cylindrical cavities and an inclusion under some specified contact conditions was analyzed in [36]. In [37], the calculation of the stress state took into account the adhesion losses of the reinforcing element with the layer. The solution of the problem of the theory of elasticity for a ball with a circular inclusion and a circular cavity under specified boundary conditions of the contact type was carried out in [38].

The review and analysis of scientific works allow us to conclude that the mentioned methods do not allow us to solve and investigate problems for elastic domains that have loads at infinity. Therefore, this work presents an innovative method that will allow us to solve problems of this type.

The aims of this work are to:

• to develop a methodology for calculating the stress-strain state of a layer with a cylindrical cavity located on two continuous supports perpendicular to the cavity and given constant stress functions on the layer surfaces;
• analysis of the stress state of a concrete slab in places of stress concentration.

2. Materials and Methods

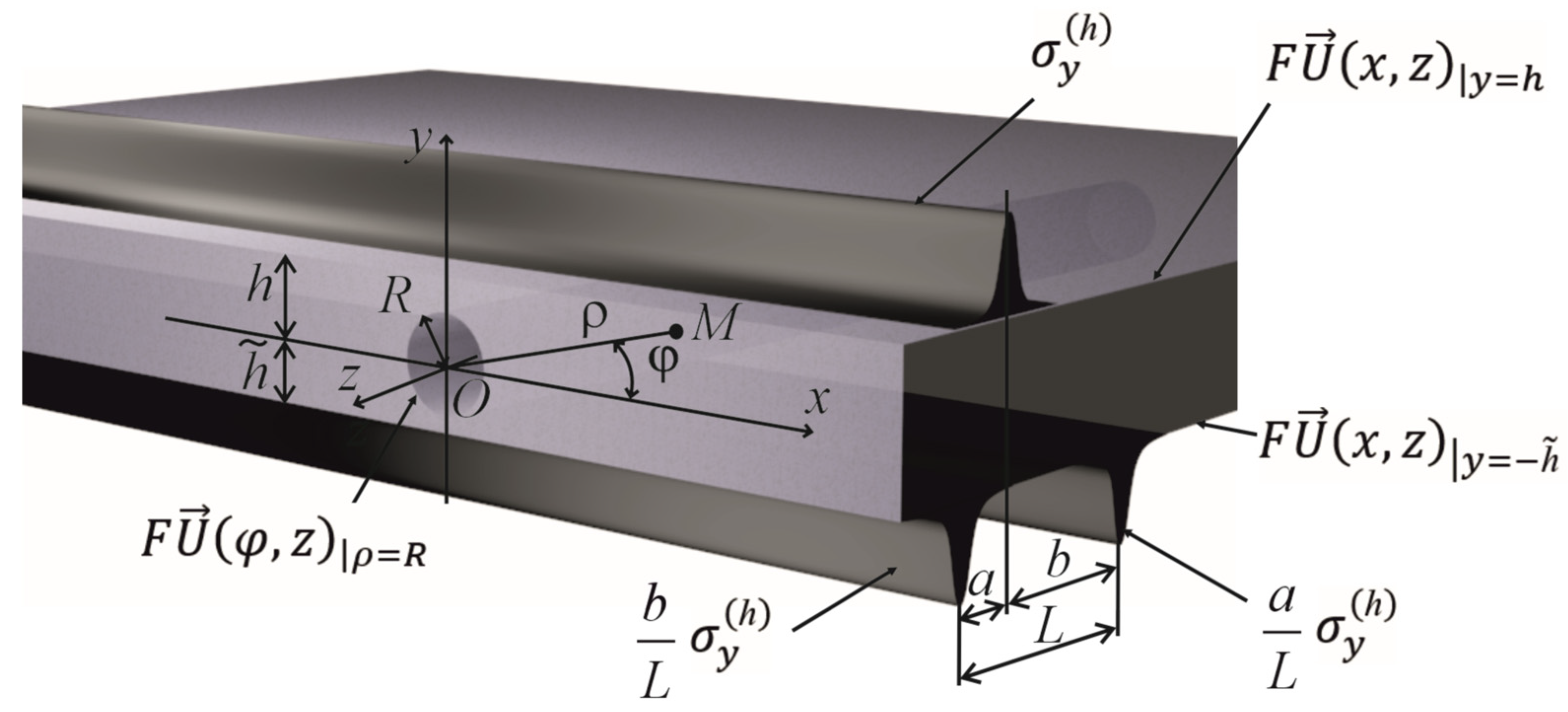
2.1. Calculation Model of a Layer with a Cylindrical Cavity, Assumptions About Elasticity and Isotropy

The purpose of this work is to perform a numerical calculation of the stress-strain state of a layer of C25/30 concrete. When calculating strength, simplified assumptions about elasticity and isotropy are used to model its behavior.

In general, concrete as a material is not perfectly elastic and isotropic. Its stress-strain diagram is nonlinear, especially under high loads. In engineering calculations, it is assumed that concrete behaves elastically at stresses not exceeding 30–40% of its maximum compressive strength (for the specified concrete class, this is 30 MPa). The modules of elasticity and tensile strength of concrete are significantly lower than its compressive strength, but elasticity theory usually uses a single modulus of elasticity (E), which is a simplification.

Concrete is inherently heterogeneous (consisting of cement stone, sand, and crushed stone) and anisotropic at the micro level. However, at the macroscopic level (when the dimensions of the element significantly exceed the dimensions of the aggregate), its properties are considered to be the same in all directions. This is a standard and very accurate assumption for ordinary concrete. The proposed model considers a body made of “pure” concrete. If it were reinforced concrete, where reinforcement creates a pronounced anisotropy, such an assumption would be incorrect.

The model is an elastic isotropic layer with a cylindrical cavity located parallel to the layer boundaries (Figure 1). Constant stresses (${\sigma }_y^{\left(h\right)}$) along the x-axis are set at the upper boundary of the layer. Linear continuous supports on the lower boundary of the layer are represented as support reactions-constant stresses that balance the given loads. The cavity is considered in the cylindrical coordinate system (ρ, φ, z). The layer is considered in the Cartesian system (x, y, z).

The cylindrical coordinate system is combined and equally oriented with the Cartesian coordinate system of the layer.

The distance from the coordinate center to the upper boundary of the layer y = h, to the lower boundary of the layer $y=-\tilde{h}$. The radius of the cylindrical cavity is R. The distances h and $\tilde{h}$ can have any values greater than R (h > R <$\widetilde{ h}$).

On the flat surfaces of the layer, the stresses vectors $F\overrightarrow{U}{\left(x,z\right)}_{\left|y=h\right.}={\overrightarrow{F}}_h^0\left(x,z\right), F\overrightarrow{U}{\left(x,z\right)}_{\left|y=-\tilde{h}\right.}={\overrightarrow{F}}_{\tilde{h}}^0\left(x,z\right)$ are given; on the surface of the cavity, the stress vector $F\overrightarrow{U}{\left(\phi ,z\right)}_{\left|\rho =R\right.}={\overrightarrow{F}}_0^{\left(p\right)}\left(\phi ,z\right)$ is given, where

$$\begin{gathered} {\overrightarrow{F}}_h^0\left(x,z\right)={\tau }_{yx}^{\left(h\right)}{\overrightarrow{e}}_x+{\sigma }_y^{\left(h\right)}{\overrightarrow{e}}_y+{\tau }_{yz}^{\left(h\right)}{\overrightarrow{e}}_z, \\ {\overrightarrow{F}}_{\tilde{h}}^0\left(x,z\right)={\tau }_{yx}^{\left(\tilde{h}\right)}{\overrightarrow{e}}_x+{\sigma }_y^{\left(\tilde{h}\right)}{\overrightarrow{e}}_y+{\tau }_{yz}^{\left(\tilde{h}\right)}{\overrightarrow{e}}_z, \\ {\overrightarrow{F}}_0^{\left(p\right)}\left(\phi ,z\right)={\sigma }_{\rho }{\overrightarrow{e}}_{\rho }+{\tau }_{\rho \phi }{\overrightarrow{e}}_{\phi }+{\tau }_{\rho z}{\overrightarrow{e}}_z. \end{gathered}$$

(1)

The functions ${\tau }_{yx}^{\left(h\right)},{\sigma }_y^{\left(h\right)},{\tau }_{yz}^{\left(h\right)},{\tau }_{yx}^{\left(\tilde{h}\right)},{\sigma }_y^{\left(\tilde{h}\right)},{\tau }_{yz}^{\left(\tilde{h}\right)}$ defined on the boundaries of the layer are constants along the x-axis and rapidly decreasing functions along the z-axis or a combination of a constant and a concentrated load.

Based on the conditions of statics, the equilibrium equations must be fulfilled for the first basic problem of elasticity theory

$${\iint }_{\left(\sigma \right)}\overrightarrow{F}\left(M\right)d\sigma =0, {\iint }_{\left(\sigma \right)}\overrightarrow{r}\times \overrightarrow{F}\left(M\right)d\sigma =0,$$

where $\sigma =\left\{{\sigma }_1\cup {\sigma }_2\right\}$, ${\sigma }_1$ is the plane on y = h, ${\sigma }_2$ is the plane on $y=-\tilde{h}$, $\overrightarrow{F}\left(M\right)=\left\{\begin{array}{c}{\overrightarrow{F}}_h^0\left(x,z\right)\hspace{0.33em}\mathrm{on} {\sigma }_1\\ {\overrightarrow{F}}_{\tilde{h}}^0\left(x,z\right)\hspace{0.33em}\mathrm{on}{ \sigma }_2\end{array}\right.,$ $\overrightarrow{r}$ is the radius vector of the point M.

2.2. Solution Method

For a highly accurate determination of the stress-strain state of this model, it is most efficient to use the generalized Fourier method by applying it to the Lamé equations.

The basic solutions of the Lamé equation are chosen in the form [16]:

$$\begin{gathered} {\overrightarrow{u}}_k^{\pm }\left(x,y,z;\lambda ,\mu \right)=N_k^{\left(d\right)}{e}^{i\left(\lambda z+\mu x\right)\pm \gamma y}; \\ {\overrightarrow{R}}_{k,m}\left(\rho ,\phi ,z;\lambda \right)=N_k^{\left(p\right)}{I}_m\left(\lambda \rho \right)e^{i\left(\lambda z+m\phi \right)}; \\ {\overrightarrow{S}}_{k,m}\left(\rho ,\phi ,z;\lambda \right)=N_k^{\left(p\right)}\left[{\left(\mathit{sign}\lambda \right)}^m{K}_m\left(\left|\lambda \right|\rho \right)e^{i\left(\lambda z+m\phi \right)}\right]; k=1,\hspace{0.33em}2,\hspace{0.33em}3; \end{gathered}$$

(2)

$$N_1^{\left(d\right)}={\displaystyle \frac{1}{\lambda }}\mathsf{\nabla }; N_2^{\left(d\right)}={\displaystyle \frac{4}{\lambda }}\left(\nu -1\right){\overrightarrow{e}}_2^{\left(1\right)}+{\displaystyle \frac{1}{\lambda }}\mathsf{\nabla }\left(y\times \right); N_3^{\left(d\right)}={\displaystyle \frac{i}{\lambda }}\mathit{rot}\left({\overrightarrow{e}}_3^{\left(1\right)}\times \right)\hspace{0.33em};$$

$$N_1^{\left(p\right)}={\displaystyle \frac{1}{\lambda }}\mathsf{\nabla }; N_2^{\left(p\right)}={\displaystyle \frac{1}{\lambda }}\left[\mathsf{\nabla }\left(\rho {\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }\rho }}\right)+4\left(\nu -1\right)\left(\mathsf{\nabla }-{\overrightarrow{e}}_3^{\left(2\right)}{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }z}}\right)\right]; N_3^{\left(p\right)}={\displaystyle \frac{i}{\lambda }}\mathit{rot}\left({\overrightarrow{e}}_3^{\left(2\right)}\times \right)\hspace{0.33em};$$

$$\gamma =\sqrt{{\lambda }^2+{\mu }^2};-\infty <\lambda ,\mu <\infty ,$$

where $I_m\left(x\right)$, $K_m\left(x\right)$ are the modified Bessel functions; $\nu$ is the Poisson’s ratio; ${\overrightarrow{S}}_{k,m}$, ${\overrightarrow{R}}_{k,m}$, $k=1,\hspace{0.33em}2,\hspace{0.33em}3$ are the external and internal solutions of the Lamé equation for cylindrical surfaces, respectively; ${\overrightarrow{u}}_k^{\left(+\right)}$ is the solution of the Lamé equation for the Cartesian coordinate system at y < 0; ${\overrightarrow{u}}_k^{\left(-\right)}$ is the solution of the Lamé equation for the Cartesian coordinate system at y > 0.

The transition formulas [16,23,26] were used to transfer these basic solutions between different coordinate systems:

-

For the transition from the solutions ${\overrightarrow{S}}_{k,m}$ of the cylindrical coordinate system to the solutions of the layer ${\overrightarrow{u}}_k^{\left(-\right)}$ (at y > 0) and ${\overrightarrow{u}}_k^{\left(+\right)}$ (at y < 0)

$$\begin{gathered} {\overrightarrow{S}}_{k,m}\left(\rho ,\phi ,z;\lambda \right)={\displaystyle \frac{{\left(-i\right)}^m}{2}}{\int }_{-\infty }^{\infty }{\omega }_{\mp }^m{\overrightarrow{u}}_k^{\left(\mp \right)}{\displaystyle \frac{d\mu }{\gamma }},k=1, 3; \\ {\overrightarrow{S}}_{2,m}\left(\rho ,\phi ,z;\lambda \right)={\displaystyle \frac{{\left(-i\right)}^m}{2}}{\int }_{-\infty }^{\infty }{\omega }_{\mp }^m\left(\left(\pm m\mu -{\displaystyle \frac{{\lambda }^2}{\gamma }}\right){\overrightarrow{u}}_1^{\left(\mp \right)}\mp {\lambda }^2{\overrightarrow{u}}_2^{\left(\mp \right)}\pm \right. \\ \left.\pm 4\mu \left(1-\nu \right){\overrightarrow{u}}_3^{\left(\mp \right)}\right){\displaystyle \frac{d\mu }{{\gamma }^2}}, \end{gathered}$$

(3)

where ${\omega }_{\mp }\left(\lambda ,\mu \right)={\displaystyle \frac{\mu \mp \gamma }{\lambda }}$, $m=0,\pm 1,\pm 2,\dots$;

-

For the transition from the solutions of ${\overrightarrow{u}}_k^{\left(+\right)}$ and ${\overrightarrow{u}}_k^{\left(-\right)}$ for the layer to the solutions of ${\overrightarrow{R}}_{k,m}$ of the cylindrical coordinate system

$$\begin{gathered} {\overrightarrow{u}}_k^{\left(\pm \right)}\left(x,y,z\right)=\sum _{m=-\infty }^{\infty }{\left(i{\omega }_{\mp }\right)}^m{\overrightarrow{R}}_{k,m},\left(k=1, 3\right); \\ {\overrightarrow{u}}_2^{\left(\pm \right)}\left(x,y,z\right)=\sum _{m=-\infty }^{\infty }\left[{\left(i{\omega }_{\mp }\right)}^m{\lambda }^{-2}\left(\left(m\mu \right){\overrightarrow{R}}_{1,m}\pm \right.\right.\left.\left.\gamma {\overrightarrow{R}}_{2,m}+4\mu \left(1-\nu \right){\overrightarrow{R}}_{3,m}\right)\right], \end{gathered}$$

(4)

where ${\overrightarrow{R}}_{k,m}={\overrightarrow{\tilde{b}}}_{k,m}\left(\rho ,\lambda \right)\times e^{i\left(m\phi +\lambda z\right)}$;

$$\begin{gathered} {\overrightarrow{\tilde{b}}}_{1,n}\left(\rho ,\lambda \right)={\overrightarrow{e}}_{\rho }{I}_n^{\prime }\left(\lambda \rho \right)+i{I}_n\left(\lambda \rho \right)\left({\overrightarrow{e}}_{\phi }{\displaystyle \frac{n}{\lambda \rho }}+{\overrightarrow{e}}_z\right); \\ {\overrightarrow{\tilde{b}}}_{2,n}\left(\rho ,\lambda \right)={\overrightarrow{e}}_{\rho }\left[\left(4\nu -3\right)I_n^{\prime }\left(\lambda \rho \right)+\lambda {\rho }_p{I}_n^{″}\left(\lambda \rho \right)\right]+ \\ +{\overrightarrow{e}}_{\phi }im\left(I_n^{\prime }\left(\lambda \rho \right)+{\displaystyle \frac{4\left(\nu -1\right)}{\lambda \rho }}{I}_n\left(\lambda \rho \right)\right)+{\overrightarrow{e}}_{z}i\lambda \rho I_n^{\prime }\left(\lambda \rho \right); \end{gathered}$$

${\overrightarrow{e}}_{\rho }$, ${\overrightarrow{e}}_{\phi }$, ${\overrightarrow{e}}_z$ are the orths of the cylindrical coordinate system.

2.3. Creating and Solving a System of Equations

The complete solution to the problem is presented in the form:

$$\overrightarrow{U}={\overrightarrow{U}}_0+{\overrightarrow{U}}_1.$$

The first part of the solution (${\overrightarrow{U}}_0$) is used to account for the given constant stresses and is an auxiliary problem. In this case, the problem is solved for a layer without a cavity in the form

$${\overrightarrow{U}}_0=\sum _{k=1}^3{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\left(H_{k,n}^{\left(0\right)}\left(\lambda \right){\overrightarrow{u}}_k^{\left(+\right)}\left(x,y,z;\lambda ,{\mu }_n\right)+\right.\left.{\tilde{H}}_{k,n}^{\left(0\right)}\left(\lambda \right){\overrightarrow{u}}_k^{\left(-\right)}\left(x,y,z;\lambda ,{\mu }_n\right)\right)d\lambda ,$$

(5)

where $H_{k,n}^{\left(0\right)}\left(\lambda \right),$ ${\widetilde{ H}}_{k,n}^{\left(0\right)}\left(\lambda \right)$ are the unknowns to be found from the boundary conditions of this auxiliary problem; ${\overrightarrow{u}}_k^{\left(+\right)}\left(x,y,z;\lambda ,\mu \right)$ and ${\overrightarrow{u}}_k^{\left(-\right)}\left(x,y,z;\lambda ,\mu \right)$ are the basic solutions of the Lamé equation for layer (2).

To determine the unknowns the stress operator is applied to solution (5), and the known functions ${\tau }_{yx}^{\left(h\right)},{\sigma }_y^{\left(h\right)},{\tau }_{yz}^{\left(h\right)},{\tau }_{yx}^{\left(\tilde{h}\right)},{\sigma }_y^{\left(\tilde{h}\right)},{\tau }_{yz}^{\left(\tilde{h}\right)}$ previously represented by the Fourier series along the x-axis and the Fourier integral along the z-axis, are substituted into the left-hand side:

$$\begin{gathered} {\overrightarrow{F}}_h^0\left(x,z\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{\overrightarrow{c}}_h^0\left(\lambda ,n\right)e^{i\left({\mu }_{n}x+\lambda z\right)}d\lambda , \\ {\overrightarrow{F}}_{\tilde{h}}^0\left(x,z\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{\overrightarrow{c}}_{\tilde{h}}^0\left(\lambda ,n\right)e^{i\left({\mu }_{n}x+\lambda z\right)}d\lambda , \end{gathered}$$

where

$$\begin{gathered} {\overrightarrow{c}}_h^0\left(\lambda ,n\right)=\left\{{\displaystyle \genfrac{}{}{0pt}{}{n=0, P_h \frac{1}{2\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\overrightarrow{F}}_h^0\left(x,z\right)e^{-i\left(\lambda z\right)}dz}{n\ne 0, 0}}\right.; \\ {\overrightarrow{c}}_{\tilde{h}}^0\left(\lambda ,n\right)=\left\{{\displaystyle \genfrac{}{}{0pt}{}{n=0, P_{\tilde{h}} \frac{1}{2\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\overrightarrow{F}}_{\tilde{h}}^0\left(x,z\right)e^{-i\left(\lambda z\right)}dz}{n\ne 0, 0}}\right.; \end{gathered}$$

(6)

$P_h{,P}_{\tilde{h}}$ are the given constants.

Getting rid of the same series, integrals and $e^{i\left({\mu }_{n}x+\lambda z\right)}$ in the right and left parts, we obtain a system of linear algebraic equations for finding $H_{k,n}^{\left(0\right)}\left(\lambda \right),$ ${\tilde{H}}_{k,n}^{\left(0\right)}\left(\lambda \right)$:

$$\left\{\begin{array}{c}{\displaystyle \sum _{s=1}^3}{H}_{k,n}^{\left(0\right)}\left(\lambda \right){\overrightarrow{d}}_s^{+}\left(h;\lambda ,{\mu }_n\right)+{\tilde{H}}_{k,n}^{\left(0\right)}\left(\lambda \right){\overrightarrow{d}}_s^{-}\left(h;\lambda ,{\mu }_n\right)={\overrightarrow{c}}_h^0\left(\lambda ,n\right),\\ {\displaystyle \sum _{s=1}^3}{H}_{k,n}^{\left(0\right)}\left(\lambda \right){\overrightarrow{d}}_s^{+}\left(-\tilde{h};\lambda ,{\mu }_n\right)+{\tilde{H}}_{k,n}^{\left(0\right)}\left(\lambda \right){\overrightarrow{d}}_s^{-}\left(-\tilde{h};\lambda ,{\mu }_n\right)={\overrightarrow{c}}_{\tilde{h}}^0\left(\lambda ,n\right),\end{array}\right.$$

(7)

where ${\overrightarrow{d}}_s^{\pm }\left(y;\lambda ,{\mu }_n\right)=N_k^{\left(d\right)}\times e^{\pm \gamma y}.$

We projected Equation (7) on the coordinate axes (equate the projections at the basis vectors ${\overrightarrow{e}}_x$, ${\overrightarrow{e}}_y$, ${\overrightarrow{e}}_z$) and express $H_{k,n}^{\left(0\right)}\left(\lambda \right)$ and ${\tilde{H}}_{k,n}^{\left(0\right)}\left(\lambda \right)$:

$$\begin{gathered} H_{j,n}^{\left(0\right)}\left(\lambda \right)=\sum _{k=1}^3{\displaystyle \frac{A_{k,j}}{D}}\left({\overrightarrow{c}}_h^0\left(\lambda ,n\right)\right){\overrightarrow{e}}_k+\sum _{k=1}^3{\displaystyle \frac{A_{k+3,j}}{D}}\left({\overrightarrow{c}}_{\tilde{h}}^0\left(\lambda ,n\right)\right){\overrightarrow{e}}_k; \\ {\tilde{H}}_{j,n}^{\left(0\right)}\left(\lambda \right)=\sum _{k=1}^3{\displaystyle \frac{A_{k,j+3}}{D}}\left({\overrightarrow{c}}_h^0\left(\lambda ,n\right)\right){\overrightarrow{e}}_k+\sum _{k=1}^3{\displaystyle \frac{A_{k+3,j+3}}{D}}\left({\overrightarrow{c}}_{\tilde{h}}^0\left(\lambda ,n\right)\right){\overrightarrow{e}}_k, \end{gathered}$$

(8)

where j = 1, 2, 3, $A_{1..6,1..6}$ and D are the algebraic complements and determinant of the system of Equation (7).

After determining the unknowns $H_{k,n}^{\left(0\right)}\left(\lambda \right)$ and ${\tilde{H}}_{k,n}^{\left(0\right)}\left(\lambda \right)$ we find the stress at the geometric location of the cavity. To do this, we apply the transition Formula (4) from the basic solutions of the layer (${\overrightarrow{u}}_k^{\left(+\right)}$ and ${\overrightarrow{u}}_k^{\left(-\right)}$) to the internal basic solutions (${\overrightarrow{R}}_{k,m}$) of the cylinder.

Having freed ourselves from the integral over λ and $e^{i\left(\lambda z+m\phi \right)}$, we obtain the stress on the plane normal to the radius at the geometric location of the cavity:

$$\begin{gathered} {\sigma }_{k,m}^{\left(0\right)}\left(\rho ,\lambda \right)=\sum _{n=-\infty }^{\infty }\left[\sum _{i=1}^3\sum _{j=1}^3\left(r_{j,k}\left(R;m,\lambda \right)f_{i,j}^{\left(0\right)}\left(\lambda ,{\mu }_n,m\right)\sum _{t=1}^3{\displaystyle \frac{A_{t,i}}{D}}\left({\overrightarrow{c}}_h^0\left(\lambda ,n\right){\overrightarrow{e}}_t\right)\right)+\right. \\ \left.+\sum _{i=1}^3\sum _{j=1}^3\left(r_{j,1}\left(R;m,\lambda \right){\tilde{f}}_{i,j}^{\left(0\right)}\left(\lambda ,{\mu }_n,m\right)\sum _{t=1}^3{\displaystyle \frac{A_{t,i+3}}{D}}\left({\overrightarrow{c}}_{\tilde{h}}^0\left(\lambda ,n\right){\overrightarrow{e}}_t\right)\right)\right], \end{gathered}$$

(9)

where for k = 1, the stress ${\sigma }_{\rho }^{\left(p\right)}$ is considered; for k = 2, the stress ${\tau }_{\rho \phi }^{\left(p\right)}$ is considered; when k = 3, the stress ${\tau }_{\rho z}^{\left(p\right)}$ is considered; ${\overrightarrow{e}}_t$, t = 1, 2, 3 are the origins of the Cartesian coordinate system; R is the radius of the cylindrical cavity;

$$\begin{gathered} f_{i,j}^{\left(0\right)}\left(\lambda ,{\mu }_n,m\right)={\left(i{\omega }_{-}\left(\lambda ,\mu \right)\right)}^m\left(\begin{array}{ccc}1& 0& 0\\ {\displaystyle \frac{m\mu }{{\lambda }^2}}& {\displaystyle \frac{\gamma }{{\lambda }^2}}& {\displaystyle \frac{4\mu \left(1-\nu \right)}{{\lambda }^2}}\\ 0& 0& 1\end{array}\right), \\ {\tilde{f}}_{i,j}^{\left(0\right)}\left(\lambda ,{\mu }_n,m\right)={\left(i{\omega }_{+}\left(\lambda ,\mu \right)\right)}^m\left(\begin{array}{ccc}1& 0& 0\\ {\displaystyle \frac{m\mu }{{\lambda }^2}}& -{\displaystyle \frac{\gamma }{{\lambda }^2}}& {\displaystyle \frac{4\mu \left(1-\nu \right)}{{\lambda }^2}}\\ 0& 0& 1\end{array}\right); \end{gathered}$$

(10)

$r_{j,k}\left(R;m,\lambda \right)$ is the tensor obtained by applying the stress operator to ${\overrightarrow{R}}_{k,m}$ and after excluding $e^{i\left(\lambda z+m\phi \right)}$; ${\overrightarrow{c}}_h^0\left(\lambda ,n\right)$, ${\overrightarrow{c}}_{\tilde{h}}^0\left(\lambda ,n\right)$ are given in Formula (7), ${\omega }_{\mp }\left(\lambda ,\mu \right)={\displaystyle \frac{\mu \mp \gamma }{\lambda }}$, $\gamma =\sqrt{{\lambda }^2+{\mu }^2}.$

The second part of the solution (${\overrightarrow{U}}_1)$ takes into account the layer with a cylindrical cavity with the stresses ${\sigma }_{k,m}^{\left(0\right)}\left(\rho ,\lambda \right)$ set on the surface of the cavity with the reverse sign. The solution for ${\overrightarrow{U}}_1$ has the form [26]:

$$\begin{gathered} {\overrightarrow{U}}_1=\sum _{k=1}^3{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}{B}_{k,m}\left(\lambda \right){\overrightarrow{S}}_{k,m}\left(\rho ,\phi ,z;\lambda \right)d\lambda + \\ +\sum _{k=1}^3{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left(H_k\left(\lambda ,\mu \right){\overrightarrow{u}}_k^{\left(+\right)}\left(x,y,z;\lambda ,\mu \right)+{\tilde{H}}_k\left(\lambda ,\mu \right){\overrightarrow{u}}_k^{\left(-\right)}\left(x,y,z;\lambda ,\mu \right)\right)\hspace{0.33em}d\mu d\lambda ; \end{gathered}$$

(11)

where $H_k\left(\lambda ,\mu \right)$, ${\tilde{H}}_k\left(\lambda ,\mu \right)$, $B_{k,m}\left(\lambda \right)$ are unknowns to be found from the boundary conditions; ${\overrightarrow{u}}_k^{\left(+\right)}\left(x,y,z;\lambda ,\mu \right)$, ${\overrightarrow{u}}_k^{\left(-\right)}\left(x,y,z;\lambda ,\mu \right)$ and ${\overrightarrow{S}}_{k,m}\left(\rho ,\phi ,z;\lambda \right)$ are the basic solutions of (2).

To fulfill the boundary conditions at the upper and lower boundaries of the layer, the vectors ${\overrightarrow{S}}_{k,m}$ in (11), using the transition Formula (3), are rewritten in the Cartesian coordinate system through the basis solutions ${\overrightarrow{u}}_k^{\left(\pm \right)}$. For the resulting vector, we will find the stress and equate it (at y = h for the upper boundary, at y =$-\tilde{h}$ for the lower boundary) to zero if nothing is specified on these surfaces except for the constant. If additional local functions are specified on the layer surfaces, we will represent these functions through a double Fourier integral and equate them to the obtained expression. After getting rid of the series and integrals on the right and left sides, we get a system of equations:

$$\begin{gathered} \sum _{k=1}^3{H}_k\left(\lambda ,\mu \right){\overrightarrow{d}}_k^{+}\left(h;\lambda ,\mu \right)+{\tilde{H}}_k\left(\lambda ,\mu \right){\overrightarrow{d}}_k^{-}\left(h;\lambda ,\mu \right)+ \\ +\sum _{k=1}^3\sum _{m=-\infty }^{\infty }{B}_{k,m}\left(\lambda \right)\sum _{n=1}^3{g}_{s,n}^m\left(\lambda ,\mu \right){\overrightarrow{d}}_n^{-}\left(h;\lambda ,\mu \right)={\overrightarrow{c}}_h^1\left(\lambda ,\mu \right), \end{gathered}$$

(12)

$$\begin{gathered} \sum _{k=1}^3{H}_k\left(\lambda ,\mu \right){\overrightarrow{d}}_k^{+}\left(-\tilde{h};\lambda ,\mu \right)+{\tilde{H}}_k\left(\lambda ,\mu \right){\overrightarrow{d}}_k^{-}\left(-\tilde{h};\lambda ,\mu \right)+ \\ +\sum _{k=1}^3\sum _{m=-\infty }^{\infty }{B}_{k,m}\left(\lambda \right)\sum _{n=1}^3{\tilde{g}}_{k,n}^m\left(\lambda ,\mu \right){\overrightarrow{d}}_n^{+}\left(-\tilde{h};\lambda ,\mu \right)={\overrightarrow{c}}_{\tilde{h}}^1\left(\lambda ,\mu \right), \end{gathered}$$

where ${\overrightarrow{d}}_k^{\pm }={\displaystyle \frac{{\overrightarrow{u}}_k^{\left(\pm \right)}}{e^{i\left(\lambda z+m\phi \right)}}}$, ${\overrightarrow{c}}_h^1\left(\lambda ,\mu \right)$, ${\overrightarrow{c}}_{\tilde{h}}^1\left(\lambda ,\mu \right)$ are the densities from the specified additional local functions (if, in addition to the constant, local loads are specified on the layer surfaces);

• $g_{k,n}^m\left(\lambda ,\mu \right)$, ${\tilde{g}}_{k,n}^m\left(\lambda ,\mu \right)$ are the elements of the matrix:

$$\begin{gathered} g_{k,n}^m\left(\lambda ,\mu \right)={\displaystyle \frac{{\left(-i{\omega }_{-}\left(\lambda ,\mu \right)\right)}^m}{2\gamma }}\left(\begin{array}{ccc}1& 0& 0\\ {\displaystyle \frac{m\mu -{\lambda }^2/\gamma }{\gamma }}& {\displaystyle \frac{-{\lambda }^2}{\gamma }}& {\displaystyle \frac{4\mu \left(1-\sigma \right)}{\gamma }}\\ 0& 0& 1\end{array}\right); \\ {\tilde{g}}_{k,n}^m\left(\lambda ,\mu \right)={\displaystyle \frac{{\left(-i{\omega }_{+}\left(\lambda ,\mu \right)\right)}^m}{2\gamma }}\left(-\begin{array}{ccc}1& 0& 0\\ {\displaystyle \frac{m\mu +{\lambda }^2/\gamma }{\gamma }}& {\displaystyle \frac{{\lambda }^2}{\gamma }}& {\displaystyle \frac{-4\mu \left(1-\sigma \right)}{\gamma }}\\ 0& 0& 1\end{array}\right). \end{gathered}$$

From the obtained equations, we find the functions $H_k\left(\lambda ,\mu \right)$ and ${\tilde{H}}_k\left(\lambda ,\mu \right)$, expressed in terms of $B_{k,m}\left(\lambda \right)$:

$$\begin{gathered} H_j\left(\lambda ,\mu \right)=\sum _{k=1}^3{\displaystyle \frac{A_{k,j}}{D}}\left({\overrightarrow{c}}_h^1\left(\lambda ,\mu \right)-\sum _{s=1}^3\sum _{m=-\infty }^{\infty }{B}_{s,m}\left(\lambda \right)\sum _{n=1}^3{g}_{s,n}^m\left(\lambda ,\mu \right){\overrightarrow{d}}_n^{-}\left(h;\lambda ,\mu \right)\right){\overrightarrow{e}}_k+ \\ +\sum _{k=1}^3{\displaystyle \frac{A_{k+3,j}}{D}}\left({\overrightarrow{c}}_{\tilde{h}}^1\left(\lambda ,\mu \right)-\sum _{s=1}^3\sum _{m=-\infty }^{\infty }{B}_{s,m}\left(\lambda \right)\sum _{n=1}^3{\tilde{g}}_{s,n}^m\left(\lambda ,\mu \right){\overrightarrow{d}}_n^{+}\left(-\tilde{h};\lambda ,\mu \right)\right){\overrightarrow{e}}_k; \end{gathered}$$

(13)

$$\begin{gathered} {\tilde{H}}_j\left(\lambda ,\mu \right)=\sum _{k=1}^3{\displaystyle \frac{A_{k,j+3}}{D}}\left({\overrightarrow{c}}_h^1\left(\lambda ,\mu \right)-\sum _{s=1}^3\sum _{m=-\infty }^{\infty }{B}_{s,m}\left(\lambda \right)\sum _{n=1}^3{g}_{s,n}^m\left(\lambda ,\mu \right){\overrightarrow{d}}_n^{-}\left(h;\lambda ,\mu \right)\right){\overrightarrow{e}}_k+ \\ +\sum _{k=1}^3{\displaystyle \frac{A_{k+3,j+3}}{D}}\left({\overrightarrow{c}}_{\tilde{h}}^1\left(\lambda ,\mu \right)-\sum _{s=1}^3\sum _{m=-\infty }^{\infty }{B}_{s,m}\left(\lambda \right)\sum _{n=1}^3{\tilde{g}}_{s,n}^m\left(\lambda ,\mu \right){\overrightarrow{d}}_n^{+}\left(-\tilde{h};\lambda ,\mu \right)\right){\overrightarrow{e}}_k, \end{gathered}$$

(14)

where ${\overrightarrow{e}}_k$, k = 1, 2, 3 are the orths of the Cartesian coordinate system; j = 1, 2, 3; $A_{1..6,1..6}$ and D are the algebraic complements and determinant of the system of Equation (12).

The system of 6 Equation (12) has the determinant [27]

$${\displaystyle \frac{64e^{-3x}{\gamma }^8{\sigma }^6\left(\left(3/4+x^2\right)\left(1-e^{2x}\right)+1/4e^{6x}-1/4\right)}{{\lambda }^4}},$$

(15)

where $x=\gamma \left(h+\tilde{h}\right)$.

To fulfill the boundary conditions on the cylinder ρ = R, the right-hand side of (11) is rewritten in the cylindrical coordinate system using the transition Formula (4) through the basis solutions ${\overrightarrow{R}}_{k,m}$, ${\overrightarrow{S}}_{k,m}$. For the resulting vector ${\overrightarrow{U}}_1$, we find the stress and equate ${\overrightarrow{h}}_m\left(\lambda \right)$—the difference between the given ${\overrightarrow{F}}_R^0\left(\phi ,z\right)$ (previously represented by the integral and Fourier series) and ${\sigma }_{k,m}^{\left(0\right)}\left(\rho ,\lambda \right)$ given in (9). After freeing the right and left sides from $e^{i\left(\lambda z+m\phi \right)}$ and the integrals over λ, we obtain a set of three systems of linear algebraic equations to determine the unknowns $B_{k,m}\left(\lambda \right)$:

$$\begin{gathered} \sum _{k=1}^3\left(B_{k,m}\left(\lambda \right)s_{k,j}\left(R;m,\lambda \right)\right)={\overrightarrow{h}}_m\left(\lambda \right){\overrightarrow{e}}_j-\sum _{k=1}^3{\int }_{-\infty }^{\infty }\left(H_k\left(\lambda ,\mu \right)\sum _{n=1}^3{r}_{n,j}\left(R;m,\lambda \right)\right.f_{k,n}^m\left(\lambda ,\mu \right)+ \\ +\left.{\tilde{H}}_k\left(\lambda ,\mu \right)\sum _{n=1}^3{r}_{n,j}\left(R;m,\lambda \right){\tilde{f}}_{k,n}^m\left(\lambda ,\mu \right)\right)d\mu , \end{gathered}$$

(16)

where $s_{k,j}\left(R;m,\lambda \right)$ is the tensor obtained by applying the stress operator to ${\overrightarrow{S}}_{k,m}\left(\rho ,\phi ,z;\lambda \right)$ and eliminating $e^{i\left(\lambda z+m\phi \right)}$; $r_{n,j}\left(R;m,\lambda \right)$ is the tensor obtained by applying the stress operator to ${\overrightarrow{R}}_{k,m}\left(\rho ,\phi ,z;\lambda \right)$ and eliminating $e^{i\left(\lambda z+m\phi \right)};$ $f_{k,n}^m\left(\lambda ,\mu \right),$ ${\tilde{f}}_{k,n}^m\left(\lambda ,\mu \right)$ presented in (10).

The determinant of the system (16) is [27]:

$$\begin{gathered} \mathrm{for} \mathrm{m} = 0 \left|{\mathsf{\Delta }}_0\right|=8\left(1-\sigma \right)x^2{K}_1^2\left(x\right)K_2\left(x\right), \\ \mathrm{for} \mathrm{m} \ge 1 \left|{\mathsf{\Delta }}_m\right|>4m{K}_{m-1}\left(x\right)K_m\left(x\right)K_{m+1}\left(x\right), x=\left|\lambda \right|\rho , \lambda \ne 0. \end{gathered}$$

(17)

We exclude the functions (13) and (14) previously found through $B_{k,m}\left(\lambda \right)$ from the system of Equation (16). As a result, we obtain a set of three infinite systems of linear algebraic equations of the second kind to determine the unknowns $B_{k,m}\left(\lambda \right)$.

For the resulting systems, using (15) and (17), we prove their unambiguous solvability. Moreover, these systems can be solved by the method of reduction, and the approximate solutions converge to the exact one.

The functions $B_{k,m}\left(\lambda \right)$ found from the infinite system of equations will be substituted into expressions (13), (14) to find $H_k\left(\lambda ,\mu \right)$ and ${\tilde{H}}_k\left(\lambda ,\mu \right)$. This will determine all the unknowns.

3. Numerical Analysis of the Stress State of the Layer

3.1. Input Data for Numerical Calculation

Numerical studies were carried out for a layer of concrete C25/30 (Figure 1), elastic modulus E = 3.25$\cdot$10⁴ MPa, Poisson’s ratio ν = 0.16.

The layer contains a cylindrical cavity of radius R = 5 cm, which is parallel to its boundaries along the z-axis. The distance from the center of the cylindrical cavity to the upper and lower boundaries of the layer h = $\tilde{h}$ = 9 cm.

The layer rests on two continuous supports along the x-axis, which are located along the z-axis at a distance L = a + b = 30 + 30 = 60 cm and are equidistant from the origin.

On the upper boundary of the layer, in the middle between the supports, there are normal stresses constant along the x-axis and in the form of a wave along the z-axis:

$${\sigma }_y^{\left(h\right)}\left(x,z\right)=-10^8{\left(z^2+10^2\right)}^{-2}.$$

(18)

Tangential stresses on this surface are zero: ${\tau }_{yx}^{\left(h\right)}\left(x,z\right)={\tau }_{yz}^{\left(h\right)}\left(x,z\right)=0$. On the lower boundary of the layer, based on the equilibrium conditions, the stresses are specified in the form of support reactions:

$${\sigma }_y^{\left(\tilde{h}\right)}\left(x,z\right)=-10^8{\left({(z-a)}^2+10^2\right)}^{-2}b/L-10^8{\left({(z+b)}^2+10^2\right)}^{-2}a/L.$$

(19)

The tangential stresses are zero: ${\tau }_{yx}^{\left(\tilde{h}\right)}\left(x,z\right)={\tau }_{yz}^{\left(\tilde{h}\right)}\left(x,z\right)=0.$ On the surface of the cavity, zero stresses are set: ${\sigma }_{\rho }={\tau }_{\rho \phi }={\tau }_{\rho z}=0$.

The infinite system of equations was truncated at m = 8 terms. With the given geometric parameters, this allowed us to obtain the fulfillment of the boundary conditions with an accuracy of 10⁻⁴ for all values from zero to one. Integration over λ and μ was performed using the Filon quadrature formulas. The number of integration points along the z-axis was taken to be 200, and the integration boundaries were chosen from −1 to 1, which ensures a highly accurate consideration of the specified function at the lower boundary of the layer.

3.2. Numerical Results Using the Finite Element Method

For comparison and validation of results, the problem was solved using the finite element method [39]. The problem solution was performed using the ANSYS 2023R1 software package. The infinite layer was truncated to a size of $\left(h+\tilde{h}\right)·10$ (Figure 2a).

In addition to the specified stresses (18) and (19), denoted as Pressure A, Pressure B, and Pressure C (Figure 2a), additional boundary conditions were applied according to the conditions of the method: on the lower edge of the end surface z = –100 (Figure 2a, Displacement D) $U_x=U_y=0$ and on the edge of the opposite end surface z = +100 (Figure 2a, Displacement E) $U_y=U_z=0$.

The following finite elements were used in solving the numerical FEM problem (Figure 2b): eight-node solid elements (SOLID186) (for 3D modeling in ANSYS). The meshing was performed for the layer automatically with a mesh size of 2 cm × 2 cm × 2 cm and for the surface of the cavity with a mesh size of 1 cm × 2 cm (Figure 2b).

The stresses ${\sigma }_x$ and ${\sigma }_z$ at the upper and lower boundaries of the layer, obtained by the finite element method, are shown in Figure 3.

The maximum stress ${\sigma }_x$ at the upper and lower boundaries is −2.14 MPa (compression) and 1.31 MPa (tension), respectively.

The stresses ${\sigma }_z$ at the upper boundary correspond to compression, with a maximum value of −4.23 MPa, while tensile stresses occur at the lower boundary of the layer, with a maximum value of 3.607 MPa.

3.3. Numerical Results of the Proposed Analytical Method

The effect of the cylindrical cavity on the stress state of the layer can be seen from the stress plot along the x-axis (Figure 4) at the upper and lower boundaries of the layer.

The cavity has the greatest influence on the stress ${\sigma }_x$ (Figure 4). Thus, within the radius of the cylindrical cavity at the upper boundary of the layer, the negative stresses ${\sigma }_x$ increase significantly to the maximum, while at the lower boundary of the layer, on the contrary, the stresses ${\sigma }_x$ decrease. At a distance from the cavity, its influence on the stress state decreases, and at distances greater than R·4, the stresses ${\sigma }_x$ almost do not change. The difference between the analytical calculation and the finite element method was 2.5%.

The cavity has a less concentrated effect on the stress ${\sigma }_z$ (Figure 4). This effect is redistributed along the axis $Ox$. Even at a distance equal to four radii, the cavity still has an effect on the stress ${\sigma }_z$. The difference between the analytical calculation and the finite element method was 4%.

At a given load, non-zero stresses ${\sigma }_z$ and ${\sigma }_{\phi }$ occur on the surface of the cylindrical cavity (Figure 5).

At the top of the cylindrical cavity, ${\sigma }_{\phi }$ and ${\sigma }_z$ have negative values, i.e., compression occurs (Figure 5). The maximum negative value of ${\sigma }_z$ occurs at $\phi ={\displaystyle \frac{\pi }{2}}$ and is equal to −1.55 MPa. The maximum negative value of ${\sigma }_{\phi }$ occurs at $\phi ={\displaystyle \frac{3\pi }{25}}$ and $\phi ={\displaystyle \frac{22\pi }{25}}$ and is equal to $-1.51$ MPa, exceeding the specified stresses. In the lower part of the cylindrical cavity, the stresses ${\sigma }_z$ have positive values, so tensile stresses occur, and on the horizontal x-axis, the stresses ${\sigma }_z$ are zero. The maximum positive value of the stress ${\sigma }_z$ takes at $\phi ={\displaystyle \frac{3\pi }{2}}$ and is equal to 1.99 MPa. The maximum positive value of the stress ${\sigma }_{\phi }$ takes at $\phi ={\displaystyle \frac{3\pi }{2}}$ and is equal to 0.71 MPa. Furthermore, the values of ${\sigma }_z$ are greater than those of ${\sigma }_{\phi }$ and exceed the calculated tensile strength of C25/30 ${(f}_{ctd})$, which is 1.8 MPa [40].

The stress state on the surface of the cylindrical cavity, the results of which were obtained using the finite element method, also have values close to the analytical calculation (the error varies from 6% to 25%). As the width and length of the plate increase, the stress values approach the analytical ones (the error decreases), with the width of the plate (along the x-axis) having a particularly strong influence. However, a further increase in these dimensions entails an increase in the size of the finite elements, which in turn affects the accuracy of the results. Thus, modeling a layer with a longitudinal cylindrical cavity and infinite loading faces the limitations of the finite element method and software, which do not allow solving problems for infinite models.

The stress state along the z-axis at the upper boundary of the layer is shown in Figure 6.

The stress state graph (Figure 6) shows the stress versus distance for three different components: ${\sigma }_x,$ ${\sigma }_y$ and ${\sigma }_{z }$. The stresses ${\sigma }_{y }$ are given and illustrate the relationship to the other stresses. The stresses ${\sigma }_x$ and ${\sigma }_{z }$, obtained as a result of the calculation, significantly exceed the specified ${\sigma }_y$, are compressive (negative values) and decrease in absolute value with distance from the center of the cavity.

The largest modulus is the stress ${\sigma }_z=-4.169$ MPa in the center of the cavity at $z=0$ (Figure 6).

At the location of the supports (z = 30), the nature of the gradual decrease in the stress state does not change.

At the lower boundary of the layer, the stress state is shown in Figure 7.

Figure 7 shows the specified stresses ${\sigma }_y$ at the lower boundary of the layer.

At the lower boundary of the layer (Figure 7), similar to the upper boundary, the tensile (positive) stress ${\sigma }_z$ in the center of the cavity at $z=0$ is of the highest value, reaching a maximum value of 3.79 MPa. This maximum value exceeds the calculated tensile strength of C25/30 class concrete [40].

In turn, the stresses ${\sigma }_x$ are much smaller in absolute value and have almost zero values in the support region.

Increasing the height of the layer reduces the stresses ${\sigma }_z$ and already at $h=\widetilde{ h}=11$ cm the maximum stresses ${\sigma }_z$ do not exceed the calculated concrete resistance.

4. Discussion

Stress analysis showed that compressive stresses dominate at the upper boundary of the layer in the cavity zone, while dangerous tensile stresses dominate at the lower boundary. The maximum tensile stresses occur on the surface of the cavity and at the lower edge of the layer directly below it, reaching values close to or even exceeding the calculated tensile strength of concrete. This determines the most vulnerable areas of the structure where cracks and destruction are likely to occur.

Numerical analysis of the stress-strain state, the results of which are presented in Figure 4, Figure 5, Figure 6 and Figure 7, clearly demonstrates that the cylindrical cavity acts as a significant stress concentrator, which radically changes their distribution in the layer and creates critical zones for the strength of the structure.

The key result of the analysis is a quantitative assessment of the maximum tensile stresses that are most dangerous for concrete. It has been established that peak values occur in two areas:

On the surface of the cavity itself (Figure 4), where the axial tensile stress σ_z reaches 1.99 MPa.

At the lower edge of the layer directly below the cavity (Figure 7), where the stress σ_z reaches an even higher value of 3.79 MPa.

A comparison of these values with the calculated tensile strength $\left(f_{ctd}\right)$, of C25/30 concrete, which is 1.8 MPa, is revealing. The calculated stress on the surface of the cavity (1.99 MPa) already exceeds the destruction threshold, indicating a high probability of microcrack formation and development in this area.

The situation is even more critical at the lower edge of the layer, where the stress (3.79 MPa) is more than twice the strength of the material. This indicates the inevitable formation of main cracks in this area under the given load conditions, which can lead to progressive destruction and loss of the load-bearing capacity of the structural element.

Thus, the results emphasize that ignoring stress concentration effects can lead to gross underestimation of risks and design errors. The proposed analytical method allows not only to identify these critical areas with high accuracy, but also to quantitatively assess the degree of danger. This is key to making informed design decisions, such as adjusting the geometry (e.g., increasing the layer thickness, as shown in the study) or introducing additional reinforcement in areas of tensile stress concentration to ensure structural reliability.

The following conclusions can also be drawn from the numerical analysis of the stress-strain state:

1

The impact of the cavity is localized but extends over a considerable distance. At a distance exceeding four radii of the cavity, the stresses σₓ are almost indistinguishable from those in a solid slab, which confirms the correctness of the model.

2

The method has proven to be effective in modeling complex boundary conditions. Calculations have shown that increasing the layer thickness (for example, to $h=11$ cm) is an effective way to reduce the maximum stresses to a safe level that does not exceed the calculated material resistance.

5. Conclusions

The paper proposes an analytical method for solving a spatial elasticity problem for a layer with a cylindrical cavity supported by linear continuous supports and subjected to infinitely distributed loads. The method is based on the generalized Fourier method and the principle of superposition, which made it possible to reduce the initial problem to two simpler ones and obtain a highly accurate solution.

Analysis of the obtained stresses allows for more effective and informed decisions regarding geometry and material selection in the early stages of design.

The proposed method is a flexible tool for engineering analysis that can be used to calculate the stress state of a layer with cylindrical inhomogeneities. The proposed solution method can be used to determine the stress state of floor slabs in construction or protective elements of aircraft in the aerospace industry.

Further investigation of this problem is interesting when the number of cavities is increased or other types of stress concentrators (solid inclusion or pipe) are used.