A Fourth-Order Parametric Iterative Approach for Solving Systems of Nonlinear Equations

Abstract

In this paper, we present a novel one-parameter family with fourth-order convergence to solve nonlinear systems, along with its convergence analysis. Several numerical experiments including a Bratu problem, a mixed Hammerstein integral equation, and nonlinear optimization problems (namely, the Broyden banded function and the Broyden tridiagonal function) as well as applications of differential equations, are analyzed using the proposed schemes to demonstrate their effectiveness. The results indicate that these methods produce more accurate approximations and exhibit greater efficiency compared to existing approaches.

1. Introduction

Nonlinear systems of equations, $F\left(\mathfrak{x}\right)=0$, where $F:\Omega \subseteq {\mathbb{R}}^n\to {\mathbb{R}}^n$, frequently arise in many fields of engineering and science [1,2]. Consequently, finding solutions to these nonlinear systems is a challenging task. Solving these systems analytically is either extremely difficult or rarely feasible. To address this, numerous researchers have proposed iterative techniques for approximating solutions to nonlinear.

One of the oldest and simplest iterative methods is Newton’s method [3,4], which is defined as follows:

$${\mathfrak{x}}^{(k+1)}={\mathfrak{x}}^{\left(k\right)}-{\left(F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right)}^{-1}F\left({\mathfrak{x}}^{\left(k\right)}\right),k=0,1,2,\dots$$

(1)

where $F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)$ represents the Jacobian matrix of F evaluated at ${\mathfrak{x}}^{\left(k\right)}$. Newton’s method exhibits quadratic convergence, provided that the root sought is simple and the initial estimate is sufficiently close to the solution.

Numerous higher-order techniques have been developed in the literature [5,6,7], many of which considered Newton’s method as a first step. However, in various practical scenarios, the first-order Fréchet derivative $F^{\prime }\left(\mathfrak{x}\right)$ either does not exist or is computationally expensive to evaluate. To address such situations, Traub [4] proposed a Jacobian-free approach, defined as follows:

$${\mathfrak{x}}^{(k+1)}={\mathfrak{x}}^{\left(k\right)}-{\left[{\mathfrak{w}}^{\left(k\right)},{\mathfrak{x}}^{\left(k\right)};F\right]}^{-1}F\left({\mathfrak{x}}^{\left(k\right)}\right),k=0,1,2,\dots$$

(2)

where $\left[{\mathfrak{w}}^{\left(k\right)},{\mathfrak{x}}^{\left(k\right)};F\right]$ represents the first-order divided difference operator of F, and ${\mathfrak{w}}^{\left(k\right)}={\mathfrak{x}}^{\left(k\right)}+\beta F\left({\mathfrak{x}}^{\left(k\right)}\right)$, with $\beta \ne 0$ being an arbitrary constant. For $\beta =1$, this method simplifies to the multidimensional Steffensen’s method, as formulated by Samanskii in [8]. These methods also have a quadratic order of convergence. We recall that the mapping $[·,·;F]:{\mathbb{R}}^n\times {\mathbb{R}}^n⟶\mathcal{L}\left({\mathbb{R}}^n\right)$ satisfies $[\mathfrak{x},\mathfrak{y};F](\mathfrak{y}-\mathfrak{x})=F\left(\mathfrak{y}\right)-F\left(\mathfrak{x}\right),$ and the components of the matrix associated with $[{\mathfrak{x}}^{\left(k\right)},{\mathfrak{y}}^{\left(k\right)};F]$ can be obtained using the formula of the divided difference operator; we utilize the following first-order divided difference operator [3]:

$${[{\mathfrak{x}}^{\left(k\right)},{\mathfrak{y}}^{\left(k\right)};F]}_{i,j}^1={\displaystyle \frac{F_i({\mathfrak{y}}_1,{\mathfrak{y}}_2,\dots ,{\mathfrak{y}}_{j-1},{\mathfrak{y}}_j,{\mathfrak{x}}_{j+1},\dots ,{\mathfrak{x}}_n)-F_i({\mathfrak{y}}_1,{\mathfrak{y}}_2,\dots ,{\mathfrak{y}}_{j-1},{\mathfrak{x}}_j,{\mathfrak{x}}_{j+1},\dots ,{\mathfrak{x}}_n)}{{\mathfrak{y}}_j-{\mathfrak{x}}_j}}.$$

(3)

Toenhance the order of convergence, several researchers have developed third-order methods [9,10,11,12], each requiring one function evaluation of F, two evaluations of its derivative $F^{\prime }$, and two matrix inversions per iteration. Cordero and Torregrosa [13] introduced two additional third-order methods: one method requiring one function evaluation F and three evaluations of $F^{\prime }$, while the other method demands one function evaluation of F and four evaluations of its Fréchet derivative $F^{\prime }$, along with two matrix inversions. Another third-order method, proposed by Darvishi and Barati [14], employs two function evaluations of F, two evaluations of $F^{\prime }$, and two matrix inversions per iteration. Further advancements in third-order methods were made by Darvishi and Barati [15], as well as Potra and Ptak [16], both introducing methods that require two function evaluations, one evaluation of the function’s derivative, and one matrix inversion per iteration.

Moreover, several higher-order iterative schemes have been developed. Babajee et al. [17] presented a fourth-order approach involving one function evaluation of F, two evaluations of $F^{\prime }$, and two matrix inversions per iteration. Another fourth-order method, proposed by Cordero et al. [18], is based on two function and two Jacobian evaluations along with one matrix inversion. Additionally, the authors in [6] introduced another fourth-order method that utilizes three function evaluations of F, one evaluation of $F^{\prime }$, and one matrix inversion per iteration.

It is evident that increasing the order of convergence in iterative methods often leads to a higher computational cost per iteration, posing a significant challenge for higher-order methods. Consequently, when developing new iterative methods, maintaining a low computational cost is essential. Motivated by this, we propose new iterative schemes that achieve fourth-order convergence while minimizing the number of function evaluations per iteration. The proposed method requires one function evaluation of F, one divided difference, and one matrix inversion of $F^{\prime }$ per iteration.

This manuscript is organized as follows. In Section 2, a new parametric fourth-order method is presented along with its convergence analysis. Section 3 discussed the efficiency index of the proposed method. In Section 4, various numerical experiments are conducted to validate the theoretical results and compare the results of the proposed algorithms with some existing methods. Finally, the paper concludes with a summary of findings.

2. Proposed Method

The proposed two-step iterative method is represented as

$$\begin{array}{cc}\hfill {\mathfrak{y}}^{\left(k\right)}& ={\mathfrak{x}}^{\left(k\right)}-{\left(F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right)}^{-1}F\left({\mathfrak{x}}^{\left(k\right)}\right),\hfill \\ \hfill {\mathfrak{x}}^{(k+1)}& ={\mathfrak{x}}^{\left(k\right)}-(\alpha {\left[{\mathfrak{x}}^{\left(k\right)},{\mathfrak{y}}^{\left(k\right)},F\right]}^{-1}+(I-\alpha )\hfill \\ \hfill & \left({\left(I-k_2\eta \right)}^{-1}\left(I-k_1\eta \right){\left(F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right)}^{-1}\right))F\left({\mathfrak{x}}^{\left(k\right)}\right),\hfill \end{array}$$

(4)

where $\eta =I-{\left(F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right)}^{-1}\left[{\mathfrak{x}}^{\left(k\right)},{\mathfrak{y}}^{\left(k\right)},F\right]$. In addition, $\left[{\mathfrak{x}}^{\left(k\right)},{\mathfrak{y}}^{\left(k\right)};F\right]={\displaystyle \frac{F\left({\mathfrak{y}}^{\left(k\right)}\right)-F\left({\mathfrak{x}}^{\left(k\right)}\right)}{{\mathfrak{y}}^{\left(k\right)}-{\mathfrak{x}}^{\left(k\right)}}}$ is a first-order finite difference. The parameters $k_1,k_2$ and $\alpha \in \mathbb{R}\setminus \left\{1\right\}$ are freely disposable. The convergence analysis is stated in the following theorem.

Theorem 1. 

Let $F:\Omega \subseteq {\mathbb{R}}^n\to {\mathbb{R}}^n$ be a function that is sufficiently differentiable in an open convex neighborhood Ω containing a zero of F and assume that $F^{\prime }\left(\mathfrak{x}\right)$ is nonsingular at $\mathfrak{x}=\xi$, and the initial guess ${\mathfrak{x}}^{\left(0\right)}$ is sufficiently close to ξ. Then, the iterative schemes defined by (4) exhibit fourth-order convergence for

$$k_1=-{\displaystyle \frac{1}{\alpha -1}},k_2={\displaystyle \frac{\alpha }{\alpha -1}},\alpha \in \mathbb{R}\setminus \left\{1\right\},$$

and the error equation is given by

$${\mathfrak{e}}^{(k+1)}=\left({\displaystyle \frac{2\alpha -1}{\alpha -1}}{B}_2^3-B_2{B}_3\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^4+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^5\right),$$

where $B_j=\left({\displaystyle \frac{1}{j!}}\right){\left[F^{\prime }\left(\xi \right)\right]}^{-1}\left[F^{\left(j\right)}\left(\xi \right)\right],j\ge 2with{\mathfrak{x}}^{\left(k\right)}-\xi ={\mathfrak{e}}^{\left(k\right)}.$

Proof. 

For the error equation of first step of Equation (4) ${\mathfrak{y}}^{\left(k\right)}={\mathfrak{x}}^{\left(k\right)}-{\left(F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right)}^{-1}F\left({\mathfrak{x}}^{\left(k\right)}\right)$, we perform the Taylor series of $F\left({\mathfrak{x}}^{\left(k\right)}\right)$ and $F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)$ around $\xi$ as follows:

$$\begin{array}{cc}\hfill F\left({\mathfrak{x}}^{\left(k\right)}\right)=& F^{\prime }\left(\xi \right)[{\mathfrak{e}}^{\left(k\right)}+B_2{\left({\mathfrak{e}}^{\left(k\right)}\right)}^2+B_3{\left({\mathfrak{e}}^{\left(k\right)}\right)}^3+B_4{\left({\mathfrak{e}}^{\left(k\right)}\right)}^4+B_5{\left({\mathfrak{e}}^{\left(k\right)}\right)}^5\hfill \\ \hfill & +B_6{\left({\mathfrak{e}}^{\left(k\right)}\right)}^6]+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^7\right),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)=& F^{\prime }\left(\xi \right)[I+2B_2{\mathfrak{e}}^{\left(k\right)}+3B_3{\left({\mathfrak{e}}^{\left(k\right)}\right)}^2+4B_4{\left({\mathfrak{e}}^{\left(k\right)}\right)}^3+5B_5{\left({\mathfrak{e}}^{\left(k\right)}\right)}^4\hfill \\ \hfill & +6B_6{\left({\mathfrak{e}}^{\left(k\right)}\right)}^5]+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^6\right).\hfill \end{array}$$

(6)

Assuming that the Jacobian matrix $F^{\prime }\left(\xi \right)$ is nonsingular, we derive the Taylor series expansion of ${\left(F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right)}^{-1}$ as follows:

$$\begin{array}{cc}\hfill {\left(F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right)}^{-1}=& {\left(F^{\prime }\left(\xi \right)\right)}^{-1}[I+C_2{\mathfrak{e}}^{\left(k\right)}+C_3{\left({\mathfrak{e}}^{\left(k\right)}\right)}^2+C_4{\left({\mathfrak{e}}^{\left(k\right)}\right)}^3+C_5{\left({\mathfrak{e}}^{\left(k\right)}\right)}^4\hfill \\ \hfill & +C_6{\left({\mathfrak{e}}^{\left(k\right)}\right)}^5]+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^6\right),\hfill \end{array}$$

(7)

where ${\mathfrak{C}}_2=-2B_2,{\mathfrak{C}}_3=4B_2^2-3B_3,$ ${\mathfrak{C}}_4=6B_3{B}_2+6B_2{B}_3-4B_4-8B_2^3+8B_4{B}_2+8B_2{B}_4-5B_5,$ ${\mathfrak{C}}_5=16B_2^4+9B_3^2-12B_3{B}_2^2-12B_2{B}_3{B}_2$ $-12B_2^2{B}_3,$ ${\mathfrak{C}}_6=-32B_2^5-18B_3^2{B}_2+24B_3{B}_2^3+24B_2{B}_3{B}_2^2$ $+24B_2^2{B}_3{B}_2-16B_4{B}_2^2-16B_2{B}_4{B}_2+10B_5{B}_2-18B_3{B}_2{B}_3$ has been determined from the following:

$$\begin{array}{c}\hfill {\left(F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right)}^{-1}{F}^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)=I_{n\times n}.\end{array}$$

Therefore,

$$\begin{array}{cc}\hfill {\left(F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right)}^{-1}& ={\left(F^{\prime }\left(\xi \right)\right)}^{-1}[I-2B_2{\mathfrak{e}}^{\left(k\right)}+\left(4B_2^2-3B_3\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^2+(6B_3{B}_2+6B_2{B}_3\hfill \\ \hfill & -4B_4-8B_2^3){\left({\mathfrak{e}}^{\left(k\right)}\right)}^3+(16B_2^4+9B_3^2-12B_3{B}_2^2-12B_2{B}_3{B}_2-12B_2^2{B}_3\hfill \\ \hfill & +8B_4{B}_2+8B_2{B}_4-5B_5){\left({\mathfrak{e}}^{\left(k\right)}\right)}^4+(-32B_2^5-18B_3^2{B}_2+24B_3{B}_2^3\hfill \\ \hfill & +24B_2{B}_3{B}_2^2+24B_2^2{B}_3{B}_2-16B_4{B}_2^2-16B_2{B}_4{B}_2+10B_5{B}_2-18B_3{B}_2{B}_3\hfill \\ \hfill & -18B_2{B}_3^2+12B_4{B}_3+24B_2^3{B}_3-16B_2^2{B}_4+12B_3{B}_4+10B_2{B}_5\hfill \\ \hfill & -6B_6\left){\left({\mathfrak{e}}^{\left(k\right)}\right)}^5\right]+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^6\right).\hfill \end{array}$$

(8)

By using (5) and (8), one can obtain

$$\begin{array}{cc}\hfill {\left(F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right)}^{-1}F\left({\mathfrak{x}}^{\left(k\right)}\right)& ={\mathfrak{e}}^{\left(k\right)}-B_2{\left({\mathfrak{e}}^{\left(k\right)}\right)}^2+2\left(B_2^2-B_3\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^3+(3B_3{B}_2+4B_2{B}_3-3B_4\hfill \\ \hfill & -4B_2^3){\left({\mathfrak{e}}^{\left(k\right)}\right)}^4+(-6B_3{B}_2^2-8B_2^2{B}_3+6B_3^2-6B_2{B}_3{B}_2+6B_2{B}_4\hfill \\ \hfill & +4B_4{B}_2+8B_2^4-4B_5){\left({\mathfrak{e}}^{\left(k\right)}\right)}^5+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^6\right).\hfill \end{array}$$

(9)

Considering the error term ${\mathfrak{e}}^{\left(k\right)}={\mathfrak{x}}^{\left(k\right)}-\xi$, the expansion of the error at the first step of the family (4) is given by the following:

$$\begin{array}{cc}\hfill {\mathfrak{y}}^{\left(k\right)}-\xi & =B_2{\left({\mathfrak{e}}^{\left(k\right)}\right)}^2-2\left(B_2^2-B_3\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^3-\left(3B_3{B}_2+4B_2{B}_3-3B_4-4B_2^3\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^4\hfill \\ \hfill & -\left(-6B_3{B}_2^2-8B_2^2{B}_3+6B_3^2-6B_2{B}_3{B}_2+6B_2{B}_4+4B_4{B}_2+8B_2^4-4B_5\right)\hfill \\ \hfill & {\left({\mathfrak{e}}^{\left(k\right)}\right)}^5+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^6\right).\hfill \end{array}$$

(10)

The Taylor’s expansion of $F\left({\mathfrak{y}}^{\left(k\right)}\right)$ around $\xi$ can be evaluated similarly to Equation (5),

$$\begin{array}{cc}\hfill F\left({\mathfrak{y}}^{\left(k\right)}\right)& =F^{\prime }\left(\xi \right)[B_2{\left({\mathfrak{e}}^{\left(k\right)}\right)}^2+2(B_3-B_2^2){\left({\mathfrak{e}}^{\left(k\right)}\right)}^3+(3B_4+5B_2^3-3B_3{B}_2-4B_2{B}_3){\left({\mathfrak{e}}^{\left(k\right)}\right)}^4\hfill \\ \hfill & +(-12B_2^4-6B_3^2+4B_5-6B_2{B}_4+10B_2^2{B}_3+6B_3{B}_2^2-4B_4{B}_2+8B_2{B}_3{B}_2)\hfill \\ \hfill & {\left({\mathfrak{e}}^{\left(k\right)}\right)}^5]+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^6\right).\hfill \end{array}$$

(11)

Using (3) on (5), (10), and (11), one can get

$$\begin{array}{cc}\hfill \left[{\mathfrak{x}}^{\left(k\right)},{\mathfrak{y}}^{\left(k\right)},F\right]=& I+B_2{\mathfrak{e}}^{\left(k\right)}+\left(B_2^2+B_3\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^2+\left(-2B_2^3+3B_2{B}_3+B_4\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^3\hfill \\ \hfill & +\left(4B_2^4-8B_2^2{B}_3+2B_3^2+4B_2{B}_4+B_5\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^4+(-8B_2^5+20B_2^3{B}_3\hfill \\ \hfill & -11B_2^2{B}_4+5B_3{B}_4+B_2\left(-9B_3^2+5B_5\right)+B_6){\left({\mathfrak{e}}^{\left(k\right)}\right)}^5+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^6\right).\hfill \end{array}$$

(12)

Now, using Equations (8) and (12), we get

$$\begin{array}{cc}\hfill \eta & =I-{\left(F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right)}^{-1}\left[{\mathfrak{x}}^{\left(k\right)},{\mathfrak{y}}^{\left(k\right)},F\right],\hfill \\ \hfill \eta & =B_2{\mathfrak{e}}^{\left(k\right)}+\left(-3B_2^2+2B_3\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^2+\left(8B_2^3-10B_2{B}_3+3B_4\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^3+(-20B_2^4\hfill \\ \hfill & +37B_2^2{B}_3-8B_3^2-14B_2{B}_4+4B_5){\left({\mathfrak{e}}^{\left(k\right)}\right)}^4+(48B_2^5-118B_2^3{B}_3+51B_2^2{B}_4-22B_3{B}_4\hfill \\ \hfill & +B_2\left(55B_3^2-18B_5\right)+5B_6){\left({\mathfrak{e}}^{\left(k\right)}\right)}^5+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^6\right).\hfill \end{array}$$

(13)

Using (13), we get

$$\begin{array}{cc}\hfill I-k_1\eta & =I-k_1{B}_2{\mathfrak{e}}^{\left(k\right)}+k_1\left(3B_2^2-2B_3\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^2-k_1\left(8B_2^3-10B_2{B}_3+3B_4\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^3\hfill \\ \hfill & -k_1(-20B_2^4+37B_2^2{B}_3-8B_3^2-14B_2{B}_4+4B_5){\left({\mathfrak{e}}^{\left(k\right)}\right)}^4-k_1(48B_2^5-118B_2^3{B}_3\hfill \\ \hfill & +51B_2^2{B}_4-22B_3{B}_4+B_2\left(55B_3^2-18B_5\right)+5B_6){\left({\mathfrak{e}}^{\left(k\right)}\right)}^5+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^6\right).\hfill \end{array}$$

(14)

In view of (8), one can obtain the following:

$$\begin{array}{cc}\hfill {\left(I-\eta \right)}^{-1}& =I+B_2{\mathfrak{e}}^{\left(k\right)}+\left(-2B_2^2+2B_3\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^2+3\left(B_2^3-2B_2{B}_3+B_4\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^3\hfill \\ \hfill & +\left(-3B_2^4+11B_2^2{B}_3-4B_3^2-8B_2{B}_4+4B_5\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^4+(-10B_2^3{B}_3+14B_2^2{B}_4\hfill \\ \hfill & +B_2\left(11B_3^2-10B_5\right)+5\left(-2B_3{B}_4+B_6\right)){\left({\mathfrak{e}}^{\left(k\right)}\right)}^5+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^6\right).\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\left(I-k_2\eta \right)}^{-1}=& I-k_2{B}_2{\mathfrak{e}}^{\left(k\right)}+k_2\left((-3+k_2)B_2^2+2B_3\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^2-k_2((8-6k_2+k_2^2)B_2^3\hfill \\ \hfill & +2(-5+2k_2)B_2{B}_3+3B_4){\left({\mathfrak{e}}^{\left(k\right)}\right)}^3+k_2((-20+25k_2-9k_2^2+k_2^3)B_2^4+\hfill \\ \hfill & (37-32k_2+6k_2^2)B_2^2{B}_3+4(-2+k_2)B_3^2+2(-7+3k_2)B_2{B}_4+B_5){\left({\mathfrak{e}}^{\left(k\right)}\right)}^4\hfill \\ \hfill & +\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^5\right).\hfill \end{array}$$

(16)

Substituting Equations (5)–(16) into the second substep of scheme (4), we obtain the error equation as follows:

$$\begin{array}{cc}\hfill {\mathfrak{e}}^{(k+1)}& =-(\alpha -1)(k_1-k_2+1)B_2{\left({\mathfrak{e}}^{\left(k\right)}\right)}^2+\left(\right(-2+k_1(-4+k_2)+4k_2-k_2^2+\alpha (3-k_1(-4\hfill \\ \hfill & +k_2)-4k_2+k_2^2\left)\right)B_2^2-2(\alpha -1)(k_1-k_2+1)B_3){\left({\mathfrak{e}}^{\left(k\right)}\right)}^3+((4-13k_2+7k_2^2-k_3^2+\hfill \\ \hfill & k_1(13-7k_2+k_2^2)+\alpha (-7+13k_2-7k_2^2+k_3^2-k_1(13-7k_2+k_2^2)))B_3^2+(-7+14k_2\hfill \\ \hfill & -4k_2^2+2k_1(-7+2k_2)+2\alpha (5+k_1(7-2k_2)-7k_2+2k_2^2))B_2{B}_3-3(\alpha -1)(k_1-k_2\hfill \\ \hfill & +1)B_4){\left({\mathfrak{e}}^{\left(k\right)}\right)}^4+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^5\right).\hfill \end{array}$$

(17)

To attain a fourth-order convergence rate, the coefficients of ${\left({\mathfrak{e}}^{\left(k\right)}\right)}^2$ and ${\left({\mathfrak{e}}^{\left(k\right)}\right)}^3$ must simultaneously vanish. By equating these coefficients to zero, we obtain the following necessary conditions:

$$k_1=-{\displaystyle \frac{1}{\alpha -1}}\mathrm{and}{k}_2=k_1+1={\displaystyle \frac{\alpha }{\alpha -1}},\mathrm{where}\alpha \in \mathbb{R}\setminus \left\{1\right\}.$$

(18)

Substituting the conditions in (18) into Equation (17), we obtain the following:

$${\mathfrak{e}}^{(k+1)}=\left({\displaystyle \frac{2\alpha -1}{\alpha -1}}{B}_3^2-B_2{B}_3\right){\left({\mathfrak{e}}^{\left(k\right)}\right)}^4+\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^5\right),$$

(19)

where $\alpha \in \mathbb{R}\setminus \left\{1\right\}$ represents a free parameter.

Hence, (19) demonstrates the fourth-order convergence of the proposed family in (4).    

Remark 1. 

A sufficient condition for the inverse ${(I-k_2\eta )}^{-1}$ to exist is $\parallel k_2\eta \parallel <1$ locally, which follows from the method’s fourth-order convergence ${\mathfrak{e}}^{(k+1)}=\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^4\right)$ and the local error bound $\parallel \eta \parallel =\mathcal{O}\left({\left({\mathfrak{e}}^{\left(k\right)}\right)}^2\right)$, ensuring $k_2\eta$ remains small near the solution.

3. Efficiency Index

The efficiency of iterative methods is a critical factor in determining their practical applicability, particularly for large-scale problems. The formula suggested by Ostrowski is the following:

$$I_E=p^{1/d},$$

where p is the order of convergence of the method and d represents the number of functional evaluations needed to perform the method per iteration.

Another classical measure of the efficiency of iterative methods is the operational efficiency index proposed by Traub, with the following expression:

$$I_O=p^{1/op},$$

where $op$ is the number of operations, expressed in units of product, needed to calculate each iteration.

In several occasions, a combination of both is also used, called the computational efficiency index, whose expression is

$$E={\rho }^{1/d+op.}$$

In general, for m nonlinear equations in m variables, it is required to compute m function evaluations for F and $m^2$ function evaluations for $F^{\prime }$. The total number of products and quotients needed for the solution linear system and linear system having identical coefficient matrix (common coefficient matrix repeated r times) are ${\displaystyle \frac{1}{3}}{m}^3+m^2-{\displaystyle \frac{1}{3}}m$ and ${\displaystyle \frac{1}{3}}{m}^3+r{m}^2-{\displaystyle \frac{1}{3}}m$, respectively, with the help of LU factorization. Because of this, the computational cost rises by $m^2$ for every system that has a matrix of common coefficients. Further, we also added $m^2$ number of evaluations for products of a matrix with a vector.

For the proposed method, which achieves a fourth-order convergence ($p=4$), the efficiency index is given by

$$E=4^{1/{\displaystyle \frac{m^3}{3}}+5m^2+2m}.$$

There are two functional evaluations and a single jacobian evaluation, so the number of functional evaluations is as follows:

$$2m+m^2$$

On the other hand, a divided difference operator is calculated and a single system is solved, so the number of operations is as follows:

$${\displaystyle \frac{m^3}{3}}+4m^2$$

Therefore, the total number of function evaluations and operations is as follows:

$$2m+m^2+{\displaystyle \frac{m^3}{3}}+4m^2={\displaystyle \frac{m^3}{3}}+5m^2+2m$$

4. Numerical Results

In this section, we examine several numerical problems to evaluate the effectiveness of the proposed methods. The newly introduced schemes, denoted as $P{M}_1$, $P{M}_2$, and $P{M}_3$, correspond to the parameter values $\alpha ={\displaystyle \frac{1}{4}}$, $\alpha ={\displaystyle \frac{1}{9}}$, and $\alpha =-{\displaystyle \frac{1}{9}}$, respectively. These methods are analyzed and compared against the following system approaches.

1.

Cordero et al. [19], denoted as ${\mathit{CL}}_{\mathbf{1}}$, ${\mathit{CL}}_{\mathbf{2}}$, respectively.

$$\begin{array}{cc}\hfill {\mathfrak{y}}^{\left(k\right)}& ={\mathfrak{x}}^{\left(k\right)}-{\left[{\mathfrak{x}}^{\left(k\right)}+\lambda H\left({\mathfrak{x}}^{\left(k\right)}\right),{\mathfrak{x}}^{\left(k\right)};F\right]}^{-1}F\left({\mathfrak{x}}^{\left(k\right)}\right),\hfill \\ \hfill {\mathfrak{x}}^{(k+1)}& ={\mathfrak{x}}^{\left(k\right)}-\left[\left({\displaystyle \frac{\beta }{6}}{G}^3+2G^2+G+1\right)\right]{\left[{\mathfrak{x}}^{\left(k\right)}+\lambda H\left({\mathfrak{x}}^{\left(k\right)}\right),{\mathfrak{x}}^{\left(k\right)};F\right]}^{-1}F\left({\mathfrak{x}}^{\left(k\right)}\right),\hfill \end{array}$$

(20)

for $\beta =1$ and $G({\mathfrak{x}}^{\left(k\right)},{\mathfrak{y}}^{\left(k\right)})=I-{\left[{\mathfrak{x}}^{\left(k\right)}+\lambda H\left({\mathfrak{x}}^{\left(k\right)}\right),{\mathfrak{x}}^{\left(k\right)};F\right]}^{-1}\left[{\mathfrak{x}}^{\left(k\right)},{\mathfrak{y}}^{\left(k\right)},F\right]$.

$$\begin{array}{cc}\hfill {\mathfrak{y}}^{\left(k\right)}& ={\mathfrak{x}}^{\left(k\right)}-{\left[{\mathfrak{x}}^{\left(k\right)}+\lambda H\left({\mathfrak{x}}^{\left(k\right)}\right),{\mathfrak{x}}^{\left(k\right)};F\right]}^{-1}F\left({\mathfrak{x}}^{\left(k\right)}\right),\hfill \\ \hfill {\mathfrak{x}}^{(k+1)}& ={\mathfrak{y}}^{\left(k\right)}-\left(3-2\Gamma \left(k\right)\right){\left[{\mathfrak{x}}^{\left(k\right)}+\lambda H\left({\mathfrak{x}}^{\left(k\right)}\right),{\mathfrak{x}}^{\left(k\right)};F\right]}^{-1}F\left({\mathfrak{y}}^{\left(k\right)}\right),\hfill \end{array}$$

(21)

where ${\Gamma }^{\left(k\right)}={\left[{\mathfrak{x}}^{\left(k\right)}+\lambda H\left({\mathfrak{x}}^{\left(k\right)}\right),{\mathfrak{x}}^{\left(k\right)};F\right]}^{-1}\left[{\mathfrak{x}}^{\left(k\right)},{\mathfrak{y}}^{\left(k\right)},F\right]$.

We note that the authors in (20) and (21) used $\lambda =0.001$ and

$$H\left({\mathfrak{x}}^{\left(k\right)}\right)={\left(f_1^m\left({\mathfrak{x}}^{\left(k\right)}\right),f_2^m\left({\mathfrak{x}}^{\left(k\right)}\right),\dots ,f_n^m\left({\mathfrak{x}}^{\left(k\right)}\right)\right)}^T,$$

with $m=2$.

2.

Grau et al. [11], denoted as $\mathit{GG}$

$$\begin{array}{cc}\hfill {\mathfrak{y}}^{\left(k\right)}& ={\mathfrak{x}}^{\left(k\right)}-{\left[F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right]}^{-1}F\left({\mathfrak{x}}^{\left(k\right)}\right),\hfill \\ \hfill {\mathfrak{x}}^{(k+1)}& ={\mathfrak{x}}^{\left(k\right)}-{\displaystyle \frac{1}{2}}\left[{\left[F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right]}^{-1}+{\left[F^{\prime }\left({\mathfrak{y}}^{\left(k\right)}\right)\right]}^{-1}\right]F\left({\mathfrak{x}}^{\left(k\right)}\right).\hfill \end{array}$$

(22)

3.

Cordero et al. [20], denoted as ${\mathit{CR}}_{\mathbf{1}}$.

$$\begin{array}{cc}\hfill {\mathfrak{y}}^{\left(k\right)}& ={\mathfrak{x}}^{\left(k\right)}-{\left[F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right]}^{-1}F\left({\mathfrak{x}}^{\left(k\right)}\right),\hfill \\ \hfill {\mathfrak{x}}^{(k+1)}& ={\mathfrak{y}}^{\left(k\right)}-{\left[F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right]}^{-1}\left(p_{k}F\left({\mathfrak{y}}^{\left(k\right)}\right)+q_{k}F\left({\mathfrak{x}}^{\left(k\right)}\right)\right),\hfill \end{array}$$

(23)

where ${\nu }_k={\displaystyle \frac{{\parallel F\left({\mathfrak{y}}^{\left(k\right)}\right)\parallel }_2}{{\parallel F\left({\mathfrak{x}}^{\left(k\right)}\right)\parallel }_2}}={\displaystyle \frac{F{\left({\mathfrak{y}}^{\left(k\right)}\right)}^{T}F\left({\mathfrak{y}}^{\left(k\right)}\right)}{F{\left({\mathfrak{x}}^{\left(k\right)}\right)}^{T}F\left({\mathfrak{x}}^{\left(k\right)}\right)}},$$K_k={\displaystyle \frac{1}{1+\lambda {\nu }_k}},$ $p_k=K_k(1+\psi {\nu }_k),$ $q_k=2K_k{\nu }_k$ and $(\lambda ,\psi )\in {\mathbb{R}}^2$

4.

Cordero et al. [21], denoted as ${\mathit{CR}}_{\mathbf{2}}$.

$$\begin{array}{cc}\hfill {\mathfrak{x}}^{(k+1)}& ={\mathfrak{y}}^{\left(k\right)}-{\omega }_k{F}^{\prime }{\left({\mathfrak{x}}^{\left(k\right)}\right)}^{-1}F\left({\mathfrak{x}}^{\left(k\right)}\right),\hfill \end{array}$$

(24)

where ${\mathfrak{y}}^{\left(k\right)}$ represents Newton’s method for systems and $(\lambda ,\psi )\in {\mathbb{R}}^2$, and ${\omega }_k={\displaystyle \frac{1+2{\mu }_k+\psi {\nu }_k}{1+\lambda {\nu }_k}}$, ${\mu }_k={\displaystyle \frac{F{\left({\mathfrak{x}}^{\left(k\right)}\right)}^{T}F\left({\mathfrak{y}}^{\left(k\right)}\right)}{{\parallel F\left({\mathfrak{x}}^{\left(k\right)}\right)\parallel }^2}},$${\nu }_k={\displaystyle \frac{{\parallel F\left({\mathfrak{y}}^{\left(k\right)}\right)\parallel }^2}{{\parallel F\left({\mathfrak{x}}^{\left(k\right)}\right)\parallel }^2}}.$

5.

Sharma and Arora [22], denoted as $\mathit{SA}$.

$$\begin{array}{cc}\hfill {\mathfrak{y}}^{\left(k\right)}& ={\mathfrak{x}}^{\left(k\right)}-{\displaystyle \frac{2}{3}}{\left[F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right]}^{-1}F\left({\mathfrak{x}}^{\left(k\right)}\right),\hfill \\ \hfill {\mathfrak{x}}^{(k+1)}& ={\mathfrak{x}}^{\left(k\right)}-\left[{\displaystyle \frac{23}{8}}I-{\left[F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right]}^{-1}{F}^{\prime }\left({\mathfrak{y}}^{\left(k\right)}\right)\left(3I-{\displaystyle \frac{9}{8}}{\left[F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right]}^{-1}{F}^{\prime }\left({\mathfrak{y}}^{\left(k\right)}\right)\right)\right]\hfill \\ & {\left[F^{\prime }\left({\mathfrak{x}}^{\left(k\right)}\right)\right]}^{-1}F\left({\mathfrak{x}}^{\left(k\right)}\right).\hfill \end{array}$$

(25)

To numerically verify the convergence order established in Theorem 1, we present the iteration number k, the error of the residual $\parallel F\left({\mathfrak{x}}^{\left(k\right)}\right)\parallel$, the error between two consecutive iterations $\parallel {\mathfrak{x}}^{k+1}-{\mathfrak{x}}^k\parallel$, and the approximate computational order of convergence (ACOC). The ACOC denoted as $\rho$ is calculated as defined in [13]:

$$\mathrm{ACOC}\approx {\displaystyle \frac{ln\frac{\parallel {\mathfrak{x}}^{k+1}-{\mathfrak{x}}^k\parallel }{\parallel {\mathfrak{x}}^k-{\mathfrak{x}}^{k-1}\parallel }}{ln\frac{\parallel {\mathfrak{x}}^k-{\mathfrak{x}}^{k-1}\parallel }{\parallel {\mathfrak{x}}^{k-1}-{\mathfrak{x}}^{k-2}\parallel }}},k=2,3,\dots$$

(26)

where ${\mathfrak{x}}^{k-2}$, ${\mathfrak{x}}^{k-1}$, ${\mathfrak{x}}^k$, and ${\mathfrak{x}}^{k+1}$ are four consecutive approximations in the iterative process.

Mathematica 11.1.1 [23] was used for all numerical computations, and stopping criteria $\parallel {\mathfrak{x}}^{k-1}-{\mathfrak{x}}^k\parallel <{10}^{-500}$ and $\parallel F\left({\mathfrak{x}}^{\left(k\right)}\right)\parallel <{10}^{-500}$ is used to reduce roundoff errors and the configurations of our computer are given below:

• A processor Intel(R) Core(TM) i3-1005G1 (Intel, Santa Clara, CA, USA).
• CPU @ 1.20 GHz (64 bit machine) (Intel, Santa Clara, CA, USA).
• Microsoft Windows 10 Pro (Microsoft Corporation, Albuquerque, NM, USA).

In all tables, $b(\pm c)$ denotes $b\times {10}^{\pm c}$. The results from

Table 1. Convergence behavior of Example 1 with ${\mathfrak{x}}^{\left(0\right)}={(sin\pi h,sin2\pi h,\dots ,sin40\pi h)}^{tr}$.

Methods	k	$\left|\left|\mathit{F}\left({\mathfrak{x}}^{\left(\mathit{k}\right)}\right)\right|\right|$	$\left|\left|{\mathfrak{x}}^{\mathit{k}+1}-{\mathfrak{x}}^{\mathit{k}}\right|\right|$	$\mathit{\rho }$
	1	$1.0(-4)$	$3.5(-2)$
$P{M}_1$	2	$7.5(-12)$	$2.6(-9)$	$3.9986$
	3	$2.1(-40)$	$7.3(-38)$
	1	$1.3(-4)$	$4.3(-2)$
$P{M}_2$	2	$1.9(-11)$	$6.6(-9)$	$3.9982$
	3	$1.1(-38)$	$3.7(-36)$
	1	$1.5(-4)$	$5.3(-2)$
$P{M}_3$	2	$4.8(-11)$	$1.7(-8)$	$3.9975$
	3	$4.9(-37)$	$1.7(-34)$
	1	$2.6(-3)$	$1.4(-1)$
$C{L}_1$	2	$3.0(-8)$	$1.6(-6)$	$4.5698$
	3	$6.8(-28)$	$3.7(-26)$
	1	$1.0(-2)$	$5.3(-1)$
$C{L}_2$	2	$6.3(-6)$	$3.5(-4)$	$4.6978$
	3	$1.9(-18)$	$1.1(-16)$
	1	$1.3(-3)$	$6.7(-2)$
$GG$	2	$2.0(-8)$	$1.1(-6)$	$3.3934$
	3	$8.2(-23)$	$4.4(-21)$
	1	$9.0(-2)$	$3.7$
$C{R}_1$	2	$1.0(-3)$	$8.2(-3)$	$2.2443$
	3	$2.4(-10)$	$1.3(-8)$
	1	$1.0(-2)$	$6.0(-1)$
$C{R}_2$	2	$4.1(-7)$	$1.6(-5)$	$2.8531$
	3	$1.1(-18)$	$5.9(-17)$
	1	$1.0(-2)$	$5.3(-1)$
$SA$	2	$6.3(-6)$	$3.5(-4)$	$4.9097$
	3	$1.9(-18)$	$1.1(-16)$

,

Table 2. Convergence behavior of Example 2 with initial guess ${\mathfrak{x}}^{\left(0\right)}={(0.5,0.5,\dots ,0.5)}^{tr}$.

Methods	k	$\left|\left|\mathit{F}\left({\mathfrak{x}}^{\left(\mathit{k}\right)}\right)\right|\right|$	$\left|\left|{\mathfrak{x}}^{\mathit{k}+1}-{\mathfrak{x}}^{\mathit{k}}\right|\right|$	$\mathit{\rho }$
	1	$7.6(-4)$	$1.6(-4)$
$P{M}_1$	2	$7.3(-19)$	$1.6(-19)$	$3.9981$
	3	$6.4(-79)$	$1.4(-79)$
	1	$7.8(-4)$	$1.7(-4)$
$P{M}_2$	2	$8.1(-19)$	$1.7(-19)$	$3.9981$
	3	$1.0(-78)$	$2.1(-79)$
	1	$7.9(-4)$	$1.7(-4)$
$P{M}_3$	2	$9.0(-19)$	$1.9(-19)$	$3.9982$
	3	$1.6(-78)$	$3.4(-79)$
	1	$2.6(-3)$	$2.0(-4)$
$C{L}_1$	2	$6.4(-18)$	$4.8(-19)$	$4.0880$
	3	$2.5(-76)$	$1.9(-77)$
	1	$2.8(-3)$	$2.2(-4)$
$C{L}_2$	2	$1.1(-17)$	$8.4(-19)$	$4.0851$
	3	$2.7(-75)$	$2.0(-76)$
	1	$4.3(-2)$	$3.2(-3)$
$GG$	2	$1.2(-9)$	$9.0(-11)$	$3.1016$
	3	$2.8(-32)$	$2.1(-33)$
	1	$9.3(-3)$	$6.9(-4)$
$C{R}_1$	2	$4.9(-12)$	$3.6(-13)$	$3.2769$
	3	$1.0(-40)$	$7.5(-42)$
	1	$7.1(-3)$	$5.4(-4)$
$C{R}_2$	2	$2.3(-14)$	$1.7(-15)$	$2.9927$
	3	$9.6(-48)$	$2.5(-49)$
	1	$2.8(-3)$	$2.2(-4)$
$SA$	2	$1.1(-17)$	$8.3(-19)$	$4.0595$
	3	$2.6(-75)$	$1.9(-76)$

,

Table 3. Convergence behavior of Example 3 with initial guess ${\mathfrak{x}}^{\left(0\right)}={(-2,-2,\dots ,-2)}^{tr}$.

Methods	k	$\left|\left|\mathit{F}\left({\mathfrak{x}}^{\left(\mathit{k}\right)}\right)\right|\right|$	$\left|\left|{\mathfrak{x}}^{\mathit{k}+1}-{\mathfrak{x}}^{\mathit{k}}\right|\right|$	$\mathit{\rho }$
	1	$1.9$	$6.4(-1)$
$P{M}_1$	2	$9.9(-5)$	$3.5(-5)$	$3.8700$
	3	$3.4(-21)$	$1.1(-21)$
	1	$2.2$	$7.4(-1)$
$P{M}_2$	2	$2.2(-4)$	$7.7(-5)$	$3.8689$
	3	$8.9(-20)$	$3.0(-20)$
	1	$2.5$	$8.2(-1)$
$P{M}_3$	2	$4.1(-4)$	$1.4(-4)$	$3.8666$
	3	$1.3(-18)$	$4.3(-19)$
	1	$40.0$	$1.3$
$C{L}_1$	2	$5.6(-2)$	$2.0(-3)$	$5.4623$
	3	$9.7(-13)$	$3.3(-14)$
	1	$45.0$	$1.4$
$C{L}_2$	2	$1.1(-1)$	$4.0(-3)$	$5.6695$
	3	$2.1(-11)$	$7.2(-13)$
	1	23	$7.8$
$GG$	2	$3.1(-3)$	$1.1(-4)$	$4.9381$
	3	$4.2(-18)$	$1.4(-19)$
	1	$29.0$	$1.1$
$C{R}_1$	2	$1.8(-1)$	$6.3(-3)$	$5.0575$
	3	$9.5(-9)$	$2.7(-10)$
	1	$17.0$	$5.7(-1)$
$C{R}_2$	2	$5.3(-3)$	$1.7(-4)$	$3.0017$
	3	$3.0(-12)$	$6.5(-14)$
	1	45	$1.4$
$SA$	2	$1.1(-1)$	$4.0(-3)$	$5.6710$
	3	$2.1(-11)$	$7.4(-13)$

,

Table 4. Convergence behavior of Example 4 with initial guess ${\mathfrak{x}}^{\left(0\right)}={(0.1,0.1,\dots ,0.1)}^{tr}$.

Methods	k	$\left|\left|\mathit{F}\left({\mathfrak{x}}^{\left(\mathit{k}\right)}\right)\right|\right|$	$\left|\left|{\mathfrak{x}}^{\mathit{k}+1}-{\mathfrak{x}}^{\mathit{k}}\right|\right|$	$\mathit{\rho }$
	1	$6.0(-7)$	$1.1(-3)$
$P{M}_1$	2	$1.4(-19)$	$2.6(-16)$	$4.0000$
	3	$4.5(-70)$	$8.2(-67)$
	1	$6.5(-7)$	$1.2(-3)$
$P{M}_2$	2	$2.1(-19)$	$3.8(-16)$	$4.0000$
	3	$2.4(-69)$	$4.5(-66)$
	1	$7.0(-7)$	$1.3(-3)$
$P{M}_3$	2	$3.1(-19)$	$5.6(-16)$	$4.0000$
	3	$1.3(-68)$	$2.3(-65)$
	1	$8.2(-6)$	$2.0(-3)$
$C{L}_1$	2	$3.0(-17)$	$7.6(-15)$	$4.2409$
	3	$6.1(-63)$	$1.5(-60)$
	1	$1.0(-5)$	$2.5(-3)$
$C{L}_2$	2	$9.8(-17)$	$2.4(-14)$	$4.2507$
	3	$8.6(-61)$	$2.2(-58)$
	1	$2.0(-5)$	$5.0(-3)$
$GG$	2	$6.5(-13)$	$1.7(-10)$	$3.2565$
	3	$2.6(-35)$	$7.0(-33)$
	1	$5.4(-5)$	$1.3(-2)$
$C{R}_1$	2	$2.0(-12)$	$3.1(-10)$	$3.0568$
	3	$4.6(-34)$	$7.7(-32)$
	1	$5.4(-5)$	$1.3(-2)$
$C{R}_2$	2	$6.8(-13)$	$1.7(-10)$	$3.1970$
	3	$3.3(-36)$	$8.6(-34)$
	1	$1.1(-5)$	$2.6(-3)$
$SA$	2	$1.2(-16)$	$2.9(-14)$	$4.2522$
	3	$1.8(-60)$	$4.5(-58)$

,

Table 5. Convergence behavior of Example 3 with initial guess ${\mathfrak{x}}^{\left(0\right)}={(-0.5,-0.5,\dots ,-0.5)}^{tr}$.

Methods	k	$\left|\left|\mathit{F}\left({\mathfrak{x}}^{\left(\mathit{k}\right)}\right)\right|\right|$	$\left|\left|{\mathfrak{x}}^{\mathit{k}+1}-{\mathfrak{x}}^{\mathit{k}}\right|\right|$	$\mathit{\rho }$
	1	$4.8(-2)$	$5.2(-3)$
$P{M}_1$	2	$5.3(-11)$	$5.8(-12)$	$3.9726$
	3	$9.3(-47)$	$1.0(-47)$
	1	$6.9(-2)$	$7.6(-3)$
$P{M}_2$	2	$3.4(-10)$	$3.7(-11)$	$3.9918$
	3	$2.2(-43)$	$2.4(-44)$
	1	$9.5(-2)$	$1.0(-2)$
$P{M}_3$	2	$1.6(-9)$	$1.7(-10)$	$3.9909$
	3	$1.3(-40)$	$1.5(-41)$
	1	$2.7(-1)$	$4.2(-2)$
$C{L}_1$	2	$9.5(-6)$	$1.5(-7)$	$4.5140$
	3	$1.8(-27)$	$2.8(-29)$
	1	$8.5$	$1.3(-1)$
$C{L}_2$	2	$1.2(-3)$	$1.8(-5)$	$4.7525$
	3	$6.4(-19)$	$1.0(-20)$
	1	$3.8(-1)$	$5.9(-3)$
$GG$	2	$8.7(-8)$	$1.4(-9)$	$3.2763$
	3	$1.1(-27)$	$1.8(-29)$
	1	$38.0$	$5.3(-1)$
$C{R}_1$	2	$2.0(-1)$	$3.3(-3)$	$4.4097$
	3	$2.1(-7)$	$3.4(-9)$
	1	$5.5$	$8.8(-2)$
$C{R}_2$	2	$3.8(-4)$	$6.0(-6)$	$3.3184$
	3	$2.5(-15)$	$4.1(-17)$
	1	$8.5$	$1.3(-1)$
$SA$	2	$1.1(-3)$	$1.8(-5)$	$4.7518$
	3	$6.1(-19)$	$9.6(-21)$

and

Table 6. Convergence behavior of Example 6 with initial guess ${\mathfrak{x}}^{\left(0\right)}={(1,1,\dots ,1)}^{tr}$.

Methods	k	$\left|\left|\mathit{F}\left({\mathfrak{x}}^{\left(\mathit{k}\right)}\right)\right|\right|$	$\left|\left|{\mathfrak{x}}^{\mathit{k}+1}-{\mathfrak{x}}^{\mathit{k}}\right|\right|$	$\mathit{\rho }$
	1	$6.2(-3)$	$1.6(-3)$
$P{M}_1$	2	$1.1(-17)$	$3.7(-17)$	$3.9840$
	3	$5.2(-72)$	$1.6(-71)$
	1	$5.8(-4)$	$1.4(-3)$
$P{M}_2$	2	$5.8(-18)$	$1.7(-17)$	$3.9812$
	3	$2.5(-73)$	$6.8(-73)$
	1	$5.3(-4)$	$1.2(-3)$
$P{M}_3$	2	$2.6(-18)$	$6.6(-18)$	$3.9757$
	3	$6.1(-75)$	$1.3(-74)$
	1	$3.5(-4)$	$1.4(-2)$
$C{L}_1$	2	$9.4(-18)$	$4.8(-17)$	$4.0028$
	3	$1.8(-71)$	$6.0(-71)$
	1	$8.0(-4)$	$3.7(-3)$
$C{L}_2$	2	$8.5(-16)$	$4.2(-15)$	$3.9996$
	3	$1.5(-63)$	$7.4(-63)$
	1	$1.1(-1)$	$2.4(-2)$
$GG$	2	$9.5(-9)$	$3.2(-9)$	$3.3369$
	3	$3.1(-29)$	$1.1(-29)$
	1	$9.3(-3)$	$3.7(-2)$
$C{R}_1$	2	$3.9(-9)$	$1.0(-8)$	$2.9306$
	3	$1.3(-28)$	$5.9(-28)$
	1	$7.5(-3)$	$3.0(-2)$
$C{R}_2$	2	$9.1(-10)$	$4.1(-9)$	$3.0092$
	3	$6.9(-31)$	$3.5(-30)$
	1	$8.8(-3)$	$3.7(-3)$
$SA$	2	$9.3(-15)$	$4.2(-15)$	$4.2917$
	3	$1.6(-62)$	$7.4(-63)$

show that the proposed methods give better results than existing methods and

Table 7. Number of iterations taken by the methods in each example, respectively.

Methods	Example 1	Example 2	Example 3	Example 4	Example 5	Example 6
$P{M}_1$	5	5	5	5	5	5
$P{M}_2$	5	5	5	5	5	5
$P{M}_3$	5	5	5	5	5	5
$C{L}_1$	6	5	6	5	6	5
$C{L}_2$	6	5	6	5	6	5
$GG$	6	6	5	6	6	6
$C{R}_1$	7	6	7	6	7	6
$C{R}_2$	6	6	6	6	7	5
$SA$	6	5	6	5	6	5

presents the number of iterations required by each method for the respective examples. A detailed discussion of the outcomes is provided separately for each example.

Example 1. 

Consider the Bratu problem [24], which has a wide range of applications, including the fuel ignition model in thermal combustion, thermal reactions, radioactive heat transfer, chemical reactor theory, the Chandrasekhar model of the universe’s expansion, and nanotechnology [25,26,27,28]. The problem is formulated as follows:

$$\begin{array}{c}\hfill {\mathfrak{y}}^{″}+C{e}^{\mathfrak{y}}=0,\mathfrak{y}\left(0\right)=\mathfrak{y}\left(1\right)=0.\end{array}$$

Using the discretization of finite differences, the boundary value problem (1) is transformed into a non-linear system of size $40\times 40$ with step size $h=1/41$. The central difference approach, which is provided as follows, has been used for the second derivative.

$${\mathfrak{y}}_k^{″}={\displaystyle \frac{{\mathfrak{y}}_{k-1}-2{\mathfrak{y}}_k+{\mathfrak{y}}_{k+1}}{h^2}},$$

which further yields the succeeding system of nonlinear equation

$${\mathfrak{y}}_{k-1}-2{\mathfrak{y}}_k+{\mathfrak{y}}_{k+1}+h^{2}C{e}_k^{\mathfrak{y}},k=1,2,\dots ,40.$$

Table 1 presents the computational comparison of the solution to this problem. The convergence of the proposed and existing schemes approaching the solution   

$$\begin{gathered} \xi =(0.0556856839360764399\dots ,0.109484517218912365\dots ,0.1612922092823206959\dots , \\ 0.2110028847969697865\dots ,0.2585096651583685153\dots ,0.3037053235694527046\dots , \\ 0.3464830109827774699\dots ,0.3867370479445188487\dots ,0.4243637749768939967\dots , \\ 0.4592624516247244838\dots ,0.4913361917742592867\dots ,0.5204929204449964016\dots , \\ 0.5466463350885622102\dots ,0.5697168526396365918\dots ,0.5896325222867928076\dots , \\ 0.6063298832873388347\dots ,0.6197547472372992549\dots ,0.6298628850887883449\dots , \\ 0.6366206009024921671\dots ,0.6400051768044093745\dots ,0.6400051768044093745\dots , \\ 0.6366206009024921671\dots ,0.6298628850887883449\dots ,0.6197547472372992549\dots , \\ 0.6063298832873388347\dots ,0.5896325222867928076\dots ,0.5697168526396365918\dots , \\ 0.5466463350885622102\dots ,0.5204929204449964016\dots ,0.4913361917742592867\dots , \\ 0.4592624516247244838\dots ,0.4243637749768939967\dots ,0.3867370479445188487\dots , \\ 0.3464830109827774699\dots ,0.3037053235694527046\dots ,0.2585096651583685153\dots , \\ 0.2110028847969697865\dots ,0.1612922092823206959\dots ,0.1094845172189123365\dots , \end{gathered}$$

${0.0556856839360764399\dots )}^{tr}$ is listed in Table 1.

The error estimates of the proposed methods outperform the existing methods from the first iteration, as shown in Table 1. Furthermore, for all proposed schemes, the estimated order of convergence aligns perfectly with the theoretical one. The approximate solution obtained with method $P{M}_1$ is shown in Figure 1.

Example 2. 

Consider the well-known Hammerstein integral equation, as described in [3], given by $\zeta \left(p\right)=1+\theta {\int }_0^{1}K(p,u){\left(\zeta \left(u\right)\right)}^{3}du$, where $\zeta \in \mathcal{C}[0,1];p,u\in [0,1]$, $\theta ={\displaystyle \frac{1}{5}}$ and

$$Kernel=K(p,u)=\left.\begin{array}{cc}& (1-p)u,u\le p,\hfill \\ & p(1-u),p\le u.\hfill \end{array}\right\}$$

This integral equation is formulated into a system of nonlinear equations by making use of Gauss Legendre quadrature formula defined as

$${\int }_0^{1}g\left(u\right)du\simeq \sum _{j=1}^8{w}_{j}g\left(u_j\right),$$

where $u_j$ and $w_j$ are the x-coordinates and the weights, respectively, at eight nodes given in the following Table. By approximating $\zeta \left(u_i\right)$ with ${\mathfrak{x}}_i$ for $i=1,2,\dots ,8$, we obtain the following system of nonlinear equations:

$$5{\mathfrak{x}}_i-5-\sum _{j=1}^8{a}_{ij}{\mathfrak{x}}_j^3=0,i=1,2,...,8$$

with $a_{ij}=\left\{\begin{array}{c}\hfill w_j{u}_j(1-u_i),j\le i,\\ \hfill w_j{u}_i(1-u_j),i<j.\end{array}\right.$

The x-coordinates and weights used in the Gauss Legendre quadrature procedure are as follows:

$Nodeno.$	$x-coordinates$	$weights$
1	$0.01985507175123188415821\dots$	$0.05061426814518812957626\dots$
2	$0.10166676129318663020422\dots$	$0.11119051722668723527217\dots$
3	$0.23723379504183550709113\dots$	$0.15685332293894364366898\dots$
4	$0.40828267875217509753026\dots$	$0.18134189168918099148257\dots$
5	$0.59171732124782490246973\dots$	$0.18134189168918099148257\dots$
6	$0.76276620495816449290886\dots$	$0.15685332293894364366898\dots$
7	$0.89833323870681336979577\dots$	$0.11119051722668723527217\dots$
8	$0.98014492824876811584178\dots$	$0.05061426814518812957626\dots$

The convergence of the proposed and existing schemes approaching the solution

$$\begin{gathered} \xi =(1.00209624503115\dots ,1.00990031618748\dots ,1.01972696099317\dots , \\ 1.02643574303062\dots ,1.02643574303062\dots ,1.01972696099317\dots , \end{gathered}$$

${1.00990031618748\dots ,1.00209624503115\dots )}^{tr}$ is listed in Table 2.

In Table 2, the error estimates of the proposed methods outperform the existing methods from the first iteration. $GG,$ $C{R}_1,$ and $C{R}_2$ provided poor results compared the remaining methods.

Example 3. 

Broyden Tridiagonal Function: The Broyden Tridiagonal Function [29] is widely used in numerical mathematics and optimization as a benchmark for testing nonlinear solvers and optimization algorithms. Its importance stems from its tridiagonal structure, sparsity, and nonlinearity, which make it a manageable yet sufficiently complex system to evaluate computational methods. The nonlinear system formed by broyden tridiagonal function is defined as follows:

$$F_i\left(\mathfrak{x}\right)=(3-2{\mathfrak{x}}_i){\mathfrak{x}}_i-{\mathfrak{x}}_{i-1}-2{\mathfrak{x}}_{i+1}+1=0,i=1,2,\dots 100.$$

The convergence of the proposed and existing schemes approaching the solution

$$\begin{gathered} \xi =(-0.5707611929747512511\dots ,-0.6819101288680880658\dots ,-0.7024860206676488739\dots , \\ -0.7062605758008976131\dots ,-0.7069518542981373673\dots ,-0.7070784178423320335\dots , \\ -0.7071015885928448094\dots ,-0.7071058305586259006\dots ,-0.7071066071515205562\dots , \\ -0.7071067493253026534\dots ,-0.7071067753535900542\dots ,-0.7071067801186861731\dots , \\ -0.7071067809910501756\dots ,-0.7071067811507571225\dots ,-0.7071067811799952717\dots , \\ -0.7071067811853480092\dots ,-0.7071067811863279549\dots ,-0.7071067811865073572\dots , \\ -0.7071067811865402011\dots ,-0.7071067811865462144\dots ,-0.7071067811865473148\dots , \\ -0.7071067811865475163\dots ,-0.7071067811865475532\dots ,-0.7071067811865475599\dots , \\ -0.7071067811865475612\dots ,-0.7071067811865475614\dots ,-0.7071067811865475615\dots , \\ -0.7071067811865475615\dots ,-0.7071067811865475615\dots ,-0.7071067811865475615\dots , \\ -0.7071067811865475615\dots ,-0.7071067811865475615\dots ,-0.7071067811865475615\dots , \\ -0.7071067811865475615\dots ,-0.7071067811865475615\dots ,-0.7071067811865475615\dots , \\ -0.7071067811865475615\dots ,-0.7071067811865475615\dots ,-0.7071067811865475615\dots , \\ -0.7071067811865475615\dots ,-0.7071067811865475615\dots ,-0.7071067811865475615\dots , \\ -0.7071067811865475615\dots ,-0.7071067811865475615\dots ,-0.7071067811865475615\dots , \\ -0.7071067811865475615\dots ,-0.7071067811865475615\dots ,-0.7071067811865475615\dots , \\ -0.7071067811865475615\dots ,-0.7071067811865475615\dots ,-0.7071067811865475615\dots , \\ -0.7071067811865475615\dots ,-0.7071067811865475615\dots ,-0.7071067811865475615\dots , \\ -0.7071067811865475615\dots ,-0.7071067811865475614\dots ,-0.7071067811865475614\dots , \\ -0.7071067811865475613\dots ,-0.7071067811865475661\dots ,-0.7071067811865475604\dots , \\ -0.7071067811865475585\dots ,-0.7071067811865475533\dots ,-0.7071067811865475392\dots , \\ -0.7071067811865475006\dots ,-0.7071067811865473953\dots ,-0.7071067811865471076\dots , \\ -0.7071067811865463218\dots ,-0.7071067811865441757\dots ,-0.7071067811865383145\dots , \\ -0.7071067811865223068\dots ,-0.7071067811864785874\dots ,-0.7071067811863591838\dots , \\ -0.7071067811860330757\dots ,-0.7071067811851424289\dots ,-0.7071067811827099488\dots , \\ -0.7071067811760665025\dots ,-0.7071067811579223241\dots ,-0.7071067811083680359\dots , \\ -0.7071067809730283466\dots ,-0.7071067806033967325\dots ,-0.7071067795938811146\dots , \\ -0.7071067768367528186\dots ,-0.7071067693066499708\dots ,-0.7071067487408863958\dots , \\ -0.7071066925729116003\dots ,-0.7071065391703262674\dots ,-0.7071061202064697042\dots , \\ -0.7071049759579877528\dots ,-0.7071018508582931619\dots ,-0.7070933157956696782\dots , \\ -0.7070700055072725268\dots ,-0.7070063430511282925\dots ,-0.7068324809375858107\dots , \\ -0.7063577059891970941\dots ,-0.7050615273253236235\dots ,-0.7015251953077047754\dots , \\ -0.6918946289504083648\dots ,-0.6657975233421828793\dots ,-0.5960353126266538993\dots , \end{gathered}$$

${-0.4164123011668417431\dots )}^{tr}$ is listed in Table 3.

It is observed in Table 3 that, for all proposed schemes, the computational order of convergence is approximately simillar with the theoretical one while all existing methods have different computational order of convergence than theoretical convergence order.

Example 4. 

Consider the Frank-Kamenetskii problem [30], which is governed by the differential equation:

$$\mathfrak{x}{\mathfrak{y}}^{″}+{\mathfrak{y}}^{\prime }+\mathfrak{x}{e}^{\mathfrak{y}}=0,{\mathfrak{y}}^{\prime }\left(0\right)=\mathfrak{y}\left(1\right)=0.$$

To transform the boundary value problem (4) into a system of nonlinear equations with 50 unknown variables, we apply a finite difference discretization using a step size of $\tilde{h}={\displaystyle \frac{1}{51}}$. Furthermore, the second derivative is approximated using the central difference scheme as follows:

$${\mathfrak{y}}_j^{″}={\displaystyle \frac{{\mathfrak{y}}_{j-1}-2{\mathfrak{y}}_j+{\mathfrak{y}}_{j+1}}{h^2}},j=1,2,\dots ,50.$$

The solution $\xi =(0.4742933\dots ,0.4738815\dots ,0.4730579\dots ,0.4718232\dots ,0.4701778\dots ,$

$0.4681227\dots ,0.4656589\dots ,0.4627878\dots ,0.4595107\dots ,0.4558294\dots ,0.4517458\dots ,$

$0.447262\dots ,0.4423803\dots ,$$0.437103\dots ,0.4314332\dots ,0.425373\dots ,0.418926\dots ,0.4120966\dots ,$

$0.4048861\dots ,0.397299\dots ,0.389338\dots ,$$0.381004\dots ,0.372319\dots ,0.3632593\dots ,0.3538470\dots ,$

$0.3440823\dots ,0.333969\dots ,0.323513\dots ,0.312719\dots ,$$0.301591\dots ,0.2901340\dots ,0.2783530\dots ,$

$0.266253\dots ,0.253839\dots ,0.241118\dots ,0.228092\dots ,0.2147698\dots ,$$0.2011542\dots ,0.1872513\dots ,$

$0.1730667\dots ,0.158605\dots ,0.143873\dots ,0.128876\dots ,0.113619\dots ,0.09810770\dots ,$$0.0823470\dots ,$

${0.06634287\dots ,0.05010065\dots ,0.03362582\dots ,0.01692381\dots )}^{tr}$ of this problem is examined and demonstrated in Table 4.

In this case, the best results were achieved by the proposed methods. Furthermore, for all the proposed schemes, the estimated order of convergence aligns perfectly with the theoretical one.

Example 5.

Broyden Banded Function: The Broyden Banded Function [29] is another benchmark problem often used in the study of numerical methods for solving nonlinear systems of equations. Unlike the Broyden Tridiagonal Function, which is tridiagonal, this function has a more general banded structure, meaning that each equation depends not just on immediate neighbors, but on a subset of variables within a certain band. The Broyden Banded Function for a system of n equations with variables $\mathfrak{x}={({\mathfrak{x}}_1,{\mathfrak{x}}_2,\dots ,{\mathfrak{x}}_n)}^{tr}$ is given by the following:

$$F_i\left(\mathfrak{x}\right)=(2+5{\mathfrak{x}}_i^2){\mathfrak{x}}_i+1-\sum _{j\in S\left(i\right)}{\mathfrak{x}}_j(1+2{\mathfrak{x}}_j),i=1,2,\dots ,50$$

where $S\left(i\right)=\{j:j\ne i,max(1,i-p)\le j\le min(n,i+p\left)\right\}$ where p is the bandwidth.

The convergence of the proposed and existing schemes approaching the solution

$$\begin{gathered} \xi =(-0.4283028635872503067\dots ,-0.4765964243562935888\dots ,-0.5196524636464013979\dots , \\ -0.5580993248561520037\dots ,-0.5925061559650828611\dots ,-0.6245037074105165235\dots , \\ -0.6232386691324512479\dots ,-0.6214196767136478016\dots ,-0.6196158428334761759\dots , \\ -0.6182260179198573987\dots ,-0.6175180248414952073\dots ,-0.6177318303186657405\dots , \\ -0.6179003162526636765\dots ,-0.6180077985633592471\dots ,-0.6180570610194790544\dots , \\ -0.6180627237744715955\dots ,-0.6180464123676292322\dots ,-0.6180369432559549751\dots , \\ -0.6180327968239003001\dots ,-0.6180320109076161335\dots ,-0.6180327484374204368\dots , \\ -0.6180336522098025557\dots ,-0.6180340391955201848\dots ,-0.6180341290746869223\dots , \\ -0.6180340902897343633\dots ,-0.6180340279672514792\dots ,-0.6180339892049930822\dots , \\ -0.6180339788606287306\dots ,-0.6180339805677721225\dots ,-0.6180339850062839112\dots , \\ -0.6180339881846647394\dots ,-0.6180339893995617135\dots ,-0.6180339894032136724\dots , \\ -0.6180339890890702474\dots ,-0.6180339888323726205\dots ,-0.6180339887160342564\dots , \\ -0.6180339886991714529\dots ,-0.6180339887199347385\dots ,-0.6180339887404800992\dots , \\ -0.6180339887510495647\dots ,-0.6180339887535674478\dots ,-0.6180339887524483498\dots , \\ -0.6180339887515573876\dots ,-0.6180339887274529494\dots ,-0.6180339894850733806\dots , \\ -0.6180339646916006426\dots ,-0.6180347757588284862\dots ,-0.6180082405037704871\dots , \end{gathered}$$

${-0.6188732808161922001\dots ,-0.5862791221249134994\dots )}^{tr}$ is listed in Table 5.

In this example, we observe again that the proposed methods achieve the best error estimates from the very first iterations.

Example 6.

Application on a Model of Nutrient Diffusion in a Biological Substrate [31].

Nutrient diffusion plays a crucial role in biological systems, affecting cellular metabolism, tissue engineering, and microbial growth. Mathematical models of nutrient diffusion help predict nutrient availability, optimize bioreactors, and enhance medical treatments such as drug delivery. Here, we explores the application of a diffusion model in a biological substrate, analyzing factors influencing diffusion rates and their implications.

Consider a two-dimensional biological substrate that acts as a growth medium or cultivation area for microorganisms. Our goal is to study the diffusion and distribution of nutrients within this medium, as they play a crucial role in the development and viability of the organisms present. The corresponding mathematical formulation is given below:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{2}u}{\partial {\mathfrak{x}}^2}}+{\displaystyle \frac{{\partial }^{2}u}{\partial {\mathfrak{y}}^2}}& =u{(\mathfrak{x},\mathfrak{y})}^3+\left|u(\mathfrak{x},\mathfrak{y})\right|,\mathrm{for}\Omega =\{(\mathfrak{x},\mathfrak{y})\in {\mathbb{R}}^2:\mathfrak{x},\mathfrak{y}\in [0,1]\},\hfill \\ \hfill u(\mathfrak{x},0)& =2{\mathfrak{x}}^2-\mathfrak{x}+1,u(\mathfrak{x},1)=2,0\le \mathfrak{x}\le 1,\hfill \\ \hfill u(0,\mathfrak{y})& =2{\mathfrak{y}}^2-\mathfrak{y}+1,u(1,\mathfrak{y})=2,0\le \mathfrak{y}\le 1.\hfill \end{array}$$

Here, $u(\mathfrak{x},\mathfrak{y})$ denotes the nutrient concentration at any location $(\mathfrak{x},\mathfrak{y})$ in the substrate. The equation models nutrient diffusion, with the term $u{(\mathfrak{x},\mathfrak{y})}^3+\left|u(\mathfrak{x},\mathfrak{y})\right|$ representing interactions between nutrient concentration and biochemical processes occurring within the medium.

The boundary conditions describe how nutrients behave at the substrate’s edges. At the lateral boundaries ($\mathfrak{x}=0$ and $\mathfrak{x}=1$), they may indicate initial concentrations or continuous nutrient supply. At the upper and lower boundaries ($\mathfrak{y}=0$ and $\mathfrak{y}=1$), they can correspond to nutrient absorption by plant roots or interactions with microorganisms present on the surface.

Solving this problem provides insights into nutrient distribution within the substrate and its influence on organism growth and health. This knowledge can contribute to optimizing agricultural methods and improving biological productivity.

As an example, the authors solve this equation for a small system using a block-wise finite difference approach. The discretization involves creating a mesh:

$$\begin{array}{cc}\hfill h& ={\displaystyle \frac{1}{n+1}},k={\displaystyle \frac{1}{m+1}},\hfill \end{array}$$

with mesh points $({\mathfrak{x}}_i,{\mathfrak{y}}_j)$ defined as ${\mathfrak{x}}_i=ih$, $i=0,\dots ,n+1$, and ${\mathfrak{y}}_j=jk$, $j=0,\dots ,m+1$. The discrete form of the equation is given by the following:

$$\begin{array}{c}\hfill u_{\mathfrak{x}\mathfrak{x}}({\mathfrak{x}}_i,{\mathfrak{y}}_j)+u_{\mathfrak{y}\mathfrak{y}}({\mathfrak{x}}_i,{\mathfrak{y}}_j)=u{({\mathfrak{x}}_i,{\mathfrak{y}}_j)}^3+\left|u({\mathfrak{x}}_i,{\mathfrak{y}}_j)\right|.\end{array}$$

This discretized representation allows us to numerically solve for $u(\mathfrak{x},\mathfrak{y})$ using computational methods. Therefore, by approximating the partial derivatives using central divided differences, we have the following:

$$\begin{array}{c}\hfill {\displaystyle \frac{u({\mathfrak{x}}_{i+1},{\mathfrak{y}}_j)-2u({\mathfrak{x}}_i,{\mathfrak{y}}_j)+u({\mathfrak{x}}_{i-1},{\mathfrak{y}}_j)}{h^2}}+{\displaystyle \frac{u({\mathfrak{x}}_i,{\mathfrak{y}}_{j+1})-2u({\mathfrak{x}}_i,{\mathfrak{y}}_j)+u({\mathfrak{x}}_i,{\mathfrak{y}}_{j-1})}{k^2}}=u{({\mathfrak{x}}_i,{\mathfrak{y}}_j)}^3+\left|u({\mathfrak{x}}_i,{\mathfrak{y}}_j)\right|,\end{array}$$

for $i=1,\dots ,n$ and $j=1,\dots ,m$.

Now, we denote $u({\mathfrak{x}}_i,{\mathfrak{y}}_j)=u_{i,j}$. Simplifying the notation, we obtain the following:

$$\begin{array}{c}\hfill 2\left(-{\displaystyle \frac{{\Lambda }^2+1}{{\Lambda }^2}}\right)u_{i,j}-{\displaystyle \frac{1}{{\Lambda }^2}}(u_{i,j+1}+u_{i,j-1})-(u_{i+1,j}+u_{i-1,j})+h^2\left(u_{i,j}^3+\left|u_{i,j}\right|\right)=0,\end{array}$$

with $\Lambda ={\displaystyle \frac{h}{k}}$, $i=1,\dots ,n$, and $j=1,\dots ,m,$ here $m=n=12$.

The convergence of the proposed and existing schemes approaching the solution

$$\begin{gathered} \xi =(0.9159579141800242144\dots ,0.9072089786307704952\dots ,0.9128728847479804976\dots , \\ 0.9369806949845996747\dots ,0.9817387686770479002\dots ,1.0485392499801558597\dots , \\ 1.1384294588808200581\dots ,1.2524247111387106228\dots ,1.3918552265712354804\dots , \\ 1.5589639444123838739\dots ,1.7582456241777705775\dots ,0.9072089786307704952\dots , \\ 0.9226014175996360779\dots ,0.9439241122376833725\dots ,0.9766415904120995219\dots , \\ 1.0242681117073024105\dots ,1.0892758524850682645\dots ,1.1736834484673403999\dots , \\ 1.2795317813663094181\dots ,1.4094228204235085911\dots ,1.567337016707685883\dots , \\ 1.7600861551188621331\dots ,0.9128728847479804976\dots ,0.9439241122376833725\dots , \\ 0.9759760675354321177\dots ,1.0146447653774112913\dots ,1.063991607220679141\dots , \\ 1.1271523601179183468\dots ,1.2068749715483895544\dots ,1.3060293623445218922\dots , \\ 1.4281978317519255005\dots ,1.5784971707380888588\dots ,1.7648499158163805706\dots , \\ 0.9369806949845996747\dots ,0.9766415904120995219\dots ,1.0146447653774112913\dots , \\ 1.0562699741873993097\dots ,1.1056547558964022744\dots ,1.1662390118051703965\dots , \\ 1.2412232244889596071\dots ,1.3340527273929771553\dots ,1.4489903276505684513\dots , \\ 1.5918786748132008886\dots ,1.7712456396452484821\dots ,0.981738768677047902\dots , \\ 1.0242681117073024105\dots ,1.0639916072206791141\dots ,1.105654755896402744\dots , \\ 1.1531829249716005428\dots ,1.2100399869774647234\dots ,1.2796254600037224161\dots , \\ 1.3657198140917823271\dots ,1.4730213214555072145\dots ,1.6078497761505851621\dots , \\ 1.7791442059653217752\dots ,1.0485392499801558597\dots ,1.0892758524850682645\dots , \\ 1.1271523601179183468\dots ,1.1662390118051703965\dots ,1.2100399869774647234\dots , \\ 1.2618193332653576622\dots ,1.3249558773708321743\dots ,1.4033536890986037907\dots , \\ 1.5019501660249639085\dots ,1.6273856823114507777\dots ,1.7889450582238398736\dots , \\ 1.1384294588808200581\dots ,1.1736834484673403999\dots ,1.206874971548389544\dots , \\ 1.2412232244889596071\dots ,1.2796254600037224161\dots ,1.3249558773708321743\dots , \\ 1.3803786842110392967\dots ,1.4497272368032708017\dots ,1.5379992136528640005\dots , \\ 1.6520291742902751577\dots ,1.8014319391776102766\dots ,1.2524247111387106228\dots , \\ 1.2795317813663094181\dots ,1.3060293623445218922\dots ,1.3340527273929771553\dots , \\ 1.3657198140917823271\dots ,1.4033536890986037907\dots ,1.4497272368032708017\dots , \\ 1.5084039721016773017\dots ,1.5842350448920806677\dots ,1.6840828331686575708\dots , \\ 1.8178602010251390389\dots ,1.3918552265712354804\dots ,1.4094228204235085911\dots , \\ 1.4281978317519255005\dots ,1.4489903276505684513\dots ,1.4730213214555072145\dots , \\ 1.5019501660249639085\dots ,1.5379992136528640005\dots ,1.584235044892080667\dots , \\ 1.6450676969911291586\dots ,1.7270705866382999624\dots ,1.8402676260652124239\dots , \\ 1.5589639444123838739\dots ,1.5673370167076855883\dots ,1.5784971707380888588\dots , \\ 1.5918786748132088866\dots ,1.6078497761505851621\dots ,1.6273856823114507777\dots , \\ 1.6520291742902751577\dots ,1.6840828331686575708\dots ,1.7270705866382999624\dots , \\ 1.7866317582138956501\dots ,1.8721986766381496795\dots ,1.758245624177770575\dots , \\ 1.7600861551188621331\dots ,1.7648499158163805706\dots ,1.7712456396452484821\dots , \\ 1.7791442059653217752\dots ,1.7889450582238398736\dots ,1.8014319391776102766\dots , \\ 1.8178602010251390389\dots ,1.8402676260652124239\dots ,1.8721986766381496795\dots , \end{gathered}$$

${1.9204682004958430305\dots )}^{tr}$ is listed in Table 6.

In this case, the best results were obtained with the proposed methods. $GG,$ $C{R}_1,$ and $C{R}_2$ showed poor results compared to the remaining methods.

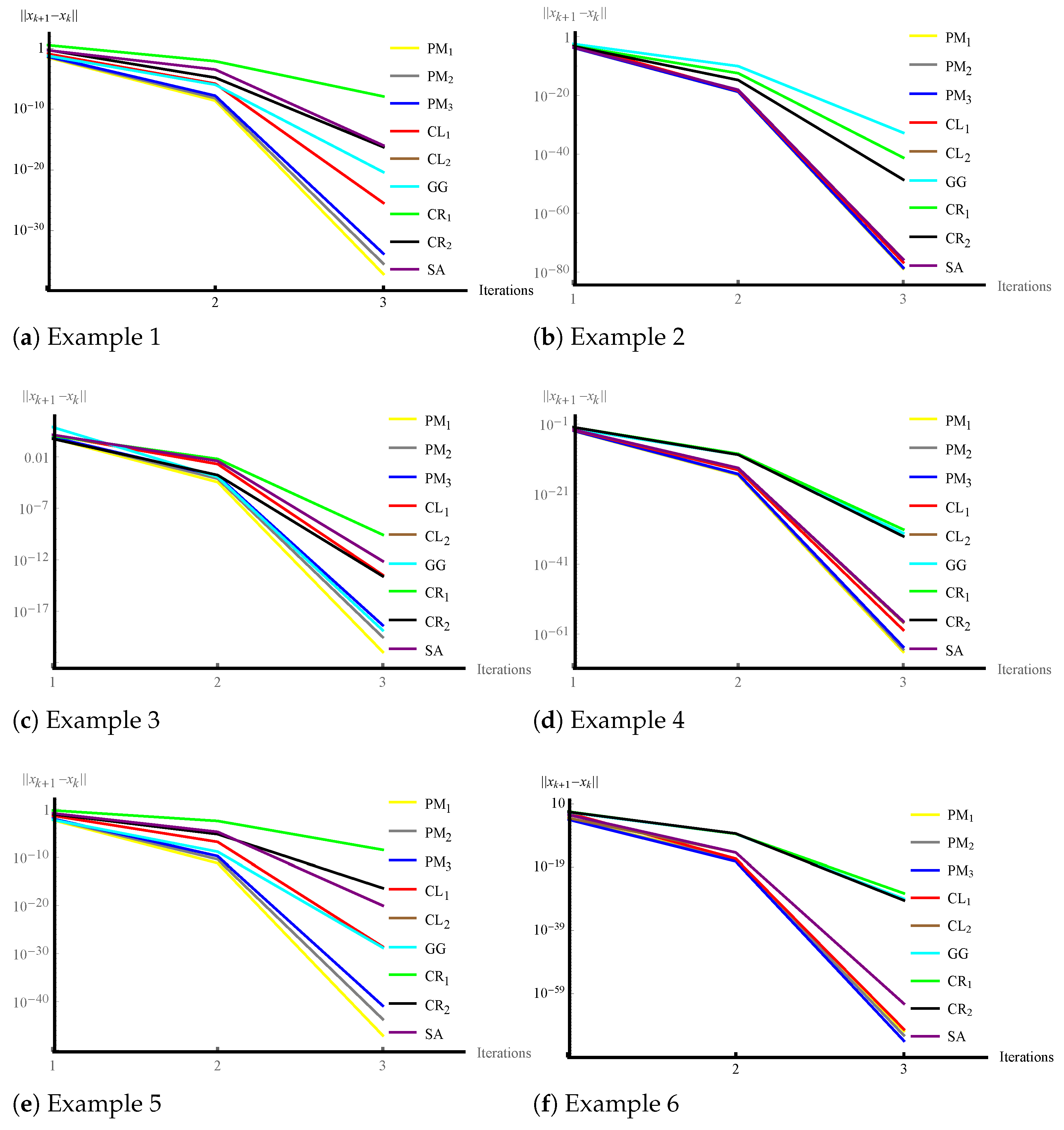
Remark 2.

The graphical error analysis for Examples 1–6 is illustrated in Figure 2. It is evident from all the subfigures in Figure 2 that our method reduces the error faster than existing techniques. Finally,

Table 8. CPU time used by the methods in each example.

Methods	Example 1	Example 2	Example 3	Example 4	Example 5	Example 6	Total Time	Average Time
$P{M}_1$	$54.311$	$1.601$	$289.503$	$83.269$	$84.861$	$881.732$	$1395.276$	$232.546$
$P{M}_2$	$55.748$	$1.727$	$291.365$	$82.354$	$85.493$	$865.837$	$1382.52$	$230.420$
$P{M}_3$	$54.523$	$1.621$	$290.154$	$82.225$	$84.908$	$885.475$	$1398.906$	$233.151$
$C{L}_1$	$60.569$	$2.203$	$489.799$	$86.236$	$87.429$	$890.662$	$1616.898$	$269.483$
$C{L}_2$	$66.117$	$2.189$	$494.327$	$86.972$	$82.168$	$892.880$	$1624.650$	$270.775$
$GG$	$60.449$	$1.871$	$260.691$	$91.487$	$93.795$	$907.086$	$1415.376$	$235.896$
$C{R}_1$	$56.037$	$1.765$	$275.593$	$86.875$	$90.081$	$898.348$	$1408.698$	$234.783$
$C{R}_2$	$56.497$	$1.634$	$272.366$	$86.858$	$90.247$	$899.627$	$1407.228$	$234.538$
$SA$	$57.489$	$1.859$	$284.298$	$90.929$	$97.864$	$888.185$	$1420.624$	$236.770$

shows the CPU times used by each method for each example. It can be seen that the proposed methods provide the best computation times.

A schematic of the algorithm for the family of proposed methods is shown in Appendix A.

5. Discussion

The numerical results demonstrate that our one-parameter family of iterative methods achieves better convergence behavior and accuracy than comparable schemes, highlighting the statistical significance of the improvements. However, a limitation of the proposed approach is that it is not globally convergent.

6. Conclusions

In this paper, we propose a family of iterative methods derived from Newton’s scheme, incorporating a real parameter $\alpha \ne 1$. The theoretical aspects of convergence and stability have been thoroughly analyzed and subsequently validated through numerical experiments in the final part of the study.

Both negative and positive values of the parameter $\alpha$ are considered to numerically compare the performance of the methods with the existing ones. These methods are applied to approximate the roots of nonlinear functions. Notably, the convergence behavior for negative values and positive values of $\alpha$ demonstrates the performance of existing methods. Additionally, a computational approximation of the order of convergence, consistent with the theoretical fourth order, is observed.