Energy-Conscious Lightweight LiDAR SLAM with 2D Range Projection and Multi-Stage Outlier Filtering for Intelligent Driving

Abstract

To meet the increasing demands of energy efficiency and real-time performance in autonomous driving systems, this paper presents a lightweight and robust LiDAR SLAM framework designed with power-aware considerations. The proposed system introduces three core innovations. First, it replaces traditional ordered point cloud indexing with a 2D range image projection, significantly reducing memory usage and enabling efficient feature extraction with curvature-based criteria. Second, a multi-stage outlier rejection mechanism is employed to enhance feature robustness by adaptively filtering occluded and noisy points. Third, we propose a dynamically filtered local mapping strategy that adjusts keyframe density in real time, ensuring geometric constraint sufficiency while minimizing redundant computation. These components collectively contribute to a SLAM system that achieves high localization accuracy with reduced computational load and energy consumption. Experimental results on representative autonomous driving datasets demonstrate that our method outperforms existing approaches in both efficiency and robustness, making it well-suited for deployment in low-power and real-time scenarios within intelligent transportation systems.

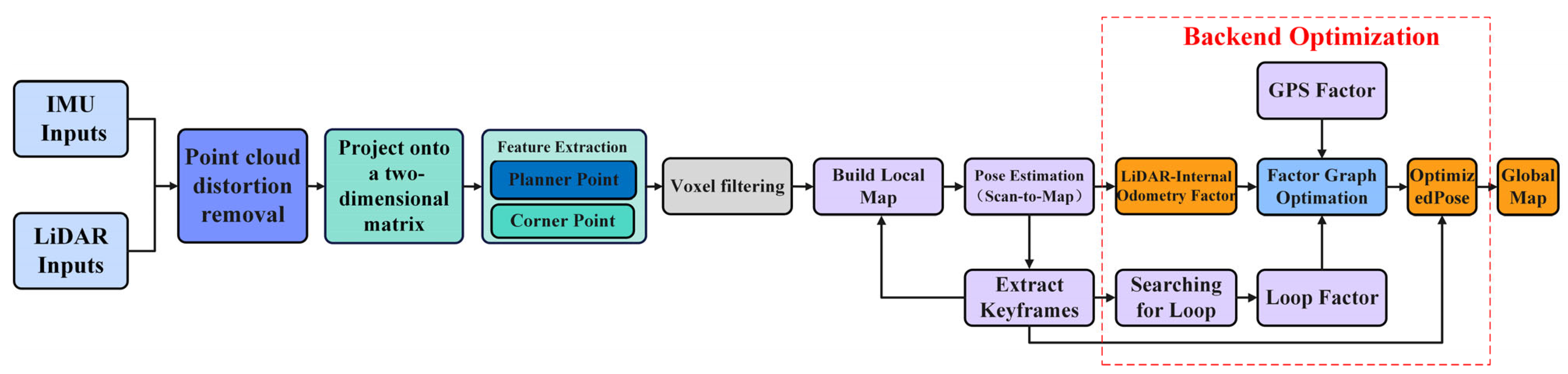
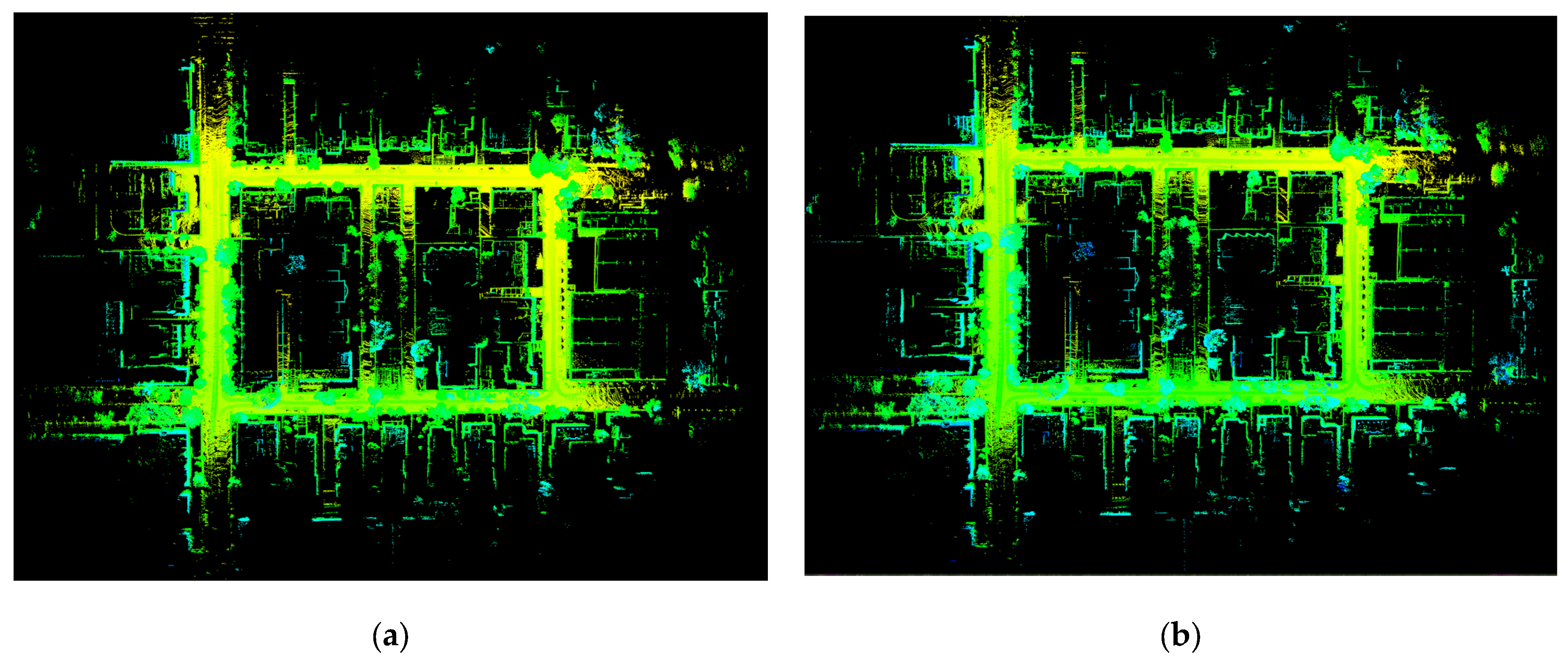1. Introduction

With the rapid advancement of autonomous driving technology, environmental perception and self-localization systems have become critical components of intelligent transportation systems. Among them, LiDAR-based Simultaneous Localization and Mapping (SLAM) techniques have attracted significant attention due to their strong adaptability to complex environments and high-precision performance [1,2]. However, mainstream SLAM algorithms often struggle to meet the practical requirements of autonomous driving scenarios, which demand high-frequency sensing and low-power operation [3,4]. These methods [5,6,7] tend to suffer from excessive computational redundancy, high memory consumption, and strong dependence on hardware resources, thus limiting their deployment on edge devices or energy-constrained platforms. Therefore, there is an urgent need for a robust yet lightweight LiDAR-internal SLAM framework that can maintain localization accuracy while effectively reducing system energy consumption and computational overhead [8,9,10,11].

In most mainstream LiDAR SLAM systems, feature extraction relies on ordered scan-line structures or neighborhood construction from raw 3D point clouds. Representative methods like LOAM [12,13,14,15] use sequential indexing to compute curvature and extract corner and planar features [16]. Specifically, the curvature calculation in LiDAR point clouds differs from the strict mathematical definition of curvature. Instead, it is approximated by measuring the variation in range values between a given point and several of its neighboring points along the same scan line. This procedure provides a fast and approximate evaluation of the local surface smoothness, where points with large curvature values correspond to edge-like structures, while those with small curvature values correspond to planar regions. By applying a simple threshold, edge and surface features can be efficiently selected. Consequently, the extraction process strongly depends on the availability of ordered scan-line structures or on the construction of local neighborhoods in the raw 3D point cloud. However, this approach suffers from low efficiency when processing large-scale or unstructured environments, and it can result in indexing mismatches under occlusion, sparsity, or motion distortion. Furthermore, traditional feature extraction pipelines often depend on OpenCV-based sorting or custom heap operations, which incur high computational and memory overhead on embedded platforms. Meeting the stringent real-time and energy-efficient requirements of autonomous driving demands a more compact and indexable point cloud structure that enables faster and more reliable feature extraction [17,18].

In real-world autonomous driving environments, LiDAR data often contains numerous outliers and noisy points caused by sensor artifacts, occlusion, or surface discontinuity. If not properly filtered, these outliers can introduce false constraints during feature association and back-end optimization, leading to inaccurate or divergent pose estimates. Most SLAM systems rely on simple single-pass filters—such as fixed depth thresholds or curvature filters—which struggle to handle complex noise distributions [12,13,14,15,19]. Although some methods employ occlusion detection or curvature-normal filtering, they lack geometric consistency validation and often retain mismatched points. Moreover, outlier rejection is usually static and lacks a hierarchical structure. A multi-stage filtering strategy that incorporates spatial, depth, and structural cues is therefore crucial for improving system robustness and energy efficiency [20].

The construction of local maps plays a central role in scan-to-map matching and back-end pose optimization [21]. Most existing SLAM frameworks use fixed-radius (spatially driven) or fixed-window (temporally driven) strategies to select historical keyframes [22]. While such methods perform well under steady linear motion, they cannot adapt to dynamic or nonlinear driving behaviors such as turning, accelerating, or stopping. In degenerate cases (e.g., repeated in-place rotation), local maps may fail to update in time, leading to pose drift or registration failure. Moreover, overly dense local maps result in unnecessary optimization load and increased power consumption. Therefore, an adaptive keyframe selection strategy that adjusts spatial coverage and density in response to vehicle motion is essential for enabling energy-efficient, high-precision SLAM in real-time driving applications.

To address these challenges, this paper proposes a lightweight and energy-efficient LiDAR SLAM framework tailored for autonomous driving scenarios. The proposed system balances localization accuracy, computational load, and robustness under diverse motion conditions. The main contributions are as follows:

(1)

Range Image-Based Feature Extraction without Ordered Indexing:

A novel projection method is introduced that transforms unordered 3D LiDAR data into a structured 2D range image. This enables efficient neighborhood access and curvature computation while preserving spatial geometry, significantly improving feature extraction speed and reducing memory overhead. The approach supports parallel implementation and is well-suited for embedded deployment.

(2)

Multi-Stage Outlier Rejection with Geometric and Structural Constraints:

A hierarchical filtering process is designed to progressively remove invalid and unstable points based on spatial proximity, depth continuity, and curvature consistency. Points affected by occlusion or geometric instability are filtered early, enhancing robustness in noisy and cluttered environments.

(3)

(Dynamically Filtered Local Map Construction for Pose Optimization:

An adaptive local mapping strategy is proposed that selects keyframes using spatial radius queries and dynamically adjusts voxel filter resolution based on system state. A temporal compensation mechanism ensures sufficient constraints during initialization. This method reduces frame redundancy and supports stable real-time optimization under varying motion conditions.

These components are integrated into a complete SLAM pipeline and evaluated on benchmark autonomous driving datasets. Experimental results demonstrate that the proposed method maintains competitive accuracy while significantly reducing computational load, making it suitable for real-time deployment on low-power autonomous platforms.

2. Lightweight and Robust Feature Extraction

This section presents an efficient and lightweight feature extraction algorithm tailored for LiDAR SLAM systems, aiming to enhance the robustness and computational efficiency of feature selection in complex driving environments. The proposed framework is implemented on top of the open-source LIO-SAM system. The method begins by projecting the raw 3D LiDAR point cloud into a structured 2D range image, significantly improving neighborhood access and reducing spatial redundancy. A novel curvature computation strategy based on 2D image neighborhoods is introduced, along with a multi-criteria feature screening mechanism that incorporates depth continuity, geometric stability, and neighborhood support. To avoid feature clustering and redundancy, a non-maximum suppression scheme is employed, ensuring spatially uniform and independent feature selection. This approach effectively suppresses false detections in occluded regions and enhances geometric consistency in sparse or distorted scans, providing high-quality, sparse, and reliable constraints for back-end pose optimization. The resulting system achieves reduced computational overhead while supporting energy-efficient and high-performance SLAM localization. Some details are in Figure 1.

2.1. Feature Point Extraction

Given an ordered point cloud $\mathcal{P}=\{p_1,p_2,\dots ,p_k\}$ that has been corrected for motion distortion, each point $p_k$ contains 3D coordinates $\left(x_k,y_k,z_k\right)$. First, the Euclidean distance of each point (i.e., the depth of each laser return in the point cloud) is computed and projected onto a two-dimensional matrix. Suppose the LiDAR sensor has $N_{scan}$ scan lines and a horizontal resolution corresponding to $N_{horiz}$ samples. If point $p_k$ corresponds to the $i$-th scan line and the $j$-th horizontal sample, then its range $r_k$ is assigned to the corresponding element of the range image as $R\left(i,j\right)$.

$$R(i,j)=r_k=\sqrt{x_k^2+y_k^2+z_k^2}$$

(1)

In this work, the raw 3D LiDAR points are first projected into a structured 2D range image, where each row corresponds to one laser scan line and each column corresponds to a horizontal sampling index. The value of each matrix element stores the depth (range) measurement of the corresponding point. This dimensionality reduction from 3D to 2D provides an efficient and ordered data structure for subsequent processing.

For invalid measurements, their values in the range image are set to a maximum constant $r_{\max }$ to facilitate subsequent processing. This 2D structure provides a foundation for efficient neighborhood access. To evaluate the smoothness of a point’s local region, this paper adopts the curvature computation method used in LOAM [13,14,15] (Lidar Odometry and Mapping). For any point $p_{i,j}$ in the range image, its curvature is defined as the squared difference between its range and the average range of its valid neighboring points in set ${\mathcal{S}}_{i,j}$. It is worth noting that in our formulation the curvature is computed using the squared depth difference, whereas the original LOAM defines curvature based on the squared difference of 3D Cartesian coordinates. This modification simplifies the computation and is more consistent with the 2D range image representation. The specific computation is given by:

$$c(p_{i,j})={\left({\displaystyle \sum _{p_{u,v}\in S_{i,j}}R}(u,v)-|{\mathcal{S}}_{i,j}|\cdot R(i,j)\right)}^2$$

(2)

Here, $R(i,j)$ is the range value of the center point $p_{i,j}$, and ${\mathcal{S}}_{i,j}$ represents the 2D valid neighborhood set of point $p_{i,j}$ in the range image. $\left|{\mathcal{S}}_{i,j}\right|$ denotes the number of valid neighboring points. The construction of the neighborhood set ${\mathcal{S}}_{i,j}$ is both dynamic and constrained. Whether a neighboring point $p_{u,v}$ can be selected as a valid neighbor of $p_{i,j}$ depends on the depth continuity between the two LiDAR points. A point $p_{u,v}$ is included in ${\mathcal{S}}_{i,j}$ if it satisfies the following condition:

$$|R(u,v)-R(i,j)|\le \alpha \cdot R(i,j)$$

(3)

where $\alpha$ is a proportional threshold factor (set to 0.1 in this paper). This condition ensures that only points lying on the same continuous surface are considered for curvature calculation, thereby significantly improving robustness against occlusion and edge discontinuities. To maintain statistical stability in curvature estimation, the valid neighboring points $p_{u,v}$ are selected as the 6 points to the left and right of $p_{i,j}$ along the scan line. Importantly, this depth continuity check (Equation (3)) also serves as the first layer of the proposed multi-stage outlier rejection strategy—one of the key innovations in this work. By enforcing strict local surface consistency at the neighborhood construction stage, the method eliminates unreliable measurements at an early stage, thereby enhancing the geometric purity of candidate features and reducing the risk of including occlusion-affected or structurally inconsistent points in subsequent processing.

To ensure the accuracy and stability of curvature statistics, points identified as geometrically unstable—primarily those near occlusions—must be excluded from feature selection. A point $p_{i,j}$ is considered an occluded or unstable point if it satisfies two conditions. First, the spatial proximity constraint requires that the point and its adjacent neighbor $p_{i,j+1}$ on the same scan line be physically continuous. This is verified by checking the index difference ${\Delta }_{\mathrm{idx}}$ in the original 1D point cloud. If this difference exceeds a threshold ${\delta }_{\mathrm{col}}$ (set to 10 in this work), the spatial continuity is violated, expressed as:

$$|I(p_{i,j+1})-I(p_{i,j})|<{\delta }_{\mathrm{col}}$$

(4)

Second, the depth discontinuity constraint ensures that even if the spatial proximity is satisfied, the two points must also have similar range values. If the absolute difference in depth exceeds a fixed threshold ${\delta }_{\mathrm{depth}}$ (set to 0.3), the point is marked as invalid. The condition is written as:

$$|R(i,j+1)-R(i,j)|>{\delta }_{\mathrm{depth}}$$

(5)

Points that meet both criteria, along with several neighboring points, are excluded from further feature extraction to avoid introducing unreliable geometric information. In addition, to guarantee the spatial uniformity of selected features, each scan line is divided into six subregions, and feature selection is performed independently within each region.

A point $p_{i,j}$ is classified as a corner point if it satisfies a set of strict geometric and statistical conditions. First, the point must exhibit a sufficiently high curvature, specifically $c(p_{i,j})>{\tau }_{\mathrm{edge}}$, where the curvature threshold ${\tau }_{\mathrm{edge}}$ is set to 0.1 in this work. Second, the point must be supported by a sufficient number of valid neighbors in its local region, requiring $|{\mathcal{S}}_{i,j}|\text{>}{N}_{\min \text{\_}\mathrm{corner}}$, with $N_{\min \text{\_}\mathrm{corner}}=10$ as defined. Third, the point must not be labeled as geometrically unstable or occluded in the earlier filtering stage. Finally, to further eliminate potential noise-induced outliers, a dynamic upper bound is imposed on the curvature value. Specifically, a point is rejected as a corner candidate if its curvature exceeds $c(p_{i,j})<\beta \cdot {(R(i,j))}^2\cdot \left|{\mathcal{S}}_{i,j}\right|$, where $\beta$ is a noise suppression coefficient set to 0.1. This composite set of criteria ensures that the extracted corner features are both geometrically distinctive and statistically reliable, even in the presence of sensor noise or environmental complexity. This adaptive curvature suppression mechanism serves as the second stage of the proposed multi-stage outlier rejection strategy. By introducing a dynamic upper bound conditioned on the local range and neighborhood density, the method effectively filters out noise-induced high-curvature points that would otherwise degrade the reliability of structural feature extraction. Together with the initial depth-based filtering, this layered design significantly enhances the robustness and selectivity of the feature screening process, which is central to the lightweight and energy-efficient SLAM framework proposed in this study.

A point $p_{i,j}$ is identified as a surface point if it meets a set of well-defined criteria. First, the point must exhibit low curvature, specifically $c(p_{i,j})<{\tau }_{surf}$, where the surface threshold ${\tau }_{surf}$ is set to 0.1 in this paper. In practice, a curvature value smaller than 0.1 is classified as a surface point, while a value greater than 1.0 is classified as a corner point. For intermediate values between 0.1 and 1.0, the points are uniformly treated as surface points. This thresholding strategy ensures a clear and robust separation of geometric features while avoiding ambiguous classifications. Second, to ensure the reliability of curvature estimation, the point must have adequate neighborhood support—meaning the number of neighboring points that pass the depth consistency check must be greater than six. Third, the point must not have been previously marked as geometrically unstable or occluded in the pre-filtering stage. Once these conditions are satisfied, the selected surface points—together with the previously extracted corner points—form two sparse and reliable sets of geometric features. These feature sets are further refined using a voxel grid filter, which reduces redundancy while preserving structural information, and are then passed to the back-end module for pose optimization. The Pseudo Code is provided in

Table 1. Pseudo Code.

Algorithm 1: Occlusion-Aware Curvature for Robust Feature Extraction

Input: Deskewed Point Cloud $\mathcal{P}$, with per-point range $r_k$ and column index.

1: Deskewed cloud $\mathcal{P}$ Project to 2D image $M_{range}$; 2: Initialize curvature array $c$ for all points in $\mathcal{P}$; 3: for each point $p_{i,j}\in \mathcal{P}$ do 4:  Initialize valid neighborhood; 5:  for each neighbor $p_{u,v}$ of $p_{i,j}$ in $M_{range}$ do 6:    if $|R(u,v)-R(i,j)|\le \alpha \cdot R(i,j)$; 7:      ${\mathcal{S}}_{i,j}\leftarrow {\mathcal{S}}_{i,j}\cup \left\{p_{u,v}\right\}$; 8:    else 9:      Marked as invalid point; 10:   end if 11: end for 12:   if $\left|{\mathcal{S}}_{i,j}\right|$ is sufficient for a stable calculation; 13:       $c\left(p_{i,j}\right)\leftarrow$ Calculate Curvature $\left({\mathcal{S}}_{i,j},p_{i,j}\right)$; 14:   else 15:      Mark as unreliable if neighborhood is ill-defined; 16:   end if 17: end for 18: Mark unstable occluded points using $M_{range}$; 19: Standard procedure using LOAM method to calculate curvatures $c\left(p_{i,j}\right)$; 20: Extract corner points and surface points based on curvature; 21: Voxel filtering;

Output: Corner Feature Set ${\mathcal{F}}_c$, Surface Feature Set ${\mathcal{F}}_s$.

.

2.2. Local Map Construction

In LiDAR-based SLAM systems, the quality of local map construction in the scan-to-map module directly influences the accuracy of pose estimation and the computational efficiency of the system. The local map is typically a spatially adjacent submap dynamically extracted from a global set of historical keyframes. Its construction involves transforming, merging, and downsampling the feature point clouds of selected keyframes [14,15]. This process is designed to ensure sufficient geometric constraints while minimizing the volume of data involved in optimization, thereby achieving a balanced trade-off between real-time performance and localization accuracy. Traditional strategies for constructing the local map generally fall into two categories, each with inherent drawbacks. Spatially driven methods select keyframes within a fixed-radius region (e.g., 30 m) around the current pose, offering rich geometric context and strong translational constraints, which are beneficial for large-scale localization. However, when the platform moves slowly or remains stationary, this strategy can lead to long periods without map updates, resulting in repeated matching against outdated observations and the accumulation of pose drift. In contrast, temporally driven strategies select the most recent $N$ keyframes based on time, ensuring that fresh observations are always incorporated and enabling rapid response to orientation changes. Nonetheless, during high-speed linear motion, these keyframes tend to be spatially concentrated, which may exclude distant but critical structural information, thereby weakening translational estimation. These limitations highlight the need for a more adaptive and context-aware local mapping strategy.

The first step in constructing the local map is to extract a subset of historical keyframes that are spatially relevant to the current pose. Let $K_p^3={\left\{p_i\right\}}_{i=1}^N$ denote the set of 3D position vectors of all $N$ stored keyframes. The position of the most recent keyframe is denoted as $p_{latest}$. To identify keyframes near the current location, the system employs a K-d tree structure to index $K_p^3$, enabling efficient spatial queries. A one-time radius search centered at $p_{latest}$ is performed to generate an initial candidate set of relevant keyframes, denoted as:

$$I_{cand}=\left\{i\right|\Vert p_i-p_{latest}\Vert \le R_{search}\}$$

(6)

where the search radius $R_{search}$ is empirically set to 50.0 m. This step ensures that only keyframes with spatial proximity to the current pose are selected for inclusion in the local map, thereby laying the foundation for a compact and context-aware local submap used in scan-to-map registration.

To prevent excessive computational overhead and redundant geometric information caused by the dense spatial clustering of selected keyframes, the system performs voxel grid downsampling on the point clouds of the candidate keyframes to regulate spatial density. The voxel size for downsampling, denoted as ${\rho }_k$, is determined dynamically based on the system state. Its baseline value ${\rho }_{base}$ is set to 0.5 m, and the adjustment strategy is as follows:

$${\rho }_k=\left\{\begin{array}{cc}0.25 \mathrm{m}& N<11\\ 0.5 \mathrm{m}& \mathrm{other}\end{array}\right.$$

(7)

Here, $N$ represents the number of keyframes currently stored. When $N<11$, the system is considered to be in an initialization phase. In this case, a finer resolution (i.e., smaller voxel size of 0.25 m) is used to preserve more keyframes in the local map, enhancing geometric constraint diversity and improving pose robustness during the early stages. This dynamic strategy ensures better stability and localization accuracy in scenarios with limited prior observations. To further reinforce system robustness in the initialization phase, an additional temporal-based keyframe supplement mechanism is introduced. Specifically, when $N<11$, a temporal window is used to include the most recent keyframes within 5.0 s. Let $I_{filtered}$ denote the index set of candidate keyframes selected through spatial search and downsampling; the final keyframe index set is defined as:

$$I_{final}=I_{filtered}\cup \left\{i\right|t_{\mathrm{curr}}-t_i|<5.0 \mathrm{s}\}$$

(8)

where $t_{\mathrm{curr}}$ is the timestamp of the current LiDAR scan and $t_i$ is the timestamp of historical keyframe iii. The 5.0 s temporal window helps ensure that temporally recent but spatially excluded keyframes are retained, which improves the richness and timeliness of the local map during initialization. In practice, the local map is maintained as a sliding window of keyframes, where the point clouds from selected frames are transformed into a common reference frame through 3D pose transformations. Following the approaches in [8,12,13,16], the transformed keyframe point clouds are then aggregated to construct the local map, which provides consistent geometric constraints for scan-to-map registration.

2.3. Scan-to-Map Registration and Pose Optimization

A Scan-to-Map registration framework is employed to perform real-time pose refinement for each incoming LiDAR scan. The core objective is to align the current LiDAR frame with a local submap constructed from historical keyframes in the global coordinate system. This alignment process is formulated as a nonlinear least-squares optimization problem, which aims to minimize the residuals between the current scan’s feature points and their corresponding planar and edge features in the local map. By minimizing both point-to-plane and point-to-edge residuals, the system obtains a precise estimation of the current pose in the global reference frame. To accelerate the correspondence search during iterative optimization, two separate K-d tree structures are built for edge and planar features, denoted as the corner map $M_c$ and surface map $M_s$, respectively. The optimization proceeds in an iterative manner until convergence is reached or a maximum number of iterations is met, which is set to 30 in this implementation.

To construct residual constraints for edge features, each extracted edge point $P_{cor}$ in the current LiDAR scan first searches for its five nearest neighbors in the local corner map $M_c$. These neighbors form a candidate set ${\mathbb{P}}_c={\left\{p_i\right\}}_{i=1}^5$, which is used to define a potential line structure $L$ via Principal Component Analysis. The mean of the five points is computed as the centroid $\overline{P}={\displaystyle \frac{1}{5}}{\displaystyle \sum _{i=1}^5{\mathrm{p}}_i}$, and a covariance matrix $H$ describing the spatial distribution of the set is constructed by [23]:

$$H={\displaystyle \sum _{i=1}^5(p_i}-\overline{p}){({\overline{p}}_i-\overline{p})}^T$$

(9)

Eigen decomposition is then performed on matrix $H$. The eigenvector $\widehat{u}$ corresponding to the largest eigenvalue ${\lambda }_1$ indicates the direction of greatest variance in the data and is taken as the direction of the candidate line. Thus, the fitted line $L$ is uniquely defined by the centroid $\overline{p}$ and the unit vector $\widehat{u}$. To ensure the reliability of this line fitting, the system evaluates the linearity of the neighbor set by comparing the dominant eigenvalue ${\lambda }_1$ with the second largest eigenvalue ${\lambda }_2$. The candidate line is deemed valid only if the condition ${\lambda }_1>k_c\cdot {\lambda }_2$ is satisfied, where $k_c$ is a curvature ratio threshold empirically set to 5.0. If the line passes this check, the point-to-line residual $d_c$ is computed as the perpendicular distance from the original point $p_{surf}$ to the line $L$, given by:

$$d_c=\Vert (p_{cor}-p)\times u\Vert$$

(10)

This residual is then incorporated into the pose optimization process. For each surface point $p_{surf}$ in the current LiDAR scan, the system searches its five nearest neighbors from the local surface point map $M_s$, forming a point set ${\mathbb{P}}_c={\left\{p_i\right\}}_{i=1}^5$. A least-squares method is then employed to fit a local 3D plane $\pi$ to this set. The general form of a plane equation is $ax+by+cz+d=0$, which can be rewritten as $ax+by+cz=-d$ [24]. Assuming $d\ne 0$, both sides can be divided by $-d$, and the normalized plane normal vector is defined as $v={[a/(-d),b/(-d),c/(-d)]}^T$. The equation becomes $p^{T}v=1$, where $p_i={[x_i,y_i,z_i]}^T$. Given the five points $p_i\in {\mathbb{P}}_s$, the system constructs an overdetermined linear system $Av=b$, where

$$A=\left[\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ ⋮& ⋮& ⋮\\ x_5& y_5& z_5\end{array}\right],b=\left[\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right]$$

(11)

This formulation allows for a closed-form least-squares solution to estimate the plane parameters from the neighborhood points, which will later be used to compute the point-to-plane residuals during pose optimization. To solve the overdetermined linear system $Av=b$, the system employs QR decomposition to obtain the least-squares solution $v_0$ that minimizes the residual norm $\Vert Av-b{\Vert }^2$. From this solution vector $v_0$, the normalized plane parameters can be recovered. Letting $\Vert v_o\Vert =ps$, the unit normal vector of the plane is defined as $\widehat{n}=v_o/ps$, and the plane’s offset from the origin is given by the constant term $d=-1/ps$. At this point, the plane $\pi$ is uniquely determined by its unit normal $\widehat{n}$ and distance $d$. To ensure the quality of the plane fitting, the system further requires that all points $p_i$ in the neighborhood used for fitting lie within a bounded distance from the estimated plane. Specifically, for all $i\in \{1,\dots ,5\}$, the point-to-plane residual must satisfy the constraint: $|{\widehat{n}}^T{p}_i+d|<{\delta }_s$, where ${\delta }_s$ is a predefined threshold for plane fitting accuracy, and is set to 0.15 in this implementation.

After obtaining the point-to-plane residuals $d_s$ for each current scan point with respect to the corresponding fitted planes $\pi$, the system calculates each residual as the perpendicular distance from the point $p_{surf}$ to the plane, using the equation [25]:

$$d_s={\widehat{n}}^T{p}_{\mathrm{surf}}+d=a\cdot x_{\mathrm{surf}}+b\cdot y_{\mathrm{surf}}+c\cdot z_{\mathrm{surf}}+d$$

(12)

where $\widehat{n}$ and $d$ are the unit normal vector and offset of the plane, respectively. Once all valid feature residuals and their corresponding Jacobian matrices are obtained, the system formulates a nonlinear least-squares optimization problem, which aims to find a pose increment $\Delta x\in {ℝ}^6$ that minimizes the sum of squared residuals: $\underset{\Delta x}{\min }{\displaystyle \sum _i\Vert d_i(}{x}_k\oplus \Delta x){\Vert }^2$. To solve this nonlinear optimization problem, the system employs the Gauss–Newton method. A first-order Taylor expansion is applied to linearize the residuals around the current pose estimate, yielding the standard Gauss–Newton equation: $(J^{T}J)\Delta x=-J^{T}r$, where $J$ is the Jacobian matrix and $r$ is the residual vector [16]. The system uses QR decomposition to solve this linear system for the pose increment $\Delta x$. The resulting pose update is then applied to the current pose estimate: $x_{k+1}=x_k\oplus \Delta x$. The optimization is deemed converged when both the rotation and translation components of $\Delta x$ fall below predefined thresholds (0.05 degrees and 0.05 m, respectively), at which point the iterative process terminates.

3. Results

The dataset used in this study is UrbanNav-HK-Data2020314, which was collected in a low-urbanization area in Kowloon, Hong Kong [26]. The environment features typical urban road scenarios and is well-suited for algorithm verification and benchmarking. As was shown in Figure 2, the data collection platform is a modified Honda Fit vehicle equipped with a range of sensors, including a Velodyne HDL-32E 3D LiDAR (360° HFOV, ±10° to ±30° VFOV, 80 m range, 10 Hz, Velodyne Lidar, Inc., San Jose, CA, USA), an Xsens MTi-10 IMU (100 Hz, AHRS, Velodyne Lidar, Inc., San Jose, CA, USA), a monocular camera with a resolution of 1920 × 1200 and a field of view of 79.4° × 96.8° at 10 Hz, and GNSS receivers such as the u-blox M8T (Velodyne Lidar, Inc., San Jose, CA, USA) and NovAtel SPAN-CPT (Velodyne Lidar, Inc., San Jose, CA, USA). The SPAN-CPT system integrates RTK GNSS and an inertial navigation system, achieving a positioning RMSE of 5 cm at 1 Hz. All sensors were mounted on the vehicle roof, with extrinsic calibrations and time synchronization completed. The data was collected on 14 March 2020, with a total size of 27.0 GB and a trajectory length of 1.21 km, covering diverse representative urban scenes. The official dataset also provides detailed sensor extrinsics, intrinsic parameters of the camera, and noise models of the IMU, serving as a reliable foundation for Scan-to-Map optimization and performance evaluation of SLAM algorithms.

This study adopts the UrbanNav-HK-Data20200314 sequence from the UrbanNav dataset for field testing [26]. The data was collected in a low-urbanization area of Kowloon, Hong Kong, featuring a diverse set of urban elements such as narrow streets, residential buildings, dense vegetation, and roadside parked vehicles. This environment poses considerable challenges and provides generality for the evaluation of SLAM and multi-sensor fusion localization algorithms. As illustrated in Figure 3, the dataset contains a closed-loop trajectory starting from Point A and passing through Points B, C, D, E, F, G, and H before returning to the starting position. The total path length is approximately 1.21 km. Eight key waypoints (A~H) are selected along the route, covering various typical scenes including intersections, curves, and straight lanes. These are used for subsequent analysis of keyframe positioning and trajectory accuracy. Figure 3b–i present real-world visual observations at each corresponding waypoint (A~H). The images reflect diverse conditions such as changes in road geometry, lighting variations, and the presence of dynamic objects like pedestrians and parked vehicles. Such complexity increases the difficulty of environmental perception and map construction, thereby offering a realistic and challenging benchmark for testing the robustness and adaptability of the Scan-to-Map method under practical urban navigation scenarios.

The experimental platform utilized in this study is a desktop computer equipped with an Intel Core i5-13400 processor, running the Ubuntu 20.04 operating system. The Robot Operating System (ROS1 Noetic) was selected as the software framework. To assess the resource efficiency of the proposed method, Energy-LIO, we conducted a quantitative comparison with the open-source LIO-SAM method using the same dataset, focusing specifically on memory consumption. The memory usage of both algorithms was recorded over a continuous runtime of approximately 800 s, as shown in Figure 4c. The horizontal axis represents the elapsed runtime of the vehicle, while the vertical axis indicates the memory occupied by the point cloud data. Throughout the entire experiment, Energy-LIO consistently maintained a lower memory footprint, generally staying below 4 MB with relatively small fluctuations. In contrast, LIO-SAM exhibited significantly higher memory demands, with a clear upward trend over time. During the early phase of the experiment (approximately the first 400 s), both methods demonstrated similar memory consumption. This is attributable to the necessity of accumulating a sufficient number of edge features (see Figure 4a) and planar features (see Figure 4b) during the initialization of the LiDAR odometry, which is essential for ensuring localization accuracy.

However, in the later phase of the experiment (after 400 s), the memory consumption of LIO-SAM increased rapidly, exceeding 5 MB and even peaking above 6 MB. In contrast, the growth of Energy-LIO’s memory usage remained more gradual and stable, indicating a more scalable and robust memory management mechanism. This memory efficiency can be largely attributed to the denoising and filtering strategies introduced in our method, which significantly reduce the backend memory load and contribute to a lightweight system architecture. The lightweight design of Energy-LIO translates directly into energy-saving benefits. By leveraging streamlined data structures and more efficient data processing pipelines, the method alleviates CPU burden associated with memory allocation and data traversal. This advantage is particularly crucial in real-world scenarios such as urban driving or highway navigation, where reducing overall computational overhead and instantaneous power consumption can extend the operational duration of autonomous vehicles and enhance the stability of long-term navigation tasks.

To further demonstrate the lightweight advantage of our proposed method, a comparative analysis of the resulting point cloud maps is conducted between Energy-LIO and LIO-SAM. This includes both an overview and close-up examinations of structural details (see Figure 5a,b). From a global perspective, the point cloud map generated by Energy-LIO (Figure 5a) exhibits superior clarity and sharpness. Structural features such as building facades, wall edges, and contours are rendered more distinctly and precisely, reflecting a higher fidelity in environmental representation. In contrast, the map produced by LIO-SAM (Figure 5b) appears less refined, with structural lines being blurrier and more dispersed. Artifacts such as “ghosting” or “dragging” effects are also observable in certain areas. This high-quality mapping performance is primarily attributed to the denoising and filtering strategies integrated into Energy-LIO. As illustrated in Figure 4a,b, our method applies multiple filtering stages during feature extraction, effectively eliminating outliers. In the backend processing stage, the algorithm emphasizes the retention of high-value edge features with strong geometric constraints, while significantly reducing the number of planar points that offer limited contribution to localization accuracy but demand substantial memory and computation.

The result is a set of rich and structured corner features that provide stronger and more deterministic constraints for pose estimation, thereby enhancing registration accuracy between successive LiDAR scans. This leads to more precise alignment and a higher-fidelity map. As shown in Figure 4b, the number of planar points processed by Energy-LIO remains significantly lower than that of LIO-SAM throughout the entire runtime. Importantly, this reduction is not a simple downsampling of the dataset; instead, it is achieved through intelligent identification and removal of unreliable planar points—often caused by dynamic objects or sensor noise.

As illustrated in Figure 4d—where the horizontal axis represents the runtime and the vertical axis indicates the number of keyframes maintained in the local map—Energy-LIO consistently sustains a significantly smaller keyframe set compared to LIO-SAM throughout the entire experiment. While LIO-SAM maintains a relatively high number of keyframes, typically ranging from 80 to 140, Energy-LIO operates within a much smaller range of 20 to 80 keyframes. On average, this represents a reduction of approximately 40% to 50% in keyframe set size. This notable decrease reflects the adoption of a more rigorous and efficient keyframe selection strategy in Energy-LIO. By maintaining a smaller yet more representative keyframe set, the system substantially reduces the computational burden associated with backend modules such as pose graph optimization and loop closure detection. Consequently, the overall computational cost and energy consumption are significantly lowered, highlighting the energy-efficient nature of the proposed method.

This strategy of “fewer but higher-quality” planar features ensures cleaner data input to the optimization backend, improving odometry accuracy while simultaneously reducing unnecessary computational overhead. In essence, the energy-efficient principle is embedded in the algorithm’s core by reducing the processing of ineffective data. Although both Energy-LIO and LIO-SAM are capable of reconstructing the overall topological structure of the environment (see Figure 5a,b), Energy-LIO demonstrates superior geometric consistency (see Figure 5e area C and D, Figure 5f area C and D). For instance, in areas featuring overpasses or parked vehicles, Energy-LIO generates sharper and more compact point cloud structures (see Figure 5c area A and B). In contrast, LIO-SAM suffers from coarser lines or duplicated boundaries, indicating the presence of accumulated pose drift over long durations (see Figure 5d area A and B). These misalignments result in slightly displaced representations of the same physical structures, degrading the geometric consistency of the reconstructed map.

The ability of Energy-LIO to achieve stable tracking with significantly fewer keyframes—as demonstrated in the aforementioned map quality analysis—stems from its intelligent keyframe selection strategy. Unlike traditional methods that rely on fixed spatial or temporal thresholds, Energy-LIO evaluates multiple criteria, including pose variation, information gain, and feature matching quality. A new frame is designated as a keyframe only if it contributes sufficient novel information to the system. This selective approach ensures that each retained keyframe carries high informational value, effectively preventing the unnecessary growth of the pose graph and avoiding redundant computations. By minimizing keyframe redundancy without compromising estimation accuracy, Energy-LIO achieves a more compact and computationally efficient backend, aligning with its core objective of energy-aware system design.

This study further employs the KITTI dataset [27,28] to conduct a more comprehensive quantitative evaluation of the proposed method in terms of odometry accuracy. The KITTI dataset was collected using a Velodyne HDL-64E 3D LiDAR scanner operating at 10 Hz, with each frame capturing approximately 100,000 three-dimensional points. These point clouds, which store the coordinates (x, y, z) along with the reflectance intensity (r), serve as the primary input data for LiDAR SLAM algorithms. Meanwhile, to provide the “ground truth” for evaluation, the vehicle was also equipped with an OXTS RT3003 high-precision GPS/IMU integrated navigation system. By combining GPS measurements with an inertial measurement unit and applying differential positioning techniques (RTK) in post-processing, this system can generate centimeter-level ground-truth vehicle poses (position and orientation). The test sequences include sequences 01, 02, 04, 05, 06, and 07, which cover different driving scenarios such as repeated-path driving in road environments (sequences 02 and 05), short straight-path driving (sequences 01 and 04), and complex-path driving (sequence 06). The experimental equipment setup is illustrated in Figure 6.

We evaluated the two methods in terms of the standard deviation (STD) and root mean square error (RMSE) of the Absolute Pose Error (APE). The results are summarized in

Table 2. Quantitative comparison between LIO-SAM and Energy-LIO on different KITTI sequences.

Seq	01			02			04
	STD	MEAN	RMSE	STD	MEAN	RMSE	STD	MEAN	RMSE
LIO-SAM	9.580841	20.16686	22.327	3.951276	9.933372	10.69039	0.135932	0.274723	0.306513
Energy-LIO	8.90709	18.90915	20.90197	3.218587	8.563033	9.147942	0.112385	0.302099	0.322326
Seq	05			06			07
	STD	MEAN	RMSE	STD	MEAN	RMSE	STD	MEAN	RMSE
LIO-SAM	1.012103	2.087631	2.320033	5.197376	13.39987	14.37252	0.448581	0.796957	0.91453
Energy-LIO	0.79129	1.789625	1.956757	5.183636	13.39703	14.3649	0.404193	0.750334	0.852275

, and the corresponding trajectory comparisons are illustrated in Figure 7. Table 1 presents the APE results across six test sequences, including the metrics RMSE, MEAN, and STD. Overall, Energy-LIO achieved consistent improvements over LIO-SAM in most sequences. Specifically, the average RMSE of Energy-LIO was reduced by approximately 6.4%, and the average STD decreased by about 12.5% compared with LIO-SAM. The most significant improvements were observed in Seq02 and Seq05, where the RMSE decreased by about 14.4% and 15.7%, respectively. These results indicate that excluding noisy points during the feature extraction stage has a substantial impact on localization accuracy, and importantly, this improvement was achieved while using fewer corner and surface points during scan-to-map matching (as demonstrated in previous experiments). However, in Seq04, the RMSE showed a slight increase of about 5.2%, while the STD decreased significantly. This can be attributed to the fact that Seq04 involves short straight-line driving (see Figure 7c), where the travel distance is limited. In such simple and short trajectories, LIO-SAM exhibited an advantage. Nevertheless, for longer and more complex driving sequences, Energy-LIO consistently demonstrated superior performance.

4. Conclusions

This study presents Energy-LIO, a lightweight and energy-conscious LiDAR SLAM framework tailored for autonomous driving in complex urban environments. By integrating range image-based feature extraction, a multi-stage outlier filtering strategy, and an adaptive keyframe selection mechanism, the proposed system effectively balances localization accuracy, computational efficiency, and memory usage. Experimental results on the UrbanNav dataset demonstrate that Energy-LIO achieves high-fidelity mapping with significantly fewer feature points and keyframes compared to LIO-SAM, while maintaining or surpassing its localization performance. Notably, the system’s memory footprint remains below 4 MB throughout long-duration operation, and the average reduction in keyframe count reaches 40~50%, reflecting substantial computational savings. The design of Energy-LIO embeds energy efficiency at its core by minimizing data redundancy, selectively processing high-value information, and avoiding unnecessary backend optimization. These characteristics make it particularly well-suited for deployment on resource-constrained platforms, such as embedded systems or autonomous vehicles with limited onboard computing capacity. Overall, Energy-LIO contributes a practical and scalable solution to real-time, power-aware SLAM and offers valuable insights into sustainable algorithm design for intelligent transportation applications.