Dual Adaptive Neural Network for Solving Free-Flow Coupled Porous Media Models Under Unique Continuation Problem
Abstract
1. Introduction
- Multiphysical coupled models contain multiple quantities to be solved. The fixed activation function may prevent the neural network from accurately capturing changes in physical quantities. It may even lead to issues such as vanishing gradients.
- In the UC problem, observational data in the boundary domain is usually unknown. This issue causes the balanced weighted loss function to develop bias during training, ultimately preventing it from fully training to optimality.
- An adaptive Swish activation function is introduced to dynamically modulate its nonlinearity, thereby enhancing the capability of neural networks to represent physical information.
- An adaptively weighted loss function is proposed for the UC problem, which dynamically balances observational data and physical constraints to improve training convergence and solution accuracy.
2. Unique Continuation Problem
2.1. The Steady Dual-Porosity–Navier–Stokes Model
2.2. The Steady Triple-Porosity–Navier–Stokes Model
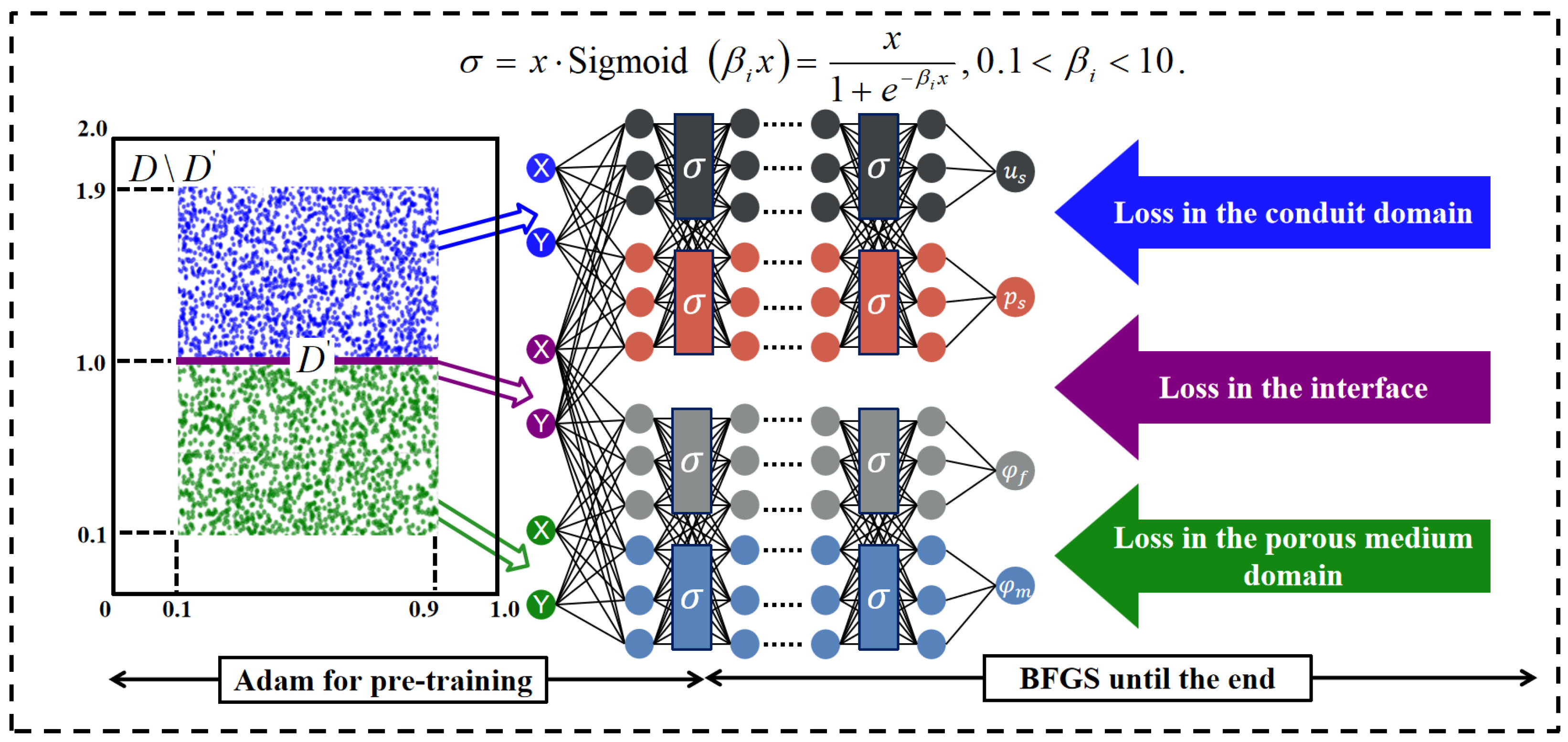
3. Dual Adaptive Neural Network Algorithm
3.1. Adaptively Weighted Loss Function
3.2. Adaptive Activation Function
- If is too small, , causing the activation function to behave nearly linearly and lose its nonlinear characteristics.
- If is too small, approaches a step function, leading to gradient explosion or training instability during the training process.
4. Theoretical Analysis
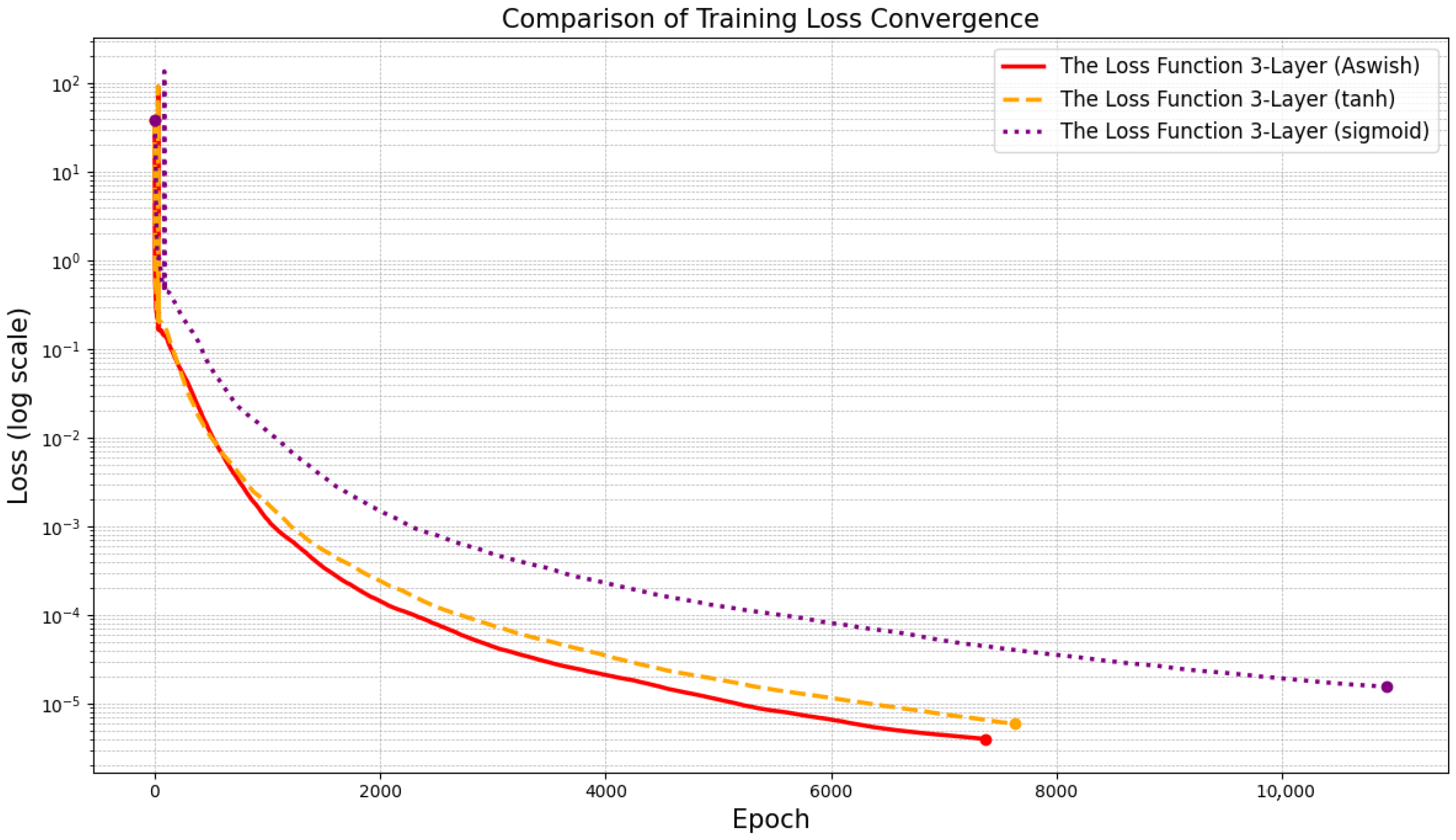
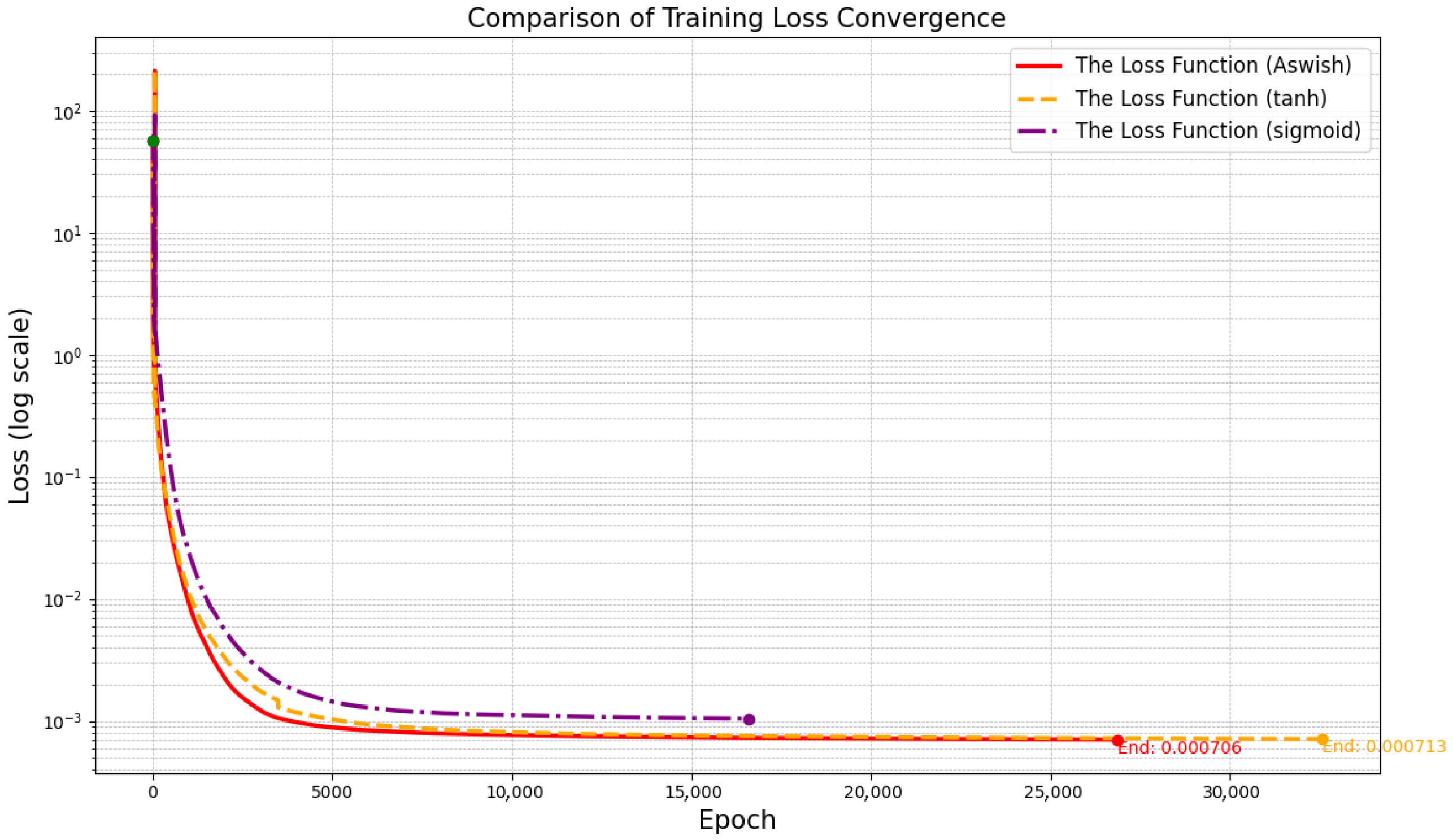
- The DANN algorithm uses an adaptively weighted loss function. This makes training adequate, meaning that the training error is small enough. We show the value of loss and plot the adaptively weighted value in the loss in the experiments in Section 5.
- The DANN algorithm uses an adaptive activation function. It excellently performs adaptive computation for different physical quantities. In Section 5, the results of the adaptive Swish activation function are preferred to Sigmoid and Tanh.
- The error estimation in Theorem 3 relies on the conditional stability for the UC problem. Thus, the generalization error achieves an efficient approximation through DANN and the conditional stability of the PDEs.
5. Numerical Experiment
5.1. Dual-Porosity–Navier–Stokes Model with Analytical Solution
5.2. Cavity Flow Test of Dual-Porosity–Navier–Stokes Model
5.3. Triple-Porosity–Navier–Stokes Model with Analytical Solution
5.4. Triple-Porosity–Navier–Stokes Model in 3D
6. Conclusions
- Explore the integration of combined activation functions (e.g., Aswish, Tanh and Sigmoid) within an adaptive framework to further enhance the performance and flexibility of the network.
- Investigate unique continuation under time-dependent problems and propose neural network or machine learning algorithms that outperform the traditional Kalman filter method.
- Explore whether deep operator networks (DeepONets) possess the capability to solve the UC problem and compare their performance with that of physics-informed neural networks (PINNs).
- Discuss the application of the UC problem in practical real-world scenarios. We will actively explore how to incorporate real observational data into our framework to further validate the practicality of the proposed method beyond analytical solution benchmarks.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, L.; Li, J. A decoupled stabilized finite element method for the dual–porosity–Navier–Stokes fluid flow model arising in shale oil. Numer. Methods Partial Differ. Equ. 2021, 37, 2357–2374. [Google Scholar] [CrossRef]
- Kashani, E.; Mohebbi, A.; Monfared, A.E.F.; de Vries, E.T.; Raoof, A. Lattice Boltzmann simulation of dissolution patterns in porous media: Single porosity versus dual porosity media. Adv. Water Resour. 2024, 188, 104712. [Google Scholar] [CrossRef]
- Yadav, M.P.; Agarwal, R.; Purohit, S.D.; Kumar, D.; Suthar, D.L. Groundwater flow in karstic aquifer: Analytic solution of dual–porosity fractional model to simulate groundwater flow. Appl. Math. Sci. Eng. 2022, 30, 598–608. [Google Scholar] [CrossRef]
- Li, J.; Gao, Z.Y.; Cao, L.L.; Chen, Z.X. A local parallel fully mixed finite element method for superposed fluid and porous layers. J. Comput. Appl. Math. 2026, 472, 116798. [Google Scholar] [CrossRef]
- Hou, J.Y.; Hu, D.; Li, X.J.; He, X.M. Modeling and a Domain Decomposition Method with Finite Element Discretization for Coupled Dual-Porosity Flow and Navier–Stokes Flow. J. Sci. Comput. 2023, 95, 67. [Google Scholar] [CrossRef]
- Hou, J.Y.; Qiu, M.L.; He, X.M.; Guo, C.H.; Wei, M.Z.; Bai, B.J. A dual–porosity–Stokes model and finite element method for coupling dual–porosity flow and free flow. SIAM J. Sci. Comput. 2016, 38, B710–B739. [Google Scholar] [CrossRef]
- Cao, L.L.; He, Y.N.; Li, J. A parallel robin–robin domain decomposition method based on modified characteristic fems for the time-dependent dual–porosity–Navier–Stokes model with the Beavers–Joseph interface condition. J. Sci. Comput. 2022, 90, 16. [Google Scholar] [CrossRef]
- Li, R.; Zhang, C.S.; Chen, Z.X. A Stokes–dual–porosity–poroelasticity model and discontinuous galerkin method for the coupled free flow and dual porosity poroelastic medium problem. J. Sci. Comput. 2025, 102, 41. [Google Scholar] [CrossRef]
- Nasu, N.J.; Al Mahbub, M.A.; Zheng, H.B. A new coupled multiphysics model and partitioned time-stepping method for the triple-porosity-Stokes fluid flow model. J. Comput. Phys. 2022, 466, 111397. [Google Scholar] [CrossRef]
- Mishra, S.; Molinaro, R. Estimates on the generalization error of physics-informed neural networks for approximating PDEs. IMA J. Numer. Anal. 2023, 43, 1–43. [Google Scholar] [CrossRef]
- Hou, Q.Z.; Li, Y.X.; Singh, V.P.; Sun, Z.W. Physics-informed neural network for diffusive wave model. J. Appl. Math. Comput. 2024, 637, 131261. [Google Scholar] [CrossRef]
- Dieva, N.; Aminev, D.; Kravchenko, M.; Smirnov, N. Overview of the Application of Physically Informed Neural Networks to the Problems of Nonlinear Fluid Flow in Porous Media. Computation 2024, 12, 69. [Google Scholar] [CrossRef]
- Frey, R.; Köck, V. Deep Neural Network Algorithms for Parabolic PIDEs and Applications in Insurance and Finance. Computation 2022, 10, 201. [Google Scholar] [CrossRef]
- Seabe, P.L.; Moutsinga, C.R.B.; Pindza, E. Forecasting Cryptocurrency Prices Using LSTM, GRU, and Bi-Directional LSTM: A Deep Learning Approach. Fractal Fract. 2023, 7, 203. [Google Scholar] [CrossRef]
- Yuan, S.H.; Liu, Y.Q.; Yan, L.M.; Zhang, R.F.; Wu, S.J. Neural Networks-Based Analytical Solver for Exact Solutions of Fractional Partial Differential Equations. Fractal Fract. 2025, 9, 541. [Google Scholar] [CrossRef]
- Pang, G.F.; Lu, L.; Karniadakis, G.E. fPINNs: Fractional physics-informed neural networks. SIAM J. Sci. Comput. 2019, 41, A2603–A2626. [Google Scholar] [CrossRef]
- Dockhorn, T. A discussion on solving partial differential equations using neural networks. arXiv 2019, arXiv:1904.07200. [Google Scholar] [CrossRef]
- Chen, N. Stochastic Methods for Modeling and Predicting Complex Dynamical Systems: Uncertainty Quantification, State Estimation, and Reduced-Order Models; Springer Nature: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Mishra, S.; Molinaro, R. Estimates on the generalization error of physics-informed neural networks for approximating a class of inverse problems for PDEs. IMA J. Numer. Anal. 2022, 42, 981–1022. [Google Scholar] [CrossRef]
- Mai, J.A.; Li, Y.; Long, L.; Huang, Y.; Zhang, H.L.; You, Y.C. Two-dimensional temperature field inversion of turbine blade based on physics-informed neural networks. Phys. Fluids. 2024, 36, 037114. [Google Scholar] [CrossRef]
- Bellassoued, M.; Imanuvilov, O.; Yamamoto, M. Carleman estimate for the Navier–Stokes equations and an application to a lateral Cauchy problem. Inverse Probl. 2016, 32, 025001. [Google Scholar] [CrossRef]
- Chaves-Silva, F.W.; Zhang, X.; Zuazua, E. Controllability of evolution equations with memory. SIAM J. Control Optim. 2017, 55, 2437–2459. [Google Scholar] [CrossRef]
- Bourgeois, L. A mixed formulation of quasi–reversibility to solve the Cauchy problem for Laplace’s equation. Inverse Probl. 2005, 21, 1087. [Google Scholar] [CrossRef]
- Badra, M.; Caubet, F.; Dardé, J. Stability estimates for Navier–Stokes equations and application to inverse problems. arXiv 2016, arXiv:1609.03819. [Google Scholar] [CrossRef]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Sci. Comput. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Wang, S.F.; Teng, Y.J.; Perdikaris, P. Understanding and mitigating gradient flow pathologies in physics-informed neural networks. SIAM J. Sci. Comput. 2021, 43, A3055–A3081. [Google Scholar] [CrossRef]
- McClenny, L.D.; Braga-Neto, U.M. Self-adaptive physics-informed neural networks. J. Comput. Phys. 2023, 474, 111722. [Google Scholar] [CrossRef]
- Aghaee, A.; Khan, M.O. Performance of Fourier-based activation function in physics-informed neural networks for patient-specific cardiovascular flows. Comput. Meth. Prog. Biomed. 2024, 247, 108081. [Google Scholar] [CrossRef]
- Wang, H.H.; Lu, L.; Song, S.J.; Gao, H. Learning specialized activation functions for physics-informed neural networks. arXiv 2023, arXiv:2308.04073. [Google Scholar]
- Jagtap, A.D.; Kawaguchi, K.; Karniadakis, G.E. Adaptive activation functions accelerate convergence in deep and physics-informed neural networks. J. Comput. Phys. 2020, 404, 109136. [Google Scholar] [CrossRef]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Swish: A self-gated activation function. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Sunkari, S.; Sangam, A.; Raman, R.; Rajalakshmi, R. A refined ResNet18 architecture with Swish activation function for Diabetic Retinopathy classification. Biomed. Signal Proces. 2024, 88, 105630. [Google Scholar] [CrossRef]
- Jais, I.K.M.; Ismail, A.R. Adam optimization algorithm for wide and deep neural network. Knowledge Engineering and Data Science. Knowl. Eng. Data Sci. 2019, 2, 10. [Google Scholar] [CrossRef]
- Zhou, W.J. A modified BFGS type quasi-Newton method with line search for symmetric nonlinear equations problems. J. Comput. Appl. Math. 2020, 367, 112454. [Google Scholar] [CrossRef]
- Stoer, J.; Bulirsch, R. introduction to numerical analysis springer-verlag. Texts Appl. Math. 2002, 12, 30. [Google Scholar]
- Cao, L.L.; Li, J.; Chen, Z.X.; Du, G.Z. A local parallel finite element method for superhydrophobic proppants in a hydraulic fracturing system based on a 2D/3D transient triple–porosity Navier–Stokes model. arXiv 2023, arXiv:2311.05170. [Google Scholar]
- Bathe, K.-J. The Inf–Sup condition and its evaluation for mixed finite element methods. Comput. Struct. 2001, 79, 243–252. [Google Scholar] [CrossRef]
- Kashefi, A.; Mukerji, T. Prediction of fluid flow in porous media by sparse observations and physics-informed PointNet. Neural Netw. 2023, 167, 80–91. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, S.X.; Yue, J. MC-CDNNs: The Monte Carlo-coupled deep neural networks approach for stochastic dual-porosity-Stokes flow coupled model. Comput. Math. Appl. 2025, 181, 1–20. [Google Scholar] [CrossRef]
- Yue, J.; Li, J.; Zhang, W.; Chen, Z.X. The coupled deep neural networks for coupling of the Stokes and Darcy–Forchheimer problems. Chin. Phys. B 2023, 32, 010201. [Google Scholar] [CrossRef]
- Bo, A.N.; Mellibovsky, F.; Bergadà, J.M.; Sang, W.M. Towards a better understanding of wall-driven square cavity flows using the lattice Boltzmann method. Appl. Math. Model. 2020, 82, 469–486. [Google Scholar] [CrossRef]




















| Max Iterations | ||||||
|---|---|---|---|---|---|---|
| 800 | 800 | 4000 | 32 | 40,000 |
| Non-Adaptive | Adaptive Swish | Adaptively Weighted | DANN | |
|---|---|---|---|---|
| Loss | ||||
| DANN (Adaptive Swish) | Tanh | Sigmoid | ||||
|---|---|---|---|---|---|---|
| Error | Error | Error | Error | Error | Error | |
| DANN (Adaptive Swish) | Tanh | Sigmoid | ||||
|---|---|---|---|---|---|---|
| Error | Error | Error | Error | Error | Error | |
| DANN (Adaptive Swish) | Tanh | Sigmoid | ||||
|---|---|---|---|---|---|---|
| Error | Error | Error | Error | Error | Error | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Wu, J. Dual Adaptive Neural Network for Solving Free-Flow Coupled Porous Media Models Under Unique Continuation Problem. Computation 2025, 13, 228. https://doi.org/10.3390/computation13100228
Liu K, Wu J. Dual Adaptive Neural Network for Solving Free-Flow Coupled Porous Media Models Under Unique Continuation Problem. Computation. 2025; 13(10):228. https://doi.org/10.3390/computation13100228
Chicago/Turabian StyleLiu, Kunhao, and Jibing Wu. 2025. "Dual Adaptive Neural Network for Solving Free-Flow Coupled Porous Media Models Under Unique Continuation Problem" Computation 13, no. 10: 228. https://doi.org/10.3390/computation13100228
APA StyleLiu, K., & Wu, J. (2025). Dual Adaptive Neural Network for Solving Free-Flow Coupled Porous Media Models Under Unique Continuation Problem. Computation, 13(10), 228. https://doi.org/10.3390/computation13100228






