MATLAB Application for Determination of 12 Combustion Products, Adiabatic Temperature and Laminar Burning Velocity: Development, Coding and Explanation
Abstract
1. Introduction
2. Materials and Methods
3. Development of the MATLAB Application
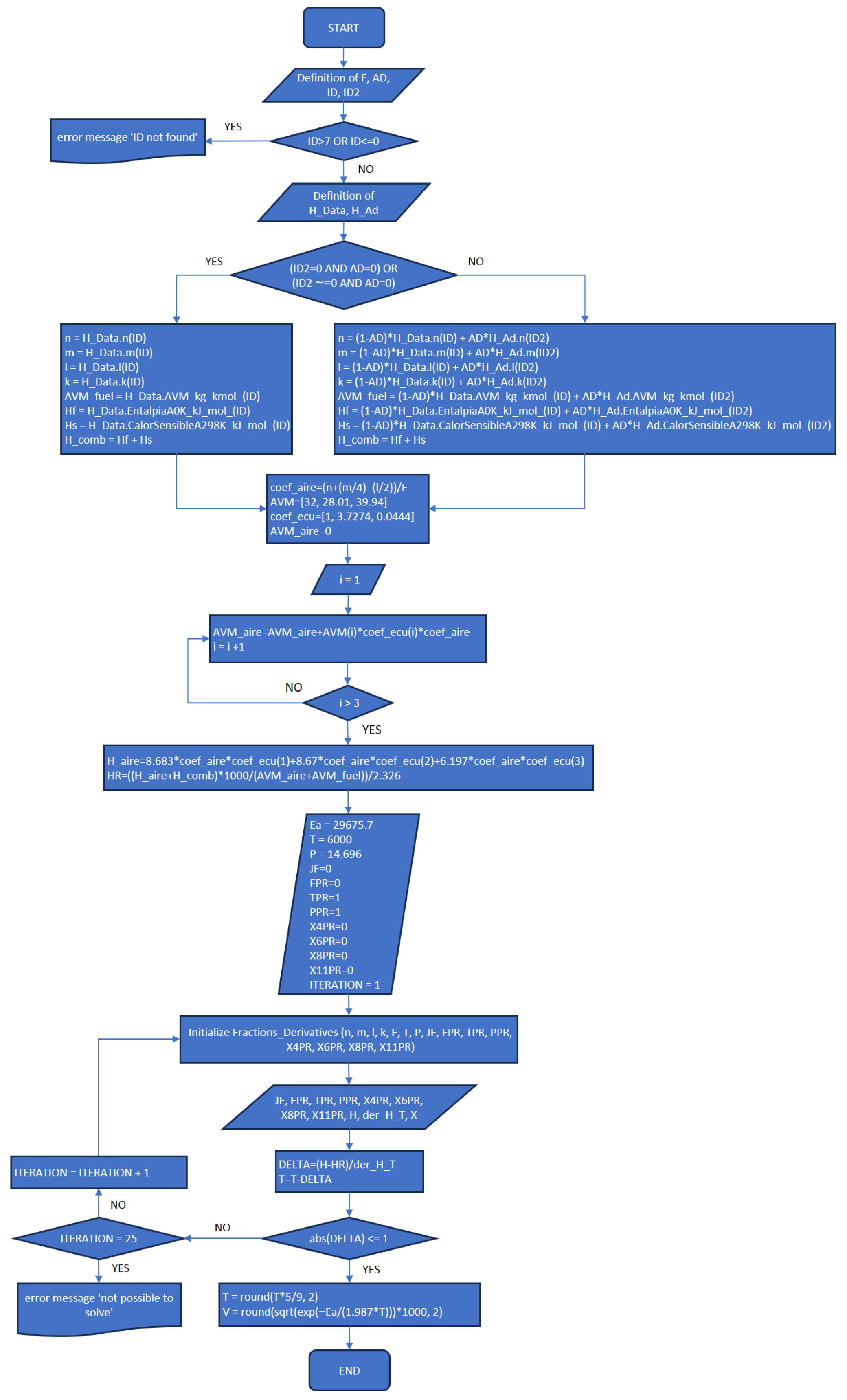
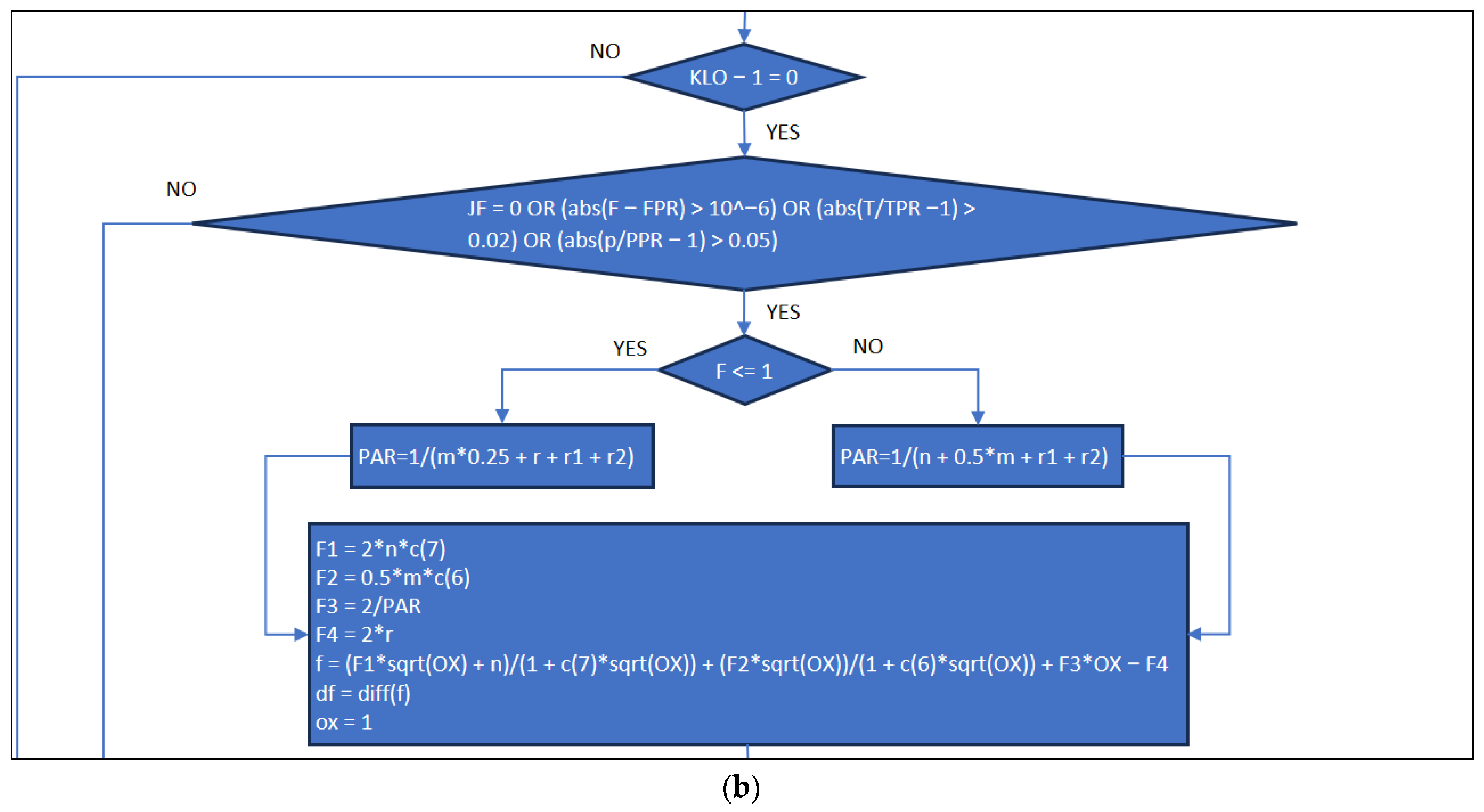
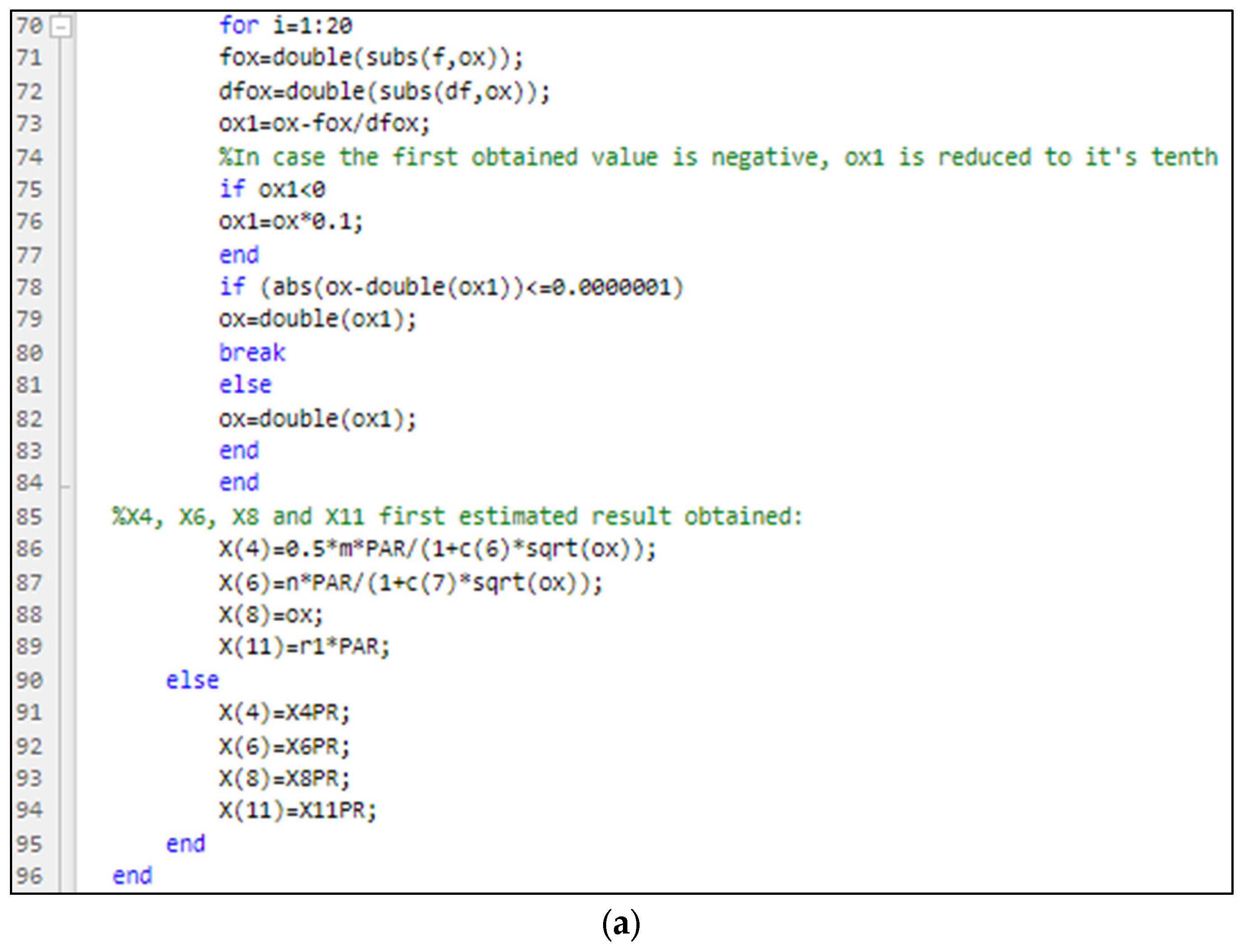
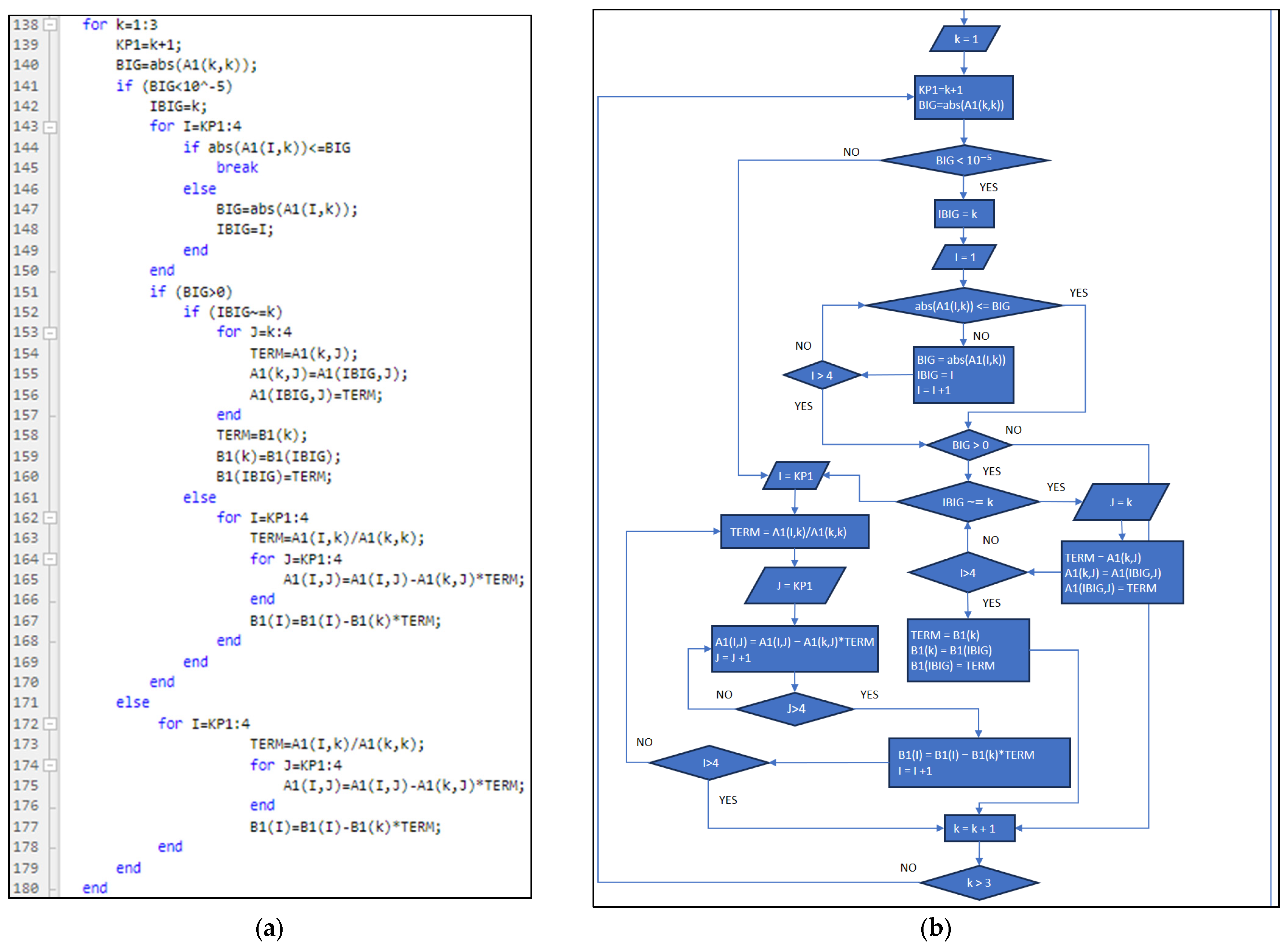
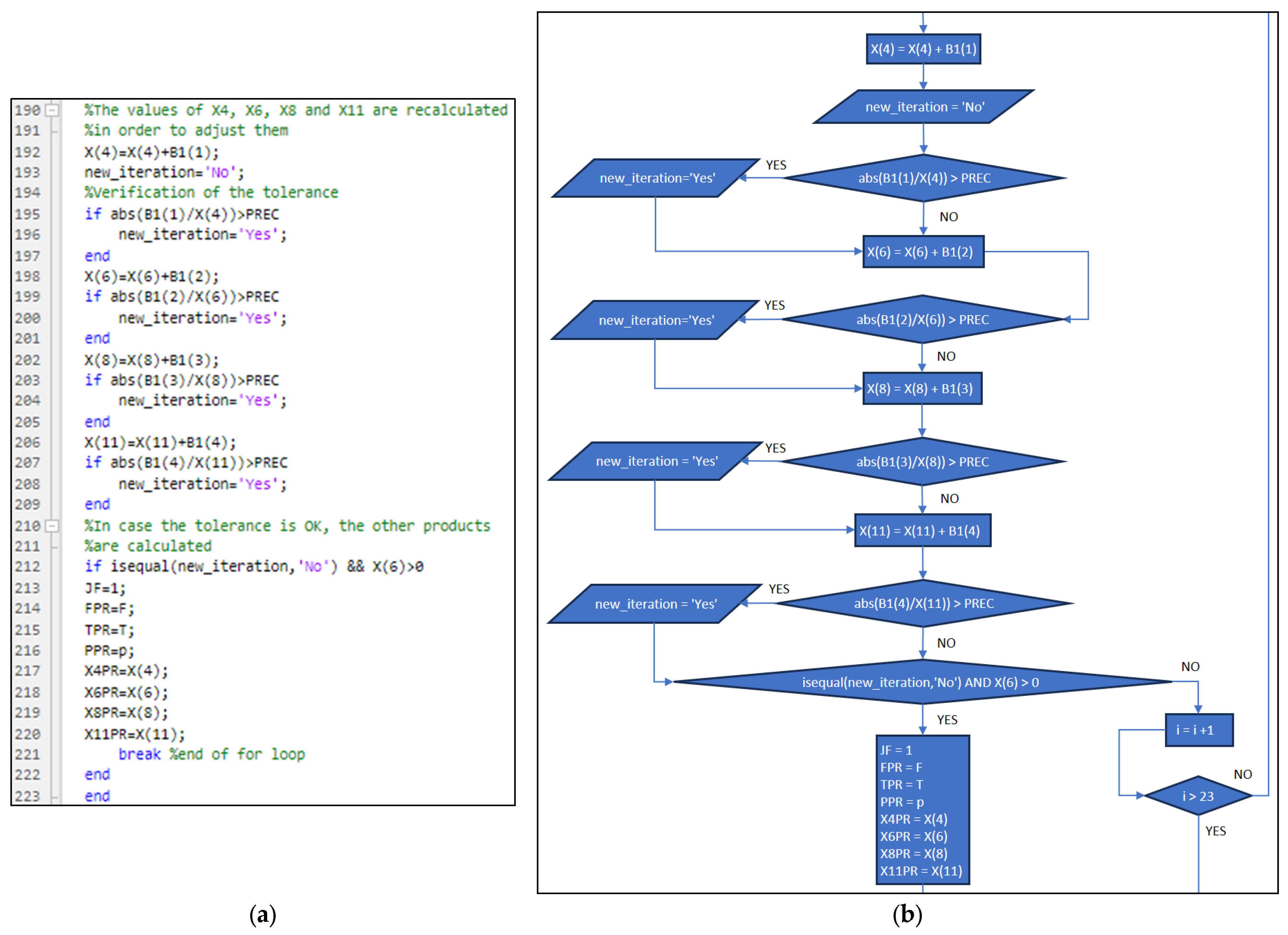
3.1. Part One: Develop of the “New_code” File
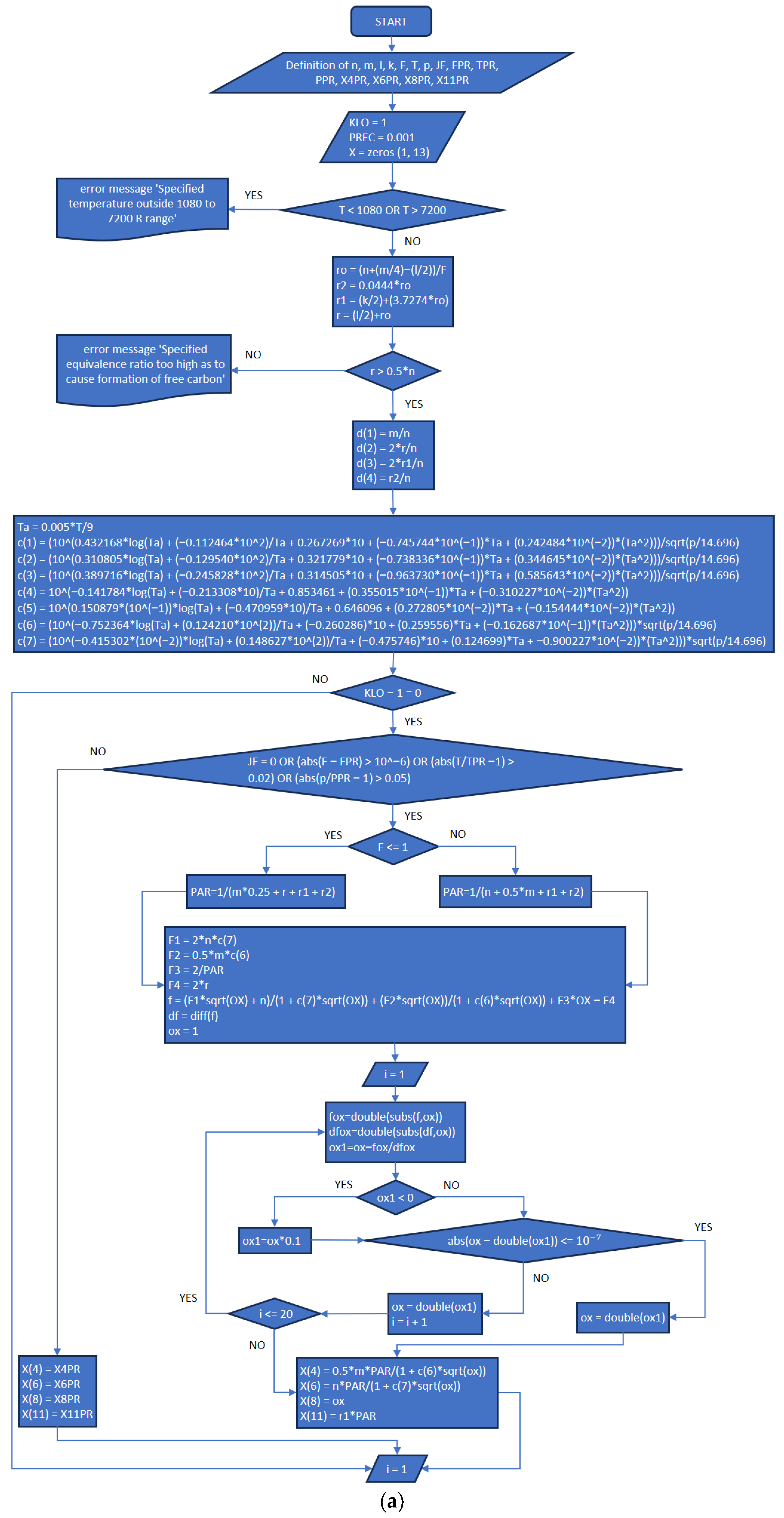
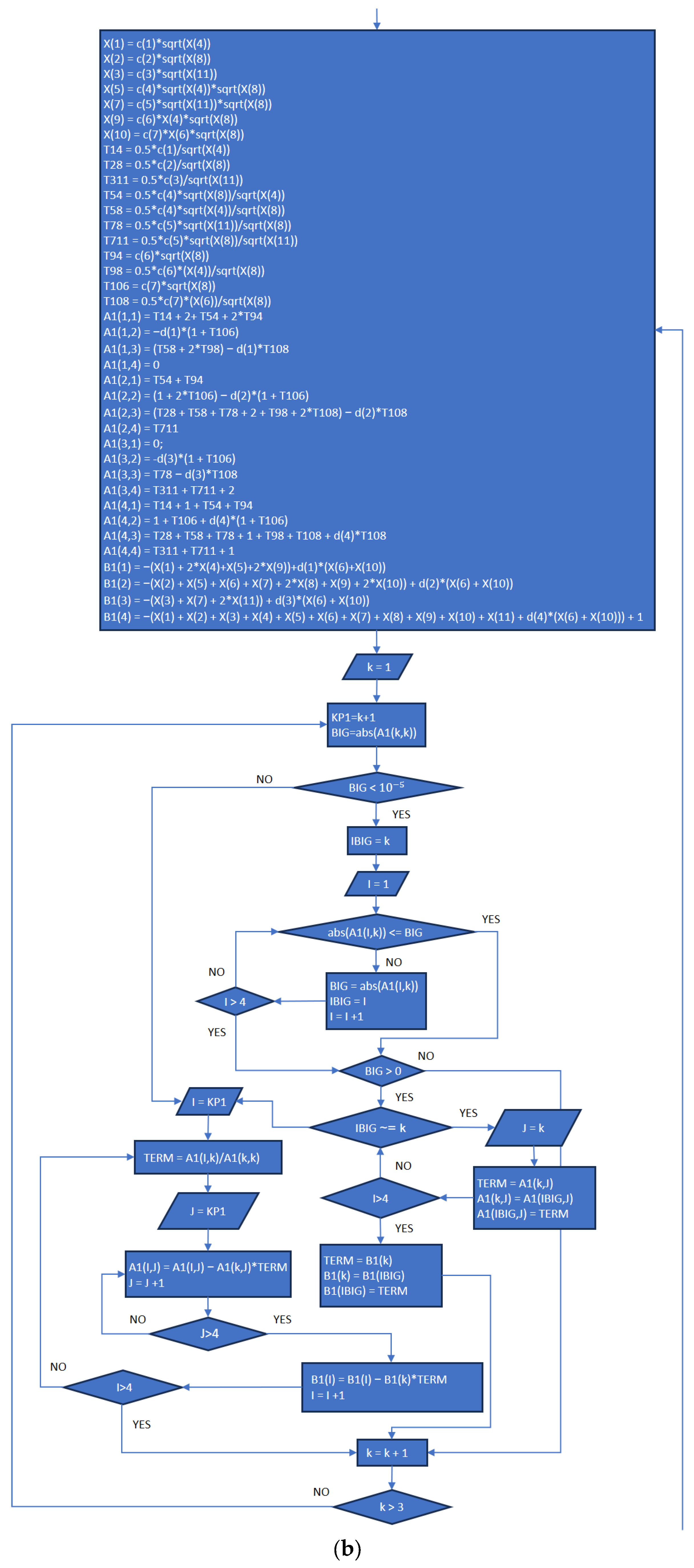
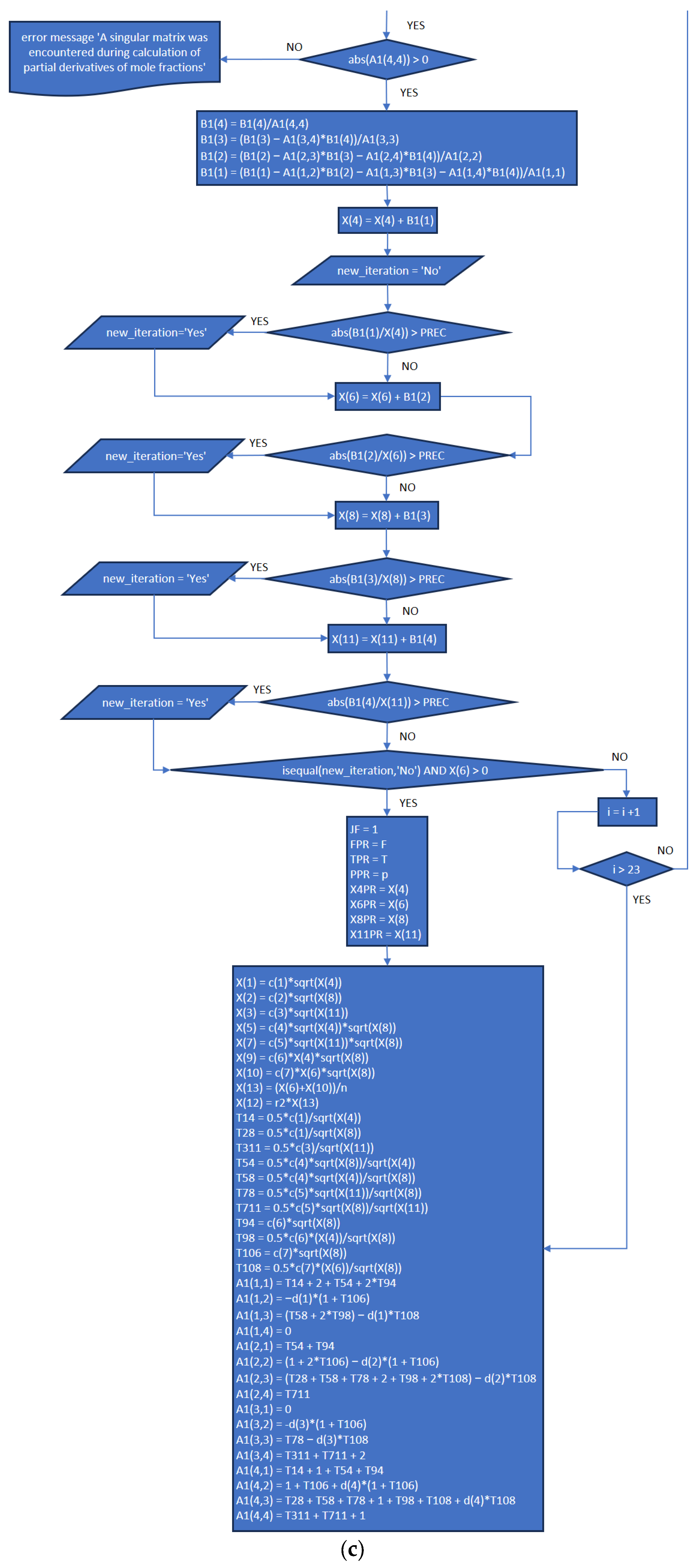
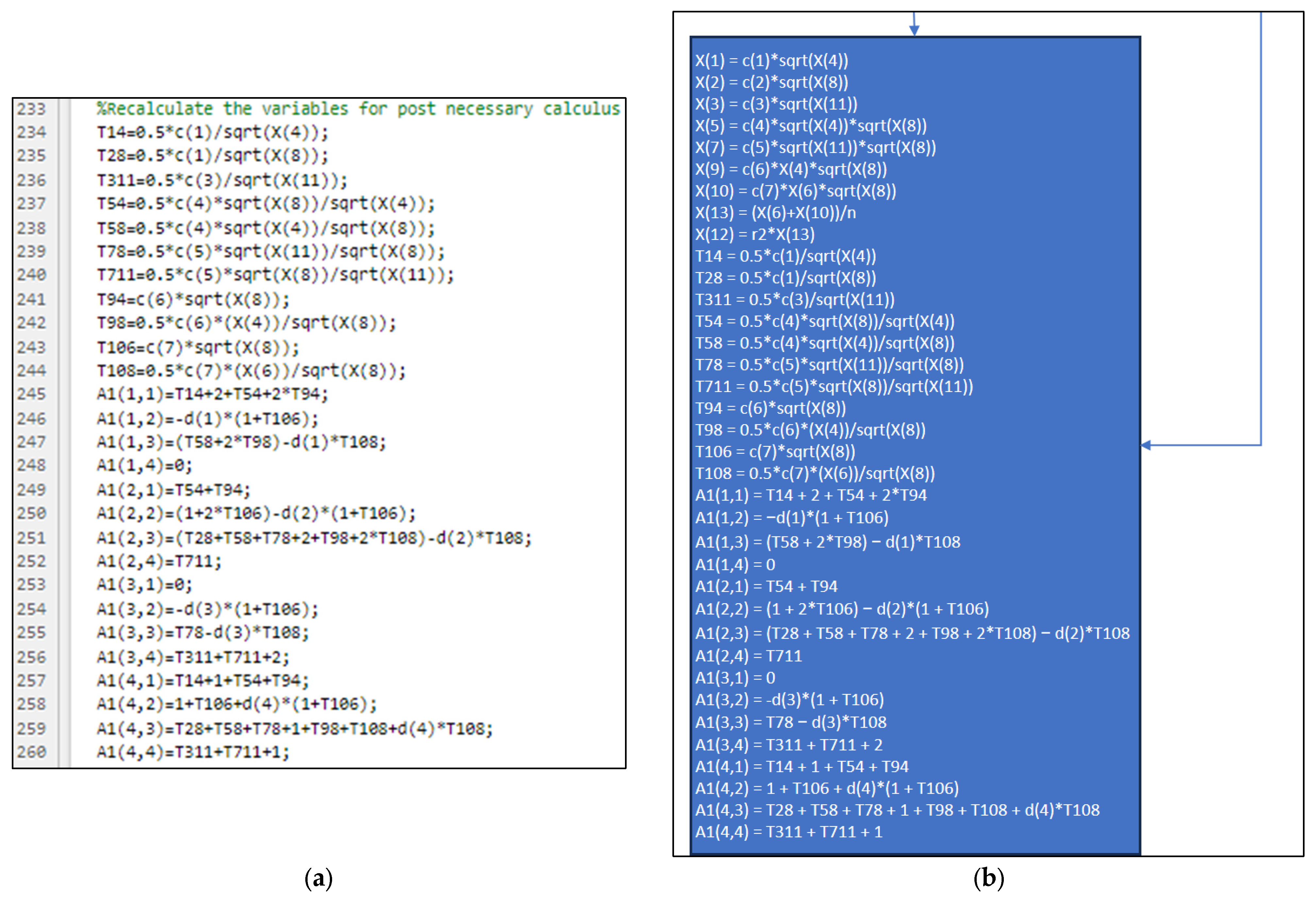
3.2. Part Two: Develop of the “Fractions_Derivatives” File
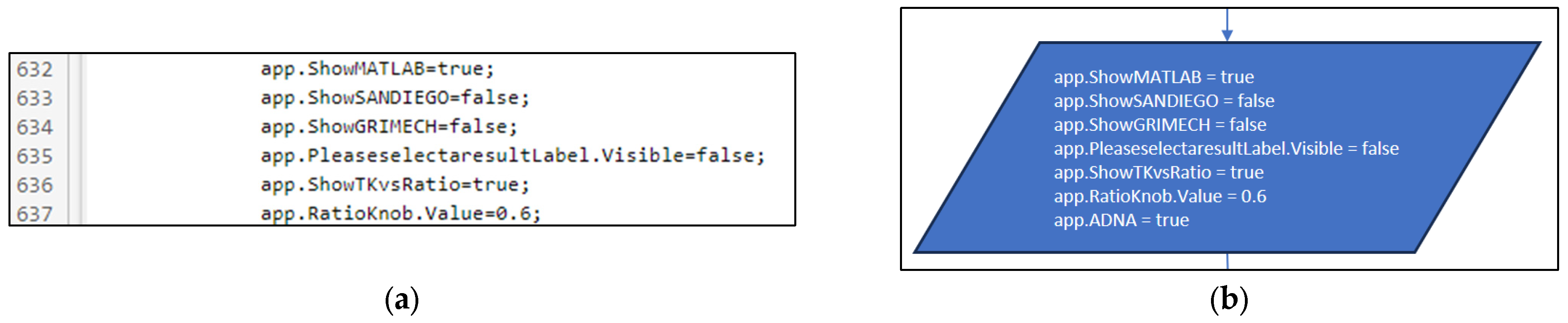
3.3. Part Three: Develop of the MATLAB Application File
4. Results and Discussions
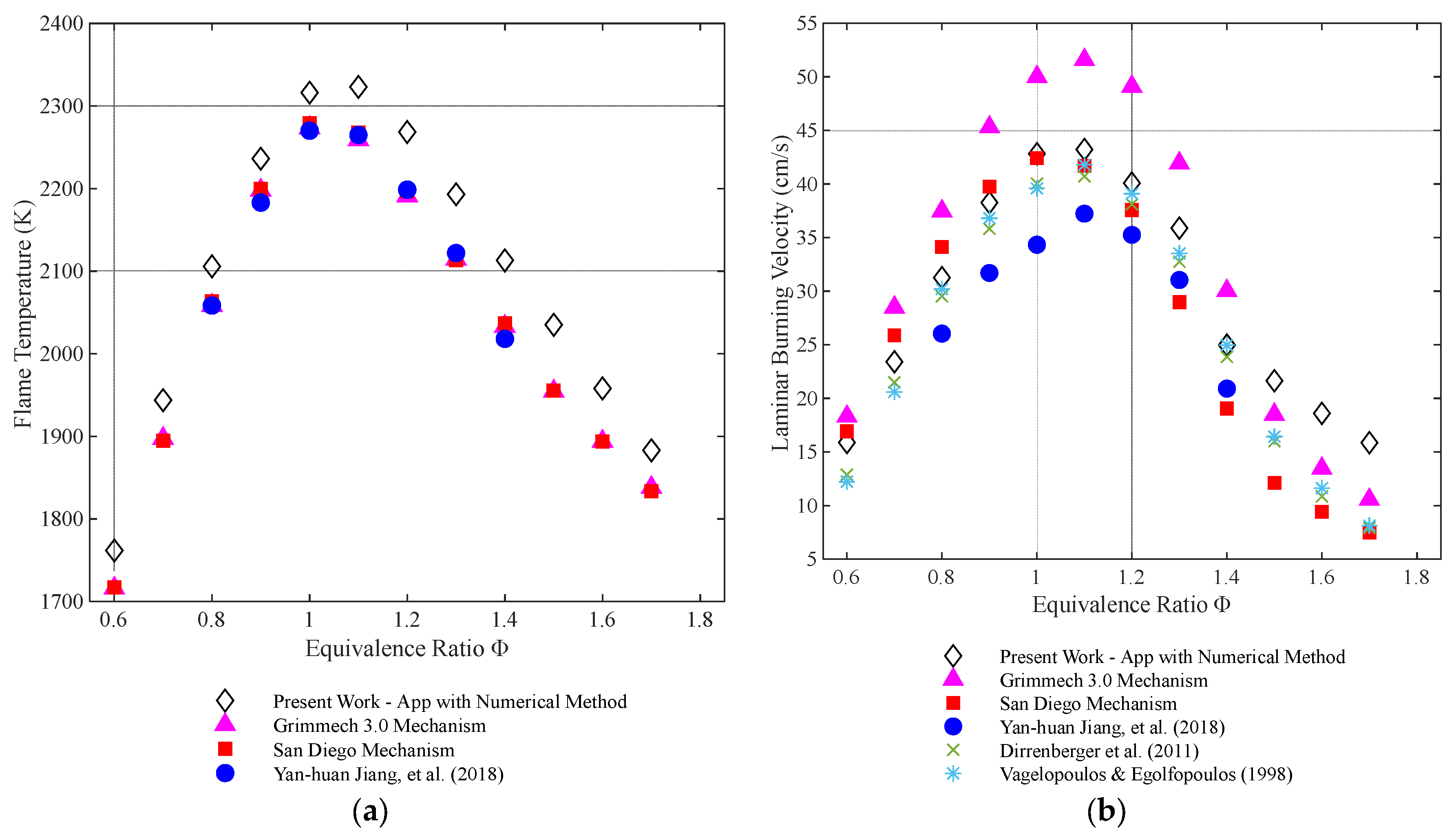
4.1. Methane
4.2. Propane
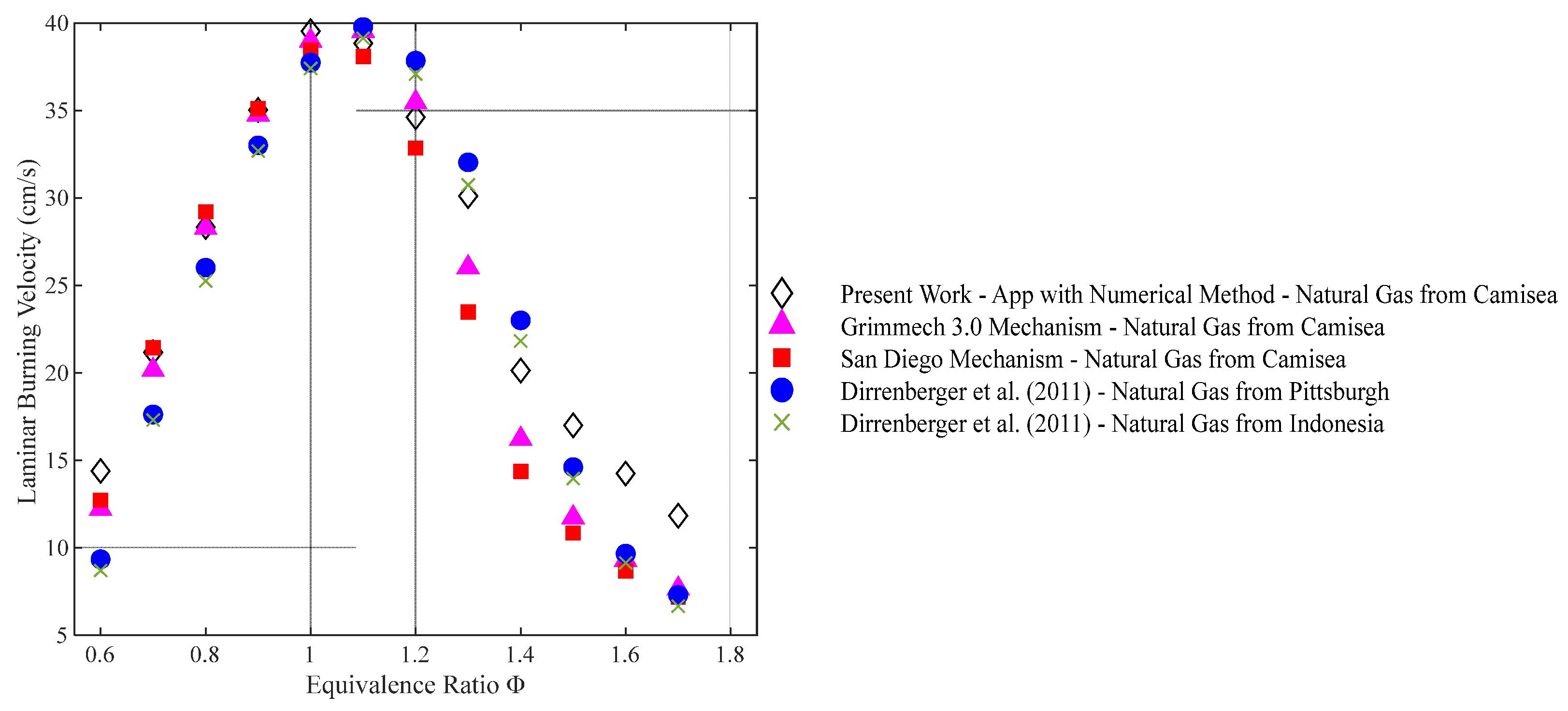
4.3. Natural Gas
5. Conclusions
- In addition to the previously published article referenced as [8], the explanation provided in the present work completes the development plan and implementation of the MATLAB application.
- The functions and execution sequence are described by using flowcharts and code extracts that allow everybody to understand how it works, and at the same time, the procedures are explicit for each part (New_code.m, Fractions_Derivatives.m, MATLAB_Application.mlapp), in order to provide the necessary information for future improvements.
- With the MATLAB application, a functional and easy-to-use interface is obtained for the visualization and analysis of the results, whose program code (Code S1, Code S2 and Code S3) is available to modify in order to increase the fuel options (6 fuels by default), add more tools or to improve the whole methodology by adding more combustion products and new equations.
- The implementation of the procedure for the determination of the laminar burning velocity as one of the novelties of this work is presented and explained as part of the New_code.m description that will allow users to improve the assumptions taken or include any other important variables not considered in the scope of the program.
- The limitations of the application are: it can be only used for hydrocarbon fuels, which can have or not have oxygen and/or nitrogen; the flame temperature must not exceed 3725 °C and must be lower than 327 °C; and the equivalence ratio must not be too high so it does not allow the formation of free carbon [8].
- The average execution time obtained by using the functions tic and toc in MATLAB when the application is initialized was 6.48 s, and when the fuel selection is changed (a new calculus is performed for the new selected fuel), it takes 6.18 s.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| F | is the equivalence ratio |
| AD | is the fraction of the diluent |
| ID | is the identifier of the selected fuel; |
| ID2 | is the identifier of the selected diluent; |
| H_Data | is the enthalpy of the fuel; |
| H_AD | is the enthalpy of the diluent; |
| n | is the carbon coefficient value of the fuel; |
| m | is the hydrogen coefficient value of the fuel; |
| l | is the oxygen coefficient value of the fuel; |
| k | is the nitrogen coefficient value of the fuel; |
| AVM | is the average molar mass |
| Ea | is the activation energy; |
| HR | is the reactants enthalpy; |
| H | is the products enthalpy; |
| der_H_T | is the derivative of enthalpy respect temperature; |
| T | is the first assumed flame temperature or a temperature iteration; |
| V | is the laminar burning velocity |
| X | is the matrix of combustion products |
| x1 | is the molar fraction of Hydrogen (H) in the products; |
| x2 | is the molar fraction of Oxygen (O) in the products; |
| x3 | is the molar fraction of Nitrogen (N) in the products; |
| x4 | is the molar fraction of Hydrogen (H2) in the products; |
| x5 | is the molar fraction of Hydroxide (OH) in the products; |
| x6 | is the molar fraction of Carbon monoxide (CO) in the products; |
| x7 | is the molar fraction of Nitric oxide (NO) in the products; |
| x8 | is the molar fraction of Oxygen (O2) in the products; |
| x9 | is the molar fraction of Dihydrogen oxide (H2O) in the products; |
| x10 | is the molar fraction of Carbon dioxide (CO2) in the products; |
| x11 | is the molar fraction of Nitrogen (N2) in the products; |
| x12 | is the molar fraction of Argon (Ar) in the products; |
| x13 | is the number of moles from fuel that gives 1 mol of products; |
| P | is the pressure; |
| Kp | is the equilibrium constants at constant pressure; |
| Ta | is the temperature for adjusting Kp; |
| PAR | first estimated value of x13; |
| f | is the general linear function composed by 4 constants (F1, F2, F3 and F4); |
| F1 | is the first constant of f equation; |
| F2 | is the second constant of f equation; |
| F3 | is the third constant of f equation; |
| F4 | is the fourth constant of f equation; |
| df | is the differential equation of f; |
| ox | is the first estimate value of x8 |
| fox | is the result of using ox as input in f; |
| dfox | is the result of using ox as input in df; |
| Bj | is the matrix equations system of molar products; |
| new iteration | is the variable that determines if a new iteration is required; |
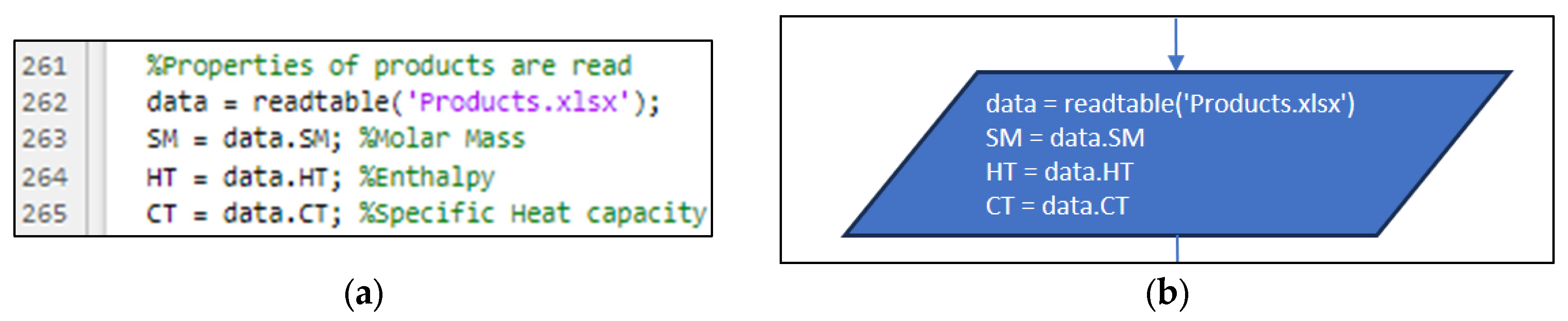
| SM | is the molar mass dataset; |
| HT | is the enthalpy dataset; |
| CT | is the specific heat capacity dataset; |
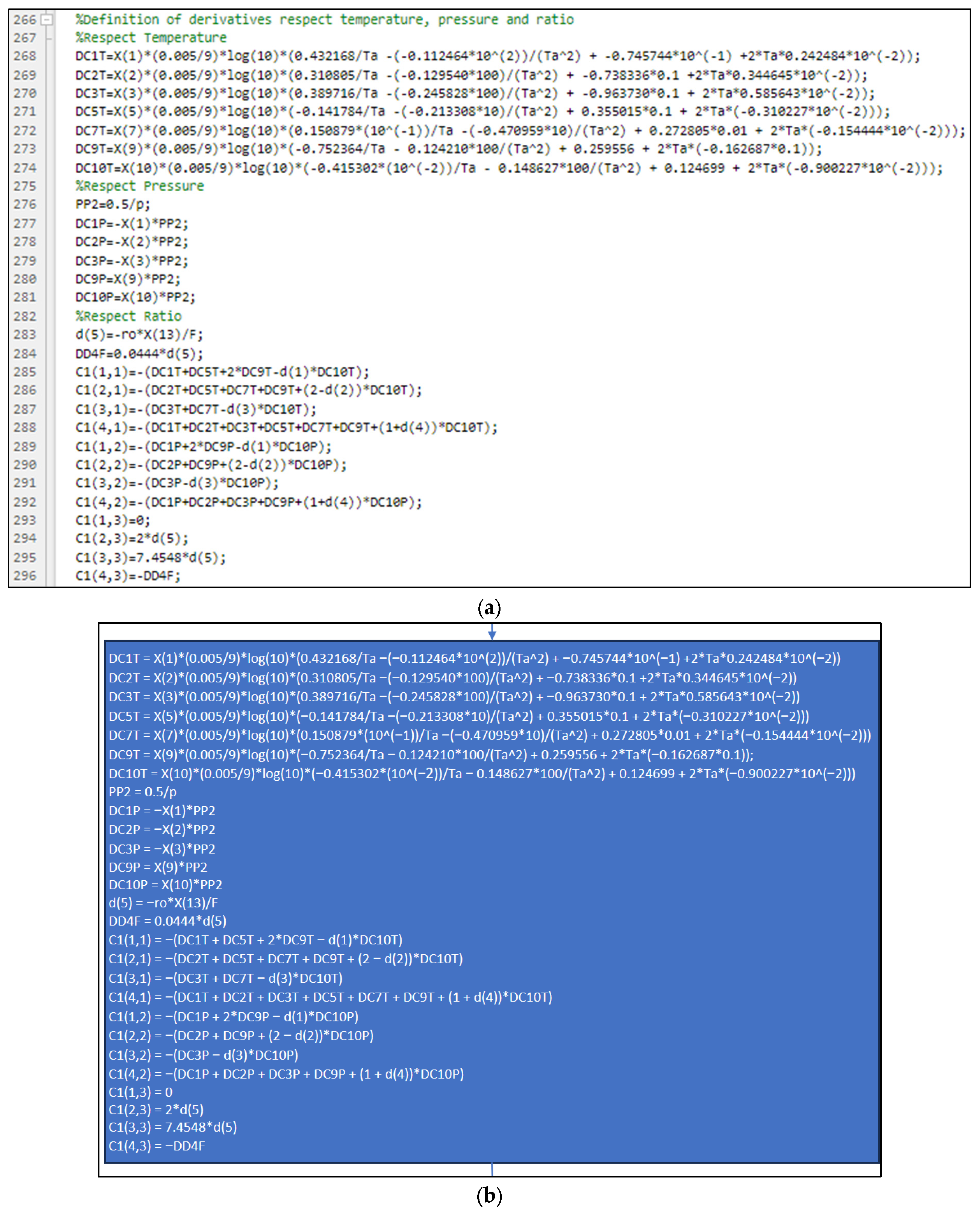
| DCT | is the matrix of derivatives respect temperature; |
| DCP | is the matrix of derivatives respect pressure; |
| DD4F | is the matrix of derivatives respect ratio; |
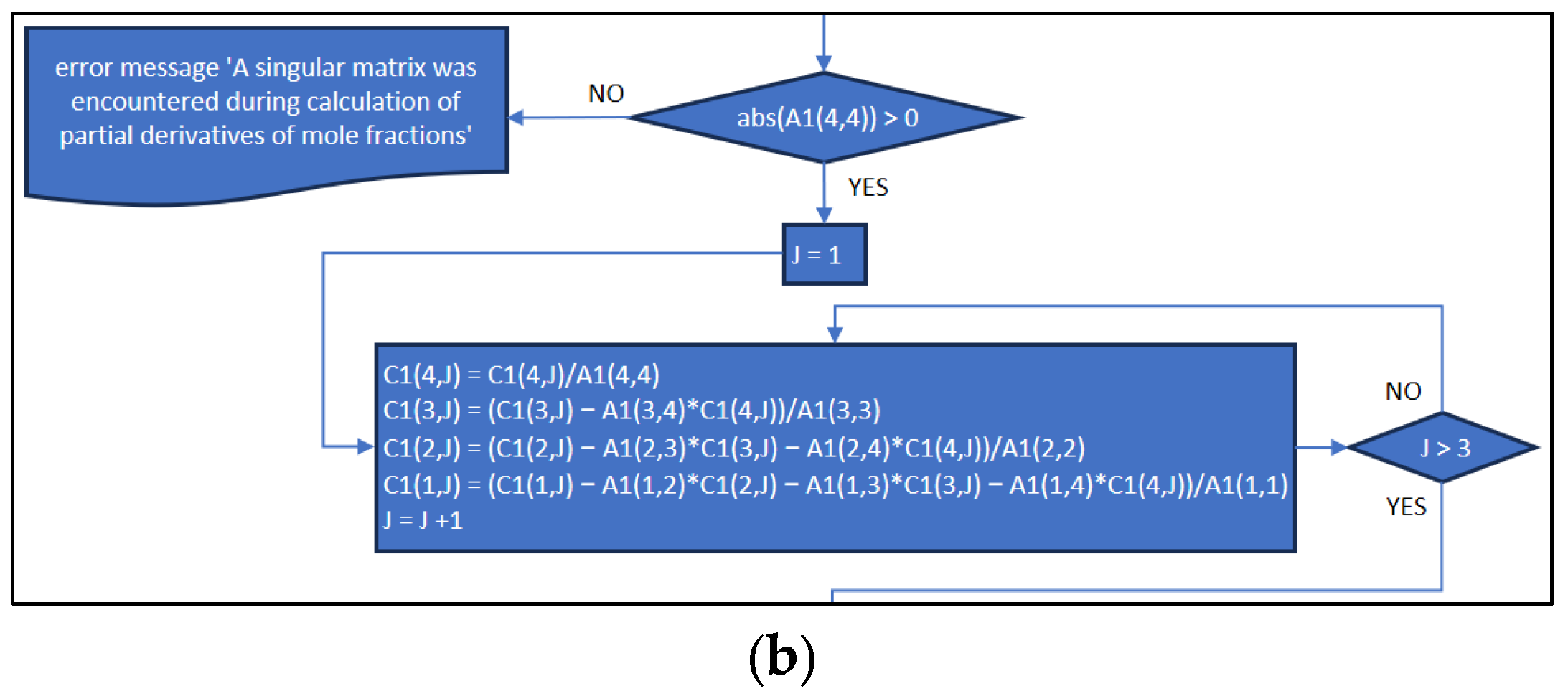
| C1 | is the equation matrix system formed by the derivatives; |
| Tk | is the temperature used as input for calculate the specific enthalpy of a product; |
| IT | is the fixed temperature to 0 decimals; |
| FR | is the fraction part of the temperature; |
| SH | is the matrix of specific enthalpy of each product; |
| CP | is the constant pressure heat; |
| Label2 | is the label that shows current date; |
| app.AD | is the value of diluent in the app; |
| app.ShowMATLAB | is the variable that shows MATLAB numerical method results; |
| app.ShowSANDIEGO | is the variable that shows Ansys Chemkin using San Diego mechanism results; |
| app.ShowGRIMMECH | is the variable that shows Ansys Chemkin using Grim 3.0 mechanism results; |
| app.PleaseselectaresultLabel | is the variable that shows a message requiring the user to select a type of plot to shown on the application; |
| app.RatioKnob | is the value set of the ratio knob |
Appendix A
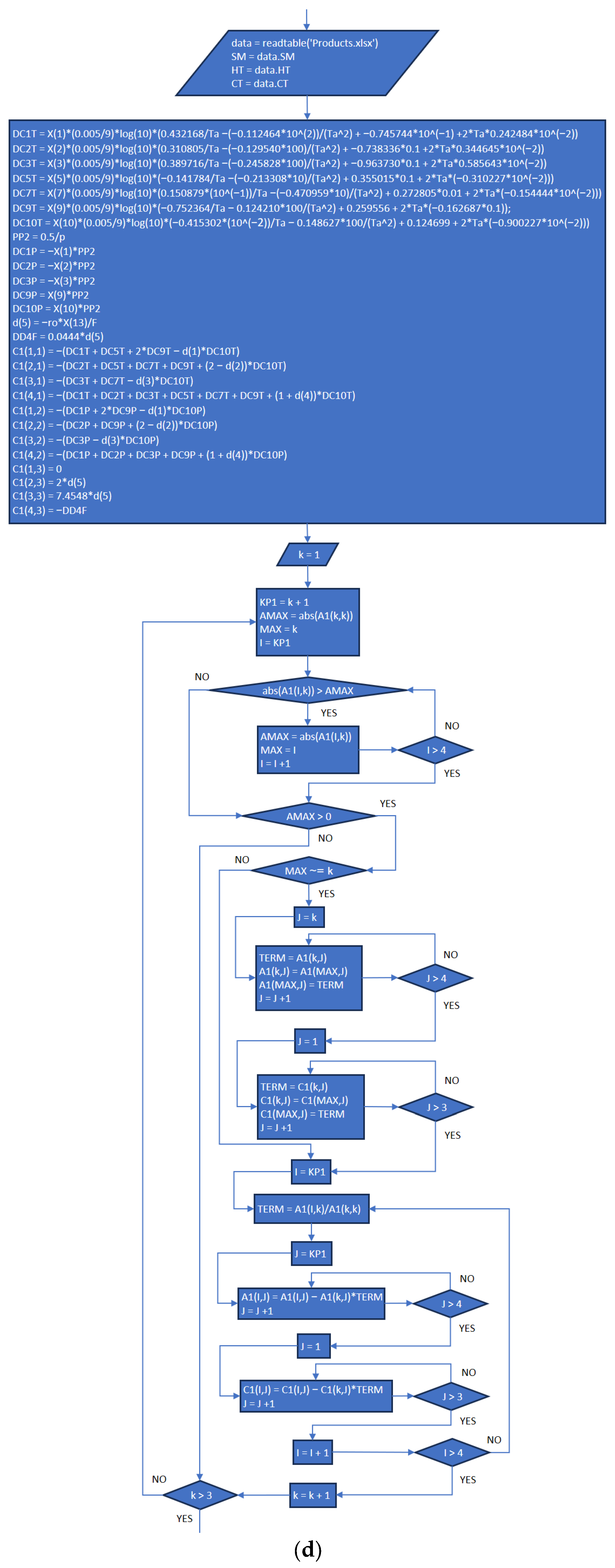
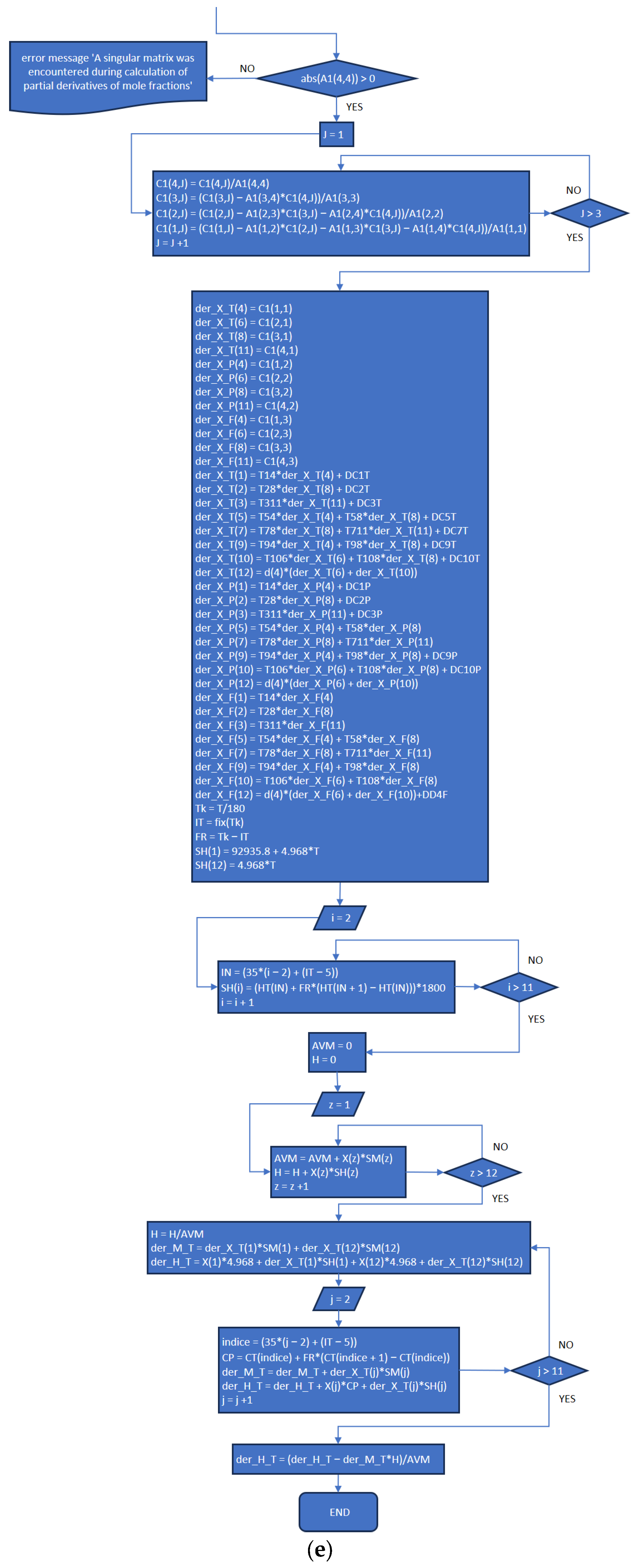
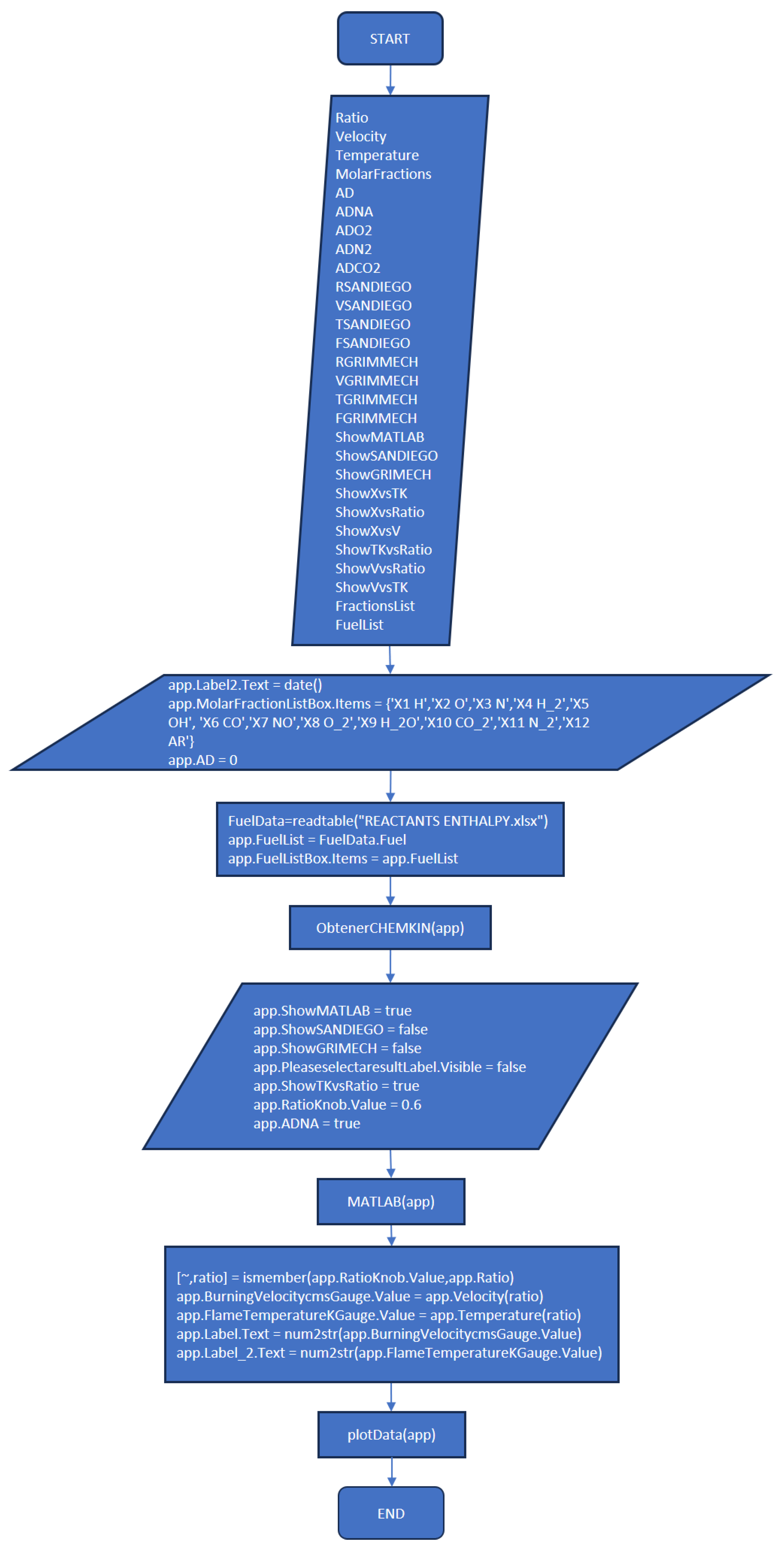
References
- Zhu, D.L.; Egolfopoulos, F.N.; Law, C.K. Experimental and numerical determination of laminar flame speeds of methane/(Ar, N2, CO2)-air mixtures as function of stoichiometry, pressure, and flame temperature. Symp. (Int.) Combust. 1989, 22, 1537–1545. [Google Scholar] [CrossRef]
- Qin, W.; Egolfopoulos, F.N.; Tsotsis, T.T. Fundamental and environmental aspects of landfill gas utilization for power generation. Chem. Eng. J. 2001, 82, 157–172. [Google Scholar] [CrossRef]
- Hu, E.; Fu, J.; Pan, L.; Jiang, X.; Huang, Z.; Zhang, Y. Experimental and numerical study on the effect of composition on laminar burning velocities of H2/CO/N2/CO2/air mixtures. Int. J. Hydrogen Energy 2012, 37, 18509–18519. [Google Scholar] [CrossRef]
- Xiang, L.; Chu, H.; Ren, F.; Gu, M. Numerical analysis of the effect of CO2 on combustion characteristics of laminar premixed methane/air flames. J. Energy Inst. 2019, 92, 1487–1501. [Google Scholar] [CrossRef]
- Xie, M.; Fu, J.; Zhang, Y.; Shu, J.; Ma, Y.; Liu, J.; Zeng, D. Numerical analysis on the effects of CO2 dilution on the laminar burning velocity of premixed methane/air flame with elevated initial temperature and pressure. Fuel 2020, 264, 116858. [Google Scholar] [CrossRef]
- Ansys, Inc. Chemkin-Pro 19.0 Theory Manual; Ansys, Inc.: Canonsburg, PA, USA, 2018. [Google Scholar]
- Olikara, C.; Borman, G.L. A Computer Program for Calculating Properties of Equilibrium Combustion Products with Some Applications to I. C. Engines. In Proceedings of the 1975 Automotive Engineering Congress and Exposition, SAE International, Detroit, MI, USA, 24–28 February 1975. [Google Scholar] [CrossRef]
- Cisneros, R.F.; Rojas, F.J. Determination of 12 Combustion Products, Flame Temperature and Laminar Burning Velocity of Saudi LPG Using Numerical Methods Coded in a MATLAB Application. Energies 2023, 16, 4688. [Google Scholar] [CrossRef]
- Combustion, R. San Diego Mechanism Web Page, Chemical-Kinetic Mechanisms for Combustion Applications, San Diego Mechanism Web Page. Available online: http://combustion.ucsd.edu (accessed on 8 June 2023).
- GRI-MECH 3.0. Available online: http://www.me.berkeley.edu/gri_mech/ (accessed on 8 June 2023).
- Bradley, D.; Hundy, G.F. Burning velocities of methane-air mixtures using hot-wire anemometers in closed-vessel explosions. Symp. (Int.) Combust. 1971, 13, 575–583. [Google Scholar] [CrossRef]
- Sakhrieh, A. The adiabatic flame temperature and laminar flame speed of methane premixed flames at varying pressures. Acta Period. Technol. 2019, 50, 220–227. [Google Scholar] [CrossRef]
- Jiang, Y.-H.; Li, G.-X.; Li, H.-M.; Li, L.; Tian, L.-L.; Huang, H.-T. Experimental and Numerical Study on the Combustion Characteristics of Propane/Air Laminar Premixed Flame at Elevated Pressure. Energy Fuels 2018, 32, 9898–9907. [Google Scholar] [CrossRef]
- Vagelopoulos, C.M.; Egolfopoulos, F.N. Direct experimental determination of laminar flame speeds. Symp. (Int.) Combust. 1998, 27, 513–519. [Google Scholar] [CrossRef]
- Dirrenberger, P.; Le Gall, H.; Bounaceur, R.; Herbinet, O.; Glaude, P.; Konnov, A.; Battin-Leclerc, F. Measurements of Laminar Flame Velocity for Components of Natural Gas. Energy Fuels 2011, 25, 3875–3884. [Google Scholar] [CrossRef]



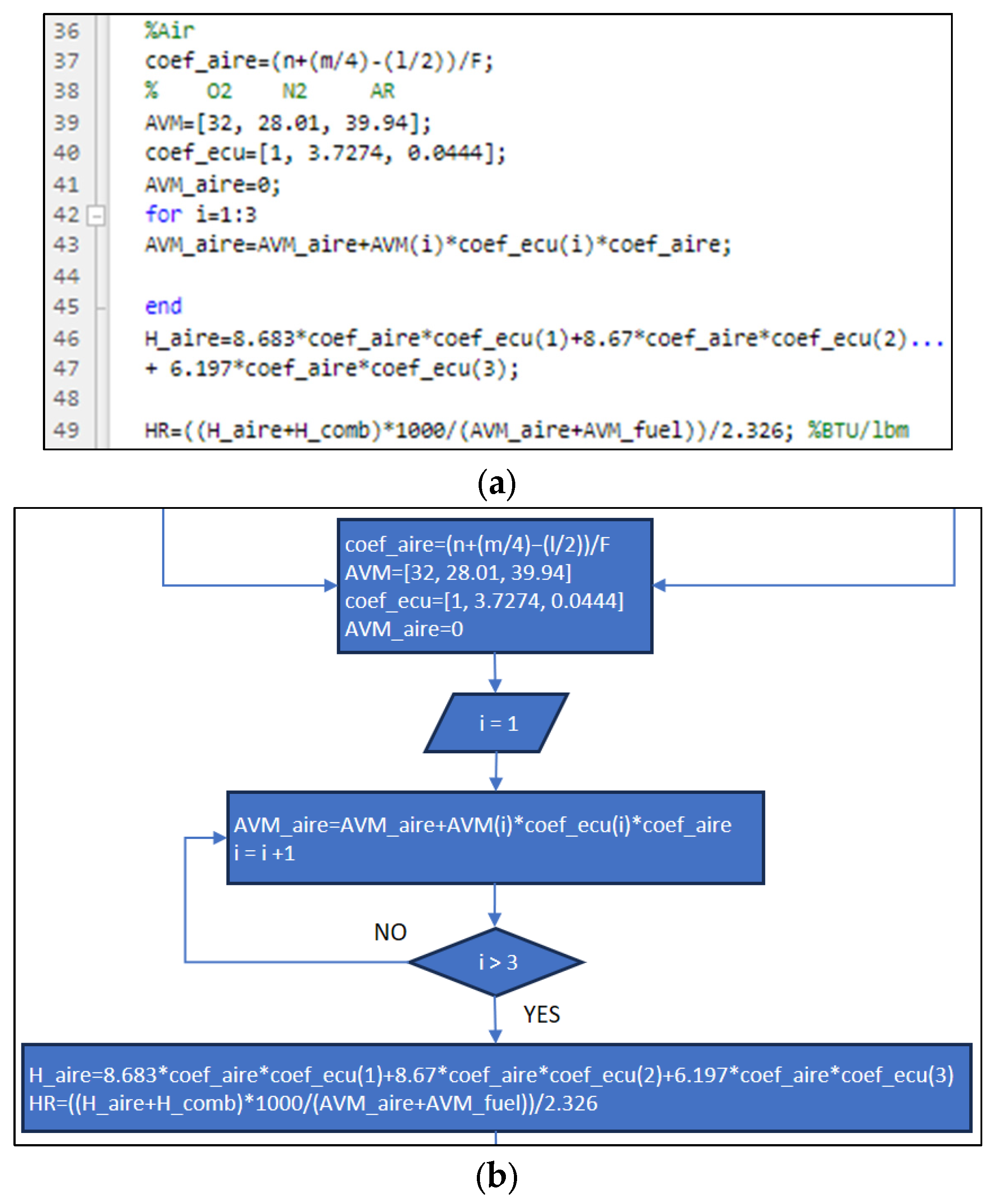

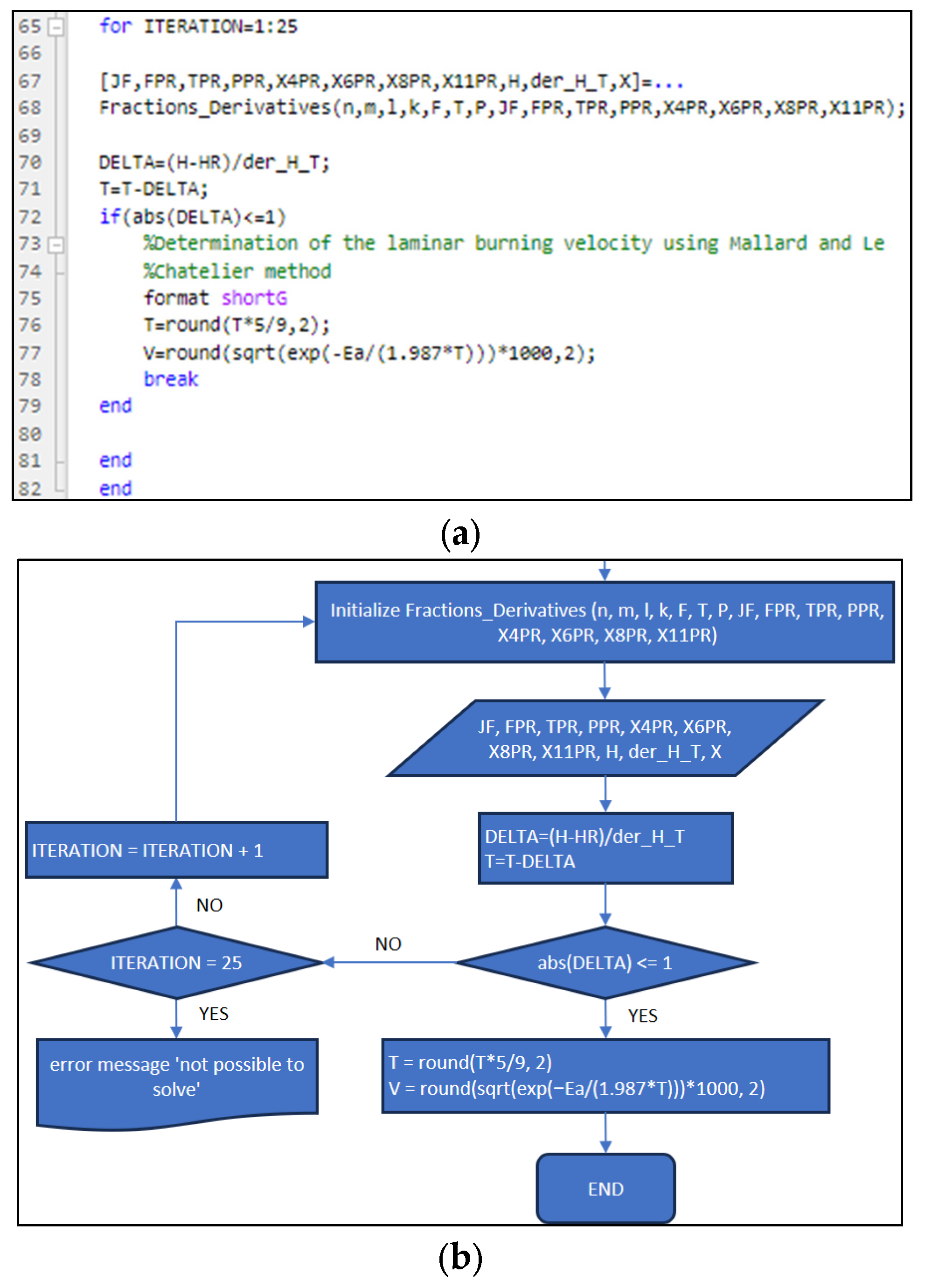
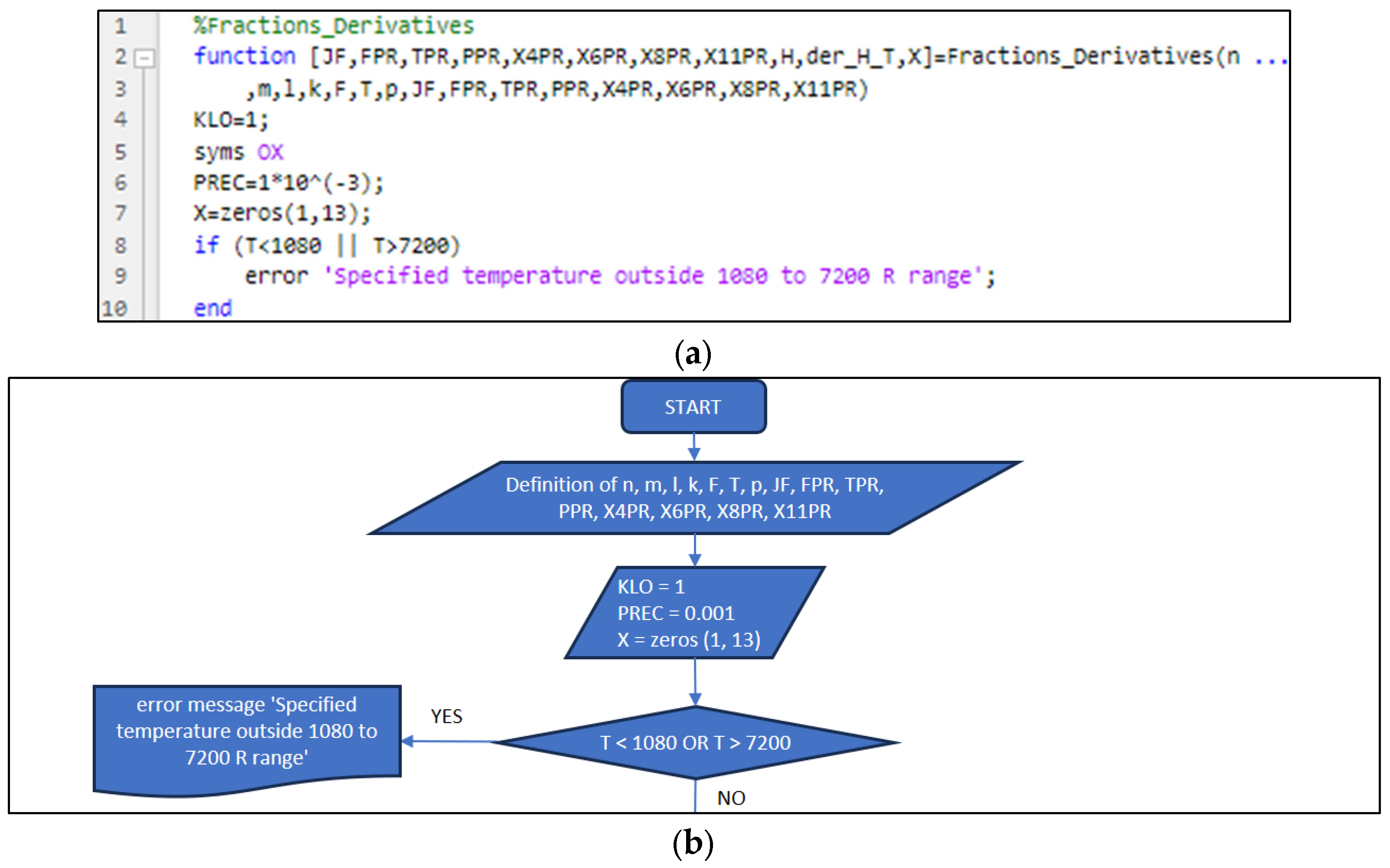
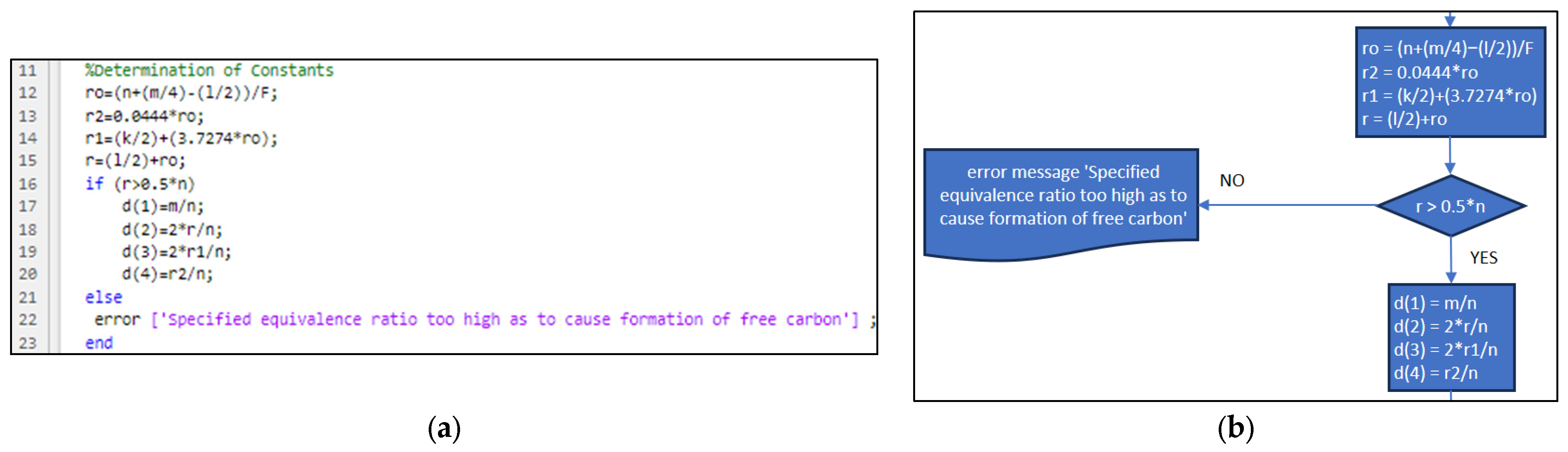















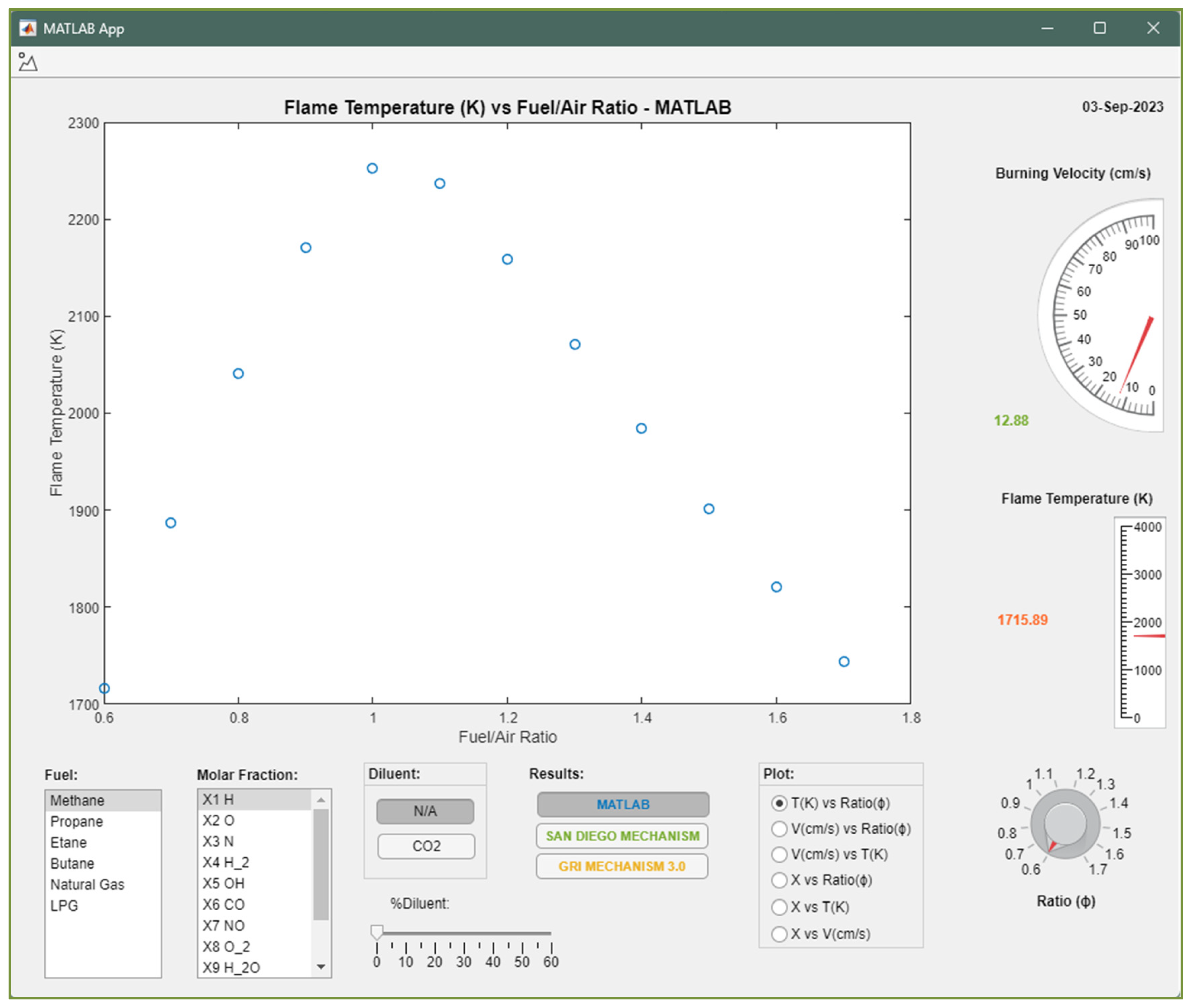

| Position | Name of Tool | Description | Selection Type |
|---|---|---|---|
| A | Fuel list | List of fuels available for calculus in the application | Unique |
| B | Molar fraction list | List of molar fractions available for plotting results | Unique |
| C | Diluent button list | List of diluents available to use in calculus | Unique |
| D | Percentage bar of diluent | Percentage of diluent by volume to be considered in fuel | Unique |
| E | Results button list | Results from resources available to be show in the plot | Multi |
| F | Plot button list | Type of plot to be show in the screen | Unique |
| G | Equivalence ratio knob | Knob that allows to see the value of laminar burning velocity and flame temperature in their respective gauges | Unique |
| H | Laminar burning velocity gauge | Laminar burning velocity value at the knob equivalence ratio value selected | NA |
| I | Flame temperature gauge | Flame temperature value at the knob equivalence ratio value selected. | NA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cisneros, R.F.; Rojas, F.J. MATLAB Application for Determination of 12 Combustion Products, Adiabatic Temperature and Laminar Burning Velocity: Development, Coding and Explanation. Computation 2024, 12, 189. https://doi.org/10.3390/computation12090189
Cisneros RF, Rojas FJ. MATLAB Application for Determination of 12 Combustion Products, Adiabatic Temperature and Laminar Burning Velocity: Development, Coding and Explanation. Computation. 2024; 12(9):189. https://doi.org/10.3390/computation12090189
Chicago/Turabian StyleCisneros, Roberto Franco, and Freddy Jesus Rojas. 2024. "MATLAB Application for Determination of 12 Combustion Products, Adiabatic Temperature and Laminar Burning Velocity: Development, Coding and Explanation" Computation 12, no. 9: 189. https://doi.org/10.3390/computation12090189
APA StyleCisneros, R. F., & Rojas, F. J. (2024). MATLAB Application for Determination of 12 Combustion Products, Adiabatic Temperature and Laminar Burning Velocity: Development, Coding and Explanation. Computation, 12(9), 189. https://doi.org/10.3390/computation12090189







