Abstract
This paper investigates the potential of utilising multilevel quasi-interpolation techniques on Chebyshev sparse grids for complex numerical computations. The paper starts by laying down the motivations for choosing Chebyshev sparse grids and quasi-interpolation methods with Gaussian kernels. It delves into the practical aspects of implementing these techniques. Various numerical experiments are performed to evaluate the efficiency and limitations of the multilevel quasi-sparse interpolation methods with dimensions two dimension and three dimension. The work ultimately aims to provide a comprehensive understanding of the computational efficiency and accuracy achievable through this approach, comparing its performance with traditional methods.
1. Introduction
Traditional interpolation methods, such as grid-based or radial basis function interpolation, encounter computational difficulties when dealing with multidimensional datasets. The computational complexity of these methods grows exponentially with the number of dimensions, rendering them similarly unfeasible on reasonable timeframes. Consequently, novel approaches are necessary to address the challenge of interpolation in multidimensional spaces.
The need for innovative solutions has driven the development of novel numerical methods that are capable of efficiently handling 2D, 3D, or high-dimensional data using higher-performance computers [1,2]. As a result, researchers have been able to make significant advancements in the various scientific domains mentioned, enabling the development of innovative solutions to complex problems [3].
2. Chebyshev Sparse Grids Technique
In the literature, a sparse grid technique has been proposed to overcome the curse of dimensionality with equally spaced grids for higher dimensional domains [4]. Georgoulis et al. [4] proposed an algorithm that reduces the requirement of a large number of data points on an equally spaced grid but keeps the simplicity of a grid structure in evaluating the interpolant. The construction of a sparse grid is defined as follows.
Define multi-index and as spatial positions. Define the point for that position as follows:
We can now define the family of uniform grids as the following set of points:
The number of points in is given as follows:
If we have , is the uniform full grid of equally spaced points of level n with distances between the points given by . The size of the grid is . We denote this full grid as . Now, we consider a sparse subset of uniform full grids, , as follows:
with . We refer to as the sparse grid of level in dimension d. Figure 1 shows a visual representation of the sparse grid for and . Notice that some of the grid points are included in more than one sub-grid; hence, there are some redundancies.

Figure 1.
Sparse grid .
In an alternative formulation of the sparse grid, there are arguments that instead of using an equally spaced grid, one can use Chebyshev points to create grids on . For the multi-index and , we can define
to have the point . Similarly, we can define the family of Chebyshev grids as follows:
and the sparse subset of Chebyshev grids as follows:
where is referred to as the sparse Chebyshev grid of level n in dimension d. Figure 2 shows a visual representation of the sparse Chebyshev grid for and . We observe that the sparse grid points are not equally spaced.

Figure 2.
Sparse Chebyshev grid .
3. Quasi-Sparse Interpolation with Gaussian Kernels
In the previous formulation of the interpolation using RBF, we observed that it is required to solve a system of N linear equations, where N is the total number of points. Using a sparse grid of points as defined in the previous sub-section will reduce the total number of points and, subsequently, the total number of equations for the higher dimension compared to a full grid of points. However, that does not fully eliminate the ill-conditioning of the problems. Another method proposed in the literature to avoid solving the system of linear equations is to use quasi-interpolation. There is extensive discussion on error estimates in quasi-interpolation in the literature [5,6,7].
We use the idea of quasi-interpolation on the sparse grid with anisotropic Gaussian basis functions. If , the distance between points and in dimension j for . Then, the diagonal matrix can be defined as follows:
where . For each multi-index ℓ, we can now define the quasi-interpolant anisiotropically:
Here, we consider the Gaussian kernel
with c determining the degree of smoothness of the interpolant.
To construct the quasi-sparse kernel-based interpolant on the sparse grid , the anisotropic interpolants on the sub-grids must be linearly combined using the following formula:
For example, the quasi-sparse kernel-based interpolation for would be
and for , it would be
In a similar fashion, we can construct the quasi-sparse kernel-based interpolation formula for the sparse grids based on Chebyshev points by replacing grids with .
4. Multilevel Quasi-Sparse Interpolation
From the construction of sparse grids, it is obvious that sparse grids from the lower level to the upper level are nested; that is,
for all . We have illustrated this nested nature in Figure 3 for equally spaced grid points. For Chebysheb points, we have also shown the nested nature of the grids, which is presented in Figure 4. Moreover, while combining kernel-based anisotropic interpolants for each subgrid, they were appropriately scaled, with the scaling being proportional to the density of the corresponding constituent subgrid. One can utilize these nested properties of the subgrids to propose a multilevel method of interpolation with them without adding any further complexity to the quasi-sparse kernel-based interpolation introduced earlier. In the earlier literature [8,9,10], multilevel methods for radial basis functions were used to combine stationary and non-stationary interpolants to accelerate convergence and to improve the numerical stability of ill-conditioned problems.
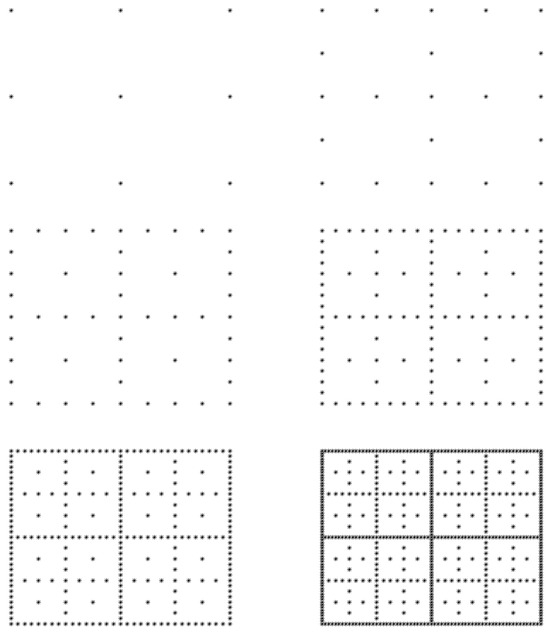
Figure 3.
Nested nature of sparse grids with equally spaced points for .

Figure 4.
Nested nature of sparse grids with Chebyshev points for .
The main idea of multilevel sparse grid-based quasi-interpolation is to interpolate the function at the lowest level, that is, for , and then update at each level of the sub-grids by computing the residuals at every level, interpolating them at the higher level. More formally, we obtain the quasi-sparse kernel-based interpolation at the coarsest level 1; that is, the coarsest level approximation is . Then, we define the residual function at level j as and interpolate the residual function as
on the level sparse grid and then update the multilevel interpolant as follows:
We refer to this algorithm as the multilevel quasi-sparse kernel-based interpolation. As the quasi-sparse kernel-based interpolation is being used at every level, the time–complexity of the multilevel method is linear with these levels. However, it takes more time than the usual quasi-sparse interpolation for a fixed level as it evaluates the residuals at every grid point. Again, the algorithm is easily amenable to parallel computing.
5. Implementation
In this article, all algorithms and numerical experiments are implemented in MATLAB software 23.2. This is necessary to be done, otherwise it will affect publication. environment. The implementation is broken down into three main parts:
- Creating sparse grids using either equally spaced grids or Chebyshev points for each level of the multilevel grid;
- Anisotropic quasi-interpolation using a Gaussian kernel;
- The development of an algorithm for quasi-sparse interpolation, which combines anisotropic quasi-interpolants, as described earlier.
For multilevel quasi-interpolation, we implement another function to apply the algorithm.
Multilevel Quasi-Sparse Interpolation
The outline for the algorithm of multilevel quasi-sparse interpolation is given in Algorithm 1. In the implementation of the multilevel quasi-sparse interpolation, after initial checks and creating a sparse grid of points, if necessary, we compute the quasi-interpolation approximation using the function QSIK for level . For all other levels , we evaluate the quasi-sparse interpolation approximation at all sparse grid points and then subtract that from the original function value to compute the residual function and then again compute the quasi-sparse approximation for the residual function at level i and add that estimate to the function approximation, where we already have up to level i. We continue computing the residual functions and updating our approximation at each level until the maximum level of evaluation n is reached. This multilevel approximation returns the function approximations at all levels . Though it requires a lot of quasi-sparse interpolation approximations at all levels, we can reduce the computation time by computing the function approximations at all levels together rather than calling the function separately for each level.
| Algorithm 1: Multilevel Quasi-Sparse Interpolation Algorithm | |
| Data: Sparse grid data decomposition | |
| Result: The multilevel quasi-sparse interpolation . | |
| 1. Initialize the first interpolation value at zero, that is . | |
| 2. Construct the nested sparse grids as . | |
| 3. for do | |
| Compute for all ; | |
| Compute using Algorithm described in Section 4; | |
| Update . | |
| end | |
6. Numerical Experiments for Quasi-Sparse Interpolation with
We now illustrate the performance of the proposed quasi-sparse kernel-based interpolation for the following test functions:
- (Franke’s function)
- .
- .
- .
Franke’s function is very commonly used as a test function in the interpolation literature with RBF kernels [11]. The others can be found in [12,13,14], respectively. These test functions are illustrated in Figure 5.
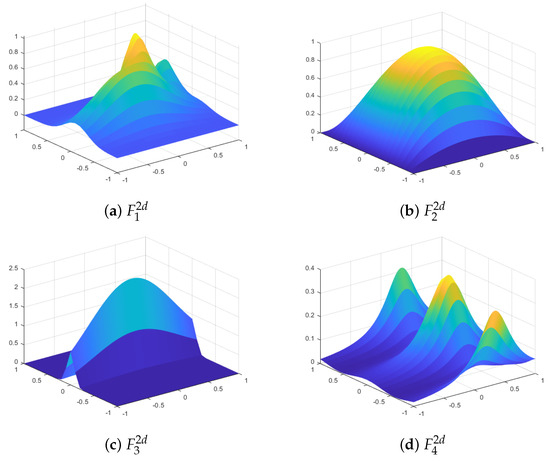
Figure 5.
Test functions in two dimensions.
In all of these numerical experiments, we have used a uniform grid of points in the rectangle . The error in approximation is reported as the maximum modulus error; that is, , and root mean square error is defined as follows:
where are the evaluation points, and is the total number of evaluation points. We also report the number of points in the sparse grid (or ) as SGnode and the number of points actually used in the computation as some of the points are revisited in the sparse grid computations as DoF.
Figure 6 shows the approximation using our proposed quasi-sparse kernel-based interpolation with an equally spaced grid for different values of n. Table 1 also shows the error estimates. We observe that the maximum error or the RMS error does not decrease substantially as we increase the sparse grid level n, but the plots show that approximations are very close to the true function for . With Chebyshev points, we observe much better approximations with both the maximum error and the RMS error decreasing with the increase in level n. The plots of the interpolating function evaluated at the grid points for the algorithm with Chebyshev points are shown in Figure 7. Again, we observe that the approximations are quite good for .
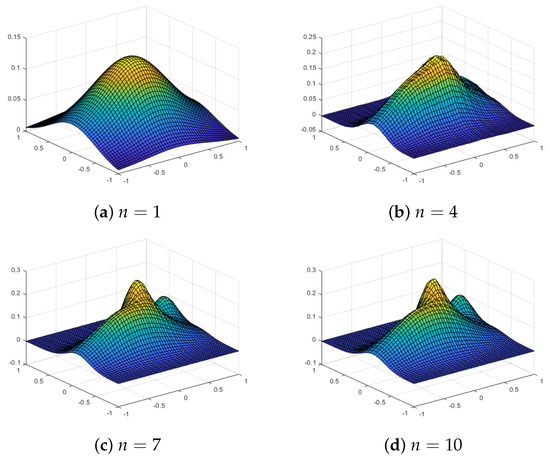
Figure 6.
Approximations using an equally spaced sparse grid with level n and a Gaussian kernel for the test function .

Table 1.
Quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev point grid results for the test function .
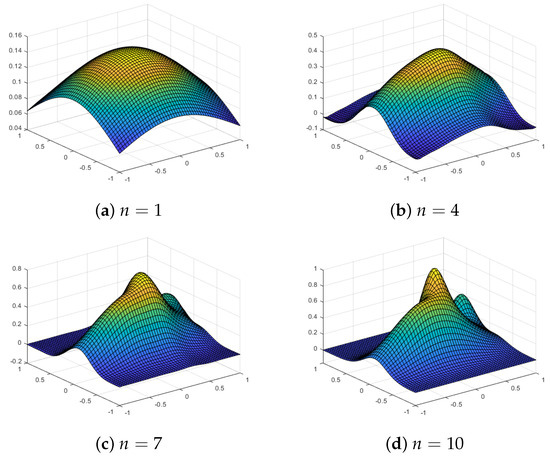
Figure 7.
Approximations using Chebyshev sparse grids with level n and a Gaussian kernel for the test function .
Figure 8 shows the approximations using our proposed quasi-sparse kernel-based interpolation with equally spaced grids for different values of n for the test function . Table 2 also shows the error estimates. We observe that the maximum error or the RMS error does not decrease substantially as we increase the grid level n, but the plots show that approximations are very close to the true function for when we use equally spaced grids. With Chebyshev points, we observe much better approximations, with both the maximum error and the RMS error decreasing with the level n. The plots of the interpolating function evaluated at grid points for the algorithm with Chebyshev points are shown in Figure 9. For , the approximations are poor, but it approximates nicely as n increases. On the other hand, when there are equally spaced grids, the interpolant starts to overfit the surface and lacks smoothness for larger values of n. Thus, by increasing the number of grid levels, the approximation actually deteriorates for equally spaced grids.
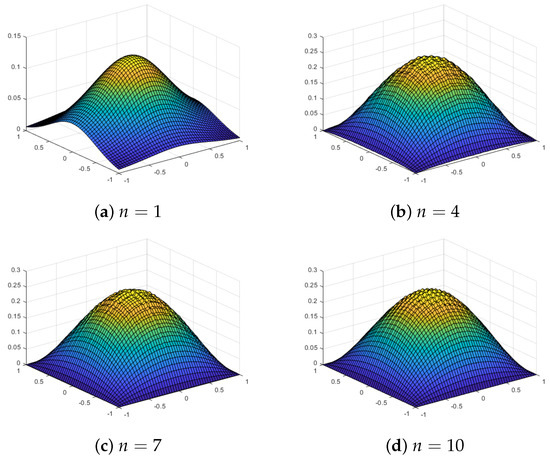
Figure 8.
Approximations using an equally spaced sparse grid with level n and a Gaussian kernel for the test function .

Table 2.
Quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev point grid results for the test function .
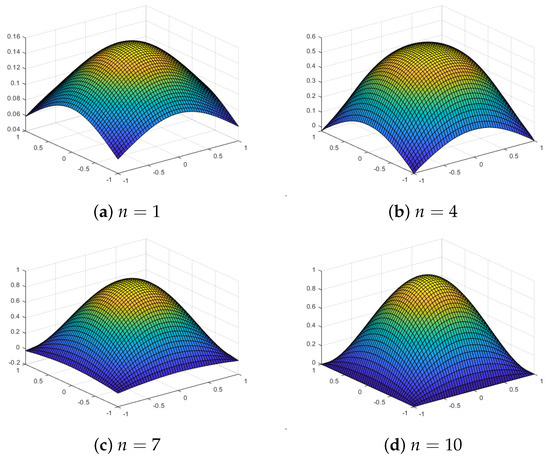
Figure 9.
Approximations using a Chebyshev sparse grid with level n and a Gaussian kernel for the test function .
Figure 10 shows the approximations using our proposed quasi-sparse kernel-based interpolation with equally spaced grids for different values of n for the test function . Table 3 shows the error estimates. We observe that the maximum error or the RMS error does not decrease substantially as we increase the grid level n, but the plots show that approximations are very close to the true function for when we use equally spaced grids. With Chebyshev points, we observe much better approximations, with both the maximum error and the RMS error decreasing with the level n. The plots of the interpolating function evaluated at grid points for the algorithm with Chebyshev points are shown in Figure 11. For , the approximations are poor, and the overall shape is not similar to the shape of the function, but it approximates nicely as n increases. On the other hand, when there are equally spaced grids, the interpolant starts to overfit the surface and lacks smoothness for larger values of n. Thus, by increasing the number of grid levels, the approximation actually deteriorates for equally spaced grids.
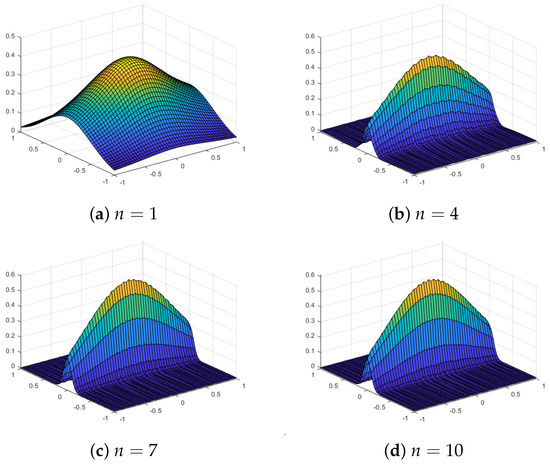
Figure 10.
Approximations using an equally spaced sparse grid with level n and a Gaussian kernel for the test function .

Table 3.
Quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev point grid results for the test function .
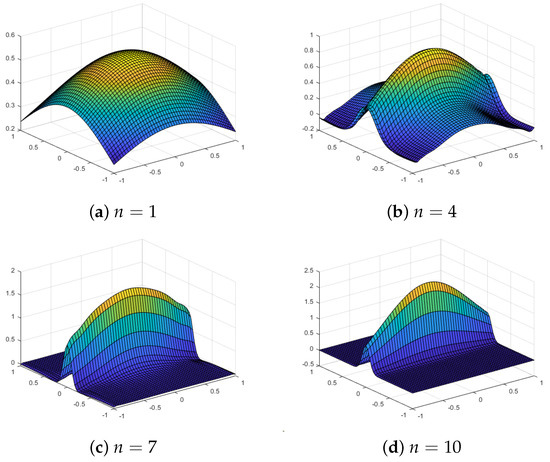
Figure 11.
Approximations using a Chebyshev sparse grid with level n and a Gaussian kernel for the test function .
Figure 12 shows the approximations using our proposed quasi-sparse kernel-based interpolation with equally spaced grids for different values of n for the test function . Table 4 shows the error estimates. We observe that the maximum error or the RMS error does not decrease substantially as we increase the grid level n, but the plots show that approximations are very close to the true function for when we use equally spaced grids. With Chebyshev points, we observe much better approximations, with both the maximum error and the RMS error decreasing with the level n. The plots of the interpolating function evaluated at grid points for the algorithm with Chebyshev points are shown in Figure 13. For , the approximations are poor, and the overall shape is not similar to the shape of the function, but it approximates nicely as n increases.
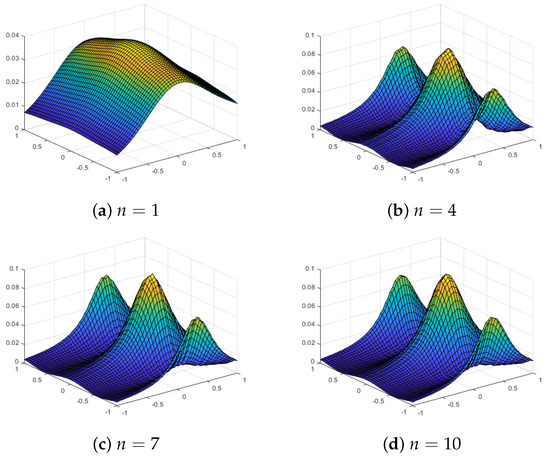
Figure 12.
Approximations using an equally spaced sparse grid with level n and a Gaussian kernel for the test function .

Table 4.
Quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev point grid results for the test function .
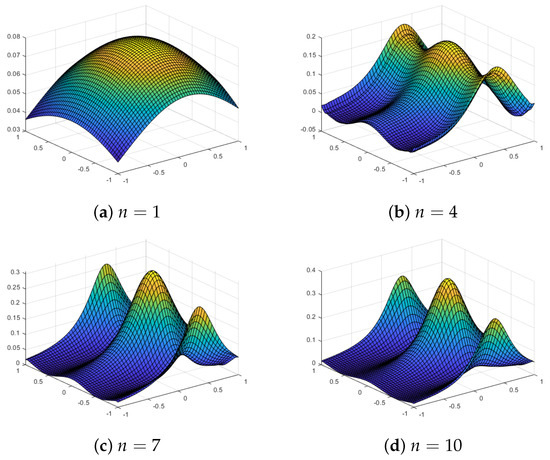
Figure 13.
Approximations using a Chebyshev sparse grid with level n and a Gaussian kernel for the test function .
In these results, quasi-sparse interpolation with equally space grids reaches a stable maximum absolute error and root mean square errors at a lower level with a small number of sparse grid points. However, the quasi-sparse interpolation with Chebyshev points attains much smaller values for maximum errors and RMS errors for all test functions and stabilizes for larger values of the level n. Additionally, since the errors remain stable when the number of grid points increases, the quasi-sparse interpolation goes well with the multilevel quasi-sparse algorithm, which will be examined in a subsequent sub-section. The main observation in these results is that quasi-sparse interpolation does not converge for equally spaced grids, but it does converge for Chebyshev grid points. The rate of convergence depends on the test function.
7. Numerical Experiments for Quasi-Sparse Interpolations with
In this section, we present the performance analysis for some test functions with domain in dimension . The following functions are used as test functions:
- (Franke’s function)
- .
- .
- .
The performance of our quasi-sparse kernel-based interpolant is evaluated in a grid of equally spaced points in the cube . The results are summarised in Table 5, Table 6, Table 7 and Table 8. Due to the long computing time and the unavailability of a parallel computing environment, we evaluate only levels for the multilevel algorithm. The results are similar to our observation for the numerical experiments in as we do not observe any convergence of the quasi-sparse interpolation with equally spaced grids, but the approximations converge for Chebyshev points in all test functions.

Table 5.
Quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev point grid results for the test function .

Table 6.
Quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev point grid results for the test function .

Table 7.
Quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev point grid results for the test function .

Table 8.
Quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev point grid results for the test function .
8. Numerical Experiments for Multilevel Quasi-Sparse Interpolation
In this section, we illustrate the performance of our proposed multilevel quasi-sparse kernel b-sed interpolation method for the same test functions, , , , and , as introduced earlier. We evaluate the interpolations at a grid of points in the rectangle . The results are shown in Table 9, Table 10, Table 11 and Table 12 for the test functions in . Some of the approximate functions are also plotted in Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21. For both equally spaced sparse grids and Chebyshev point-based sparse grids, we observe that the maximum error and the root mean square error decrease with the increase in level n. The multilevel quasi-sparse interpolation results are even better with Chebyshev points instead of equally spaced grids.

Table 9.
Multilevel quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev grid results for the test function .

Table 10.
Multilevel quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev grid results for the test function .

Table 11.
Multilevel quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev grid results for the test function .

Table 12.
Multilevel quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev grid results for the test function .
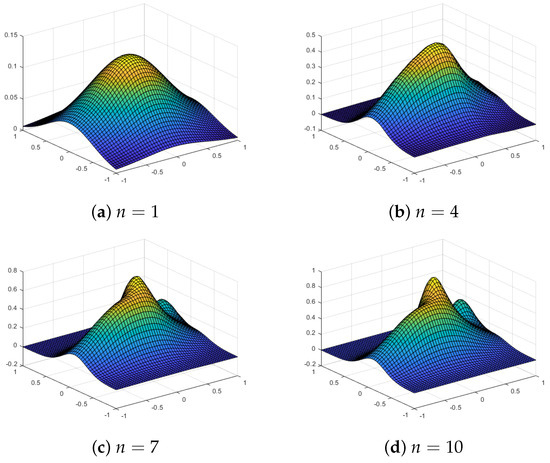
Figure 14.
Multilevel quasi-sparse approximations using an equally spaced grid with level n and a Gaussian kernel for the test function .
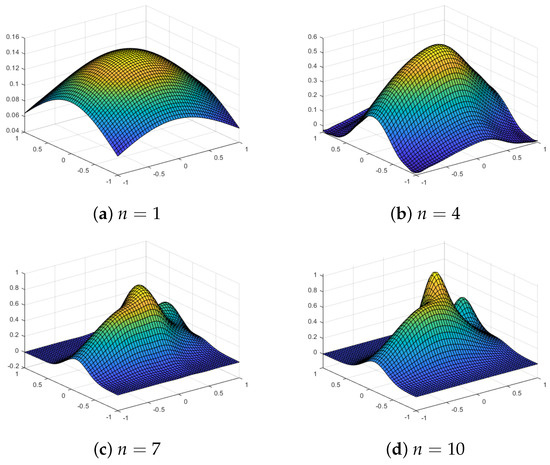
Figure 15.
Multilevel quasi-sparse approximations using a Chebyshev grid with level n and a Gaussian kernel for the test function .
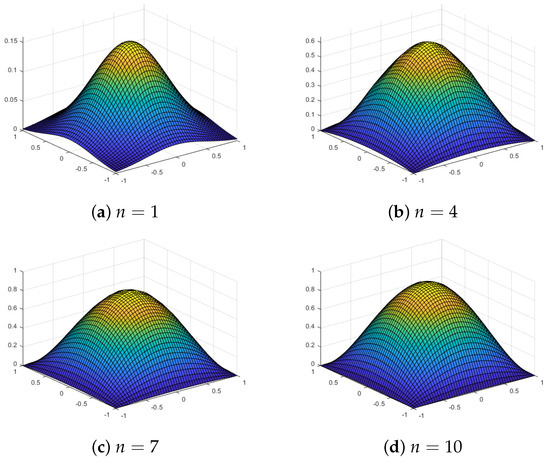
Figure 16.
Multilevel quasi-sparse approximations using an equally spaced grid with level n and a Gaussian kernel for the test function .
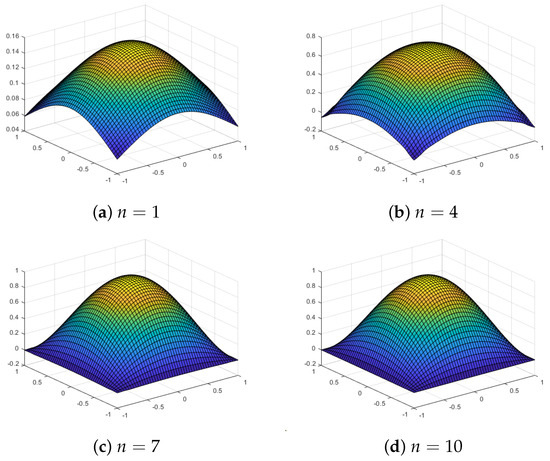
Figure 17.
Multilevel quasi-sparse approximations using a Chebyshev grid with level n and a Gaussian kernel for the test function .
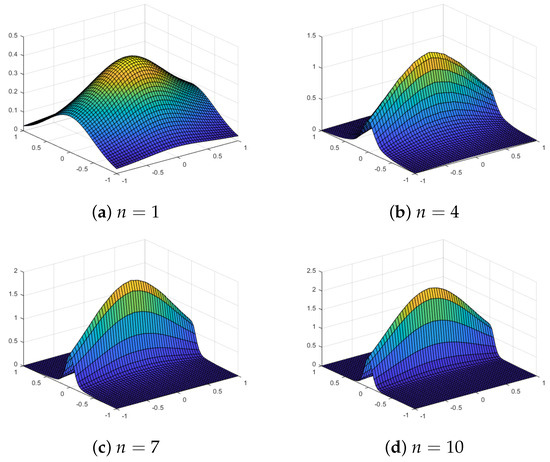
Figure 18.
Multilevel quasi-sparse approximations using an equally spaced grid with level n and a Gaussian kernel for the test function .
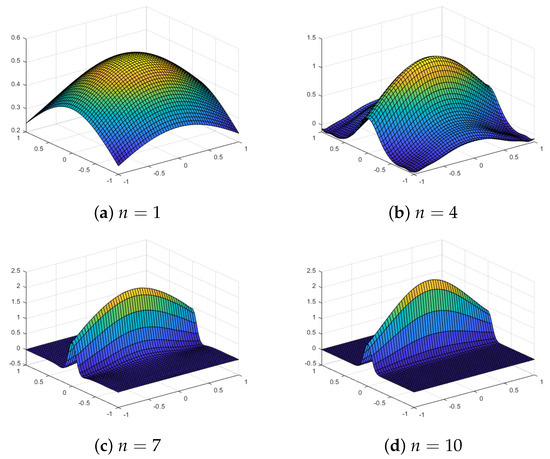
Figure 19.
Multilevel quasi-sparse approximations using a Chebyshev grid with level n and a Gaussian kernel for the test function .
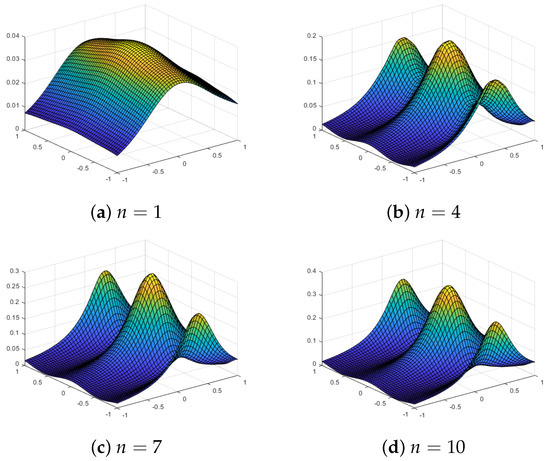
Figure 20.
Multilevel quasi-sparse approximations using an equally spaced grid with level n and a Gaussian kernel for the test function .
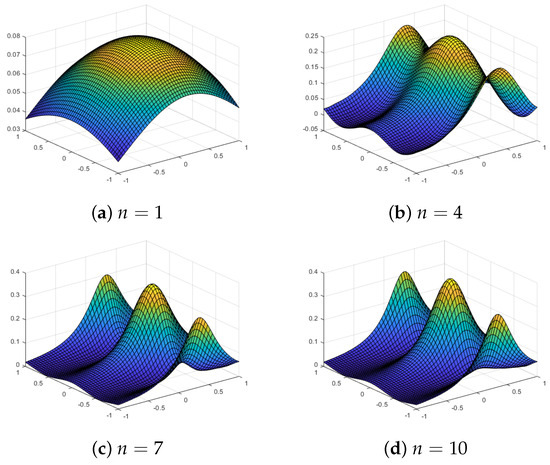
Figure 21.
Multilevel quasi-sparse approximations using a Chebyshev grid with level n and a Gaussian kernel for the test function .
Next, we illustrate the application of our multilevel quasi-sparse interpolation with a Gaussian kernel for the test functions , , , and in dimension , as introduced earlier. For , we evaluate the multilevel interpolation using a grid of points in the cube . Table 13, Table 14, Table 15 and Table 16 show the error estimates with maximum absolute error and root mean square errors for the proposed interpolant for levels up to . Again, we observe that the errors decrease with the level n for the multilevel procedure for both equally spaced grids and Chebyshev points. However, errors are much smaller for Chebyshev points at higher levels.

Table 13.
Multilevel quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev grid results for the test function .

Table 14.
Multilevel quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev grids results for the test function .

Table 15.
Multilevel quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev grid results for the test function .

Table 16.
Multilevel quasi-sparse interpolation with a Gaussian kernel using equally spaced grids and Chebyshev grid results for the test function .
9. Convergence with Computation Time
In Figure 22, the root mean square (RMS) error is plotted against the computation time for the same test functions in , and similar plots of RMS error against time for the test functions in are plotted in Figure 23. These figures show that the quasi-sparse interpolation with equally spaced grids does not converge in error as computational time increases. On the other hand, the errors decrease quite fast and converge for quasi-sparse interpolation with Chebyshev points. Multilevel quasi-sparse interpolation with an equally spaced grid improves errors in approximation and shows some convergence. Still, Chebyshev points present much better convergence results than equally spaced points. It is also interesting to note that, at a similar computational time (in seconds), quasi-sparse interpolation with Chebyshev points yields better results than the multilevel method, though multilevel methods execute only at a smaller number of levels at a comparable time.
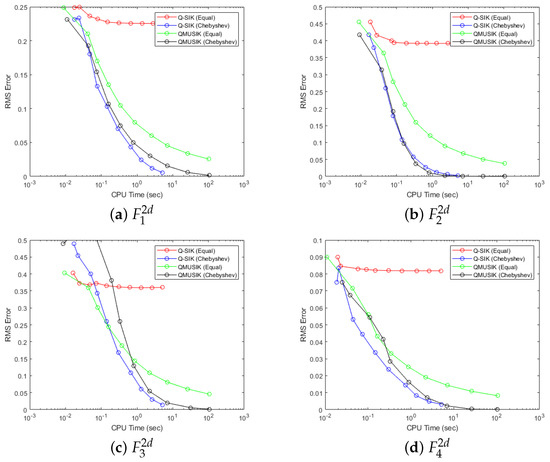
Figure 22.
RMS error against the computation time for the test functions in .
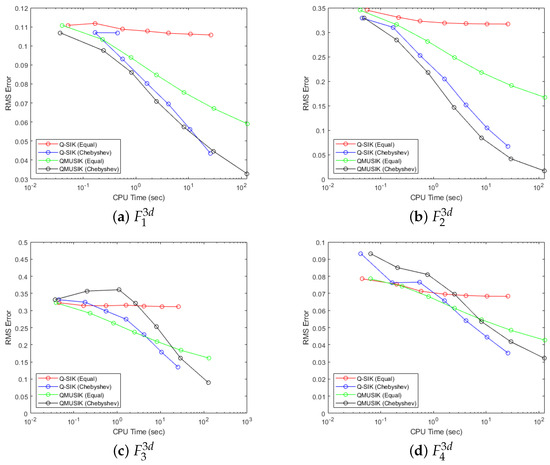
Figure 23.
RMS error against the computation time for the test functions in .
Figure 23 shows the RMS error in approximation against the computational time (in seconds) for the test functions in dimension . Here, we do not observe the convergence in any of the algorithms as all except equally spaced points with quasi-sparse interpolation are show a decreasing trend in errors with computational time. Here, better performance is also obtained for Chebyshev points and Chebyshev points with only quasi-sparse interpolations, which are competitive with multilevel algorithms for a similar computational time and better than multilevel algorithms with equally spaced points.
10. Discussion and Findings
In this article, we explored an algorithm for quasi-interpolation with a Gaussian kernel based on sparse grids. We observed that quasi-sparse kernel-based interpolation approximates two- and three-dimensional functions quite reasonably. However, quasi-interpolation is not guaranteed to converge. We observed that even for large values of the level n of the grids, the root mean square error of the approximation does not converge to 0 if we use equally spaced sparse grids. However, if we use Chebyshev points, the root mean square error of the approximation steadily decreases with level n. We obtain a much better approximation with Chebyshev points than an equally spaced grid for larger values of n. However, Chebyshev points are more dense along the boundary of the domain and more sparse in the centre. For this reason, Chebyshev points yield a very poor approximation in the centre for smaller values of n, which is evident from the plots with Chebyshev approximations with or .
The way grids are constructed, it is possible to implement the algorithm in parallel to make it faster. Otherwise, the repeat of evaluation of the anisotropic interpolant at many grid points for different values of n slows down the execution. We can see that for , the level has 13313 distinct points only, but these points are revisited many times, yielding a total number of 35851 points used for computation. This increases the function evaluation by nearly three times. For and the level , the number of unique grid points is only 8961, but the points used for computation reach 38868. Due to this, the time–complexity of the algorithm increases by many times; one should either implement the algorithm for parallel computing only or improve the algorithm to avoid revisiting grid points for different multi-index ℓ.
In this article, we also proposed multilevel quasi-sparse kernel-based interpolation based on equally spaced grids as well as sparse grids based on Chebyshev points. We illustrated our proposed methods using some numerical test functions. We observed that the proposed multilevel quasi-procedure performs better than the proposed quasi-sparse interpolation method. However, the computational time for the multilevel method is considerably higher than for simple quasi-sparse interpolation. This is because the multilevel method requires residual functions to be evaluated at every sparse grid point, and as the level n increases, the number of sparse grid points also increases exponentially, which leads to a huge increase in computational time. On a positive note, we would like to mention that due to the nature of sparse grid construction, it is possible to implement the algorithm for parallel computing, which will reduce the computational time considerably.
Furthermore, the multilevel quasi-sparse algorithm requires substantially less computational time compared to other multilevel methods proposed in the literature as it does not require solving a system of linear equations at every level of approximations with the residual functions. Due to the implementation of the quasi-sparse algorithm at every level, the proposed multilevel quasi-sparse method will have linear time complexity with the level n.
11. Conclusions
The paper has successfully demonstrated the viability and advantages of using multilevel quasi-interpolation techniques on Chebyshev sparse grids. In comparison to conventional methods, the multilevel quasi-sparse interpolation with Gaussian kernels showed promising performance metrics. This paper also elaborated on the implementation complexities and challenges, providing an efficient way to construct sparse grids and compute anisotropic quasi-interplants. While the methodology was effective in lower dimensions, i.e., two dimensions and three dimensions, limitations began to appear as the computational time and complexity increased, indicating areas for future research and optimisation.
The numerical experiments yielded insightful data on the performance of this technique, showcasing its capacity for faster convergence with computation time in specific settings. The study acts as a foundational resource for future research aiming to employ multilevel quasi-interpolation techniques for various applications, especially in high-dimensional computational problems.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The author is thankful to the University of Leicester for providing the academic environment and resources. Additionally, sincere appreciation goes to his supervisors, Ruslan Davidchack and Jeremy Levesley, for their invaluable guidance and mentorship. Special thanks are also extended to Taibah University for their generous financial support throughout his doctoral studies.
Conflicts of Interest
The author declares no conflict of interest.
References
- Alsharif, F. Multilevel Quasi-Interpolation With a Gaussian Kernel Using Chebyshev Points—Numerical and Theoretical Studies Using the Radial Basis Function Approach. Ph.D. Thesis, University of Leicester, Leicester, UK, 2023. [Google Scholar] [CrossRef]
- Alsharif, F. Quasi-Interpolation on Chebyshev Grids with Boundary Corrections. Computation 2024, 12, 100. [Google Scholar] [CrossRef]
- Franz, T.; Wendland, H. Multilevel quasi-interpolation. IMA J. Numer. Anal. 2022, 43, 2934–2964. [Google Scholar] [CrossRef]
- Georgoulis, E.; Levesley, J.; Subhan, F. Multilevel sparse kernel based interpolation. SIAM J. Sci. Comput. 2013, 35, 815–832. [Google Scholar] [CrossRef]
- Beatson, R.; Powell, M. Univariate multiquadric approximation: Quasi-interpolation to scattered data. Constr. Approx 1992, 8, 275–288. [Google Scholar] [CrossRef]
- Wu, Z.; Robert, S. Shape preserving properties and convergence of univariate multiquadric quasi-interpolation. Acta Math. Appl. Sin. 1994, 10, 441–446. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, J. Generalized strang-fix condition for scattered data quasi-interpolation. Adv. Comput. Math. 2005, 23, 201–214. [Google Scholar] [CrossRef]
- Floater, M.S.; Iske, A. Multistep scattered data interpolation using compactly supported radial basis functions. J. Comput. Appl. Math 1996, 73, 65–78. [Google Scholar] [CrossRef]
- Hales, S.J.; Levesley, J. Error estimates for multilevel approximation using polyharmonic splines. Numer. Algorithms 2002, 30, 1–10. [Google Scholar] [CrossRef]
- Hubbert, S.; Levesley, J. Convergence of Multilevel Stationary Gaussian Quasi-Interpolation. arXiv 2017, arXiv:1609.02457. [Google Scholar]
- Franke, R. Scattered data interpolation: Tests of some methods. Math. Comput. 1982, 38, 181–200. [Google Scholar]
- Fasshauer, G.E. Meshfree Approximation Methods with MATLAB of Interdisciplinary Mathematical Sciences; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2007; Volume 6. [Google Scholar]
- Beatson, R.; Davydov, D.; Levesley, J. Error bounds for anisotropic rbf interpolation. J. Approx. Theory 2010, 162, 512–527. [Google Scholar] [CrossRef]
- Casciola, G.; Montefusco, L.B.; Morigi, S. The regularizing properties of anisotropic radial basis functions. Appl. Math. Comput. 2007, 190, 1050–1062. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).