Abstract
This paper provides a new fractional boundary element method (BEM) solution for nonlinear nonlocal thermoelastic problems with anisotropic fibrous polymer nanoparticles. This comprehensive BEM solution comprises two solutions: the anisotropic fibrous polymer nanoparticles problem solution and the nonlinear nonlocal thermoelasticity problem. The nonlinear nonlocal thermoelasticity problem solution separates the displacement field into complimentary and specific components. The overall displacement is obtained using the boundary element methodology, which solves a Navier-type problem, and the specific displacement is derived using the local radial point interpolation method (LRPIM). The new modified shift-splitting (NMSS) technique, which minimizes memory and processing time requirements, was utilized to solve BEM-created linear systems. The performance of NMSS was evaluated. The numerical results show how fractional and graded parameters influence the thermal stresses of nonlinear nonlocal thermoelastic issues involving anisotropic fibrous polymer nanoparticles. The numerical findings further reveal that the BEM results correlate very well with the finite element method (FEM) and analytical results, demonstrating the validity and correctness of the proposed methodology.
1. Introduction
In recent decades, discrete nanofibers of an anisotropic polymeric matrix created by electrospinning have received a lot of attention in a variety of scientific and technical fields, including thermal insulators, polymer acts, and other devices. The study focuses on the challenges that arise when fractional thermal loading is applied to an anisotropic fiber polymeric material. Because of their numerous real-world applications, fibrous polymer materials have received increased attention for thermal analysis. We are interested in stochastic structures known as fractals, which can properly represent complex geometries or physical processes. Certain parts of polymer nanocomposites can be described as “fractal-like” at times. We are interested in the qualities that these structured polymeric materials exhibit both naturally and when heated. The prospect of fractional thermoelasticity motivates research into the thermal field of a built polymeric matrix (or future goods containing nano-constituents) [1,2].
This comprehensive research is largely supported by the fact that stress fields or stress components play a key role in the understanding of mechanical and thermal links in composite materials. Many academics are interested in defining the dynamic response of recent research materials and material properties at different scales. Thermoelastic behavior, including thermal end effect analysis of emerging materials such as polymer micro- and nanofibers, nanostructures, nanowires, and nanomaterials, because of mechanical and thermal loads, is a significant problem in emerging thermal mechanics that requires further investigation. There are a few studies in the literature that look at the thermomechanical and damping behavior of micro- and nanomaterials; however, they all rely on the local theory notion [3,4].
In recent years, numerous researchers have focused on the effect of scale on nanomaterials’ mechanical and thermal properties. The size of the material at the nanoscale has been discovered to have a considerable influence on its thermoelastic characteristics. Nanoscale theories often use continuum mechanics, which assumes a local configuration and includes continuous material properties and pointwise temperatures. As we know, macroscopic material mechanics is ineffective for deformation, stress field, displacement field, and thermal end effect analysis. In the case of very heterogeneous materials, Eshelby’s technique, as stated in the fourth moment theory, is valid in the formation of phase material stress, strain, and displacement fields [5,6].
Because of the greater surface energy, several anomalous events develop, particularly in small nanomaterials on the scale of a nanometer. As a result, numerous thermomechanical properties of the constituent materials, as well as the efficiency of those materials, have been extensively researched in several attempts to construct a nanomaterial. Among its prospective applications, fibrous polymer nanoparticles are primarily intended for soft tissue replacement, such as tendon and ligament tissue. This is simply owing to the morphological resemblance in micro- and nanostructures of well-aligned collagen fibers found in soft tissues. The incredible advancement of plastic surgery has resulted in an increased demand for appropriate fiber-reinforced materials for soft tissue replacement. For hard tissue (e.g., joint replacement), the utilization of long fibers (hydrogel and bone scaffold), known as nanocomposites, has an advantage over current microsized fibers. Fibrous polymer nanomaterials are largely used in hard and soft tissue replacements, as well as in tissue engineering [7,8].
Nanomaterials differ from macroscale equivalents primarily in terms of critical dimensions, which are often measured in nanometers. They have gained significant attention for extending the degree of material nonlocality beyond the nanoscale to nanocomposite materials. Because of the complex structure and properties of nanomaterials, the materials that make up nanostructured materials have a nonlocal distribution and interact with the materials’ boundary surfaces. In the nonlocal field, constitutive materials are represented by a nonlocal damage known as the internal length. However, in the entire field, constitutive materials are ignored, but their effects can still be described as a nonlocal field. As a result, the materials of the nonlocal thermomaterial should be considered nonlocal thermosolids to refine the fields of temperature and deformation using Eringen’s nonlocal model [9,10,11]. Soleiman et al. [12] examined the thermomechanical behaviour of functionally graded nanoscale beams under the fractional heat transfer model using a two-parameter Mittag-Leffler function. Fahmy proposed unique boundary element solutions to thermoelastic nanostructure problems [13,14].
The examination of nonlocal problems of anisotropic fibrous polymer nanomaterials with various boundary conditions includes several particularly interesting topics. The current study introduces a novel mathematical model that is consistent with the non-local thermoelasticity theory for describing the investigated anisotropic fibrous polymer nanomaterials with surface stress and a small-scale parameter. The proposed model may be used to supplement nonlocal continuum models for solely mechanical or thermal boundary value concerns. Furthermore, the nonlocal issue of an anisotropic fibrous polymer nanomaterial with mass diffusion is addressed. Finally, the nonlocal problem defining the combined thermo-chemo-mechanical fuel stress, heat transfer, and mass diffusion phenomenon is investigated using nonlocal completeness, with a focus on surface-stress problems [15,16].
Boundary element analysis has grown in prominence as a useful method for dealing with problems involving convoluted borders in complex geometries [17,18,19,20]. Extensive research has focused on determining the dynamic behavior of various domain models and elastic or inelastic fractures in metallic, geometrically complex, anisotropic fibrous polymeric materials using a variety of interfaces in a more accurate and cost-effective manner by employing methods that allow for the use of available or easily inferred specific boundary conditions. This paper investigates specific mixed boundary value problems in a nonlocal anisotropic fibrous polymeric matrix. More broadly, for subsurface cosine-material composites, we want to determine the mean values of several significant physical fields in space and time that result from thermo-mechanical boundary value problems connected to the generalized nonlocal couple stress theory. We are particularly interested in the polymer-reinforced constituent porous materials with fractal-shaped microstructures, as well as the interface’s defective nonhomogeneity and the nonuniform initial border straightening of conflicts [21,22].
In this paper, we present a novel fractional boundary element solution for nonlinear nonlocal thermoelastic problems employing anisotropic fibrous polymer nanomaterials. This method consists of two steps. First, we handle the anisotropic fibrous polymer nanoparticle problem. Second, we apply the solution of the anisotropic fibrous polymer nanomaterial problem to the nonlinear nonlocal thermoelasticity equation. The numerical results show how fractional and graded parameters influence the thermal stresses of anisotropic size- and temperature-dependent fibrous polymer nanomaterials, demonstrating the accuracy and validity of the proposed methodology.
Let us consider a fibrous polymer nanomaterial in the , occupying the region that is bounded by . The governing equations of fractional size- and temperature-dependent polymer problems of nonlinear nonlocal elasticity can be expressed as the following [13,14]:
The force equilibrium equation:
The fractional-order temperature-dependent heat equation:
where
2. Numerical Solution
In this section, we will determine the general fractional BEM solution to our studied problem, which is composed of the sum of the polymer thermoelastic solution, fractional size- and temperature-dependent solution, and nonlinear nonlocal elasticity solution.
2.1. Polymer Thermoelastic Solution (PTES)
Polymer thermoelasticity refers to the study of the mechanical behavior of polymers under the influence of temperature variations. This phenomenon is critical in various applications such as in the design of smart materials and in the manufacturing of polymer-based products. Understanding how these thermodynamic properties influence the thermoelastic behavior of polymers is essential for their effective utilization in practical applications.
In this subsection, we analyze the mechanical deformation of a fibrous polymer nanomaterial of nonlinear nonlocal thermoelasticity, which is shown in Figure 1, where end-to-end vector R connects the start to the end of the chain.
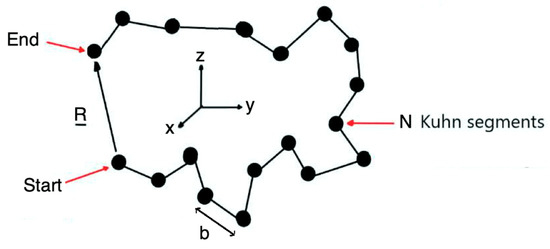
Figure 1.
Polymer chain’s elasticity configuration of Kuhn segments of length , with end-to-end vector , and contour length .
The polymer’s energy in terms of the end-to-end vector is the following [23]:
which can be expressed as
The constitutive equation for polymer elasticity is the following [23]:
where
and
Thus, from Equation (7), we can calculate the displacement, which is a polymer thermoelastic solution from strain .
2.2. Fractional Size- and Temperature-Dependent Solution (FSTDS)
Size-dependent phenomena refer to the changes in the properties of materials as their size is altered, whether at the macroscopic, microscopic, or nanoscopic level. On the other hand, temperature-dependent phenomena encompass the alterations in material properties as a result of changes in temperature. The significance of studying these phenomena lies in their profound implications for the design, fabrication, and application of materials in diverse industries, including electronics, healthcare, energy, and transportation.
The couple stress, force traction, and couple traction are the following [13]:
in which
The considered boundary conditions are
The governing Equations (1) and (2) can be expressed as [13,14]
In which
According to [14], Equation (2) yields
in which
The integral equation corresponding to (32) can be defined as [13]
To solve the domain integrals in Equation (35), we used the same process as Fahmy [14] and the techniques from [24,25] to obtain the following system:
According to [14], that can also be expressed as
Thus, we obtain the fractional size- and temperature-dependent solution .
2.3. Nonlinear Nonlocal Elasticity Solution (NNES)
Nonlinear nonlocal elasticity deals with the mechanical behavior of materials that cannot be accurately described by linear elasticity theory. Instead, it takes into account nonlocal effects, meaning that the deformation at a point is influenced by the state of stress and strain at all other points in the material. This contrasts with classical elasticity, which assumes that the state of stress at a point is only influenced by the deformation in the immediate vicinity.
According to Eringen’s nonlocal elasticity model, we consider the stress–strain relation (8) and the attenuation function of Lazar et al. [26] with the following properties:
- (I)
- The nonlocal kernel must depend on the internal length;
- (II)
- ;
- (II)
- It should satisfy , .
Also, Dirac delta function at (local elasticity).
The following attenuation function is used in this paper:
such that
where .
According to Polizzotto et al. [27], a stress–strain relation can be expressed as the following:
where
and
The local governing equation can be expressed as the following:
Equation (40) can be expressed as the following:
with .
The field Equation (41) is written as the following:
Liu and Gu [28] suggested a weak-strong form point collocation method for solving Equation (43). In addition, Schwartz et al. [29] presented the strong-form local radial point interpolation method (LRPIM) for solving Equation (43). This work introduces a BEM based on the strong-form LRPIM.
A nonlinear nonlocal elasticity displacement solution is created by adding a complementary displacement and a particular displacement . Thus, from Equation (43), we obtain the following:
To obtain a complementary solution , Equation (44) has been written in the following form [30]:
According to the local radial point interpolation of Liu and Gu [31], the kinematical field can be interpolated as follows:
where
where
and
Approximation (47) is now written as the following [29]:
or
By using interpolation (54), Equation (45) has been written as the following:
which can be written as the following:
Now, to obtain a particular solution, we assume that ; thus, we have the following:
The boundary traction can be expressed more compactly as the following [29]:
where
Now, Equation (46) can be rewritten as the following [29]:
By using Equations (57), (59), and (60), we have the following final BEM equation:
The nonlinear nonlocal elasticity solution is obtained by adding the complementary solution and particular solution together.
Hence, from Equations (7), (35), and (62), we obtain general solution of the considered problem as follows:
where the general solution of our considered problem is constructed as the sum of the following three solutions: polymer thermoelastic solution , fractional size- and temperature-dependent solution , and nonlinear nonlocal elasticity solution . The new modified shift-splitting (NMSS) [32] technique was used to solve the resulting linear Equations (7), (35), and (62) arising from BEM.
3. Numerical Results and Discussion
This study considered the generalized radial basis functions and with the anisotropy constant of magnetite nanoparticles given in [33] and the following parameters: , , and . This study considered the computational domain, which has 40 boundary nodes and 90 internal nodes as illustrated in Figure 2.

Figure 2.
Boundary element model.
This study also considered the reinforcing factors , , and , as well as the following anisotropic fibrous behavior:
The proposed methodology is applicable to a wide range of fibrous polymer nanomaterial issues, including nonlinear nonlocal elasticity. The numerical results demonstrate the computational performance of the proposed methodology, as shown in Table 1 and Table 2 below. The new modified shift-splitting (NMSS) technique [32] was applied to reduce memory and processing time requirements. Figures depict the numerical results, which highlight the effects of fractional and graded parameters on the thermal stresses of anisotropic fractional size and temperature-dependent fibrous polymer nanomaterials with nonlinear nonlocal elasticity.

Table 1.
CPU timings and iteration counts for regularized, GMSS, and NMSS models.

Table 2.
A comparison of the computational resources needed to model nonlinear nonlocal thermoelastic problems of anisotropic fibrous polymer nanomaterials.
Table 1 illustrates the CPU time and iteration number for new modified shift-splitting (NMSS) [32], generalized modified shift-splitting (GMSS) [34], and regularized [35] iterative methods at every discretization level, where the number of the equation is represented between parentheses. This table demonstrates the superiority of the NMSS over the regularized and GMSS approaches.
Figure 3 depicts the fluctuation of thermal stress along the -axis for various fractional order parameters . This figure demonstrates that when the fractional order parameter increases, the thermal stress decreases.
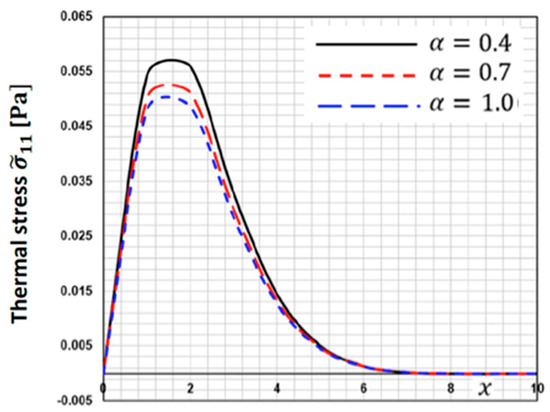
Figure 3.
Thermal stress distribution along the -axis for different fractional order parameters.
Figure 4 depicts the fluctuation of thermal stress along the -axis for various fractional order parameters . This figure demonstrates that when the fractional order parameter increases, the thermal stress increases.
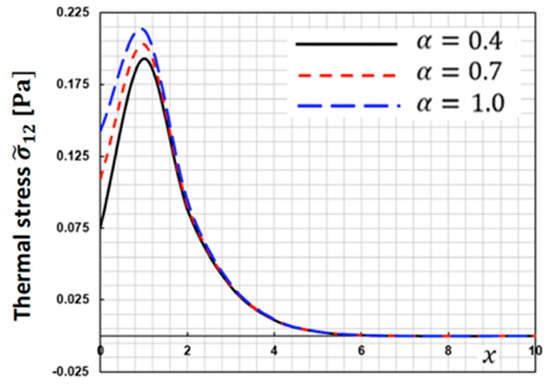
Figure 4.
Thermal stress distribution along the -axis for different fractional order parameters.
Figure 5 depicts the fluctuation of thermal stress along the -axis for various fractional order parameters . This figure demonstrates that when the fractional order parameter increases, the thermal stress decreases.
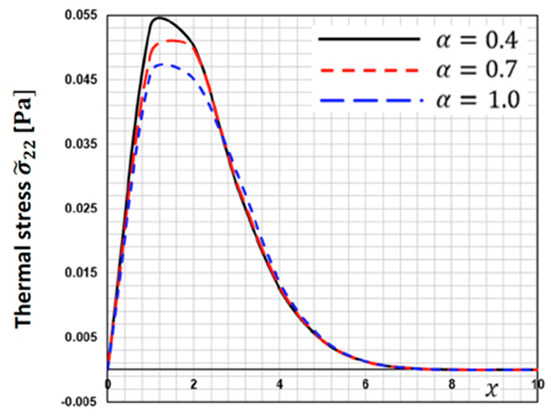
Figure 5.
Thermal stress distribution along the -axis for different fractional order parameters.
Figure 6 depicts the fluctuation of thermal stress along the -axis for various fractional order parameters . This figure demonstrates that when the functionally graded parameter increases, the thermal stress decreases.
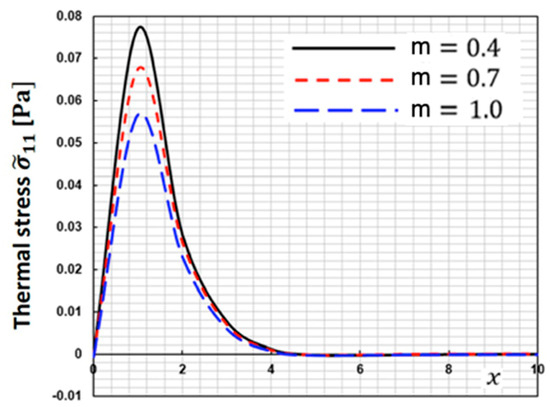
Figure 6.
Thermal stress distribution along the -axis for different fractional order parameters.
Figure 7 depicts the fluctuation of thermal stress along the -axis for various fractional order parameters . This figure demonstrates that when the functionally graded parameter increases, the thermal stress decreases.
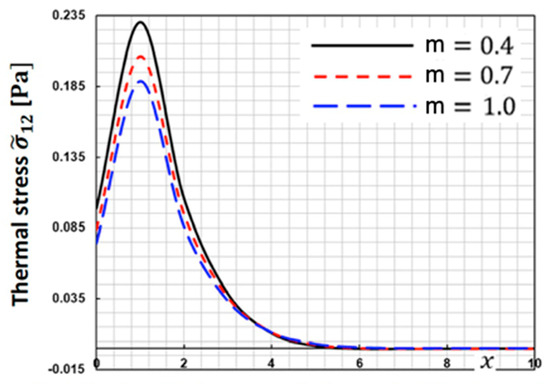
Figure 7.
Thermal stress distribution along the -axis for different fractional order parameters.
Figure 8 depicts the fluctuation of thermal stress along the -axis for various fractional order parameters . This figure demonstrates that when the functionally graded parameter increases, the thermal stress increases.
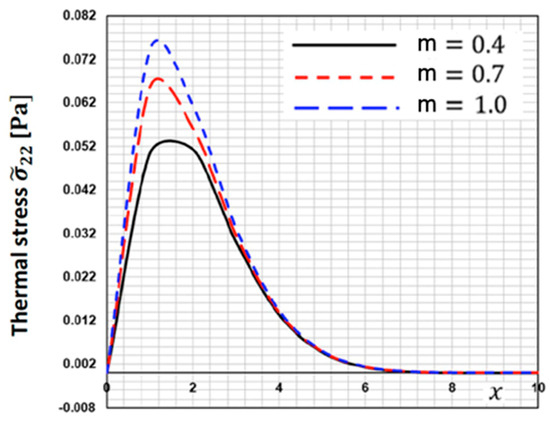
Figure 8.
Thermal stress distribution along the -axis for different fractional order parameters.
The current BEM approach strategy’s validity and accuracy have not been shown by any published data. However, in the context of this current broad investigation, some works can be considered special cases.
Figure 9, Figure 10 and Figure 11 display the change in special case thermal stresses , and along the x-axis for the suggested BEM, finite element method (FEM) of Sidhardh et al. [36], and analytical (Analytical) solution of Kumar and Mukhopadhyay [37], which are some special cases of our study. These figures show that the BEM results of the proposed technique match well with the FEM and Analytical results, validating the technique’s validity and accuracy.
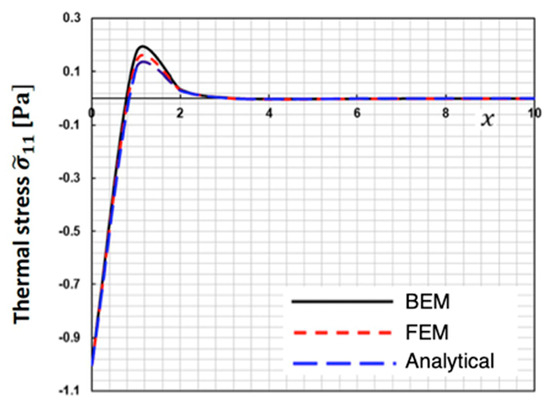
Figure 9.
Thermal stress distribution along the -axis for BEM, FEM, and Analytical.
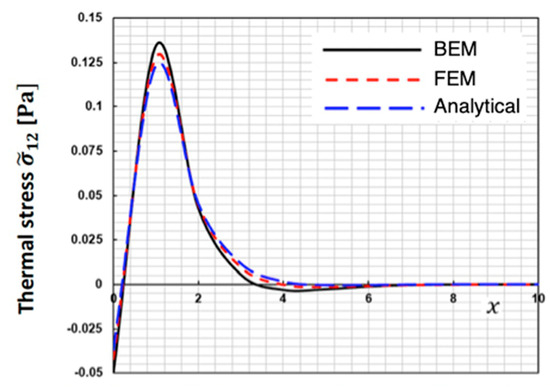
Figure 10.
Thermal stress distribution along the -axis for BEM, FEM, and Analytical.
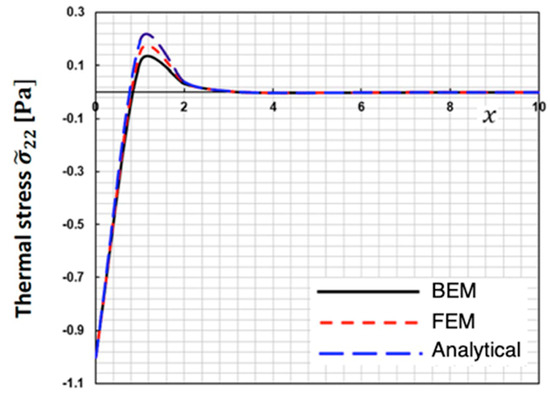
Figure 11.
Thermal stress distribution along the -axis for BEM, FEM, and Analytical.
Table 2 compares computer resources needed to model nonlinear nonlocal thermoelastic problems of anisotropic fibrous polymer nanomaterials for current BEM and the finite element method (FEM). This table shows the effectiveness of our suggested BEM technique.
4. Conclusions
Some of the inferences that can be drawn from the current study are as follows:
- A new fractional boundary element model was used to solve the nonlinear nonlocal size- and temperature-dependent thermoelastic problems of anisotropic fibrous polymer nanomaterials.
- Th proposed BEM technique was used first to solve the anisotropic fibrous polymer nanoparticle problem. Then, we used the solution of the anisotropic fibrous polymer nanomaterial problem to solve the nonlinear nonlocal thermoelasticity problem.
- The nonlocal elastic technique separates the displacement field into a complementary component and a particular component.
- The overall displacement is obtained using the boundary element technique, which solves a Navier-type problem, whereas the individual displacement is derived using local radial points.
- The new modified shift-splitting (NMSS) technique which reduces memory and processing time requirements was used to solve linear systems created by BEM.
- The numerical findings were depicted graphically to display the influences of the fractional and graded parameters on the thermal stresses of anisotropic fibrous polymer nanomaterials.
- The numerical findings also show the differences between the regularized, generalized modified shift-splitting, and new modified shift-splitting iterative methods, and they verified the validity, accuracy, and effectiveness of the developed fractional boundary element technique.
- The main advantages of the current HBEM model are its generality and simplicity. The numerical findings supported the claim that the proposed method offers more advantages than other domain discretization techniques.
- A comparison of the computational resources needed to solve nonlinear nonlocal thermoelastic problems of anisotropic fibrous polymer nanomaterials was performed for current fractional BEM and the finite element method (FEM).
- The findings of this paper contribute to the development of mathematical models that can be applied in food packaging, phones, soda and water bottles, films, agriculture, biomedical devices, coating, paints, blending, airplanes, textile fibers, the automotive industry, consumer goods, industrial, recreational vehicles, effective actuators, fluorescence imaging, photodynamic therapy, hydrogels, electronic devices, engineering resins and polyolefins, and computers, among others.
- In future work, we suggest expanding the boundary element technique proposed in this research for applications in three-dimensional thermoelastic problems of anisotropic fibrous polymer nanomaterials, which include multilayer difficulties, complex geometries, and the inclusion of convective factors.
Author Contributions
Conceptualization, M.A.F.; methodology, M.A.F.; software, M.A.F.; validation, M.A.F.; formal analysis, M.A.F.; investigation, M.A.F.; resources, M.A.F.; data curation, M.A.F.; writing—original draft preparation, M.A.F. and M.T.; writing—review and editing, M.A.F. and M.T.; visualization, M.A.F. and M.T.; supervision, M.A.F. and M.T.; project administration, M.A.F. and M.T.; funding acquisition, M.A.F. and M.T. All authors have read and agreed to the published version of the manuscript.
Funding
The authors did not receive support from any organization for the submitted work.
Data Availability Statement
All data generated or analyzed during this study are included in this published article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Thermal expansion | Pseudo mean curvature tensor | ||
| Thermal shear strain | Internal length of considered material | ||
| Boundary | Couple traction | ||
| Kronecker delta function | Monomials number | ||
| Strain tensor | True couple-stress vector | ||
| Couple stress parameter | Pseudo couple-stress tensor | ||
| Yield stress | Functionally graded parameter | ||
| Total force-stress tensor | Outward unit normal vector | ||
| Symmetric force-stress tensor | Nodes number | ||
| Skew-symmetric force-stress tensor | P | Pressure | |
| Rotation | Point couple kernel function | ||
| Spherical region | Monomials | ||
| Shape parameters | External heat source | ||
| Heat capacity | Euclidian distance | ||
| Point force kernel function | Radius of spherical region | ||
| Fourth-order constant stiffness tensor | Radial basis function | ||
| Young’s modulus | Traction | ||
| Body force vector | Displacement vector | ||
| Strain hardening | Kelvin fundamental solution | ||
| I | Identity tensor | Poisson’s ratio | |
| Boltzmann’s constant | Evaluation point | ||
| Mean curvature vector | Center point | ||
| Field point |
References
- Kong, B.; Liu, R.; Guo, J.; Lu, L.; Zhou, Q.; Zhao, Y. Tailoring micro/nano-fibers for biomedical applications. Bioact. Mater. 2023, 19, 328–347. [Google Scholar] [CrossRef]
- Deng, R.; Luo, Z.; Rao, Z.; Lin, Z.; Chen, S.; Zhou, J.; Zhu, Q.; Liu, X.; Bai, Y.; Quan, D. Decellularized extracellular matrix containing electrospun fibers for nerve regeneration: A comparison between core–shell structured and preblended composites. Adv. Fiber Mater. 2022, 4, 503–519. [Google Scholar] [CrossRef]
- Lu, C.; Shao, H.; Bi, S.; Chen, N.; Shao, G.; Jiang, J. Estimation of transverse thermoelastic properties of polyimide fibers based on micromechanical models. Compos. Sci. Technol. 2024, 250, 110541. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Ahmad, H.; Nofal, T.A.; Abu-Zinadah, H. Thermo-viscoelastic fractional model of rotating nanobeams with variable thermal conductivity due to mechanical and thermal loads. Mod. Phys. Lett. B 2021, 35, 2150297. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Marin, M. The size-dependent thermoelastic vibrations of nanobeams subjected to harmonic excitation and rectified sine wave heating. Mathematics. Mathematics 2020, 8, 1128. [Google Scholar] [CrossRef]
- Huang, K.; Xu, W. A Nonlinear Nonlocal Thermoelasticity Euler–Bernoulli Beam Theory and Its Application to Single-Walled Carbon Nanotubes. Nanomaterials 2023, 13, 721. [Google Scholar] [CrossRef] [PubMed]
- Pryjmaková, J.; Kaimlová, M.; Hubáček, T.; Švorčík, V.; Siegel, J. Nanostructured materials for artificial tissue replacements. Int. J. Mol. Sci. 2020, 21, 2521. [Google Scholar] [CrossRef]
- Mosaad, K.E.; Shoueir, K.R.; Saied, A.H.; Dewidar, M.M. New prospects in nano phased co-substituted hydroxyapatite enrolled in polymeric nanofiber mats for bone tissue engineering applications. Ann. Biomed. Eng. 2021, 49, 2006–2029. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Lu, Y.; He, T. An investigation into size-dependent dynamic mechanical-diffusion responses of multi-layered laminated sandwich-like nanocomposites under shock loadings of molar concentration for vibration control based on nonlocal diffusion-elasticity theory. Mech. Adv. Mater. Struct. 2023, 30, 647–660. [Google Scholar] [CrossRef]
- Tchepemen, N.; Balasubramanian, S.; Kanagaraj, N.; Kengne, E. Modulational instability in a coupled nonlocal media with cubic, quintic and septimal nonlinearities. Nonlinear Dyn. 2023, 111, 20311–20329. [Google Scholar] [CrossRef]
- Arash, B.; Unger, R.; Exner, W.; Rolfes, R. A finite deformation gradient-enhanced damage model for nanoparticle/polymer nanocomposites: An atomistically-informed multiscale approach. Compos. Struct. 2021, 258, 113211. [Google Scholar] [CrossRef]
- Soleiman, A.; Abouelregal, A.E.; Fahmy, M.A.; Sedighi, H.M. Thermomechanical Behavior of Functionally Graded Nanoscale Beams Under Fractional Heat Transfer Model with a Two-Parameter Mittag-Leffler Function. Iran. J. Sci. Technol. Trans. Mech. Engineering. 2023. [Google Scholar] [CrossRef]
- Fahmy, M.A. A new BEM modeling algorithm for size-dependent thermopiezoelectric problems in smart nanostructures. CMC-Comput. Mater. Contin. 2021, 69, 931–944. [Google Scholar] [CrossRef]
- Fahmy, M.A. Fractional Temperature-Dependent BEM for Laser Ultrasonic Thermoelastic Propagation Problems of Smart Nanomaterials. Fractal Fract. 2023, 7, 536. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Rabih, M.N.A.; Alharbi, H.A.; Megahid, S.F. A modified couple stress model to analyze the effect of size-dependent on thermal interactions in rotating nanobeams whose properties change with temperature. Math. Mech. Solids 2024. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Mohamed, B.O.; Sedighi, H.M. Thermoelastic deformation properties of non-localized and axially moving viscoelastic Zener nanobeams. Adv. Nano Res. 2024, 16, 141–154. [Google Scholar] [CrossRef]
- Fahmy, M.A. A new boundary element formulation for modeling and simulation of three-temperature distributions in carbon nanotube fiber reinforced composites with inclusions. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Fahmy, M.A. 3D Boundary Element Model for Ultrasonic Wave Propagation Fractional Order Boundary Value Problems of Functionally Graded Anisotropic Fiber-Reinforced Plates. Fractal Fract. 2022, 6, 247. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Almehmadi, M.M. Boundary element analysis of rotating functionally graded anisotropic fiber-reinforced magneto-thermoelastic composites. Open Eng. 2022, 12, 313–322. [Google Scholar] [CrossRef]
- Fahmy, M.A. Three-Dimensional Boundary Element Strategy for Stress Sensitivity of Fractional-Order Thermo-Elastoplastic Ultrasonic Wave Propagation Problems of Anisotropic Fiber-Reinforced Polymer Composite Material. Polymers 2022, 14, 2883. [Google Scholar] [CrossRef]
- Ren, B.; Wu, C.T.; Seleson, P.; Zeng, D.; Nishi, M.; Pasetto, M. An FEM-Based Peridynamic Model for Failure Analysis of Unidirectional Fiber-Reinforced Laminates. J. Peridynamics Nonlocal Model. 2022, 4, 139–158. [Google Scholar] [CrossRef]
- Eshmatov, B.K.; Abdikarimov, R.; Amabili, M.; Vatin, N.I. Nonlinear vibrations and dynamic stability of viscoelastic anisotropic fiber reinforced plates. Mag. Civ. Eng. 2023, 118, 11811. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Elasticity of Polymer Networks. Macromolecules 2002, 35, 6670–6686. [Google Scholar] [CrossRef]
- Hematiyan, M.R. Exact transformation of a wide variety of domain integrals into boundary integrals in boundary element method. Commun. Numer. Methods Eng. 2008, 24, 1497–1521. [Google Scholar] [CrossRef]
- Hadjesfandiari, A.R.; Dargush, G.F. Fundamental solutions for isotropic size-dependent couple stress elasticity. Int. J. Solids Struct. 2013, 50, 1253–1265. [Google Scholar] [CrossRef]
- Lazar, M.; Maugin, G.A.; Aifantis, E.C. On a theory of nonlocal elasticity of biHelmholtz type and some applications. Int. J. Solids Struct. 2006, 43, 1404–1421. [Google Scholar] [CrossRef]
- Polizzotto, C.; Fushi, P.; Pisano, A.A. A strain-difference-based nonlocal elasticity model. Int. J. Solids Struct. 2004, 41, 2383–2401. [Google Scholar] [CrossRef]
- Liu, G.R.; Gu, Y.T. A meshfree method: Meshfree weak-strong (MWS) form method for 2-D solids. Comput. Mech. 2003, 33, 2–14. [Google Scholar] [CrossRef]
- Schwartz, M.; Niane, N.; Njiwa, R.K. A simple solution method to 3D integral nonlocal elasticity: Isotropic-BEM coupled with strong form local radial point interpolation. Eng. Anal. Bound. Elements 2011, 36, 606–612. [Google Scholar] [CrossRef]
- Brebbia, C.A.; Dominguez, J. Boundary Elements. An Introductory Course; Computational Mechanics Publications: Southampton, UK, 1992. [Google Scholar]
- Liu, G.R.; Gu, Y.T. A local radial point interpolation method (LRPIM) for free vibration analyses of 2-D solids. J. Sound Vib. 2001, 246, 29–46. [Google Scholar] [CrossRef]
- Badahmane, A. Regularized preconditioned GMRES and the regularized iteration method. Appl. Numer. Math. 2020, 152, 159–168. [Google Scholar] [CrossRef]
- Victoria, L.; del Castillo, C.D.; Rinaldi, C. Effect of Sample Concentration on the Determination of the Anisotropy Constant of Magnetic Nanoparticles. IEEE Trans. Magn. 2010, 46, 852–859. [Google Scholar] [CrossRef]
- Huang, Z.G.; Wang, L.G.; Xu, Z.; Cui, J.J. The generalized modified shift-splitting preconditioners for nonsymmetric saddle point problems. Appl. Math. Comput. 2017, 299, 95–118. [Google Scholar] [CrossRef]
- Ardeshiry, M.; Goughery, H.S.; Pour, H.N. New modified shift-splitting preconditioners for non-symmetric saddle point problems. Arab. J. Math. 2020, 9, 245–257. [Google Scholar] [CrossRef]
- Sidhardh, S.; Patnaik, S.; Semperlotti, F. Thermodynamics of fractional-order nonlocal continua and its application to the thermoelastic response of beams. Eur. J. Mech./A Solids 2021, 88, 104238. [Google Scholar] [CrossRef]
- Kumar, H.; Mukhopadhyay, S. Size-dependent thermoelastic damping analysis in nanobeam resonators based on Eringen’s nonlocal elasticity and modified couple stress theories. J. Vib. Control. 2022, 29, 1510–1523. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).