Abstract
Three-dimensional porous scaffolds are substitutes for traditional bone grafts in bone tissue engineering (BTE) applications to restore and treat bone injuries and defects. The use of computational modelling is gaining momentum to predict the parameters involved in tissue healing and cell seeding procedures in perfusion bioreactors to reach the final goal of optimal bone tissue growth. Computational modelling based on finite element method (FEM) and computational fluid dynamics (CFD) are two standard methodologies utilised to investigate the equivalent mechanical properties of tissue scaffolds, as well as the flow characteristics inside the scaffolds, respectively. The success of a computational modelling simulation hinges on the selection of a relevant mathematical model with proper initial and boundary conditions. This review paper aims to provide insights to researchers regarding the selection of appropriate finite element (FE) models for different materials and CFD models for different flow regimes inside perfusion bioreactors. Thus, these FEM/CFD computational models may help to create efficient designs of scaffolds by predicting their structural properties and their haemodynamic responses prior to in vitro and in vivo tissue engineering (TE) applications.
1. Introduction
Bones are one of the most vital organs in the human body. They contain a reservoir of minerals that provide protection for inner organs and support for muscles and physical activities. Bone tissue is arranged as inner spongy cancellous bone of 75% to 95% porosity with a mean pore size of 200 µm to 600 µm diameter and outer compact cortical bone of 5% to 10% porosity with 10 µm to 100 µm pore diameter [1]. Ageing, trauma, bone loss, cancer, infection, and metabolic bone disorders are causes of bone defects and injuries. Bone grafts are conventionally used for bone tissue reconstruction. However, they come with disadvantages such as infection, immune rejection on the host site, lack of vascularisation, disease transmission and increased patient morbidity [2].
Bone tissue engineering (BTE) is an interdisciplinary bioengineering field that combines life sciences, engineering, materials, and physio-chemical and biological components to restore and replace injured and damaged bone tissues with new biological tissues [3,4,5]. BTE procedures typically utilise three-dimensional (3D) porous temporary support structures known as scaffolds made of various materials to neo-tissues during regeneration (Figure 1). These scaffolds assist stem cells in surviving, proliferating, migrating, and differentiating into various functional tissues [6]. They achieve this by providing a network of interconnected pores and struts that not only support mechanical loading but also enable efficient mass transport, allowing for the movement of nutrients and waste materials [7,8]. The degradation rate of scaffolds must be near the neo-tissue growth rate in the regeneration of bone tissues (Figure 1 and Figure 2). Ensuring that the degradation rates are synchronised with new tissue growth is crucial for maintaining structural integrity and supporting the healing process [9,10]. This synchronisation minimises the inflammation risk and mechanical failure while promoting natural and efficient tissue regeneration [11].
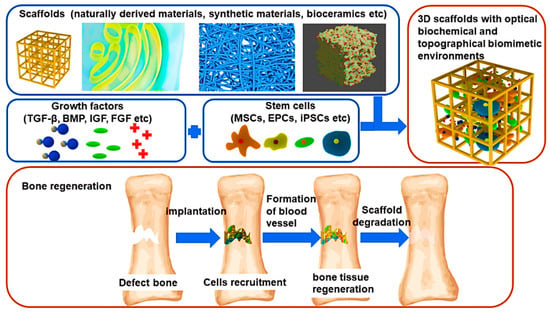
Figure 1.
Illustration of scaffolds-based BTE. TGF-β: Transforming Growth Factor-β, BMP: Bone Morphogenetic Proteins, IGF: Insulin-like Growth Factor, FGF: Fibroblast Growth Factor, MSCs: Mesenchymal Stem Cells, EPC: Endothelial Progenitor Cell, iPSC: Induced Pluripotent Stem Cells. Reproduced with permission from Ref. [12] CC BY 4.0.
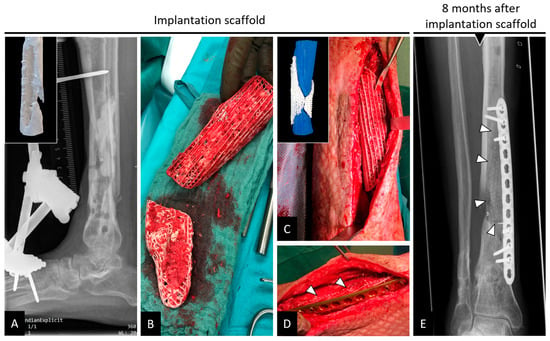
Figure 2.
(A–D) Implantation of a composite scaffold on a tibial bone defect region. (E) Bone remodelling in and out of the scaffold with white triangles denoting the external boundaries of the scaffold. Reproduced with permission from Ref. [13] CC BY 4.0.
Computational modelling utilises mathematical models to study the complex processes of a physical system using high-end computational resources. This technique involves modifying inputs and boundary conditions within computer simulations to facilitate the exploration and analysis of different scenarios and outcomes in the models [14,15,16]. The advantage of simulation is that one can evaluate the designed scaffolds before fabrication, ex vivo testing and in vivo implantation to save time and cost while obtaining valuable information about scaffold designs [17,18]. The other advantage is that one can virtually evaluate many scaffolds without fabrication by changing the related geometry and material properties [19,20]. The results from the computational simulation are usually validated through comparison with experimental studies [21,22]. Computational methods have been used to design scaffold architectures [23,24], to predict equivalent mechanical properties of scaffolds under diverse loading conditions using the finite element method (FEM) [25,26,27], and to predict their flow properties under different flow scenarios using computational fluid dynamics (CFD) [28,29]. They are also applied to model the degradation profiles of scaffolds in hydrolytic degradation and erosion environments [30,31], to simulate bone ingrowth or bone remodelling within scaffolds [32] and to simulate the vascularisation of blood vessels [33]. The advantage of such computational modelling lies in its capacity to predict scenarios that cannot otherwise be monitored in real-time, contributing proactive knowledge into potential outcomes; the key to successful prediction depends on choosing suitable models for given problems. The research questions which are addressed in this review article for computational modelling in BTE are:
- How do a scaffold’s architecture and morphological parameters affect its equivalent mechanical properties and permeability?
- How do the scaffolds behave under different loading conditions and different fluid flow conditions while transporting materials such as nutrients and waste materials? How do their equivalent mechanical properties and flow properties vary in such scenarios?
- What kind of material models can be applied for FEM-based structural analysis of scaffolds, and what kind of fluid flow models can be utilised for CFD-based permeability analysis of scaffolds?
2. Computational Modelling of Mechanical Behaviour and Permeability of Scaffolds
2.1. Design of Scaffolds
2.1.1. Essentials of Scaffolds
Scaffolds for BTE are temporary porous biomaterial structures that act as supporting frameworks for incoming cells to adhere to, multiply and finally differentiate into different functional bone tissues. They must be: (i) nontoxic to host tissues (i.e., biocompatible), (ii) able to degrade their structure to give space for the growing bone cells (i.e., biodegradable) [34], (iii) able to permit the cells to stick and multiply on their surfaces to generate extracellular matrix (i.e., osteoconductive) [35], (iv) able to induce neo-bone tissues through mechanical stimulus (i.e., osteoinductive) [36], (v) able to form bone materials with the help of bone-forming cells ‘osteoblasts’ (i.e., osteogenic), (vi) able to integrate existing osseous tissues with their load-bearing surfaces (osteointegration) [37], (vii) exhibit appropriate morphological characteristics like pore size, porosity, and pore connectivity [38], and (viii) mirror the mechanical properties of the host tissues, including Young’s modulus and compressive strength. These properties of scaffolds are influenced by their materials, such as synthetic and natural polymers, bio-composites, metal alloys and ceramics (Figure 3 and Figure 4) [39,40,41].

Figure 3.
The characteristics of a BTE scaffold and its related supportive functions [42].
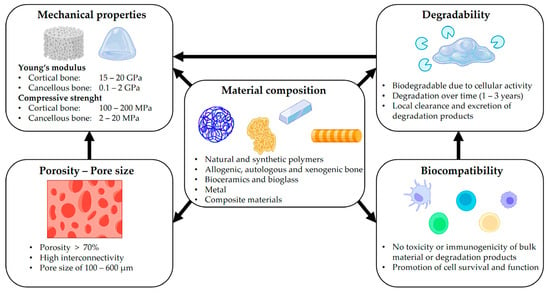
Figure 4.
Factors required for designing scaffolds. Reproduced with permission from Ref. [43] CC BY 4.0.
2.1.2. Types of Designs
There are two types of scaffold designs based on the architecture: non-parametric and parametric (Figure 5) [44]. Non-parametric designs are based on traditional lattice geometries such as simple cubic, body-centred cubic (BCC), face-centred cubic (FCC) [45,46], octet, truncated octahedron [47], diamond, truncated cube [48], fluorite, kelvin cell [49], iso truss, re-entrant, Weaire–Phelan and honeycomb [50]. An advantage of non-parametric design is that the scaffolds are more accessible to manufacture due to their simple geometries, as they do not require specialised algorithms to generate. Parametric designs, on the other hand, leverage more complex algorithms to create complicated structures, such as Triply Periodic Minimal Surfaces (TPMS) [51] and Voronoi structures [52,53]. Modern additive manufacturing technologies (AM) are capable of producing such complex designs [54,55]. Scaffolds based on TPMS can be generated through trigonometric equations and provide a smooth surface devoid of sharp edges, zero mean curvature, a high surface-to-area ratio, well-interconnected non-tortuous pores, and superior material permeability compared to scaffolds based on non-parametric designs [56,57]. Voronoi scaffolds are designed based on Voronoi tessellation using randomly distributed seeding points to create polyhedral cells scaled to form pores and struts of structures similar to trabecular bones [58,59]. Apart from TPMS and Voronoi structures, distinct research works are being performed to design unique stochastical structures to mimic the bone structures using level set equations with weight functions [60], an anisotropic spinodal phase decomposition with Gaussian random fields (GRF) [61,62,63], and an iterative topological network optimisation based on a graph of trabecular bone [64,65].
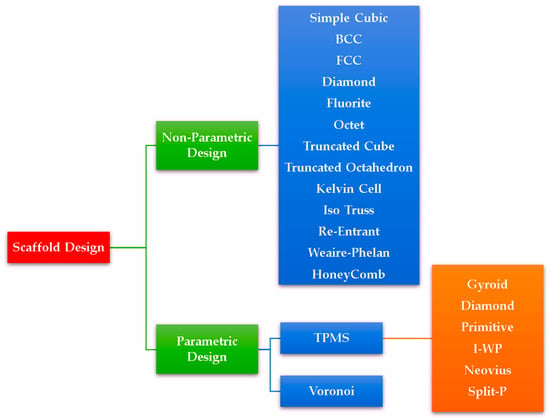
Figure 5.
Types of scaffold designs based on their architectures. Their related structures can be viewed in Supplementary Materials Figures S1–S3.
Further, the scaffolds can be classified into uniform and functionally graded scaffolds (FGS). Uniform scaffolds have the same porosity throughout their structure, whereas FGS have gradient porosities based on relative density or cell size variation [66,67]. The gradient in an FGS may be designed to imitate the characteristics of native tissues. Usually, scaffold design begins with obtaining anatomical shapes from imaging tools like computer tomography (CT) [68,69] and magnetic resonance imaging (MRI), or modelling cellular lattices using computer-aided design (CAD) software or specialised programs (Supplementary Materials Table S1).
2.1.3. Influence of Morphological Parameters on Mechanical Behaviour and Permeability
The morphological parameters of scaffolds, such as pore size, porosity, pore interconnections and pore shape, all influence osteogenesis. A large pore size, for example, leads to higher porosity and a larger surface area for the cells to live, multiply and differentiate into specialised bone tissues. The morphology of scaffolds and their effective pore interconnections play a crucial role in facilitating oxygen exchange and nutrient delivery within the scaffolds for cell growth, which is essential for successful tissue regeneration [70]. However, increased porosity compromises mechanical strength, impacting the scaffold’s ability to withstand applied loads [71].
2.2. Simulation of Mechanical Behaviour of BTE Scaffolds
FEM for Prediction of Mechanical Properties
The mechanical properties of the scaffolds, such as effective elastic modulus compressive and tensile strengths, depend on their material properties and architectures [72]. Scaffolds are subjected to various types of loading, including shear, bending, torsion, tension, and compression, after they are implanted inside the body [73,74]. In load bearing BTE applications, scaffolds must support loads ranging from hundreds to thousands of newtons, making their mechanical properties crucial [75,76]. It is indispensable for the scaffolds to withstand significant loads without collapsing to achieve the goal of bone tissue generation. FEM is a numerical tool used to solve partial differential equations (PDEs) in real-time engineering problems, enabling the prediction of mechanical properties. This capability is valuable for optimising the scaffolds by modifying their morphological parameters [77,78]. In FEM, the scaffold geometry is partitioned into a finite number of elements using the process of meshing. Generally, increasing the number of finite elements improves the accuracy and fidelity of simulation results but also leads to an increase in computation time [79]. An FE model combines FE meshes and material properties such as Poisson’s ratio and Young’s modulus. The choice of model depends on scaffold materials, which vary from elastic, plastic, hyperelastic, poor elastic, and elastoplastic to viscoelastic models, which can express one or more linear, bilinear, multilinear, and non-linear behaviours (Figure 6) (Table 1). By applying boundary conditions such as force, acceleration loads, pressure and displacement restraints to FE models, various mechanical properties, including displacement, principal strain, component strain, principal stress, von Mises stress and component stress are computed for different materials [80,81]. These calculations are conducted through static, quasi-static, and buckling analyses. The workflow (Figure 7) of an imaging-based FEM computational modelling process of TE scaffolds is given by Imran et al. [82].
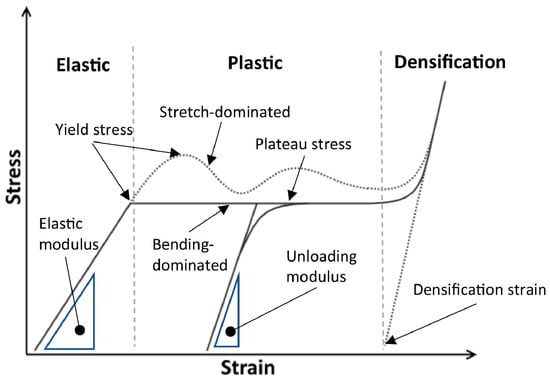
Figure 6.
Different stages of compressive behaviour of lattice structures. Reproduced with permission from Ref. [83] CC BY-NC-ND 4.0.
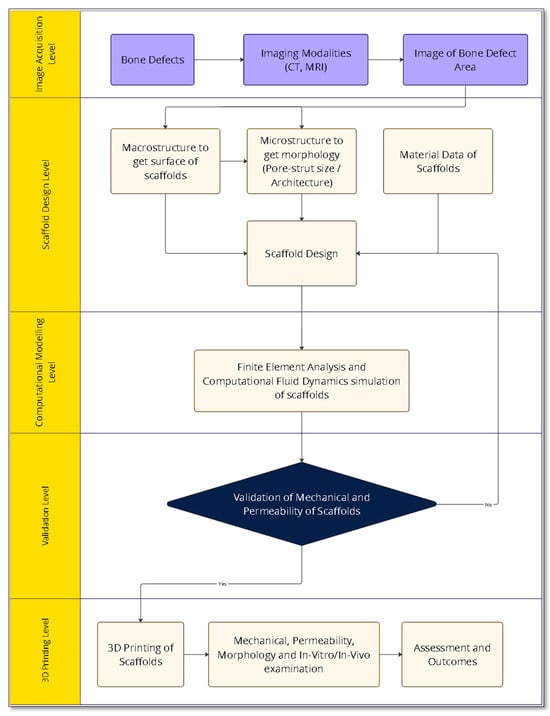
Figure 7.
An image-based FEM computational workflow for BTE scaffolds using FEM and CFD modelling [82].
One of the basic FEM-based material models for structural analysis is a linear model which obeys Hooke’s Law. This linear model substantiates a linear association between the applied force and the resulting displacement. In a linear isotropic material model, the properties of materials do not change with direction. Musthafa et al. [84] designed gyroid-based TPMS scaffolds of titanium alloys with different pore sizes using the signed distance field method and applied compressive loading using linear elastic FEM-based simulation to evaluate their effective elastic modulus for BTE applications. In this research, methods to create surface/volume/FE meshes from a gyroid lattice were explained to create FE models for the compressive loading simulation (Figure 8). The results revealed that the predicted elastic moduli of the scaffolds were in the range of 0.05 to 1.93 GPa and gave an insight into how the required mechanical properties can be achieved by tuning the morphological parameters of the scaffold [84]. However, it is imperative to note that this linearity holds only within the linear elastic region of a material. Linear elastic models are suitable only for small deformations, while summations involving large deformations necessitate the use of non-linear elastic models to predict yielding behaviour accurately [85]. A similar linear isotropic elastic trend was found in Ti6Al4V scaffolds based dental implants for periodontal diseases (Figure 9).
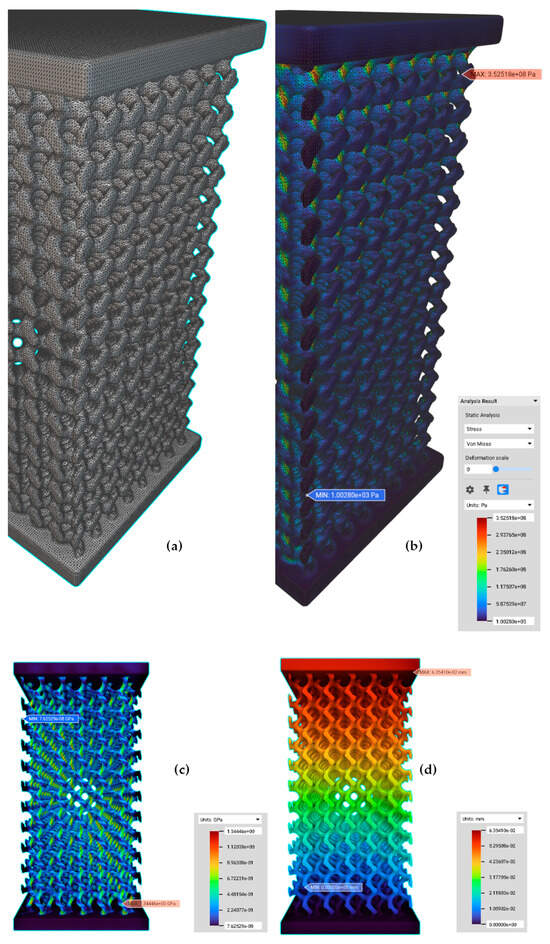
Figure 8.
(a) An FE volume mesh for an FE model from an implicit body of a cuboid gyroid scaffold (conversion of the given implicit body to a surface mesh, to a volume mesh with tetrahedral elements and a FE volume mesh with quadratic order), (b) structural analysis of an FE model under compressive loading. (c) von Mises contour of PS550 (Pore size 500 µm and Strut size 300 µm) gyroid scaffold, and (d) displacement contour of PS550. Reproduced with permission from Ref. [84] CC BY 4.0.
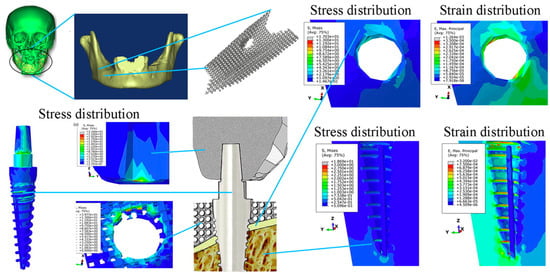
Figure 9.
Prediction of von Mises stress (S) and max principal strain (E) of scaffolds attached to dental implants using FEM-based linear isotropic models. Reproduced with permission from Ref. [86] CC BY-NC-ND 4.0.
In bilinear isotropic (BISO) hardening models, the stress and strain vary even after attaining maximum plastic deformation. A bilinear isotropic hardening model was applied with quasi-static compressive loading-based simulation using FEM by Zhang et al. [87] to predict local strain distributions, effective Young’s modulus, and compressive strength of poly (ε-caprolactone)/nanohydroxyapatite scaffolds for osteochondral bone defects. The objective of this work was to evaluate the effects of pore shape on scaffolds’ mechanical properties. A mesh size of 0.125 mm was utilised for linear tetrahedral elements to create FE meshes of scaffolds, ensuring convergence in FE modelling. The FE outcomes displayed a linear correlation between the porosities and Young’s moduli of the scaffolds, similar to that of osteochondral bone [87].
In elastoplastic materials models, the non-linear performance of the materials is described as bilinear [88] or multilinear [89] following the onset of plastic deformation, during which they endure permanent deformation after the loads are applied. A linear elastic FEM must be initially performed to determine whether the predicted stress is larger than the yield strength of the material. Then, a non-linear static FEM can be performed to predict its behaviour in the plastic regime [90]. A series of static analyses are conducted to analyse time-dependent non-linear behaviours of materials like plasticity and viscoelasticity. In each successive time step within the series, boundary conditions are adjusted without consideration of inertial forces, frequency, or damping effects [91].
Rezapourian et al. [92] designed TPMS-based Split-P scaffolds of porosities in a range from 75% to 90% and applied a multilinear isotropic elastoplastic model to predict the behaviour of Ti6Al4V scaffolds under compressive loading. Linear tetrahedral meshes (with an element size of 0.2 mm) of the scaffolds were placed between a fixed bottom plate and a movable top plate, subject to a velocity of 2 ms−1, to simulate the compressive behaviour at different strains. The assessment of the simulation results disclosed that the Split-P scaffolds exhibited adequate stress transfer necessary for enhanced load-supporting capability in trabecular and cortical bone applications, displaying fracture characteristics capable of sustaining normal biomechanical loads [92].
Verma et al. [93] utilised a non-linear isotropic hardening elastoplastic model for FE simulations involving diverse compressive loading scenarios. These simulations focused on a Ti6Al4V primitive (P) TPMS scaffold with 80% porosity fixed within a segmental bone defect region of a femur. The authors compared its performance against scaffolds placed within femoral defects (Figure 10). The simulation results indicated that the porous P scaffolds provided beneficial mechanical stimuli to the neighbouring bone tissues and transferred more stress to these tissues due to the matching effective elastic modulus [93].
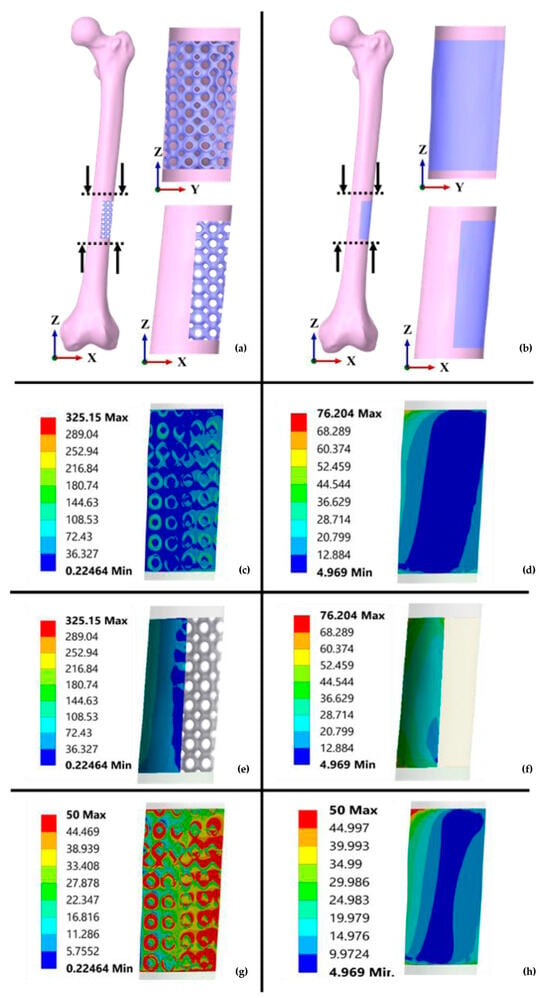
Figure 10.
FEA of solid and porous TPMS scaffolds based on segmental femur defect for BTE and its related stress contours (units are given in MPa): (a,b) Implantation of P-TPMS and solid scaffolds, (c,d) stress distribution contours on the bone, (e,f) von Mises stress contours of P and solid scaffolds, (g,h) stress distribution contours for P and solid scaffolds at 50 MPa. Reproduced with permission from Ref. [93] CC BY 4.0.
A BISO model with Maxwell’s criterion was used by Vance et al. [94] to predict the elastoplastic mechanical behaviour of customised Ti6Al4V (Ti64) sheathed scaffold implants obtained from X-ray CT for segmental bone defect repair. The simulation results predicted the Young’s modulus of the implant at 11.94 GPa, comparable with that of experimental testing (14.58 GPa). Given that its stiffness is lower than Young’s modulus of the tibia bone (18.01 GPa), this suggests that the bone implant is a potential candidate with the requisite lower stiffness required for osseointegration and bone regeneration (Figure 11) [94].

Figure 11.
FEM-based BISO elastoplastic model prediction of scaffolds for tibial bone defect repair. Reproduced with permission from Ref. [94] CC BY-NC-ND 4.0.
Huang et al. [95] comprehensively reviewed several biomaterial scaffolds for applications of maxillofacial BTE. They explained the technical considerations of physical properties (shape, porous structure, microarchitecture and mechanical), biological properties and biomaterials (metals, polymers, ceramics, and composites) required for essential cell proliferation, angiogenesis, and osteogenesis [95]. Polymeric materials give more control over morphological parameters, biocompatibility, and biodegradation [96]. In quasi-static compressive loading, polymer-based scaffolds undergo viscoelastic deformation after yielding. This viscoelastic behaviour can be simulated using the Prony series relaxation model, in which the shear and bulk moduli are described via the Prony series with the help of volumetric and deviatoric viscosities of materials [97,98]. The polymer-based scaffolds with increasing porosity lack sufficient mechanical strength for loadbearing bone applications [99].

Table 1.
Computational modelling of mechanical behaviour using FEM.
Table 1.
Computational modelling of mechanical behaviour using FEM.
| Model | Predicted Mechanical Properties | Material * | Remarks |
|---|---|---|---|
| Linear isotropic elastic model | Young’s modulus (2D and 3D compressive responses) | PCL | Relationship between compressive modulus and porosities of uniform and gradient diamond pored scaffolds for tissue-engineered meniscus applications [100] |
| BISO model | Effective plastic strain | Twinning-induced plasticity steel | Evaluation of morphological properties on quasi-static behaviour of hallow walled lattice structures under compressive loading [101] |
| Linear isotropic Reuss model | Equivalent Young’s modulus, compression Stiffness | PCL-ACP | Prediction of compressive stiffness of non-parametric scaffolds under linear compressive loading for BTE applications [102] |
| Multilinear isotropic, elastoplastic model | von Mises stress, equivalent plastic strain distributions | Ti6Al4V | Prediction of elastoplastic nature of Split-P TPMS scaffolds for cortical and trabecular bone applications [92] |
| Non-linear elastoplastic model | Plastic deformation | 316L SS | Evaluating the influence of gradient properties of TPMS and circular loading scaffolds on their elastoplastic properties under static compressive loading [103] |
| Raghava–Hill Plasticity Model | Compressive stiffness and strength | Ti-42Nb alloy | Evaluation of effects of unit cells of gyroid and I-WP-based bone scaffolds on their mechanical properties under quasi-static compression [104] |
| Bilinear plasticity model with isotropic hardening (Li–Guo–Shim Model) | Plastic deformation | SS316 Stainless Steel | Prediction of plastic behaviour of Voronoi-based honeycomb scaffolds [105] |
| One term Ogden hyper elastic model | Effective compressive modulus, shear modulus | AG hydrogels | Prediction of non-linear mechanical properties of mesostructure-based hydrogel scaffolds using inverse FE simulations for TE applications [106] |
| 5-term Mooney–Rivlin and 2-term Ogden models | Stress relaxation | AG hydrogels | Evaluation of the hyper-viscoelastic response of hydrogels in compression and tension loading for human articular cartilage [107] |
| 5-term Mooney–Rivlin model, Prony series relaxation model and Generalised Maxwell Model (GMM) | Tensile strength and storage modulus | PLA | Prediction of elastic and viscoelastic behaviours of dog bone-shaped structures under tensile loading [108] |
| Burgers and Maxwell viscoelastic models | Linear viscoelastic behaviour (creep and recovery) | Polypropylene | Prediction of viscoelastic deformation at different pressure levels [109] |
| Riemann–Liouville-based fractional viscoelastic model | Viscoelastic (creep recovery and cyclic response) deformations | POM | Development of a non-linear multiaxial viscoelastic model to evaluate time-dependent responses of isotropic materials under small deformation gradients [110] |
| Maxwell, Kelvin, and Burger models | Storage and loss moduli | PLA | Prediction of time-dependent viscoelastic behaviour of orthotropic viscoelastic materials [111] |
| Mori–Tanaka model | Effective elastic moduli (Young’s modulus) and Poisson’s ratio | Acrylic-based photopolymers | Prediction of mechanical properties of mix-materials composites based foams with different porosities [112] |
| Crushable foam plasticity model | Elastic modulus under quasi-static compression | VeroClear | Prediction of damage behaviour of polymer bone scaffolds with cubic and hexagonal architecture [113] |
| Johnson–Cook (JC) damage deformation model | Compressive stress distribution | Ti6Al4V-PCL | Performance evaluation of failure and mechanical strength mechanisms of interpenetrating phase composites (IPCs) under compressive loading for orthopaedic implants [114] |
| Arruda–Boyce (AB) Model | Compressive uniaxial modulus and strength | PA-12 | Prediction of viscoelastic behaviour of polymeric gyroid scaffolds of sheet network architecture with non-identical relative densities [115] |
* PCL-ACP: Polycaprolactone and amorphous calcium phosphate, PCL: Polycaprolactone, PLA: Polylactic Acid, LSCF: Lanthanum strontium cobalt ferrite, PHBV: Poly(3-hydroxybutyrate-co-3-hydroxy valerate), ABS: Acrylonitrile Butadiene Styrene, ITO: Indium Tin Oxide, Ti6Al4V: Titanium–Aluminium–Vanadium alloy, PEEK: Polyether ether ketone, Ti-4Nb: Titanium–Niobium alloy, N/A: Not Applicable; PA: Polyamide; AG: Alginate–Gelatin; POM: Polyoxymethylene; SS: Stainless Steel.
2.3. Simulation of Permeability of BTE Scaffolds
Need for Permeability Simulation
Scaffolds permit the transport of nutrients from nearby tissues and provide a pathway to eliminate waste products from the cells. Permeability refers to the ability of materials to flow through the scaffolds and is primarily dependent on the architecture of the scaffolds. When scaffolds possess high permeabilities and well-interconnected pore networks, a more significant number of cells and nutrients can infiltrate the scaffolds, leading to enhanced tissue growth [116,117]. Shear flow refers to the movement of a fluid induced by forces within it. Wall shear stress (WSS) is a specific type of shear stress that occurs due to varying fluid velocities along the inner surfaces of scaffold walls. WSS provides mechanical stimuli that encourage cells to grow and differentiate into functional tissues [118,119]. Therefore, altering design parameters like pore size, architecture, and pore interconnectivity in scaffolds can result in a different average WSS, which is instrumental in guiding cell differentiation within these structures [120,121].
CFD is a numerical approach applied to simulate the nature of fluid flow inside scaffolds and their related fluidic environments. CFD simulation solves the governing mathematical equations that characterise the physical nature of fluids (e.g., pressure and velocity) using an in silico depiction of fluidic nature in different flow situations. This technique can be used to optimise the design of scaffolds and improve their permeability for successful bone tissue regeneration [122,123]. For CFD simulations, two types of fluids are considered: Newtonian and non-Newtonian fluids [124,125]. Newtonian fluids such as water, alcohol, and glycerol have constant viscosity at constant temperatures and obey the Newtonian law of viscosity. This law states that their shear stress is directly proportional to the rate of change in fluid velocity. Non-Newtonian fluids such as blood and cell culture media, which do not obey Newton’s law of viscosity, have variable viscosities dependent on shear rate (Table 2 and Table 3).

Table 2.
Flow parameters in BTE from the literature.
Newtonian fluids, with their constant viscosity at a constant temperature, flow more readily through permeable networks, while non-Newtonian fluids, owing to their variable viscosity, exhibit higher levels of WSS. CFD simulations based on non-Newtonian fluids give more realistic fluid flow behaviour predictions, especially in biomedical applications, due to their more realistic representation of the variable viscosity characteristics of biological fluids [129]. Values of WSS greater than 30 mPa have been shown to be beneficial for the growth of cells [130].
Suffo et al. discussed the differences between various turbulent flow modelling methods (Figure 12) [131]. These methods include Reynolds averaged Navier–Stokes (RANS) such as k-ε, k-ω (Wilcox model) and k-ω SST (shear stress transport), Reynolds stress models (RSM), large eddy simulation (LES), direct numerical simulation (DNS), the scale adaptive simulation (SAS), and detached eddy simulation (DES) models. The authors applied these models to different turbulent flows and utilised the knowledge of CFD simulation with Fluid–Structural Interaction (FSI) techniques [132,133]. This integration was specifically employed for turbulence flow modelling of PLA scaffolds, facilitating the study of their flow properties.

Figure 12.
Principal turbulent CFD methods (from top to bottom: lowest to highest computational cost) [131].
Pires et al. [134] provided a review of the challenges encountered in designing CFD applications for BTE. Notably, they explained how scaffold design parameters affect both mechanical and permeability properties, as well as how CFD and FEM simulation studies optimise scaffold designs to achieve the goal of bone tissue regeneration [134].
In BTE, bioreactors are employed to grow functional tissues from MSCs in controlled in vitro conditions. This process provides a continuous supply of nutrients and the removal of waste products prior to in vivo implantation at bone defect sites [135,136]. Implementing a mathematical model of the process in a CFD simulation involves four key steps: designing the geometries of scaffolds and complimentary bioreactors, selecting the appropriate flow equations, and determining the boundary and initial conditions (Figure 13) [137,138]. Thus, the fundamentals of CFD simulations can be described in three modules:
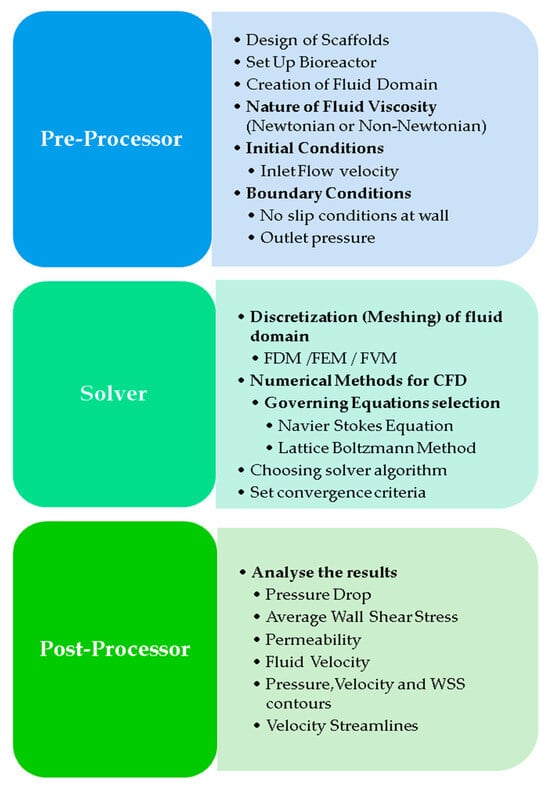
Figure 13.
Steps in formulating a mathematical model in a CFD simulation [137].
- (i)
- Preprocessing: This initial phase involves designing the scaffold geometry and setting up the bioreactor geometry. Then, the fluid domain or volume is extracted using Boolean differentiation of scaffold geometry with the bioreactor geometry (Figure 14). The flow of either Newtonian or non-Newtonian fluids must be represented in terms of boundary conditions, including the inlet flow velocity, the outlet pressure, and the viscosity of the given fluid. These boundary conditions describe the given fluid’s interaction with the scaffold’s surface [139,140].
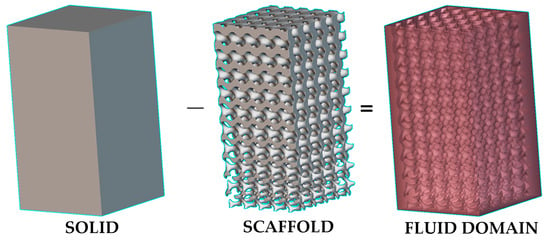 Figure 14. An illustration (designed using nTopology software version 4.22.2) of creating a fluid domain for CFD by using Boolean subtraction of solid (bioreactor) by scaffold lattice; the top region of the fluid domain can be used as a velocity inlet of flow, and its bottom region can be used as a pressure outlet.
Figure 14. An illustration (designed using nTopology software version 4.22.2) of creating a fluid domain for CFD by using Boolean subtraction of solid (bioreactor) by scaffold lattice; the top region of the fluid domain can be used as a velocity inlet of flow, and its bottom region can be used as a pressure outlet. - (ii)
- Solver: This module focuses on applying numerical methods within CFD to solve the governing equations, such as the Navier–Stokes (NS) equations [141] for continuous flow modelling or the Lattice Boltzmann Method (LBM) for discrete flow modelling [142]. Traditionally, finite difference methods (FDM) using grids for the discretisation of a given geometry were applied to solve the governing equations, but they were inefficient for complex geometries [143]. The methods of FEM and the finite volume method (FVM) have since gained popularity in CFD simulations for complex and curved geometries. In FEM, geometry is divided into more minor finite elements, primarily using mesh nodes. At the same time, FVM discretises the problem into small control volumes centred around mesh points, focusing on the conservation of physical quantities across each volume [144]. FEM is highly versatile and is particularly effective for problems involving complex geometries and irregular shapes. However, it becomes very computationally expensive for models with a large number of elements. Comparatively, FVM is often considered more efficient for problems involving fluid dynamics and heat transfer, mainly because it directly applies the conservation laws of mass, momentum, and energy over control volumes [145]. This type makes it naturally suited for the analysis of flow problems and can lead to more accurate results in these cases with less computational effort.
- (iii)
- Post Processing: After the CFD simulation, a post-processing module is used to analyse the results, including the velocity streamlines, the average WSS, and pressure and velocity contours. This analysis provides insights into how a scaffold’s architecture affects fluid flow, offering valuable information about permeability, fluid velocity, and WSS [146,147].
In fluid dynamics, a laminar flow occurs when the fluid flows smoothly without any disturbance or deviation from its path. This type of flow typically happens at low velocities or with high-viscosity fluids. Usually, the laminar occurs when a Reynolds number is lower than a critical value of 2300. In contrast, fluid flows with a Reynolds number larger than 4000 are considered turbulent flow and generally involve swirling motions (eddies) and deviations from the standard flow pattern. Fluid flow with a Reynolds number between 2300 and 3000 is considered transitional, indicating a shift from laminar to turbulent flow characteristics [148,149].
Wang et al. [150] conducted a study using water as an incompressible fluid with an inlet velocity of 1 mm/s and a zero-outlet pressure in their laminar CFD model to predict permeability and the WSS of honeycomb structures in the context of cancellous bone repair applications. This study concluded that the permeability of scaffolds between 15 and 48 µm2 has a positive influence on cancellous bone tissue regeneration. At the same time, a WSS value between 2.8 and 42.8 mPa can simulate cell growth inside scaffolds (Figure 15) [150].
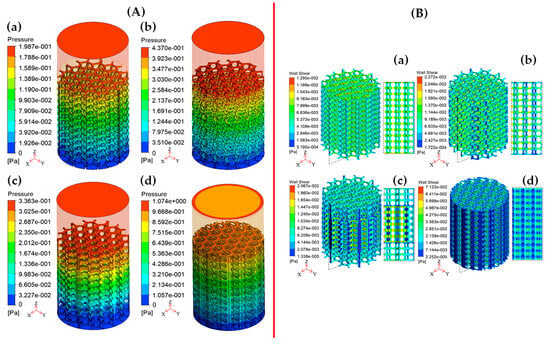
Figure 15.
(A) Pressure drops and (B) WSS contours of hexagonal honeycomb scaffolds based on (a) Simple Uniform structure, (b) Overlapping Simple Curved structure, (c) Simple Gradient structure, and (d) Simple Internal Curved structure. Reproduced with permission from Ref. [150] CC BT-NC-ND 4.0.
Using blood as the fluid material in simulations, rather than water, offers more realistic predictions of permeability and WSS within scaffolds. This simulation type is particularly relevant as turbulence flow is a crucial characteristic of blood circulation [151]. Omar et al. [130] utilised a k-ω SST turbulence CFD model to predict flow velocities, pressure drops and WSS in anatomically shaped bone scaffolds. In their model, they varied inlet blood flow velocities from 1 to 9 mm/s and employed a convergence criterion of 10−4 for residual monitoring. Their findings indicated that for blood velocities ranging from 1 to 5 mm/s, the predicted WSS value was lower than 30 mPa. In contrast, for velocities exceeding 5 mm/s, the predicted WSS value was higher than 30 mPa. The study also observed that the value of WSS was generally lower in the centre of scaffolds and increased near the wall of scaffolds (Figure 16) [130].
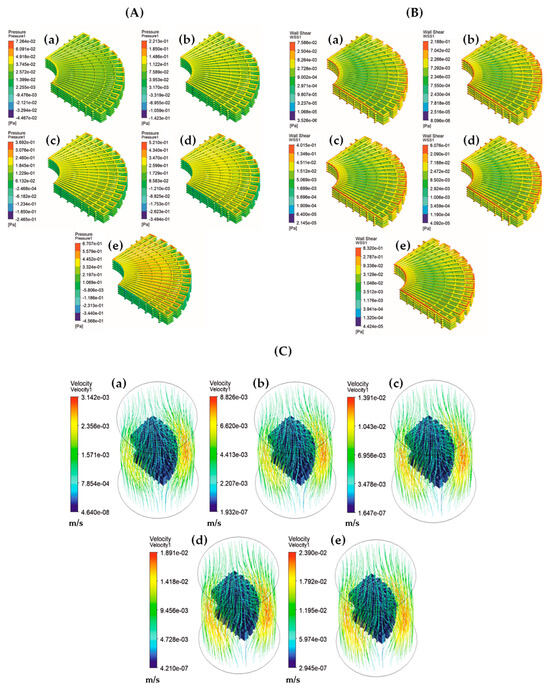
Figure 16.
(A) Pressure drops, (B) WSS and (C) velocity contours of anatomically shaped BTE scaffolds for inlet blood velocities: (a) 1 mm/s, (b) 3 mm/s, (c) 5 mm/s, (d) 7 mm/s and (e) 9 mm/s. Reproduced with permission from Ref. [130] CC BY 4.0.
Blood is composed of plasma, ‘thrombocytes (platelets), leukocytes (white blood cells), and erythrocytes (red blood cells)’ [152]. As previously mentioned, blood exhibits non-Newtonian flow characteristics due to well-deformed high clusters of erythrocytes [153]. Various non-Newtonian blood viscosity models have been employed, such as the power law, generalised power law, Casson, Carreau, and Carreau–Yasuda models to model blood flow and WSS distributions in blood vessels [154,155].
Seehanam et al. [156] applied the Carreau–Yasuda viscosity model on sheet-based gyroid scaffolds to predict pressure drops, velocity profiles and fluid-induced WSS in comparison with a Newtonian flow model. This model was performed to study the influence of shear rate on blood viscosity. The findings revealed that the predicted parameters from the non-Newtonian model were twice those predicted using the Newtonian model. Additionally, both models predicted shear stress in the range between 0.05 and 10 mPa, which is considered beneficial for the promotion of bone cell proliferation (Figure 17) [156].
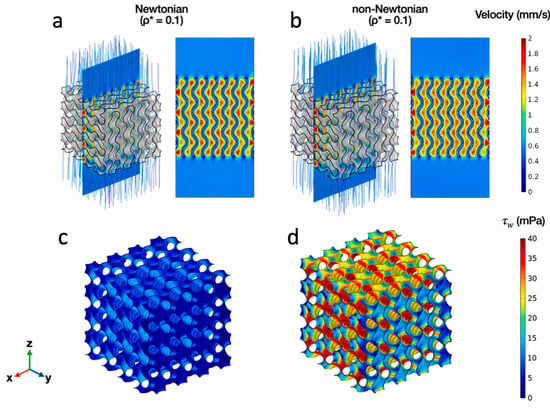
Figure 17.
(a,b) Velocity contours and (c,d) WSS contours of Newtonian and non-Newtonian CFD models of gyroid scaffolds with relative density 0.1. Reproduced with permission from Ref. [156] CC BY-NC-ND 4.0.
A significant challenge in CFD simulation is generating clean meshes for complex geometry structures such as TPMS structures and Voronoi lattices when computational power is limited [157]. To overcome this limitation, Reduan et al. developed a new analytical model based on Hagen–Poiseuille’s law for permeability prediction of TPMS-based bone scaffolds, which relies on morphological parameters. This model utilises pressure drop values derived from CFD analysis to calibrate and refine the analytical model, thus offering an effective workaround for computational limitations in the analysis of complex scaffolds (Figure 18) [158].
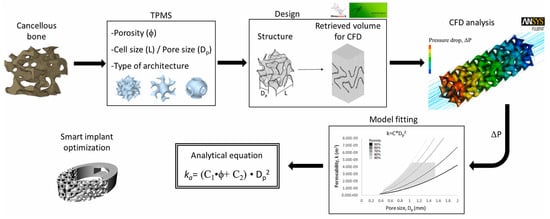
Figure 18.
CFD for permeability prediction of TPMS scaffolds to optimise innovative BTE implants. Reproduced with permission from Ref. [158] CC BY-NC-ND 4.0.

Table 3.
CFD modelling of fluid behaviour.
Table 3.
CFD modelling of fluid behaviour.
| Model | Predicted Fluid and Other Properties | Fluid Material * | Remarks |
|---|---|---|---|
| Steady-state Laminar fluid flow model | Permeability and WSS | Blood (Density: 1050 kg/m3, viscosity: 0.004 kg/(m.s), inlet velocity: 0.3 mL/min) | Evaluation of the influence of morphological parameters of uniform and graded Schwartz-Primitive scaffolds on their permeability properties for trabecular bone applications [159] |
| Pressure drops, permeability, and WSS | Blood (Viscosity: 3.2 × 10−3 Pa.s, density: 1060 kg/m3, inlet velocity: 1 mm/s) | Evaluation of fluid transport properties of Tra-PLA/PDA/COS@EU scaffolds for trabecular bone repair [116] | |
| Laminar fluid flow model with Wang–Tarbell formula for permeability | WSS, flow rate, permeability, and mass flow | α-MEM (Density: 1000 kg/m3, viscosity: 1.45 × 10−3 Pa.s, inlet velocity: 1 mm/s) | Prediction of hydrodynamic responses for osteogenesis inside titanium alloy-based TPMS and Voronoi scaffolds [160] |
| Incompressible Laminar Newtonian fluid model and Discrete phase model (DPM) | Permeability, FSS, and distribution of stem cells | Blood (Density: 1060 kg/cm3, viscosity: 0.003 kg/m/s) MSCs (Diameter: 12.7 µm, and density: 1140 kg(m3) | Prediction of fluid shear stress on Voronoi scaffold surface, MSCs attachment on the scaffold and mechano-regulation osteoblast differentiation (MrOD) [161] |
| Incompressible Newtonian fluid model and Machine Learning (ML) | Permeability, pressure drop and specific surface area | Body Fluid (Density: 1056 kg/m3, viscosity: 0.0045 Pa.s) | Prediction of WSS using support vector machines and eXtreme Gradient Boosting ML models to minimise the computational cost of CFD simulations [162] |
| Power law models for incompressible non-Newtonian fluid | Permeability and WSS | Blood (Density: 1050 kg/m3, minimum and maximum dynamic viscosities: 0.001 and 0.708 kg/m/s, consistency index: 0.017 kg.sn−2/m, power law exponent: 0.708) | Prediction of transport properties inside open cell Neovius TPMS scaffolds for BTE [163] |
| Carreau–Yasuda non-Newtonian flow model and DPM | Pressure drops, specific surface area, and cell seeding efficiency | Blood (Density: 1050 kg/m3, inlet velocity: 0.1 mm/s, lower and upper viscosities: 0.25 and 0.0035 Pa.s) MSCs (density: 1130 kg/m3, diameter: 10 µm and initial cell number: 3600) | Influence of pore size of TPMS scaffolds on cell seeding [164] |
| FEM-based CFD model with Brinkmann equation for shear stress in scaffold medium | Flow velocity and shear stress | Culture medium (Inlet flow rate: 2 mL/min) | Development of CFD models for evaluation of perfusion bioreactor systems to predict flow parameters of β-Tricalcium phosphate scaffolds in BTE [165] |
| RANS K-Turbulence model and Transport of diluted specimen model | Shear stress, flow distribution and glucose diffusion | Water (Mass inflow: 1.5 g/min), Glucose in tissues (Diffusion coefficient: 6 × 10–10 m2/s, elimination rate: −1.157 + 10−4 mol/(m3.s)) | Prediction of shear stress and nutrient distribution into tissues in a perfusion bioreactor [166] |
| SST K-ω Turbulence Model | Pressure drops, Flow velocity distribution and WSS | DMEM (Density: 1 g/cm3, dynamic viscosity: 1.45 mPa.s, inlet velocity: 0.1, 1 to 10 mm/s, Thermal conductivity: 91 W/(mK), Specific Heat: 1050 J/(kg K), Electrical resistivity: 6.20 × 10−8 Ω m) | Prediction of permeability of Magnesium-based trabecular bone implants [167] |
| Vertex hydrodynamics (VH) model | Elastic energy (Cell distribution), Total/specific number of cells, intracellular pressure, and normalised shear stress | Water | Simulation of tissue growth at FGS in perfusion bioreactors [168] |
| LBM-based mesoscopic model | Cell attachment rate and seeding efficiency | MSCs (Stiffness: 50 to 150 µN, bond strength: 0.025 to 0.125 pN/nm, Binding force: 10 to 50 pN) | Simulation of MSCs seeding on uniform pore scaffold to evaluate cell deformation and attachment [169] |
| Two-relaxation time (TRT) LBM with Michaelis–Menten-like kinetic model | Fluid flow and oxygen transport | α-MEM (Density: 993 kg/m3, viscosity: 10−3 Pa.s, inlet velocity: 1.47 mm/s, oxygen diffusion coefficient: 3 × 10−9 m2/s) | Prediction of oxygen consumption to the cells (MC3T3E1 Preosteoblasts) for optimal in vitro BTE methods of polysaccharide hydrogel scaffolds [170] |
* α-MEM: α-Modified Eagle’s Minimum cell culture medium with less vitamins, amino acids, and glucose; MEM: Modified Eagle’s Minimum cell culture medium with more vitamins, amino acids, and glucose; DMEM: Dulbecco’s Modified Eagle’s Medium; Tra-PLA/PDA/COS@EU: PLA with polydopamine and Chito Oligosaccharide-based europium (III) organic ligands.
3. Conclusions
This review article has given an extensive analysis of the studies in FEM/CFD computational modelling of scaffolds in BTE. It also gives introductory details about different scaffold types based on parametric, non-parametric and stochastic designs to achieve simple to complex structures. The main challenge for computational engineers in BTE is to select the appropriate material models for different mechanical loading in the case of FEM modelling and to choose the suitable flow models for both Newtonian and non-Newtonian fluids in the case of CFD modelling. Knowing the suitable models for the given problems helps to accurately predict the equivalent mechanical properties and flow properties to enhance scaffold designs, as well as to improve the bioreactor environment. Thus, the prediction of these properties using computational modelling may be helpful in reducing the cost of in vivo and in vitro examinations.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/computation12040074/s1, Figure S1: non-parametric designs of scaffolds; Figure S2: parametric designs of scaffolds—TPMS; Figure S3: parametric designs of scaffolds—Voronoi; Table S1: software tools to design TPMS/lattice-based scaffolds; Table S2: list of FEM software; Table S3: list of CFD software.
Author Contributions
Conceptualisation, methodology, software, formal analysis, investigation, resources, data curation, writing—original draft preparation, visualisation, H.-S.N.M.; writing—review and editing, J.W. and M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No data is associated for this review article.
Acknowledgments
(1.) I acknowledge Oraib Al-Ketan (New York University, Abu-Dhabi, UAE) for providing his honest feedback for this manuscript and for providing ‘MSLattice PRO’ software to design the TPMS gyroid scaffolds given in Supplementary Materials Figure S2g,h. (2.) I acknowledge my academic supervisors, Dhayalan Velauthapillai/Talal Rahman (Western Norway University of Applied Sciences, Bergen, Norway) and Kamal Mustafa (University of Bergen, Bergen, Norway) for their academic support. (3.) I acknowledge nTopology Inc. (New York, USA) for providing a non-commercial license of nTop software to design the scaffolds given in Figure 13, Supplementary Materials Figures S1, S2a–f and S3.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Martin Bruce, R.; Burr David, B.; Sharkey, N.A.; Fyhrie David, P. Skeletal Tissue Mechanics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Heimes, D.; Pabst, A.; Becker, P.; Hartmann, A.; Kloss, F.; Tunkel, J.; Smeets, R.; Kämmerer, P.W. Comparison of Morbidity-Related Parameters between Autologous and Allogeneic Bone Grafts for Alveolar Ridge Augmentation from Patients’ Perspective—A Questionnaire-Based Cohort Study. Clin. Implant. Dent. Relat. Res. 2024, 26, 170–182. [Google Scholar] [CrossRef]
- Wu, Y.; Ji, Y.; Lyu, Z. 3D Printing Technology and Its Combination with Nanotechnology in Bone Tissue Engineering. Biomed. Eng. Lett. 2024, 1–14. [Google Scholar] [CrossRef]
- Gou, Y.; Huang, Y.; Luo, W.; Li, Y.; Zhao, P.; Zhong, J.; Dong, X.; Guo, M.; Li, A.; Hao, A.; et al. Adipose-Derived Mesenchymal Stem Cells (MSCs) Are a Superior Cell Source for Bone Tissue Engineering. Bioact. Mater. 2024, 34, 51–63. [Google Scholar] [CrossRef]
- Zhang, J.; Suttapreyasri, S.; Leethanakul, C.; Samruajbenjakun, B. Fabrication of Vascularized Tissue-Engineered Bone Models Using Triaxial Bioprinting. J. Biomed. Mater. Res. A 2024, 1–14. [Google Scholar] [CrossRef]
- Liu, T.; Wang, Y.; Kuang, T. Oriented Porous Polymer Scaffolds in Tissue Engineering: A Comprehensive Review of Preparation Strategies and Applications. Macromol. Mater. Eng. 2024, 309, 2300246. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, S.; Ding, W.; Du, H.; Li, M.; Li, Z.; Chen, M. Additively-Manufactured Gradient Porous Bio-Scaffolds: Permeability, Cytocompatibility and Mechanical Properties. Compos. Struct. 2024, 336, 118021. [Google Scholar] [CrossRef]
- Mostajeran, H.; Baheiraei, N.; Bagheri, H. Effects of Cerium-Doped Bioactive Glass Incorporation on an Alginate/Gelatin Scaffold for Bone Tissue Engineering: In Vitro Characterizations. Int. J. Biol. Macromol. 2024, 255, 128094. [Google Scholar] [CrossRef]
- Abdollahi, F.; Saghatchi, M.; Paryab, A.; Malek Khachatourian, A.; Stephens, E.D.; Toprak, M.S.; Badv, M. Angiogenesis in Bone Tissue Engineering via Ceramic Scaffolds: A Review of Concepts and Recent Advancements. Biomater. Adv. 2024, 159, 213828. [Google Scholar] [CrossRef]
- Zhang, T.; Li, J.; Wang, Y.; Han, W.; Wei, Y.; Hu, Y.; Liang, Z.; Lian, X.; Huang, D. Hydroxyapatite/Polyurethane Scaffolds for Bone Tissue Engineering. Tissue Eng. Part. B Rev. 2024, 30, 60–73. [Google Scholar] [CrossRef]
- Han, X.; Saiding, Q.; Cai, X.; Xiao, Y.; Wang, P.; Cai, Z.; Gong, X.; Gong, W.; Zhang, X.; Cui, W. Intelligent Vascularized 3D/4D/5D/6D-Printed Tissue Scaffolds. Nano-Micro Lett. 2023, 15, 239. [Google Scholar] [CrossRef]
- Qi, J.; Yu, T.; Hu, B.; Wu, H.; Ouyang, H. Current Biomaterial-Based Bone Tissue Engineering and Translational Medicine. Int. J. Mol. Sci. 2021, 22, 10233. [Google Scholar] [CrossRef]
- Laubach, M.; Suresh, S.; Herath, B.; Wille, M.L.; Delbrück, H.; Alabdulrahman, H.; Hutmacher, D.W.; Hildebrand, F. Clinical Translation of a Patient-Specific Scaffold-Guided Bone Regeneration Concept in Four Cases with Large Long Bone Defects. J. Orthop. Translat. 2022, 34, 73–84. [Google Scholar] [CrossRef]
- D’Andrea, L.; Gastaldi, D.; Baino, F.; Verné, E.; Schwentenwein, M.; Örlygsson, G.; Vena, P. Computational Models for the Simulation of the Elastic and Fracture Properties of Highly Porous 3D-Printed Hydroxyapatite Scaffolds. Int. J. Numer. Method. Biomed. Eng. 2024, 40, e3795. [Google Scholar] [CrossRef]
- Wang, M.; Jiang, G.; Yang, H.; Jin, X. Computational Models of Bone Fracture Healing and Applications: A Review. Biomed. Tech. 2024. [Google Scholar] [CrossRef]
- Drakoulas, G.; Gortsas, T.; Polyzos, E.; Tsinopoulos, S.; Pyl, L.; Polyzos, D. An Explainable Machine Learning-Based Probabilistic Framework for the Design of Scaffolds in Bone Tissue Engineering. Biomech. Model. Mechanobiol. 2024, 2024, 1–26. [Google Scholar] [CrossRef]
- Kallivokas, S.V.; Kontaxis, L.C.; Psarras, S.; Roumpi, M.; Ntousi, O.; Kakkos, I.; Deligianni, D.; Matsopoulos, G.K.; Fotiadis, D.I.; Kostopoulos, V. A Combined Computational and Experimental Analysis of PLA and PCL Hybrid Nanocomposites 3D Printed Scaffolds for Bone Regeneration. Biomedicines 2024, 12, 261. [Google Scholar] [CrossRef]
- Huo, L.; Li, Q.; Jiang, L.; Jiang, H.; Zhao, J.; Yang, K.; Dong, Q.; Shao, Y.; Chu, C.; Xue, F.; et al. Porous Mg–Zn–Ca Scaffolds for Bone Repair: A Study on Microstructure, Mechanical Properties and in Vitro Degradation Behavior. J. Mater. Sci. Mater. Med. 2024, 35, 1–8. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Z.; Chen, X.; Zhao, R. Design and Evaluation of TPMS-Inspired 3D-Printed Scaffolds for Bone Tissue Engineering: Enabling Tailored Mechanical and Mass Transport Properties. Compos. Struct. 2024, 327, 117638. [Google Scholar] [CrossRef]
- Khoshgoftar, M.J.; Ansari, H. Design and Analysis of Unit Cell Geometry to Improve Mechanical Properties and Surface-to-Volume Ratio of Used Scaffold in Treating Damaged Bone Tissue. Adv. Eng. Mater. 2024, 26, 2301600. [Google Scholar] [CrossRef]
- Peng, X.; Li, S.; He, D.; Li, J.; Qu, S.; Jin, Z. Expanding the Mechanical and Mass-Transport Combination for Bone Scaffolds: Through Stretched Structure. Compos. Struct. 2024, 329, 117783. [Google Scholar] [CrossRef]
- Bowlin, G.L.; Lee, M.-C.; Pan, C.-T.; Chen, W.-F.; Lin, M.-C.; Shiue, Y.-L. Design, Manufacture, and Characterization of a Critical-Sized Gradient Porosity Dual-Material Tibial Defect Scaffold. Bioengineering 2024, 11, 308. [Google Scholar] [CrossRef]
- Luo, Y.; Kim, J. Achieving the Ideal Balance between Biological and Mechanical Requirements in Composite Bone Scaffolds through a Voxel-Based Approach. Biomech. Model. Mechanobiol. 2024, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Acar, A.A.; Daskalakis, E.; Bartolo, P.; Weightman, A.; Cooper, G.; Blunn, G.; Koc, B. Customized Scaffolds for Large Bone Defects Using 3D-Printed Modular Blocks from 2D-Medical Images. Biodes Manuf. 2024, 7, 74–87. [Google Scholar] [CrossRef]
- Zou, Z.; Cheong, V.S.; Fromme, P. Bone Remodelling Prediction Using Mechanical Stimulus with Bone Connectivity Theory in Porous Implants. J. Mech. Behav. Biomed. Mater. 2024, 153, 106463. [Google Scholar] [CrossRef] [PubMed]
- Shalimov, A.; Tashkinov, M.; Silberschmidt, V.V. Failure of Trabecular Bone: XFEM Modelling of Multiple Crack Growth. Theor. Appl. Fract. Mech. 2024, 130, 104338. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, Q.; Zhou, H.; Zhao, C.; Wu, L. Investigation on Mechanical Properties of Ti-6Al-4 V Multilayer Micro-Lattice Biomaterials under Dynamic Compression Loading. J. Alloys Compd. 2024, 977, 173419. [Google Scholar] [CrossRef]
- Mao, R.; Lai, Y.; Li, D.; Huang, Y.; Wang, L.; Luo, F.; Chen, Y.; Lu, J.; Ge, X.; Liu, Y.; et al. Flow Channel Performance in 3D Printed Hydroxyapatite Scaffolds to Improve Metabolism and Tissue Ingrowth in Flat Bone Repair. Compos. B Eng. 2023, 259, 110727. [Google Scholar] [CrossRef]
- Drakoulas, G.; Gortsas, T.; Tsinopoulos, S.; Polyzos, D. A Numerical Study on the Early-Stage Performance of 3D Composite PLA/316L Scaffolds in Tissue Engineering. In Advances in Computational Mechanics and Applications; Springer: Berlin/Heidelberg, Germany, 2024; pp. 28–44. [Google Scholar] [CrossRef]
- Tajvar, S.; Hadjizadeh, A.; Samandari, S.S. Scaffold Degradation in Bone Tissue Engineering: An Overview. Int. Biodeterior. Biodegrad. 2023, 180, 105599. [Google Scholar] [CrossRef]
- Sestito, J.M.; Harris, T.A.L.; Wang, Y. Structural Descriptor and Surrogate Modeling for Design of Biodegradable Scaffolds. J. Mech. Behav. Biomed. Mater. 2024, 152, 106415. [Google Scholar] [CrossRef]
- Asbai-Ghoudan, R.; Nasello, G.; Pérez, M.Á.; Verbruggen, S.W.; Ruiz de Galarreta, S.; Rodriguez-Florez, N. In Silico Assessment of the Bone Regeneration Potential of Complex Porous Scaffolds. Comput. Biol. Med. 2023, 165, 107381. [Google Scholar] [CrossRef]
- Alshammari, A.; Alabdah, F.; Wang, W.; Cooper, G. Virtual Design of 3D-Printed Bone Tissue Engineered Scaffold Shape Using Mechanobiological Modeling: Relationship of Scaffold Pore Architecture to Bone Tissue Formation. Polymers 2023, 15, 3918. [Google Scholar] [CrossRef] [PubMed]
- Boaretti, D.; Marques, F.C.; Ledoux, C.; Singh, A.; Kendall, J.J.; Wehrle, E.; Kuhn, G.A.; Bansod, Y.D.; Schulte, F.A.; Müller, R. Trabecular Bone Remodeling in the Aging Mouse: A Micro-Multiphysics Agent-Based in Silico Model Using Single-Cell Mechanomics. Front. Bioeng. Biotechnol. 2023, 11, 1091294. [Google Scholar] [CrossRef] [PubMed]
- Rosa, N.; Pouca, M.V.; Torres, P.M.C.; Olhero, S.M.; Jorge, R.N.; Parente, M. Influence of Structural Features in the Performance of Bioceramic-Based Composite Scaffolds for Bone Engineering Applications: A Prediction Study. J. Manuf. Process. 2023, 90, 391–405. [Google Scholar] [CrossRef]
- Beheshtizadeh, N.; Farzin, A.; Rezvantalab, S.; Pazhouhnia, Z.; Lotfibakhshaiesh, N.; Ai, J.; Noori, A.; Azami, M. 3D Printing of Complicated GelMA-Coated Alginate/Tri-Calcium Silicate Scaffold for Accelerated Bone Regeneration. Int. J. Biol. Macromol. 2023, 229, 636–653. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wang, K.; Wang, R.; Yin, Z.; Zhou, X.; Xu, A.; Zhang, X.; Li, Y.; Wang, R.; Zhang, S.; et al. Effect of Lattice Type on Biomechanical and Osseointegration Properties of 3D-Printed Porous Ti6Al4V Scaffolds. Int. J. Bioprinting 2024, 10, 1698. [Google Scholar] [CrossRef]
- Mashhadi Keshtiban, M.; Taghvaei, H.; Noroozi, R.; Eskandari, V.; Arif, Z.U.; Bodaghi, M.; Bardania, H.; Hadi, A. Biological and Mechanical Response of Graphene Oxide Surface-Treated Polylactic Acid 3D-Printed Bone Scaffolds: Experimental and Numerical Approaches. Adv. Eng. Mater. 2024, 26, 2301260. [Google Scholar] [CrossRef]
- Velasco, M.A.; Narváez-Tovar, C.A.; Garzón-Alvarado, D.A. Review Article Design, Materials, and Mechanobiology of Biodegradable Scaffolds for Bone Tissue Engineering. BioMed. Res. Int. 2015, 2015, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Al-Allaq, A.A.; Kashan, J.S.; Abdul-Kareem, F.M. In Vivo Investigations of Polymers in Bone Tissue Engineering: A Review Study. Int. J. Polym. Mater. Polym. Biomater. 2024, 1–16. [Google Scholar] [CrossRef]
- Katebifar, S.; Arul, M.; Abdulmalik, S.; Yu, X.; Alderete, J.F.; Kumbar, S.G. Novel High-Strength Polyester Composite Scaffolds for Bone Regeneration. Polym. Adv. Technol. 2023, 34, 3770–3791. [Google Scholar] [CrossRef]
- Paltanea, G.; Manescu, V.; Antoniac, I.; Antoniac, A.; Nemoianu, I.V.; Robu, A.; Dura, H. A Review of Biomimetic and Biodegradable Magnetic Scaffolds for Bone Tissue Engineering and Oncology. Int. J. Mol. Sci. 2023, 24, 4312. [Google Scholar] [CrossRef]
- Schulze, F.; Lang, A.; Schoon, J.; Wassilew, G.I.; Reichert, J. Scaffold Guided Bone Regeneration for the Treatment of Large Segmental Defects in Long Bones. Biomedicines 2023, 11, 325. [Google Scholar] [CrossRef] [PubMed]
- Ataollahi, S. A Review on Additive Manufacturing of Lattice Structures in Tissue Engineering. Bioprinting 2023, 35, e00304. [Google Scholar] [CrossRef]
- Liu, K.; Zhou, Q.; Zhang, X.; Ma, L.; Xu, B.; He, R. Morphologies, Mechanical and in Vitro Behaviors of DLP-Based 3D Printed HA Scaffolds with Different Structural Configurations. RSC Adv. 2023, 13, 20830–20838. [Google Scholar] [CrossRef] [PubMed]
- Pasini, C.; Pandini, S.; Ramorino, G.; Sartore, L. Tailoring the Properties of Composite Scaffolds with a 3D-Printed Lattice Core and a Bioactive Hydrogel Shell for Tissue Engineering. J. Mech. Behav. Biomed. Mater. 2024, 150, 106305. [Google Scholar] [CrossRef] [PubMed]
- Ali, D. The Behaviour of Scaffolds for Bone under Torsional Loading with Different Architectures: A Numerical Analysis. In 2020 Medical Technologies Congress (TIPTEKNO), Anatalya, Turkey; IEEE: New York, NY, USA, 2020; pp. 1–3. [Google Scholar] [CrossRef]
- Karri, C.P.; Kambagowni, V. Finite Element Analysis Approach for Optimal Design and Mechanical Performance Prediction of Additive Manufactured Sandwich Lattice Structures. J. Inst. Eng. (India) Ser. D, 2024; 1–16. [Google Scholar] [CrossRef]
- Roohani, I.; Entezari, A.; Zreiqat, H. Liquid Crystal Display Technique (LCD) for High Resolution 3D Printing of Triply Periodic Minimal Surface Lattices Bioceramics. Addit. Manuf. 2023, 74, 103720. [Google Scholar] [CrossRef]
- Talebi, S.; Sadighi, M. Simulation of Compression Behavior of Porous Structure Based on Different Space-Filling Unit Cells under Quasi-Static Loading. Mech. Based Des. Struct. Mach. 2023, 51, 2535–2549. [Google Scholar] [CrossRef]
- Li, L.; Wang, P.; Liang, H.; Jin, J.; Zhang, Y.; Shi, J.; Zhang, Y.; He, S.; Mao, H.; Xue, B.; et al. Design of a Haversian System-like Gradient Porous Scaffold Based on Triply Periodic Minimal Surfaces for Promoting Bone Regeneration. J. Adv. Res. 2023, 54, 89–104. [Google Scholar] [CrossRef] [PubMed]
- Araya, M.; Jaskari, M.; Rautio, T.; Guillén, T.; Järvenpää, A. Assessing the Compressive and Tensile Properties of TPMS-Gyroid and Stochastic Ti64 Lattice Structures: A Study on Laser Powder Bed Fusion Manufacturing for Biomedical Implants. J. Sci. Adv. Mater. Devices 2024, 9, 100663. [Google Scholar] [CrossRef]
- Vaiani, L.; Uva, A.E.; Boccaccio, A. Structural and Topological Design of Conformal Bilayered Scaffolds for Bone Tissue Engineering. Thin-Walled Struct. 2023, 192, 111209. [Google Scholar] [CrossRef]
- Song, J.; Li, L.; Fang, L.; Zhang, E.; Zhang, Y.; Zhang, Z.; Vangari, P.; Huang, Y.; Tian, F.; Zhao, Y.; et al. Advanced Strategies of Scaffolds Design for Bone Regeneration. BMEMat 2023, 1, e12046. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, M.; Wu, R.; Guo, J.; Sun, A.; Li, Z.; Ye, R.; Xu, G.; Cheng, Y. From Materials to Clinical Use: Advances in 3D-Printed Scaffolds for Cartilage Tissue Engineering. Phys. Chem. Chem. Phys. 2023, 25, 24244–24263. [Google Scholar] [CrossRef]
- Vigil, J.; Lewis, K.; Norris, N.; Karakoç, A.; Becker, T.A. Design, Fabrication, and Characterisation of 3D-Printed Multiphase Scaffolds Based on Triply Periodic Minimal Surfaces. Adv. Polym. Technol. 2024, 2024, 1–7. [Google Scholar] [CrossRef]
- Gao, T.; Liu, K.; Wang, X.; Wei, K.; Wang, Z. Multi-Level Mechanism of Biomimetic TPMS Hybridizations with Tailorable Global Homogeneity and Heterogeneity. Extreme Mech. Lett. 2024, 68, 102136. [Google Scholar] [CrossRef]
- Zhou, Y.; Isaksson, P.; Persson, C. An Improved Trabecular Bone Model Based on Voronoi Tessellation. J. Mech. Behav. Biomed. Mater. 2023, 148, 106172. [Google Scholar] [CrossRef]
- Liu, B.; Wei, X.; Cao, W.; Lu, P.; Wang, X. A Novel Method to Design Gradient Porous Structures with Conformal Density. Thin-Walled Struct. 2024, 197, 111623. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Lee, D.-W.; Abu Al-Rub, R.K. Mechanical Properties of Additively-Manufactured Sheet-Based Gyroidal Stochastic Cellular Materials. Addit. Manuf. 2021, 48, 102418. [Google Scholar] [CrossRef]
- Vafaeefar, M.; Moerman, K.M.; Vaughan, T.J. Experimental and Computational Analysis of Energy Absorption Characteristics of Three Biomimetic Lattice Structures under Compression. J. Mech. Behav. Biomed. Mater. 2024, 151, 106328. [Google Scholar] [CrossRef]
- He, L.; Zhao, M.; Cheung, J.P.Y.; Zhang, T.; Ren, X. Gaussian Random Field-Based Characterization and Reconstruction of Cancellous Bone Microstructure Considering the Constraint of Correlation Structure. J. Mech. Behav. Biomed. Mater. 2024, 152, 106443. [Google Scholar] [CrossRef]
- Deng, W.; Kumar, S.; Vallone, A.; Kochmann, D.M.; Greer, J.R. AI-Enabled Materials Design of Non-Periodic 3D Architectures With Predictable Direction-Dependent Elastic Properties. Adv. Mater. 2024, 2308149. [Google Scholar] [CrossRef]
- Alsheghri, A.; Reznikov, N.; Piché, N.; McKee, M.D.; Tamimi, F.; Song, J. Optimization of 3D Network Topology for Bioinspired Design of Stiff and Lightweight Bone-like Structures. Mater. Sci. Eng. C 2021, 123, 112010. [Google Scholar] [CrossRef]
- Rajaraman, S.; Rakshit, S. Multiscale Topology Optimization of Pelvic Bone for Combined Walking and Running Gait Cycles. Comput. Methods Biomech. Biomed. Eng. 2023, 1–17. [Google Scholar] [CrossRef]
- Pugliese, R.; Graziosi, S. Biomimetic Scaffolds Using Triply Periodic Minimal Surface-Based Porous Structures for Biomedical Applications. SLAS Technol. 2023, 28, 165–182. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Z.; Chen, X.; Zhao, R. Multi-Objective Optimization for Designing Porous Scaffolds with Controllable Mechanics and Permeability: A Case Study on Triply Periodic Minimal Surface Scaffolds. Compos. Struct. 2024, 333, 117923. [Google Scholar] [CrossRef]
- Pemmada, R.; Telang, V.S.; Tandon, P.; Thomas, V. Patient-Specific Mechanical Analysis of PCL Periodontal Membrane: Modeling and Simulation. J. Mech. Behav. Biomed. Mater. 2024, 151, 106397. [Google Scholar] [CrossRef]
- Vaquette, C.; Carluccio, D.; Batstone, M.; Ivanovski, S. Workflow for Fabricating 3D-Printed Resorbable Personalized Porous Scaffolds for Orofacial Bone Regeneration. Methods Mol. Biol. 2023, 2588, 485–492. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Jiang, S.; Zhong, C.; Zhao, C.; Jiao, Y.; Shen, J.; Chen, H.; Ye, M.; Zhou, J.; et al. The Design of Strut/TPMS-Based Pore Geometries in Bioceramic Scaffolds Guiding Osteogenesis and Angiogenesis in Bone Regeneration. Mater. Today Bio. 2023, 20, 100667. [Google Scholar] [CrossRef]
- Wang, C.; Liu, J.; Min, S.; Liu, Y.; Liu, B.; Hu, Y.; Wang, Z.; Mao, F.; Wang, C.; Ma, X.; et al. The Effect of Pore Size on the Mechanical Properties, Biodegradation and Osteogenic Effects of Additively Manufactured Magnesium Scaffolds after High Temperature Oxidation: An in Vitro and in Vivo Study. Bioact. Mater. 2023, 28, 537–548. [Google Scholar] [CrossRef]
- Eivazzadeh-Keihan, R.; Sadat, Z.; Lalebeigi, F.; Naderi, N.; Panahi, L.; Ganjali, F.; Mahdian, S.; Saadatidizaji, Z.; Mahdavi, M.; Chidar, E.; et al. Effects of Mechanical Properties of Carbon-Based Nanocomposites on Scaffolds for Tissue Engineering Applications: A Comprehensive Review. Nanoscale Adv. 2024, 6, 337–366. [Google Scholar] [CrossRef]
- Naghavi, S.A.; Tamaddon, M.; Marghoub, A.; Wang, K.; Bahrami Babam-Iri, B.; Hazeli, K.; Xu, W.; Lu, X.; Sun, C.; Wang, L.; et al. Mechanical Characterisation and Numerical Modelling of TPMS-Based Gyroid and Diamond Ti6Al4V Scaffolds for Bone Implants: An Integrated Approach for Translational Consideration. Bioengineering 2022, 2022, 504. [Google Scholar] [CrossRef]
- Papazoglou, D.P.; Neidhard-Doll, A.T.; Pinnell, M.F.; Erdahl, D.S.; Osborn, T.H. Compression and Tensile Testing of L-PBF Ti-6Al-4V Lattice Structures with Biomimetic Porosities and Strut Geometries for Orthopedic Implants. Metals 2024, 14, 232. [Google Scholar] [CrossRef]
- Zhang, S.; Vijayavenkataraman, S.; Lu, W.F.; Fuh, J.Y.H. A Review on the Use of Computational Methods to Characterise, Design, and Optimise Tissue Engineering Scaffolds, with a Potential in 3D Printing Fabrication. J. Biomed. Mater. Res. B Appl. Biomater. 2019, 107, 1329–1351. [Google Scholar] [CrossRef]
- Liu, B.; Liu, J.; Wang, C.; Wang, Z.; Min, S.; Wang, C.; Zheng, Y.; Wen, P.; Tian, Y. High Temperature Oxidation Treated 3D Printed Anatomical WE43 Alloy Scaffolds for Repairing Periarticular Bone Defects: In Vitro and in Vivo Studies. Bioact. Mater. 2024, 32, 177–189. [Google Scholar] [CrossRef]
- Shirzad, M.; Bodaghi, M.; Oh, D.; Yi, M.; Nam, S.Y. Design and Optimization of Bioinspired Auxetic Structure for Biomedical Applications. Eur. J. Mech. A/Solids 2024, 103, 105139. [Google Scholar] [CrossRef]
- Kong, D.; Wang, Q.; Huang, J.; Zhang, Z.; Wang, X.; Han, Q.; Shi, Y. A Biomimetic Structural Material with Adjustable Mechanical Property for Bone Tissue Engineering. Adv. Funct. Mater. 2024, 34, 2305412. [Google Scholar] [CrossRef]
- Sorgente, T.; Biasotti, S.; Manzini, G.; Spagnuolo, M. A Survey of Indicators for Mesh Quality Assessment. Comput. Graph. Forum. 2023, 42, 461–483. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, W.; Liu, S.; Liu, Z.; Yan, Z.; Yu, A.; Liu, B.; Xu, J.; Lu, X.; Liu, Y.; et al. Effects of Elastic Modulus of Porous Implants on Success Rate of Implant Surgery – An in Vivo Study Using Miniature Swine Model. Mater. Des. 2024, 239, 112819. [Google Scholar] [CrossRef]
- Kalsi, S.; Singh, J.; Sharma, N.K. Evaluation of Mechanical Properties of Anatomically Designed Scaffolds to Repair the Femur Bone Using FEM. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Imran, R.; Al Rashid, A.; Koç, M. Review on Computational Modeling for the Property, Process, Product and Performance (PPPP) Characteristics of Additively Manufactured Porous Magnesium Implants. Bioprinting 2022, 28, e00236. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM Lattice Structures: Properties, Performance, Applications and Challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Musthafa, H.-S.N.; Walker, J.; Rahman, T.; Bjørkum, A.; Mustafa, K.; Velauthapillai, D. In-Silico Prediction of Mechanical Behaviour of Uniform Gyroid Scaffolds Affected by Its Design Parameters for Bone Tissue Engineering Applications. Computation 2023, 11, 181. [Google Scholar] [CrossRef]
- Roldán, E.; Reeves, N.D.; Cooper, G.; Andrews, K. 2D and 3D PVA Electrospun Scaffold Evaluation for Ligament Implant Replacement: A Mechanical Testing, Modelling and Experimental Biomechanics Approach. Materialia 2024, 33, 102042. [Google Scholar] [CrossRef]
- de Ullola, J.L.; González, J.E.; Beltrán, A.M.; Avés, E.P.; Rodríguez-Guerra, J.; Torres, Y. Biomechanical Behavior of Customized Scaffolds: A Three-Dimensional Finite Element Analysis. Mater. Des. 2022, 223, 111173. [Google Scholar] [CrossRef]
- Zhang, B.; Guo, L.; Chen, H.; Ventikos, Y.; Narayan, R.J.; Huang, J. Finite Element Evaluations of the Mechanical Properties of Polycaprolactone/Hydroxyapatite Scaffolds by Direct Ink Writing: Effects of Pore Geometry. J. Mech. Behav. Biomed. Mater. 2020, 104, 103665. [Google Scholar] [CrossRef]
- Jiang, W.Z.; Teng, X.C.; Ni, X.H.; Zhang, X.G.; Cheng, X.; Jiang, W.; Han, D.; Zhang, Y.; Ren, X. An Improved Re-Entrant Honeycomb with Programmable Densification and Multistage Energy-Absorbing Performance. Eng. Struct. 2024, 301, 117318. [Google Scholar] [CrossRef]
- Adibeig, M.R.; Saeimi-Sadigh, M.-A.; Vakili-Tahami, F.; Karimani, M.R.; Marami, G. Quasi-Static Simulation and Fatigue Life Estimation of Fused Filament Fabrication of Polylactic Acid Specimens Using Finite Element Method. J. Manuf. Process. 2023, 106, 202–213. [Google Scholar] [CrossRef]
- Cantaboni, F.; Battini, D.; Hauber, K.Z.; Ginestra, P.S.; Tocci, M.; Avanzini, A.; Ceretti, E.; Pola, A. Mechanical and Microstructural Characterization of Ti6Al4V Lattice Structures with and without Solid Shell Manufactured via Electron Beam Powder Bed Fusion. Int. J. Adv. Manuf. Technol. 2024, 131, 1289–1301. [Google Scholar] [CrossRef]
- Böker, A.; De Santis, R.; Harish, A.; Alsaleh, N.A.; Ahmadein, M.; Elfar, A.A.; Djuansjah, J.; Hassanin, H.; El-Sayed, M.A.; Essa, K.; et al. Designing Lightweight 3D-Printable Bioinspired Structures for Enhanced Compression and Energy Absorption Properties. Polymers 2024, 16, 729. [Google Scholar] [CrossRef]
- Rezapourian, M.; Jasiuk, I.; Saarna, M.; Hussainova, I. Selective Laser Melted Ti6Al4V Split-P TPMS Lattices for Bone Tissue Engineering. Int. J. Mech. Sci. 2023, 251, 108353. [Google Scholar] [CrossRef]
- Verma, R.; Kumar, J.; Singh, N.K.; Rai, S.K.; Saxena , K.K.; Xu, J. Design and Analysis of Biomedical Scaffolds Using TPMS-Based Porous Structures Inspired from Additive Manufacturing. Coatings 2022, 12, 839. [Google Scholar] [CrossRef]
- Vance, A.; Bari, K.; Arjunan, A. Compressive Performance of an Arbitrary Stiffness Matched Anatomical Ti64 Implant Manufactured Using Direct Metal Laser Sintering. Mater. Des. 2018, 160, 1281–1294. [Google Scholar] [CrossRef]
- Huang, X.; Lou, Y.; Duan, Y.; Liu, H.; Tian, J.; Shen, Y.; Wei, X. Biomaterial Scaffolds in Maxillofacial Bone Tissue Engineering: A Review of Recent Advances. Bioact. Mater. 2024, 33, 129–156. [Google Scholar] [CrossRef]
- Costantino, D.; Gaudio, L.; Di, S.; Baiguera, S.; Górnicki, T.; Lambrinow, J.; Golkar-Narenji, A.; Data, K.; Domagała, D.; Niebora, J.; et al. Biomimetic Scaffolds—A Novel Approach to Three Dimensional Cell Culture Techniques for Potential Implementation in Tissue Engineering. Nanomaterials 2024, 14, 531. [Google Scholar] [CrossRef]
- Galadima, Y.K.; Oterkus, S.; Oterkus, E.; Amin, I.; El-Aassar, A.H.; Shawky, H. Modelling of Viscoelastic Materials Using Non-Ordinary State-Based Peridynamics. Eng. Comput. 2024, 40, 527–540. [Google Scholar] [CrossRef]
- Raj, G.B.; Saludheen, A.; Arumugham-Achari, A.K.; George, N.; Chacko, T. Simulations for Mechanical Properties of Polymer Composites: Investigations into Suitability of Numerical Models for TPU-CNT with Mooney–Rivlin (N = 1) and Friction. Mech. Time Depend. Mater. 2023, 27, 705–726. [Google Scholar] [CrossRef]
- Koushik, T.M.; Miller, C.M.; Antunes, E. Bone Tissue Engineering Scaffolds: Function of Multi-Material Hierarchically Structured Scaffolds. Adv. Healthc. Mater. 2023, 12, 2202766. [Google Scholar] [CrossRef]
- Du, M.; Liu, K.; Lai, H.; Qian, J.; Ai, L.; Zhang, J.; Yin, J.; Jiang, D. Functional Meniscus Reconstruction with Biological and Biomechanical Heterogeneities through Topological Self-Induction of Stem Cells. Bioact. Mater. 2024, 36, 358–375. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, B.; Zhou, S.; Luo, M.; Han, F.; Chai, C.; Wang, J.; Yang, X. Superior Energy Absorption Characteristics of Additively-Manufactured Hollow-Walled Lattices. Int. J. Mech. Sci. 2024, 264, 108834. [Google Scholar] [CrossRef]
- Liu, J.; Roque, R.; Barbosa, G.F.; Malavolta, A.T. Compression Stiffness Evaluation of Polycaprolactone-Amorphous Calcium Phosphate 3D-Designed Scaffolds Oriented by Finite Element Analysis. J. Appl. Polym. Sci. 2021, 138, 51245. [Google Scholar] [CrossRef]
- Cheng, F.; Zhao, Q.; Mao, Z.; Wang, F. Mechanical Response of Gradient Lattice Structures Based on Topology Optimization. Adv. Eng. Mater. 2024, 2301887. [Google Scholar] [CrossRef]
- Günther, F.; Pilz, S.; Hirsch, F.; Wagner, M.; Kästner, M.; Gebert, A.; Zimmermann, M. Experimental and Numerical Characterization of Imperfect Additively Manufactured Lattices Based on Triply Periodic Minimal Surfaces. Mater. Des. 2023, 233, 112197. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, S.; Sun, Z.; Shim, V.P.W. Density-Graded Voronoi Honeycombs – A Local Transversely Isotropic Description. Int. J. Solids Struct. 2023, 285, 112555. [Google Scholar] [CrossRef]
- Soufivand, A.A.; Budday, S. Predicting the Hyperelastic Properties of Alginate-Gelatin Hydrogels and 3D Bioprinted Mesostructures. Sci. Rep. 2023, 13, 21858. [Google Scholar] [CrossRef]
- Weizel, A.; Distler, T.; Detsch, R.; Boccaccini, A.R.; Seitz, H.; Budday, S. Time-Dependent Hyper-Viscoelastic Parameter Identification of Human Articular Cartilage and Substitute Materials. J. Mech. Behav. Biomed. Mater. 2023, 138, 105618. [Google Scholar] [CrossRef]
- Issabayeva, Z.; Shishkovsky, I. Prediction of The Mechanical Behavior of Polylactic Acid Parts with Shape Memory Effect Fabricated by FDM. Polymers 2023, 15, 1162. [Google Scholar] [CrossRef]
- Gebrehiwot, S.Z.; Espinosa-Leal, L. Characterising the Linear Viscoelastic Behaviour of an Injection Moulding Grade Polypropylene Polymer. Mech. Time Depend. Mater. 2022, 26, 791–814. [Google Scholar] [CrossRef]
- Muliana, A. A Fractional Model of Non-linear Multiaxial Viscoelastic Behaviors. Mech. Time Depend. Mater. 2023, 27, 1187–1207. [Google Scholar] [CrossRef]
- Anoop, M.S.; Senthil, P.; Sooraj, V.S. An Investigation on Viscoelastic Characteristics of 3D-Printed FDM Components Using RVE Numerical Analysis. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 38. [Google Scholar] [CrossRef]
- Kornfellner, E.; Königshofer, M.; Krainz, L.; Krause, A.; Unger, E.; Moscato, F. Measured and Simulated Mechanical Properties of Additively Manufactured Matrix-Inclusion Multimaterials Fabricated by Material Jetting. 3D Print. Med. 2024, 10, 4. [Google Scholar] [CrossRef]
- Rasheed, S.; Lughmani, W.A.; Khan, M.M.; Brabazon, D.; Obeidi, M.A.; Ahad, I.U. The Porosity Design and Deformation Behavior Analysis of Additively Manufactured Bone Scaffolds through Finite Element Modelling and Mechanical Property Investigations. J. Funct. Biomater. 2023, 14, 496. [Google Scholar] [CrossRef]
- Xie, H.; Chen, J.; Liu, F.; Luo, T.; Wang, Y.; Tang, Y. Design of the Ti-PCL Interpenetrating Phase Composites with the Minimal Surface for Property Enhancement of Orthopedic Implants. J. Phys. Conf. Ser. 2024, 2713, 012047. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Elhebeary, M.; Shiang, C.S.; Pang, S.; Abu Al-Rub, R.K.; Jasiuk, I.M. Mechanical Properties of 3D Printed Polymeric Gyroid Cellular Structures: Experimental and Finite Element Study. Mater. Des. 2019, 165, 107597. [Google Scholar] [CrossRef]
- Huang, X.; Zheng, L.; Li, P.; Lin, Z.; Huang, S.; Zhou, C. Fabrication of 3D Printed Trabecular Bone-Templated Scaffolds Modified with Rare Earth Europium (III)-Based Complex for Enhancing Mitochondrial Function in Bone Regeneration. Appl. Mater. Today 2024, 37, 102130. [Google Scholar] [CrossRef]
- Yánez, A.; Cuadrado, A.; Martel, O.; Fiorucci, M.P.; Deviaene, S. Mechanical and Permeability Properties of Skeletal and Sheet Triply Periodic Minimal Surface Scaffolds in Bone Defect Reconstruction. Results Eng. 2024, 21, 101883. [Google Scholar] [CrossRef]
- Basri, H.; Prakoso, A.T.; Abidin, Z.; Syahrom, A.; Akbar, I.; Adanta, D. The Effect of Tortuosity on Wall Shear Stress of Porous Scaffold. CFD Lett. 2023, 15, 61–73. [Google Scholar] [CrossRef]
- Azizi, P.; Drobek, C.; Budday, S.; Seitz, H. Simulating the Mechanical Stimulation of Cells on a Porous Hydrogel Scaffold Using an FSI Model to Predict Cell Differentiation. Front. Bioeng. Biotechnol. 2023, 11, 1249867. [Google Scholar] [CrossRef]
- Liu, Z.; Gong, H.; Gao, J.; Liu, L. Bio-Inspired Design, Mechanical and Mass-Transport Characterizations of Orthotropic TPMS-Based Scaffold. Compos. Struct. 2023, 321, 117256. [Google Scholar] [CrossRef]
- Altunbek, M.; Afghah, S.F.; Fallah, A.; Acar, A.A.; Koc, B. Design and 3D Printing of Personalised Hybrid and Gradient Structures for Critical Size Bone Defects. ACS Appl. Bio Mater. 2023, 6, 1873–1885. [Google Scholar] [CrossRef]
- Liu, S.; Feng, J.; Zhang, F.; Jiang, W.; Vasilieva, T.M.; Lu, P.; Lu, S. Parametric Design and Performance Study of Continuous Gradient Triply Periodic Minimal Surface Bone Scaffold. IJB 2024, 2306. [Google Scholar] [CrossRef]
- Gupta, A.; Rana, M.; Mondal, N. Determination of Optimum Design Parameters for Gyroid Scaffolds to Mimic a Real Bone-Like Condition In Vitro: A Fluid Structure Interaction Study. J. Eng. Sci. Med. Diagn. Ther. 2023, 6, 1–33. [Google Scholar] [CrossRef]
- de Wildt, B.W.M.; Zhao, F.; Lauwers, I.; van Rietbergen, B.; Ito, K.; Hofmann, S. Characterization of Three-Dimensional Bone-like Tissue Growth and Organization under Influence of Directional Fluid Flow. Biotechnol. Bioeng. 2023, 120, 2013–2026. [Google Scholar] [CrossRef]
- Deshmukh, K.; Mitra, K.; Bit, A. Influence of Non-Newtonian Viscosity on Flow Structures and Wall Deformation in Compliant Serpentine Microchannels: A Numerical Study. Micromachines 2023, 14, 1661. [Google Scholar] [CrossRef]
- Iversen, P.; Nicolaysen, G.; Benestad, H. Blood Flow to Bone Marrow During Development of Anemia or Polycythemia in the Rat. Blood 1992, 79, 594–601. [Google Scholar] [CrossRef]
- Pal, S. Mechanical Properties of Biological Materials. In Design of Artificial Human Joints & Organs; Springer US: New York, NY, USA, 2014; pp. 23–40. [Google Scholar] [CrossRef]
- Bixel, M.G.; Kusumbe, A.P.; Ramasamy, S.K.; Sivaraj, K.K.; Butz, S.; Vestweber, D.; Adams, R.H. Flow Dynamics and HSPC Homing in Bone Marrow Microvessels. Cell Rep. 2017, 18, 1804–1816. [Google Scholar] [CrossRef]
- Kumar, R. Computer Model of Non-Newtonian Canalicular Fluid Flow in Lacunar–Canalicular System of Bone Tissue. Comput. Methods Biomech. Biomed. Eng. 2024, 1–15. [Google Scholar] [CrossRef]
- Omar, A.M.; Hassan, M.H.; Daskalakis, E.; Ates, G.; Bright, C.J.; Xu, Z.; Powell, E.J.; Mirihanage, W.; Bartolo, P.J.D.S. Geometry-Based Computational Fluid Dynamic Model for Predicting the Biological Behavior of Bone Tissue Engineering Scaffolds. J. Funct. Biomater. 2022, 13, 104. [Google Scholar] [CrossRef]
- Suffo, M.; López-Marín, C.J. A Comparative Study of Turbulence Methods Applied to the Design of a 3D-Printed Scaffold and the Selection of the Appropriate Numerical Scheme to Simulate the Scaffold for Tissue Engineering. Appl. Sci. 2021, 12, 191. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.; Xu, Z.; Yang, Y.; Wang, Y.; Zhu, J.; Guo, X.; Tang, D.; Gu, Z. A New Approach of Using Organ-on-a-Chip and Fluid–Structure Interaction Modeling to Investigate Biomechanical Characteristics in Tissue-Engineered Blood Vessels. Front. Physiol. 2023, 14, 1–9. [Google Scholar] [CrossRef]
- Fu, M.; Qiu, S.; Wang, F.; Lin, G.; Shi, Y.; Qin, Z.; Tang, B.; Li, X.; Zhang, J. Enhanced Osteogenic Properties of Bone Repair Scaffolds through Synergistic Effects of Mechanical and Biochemical Stimulation. Adv. Eng. Mater. 2023, 25, 2200885. [Google Scholar] [CrossRef]
- Pires, T.; Dunlop, J.W.C.; Fernandes, P.R.; Castro, A.P.G. Challenges in Computational Fluid Dynamics Applications for Bone Tissue Engineering. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2022, 478, 1–20. [Google Scholar] [CrossRef]
- Watson, E.; Mikos, A.G. Advances in In Vitro and In Vivo Bioreactor-Based Bone Generation for Craniofacial Tissue Engineering. BME Front. 2023, 4, 4. [Google Scholar] [CrossRef]
- D’Adamo, A.; Salerno, E.; Corda, G.; Ongaro, C.; Zardin, B.; Ruffini, A.; Orlandi, G.; Bertacchini, J.; Angeli, D. Experimental Measurements and CFD Modelling of Hydroxyapatite Scaffolds in Perfusion Bioreactors for Bone Regeneration. Regen. Biomater. 2023, 10, rbad002. [Google Scholar] [CrossRef]
- Burova, I.; Wall, I.; Shipley, R.J. Mathematical and Computational Models for Bone Tissue Engineering in Bioreactor Systems. J. Tissue Eng. 2019, 10, 1–25. [Google Scholar] [CrossRef]
- Kozaniti, F.K.; Manara, A.E.; Kostopoulos, V.; Mallis, P.; Michalopoulos, E.; Polyzos, D.; Deligianni, D.D.; Portan, D.V. Computational and Experimental Investigation of the Combined Effect of Various 3D Scaffolds and Bioreactor Stimulation on Human Cells’ Feedback. Appl. Biosci. 2023, 2, 249–277. [Google Scholar] [CrossRef]
- Channasanon, S.; Kaewkong, P.; Chantaweroad, S.; Tesavibul, P.; Pratumwal, Y.; Otarawanna, S.; Kirihara, S.; Tanodekaew, S. Scaffold Geometry and Computational Fluid Dynamics Simulation Supporting Osteogenic Differentiation in Dynamic Culture. Comput. Methods Biomech. Biomed. Eng. 2023, 1–12. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, H.; Zhang, J.; Qin, S.; Duan, M. Study on Flow Field Characteristics of TPMS Porous Materials. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 188. [Google Scholar] [CrossRef]
- Wang, X.; Chen, J.; Guan, Y.; Sun, L.; Kang, Y. Internal Flow Field Analysis of Heterogeneous Porous Scaffold for Bone Tissue Engineering. Comput. Methods Biomech. Biomed. Eng. 2023, 26, 807–819. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Pham, N.H.; Papavassiliou, D.V. Relationship between Pore Fluid Velocity Distribution and Pore Size Distribution. AIChE J. 2023, 69, e17987. [Google Scholar] [CrossRef]
- Ji, G.; Zhang, M.; Lu, Y.; Dong, J. The Basic Theory of CFD Governing Equations and the Numerical Solution Methods for Reactive Flows. In Computational Fluid Dynamics; Ji, G., Dong, J., Eds.; IntechOpen: Rijeka, Croatia, 2023. [Google Scholar] [CrossRef]
- Akhtar, S.; Hussain, Z.; Nadeem, S.; Najjar, I.M.R.; Sadoun, A.M. CFD Analysis on Blood Flow inside a Symmetric Stenosed Artery: Physiology of a Coronary Artery Disease. Sci. Prog. 2023, 106, 00368504231180092. [Google Scholar] [CrossRef]
- Van Hoecke, L.; Boeye, D.; Gonzalez-Quiroga, A.; Patience, G.S.; Perreault, P. Experimental Methods in Chemical Engineering: Computational Fluid Dynamics/Finite Volume Method—CFD/FVM. Can. J. Chem. Eng. 2023, 101, 545–561. [Google Scholar] [CrossRef]
- Ye, J.; He, W.; Wei, T.; Sun, C.; Zeng, S. Mechanical Properties Directionality and Permeability of Fused Triply Periodic Minimal Surface Porous Scaffolds Fabricated by Selective Laser Melting. ACS Biomater. Sci. Eng. 2023, 9, 5084–5096. [Google Scholar] [CrossRef]
- Tang, Z.; Zhou, Y.; Ma, L.; Li, J. Flow Performance of Porous Implants with Different Geometry: Line, Surface, and Volume Structures. IJB 2023, 9, 700. [Google Scholar] [CrossRef]
- Stewart, S.; Chuckravanen, D. Novel Method Employing Accelerated-Oscillated Wave Saline Solutions to Unblock Blood Vessels—Physics and Fluid Dynamics Perspectives and Simulations. Open J. Biophys. 2021, 11, 415–424. [Google Scholar] [CrossRef]
- Selvan, R.; Bhattacharya, S. Human Red Blood Cell Membrane Stiffness: Why Should We Study It and How? Eur. Phys. J. Spec. Top. 2024, 1–15. [Google Scholar] [CrossRef]
- Wang, S.; Shi, Z.; Liu, L.; Huang, Z.; Li, Z.; Liu, J.; Hao, Y. Honeycomb Structure Is Promising for the Repair of Human Bone Defects. Mater. Des. 2021, 207, 109832. [Google Scholar] [CrossRef]
- Alimov, N. Blood supply to the human body, vascular anatomy and blood components. West. Eur. J. Med. Med. Sci. 2023, 1, 4–14. [Google Scholar]
- Almadhor, A.; Sattar, U.; Al Hejaili, A.; Ghulam Mohammad, U.; Tariq, U.; Ben Chikha, H. An Efficient Computer Vision-Based Approach for Acute Lymphoblastic Leukemia Prediction. Front. Comput. Neurosci. 2022, 16, 1083649. [Google Scholar] [CrossRef]
- Oh, D.; Ii, S.; Takagi, S. Numerical Study of Particle Margination in a Square Channel Flow with Red Blood Cells. Fluids 2022, 7, 96. [Google Scholar] [CrossRef]
- Ahadi, F.; Biglari, M.; Azadi, M.; Bodaghi, M. Computational Fluid Dynamics of Coronary Arteries with Implanted Stents: Effects of Newtonian and Non-Newtonian Blood Flows. Eng. Rep. 2023, e12779. [Google Scholar] [CrossRef]
- Muhammad Fahim, M.S.; Ali, N. Pulsatile Pressure-Driven Non-Newtonian Blood Flow through a Porous Stenotic Artery: A Computational Analysis. Numeri Heat. Transf. A Appl. 2024, 1–21. [Google Scholar] [CrossRef]
- Seehanam, S.; Chanchareon, W.; Promoppatum, P. Assessing the Effect of Manufacturing Defects and Non-Newtonian Blood Model on Flow Behaviors of Additively Manufactured Gyroid TPMS Structures. Heliyon. 2023, 9, e15711. [Google Scholar] [CrossRef]
- Li, M.; Hu, J.; Chen, W.; Kong, W.; Huang, J. Explicit Topology Optimization of Voronoi Foams. IEEE Trans. Vis. Comput. Graph. 2024, PP, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Asbai-Ghoudan, R.; Ruiz de Galarreta, S.; Rodriguez-Florez, N. Analytical Model for the Prediction of Permeability of Triply Periodic Minimal Surfaces. J. Mech. Behav. Biomed. Mater. 2021, 124, 104804. [Google Scholar] [CrossRef] [PubMed]
- Kadir Hussein, N.A.; Noordin, M.A.; Md Saad, A.P. Influence of Conical Graded Porous Architecture on the Mechanical, Failure Behavior and Fluid-Flow Properties for Bone Scaffold Application. Eng. Fail. Anal. 2024, 157, 107893. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Sun, Z.; Peng, K.; Liu, K.; Xu, P.; Li, J.; Wei, X.; He, X. Integrated Evaluation of Biomechanical and Biological Properties of the Biomimetic Structural Bone Scaffold: Biomechanics, Simulation Analysis, and Osteogenesis. Mater. Today Bio. 2024, 24, 100934. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Sun, Z.; Jia, C.; Ren, J.; Li, J.; Ma, Z.; Zhang, J.; Li, J.; Zhang, T.; Zang, Q.; et al. Roles of Irregularity of Pore Morphology in Osteogenesis of Voronoi Scaffolds: From the Perspectives of MSC Adhesion and Mechano-Regulated Osteoblast Differentiation. J. Biomech. 2023, 151, 111542. [Google Scholar] [CrossRef] [PubMed]
- Sudalai, M.E.; Thirumarimurugan, M.; Gnanaprakasam, A.; Satthiyaraju, M. Computational Fluid Dynamics Study on Three-Dimensional Polymeric Scaffolds to Predict Wall Shear Stress Using Machine Learning Models for Bone Tissue Engineering Applications. Asia-Pac. J. Chem. Eng. 2023, e3017. [Google Scholar] [CrossRef]
- Singh, S.; Yadav, S.K.; Meena, V.K.; Vashisth, P.; Kalyanasundaram, D. Orthopedic Scaffolds: Evaluation of Structural Strength and Permeability of Fluid Flow via an Open Cell Neovius Structure for Bone Tissue Engineering. ACS Biomater. Sci. Eng. 2023, 9, 5900–5911. [Google Scholar] [CrossRef] [PubMed]
- Seehanam, S.; Khrueaduangkham, S.; Sinthuvanich, C.; Sae-Ueng, U.; Srimaneepong, V.; Promoppatum, P. Evaluating the Effect of Pore Size for 3d-Printed Bone Scaffolds. Heliyon 2024, 10, e26005. [Google Scholar] [CrossRef]
- Nokhbatolfoghahaei, H.; Bohlouli, M.; Adavi, K.; Paknejad, Z.; Rezai Rad, M.; Khani, M.M.; Salehi-Nik, N.; Khojasteh, A. Computational Modeling of Media Flow through Perfusion-Based Bioreactors for Bone Tissue Engineering. J. Eng. Med. 2020, 234, 1397–1408. [Google Scholar] [CrossRef]
- Gensler, M.; Malkmus, C.; Ockermann, P.; Möllmann, M.; Hahn, L.; Salehi, S.; Luxenhofer, R.; Boccaccini, A.R.; Hansmann, J. Perfusable Tissue Bioprinted into a 3D-Printed Tailored Bioreactor System. Bioengineering 2024, 11, 68. [Google Scholar] [CrossRef]
- Manescu, V.; Paltanea, G.; Antoniac, A.; Gruionu, L.G.; Robu, A.; Vasilescu, M.; Laptoiu, S.A.; Bita, A.I.; Popa, G.M.; Cocosila, A.L.; et al. Mechanical and Computational Fluid Dynamic Models for Magnesium-Based Implants. Materials 2024, 17, 830. [Google Scholar] [CrossRef]
- Krasnyakov, I.; Bratsun, D. Cell-Based Modeling of Tissue Developing in the Scaffold Pores of Varying Cross-Sections. Biomimetics 2023, 8, 562. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, J.; Liu, Y.; Shao, J.; Xie, S. Effects of Cell Deformability and Adhesion Strength on Dynamic Cell Seeding: Cell-Scale Investigation via Mesoscopic Modeling. J. Biomech. 2023, 153, 111589. [Google Scholar] [CrossRef]
- Grenier, J.; David, B.; Journé, C.; Cicha, I.; Letourneur, D.; Duval, H. Perfusion of MC3T3E1 Preosteoblast Spheroids within Polysaccharide-Based Hydrogel Scaffolds: An Experimental and Numerical Study at the Bioreactor Scale. Bioengineering 2023, 10, 849. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).