Multi-Directional Functionally Graded Sandwich Plates: Buckling and Free Vibration Analysis with Refined Plate Models under Various Boundary Conditions

Abstract

This study conducts buckling and free vibration analyses of multi-directional functionally graded sandwich plates subjected to various boundary conditions. Two scenarios are considered: a functionally graded (FG) skin with a homogeneous hard core, and an FG skin with a homogeneous soft core. Utilizing refined plate models, which incorporate a parabolic distribution of transverse shear stresses while ensuring zero shear stresses on both the upper and lower surfaces, equations of motion are derived using Hamilton’s principle. Analytical solutions for the buckling and free vibration analyses of multi-directional FG sandwich plates under diverse boundary conditions are developed and presented. The obtained results are validated against the existing literature for both the buckling and free vibration analyses. The composition of metal–ceramic-based FG materials varies longitudinally and transversely, following a power law. Various types of sandwich plates are considered, accounting for plate symmetry and layer thicknesses. This investigation explores the influence of several parameters on buckling and free vibration behaviors.

1. Introduction

Composite materials blend two or more substances with varying properties to create unique characteristics absent in their individual components. Functionally graded materials (FGMs) represent a specific class of composites distinguished by directional variations in their material properties [1]. While unidirectional FGMs vary their properties along a single axis, multi-directional (MD) graded materials introduce variations along multiple axes, enhancing their performance [2].

Various methodologies have been proposed for analyzing the free vibration of plates, beams, and shells, including the energy method for plates [3], Galerkin–Vlasov’s method for tapered plates [4], and the Rayleigh–Ritz method for rotating hard-coating cylindrical shells [5]. For 2-D FGMs, studies have explored their free vibration behavior under different boundary conditions, revealing variations in their frequency based on the boundary conditions [6]. A semi-analytical numerical method was employed in solving the problems of the bending analysis of 2-D functionally graded (FG) circular and annular plates [7] and their impact analysis [8].

Buckling and frequency analyses were conducted on a two-directional (2-D) FG circular plate using the differential quadrature method (DQM) for both clamped and simply supported boundary conditions. The results indicated a higher critical buckling load for the clamped plate compared to the simply supported configuration [9]. Additionally, finite element analysis and analytical techniques like the third-order shear deformation plate theory have provided us with understanding of the static deflection and buckling characteristics of FGM plates [10,11].

The free vibration and buckling of 2-D FGM plates were investigated using a non-uniform rational B-spline technique [12]. Estimating the material properties of FGMs is crucial, with empirical relationships available for ideal FGMs. However, certain parameters like the stress–strain transfer ratio (q) remain mathematically unquantifiable, necessitating experimental validation [13]. Several material combination experiments have been conducted to explore the parameter q empirically [14].

A free vibration analysis of multi-directional FG piezoelectric annular plates has been conducted using the differential quadrature method (DQM). Radial and thickness gradations were incorporated, revealing that radial gradation enhances plate stiffness, resulting in higher frequency responses [15]. Static and dynamic analyses of three-dimensional shells composed of multi-directional FG material (MD FGM) have been carried out using polyhedral finite element methods. That study explored the effects of shell thickness and slenderness on structural behavior [16]. The bending analysis of multilayer panels of FGMs was performed using a higher-order layer-wise model, with Young’s modulus determined via the Halpin–Tsai method and Poisson’s ratio via the rule of mixture [17]. In a thermal environment, numerical and experimental investigations were used to examine the free vibration of unidirectional and bi-directional porous FG curved panels. The evaluation of temperature-dependent (TD) material properties showed lower frequencies compared to temperature-independent (TID) properties [18]. A strain gradient elasticity theory was employed to study the dynamic response of square microplates with multi-directional FGM properties under a moving concentrated load [19]. The optimization of multi-directional FG plates under thermal effects was achieved through free vibration analysis [20]. Furthermore, a free vibration analysis of tri-directional FG beams under magneto-electro-elastic fields utilized the DQM and higher-order deformation theory [21,22]. In another study, the analysis of MD FG sandwich plates covered both FG skin with a homogeneous core and FG cores with homogeneous skin configurations, with the former demonstrating higher natural frequencies [23].

Singh and Kumari [24] proposed an approximate analytical solution for analyzing the free vibration of composite FG rectangular plates. By applying a modified version of Hamilton’s principle, they derived governing equations, considering all stresses and displacements as primary variables. The solution was obtained using the extended Kantorovich method, along with Fourier and power series approaches. Singh et al. [25] introduced a framework for accurately analyzing the free vibration of in-plane FG orthotropic rectangular plates integrated with piezoelectric sensory layers, considering both their elastic and viscoelastic properties. Numerical studies have explored the effects of in-plane gradation and viscoelasticity on vibration responses, revealing significant alterations in flexural frequencies and mode shapes. Vaishali et al. [26] proposed an innovative multi-physical probabilistic vibration analysis approach for FG materials. They combined Gaussian Process Regression (GPR) with finite element simulations, aided by a Monte Carlo Simulation, resulting in significant computational efficiency. By integrating machine learning with physics-based modeling, system uncertainty can be efficiently quantified.

Malikan and Eremeyev [27] developed a novel hyperbolic, polynomial higher-order elasticity theory for thick FGM beams. Their model addressed a critical drawback in material composition and incorporated a unique shape function for shear stress distribution. Through rigorous validation and comparative analyses, they demonstrated the efficacy of their approach. Their findings underscored the significance of higher-order beam theories and stretching effects. Importantly, their investigation into FGM beams with different boundary conditions revealed the marked effects of material imperfections, emphasizing the practical implications of their work for structural mechanics and material engineering.

Functionally graded materials undergo changes in their properties through adjustments in their microstructure, material composition, and porosity. Manufacturing techniques such as solid-state, liquid-state, or deposition processes enable the fabrication of these materials [28,29]. The research on FG structures, including plates, disks, and beams, has predominantly focused on unidirectional FGMs, as evidenced by the existing literature [30,31,32]. Fabrication methods must minimize the delamination that results from differences in the materials’ physical and chemical characteristics, necessitating techniques that ensure consistent thermo-mechanical properties [33]. While existing methods suit the fabrication of unidirectional FGMs, multi-directional gradation poses unique challenges. Functionally graded additive manufacturing (FGAM) emerges as a promising solution due to its ability to produce components with material gradients in various directions, offering advantages such as reduced material wastage, the absence of tooling requirements, and decreased manufacturing time and costs [34]. Various material modeling techniques exist, with rule of mixture (ROM) models often providing the best results for material combinations when compared to experimental data [35].

A delamination analysis within multilayered FG beam configurations was performed with a specific emphasis on understanding the time-dependent strain energy release rate. The study included different models of nonlinear creep behavior, particularly in tension and compression scenarios [36]. Dastjerdi et al. [37] employed a highly efficient quasi-3D theory to investigate the nonlinear hygro-thermo-mechanical bending analysis of a thick FGM rotating disk in a hygro-thermal environment, taking porosity into account as a structural defect. Their analysis incorporates two applied quasi-3D displacement fields, where the strain along the thickness is non-zero, unlike in conventional plate theories. Karami and Ghayesh [38] explored the significance of micromechanical models in analyzing the forced vibrations of multi-layered microplates subjected to a moving load. Their microplate comprised an FGM core and metal foam face sheets. The problem was modelled using a quasi-3D shear deformable method and modified couple stress theory. The same authors [39] investigated the vibrations of sandwich microshells featuring porous FG face sheets, considering in-surface curvilinear motions. The motion equations were derived using Hamilton’s principle, employing a curvilinear framework for a modified couple stress scheme that incorporated length-scale parameters. The vibration modes for curvilinear and normal displacements were assumed using trigonometric functions, and natural frequencies were determined numerically.

Despite the extensive research on unidirectional graded plates, research on multi-directional gradation remains limited. Multi-directional gradation promises optimized structures with enhanced performance compared to unidirectional grading. Thus, this paper investigates the free vibration and buckling analysis of multi-directional FG plates using refined plate theories. Our analysis considers a face sheet made of FGM with a homogeneous core composed of ceramic (hard core) or metal (soft core). The results of the proposed methods are validated against the existing literature for both buckling and free vibration analyses. Furthermore, a detailed parametric analysis explores the effects of grading index and geometry on the frequency and buckling load of multi-directional FG plates.

2. Mathematical Modeling

2.1. Preliminary Concepts and Definitions

Figure 1 depicts a multi-directional FGM sandwich plate with its dimensions along the x, y, and z axes denoted as length (a), width (b), and thickness (h), respectively. The sandwich plate comprises two face sheets (top and bottom) sandwiching a core layer. In Figure 1, the x and y axes represent the midplane, while the z axis is perpendicular to the midplane.

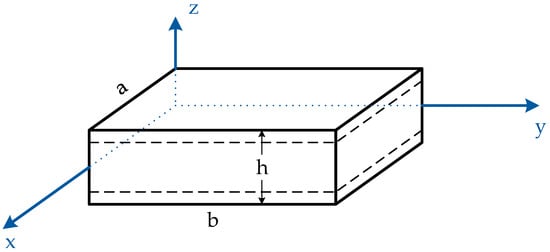
Figure 1. Multi-directional FGM sandwich plate.

A power law variation in the volume fraction of the FGM’s metal and ceramic constituents is represented by Equations (1) and (2). This investigation focuses on metal (Al) and ceramic (Al₂O₃), with their compositions varying longitudinally (p_x) and transversely (p_z). The material properties of the FGM sandwich plate are influenced by the volume fractions of these constituents along both its longitudinal and transverse directions, following a power law relationship. The volume fraction of metal in a multi-directional sandwich plate is expressed as shown in Equation (1):

$$\begin{array}{l}{V}^{(1)}\left(x,z\right)={\left(\frac{z-h_1}{h_1-h_2}\right)}^{p_z}{\left(1-\frac{x}{2a}\right)}^{p_x}\\ V^{(2)}\left(x,z\right)=1\\ V^{(3)}\left(x,z\right)={\left(\frac{z-h_4}{h_3-h_4}\right)}^{p_z}{\left(1-\frac{x}{2a}\right)}^{p_x}\end{array}$$

(1)

where V⁽ⁿ⁾ (n = 1, 2, 3) represents the volume fraction function of Layer n, while p_z and p_x denote the volume fraction indices in the transverse and longitudinal directions, respectively. Type A has an FG face sheet and homogeneous hard core, while Type B has an FG face sheet and homogeneous soft core. Figure 2 presents the different layers of the material. The layer thicknesses, denoted by the coordinate points h₁ = −h/2, h₂, h₃, and h₄ = h/2 in the z direction, determine the sandwich configuration.

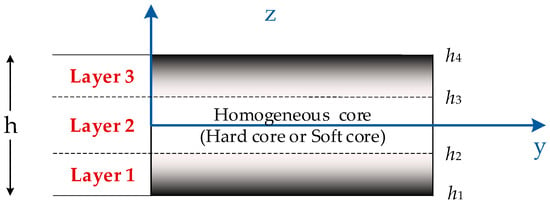
Figure 2. Material variation with thickness of multi-directional FGM sandwich plate: FGM containing face sheets and a homogeneous core (Type A: hard core, Type B: soft core).

2.2. Modeling of FG Sandwich Plate

The effective material properties of the plate, i.e., its Young’s modulus E, Poisson’s ratio ν, and mass density ρ, can be expressed by the rule of mixture, as shown in Equation (2) [40].

$$P^{(n)}\left(x,z\right)=\left(P_1-P_2\right)V^{(n)}\left(x,z\right)+P_2$$

(2)

where P⁽ⁿ⁾ is the effective material property of the FGM of Layer n. For Type A, P₁ and P₂ are the properties of the top and bottom faces of Layer 1, respectively, and vice versa for Layer 3, depending on the volume fraction V⁽ⁿ⁾ (n = 1, 2, 3). For Type B, P₁ and P₂ are the properties of Layer 3 and Layer 1, respectively. The discussion of the two types of FGM sandwich plates, Type A with a hard core and Type B with a soft core, will be presented in subsequent sections. In this study, the Poisson’s ratio of the plate is considered constant, as its impact on deformation is deemed significantly less impactful than that of Young’s modulus [41].

2.3. Displacement Field and Strains

In the multi-directional FGM sandwich plate, the in-plane displacements u and v are accounted for in the x and y directions, respectively, while the transverse displacement w occurs in the z direction. These displacements can be expressed as follows, using refined shear deformation theory, as shown in Equations (3)–(6):

$$\begin{array}{l}u(x,y,z,t)=u_0(x,y,t)-z\frac{\partial w_b}{\partial x}-f\left(z\right)\frac{\partial w_b}{\partial x}\\ v(x,y,z,t)=v_0(x,y,t)-z\frac{\partial w_b}{\partial y}-f\left(z\right)\frac{\partial w_b}{\partial y}\\ w(x,y,z,t)=w_b(x,y,t)+w_s(x,y,t)\end{array}$$

(3)

In this study, two different shape functions are considered, as follows:

$$\begin{array}{l}f(z)=-\frac{1}{4}z+\frac{5}{3}z{\left(\frac{z}{h}\right)}^2 \mathrm{for} \mathrm{Model} 1\\ f(z)=z-\frac{h}{\pi }\sin \left(\frac{\pi z}{h}\right) \mathrm{for} \mathrm{Model} 2\end{array}$$

(4)

where u₀, v₀, w_b, and w_s are the in-plane and transverse displacements of the middle plane. The strains associated with the displacements in Equation (3) are given by Equations (5) and (6):

$$\begin{array}{l}{\epsilon }_x={\epsilon }_x^0+z k_x^b+f k_x^s\\ {\epsilon }_y={\epsilon }_y^0+z k_y^b+f k_y^s\\ {\gamma }_{xy}={\gamma }_{xy}^0+z k_{xy}^b+f k_{xy}^s\\ {\gamma }_{yz}=g {\gamma }_{yz}^s\\ {\gamma }_{xz}=g {\gamma }_{xz}^s\\ {\epsilon }_z=0\end{array}$$

(5)

where

$$\begin{array}{l}{\epsilon }_x^0=\frac{\partial u_0}{\partial x},\hspace{1em}{k}_x^b=-\frac{{\partial }^2{w}_b}{\partial x^2},\hspace{1em}{k}_x^s=-\frac{{\partial }^2{w}_s}{\partial x^2}\\ {\epsilon }_y^0=\frac{\partial v_0}{\partial y},\hspace{1em}{k}_y^b=-\frac{{\partial }^2{w}_b}{\partial y^2},\hspace{1em}{k}_y^s=-\frac{{\partial }^2{w}_s}{\partial y^2}\\ {\gamma }_{xy}^0=\frac{\partial u_0}{\partial y}+\frac{\partial v_0}{\partial x},\hspace{1em}{k}_{xy}^b=-2\frac{{\partial }^2{w}_b}{\partial x\partial y},\hspace{1em}{k}_{xy}^s=-2\frac{{\partial }^2{w}_s}{\partial x\partial y}\\ {\gamma }_{yz}^s=\frac{\partial w_s}{\partial y},\hspace{1em}{\gamma }_{xz}^s=\frac{\partial w_s}{\partial x}\\ g\left(z\right)=1-f^{\prime }\left(z\right),\hspace{1em}{f}^{\prime }\left(z\right)=\frac{df\left(z\right)}{dz}\end{array}$$

(6)

The stress–strain relationship of a multi-directional FGM sandwich plate can be expressed as shown in Equations (7) and (8):

$$\begin{array}{l}{\left\{\begin{array}{c}{\sigma }_x\\ {\sigma }_y\\ {\tau }_{xy}\end{array}\right\}}^{(n)}={\left[\begin{array}{ccc}{Q}_{11}& Q_{12}& 0\\ Q_{12}& Q_{22}& 0\\ 0& 0& Q_{66}\end{array}\right]}^{(n)}\left\{\begin{array}{c}{\epsilon }_x\\ {\epsilon }_y\\ {\gamma }_{xy}\end{array}\right\} \\ \mathrm{and} {\left\{\begin{array}{c}{\tau }_{yz}\\ {\tau }_{zx}\end{array}\right\}}^{\left(n\right)}={\left[\begin{array}{cc}{Q}_{44}& 0\\ 0& Q_{55}\end{array}\right]}^{\left(n\right)}\left\{\begin{array}{c}{\gamma }_{yz}\\ {\gamma }_{zx}\end{array}\right\}\end{array}$$

(7)

where

$$\begin{array}{l}{Q}_{11}^{\left(n\right)}\left(x,z\right)=Q_{22}^{\left(n\right)}\left(x,z\right)=\frac{E^{\left(n\right)}(x,z)}{1-{\nu }^2}\\ Q_{12}=\nu \cdot Q_{11}^{\left(n\right)}\left(x,z\right)\\ Q_{44}^{\left(n\right)}\left(x,z\right)=Q_{55}^{\left(n\right)}=Q_{66}^{\left(n\right)}=\frac{E^{\left(n\right)}(x,z)}{2\left(1+\nu \right)}\end{array}$$

(8)

2.4. Governing Equations

Hamilton’s principle (Equation (9)) is employed here to derive the equations of motion:

$$0={\displaystyle \underset{0}{\overset{t}{\int }}(\delta U+\delta V-\delta K) dt}$$

(9)

Here, δU represents the variation of strain energy, δV denotes the variation of work done, and δK signifies the variation of kinetic energy. The variation of the strain energy of the plate is expressed as shown in Equation (10):

$$\begin{array}{ll}\delta U& ={\displaystyle \underset{V}{\int }\left[{\sigma }_x\delta {\epsilon }_x+{\sigma }_y\delta {\epsilon }_y+{\tau }_{xy}\delta {\gamma }_{xy}+{\tau }_{yz}\delta {\gamma }_{yz}+{\tau }_{xz}\delta {\gamma }_{xz}\right]} dV\\ & ={\displaystyle \underset{A}{\int }\left[N_x\delta {\epsilon }_x^0+N_y\delta {\epsilon }_y^0+N_{xy}\delta {\gamma }_{xy}^0+M_x^b\delta k_x^b+M_y^b\delta k_y^b+M_{xy}^b\delta k_{xy}^b\right.}\\ & \left.\hspace{1em}+M_x^s\delta k_x^s+M_y^s\delta k_y^s+M_{xy}^s\delta k_{xy}^s+S_{yz}^s\delta {\gamma }_{yz}^s+S_{xz}^s\delta {\gamma }_{xz}^s\right] dA=0\end{array}$$

(10)

where A is the top surface and the stress resultants N, M, and S are defined as

$$\begin{array}{l}\left(N_i,M_i^b,M_i^s\right)={\displaystyle \sum _{n=1}^3{\displaystyle \underset{h_n}{\overset{h_{n+1}}{\int }}\left(1,z,f\right){\sigma }_{i}dz}},\hspace{1em}\left(i=x,y,xy\right)\\ \left(S_{xz}^s,S_{yz}^s\right)={\displaystyle \sum _{n=1}^3{\displaystyle \underset{h_n}{\overset{h_{n+1}}{\int }}g\left({\tau }_{xz},{\tau }_{yz}\right)dz}}\end{array}$$

(11)

The variation of the work done by the in-plane load $\left(N_x^0,N_y^0,N_{xy}^0\right)$ can be expressed as

$$\delta V=-{\displaystyle \underset{A}{\int }\overline{N}\delta \left(w_b+w_s\right)}dA$$

(12)

with

$$\overline{N}=\left[N_x^0\frac{{\partial }^2\left(w_b+w_s\right)}{\partial x^2}+N_y^0\frac{{\partial }^2\left(w_b+w_s\right)}{\partial y^2}+2N_{xy}^0\frac{{\partial }^2\left(w_b+w_s\right)}{\partial x\partial y}\right]$$

(13)

The variation in the kinetic energy of the plate can be expressed as

$$\begin{array}{l}\delta K=\underset{-h/2}{\overset{h/2}{\int }}\underset{A}{\int }\left(\dot{u}\delta \dot{u}+\dot{v}\delta \dot{v}+\dot{w}\delta \dot{w}\right) \rho (z) dA dz\\ =\underset{A}{\int }\{I_0\left[{\dot{u}}_0\delta {\dot{u}}_0+{\dot{v}}_0\delta {\dot{v}}_0+\left({\dot{w}}_b+{\dot{w}}_s\right)\left(\delta {\dot{w}}_b+\delta {\dot{w}}_s\right)\right]\\ -I_1\left({\dot{u}}_0\frac{\partial \delta {\dot{w}}_b}{\partial x}+\frac{\partial {\dot{w}}_b}{\partial x}\delta {\dot{u}}_0+{\dot{v}}_0\frac{\partial \delta {\dot{w}}_b}{\partial y}+\frac{\partial {\dot{w}}_b}{\partial y}\delta {\dot{v}}_0\right)\\ -I_2\left({\dot{u}}_0\frac{\partial \delta {\dot{w}}_s}{\partial x}+\frac{\partial {\dot{w}}_s}{\partial x}\delta {\dot{u}}_0+{\dot{v}}_0\frac{\partial \delta {\dot{w}}_s}{\partial y}+\frac{\partial {\dot{w}}_s}{\partial y}\delta {\dot{v}}_0\right)\\ +J_1\left(\frac{\partial {\dot{w}}_b}{\partial x}\frac{\partial \delta {\dot{w}}_b}{\partial x}+\frac{\partial {\dot{w}}_b}{\partial y}\frac{\partial \delta {\dot{w}}_b}{\partial y}\right)+K_2\left(\frac{\partial {\dot{w}}_s}{\partial x}\frac{\partial \delta {\dot{w}}_s}{\partial x}+\frac{\partial {\dot{w}}_s}{\partial y}\frac{\partial \delta {\dot{w}}_s}{\partial y}\right)\\ +J_2\left(\frac{\partial {\dot{w}}_b}{\partial x}\frac{\partial \delta {\dot{w}}_s}{\partial x}+\frac{\partial {\dot{w}}_s}{\partial x}\frac{\partial \delta {\dot{w}}_b}{\partial x}+\frac{\partial {\dot{w}}_b}{\partial y}\frac{\partial \delta {\dot{w}}_s}{\partial y}+\frac{\partial {\dot{w}}_s}{\partial y}\frac{\partial \delta {\dot{w}}_b}{\partial y}\right)\}dA\end{array}$$

(14)

The notation with a dot superscript denotes differentiation with respect to the time variable t, where ρ(z) represents the mass density defined by Equation (3) and (I_i, J_i, K_i) denote mass inertias, expressed as

$$\begin{array}{l}\left(I_0,I_1,I_2\right)={\displaystyle \sum _{n=1}^3{\displaystyle \underset{h_n}{\overset{h_{n+1}}{\int }}\left(1,z,z^2\right)\rho (z)dz}}\\ \left(J_1,J_2,K_2\right)={\displaystyle \sum _{n=1}^3{\displaystyle \underset{h_n}{\overset{h_{n+1}}{\int }}\left(f,z f,f^2\right)\rho (z)dz}}\end{array}$$

(15)

By substituting Equations (10), (12), and (14) into Equation (9), the following can be derived:

$$\begin{array}{l}\delta u_0: \frac{\partial N_x}{\partial x}+\frac{\partial N_{xy}}{\partial y}=I_0{\ddot{u}}_0-I_1\frac{\partial {\ddot{w}}_b}{\partial x}-J_1\frac{\partial {\ddot{w}}_s}{\partial x}\\ \delta v_0: \frac{\partial N_{xy}}{\partial x}+\frac{\partial N_y}{\partial y}=I_0{\ddot{v}}_0-I_1\frac{\partial {\ddot{w}}_b}{\partial y}-J_1\frac{\partial {\ddot{w}}_s}{\partial y}\\ \delta w_b: \frac{{\partial }^2{M}_x^b}{\partial x^2}+2\frac{{\partial }^2{M}_{xy}^b}{\partial x\partial y}+\frac{{\partial }^2{M}_y^b}{\partial y^2}+\overline{N}=I_0\left({\ddot{w}}_b+{\ddot{w}}_s\right)+I_1\left(\frac{\partial {\ddot{u}}_0}{\partial x}+\frac{\partial {\ddot{v}}_0}{\partial y}\right)-I_2{\nabla }^2{\ddot{w}}_b-J_2{\nabla }^2{\ddot{w}}_s\\ \delta w_s: \frac{{\partial }^2{M}_x^s}{\partial x^2}+2\frac{{\partial }^2{M}_{xy}^s}{\partial x\partial y}+\frac{{\partial }^2{M}_y^s}{\partial y^2}+\frac{\partial S_{xz}^s}{\partial x}+\frac{\partial S_{yz}^s}{\partial y}+\overline{N}=I_0\left({\ddot{w}}_b+{\ddot{w}}_s\right)+J_1\left(\frac{\partial {\ddot{u}}_0}{\partial x}+\frac{\partial {\ddot{v}}_0}{\partial y}\right)-J_2{\nabla }^2{\ddot{w}}_b-K_2{\nabla }^2{\ddot{w}}_s\end{array}$$

(16)

By substituting Equation (7) into Equation (11) and integrating across the thickness of the plate, the stress resultants can be expressed compactly in terms of strains as follows:

$$\left\{\begin{array}{c}N\\ M^b\\ M^s\end{array}\right\}=\left[\begin{array}{ccc}A& B& B^s\\ B& D& D^s\\ B^s& D^s& H^s\end{array}\right]\left\{\begin{array}{c}\epsilon \\ k^b\\ k^s\end{array}\right\}$$

(17)

in which

$$\begin{array}{l}N={\left\{N_x,N_y,N_{xy}\right\}}^t,\hspace{1em}{M}^b={\left\{M_x^b,M_y^b,M_{xy}^b\right\}}^t,\hspace{1em}{M}^s={\left\{M_x^s,M_y^s,M_{xy}^s\right\}}^t\\ \epsilon ={\left\{{\epsilon }_x^0,{\epsilon }_y^0,{\gamma }_{xy}^0\right\}}^t,\hspace{1em}{k}^b={\left\{k_x^b,k_y^b,k_{xy}^b\right\}}^t,\hspace{1em}{k}^s={\left\{k_x^s,k_y^s,k_{xy}^s\right\}}^t\\ A=\left[\begin{array}{ccc}{A}_{11}& A_{12}& 0\\ A_{12}& A_{22}& 0\\ 0& 0& A_{66}\end{array}\right],\hspace{1em}B=\left[\begin{array}{ccc}{B}_{11}& B_{12}& 0\\ B_{12}& B_{22}& 0\\ 0& 0& B_{66}\end{array}\right],\hspace{1em}D=\left[\begin{array}{ccc}{D}_{11}& D_{12}& 0\\ D_{12}& D_{22}& 0\\ 0& 0& D_{66}\end{array}\right]\\ B^s=\left[\begin{array}{ccc}{B}_{11}^s& B_{12}^s& 0\\ B_{12}^s& B_{22}^s& 0\\ 0& 0& B_{66}^s\end{array}\right],\hspace{1em}{D}^s=\left[\begin{array}{ccc}{D}_{11}^s& D_{12}^s& 0\\ D_{12}^s& D_{22}^s& 0\\ 0& 0& D_{66}^s\end{array}\right],\hspace{1em}{H}^s=\left[\begin{array}{ccc}{H}_{11}^s& H_{12}^s& 0\\ H_{12}^s& H_{22}^s& 0\\ 0& 0& H_{66}^s\end{array}\right]\\ S={\left\{S_{xz}^s,S_{yz}^s\right\}}^t,\hspace{1em}\gamma ={\left\{{\gamma }_{xz}^0,{\gamma }_{yz}^0\right\}}^t,\hspace{1em}{A}^s=\left[\begin{array}{cc}{A}_{44}^s& 0\\ 0& A_{55}^s\end{array}\right]\end{array}$$

(18)

The stiffness components are given as

$$\begin{array}{l}\left\{\begin{array}{cccccc}{A}_{11}& B_{11}& D_{11}& B_{11}^s& D_{11}^s& H_{11}^s\\ A_{12}& B_{12}& D_{12}& B_{12}^s& D_{12}^s& H_{12}^s\\ A_{66}& B_{66}& D_{66}& B_{66}^s& D_{66}^s& H_{66}^s\end{array}\right\}=\underset{-h/2}{\overset{h/2}{\int }}{Q}_{11}\left(1,z,z^2,f(z),z f(z),f^2(z)\right)\left\{\begin{array}{c}1\\ \nu \\ \frac{1-\nu }{2}\end{array}\right\}dz\\ \left(A_{22},B_{22},D_{22},B_{22}^s,D_{22}^s,H_{22}^s\right)=\left(A_{11},B_{11},D_{11},B_{11}^s,D_{11}^s,H_{11}^s\right)\\ A_{44}^s=A_{55}^s=\underset{-h/2}{\overset{h/2}{\int }}{Q}_{44}{\left[g(z)\right]}^{2}dz\end{array}$$

(19)

By introducing Equation (17) into Equation (16), the equations of motion can be rephrased in terms of displacements (u₀, v₀, w_b, w_s). The resulting equations take the following forms:

$$\begin{array}{l}{A}_{11}\frac{{\partial }^2{u}_0}{\partial x^2}+A_{66}\frac{{\partial }^2{u}_0}{\partial y^2}+\left(A_{12}+A_{66}\right)\frac{{\partial }^{2}v}{\partial x\partial y}-B_{11}\frac{{\partial }^3{w}_b}{\partial x^3}-\left(B_{12}+2B_{66}\right)\frac{{\partial }^3{w}_b}{\partial x\partial y^2} \\ \hspace{1em}\hspace{1em}-B_{11}^s\frac{{\partial }^3{w}_s}{\partial x^3}-\left(B_{12}^s+2B_{66}^s\right)\frac{{\partial }^3{w}_s}{\partial x\partial y^2}=I_0{\ddot{u}}_0-I_1\frac{\partial {\ddot{w}}_b}{\partial x}-J_1\frac{\partial {\ddot{w}}_s}{\partial x}\\ \left(A_{12}+A_{66}\right)\frac{{\partial }^2{u}_0}{\partial x\partial y}+A_{66}\frac{{\partial }^2{v}_0}{\partial x^2}+A_{22}\frac{{\partial }^2{v}_0}{\partial y^2}-\left(B_{12}+2B_{66}\right)\frac{{\partial }^3{w}_b}{\partial x^2\partial y}-B_{22}\frac{{\partial }^3{w}_b}{\partial y^3}\\ \hspace{1em}\hspace{1em}-B_{22}^s\frac{{\partial }^3{w}_s}{\partial y^3}-\left(B_{12}^s+2B_{66}^s\right)\frac{{\partial }^3{w}_s}{\partial x^2\partial y}=I_0{\ddot{v}}_0-I_1\frac{\partial {\ddot{w}}_b}{\partial y}-J_1\frac{\partial {\ddot{w}}_s}{\partial y}\\ B_{11}\frac{{\partial }^3{u}_0}{\partial x^3}+\left(B_{12}+2B_{66}\right)\frac{{\partial }^3{u}_0}{\partial x\partial y^2}+\left(B_{12}+2B_{66}\right)\frac{{\partial }^3{v}_0}{\partial x^2\partial y}+B_{22}\frac{{\partial }^3{v}_0}{\partial y^3}-D_{11}\frac{{\partial }^4{w}_b}{\partial x^4}\\ \hspace{1em}\hspace{1em}-2\left(D_{12}+2D_{66}\right)\frac{{\partial }^4{w}_b}{\partial x^2\partial y^2}-D_{22}\frac{{\partial }^4{w}_b}{\partial y^4}-D_{11}^s\frac{{\partial }^4{w}_s}{\partial x^4}-2\left(D_{12}^s+2D_{66}^s\right)\frac{{\partial }^4{w}_s}{\partial x^2\partial y^2}\\ \hspace{1em}\hspace{1em}-D_{22}^s\frac{{\partial }^4{w}_s}{\partial y^4}+\overline{N}=I_0\left({\ddot{w}}_b+{\ddot{w}}_s\right)+I_1\left(\frac{\partial {\ddot{u}}_0}{\partial x}+\frac{\partial {\ddot{v}}_0}{\partial y}\right)-I_2{\nabla }^2{\ddot{w}}_b-J_2{\nabla }^2{\ddot{w}}_s\\ B_{11}^s\frac{{\partial }^3{u}_0}{\partial x^3}+\left(B_{12}^s+2B_{66}^s\right)\frac{{\partial }^3{u}_0}{\partial x\partial y^2}+\left(B_{12}^s+2B_{66}^s\right)\frac{{\partial }^3{v}_0}{\partial x^2\partial y}+B_{22}^s\frac{{\partial }^3{v}_0}{\partial y^3}-D_{11}^s\frac{{\partial }^4{w}_b}{\partial x^4}\\ \hspace{1em}\hspace{1em}-2\left(D_{12}^s+2D_{66}^s\right)\frac{{\partial }^4{w}_b}{\partial x^2\partial y^2} -D_{22}^s\frac{{\partial }^4{w}_b}{\partial y^4}-H_{11}^s\frac{{\partial }^4{w}_s}{\partial x^4}-2\left(H_{12}^s+2H_{66}^s\right)\frac{{\partial }^4{w}_s}{\partial x^2\partial y^2}-H_{22}^s\frac{{\partial }^4{w}_s}{\partial y^4}\\ \hspace{1em}\hspace{1em}+A_{55}^s\frac{{\partial }^2{w}_s}{\partial x^2}+A_{44}^s\frac{{\partial }^2{w}_s}{\partial y^2}+\overline{N}=I_0\left({\ddot{w}}_b+{\ddot{w}}_s\right)+J_1\left(\frac{\partial {\ddot{u}}_0}{\partial x}+\frac{\partial {\ddot{v}}_0}{\partial y}\right)-J_2{\nabla }^2{\ddot{w}}_b-K_2{\nabla }^2{\ddot{w}}_s\end{array}$$

(20)

The exact solution to the set of Equation (20), describing the P-FGMs multi-directional functionality graded sandwich plate under various boundary conditions, can be derived. The boundary conditions for an arbitrary edge include both its simply supported and clamped conditions:

• Clamped (C):

  $$\begin{array}{l}{u}_0=v_0=w_b=\partial w_b/\partial x=\partial w_b/\partial y=w_s=\partial w_s/\partial x=\partial w_s/\partial y=0,\\ \mathrm{at} x=0, y=0,b\end{array}$$

  (21)
• Simply supported (S):

  $$\begin{array}{l}{v}_0=w_b=\partial w_b/\partial y=w_s=\partial w_s/\partial y=0,\hspace{1em}\hspace{1em}\mathrm{at} x=0,a\\ u_0=w_b=\partial w_b/\partial x=w_s=\partial w_s/\partial x=0,\hspace{1em}\hspace{1em}\mathrm{at} y=0,b\end{array}$$

  (22)

The following representation of the displacement quantities that fulfill the aforementioned boundary conditions is applicable to our specific problem:

$$\left\{\begin{array}{c}{u}_0\\ v_0\\ w_b\\ w_s\end{array}\right\}=\left\{\begin{array}{l}{U}_{mn}\frac{\partial X_m\left(x\right)}{\partial x}{Y}_n\left(y\right)e^{i\omega t}\\ V_{mn}{X}_n\left(x\right)\frac{\partial Y_n\left(y\right)}{\partial y}{e}^{i\omega t}\\ W_{bmn}{X}_n\left(x\right)Y_n\left(y\right)e^{i\omega t}\\ W_{smn}{X}_n\left(x\right)Y_n\left(y\right)e^{i\omega t}\end{array}\right\}$$

(23)

where U_mn, V_mn, W_bmn, and W_smn are arbitrary parameters and ω = ω_mn denotes the eigenfrequency associated with the (m,n)^th eigenmode. The functions X_m(x) and Y_n(y) are suggested here to satisfy, at least, the geometric boundary conditions given in Equations (21) and (22) and represent the approximate shapes of the deflected surface of the plate. These functions, for the different boundary condition cases, are listed in Table 1. Note that λ = mπ/a and μ = nπ/b.

Table 1. The admissible functions for the various boundary conditions [42].

Boundary Conditions	x = 0	y = 0	x = a	y = b	Xm(x)	Yn(y)
SSSS	S	S	S	S	sin(λx)	sin(μx)
CSCS	C	S	C	S	sin2(λx)	sin(μx)
CCCC	C	C	C	C	sin2(λx)	sin2(μx)
FCFC	F	C	F	C	cos2(λx)·[sin2(λx) + 1]	sin2(μx)

By substituting Equation (23) into the governing Equation (20) and multiplying each equation by its corresponding eigenfunction, and then integrating over the solution domain, we can derive the following equations after performing certain mathematical manipulations:

$$\left(\right[\begin{array}{cccc}{a}_{11}& a_{12}& a_{13}& a_{14}\\ a_{21}& a_{22}& a_{23}& a_{24}\\ a_{31}& a_{32}& a_{33}-\beta N& a_{34}-\beta N\\ a_{41}& a_{42}& a_{43}-\beta N& a_{44}-\beta N\end{array}]-{\omega }^2\left[\begin{array}{cccc}{m}_{11}& 0& m_{13}& m_{14}\\ 0& m_{22}& m_{23}& m_{24}\\ m_{31}& m_{32}& m_{33}& m_{34}\\ m_{41}& m_{42}& m_{43}& m_{44}\end{array}\right])·\left\{\begin{array}{c}{U}_{\mathit{mn}}\\ V_{\mathit{mn}}\\ W_{\mathit{mn}}\\ X_{\mathit{mn}}\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right\}$$

(24)

in which

$$\begin{array}{llll}\hspace{1em}{a}_{11}=A_{11}{\alpha }_{12}+A_{66}{\alpha }_8& \hspace{1em}{a}_{12}=\left(A_{12}+A_{66}\right){\alpha }_8& \hspace{1em}{a}_{13}=-B_{11}{\alpha }_{12}-\left(B_{12}+2B_{66}\right){\alpha }_8& \hspace{1em}{a}_{14}=-\left(B_{12}^s+2B_{66}^s\right){\alpha }_8-B_{11}^s{\alpha }_{12}\\ \hspace{1em}{a}_{21}=\left(A_{12}+A_{66}\right){\alpha }_{10}& \hspace{1em}{a}_{22}=A_{22}{\alpha }_4+A_{66}{\alpha }_{10}& \hspace{1em}{a}_{23}=-B_{22}{\alpha }_4-\left(B_{12}+2B_{66}\right){\alpha }_{10}& \hspace{1em}{a}_{24}=-\left(B_{12}^s+2B_{66}\right){\alpha }_{10}-B_{22}^s{\alpha }_4\\ a_{31}=B_{11}{\alpha }_{13}+\left(B_{12}+2B_{66}\right){\alpha }_{11}& \begin{array}{c}{a}_{32}=\left(B_{12}+2B_{66}\right){\alpha }_{11}\hfill \\ +B_{22}{\alpha }_5\hfill \end{array}& \begin{array}{c}{a}_{33}=-D_{11}{\alpha }_{13}-2\left(D_{12}+2D_{66}\right){\alpha }_{11}\hfill \\ -D_{22}{\alpha }_5\hfill \end{array}& \begin{array}{c}{a}_{34}=-D_{11}^s{\alpha }_{13}-2\left(D_{12}^s+2D_{66}^s\right){\alpha }_{11}\hfill \\ -D_{66}^s{\alpha }_5\hfill \end{array}\\ a_{41}=B_{11}^s{\alpha }_{13}+\left(B_{12}^s+2B_{66}^s\right){\alpha }_{11}& \begin{array}{c}{a}_{42}=\left(B_{12}^s+2B_{66}^s\right){\alpha }_{11}\hfill \\ +B_{22}^s{\alpha }_5\hfill \end{array}& \begin{array}{c}{a}_{43}=-D_{11}^s{\alpha }_{13}-2\left(D_{12}^s+2D_{66}^s\right){\alpha }_{11}\hfill \\ -D_{22}^s{\alpha }_5\hfill \end{array}& \begin{array}{c}{a}_{44}=-H_{11}^s{\alpha }_{13}-2\left(H_{12}^s+2H_{66}^s\right){\alpha }_{11}\hfill \\ -H_{22}^s{\alpha }_5+A_{44}^s{\alpha }_9+A_{55}^s{\alpha }_3\hfill \end{array}\\ N=N_x^0\\ {\xi }_1=N_y^0/N_x^0\end{array}$$

(25)

and

$$\begin{array}{l}{m}_{11}=-I_0{\alpha }_6\\ m_{13}=-I_1{\alpha }_6,\hspace{1em}{m}_{32}=-I_1{\alpha }_3\\ m_{14}=J_1{\alpha }_6,\hspace{1em}{m}_{33}=-I_0{\alpha }_1+I_2\left({\alpha }_3+{\alpha }_9\right)\\ m_{22}=-I_0{\alpha }_2,\hspace{1em}{m}_{34}=-I_0{\alpha }_1+J_2\left({\alpha }_3+{\alpha }_9\right)\\ m_{23}=I_1{\alpha }_2,\hspace{1em}{m}_{41}=-J_1{\alpha }_9\\ m_{24}=J_1{\alpha }_2,\hspace{1em}{m}_{42}=-J_1{\alpha }_3\\ m_{31}=-I_1{\alpha }_9,\hspace{1em}{m}_{44}=-I_0{\alpha }_1+K_2\left({\alpha }_3+{\alpha }_9\right)\end{array}$$

(26)

with

$$\begin{array}{l}\beta ={\xi }_1{\alpha }_3+{\alpha }_9\\ \left({\alpha }_1,{\alpha }_3,{\alpha }_5\right)=\underset{0}{\overset{b}{\int }}\underset{0}{\overset{a}{\int }}\left(X_m{Y}_n,X_m{Y}_n^{″},X_m{Y}_n^{⁗}\right)X_m{Y}_{n}dxdy\\ \left({\alpha }_2,{\alpha }_4,{\alpha }_{10}\right)=\underset{0}{\overset{b}{\int }}\underset{0}{\overset{a}{\int }}\left(X_m{Y}_n^{\prime },X_m{Y}_n^{″},X_m^{″}{Y}_n^{\prime }\right)X_m{Y}_n^{\prime }dxdy\\ \left({\alpha }_6,{\alpha }_8,{\alpha }_{12}\right)=\underset{0}{\overset{b}{\int }}\underset{0}{\overset{a}{\int }}\left(X_m^{\prime }{Y}_n,X_m^{\prime }{Y}_n^{″},X_m^{‴}{Y}_n\right)X_m^{\prime }{Y}_{n}dxdy\\ \left({\alpha }_7,{\alpha }_9,{\alpha }_{11},{\alpha }_{13}\right)=\underset{0}{\overset{b}{\int }}\underset{0}{\overset{a}{\int }}\left(X_m^{\prime }{Y}_n^{\prime },X_m^{″}{Y}_n,X_m^{\prime }{Y}_n^{″},X_m^{⁗}{Y}_n\right)X_m{Y}_{n}dxdy\end{array}$$

(27)

3. Numerical Results and Discussion

In this section, we explore several numerical examples to assess the accuracy of the two proposed theories in analyzing the buckling and free vibration of multi-directional FG sandwich plates under different boundary conditions. A range of sandwich plate configurations, comprising both symmetric and non-symmetric FGMs, are examined to demonstrate the versatility of these theories.

The subsequent discussions aim to underscore the precision and relevance of the presented theories in capturing the plate’s behavior under varied conditions. The considered configuration schemes of the sandwich plates include:

• (1-0-1) FGM sandwich plate, consisting of two layers of equal thickness without a core, where h₁ = h₂ = 0.
• (1-2-1) FGM sandwich plate, with the core thickness equal to the sum of the face thicknesses: h₂ = −h/4, h₃ = h/4.
• (1-1-1) FGM sandwich plate, comprising three equal-thickness layers: h₂ = −h/6, h₃ = h/6.
• (2-2-1) FGM sandwich plate, featuring a core thickness twice that of the upper face and equal to the lower one, defined by h₂ = −h/10, h₃ = 3h/10.
• (1-1-2) FGM sandwich plate, with a core thickness equal to that of the lower face and with the thickness of the upper face twice that of the core: h₂ = −h/4, h₃ = 0.

The material combinations include aluminum and alumina, each with the following properties [23]:

• Ceramic (alumina, Al₂O₃): Young’s modulus E_c = 380 GPa, Poisson’s ratio v_c = 0.3, density ρ_c = 3800 kg/m³;
• Metal (aluminum, Al): Young’s modulus E_m = 70 GPa, Poisson’s ratio v_m = 0.3, density ρ_m = 2702 kg/m³.

3.1. FG Sandwich Plates

3.1.1. Free Vibration Analysis of FG Sandwich Plates

The face sheet comprises a functionally graded material with properties varying along the p_z direction. A power law distribution is utilized for the FG face sheet, while the core consists of a homogeneous material. When the core material is pure ceramic (alumina), it is referred to as “hard-core”, and when it is pure metal (aluminum) it is called “soft-core”. Table 2 displays the fundamental frequency results obtained from the two proposed methods for a/h = 10 and p_x = 0, in the case of a hard core. The results indicate that the sandwich plate with the (1-2-1) scheme exhibits the highest frequency because of its thicker ceramic core, leading to greater stiffness. Subsequently, a decrease in natural frequency was observed for the (2-2-1) scheme, followed by the (1-1-1), (2-1-2), and (1-0-1) schemes. Their frequency diminishes with an increase in the grading parameter p_z.

Table 2. Dimensionless fundamental frequency $\overline{\omega }$ of FG sandwich plates (a/h = 10 and p_x = 0). Type A: hard core.

pz	Theory	1-0-1	2-1-2	1-1-1	2-2-1	1-2-1
0	3D [43]	1.8268	1.8268	1.8268	1.8268	1.8268
	SSDT [44]	1.8245	1.8245	1.8245	1.8245	1.8245
	TSDT [44]	1.8245	1.8245	1.8245	1.8245	1.8245
	FSDT [44]	1.8244	1.8244	1.8244	1.8244	1.8244
	NFSDT [45]	1.8244	1.8244	1.8244	1.8244	1.8244
	Present 1	1.8245	1.8245	1.8245	1.8245	1.8245
	Present 2	1.8245	1.8245	1.8245	1.8245	1.8245
0.5	3D [43]	1.4461	1.4861	1.5213	1.5493	1.5767
	SSDT [44]	1.4444	1.4842	1.5193	1.5520	1.5745
	TSDT [44]	1.4442	1.4841	1.5192	1.5520	1.5727
	FSDT [44]	1.4417	1.4816	1.5170	1.5500	1.5727
	NFSDT [45]	1.4442	1.4841	1.5192	1.5471	1.5745
	Present 1	1.4446	1.4844	1.5195	1.5474	1.5747
	Present 2	1.4447	1.4845	1.5195	1.5474	1.5747
1	3D [43]	1.2447	1.3018	1.3552	1.3976	1.4414
	SSDT [44]	1.2434	1.3002	1.3534	1.4079	1.4393
	TSDT [44]	1.2432	1.3001	1.3533	1.4079	1.4393
	FSDT [44]	1.2403	1.2973	1.3507	1.4056	1.4372
	NFSDT [45]	1.2429	1.3000	1.3533	1.3956	1.4393
	Present 1	1.2437	1.3005	1.3537	1.3959	1.4396
	Present 2	1.2438	1.3006	1.3537	1.3959	1.4396
5	3D [43]	0.9448	0.9810	1.0453	1.1098	1.1757
	SSDT [44]	0.9463	0.9821	1.0448	1.1474	1.1740
	TSDT [44]	0.9460	0.9818	1.0447	1.1473	1.1740
	FSDT [44]	0.9426	0.9787	1.0418	1.1447	1.1716
	NFSDT [45]	0.9431	0.9796	1.0435	1.1077	1.1735
	Present 1	0.9467	0.9824	1.0451	1.1094	1.1743
	Present 2	0.9469	0.9826	1.0453	1.1095	1.1744

Additionally, an analysis was conducted for a/h = 5 and p_x = 0 for both hard-core and soft-core materials, as presented in Table 3 and Table 4. The analysis reveals that the soft-core material yields lower frequencies than the hard-core material for homogeneous materials. Moreover, as the plate thickness transitions from a/h = 10 to a/h = 5, there is a noticeable decrease in the frequency outcomes.

Table 3. Dimensionless fundamental frequency $\overline{\omega }$ of FG sandwich plates (a/h = 5 and n_x = 0). Type A: hard core.

nz	Theory	1-0-1	2-1-2	1-1-1	2-2-1	1-2-1
0	3D [43]	1.6771	1.6771	1.6771	1.6771	1.6771
	NFSDT [45]	1.6697	1.6697	1.6697	1.6697	1.6697
	Present 1	1.6701	1.6701	1.6701	1.6701	1.6701
0.5	3D [43]	1.3536	1.3905	1.4218	1.4454	1.4694
	NFSDT [45]	1.3473	1.3841	1.4152	1.4386	1.4626
	Present 1	1.3478	1.3844	1.4154	1.4388	1.4628
1	3D [43]	1.1749	1.2292	1.2777	1.3143	1.3534
	NFSDT [45]	1.1691	1.2232	1.2714	1.3078	1.3467
	Present 1	1.1703	1.2238	1.2717	1.3082	1.3471
5	3D [43]	0.8909	0.9336	0.9980	1.0561	1.1190
	NFSDT [45]	0.8853	0.9286	0.9916	1.0488	1.1118
	Present 1	0.89528	0.9365	0.9959	1.0533	1.1136
10	3D [43]	0.8683	0.8923	0.9498	1.0095	1.0729
	NFSDT [45]	0.8599	0.8860	0.9428	1.0012	1.0648
	Present 1	0.8725	0.8998	0.9508	1.0095	1.0679

Table 4. Dimensionless fundamental frequency $\overline{\omega }$ of FG sandwich plates (a/h = 5 and n_x = 0). Type B: soft core.

nz	Theory	1-0-1	2-1-2	1-1-1	2-2-1	1-2-1
0	3D [43]	0.8529	0.8529	0.8529	0.8529	0.8529
	NFSDT [45]	0.8491	0.8491	0.8491	0.8491	0.8491
	Present 1	0.8501	0.8501	0.8501	0.8501	0.8501
0.5	3D [43]	1.3789	1.3206	1.2805	1.2453	1.2258
	NFSDT [45]	1.3686	1.3115	1.2729	1.2380	1.2185
	Present 1	1.3829	1.3284	1.2859	1.2509	1.2255
1	3D [43]	1.5090	1.4333	1.3824	1.3420	1.3213
	NFSDT [45]	1.4915	1.4156	1.3702	1.3302	1.3104
	Present 1	1.5176	1.4557	1.4036	1.3625	1.3289
5	3D [43]	1.6587	1.5801	1.5028	1.4601	1.4267
	NFSDT [45]	1.6305	1.5125	1.4589	1.4195	1.4026
	Present 1	1.6585	1.6181	1.5665	1.5212	1.4748
10	3D [43]	1.6728	1.6091	1.5267	1.4831	1.4410
	NFSDT [45]	1.6495	1.5196	1.4642	1.4266	1.4101
	Present 1	1.6679	1.6394	1.5931	1.5484	1.5018

When n_z = 0.5, the hard-core plate exhibits higher frequencies than the soft-core plate for all instances, except for the 1-0-1 scheme, where the soft core demonstrates higher frequencies. Conversely, at n_z = 1, the soft core demonstrates higher frequencies than the hard core, except for the 1-2-1 scheme. Beyond n_z > 5, it is observed that the soft-core material consistently yields higher frequencies than the hard-core material.

3.1.2. Buckling Analysis of FG Sandwich Plates

The buckling analysis results mirror the trends observed in the frequency analysis, as summarized in Table 5. Similar to the frequency outcomes, the buckling analysis focuses on a square plate with a hard core material undergoing uniaxial compression, particularly at a/h = 10. Among the different schemes examined, the (1-2-1) configuration demonstrates the highest buckling load, followed by (2-2-1), (1-1-1), (2-1-2), and (1-0-1), in descending order of buckling strength. Notably, there is a consistent decrease in buckling load with the increasing grading parameter p_z. This pattern underscores the significant influence of the grading parameter on the buckling behavior of square plates with a hard core material under uniaxial compression, with various schemes exhibiting distinct levels of structural stability.

Table 5. Dimensionless buckling load $\overline{N}$ of square plates under uniaxial compression (ξ₁ = 0, a/h = 10). Type A: hard core.

nz	Theory	1-0-1	2-1-2	1-1-1	2-2-1	1-2-1
0	SSDT [44]	13.0061	13.0061	13.0061	13.0061	13.0061
	TSDT [44]	13.0050	13.0050	13.0050	13.0050	13.0050
	FSDT [44]	13.0045	13.0045	13.0045	13.0045	13.0045
	NFSDT [45]	13.0045	13.0045	13.0045	13.0045	13.0045
	Present 1	13.0049	13.0049	13.0049	13.0049	13.0049
	Present 2	13.0061	13.0061	13.0061	13.0061	13.0061
0.5	SSDT [44]	7.3657	7.9420	8.4371	8.8104	9.2167
	TSDT [44]	7.3644	7.9408	8.4365	8.8100	9.2168
	FSDT [44]	7.3373	7.9132	8.4103	8.7867	9.1952
	NFSDT [45]	7.3634	7.9403	8.4361	8.8095	9.2162
	Present 1	7.3644	7.9408	8.4365	8.8099	9.2168
	Present 2	7.3657	7.9419	8.4371	8.8104	9.2167
1	SSDT [44]	5.1685	5.8412	6.4654	6.9498	7.5063
	TSDT [44]	5.1671	5.8401	6.4647	6.9494	7.5066
	FSDT [44]	5.1424	5.8138	6.4389	6.9257	7.4837
	NFSDT [45]	5.1648	5.8387	6.4641	6.9485	7.5056
	Present 1	5.1671	5.8401	6.4647	6.9494	7.5066
	Present 2	5.1685	5.8412	6.4654	6.9498	7.5063
5	SSDT [44]	2.6601	3.0441	3.5806	4.1129	4.7349
	TSDT [44]	2.6582	3.0426	3.5796	4.1121	4.7347
	FSDT [44]	2.6384	3.0225	3.5596	4.0929	4.7148
	NFSDT [45]	2.6415	3.0282	3.5710	4.1024	4.7305
	Present 1	2.6582	3.0426	3.5796	4.1121	4.7347
	Present 2	2.6601	3.0441	3.5806	4.1129	4.7349

Moreover, a buckling analysis of square FG plates under biaxial compression was conducted, as indicated in Table 6. This table provides a comprehensive comparison of the dimensionless buckling loads for square plates across various theories and conditions, offering insights into the impact of the grading parameter on the structural stability of the plate. Similar to unidirectional loading, biaxial loading also results in a noticeable decrease in the dimensionless buckling loads for all the schemes considered.

Table 6. Dimensionless buckling load $\overline{N}$ of square plates under biaxial compression (ξ₁ = 1, a/h = 10). Type A: hard core.

nz	Theory	1-0-1	2-1-2	1-1-1	2-2-1	1-2-1
0	SSDT [44]	6.5030	6.5030	6.5030	6.5030	6.5030
	TSDT [44]	6.5025	6.5025	6.5025	6.5025	6.5025
	FSDT [44]	6.5022	6.5022	6.5022	6.5022	6.5022
	NFSDT [45]	6.5022	6.5022	6.5022	6.5022	6.5022
	Present 1	6.5025	6.5025	6.5025	6.5025	6.5025
	Present 2	6.5030	6.5030	6.5030	6.5030	6.5030
0.5	SSDT [44]	3.6828	3.9710	4.2186	4.4052	4.6084
	TSDT [44]	3.6822	3.9704	4.2182	4.4050	4.6084
	FSDT [44]	3.6687	3.9566	4.2052	4.3934	4.5976
	NFSDT [45]	3.6817	3.9702	4.2181	4.4047	4.6081
	Present 1	3.6822	3.9704	4.2182	4.4049	4.6084
	Present 2	3.6828	3.9709	4.2185	4.4052	4.6083
1	SSDT [44]	2.5842	2.9206	3.2327	3.4749	3.7531
	TSDT [44]	2.5836	2.9200	3.2324	3.4747	3.7533
	FSDT [44]	2.5712	2.9069	3.2195	3.4629	3.7418
	NFSDT [45]	2.5824	2.9193	3.2320	3.4742	3.7528
	Present 1	2.5835	2.9200	3.2323	3.4747	3.7533
	Present 2	2.5842	2.9206	3.2327	3.4749	3.7531
5	SSDT [44]	1.3300	1.5220	1.7903	2.0564	2.3674
	TSDT [44]	1.3291	1.5213	1.7898	2.0561	2.3673
	FSDT [44]	1.3192	1.5113	1.7798	2.0464	2.3574
	NFSDT [45]	1.3208	1.5141	1.7855	2.0512	2.3652
	Present 1	1.3291	1.5213	1.7898	2.0560	2.3673
	Present 2	1.3300	1.5220	1.7903	2.0564	2.3674

3.2. Multi-Directional FG Sandwich Plates

3.2.1. Free Vibration Analysis of Multi-Directional FG Sandwich Plates

The free vibration analysis of a multi-directional FG skin with a homogeneous hard core was conducted under various boundary conditions. Multi-directional gradation was achieved by adjusting the parameters p_x and p_z. The results are presented in Table 7. Across all boundary conditions, the (1-2-1) scheme exhibits the highest frequency, followed by (2-2-1), (1-1-1), (2-1-2), and (1-0-1). In all scenarios, maintaining a constant and zero value for the parameter p_x while increasing p_z from 0.5 to 1 and 5 results in a decrease in frequency. Similarly, increasing p_x from 0 to 0.5 and up to 2 and then varying p_z also leads to a decreasing trend in frequency.

Table 7. Dimensionless fundamental frequency $\overline{\omega }$ of square plates under various boundary conditions (a/h = 10). Type A: hard core.

Boundary Conditions	px	pz	1-0-1	2-1-2	1-1-1	2-2-1	1-2-1
SSSS	0	0.5	1.4446	1.4844	1.5195	1.5474	1.5747
	0	1	1.2437	1.3005	1.3537	1.3959	1.4396
	0	5	0.9467	0.9824	1.0451	1.1094	1.1743
	0.5	0.5	1.3965	1.4302	1.4635	1.4949	1.5216
	0.5	1	1.2113	1.2606	1.3109	1.3556	1.3983
	0.5	5	0.9451	0.9748	1.0338	1.0981	1.1613
	2	0.5	1.2835	1.3046	1.3353	1.3749	1.4024
	2	1	1.1378	1.1708	1.2156	1.2655	1.3076
	2	5	0.9414	0.9590	1.0103	1.0745	1.1341
CSCS	0	0.5	2.1285	2.1868	2.2375	2.2772	2.3165
	0	1	1.8379	1.9218	1.9992	2.0599	2.1231
	0	5	1.4017	1.4583	1.5511	1.6446	1.7399
	0.5	0.5	2.0571	2.1080	2.1569	2.2018	2.2407
	0.5	1	1.7894	1.8634	1.9373	2.0015	2.0638
	0.5	5	1.3983	1.4469	1.5345	1.6280	1.7208
	2	0.5	1.8894	1.9256	1.9718	2.0288	2.0697
	2	1	1.6788	1.7321	1.7988	1.8708	1.9329
	2	5	1.3899	1.4234	1.4999	1.5934	1.6813
CCCC	0	0.5	2.6386	2.7106	2.7725	2.8205	2.8684
	0	1	2.2834	2.3877	2.4827	2.5565	2.6338
	0	5	1.7439	1.8180	1.9334	2.0482	2.16583
	0.5	0.5	2.5497	2.6139	2.6744	2.7287	2.7767
	0.5	1	2.2225	2.3157	2.4069	2.4850	2.5616
	0.5	5	1.7387	1.8038	1.9129	2.0277	2.1425
	2	0.5	2.3406	2.3902	2.4486	2.5178	2.5689
	2	1	2.0835	2.1538	2.2371	2.3250	2.4021
	2	5	1.7257	1.7741	1.8701	1.9849	2.0939
FCFC	0	0.5	2.7884	2.8643	2.9290	2.9788	3.0289
	0	1	2.4168	2.5271	2.6268	2.7038	2.7847
	0	5	1.8478	1.9289	2.0510	2.1715	2.2954
	0.5	0.5	2.6941	2.7629	2.8266	2.8830	2.9335
	0.5	1	2.3519	2.4514	2.5474	2.6289	2.7094
	0.5	5	1.8415	1.9137	2.0294	2.1499	2.2709
	2	0.5	2.4724	2.5282	2.5906	2.6628	2.7171
	2	1	2.2035	2.2809	2.3695	2.4614	2.5428
	2	5	1.8257	1.8821	1.9843	2.1048	2.2199

Notably, the results reveal an intriguing observation: an increase in the parameter p_z has a more pronounced effect on the frequency parameter compared to p_x. Thus, enhancing the ceramic composition of the material in its transverse direction demonstrates a more significant influence on frequency than varying the ceramic composition of its longitudinal direction. The frequency is observed to be at its maximum for the FCFC condition, followed by the CCCC, CSCS, and SSSS conditions.

The free vibration analysis of a multi-directional FG skin combined with a homogeneous soft core was also conducted under various boundary conditions for different values of p_x and p_z. The results are presented in Table 8. In contrast to the hard-core sandwich plate, the maximum frequency was observed for the (1-0-1) configuration, followed by (2-1-2), (1-1-1), (2-2-1), and (1-2-1). Similar to the hard-core case, the soft-core frequency is highest for the FCFC condition, followed by the CCCC, CSCS, and SSSS conditions.

Table 8. Dimensionless fundamental frequency $\overline{\omega }$ of square plates under various boundary conditions (a/h = 10). Type B: soft core.

Boundary Conditions	px	pz	1-0-1	2-1-2	1-1-1	2-2-1	1-2-1
SSSS	0	0.5	1.5758	1.5299	1.4876	1.4372	1.4173
	0	1	1.7263	1.6846	1.6405	1.5798	1.5619
	0	5	1.8422	1.8421	1.8179	1.7541	1.7494
	0.5	0.5	1.6232	1.5879	1.5507	1.4986	1.4828
	0.5	1	1.7452	1.7137	1.6749	1.6146	1.6000
	0.5	5	1.8401	1.8441	1.8228	1.7601	1.7570
	2	0.5	1.7017	1.6887	1.6627	1.6085	1.6006
	2	1	1.7762	1.7652	1.7382	1.6791	1.6714
	2	5	1.8354	1.8476	1.8323	1.7718	1.7720
CSCS	0	0.5	2.2702	2.1949	2.1305	2.0639	2.0299
	0	1	2.4889	2.4125	2.3402	2.2608	2.2229
	0	5	2.6799	2.6551	2.6007	2.5159	2.4809
	0.5	0.5	2.3500	2.2855	2.2237	2.1542	2.1209
	0.5	1	2.5258	2.4619	2.3942	2.3144	2.2771
	0.5	5	2.6796	2.6609	2.6105	2.5266	2.4932
	2	0.5	2.4776	2.4404	2.3886	2.3152	2.2845
	2	1	2.5842	2.5476	2.4923	2.4127	2.3788
	2	5	2.6778	2.6715	2.6289	2.5474	2.5171
CCCC	0	0.5	2.7695	2.6701	2.5885	2.5124	2.4665
	0	1	3.0378	2.9312	2.8358	2.7455	2.6897
	0	5	3.2917	3.2401	3.1577	3.0599	2.9948
	0.5	0.5	2.8767	2.7864	2.7043	2.6239	2.5747
	0.5	1	3.0912	2.9977	2.9053	2.8136	2.7552
	0.5	5	3.2937	3.2499	3.1717	3.0748	3.0107
	2	0.5	3.0449	2.9835	2.9084	2.8226	2.7694
	2	1	3.1743	3.1116	3.0305	2.9380	2.8782
	2	5	3.2958	3.2674	3.1982	3.1032	3.0417
FCFC	0	0.5	2.8951	2.7859	2.6987	2.6225	2.5716
	0	1	3.1767	3.0559	2.9515	2.8615	2.7965
	0	5	3.4568	3.3879	3.2907	3.1924	3.1092
	0.5	0.5	3.0140	2.9116	2.8210	2.7402	2.6828
	0.5	1	3.2383	3.1298	3.0265	2.9346	2.8647
	0.5	5	3.4606	3.3999	3.3068	3.2091	3.1264
	2	0.5	3.1988	3.1233	3.0364	2.9495	2.8830
	2	1	3.3337	3.2555	3.1613	3.0677	2.9926
	2	5	3.4659	3.4215	3.3372	3.2410	3.1601

Across all boundary conditions, maintaining a fixed and zero value for the parameter p_x while increasing p_z from 0.5 to 1 and 5 results in an increase in frequency. Conversely, increasing p_x from 0 to 0.5 and up to 2 and varying p_z leads to a similar increase in frequency. The results underscore the fact that the parameter p_z has a more significant influence on the frequency parameter compared to p_x.

3.2.2. Buckling Analysis of Multi-Directional Sandwich Plates

Likewise, a buckling analysis was carried out for a multi-directional FG skin paired with a homogeneous hard core under various boundary conditions, incorporating different values of p_x and p_z. Across all boundary conditions, the (1-2-1) scheme consistently demonstrated the highest frequency, followed by (2-2-1), (1-1-1), (2-1-2), and (1-0-1). The results are presented in Table 9.

Table 9. Dimensionless buckling load $\overline{N}$ of square plates under various boundary conditions (ξ₁ = 1, a/h = 10). Type A: hard core.

Boundary Conditions	px	pz	1-0-1	2-1-2	1-1-1	2-2-1	1-2-1
SSSS	0	0.5	3.6822	3.9704	4.2182	4.4049	4.6084
	0	1	2.5836	2.9200	3.2324	3.4747	3.7533
	0	5	1.3291	1.5213	1.7898	2.0560	2.3673
	0.5	0.5	3.3400	3.6008	3.8391	4.0419	4.2426
	0.5	1	2.3939	2.6942	2.9871	3.2338	3.5029
	0.5	5	1.3132	1.4882	1.7421	2.0049	2.3062
	2	0.5	2.6494	2.8539	3.0711	3.3002	3.5003
	2	1	2.0109	2.2382	2.4909	2.7428	2.9958
	2	5	1.2799	1.4213	1.6460	1.9017	2.1826
CSCS	0	0.5	6.8605	7.3953	7.8497	8.1872	8.5586
	0	1	4.8432	5.4737	6.0517	6.4943	7.0067
	0	5	2.5016	2.8785	3.3849	3.8795	4.4612
	0.5	0.5	6.2201	6.7143	7.1567	7.5246	7.8959
	0.5	1	4.4844	5.0537	5.5993	6.0509	6.5494
	0.5	5	2.4677	2.8154	3.2956	3.7841	4.3477
	2	0.5	4.9270	5.3365	5.7488	6.1675	6.5439
	2	1	3.7581	4.2053	4.6824	5.1459	5.6195
	2	5	2.3949	2.6880	3.1153	3.5909	4.1184
CCCC	0	0.5	9.2373	9.9552	10.5596	11.0035	11.4961
	0	1	6.5513	7.4037	8.1779	8.7647	9.4479
	0	5	3.3941	3.9213	4.6095	5.2737	6.0585
	0.5	0.5	8.3721	9.0459	9.6401	10.1254	10.6224
	0.5	1	6.0623	6.8391	7.5736	8.1735	8.8414
	0.5	5	3.3439	3.8349	4.4887	5.1449	5.9063
	2	0.5	6.6247	7.2047	7.7675	8.3230	8.8337
	2	1	5.0717	5.6980	6.3470	6.9651	7.6049
	2	5	3.2349	3.6606	4.2447	4.8841	5.5985
FCFC	0	0.5	10.8692	11.7121	12.4173	12.9312	13.5048
	0	1	7.7331	8.7391	9.6467	10.3296	11.1282
	0	5	4.0148	4.6515	5.4666	6.2465	7.1712
	0.5	0.5	9.8488	10.6484	11.3463	11.9092	12.4918
	0.5	1	7.1529	8.0755	8.9396	9.6388	10.4219
	0.5	5	3.9521	4.5488	5.3239	6.0947	6.9926
	2	0.5	7.7875	8.4932	9.1618	9.8086	10.4127
	2	1	5.9771	6.7339	7.5029	8.2251	8.9797
	2	5	3.8149	4.3412	5.0358	5.7873	6.6313

The buckling load undergoes a notable decrease when p_x remains at zero and p_z varies from 0.5 to 5. Additionally, as both p_x and p_z are incrementally adjusted, the buckling load decreases, with p_z exerting a more significant influence than p_x. The maximum buckling load was observed under the FCFC boundary condition, followed by the CCCC, CSCS, and SSSS conditions.

The buckling analysis of a multi-directional FG skin with a homogeneous soft core was conducted using similar parameter values. The results are presented in Table 10. Across all boundary conditions, the (1-0-1) scheme consistently exhibits the highest buckling load, followed by (2-1-2), (1-1-1), (2-2-1), and (1-1-1). The buckling load experiences a significant increase when p_x is maintained at zero and p_z varies from 0.5 to 5. Furthermore, incremental adjustments in both p_x and p_z result in an increased buckling load. The maximum buckling load was observed under the FCFC condition, followed by the CCCC, CSCS, and SSSS conditions.

Table 10. Dimensionless buckling load $\overline{N}$ of square plates under various boundary conditions (ξ₁ = 1, a/h = 10). Type B: soft core.

Boundary Conditions	px	pz	1-0-1	2-1-2	1-1-1	2-2-1	1-2-1
SSSS	0	0.5	3.9158	3.6018	3.3496	3.1017	2.9770
	0	1	4.9809	4.5812	4.2423	3.8888	3.7302
	0	5	6.3116	5.9908	5.6258	5.1429	4.9673
	0.5	0.5	4.2926	3.9860	3.7234	3.4429	3.3158
	0.5	1	5.2096	4.8331	4.4959	4.1236	3.9641
	0.5	5	6.3410	6.0394	5.6855	5.2028	5.0310
	2	0.5	5.0219	4.7482	4.4749	4.1298	3.9982
	2	1	5.6446	5.3254	5.0012	4.5931	4.4361
	2	5	6.3969	6.1343	5.8037	5.3219	5.1589
CSCS	0	0.5	6.9651	6.3522	5.8856	5.4808	5.2319
	0	1	8.8733	8.0495	7.3940	6.8224	6.4704
	0	5	11.4549	10.6674	9.8643	9.0650	8.5544
	0.5	0.5	7.7135	7.0766	6.5604	6.0956	5.8111
	0.5	1	9.3552	8.5479	7.8692	7.2585	6.8763
	0.5	5	11.5328	10.7791	9.9902	9.1863	8.6741
	2	0.5	9.1297	8.5002	7.9139	7.3319	6.9766
	2	1	10.2468	9.5073	8.8092	8.1261	7.6953
	2	5	11.6792	10.9948	10.2374	9.4264	8.9138
CCCC	0	0.5	9.0716	8.2251	7.6020	7.1061	6.7586
	0	1	11.5691	10.3968	9.4986	8.8027	8.2856
	0	5	15.1311	13.9037	12.7229	11.7333	10.9025
	0.5	0.5	10.1175	9.2048	8.4892	7.9139	7.4925
	0.5	1	12.2651	11.0898	10.1375	9.3863	8.8056
	0.5	5	15.2571	14.0721	12.9036	11.9041	11.0635
	2	0.5	12.0741	11.1201	10.2665	9.5369	8.9691
	2	1	13.5375	12.4139	11.3971	10.5446	9.8545
	2	5	15.4932	14.3959	13.2576	12.2414	11.3854
FCFC	0	0.5	10.4404	9.4306	8.7022	8.1545	7.7373
	0	1	13.3239	11.9014	10.8357	10.0699	9.4331
	0	5	17.5759	16.0092	14.5512	13.4495	12.3755
	0.5	0.5	11.6978	10.5847	9.7294	9.0892	8.5673
	0.5	1	14.1765	12.7309	11.5854	10.7529	10.0252
	0.5	5	17.7400	16.2199	14.7711	13.6554	12.5642
	2	0.5	14.0361	12.8349	11.7854	10.9667	10.2366
	2	1	15.7264	14.3105	13.0605	12.1066	11.2195
	2	5	18.0477	16.6251	15.2018	14.0618	12.9413

4. Conclusions

The comprehensive investigation outlined in this paper provides pivotal insights into the buckling and free vibration behavior of multi-directional FG sandwich plates under a spectrum of boundary conditions. Our rigorous validation process and in-depth analyses offer a clear understanding of the materials’ responses across various load applications. The consistency between the results of different shape function models underscores the reliability of our analytical approach. The implications of this research are particularly salient for design engineers and materials scientists focusing on the development of unidirectional and multi-directional FG sandwich panels custom-designed for specialized applications.

The primary conclusions drawn from this study can be summarized as follows:

• The boundary condition of FCFC invariably results in the highest frequency and buckling load values when compared to other tested conditions such as CCCC, CSCS, and SSSS. Noteworthy is the observation that the transverse grading parameter p_z demonstrates a more significant effect than the longitudinal grading parameter p_x on these outcomes.
• In the context of sandwich plates with a hard core, an increment in the values of both p_x and p_z is associated with a reduction in the plates’ natural frequency and buckling load. This situation is reversed for materials with a soft core, where an increase in p_x and p_z corresponds to a decrease in their frequency and buckling load. This inverse relationship is due to the increased presence of ceramic constituents in the FG material, which are introduced as the grading parameters p_x and p_z rise, thereby enhancing the natural frequency due to their higher stiffness relative to metals.
• Structural configurations that have a thicker core are shown to yield a higher stiffness. Specifically, for cores predominantly made of ceramic, enhancing the ceramic layer thickness effectively introduces additional stiffness akin to rigid plates, which elevates their natural frequencies. In contrast, for metal-based core configurations, an increase in metal core thickness imparts greater flexibility to the structure, leading to a decrease in its natural frequencies.

The insights gleaned from our research extend the existing knowledge base and provide a robust foundation for the optimized design of FG sandwich plates, catering to the evolving demands of advanced engineering applications. We anticipate that our findings will spur further studies, potentially exploring even wider parameter spaces and boundary conditions to enrich our understanding of the structural applications of FG materials.