Abstract
We systematically investigate the performance of numerical methods to solve Fisher’s equation, which contains a linear diffusion term and a nonlinear logistic term. The usual explicit finite difference algorithms are only conditionally stable for this equation, and they can yield concentrations below zero or above one, even if they are stable. Here, we collect the stable and explicit algorithms, most of which we invented recently. All of them are unconditionally dynamically consistent for Fisher’s equation; thus, the concentration remains in the unit interval for arbitrary parameters. We perform tests in the cases of 1D and 2D systems to explore how the errors depend on the coefficient of the nonlinear term, the stiffness ratio, and the anisotropy of the system. We also measure running times and recommend which algorithms should be used in specific circumstances.
1. Introduction
Fisher’s equation, sometimes also called the Fisher–Kolmogorov–Petrovsky–Piskunov equation [1], includes an additional logistic reaction term in addition to the standard diffusion term:
Here u is the unknown function, which usually represents the concentration. In this case, the range of u is the unit interval [0, 1]. Without the logistic term, the equation is the common heat equation, where u is the temperature, often measured in Kelvin units. Equation (1) is proposed to model how gene-variants spread in space, how misfolded proteins grow and spread in neurophysiology [2], and how fronts propagate in combustion processes [3]. Some chemotaxis models [4,5] can be considered further generalizations of Fisher’s equation.
It is worth mentioning that traveling wave analytical solutions for a kind of Kolmogorov–Petrovsky–Piskunov equation (generalized Fisher’s equation) were achieved through Cole–Hopf transformation in [6]. Solutions for time-dependent coefficients were constructed by Hammond and Bortz [7]. In our work, we will use another analytical solution [8,9] as a reference solution to calculate the numerical errors.
Fisher’s equation has been solved numerically by several research groups. For example, a Petrov–Galerkin finite element method, including Gaussian elimination, was used by Tang and Weber [10]. Chandraker et al. [11] designed a semi-implicit finite difference scheme in one dimension with first-order accuracy in time and second-order accuracy in space. An exponential B-spline collocation method was proposed by Dag and Ersoy [12] that uses the exponential cubic B-spline in space and the Crank–Nicolson method in time. Tamsir and Huntul suggested [13] a new hybrid method based on cubic uniform algebraic trigonometric tension B-spline functions and the differential quadrature method.
It is commonly known that the true solution of the diffusion or heat equation always follows the minimum and maximum principles [14] (p. 87). The minimum principle implies the so-called positivity-preserving property, i.e., that the equation does not yield negative values if the initial and boundary values are non-negative. When a source or reaction term exists in the diffusion equation, these rules generally do not apply. However, in the case of Fisher’s equation, a similar phenomenon is present due to the logistic nature of the reaction term. In the case of Equation (1), if the initial and boundary values of the u variable are in the unit interval, then u remains in this interval for any non-negative values of the parameter β. Therefore, the applied numerical schemes should also preserve this property of the solution, which may be called dynamical consistency. We note that the property ‘dynamical consistency’ of numerical algorithms can have several definitions [15], formulating that the numerical solutions reflect important properties of the true solutions of the original system. In this paper, in connection with Fisher’s equation, we will use the above-mentioned meaning. In the case of standard finite difference or finite element methods, dynamical consistency is not guaranteed. Thus, the solutions produced by these algorithms can occasionally provide negative and non-physical numbers. Subsequently, the solutions may begin to oscillate, resulting in numerical instabilities. This is especially frequent in the case of the common explicit methods since they are mostly unstable for the linear diffusion equation if the time step size is above the mesh Fourier number or, in other terminology, the CFL limit. Implicit methods, on the other hand, have better stability features, but they require solving a system of algebraic equations, which can be very demanding if the size of the system is large.
There are some researchers working with unconditionally positive methods [16,17,18] to solve similar equations. The positivity of solutions has also been included in numerical techniques for solving ordinary differential equations [19]. A positivity-preserving technique for a system of advection–reaction–diffusion equations defining chemotaxis/haptotaxis models was devised by Chertock and Kurganov [20]. However, their method is positivity-maintaining only when the time step size is smaller than the CFL number, which is rather low. The same can be said about those nonstandard finite difference schemes (NSFD) that have been used to solve the Fisher and Nagumo problem by Agbavon et al. [9,21] and to solve cross-diffusion equations by Songolo [22] and by Chapwanya et al. [23].
In this work, we deal only with methods that are unconditionally dynamically consistent. This paper may be seen as a substantial extension of our earlier publication [24], where we performed tests of some positivity-preserving methods with a first or second order of convergence for the linear heat or diffusion equation. Since then, we have constructed third- and fourth-order numerical methods [25] that can solve some nonlinear equations as well, with the property of dynamical consistency. In this research paper, we involve these methods as well and focus on Fisher’s equation. We conduct systematic testing by sweeping specific parameters to investigate the performance of the various algorithms to see which of them is optimal in various scenarios.
The paper’s outline is as follows. In Section 2, the spatial discretization of Fisher’s equation is considered both in the simplest one-dimensional case as well as in a very general case. In Section 3, we first briefly recall the 12 numerical schemes that can be applied to the diffusion equation. Then, six different operator-splitting treatments of the nonlinear term are presented with analytical results. In Section 4, we verify our code by testing the 72 obtained algorithm combinations using an analytical reference solution and keep only 24 of them for further tests. In Section 5, tests with running-time measurements are performed for a stiff and for an anisotropic 2D system to select the top 10 methods. Section 6 presents three further numerical tests with a parameter sweep for the stiffness ratio, nonlinear coefficient β, and anisotropy ratio. Section 7 summarizes our conclusions and recommendations about the numerical techniques used.
2. The Studied Equation and Its Space Discretization
Let us discretize the time variable uniformly, which means , and
First, an equidistant discretization of the interval is constructed:
The application of the usual central difference approximation of the second space derivatives yields a system of ordinary differential equations (ODEs) for nodes :
In the case of Dirichlet boundary conditions, the time development of the first and last node will be given. We define a matrix M with the following elements:
This matrix is tridiagonal in the one-dimensional case. Now, equation system (2) can be written in matrix form:
If the diffusivity of the media depends on space, the following PDE can be used:
We discretize the function α and, simultaneously, in Equation (5) to obtain
If the diffusivity between cell i and its (right) neighbor is denoted by , then, instead of (2), we obtain
Now, one can introduce a resistance–capacitance model by introducing cells instead of nodes. One can define the capacity of the cell, which, in the simplest case, is the same as the volume of the cell and can be given as . The resistances are calculated as follows:
Now the time derivative of each cell-concentration is determined by the equation
which can be written in a similar matrix form as (4). This ODE system can be easily generalized to two or three space dimensions:
In two space dimensions, the numbering of the cells is along the horizontal (x-directional) rows from 1 to and then from to , etc. We note that the definitions of the resistances and capacitances of the cells are not so simple in complicated cases, e.g., in porous materials, where the porosity and other factors must be taken into account (see [26] and the references therein). Either way, the resistance–capacitance model is very flexible and easy to adapt to various circumstances.
The eigenvalues of the system matrix M with the (nonzero) smallest and biggest absolute values are denoted by λMIN and λMAX, respectively. The system’s stiffness ratio can now be found using SR = λMAX/λMIN, and the maximum time step size that the FTCS (explicit Euler) scheme can use for the pure diffusion problem is precisely provided by , beyond which the solutions are predicted to diverge owing to instability. Referred to the CFL limit or mesh Fourier number, this threshold time step size is also valid for second-order explicit Runge–Kutta (RK) algorithms. While we emphasize once more that this constraint does not apply to any of the methods shown here, these two numbers provide insight into the problem’s degree of difficulty.
3. The Tested Methods
We begin with the brief presentation of the numerical schemes for the linear diffusion equation, and only after this, the treatments of the nonlinear term will be described. For a one-space-dimensional equidistant mesh with constant diffusivity, is the widely used mesh ratio. The case of the general mesh can be simply handled if one introduces the following notations:
The first quantity is the generalization of r (defined above) while the second one reflects the state and the effect of the neighbors of cell i as well. Therefore, in this simple case,
Keeping these in mind, it is enough to present the generalized formula of the numerical schemes.
3.1. The Applied 12 Convex Combination Scheme for the Diffusion Equation
1. The UPFD method [16] is a simple one-stage algorithm with the formula
2. The constant neighbor (CNe) method for Equation (1) is
3. The LH-CNe belongs to the family of odd–even hopscotch methods; thus, the space must be discretized by a special, so-called bipartite grid. The cells are labelled as odd and even, and all the nearest neighbors of the odd nodes are even and vice versa. In the case of the leapfrog–hopscotch (LH) structure, one starts with a half time step, e.g., with the even cells, then full time steps come strictly alternately for the odd and even cells until the end of the last timestep, which should be halved for the even cells to reach at exactly the same final time as the odd cells do. The main point is that when a new value of ui is calculated, always the latest values of the neighbors must be used, which ensures stability and rather fast convergence at the same time. In the case of the LH-CNe method examined in this work, the CNe formula is used in each stage with the appropriate time step size. A pseudocode of this method is presented in Appendix A that includes the treatment of the nonlinear term.
4. The CpC algorithm calculates new predictor values of the variables with the CNe formula, but with a time step:
In the second stage, we can use (10) and take a full time-step-size corrector step using the CNe formula again. Thus, the final values at the end of the time step are
where, of course, the predictor values are used to obtain the quantities.
5. The linear-neighbor (LNe or sometimes LNe2) method is also a kind of predictor-corrector method. Its first stage uses the CNe method to calculate the new values for the final time of the actual time step. Using these predictor values one can calculate
and then the corrector values are obtained as follows:
6. The values provided by Equation (14) can be used to calculate again; thus, one can repeat (13) and (14) to refine the results. Since in this case, there are three stages altogether, the algorithm is called LNe3.
7–8. The LNe4 (LNe5) method is a four (five)-stage algorithm that is obtained by repeating the procedure explained in the previous point after the calculations of the LNe3 (LNe4) scheme. These iterations, unfortunately, do not improve the order, but increase the accuracy of the results.
9. The first two stages of the three-stage Constant-Linear-Quadratic-neighbor (CLQ) method [25] are the same as those of the LNe method, with the exception that the second LNe stage has to be made with not only a full but also a half time step size using (16). If we denote these results using and , respectively, then one can use these to calculate and , such as in Equation (13), and then and , where is calculated at the beginning of the first stage. The final concentration values at the end of the time step are given by
10. One can use the CLQ function values obtained above to add one more stage, with which we will have a four-stage scheme called the CLQ2 method. For this, the midpoint values must be calculated after the third stage as follows:
Then, in Stage 4, we repeat the calculations of the third stage, but we use and to obtain the new values of S and W, etc.
11–12. This iteration can be further repeated in the very same way as in point 10 above. In this way, one can obtain the CLQ3 algorithm (five stages altogether) and the CLQ4 algorithm (six stages altogether) [25].
The UPFD and the CNe algorithms are first-order; the LH-CNe, CpC, and LNe-LNe5 algorithms are second-order; the CLQ is third-order; and the CLQ2-4 is fourth-order in time. Their exceptional stability is the consequence of the following property:
Theorem 1.
If Schemes 1–8 are applied to the spatially discretized linear diffusion in Equation (2) or (6), then the new
values are the convex combinations of the initial values . The same is true when the CLQ–CLQ4 schemes are applied to Equation (2).
The proof of the theorem, as well as some more detailed descriptions of the discretization and the methods can be found in our earlier publications, e.g., [24,25], and the references therein.
According to all of our numerical experiments, the statement in Theorem 1 holds for the CLQ-CLQ4 algorithms in the case of the generalized Equation (6), but this has not been proved analytically yet.
Due to Theorem 1, all the methods used are unconditionally stable for the linear heat conduction equation, implying that the above-mentioned mesh Fourier number or CFL limit does not affect their stability. However, as we will observe, it does affect their accuracy. The price one must pay for unconditional stability is conditional consistency in the sense that the refinement of the spatial mesh without decreasing the time step size does not yield better accuracy. This is due to some extra terms in the truncation error that contain the combination of the space and time step sizes. This phenomenon has been investigated analytically and numerically in our previous works (e.g., [25,27]), and it has nothing to do with the dynamical consistency of the methods. It must be underlined again that only a small portion of the explicit methods are unconditionally stable, and only a few of the unconditionally stable schemes have the convex combination property.
3.2. The Numerical Treatments of the Nonlinear Term
The nonlinear logistic term is implemented via operator splitting, whereby we address the effect of the diffusion term and the nonlinear term independently. The diffusion term is handled in the 12 above-listed ways. The outcome of those algorithms can be denoted by , which represents the concentration value when the diffusion term is fully considered. The effect of the reaction term, which has the form
is calculated in two ways. The first way is called “pseudo-implicit” treatment [25] and involves a selective replacement of u in the right-hand side of (17) with the values and the new, unknown value to obtain
This can be simply rearranged to take on a completely explicit form:
Note that no negative terms appear on the right-hand side of this formula.
The other way is obtained if we solve the ODE
analytically. To be more exact, the appropriate initial value problem is solved in which the initial time is the first point of the actual time step and the values are the initial values of u for each cell. This yields the formula
The advantage of this so-called quasi-exact way is that it avoids approximation and linearization, aside from the operator splitting itself. However, for some more complicated nonlinear terms, e.g., in the Nagumo equation, the analytical solution does not exist, but the pseudo-implicit treatment can be used without difficulties [25]. We note that Ramos [28] used linearization techniques slightly similar to our pseudo-implicit treatment, which, however, are not dynamically consistent.
Remark 1.
Suppose that . Now, it is clear from looking at the coefficient of that both the numerators as well as the denominators in Equations (19) and (21) are always positive, and the denominators cannot be greater than the numerators. Additionally, the right-hand sides never exceed one. These immediately imply that the new value cannot be negative or less than the value , and therefore, .
In the case of the simple operator splitting, a time step starts with one of the algorithms listed in Section 3.1, and then the operation (19) or (21) is performed as an extra step. We also apply Strang splitting, where operations (19) and (21) are performed twice in one time step: before and after the calculation of the effect of diffusion. In these cases, the substitution must be performed in (19) and (21). Strang splitting also allows us to mix (hybridize) the pseudo-implicit and the quasi-exact treatments, e.g., perform (19) with halved h before and (21) after the scheme (1–12) for the diffusion equation.
Theorem 2.
(The methods’ dynamical consistency.) Assume one solves Fisher’s Equation (1) using Schemes 1–12 with treatments (19) or (21) with or without Strang splitting. If the starting values of the concentration fall within the unit interval
, then the values of u stay within this interval for any non-negative β and time step size h for the whole duration of the calculation. Furthermore, the existence of the Fisher term (increasing β from zero to arbitrary positive value) can cause only an increase, and never the decrease, in the u values, which faithfully reflects a dynamical property of PDE (1).
Proof of Theorem 2.
The statement is immediately yielded by Theorem 1 and Remark 1. □
Theorem 2 inherently implies unconditional stability and is comparable to the maximum and minimum principles valid for the pure diffusion equation. The statements of Theorem 2 were published in our paper [25] for only a few of the 12 schemes listed above and without mentioning Strang splitting.
4. Verification in 1D
Experiment 1: One Space Dimension Using an Exact Solution
The analytical solution [8,9], valid for , is presented below:
This is used as the reference solution for PDE (1). The initial condition is obtained simply by substituting the initial time into Equation (22). The appropriate Dirichlet boundary conditions are prescribed by the substitution of the left- and right-side coordinates of the examined interval, which are .This is discretized by dividing the interval into 100 equal parts: . The initial and the final times are and . The nonlinear coefficient is quite large: .
The maximum numerical errors are calculated by comparing the numerical solutions produced using the examined method with the analytical reference solution at the final time using the formula
In our experiments, we calculated the error for S = 13 different time step sizes for all the examined methods. The results for three different kinds of treatment are presented in Figure 1, Figure 2 and Figure 3. Very similar plots have been obtained for the three other treatments and for other values of parameters such as β, , etc. The algorithms exhibit smooth convergence and show no signs of instability. However, as noted above, the inconsistent terms in the truncation error cause this convergence to be slow for larger time step sizes.
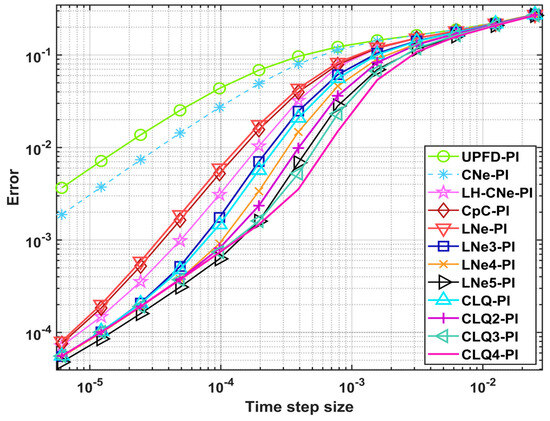
Figure 1.
Maximum error as a function of the time step size for PI treatment.

Figure 2.
Maximum error as a function of the time step size for QE treatment.

Figure 3.
Maximum error as a function of the time step size for QE-St treatment.
In order to compare the overall accuracy of the 72 different combinations, we introduce the so-called aggregated errors (AgE). In the case of the maximum errors, they are given by the following formula:
A similar aggregated error can be calculated using the average absolute error:
The third possibility provides the energy error in the case of the heat equation; thus, we traditionally refer to it as the energy error:
Lastly, it is also possible to compute the three types of the errors’ simple average:
It is obvious that algorithm combinations with larger absolute values of AgE are more accurate. The AgE values are tabulated in Table 1 and visualized in Figure 4. One can observe that the quasi-exact treatment is almost always more accurate than the pseudo-implicit one. Strang splitting yields significantly larger accuracy, usually for the higher-order, more accurate methods, e.g., for the CLQ3 and CLQ4 schemes. The mixed treatments are rarely competitive, and since they are more complicated to code, we omit them from future investigations. Only the QE and QE-Strang treatments for all the 12 methods, comprising 24 combinations altogether, will be carried forward to further examinations.

Table 1.
Aggregated error (AgE) values for each method combined with each different treatment in Experiment 1.

Figure 4.
AgE errors for the methods and for all treatments of the nonlinear term in Experiment 1.
5. Testing of Performance with Running Time Measurements
From this point, we will have two space dimensions and we will use the capacity–resistivity model explained in Section 2. We generate random values for the capacities and the resistances with a log-uniform distribution as follows:
By varying the a and b parameters, we are able to produce highly different test problems. Here rand comprises random numbers generated using MATLAB in the unit interval. The running times are measured using the tic-toc function of MATLAB. In order to minimize the effects of the random fluctuations, the calculations are performed 100 times subsequently, and then the average running times are calculated. From this point, the reference solution is provided by the MATLAB R2020b ode15 solver with a very stringent tolerance.
5.1. Experiment 2: Stiff System
Now, PDE (1) with is going to be solved using 24 algorithm combinations. The used system size and final time are while , and . These parameters yield , which means that the system is rather stiff. The initial concentrations are random numbers: . We present the obtained errors as a function of the running times. Since the curves are very close to one another, we separately display the low-accuracy and the high-accuracy parts in Figure 5 and Figure 6, respectively. One can see that the methods behave well in these cases as well.

Figure 5.
Maximum error as a function of the running time for Experiment 2: low-accuracy part.

Figure 6.
Maximum error as a function of the running time for Experiment 2: high-accuracy part.
5.2. Experiment 2: Anysotropic System
In this case, the used system size and final time are the coefficient of the Fisher term is , and the exponents are and . These parameters give and , which means that the system is only moderately stiff. However, the resistances in the x direction are two orders of magnitude larger than in the z direction; therefore, the system is quite anisotropic. The initial concentrations are random numbers in the left half of the unit interval . We present the maximum error as a function of the running time in Figure 7.

Figure 7.
Maximum error as a function of the running time for Experiment 3.
One can see that all of the examined 24 combinations behave well in this case as well. In Experiments 2 and 3, the LH method is the most efficient with and without Strang splitting when only low accuracy is required. The LNe and CpC methods also have acceptable performance. For high accuracy, the CLQ family with Strang splitting clearly outperforms the other methods. Based on the results of Experiments 1, 2, and 3, we choose LH-CNE-Qe, LH-CNe-QE-St, CpC-QE, LNe3-QE-St, LNe4-QE-St, LNe5-QE-St, CLQ-QE-St, CLQ2-QE-St, CLQ3-QE-St, and CLQ4-QE-St as the top 10 methods for further investigation.
We note that we performed these running time measurements in the case of the PI treatments just to check whether this treatment type is not significantly faster than the QE treatment. We found that choosing QE or PI does not noticeably influence the running times, which is logical since the exponential expression does not depend on time or space and thus has to be calculated only once. However, in cases where the coefficient β depends on both space and time, calling the exponential function could significantly slow down the calculations when they use the QE treatment, and thus, the PI could become competitive.
6. Testing of Performance with Parameter Sweep for the Top 10 Methods
6.1. Comparison of the AgE Errors as Functions of the Stiffness Ratios
Test problems with different stiffness ratios have been constructed using the exponents of the mesh-cell data distribution. To be more specific, we have made use of the factors listed in Table 2. The nonlinear coefficient is , the sizes of the grid are fixed to and , the initial values are , and the final time is . We have applied S = 15 different time step sizes and then applied Formula (27) for the aggregated error.

Table 2.
The exponents of the capacities and resistances.
The AgE error as a function of the stiffness ratio is displayed in Figure 8 and Table 3. We see that the methods’ accuracy values decrease with rising stiffness ratios and decreasing CFL limits as expected. For low stiffness, the Strang splitting treatment has a substantial advantage, which is diminishing with increasing stiffness. The relative advantage of the high-order CLQ family is large for medium stiffness, but starts to vanish for very high values of the stiffness ratio due to the so-called order reduction.

Figure 8.
The AgE error as a function of stiffness in the case of the positivity-preserving methods.

Table 3.
Aggregated error (AgE) values for positivity-preserving methods of different treatments.
6.2. Comparison of the AgE Errors as Functions of the β Parameter
Here, we have used the values of the nonlinear coefficient to calculate the AgE values. All a and b exponents are zero, which means for all cells. The sizes of the grid are fixed to and , and the final time is . The initial values are .
The AgE error as a function of the β parameter is displayed in Figure 9. We see that the accuracy of the methods becomes worse when the value of the β parameter is increasing.

Figure 9.
AgE error as a function of the β parameter in the case of the positivity-preserving methods.
6.3. Comparison of the AgE Errors as Functions of the Anisotropy Coefficients (ACs)
Here, the sizes of the grid have been fixed to and , and the final time is . We have used the , and parameters. To perform the parameter sweep for the anisotropy, the following anisotropy coefficient has been introduced:
The horizontal and vertical resistances have been adjusted to obtain an increasing series for this AC parameter as displayed in Table 4. The aggregated error as a function of the anisotropy coefficient AC is also tabulated in Table 4, as well as in Figure 10.

Table 4.
The different anisotropy coefficients (AC) used in the simulation.

Figure 10.
The AgE error as a function of anisotropy coefficient.
For large values of the anisotropy coefficient, we notice that the relative advantage of the CLQ3-QE-St and CLQ4-QE-St methods increases compared to the LNe group and the CLQ-QE-St method, but decreases compared to the methods without Strang splitting. Even more remarkable is the decreasing advantage of the LH-CNe-QE-St algorithm for an increasing AC value.
7. Discussion and Conclusions
We have studied numerical methods about which it has analytically proven that they keep the values of the concentration function in the unit interval for arbitrary time step sizes and arbitrary values of the nonlinear parameter β when they are applied to Fisher’s equation. The numerical case studies have confirmed these results since all methods have behaved well without the slightest sign of instability.
According to the running time measurements, generally, the LH-CNe is the most efficient among the methods since it serves rather accurate results in a very short time. However, if stiffness or anisotropy increases, its advantage vanishes. In those cases, the CLQ or the CLQ2 methods constitute the optimal choice.
When the nonlinearity is strong, i.e., the β coefficient is large, the quasi-exact treatment of the nonlinear term combined with Strang splitting is recommended, especially when the method for the diffusion part is relatively accurate, usually due to a higher order of convergence. However, if the accuracy is limited by the anisotropy or, more importantly, by the stiffness of the problem, Strang splitting can be a waste of time and the time step size should be decreased instead.
Author Contributions
Conceptualization, methodology, supervision, project administration, and resources, E.K.; software, H.K. and I.O.; validation and investigation, H.K.; formal analysis, E.K.; writing—original draft preparation, E.K. and I.O.; writing—review and editing, E.K. and H.K.; visualization, H.K. and I.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data are available from the authors on reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
We present a pseudocode to help understand the most sophisticated combinations, labelled with LH-CNe-St. We note that for the sake of simplicity and speed, the number of cells in the x (horizontal) direction is always odd. This ensures that the vertical (z-directional) neighbors of odd cells are automatically even and vice versa. Otherwise, the parity of each cell should be checked in each stage, which would be more difficult to code and also would increase running times.
ULH(:)=U0(:); % Initialization
ES=exp(-beta*h/2);
ESh=exp(-beta*h/4);
ULH=ULH./(ULH+(1-ULH).*ESh); % Formula (21) with quarter time step size
for i=2:2:N % zeroth time step for the even nodes
A(i) is calculated using the initial conditions
CNe Formula (13) is calculated % half time step
end
ULH=ULH./(ULH+(1-ULH).*ESh); % Formula (21) with quarter time step size
for t=1:1:T-1 % BIG LOOP FOR TIME STARTS
for i=1:2:N % odd nodes
A(i) is calculated using the latest values of the even nodes
CNe Formula (12) is calculated % full time step
end
if (taxis(t+1)<tf-0.9*h)
ULH=ULH./(ULH+(1-ULH).*ES); % Formula (21) with half time step size
for i=2:2:N %%% even
A(i) is calculated using the latest values of the odd nodes
CNe Formula (12) is calculated % full time step
end
ULH=ULH./(ULH+(1-ULH).*ES); % Formula (21) with half time step size
else
ULH=ULH./(ULH+(1-ULH).*ESh); % Formula (21) with quarter time step size
for i=2:2:N %% even
A(i) is calculated using the latest values of the even nodes
CNe Formula (13) is calculated % half time step
end
ULH=ULH./(ULH+(1-ULH).*ESh); % Formula (21) with quarter time step size
end
end
References
- Li, Y.; van Heijster, P.; Marangell, R.; Simpson, M.J. Travelling wave solutions in a negative nonlinear diffusion–reaction model. J. Math. Biol. 2020, 81, 1495–1522. [Google Scholar] [CrossRef]
- Weickenmeier, J.; Jucker, M.; Goriely, A.; Kuhl, E. A physics-based model explains the prion-like features of neurodegeneration in Alzheimer’s disease, Parkinson’s disease, and amyotrophic lateral sclerosis. J. Mech. Phys. Solids 2019, 124, 264–281. [Google Scholar] [CrossRef]
- Campos, D.; Llebot, J.E.; Fort, J. Reaction–diffusion pulses: A combustion model. J. Phys. A Math. Gen. 2004, 37, 6609–6621. [Google Scholar] [CrossRef]
- Columbu, A.; Frassu, S.; Viglialoro, G. Refined criteria toward boundedness in an attraction–repulsion chemotaxis system with nonlinear productions. Appl. Anal. 2024, 103, 415–431. [Google Scholar] [CrossRef]
- Li, T.; Frassu, S.; Viglialoro, G. Combining effects ensuring boundedness in an attraction–repulsion chemotaxis model with production and consumption. Z. Angew. Math. Phys. 2023, 74, 109. [Google Scholar] [CrossRef]
- Ma, W.; Fuchssteiner, B. Explicit and exact solutions to a Kolmogorov-Petrovskii-Piskunov equation. Int. J. Non-Linear Mech. 1996, 31, 329–338. [Google Scholar] [CrossRef]
- Hammond, J.F.; Bortz, D.M. Analytical solutions to Fisher’s equation with time-variable coefficients. Appl. Math. Comput. 2011, 218, 2497–2508. [Google Scholar] [CrossRef]
- Bastani, M.; Salkuyeh, D.K. A highly accurate method to solve Fisher’s equation. Pramana 2012, 78, 335–346. [Google Scholar] [CrossRef]
- Agbavon, K.M.; Appadu, A.R.; Khumalo, M. On the numerical solution of Fisher’s equation with coefficient of diffusion term much smaller than coefficient of reaction term. Adv. Differ. Equ. 2019, 2019, 146. [Google Scholar] [CrossRef]
- Tang, S.; Weber, R.O. Numerical study of Fisher’s equation by a Petrov-Galerkin finite element method. J. Aust. Math. Soc. Ser. B Appl. Math. 1991, 33, 27–38. [Google Scholar] [CrossRef]
- Chandraker, V.; Awasthi, A.; Jayaraj, S. A Numerical Treatment of Fisher Equation. Procedia Eng. 2015, 127, 1256–1262. [Google Scholar] [CrossRef]
- Dag, I.; Ersoy, O. The exponential cubic B-spline algorithm for Fisher equation. Chaos Solitons Fractals 2016, 86, 101–106. [Google Scholar] [CrossRef]
- Tamsir, M.; Huntul, M. A numerical approach for solving Fisher’s reaction–diffusion equation via a new kind of spline functions. Ain Shams Eng. J. 2021, 12, 3157–3165. [Google Scholar] [CrossRef]
- Holmes, M.H. Introduction to Numerical Methods in Differential Equations; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Anguelov, R.; Lubuma, J.M.-S.; Shillor, M.; Anguelov, R.; Lubuma, J.M.-S.; Shillor, M. Dynamically consistent nonstandard finite difference schemes for continuous dynamical systems. Conf. Publ. 2009, 2009, 34–43. [Google Scholar] [CrossRef]
- Chen-Charpentier, B.M.; Kojouharov, H.V. An unconditionally positivity preserving scheme for advection–diffusion reaction equations. Math. Comput. Model. 2013, 57, 2177–2185. [Google Scholar] [CrossRef]
- Appadu, A.R. Performance of UPFD scheme under some different regimes of advection, diffusion and reaction. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 1412–1429. [Google Scholar] [CrossRef]
- Drljača, B.; Savović, S. Unconditionally positive finite difference and standard explicit finite difference schemes for power flow equation. Univ. Thought-Publ. Nat. Sci. 2019, 9, 75–78. [Google Scholar] [CrossRef]
- Dimitrov, D.T.; Kojouharov, H.V. Positive and elementary stable nonstandard numerical methods with applications to predator–prey models. J. Comput. Appl. Math. 2006, 189, 98–108. [Google Scholar] [CrossRef]
- Chertock, A.; Kurganov, A. A second-order positivity preserving central-upwind scheme for chemotaxis and haptotaxis models. Numer. Math. 2008, 111, 169–205. [Google Scholar] [CrossRef]
- Agbavon, K.M.; Appadu, A.R. Construction and analysis of some nonstandard finite difference methods for the FitzHugh–Nagumo equation. Numer. Methods Partial. Differ. Equ. 2020, 36, 1145–1169. [Google Scholar] [CrossRef]
- Songolo, M.E. A Positivity-Preserving Nonstandard Finite Difference Scheme for Parabolic System with Cross-Diffusion Equations and Nonlocal Initial Conditions. Am. Sci. Res. J. Eng. Technol. Sci. 2016, 18, 252–258. [Google Scholar]
- Chapwanya, M.; Lubuma, J.M.-S.; Mickens, R.E. Positivity-preserving nonstandard finite difference schemes for cross-diffusion equations in biosciences. Comput. Math. Appl. 2014, 68, 1071–1082. [Google Scholar] [CrossRef]
- Omle, I.; Askar, A.H.; Kovács, E. Systematic testing of explicit positivity preserving algorithms for the heat-equation. J. Math. Comput. Sci. 2022, 12, 162. [Google Scholar] [CrossRef]
- Kovács, E.; Majár, J.; Saleh, M. Unconditionally Positive, Explicit, Fourth Order Method for the Diffusion- and Nagumo-Type Diffusion–Reaction Equations. J. Sci. Comput. 2024, 98, 39. [Google Scholar] [CrossRef]
- Murray, M.Y. Comprehensive Biotechnology, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2011; Volume 1–6, pp. 1–4729. [Google Scholar]
- Nagy, Á.; Majár, J.; Kovács, E. Consistency and Convergence Properties of 20 Recent and Old Numerical Schemes for the Diffusion Equation. Algorithms 2022, 15, 425. [Google Scholar] [CrossRef]
- Ramos, J. A piecewise time-linearized method for the logistic differential equation. Appl. Math. Comput. 1998, 93, 139–148. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).