Design of Trabecular Bone Mimicking Voronoi Lattice-Based Scaffolds and CFD Modelling of Non-Newtonian Power Law Blood Flow Behaviour

Abstract

Designing scaffolds similar to the structure of trabecular bone requires specialised algorithms. Existing scaffold designs for bone tissue engineering have repeated patterns that do not replicate the random stochastic porous structure of the internal architecture of bones. In this research, the Voronoi tessellation method is applied to create random porous biomimetic structures. A volume mesh created from the shape of a Zygoma fracture acts as a boundary for the generation of random seed points by point spacing to create Voronoi cells and Voronoi diagrams. The Voronoi lattices were obtained by adding strut thickness to the Voronoi diagrams. Gradient Voronoi scaffolds of pore sizes (19.8 µm to 923 µm) similar to the structure of the trabecular bone were designed. A Finite Element Method-based computational fluid dynamics (CFD) simulation was performed on all designed Voronoi scaffolds to predict the pressure drops and permeability of non-Newtonian blood flow behaviour using the power law material model. The predicted permeability (0.33 × 10⁻⁹ m² to 2.17 × 10⁻⁹ m²) values of the Voronoi scaffolds from the CFD simulation are comparable with the permeability of scaffolds and bone specimens from other research works.

1. Introduction

A human bone is a stiff organ with outer concentrated tissues (cortical bone) and inner spongy tissues (trabecular bone/cancellous bone). Trabecular bone patterns such as the femur (thigh bone) and the zygoma (cheekbone) (Figure 1 and Figure 2) possess distinct random and interconnected irregular porous arrangements of different thicknesses (50 to 300 µm) and pore sizes [1]. Bones, which protect internal organs such as the brain, lungs, and heart, act as a storehouse of minerals and a production site of red blood cells. Bone defects occur due to infections, genetic disorders, trauma, diseases, and tumours. Although bone grafts are the gold standard in the repair of bone defects, they have demerits of limited bone tissue availability, donor site morbidity, immune rejection of transplanted cells, long recovery times, and transmission of infections [2]. Three-dimensional (3D) scaffolds, which are porous temporary structures that are utilised in bone tissue engineering (BTE), are alternatives to bone grafts for replacement, repair, and regeneration of bone tissues in bone defects, trauma and injuries [3,4,5]. BTE scaffolds have been applied in various applications, such as large segmental defects in long bones [6], oral and maxillofacial defects [7], articular osteochondral defects (OCD) [8] and ipsilateral femoral bone defects [9]. These scaffolds provide support to withstand the applied mechanical loading, mass transport of nutrients, biofactors, cells, and the removal of wastes to achieve the goal of bone tissue regeneration. Mechanical loading and fluid flow shear stress act as mechanical stimuli transduced into various biophysical factors for osteogenesis to proliferate and differentiate implanted stem cells into functional bone tissues and de novo blood vessels (angiogenesis) [10,11,12].

With modern additive manufacturing (3D printing) machines, manufacturing complex geometries of tissue engineering scaffolds is practically feasible [17,18]. The design of scaffolds for BTE is highly demanding in creating a structure that mimics the architecture of natural trabecular bone [19,20]. The scaffold architecture must be able to replicate the in vivo nature of bones by providing adequate pore distribution with the required structural integrity and maintaining permeability between scaffolds and native bone tissues [21,22]. It is also vital for cell attachment, proliferation (multiplication of cells), and cell differentiation into functional bone tissues. It is feasible to distinguish BTE scaffold designs into two rudimentary groups: one is nonparametric design, such as cubic [23], diamond, or honeycomb [24,25], and the other is parametric design, such as triply periodic minimal surfaces (TPMS) [26,27,28,29]. Unfortunately, the nonparametric and TPMS-based scaffolds are not able to fully replicate the non-periodic and irregular porous microarchitecture of the natural bones. There is a need for a design of scaffolds to mimic the architecture of trabecular bone, which has gradient porous structures that enhance bone regeneration activities such as cell attachment on the scaffold surface, cell growth, and osteogenesis. Such irregular stochastic designs require complex algorithms, which are complicated, and the scaffold design based on the Voronoi tessellation method is one of the possibilities to achieve the biomimetic structure of bones, providing realistic physiological habitat for human cells [30].

The Voronoi tessellation (tiling) method is based on a Voronoi diagram, where several points (seeds) are distributed in a given plane. A circle is drawn around every seed, and it extends until two circles touch each other to form an edge or boundary, further extending to create polygons. The graph formed from the seeds given is known as the Voronoi diagram. The given plane is, therefore, divided into several regions known as Voronoi cells or Thiessen polygons [31]. Each polygon surrounds a point, and the boundary between two or more points is equal to their distance (Figure 3). This concept of Voronoi diagrams can be extended to a 3D space for a given random point cloud to create a stochastic random polyhedral lattice structure that can resemble the internal architecture of a trabecular bone for BTE applications (Figure 4) [32,33,34,35]. Nguyen et al. generated 3D random lattice geometrical models based on Voronoi diagrams for additive manufacturing and presented a workflow to create a final assembled product from random points [36]. Rezapourian et al. performed a numerical study for orthopaedic applications using finite element analysis (FEA) to examine the variation of mechanical properties of Hydroxyapatite based irregular Voronoi lattice bone scaffolds by altering their morphological parameters, such as the thickness of the trabeculae and the point spacing distance [37]. Liu et al. combined the topological optimisation method with Voronoi-based random porous structures generated from Voronoi diagrams using the surface mesh superposition concept for medical applications [38]. Xiao et al. studied the effect of the variation of porosity of Voronoi tessellation-based random pore structured geometry models on their permeabilities using the Lattice Boltzmann method (LBM) [39].

Permeability is a measure for scaffolds to allow the mass transport movement of biological cells, oxygen, nutrients for activities of the cells, and waste materials [41,42]. It depends on the microstructure, the shape of the scaffolds and well-interconnected pores, which allow substantial fluid transport to enrich bone tissue regeneration [43,44]. Large pores and higher porosity of scaffolds lead to higher permeability due to a high quantity of mass transfer but with a reduction in mechanical strength. Jiao et al. concluded that the trabecular porous scaffolds of higher porosities have superior bone integration, bone formation and bone ingrowth than the scaffolds with lower porosities in defects of femoral bones [45]. However, higher permeabilities can cause increased cell washout by the fluid and non-adhesion to the scaffolds, while lower permeabilities can lead to malnutrition, which hinders bone tissue growth.

Computational fluid dynamics (CFD) is a numerical modelling scheme for the prediction of flow properties such as permeability, tortuosity, wall shear stress (WSS), and fluid pressure within scaffolds [46,47]. As the governing equations of fluid flow related to partial difference Equations (PDEs), numerical methods involving finite difference methods (FDM), finite volume methods (FVM), and finite element methods (FEM) have been applied to solve these equations. The problem with FDM methods is that they apply structured grids for discretising the given fluid domain, and they have difficulty approximating complex geometries. This problem is solved by FVM and FEM, which use unstructured meshes with tetrahedral, hexahedral, and polyhedral elements [48]. Even though tetrahedral meshes are convenient for discretising complex geometry, their discretised cells are overstretched in highly curved structures. Such meshes have a large aspect ratio and are not aligned with the direction of flow, causing false diffusion while dealing with advection terms and making the solution diverge in the case of FVM [49]. FEM applies several streamline upwinding advection dominated PDE methods such as monotone streamline upwind method [50,51], streamline upwind Petrov–Galerkin (SUPG) stabilisation method [52,53], min-mod Petrov–Galerkin method, flux-corrected transport (FCT) stabilisation method [54,55], and the discontinuous Petrov–Galerkin (DPG) method [56] to achieve numerical stability to make the solution converge while dealing with unstructured tetrahedral meshes [57]. Many previous CFD simulation research works used a Newtonian fluid material such as water to predict the flow properties of permeable BTE scaffolds [58,59,60]. However, having a non-Newtonian fluid of varying viscosity, such as blood—due to constituents of plasma, platelets, white blood cells (WBCs), and red blood cells (RBCs)—gives realistic predictions of flow properties [61,62,63]. Different blood viscosity models such as Casson, Cross, Powell–Erying, Carreau, Carreau–Yasuda [64,65], Generalised power law, and Power law have been applied in CFD simulation research applications. The power law model is the simplest model, which requires only two parameters: consistency index and power law index, and other non-Newtonian models require four to five parameters, such as zero shear rate viscosity, infinite shear rate viscosity, yield stress and relaxation time [66]. The power law model is apt for non-Newtonian fluids with lower ranges of shear rates, as the blood exhibits non-Newtonian behaviour, such as shear thinning at shear rates less than 100 s⁻¹ [67]. Blood plays a significant role in transporting stem cells, growth factors, and oxygen to the scaffolds for cell adhesion, proliferation and cell differentiation, as well as the removal of toxins and waste metabolites [68]. Ali et al. applied power law-based non-Newtonian models to rectangular pore lattice and gyroid scaffolds to predict their permeability and WSS [69]. Mahammod et al. also applied a power law model to predict the permeability of irregularly shaped scaffolds designed from computed tomography (CT) images of composite scaffolds manufactured from solvent-leaching techniques [70]. Singh et al. utilised power law-based CFD models to simulate the flow behaviour of non-Newtonian blood on open cell neovius TPMS structures for BTE applications [71]. CFD was applied on Voronoi lattice scaffolds using Newtonian fluid models to study the properties of fluid flow affected by the morphological parameters of scaffolds in applications of osteogenesis [72] and using discrete phase model to study the ability of adhesion of stem cells on the scaffolds [73]. The prediction of fluid flow properties using CFD modelling for non-Newtonian viscosity models of Voronoi scaffolds for BTE applications has not been widely reported in the literature.

The goal of this research is to develop a Voronoi lattice-based scaffold design that mimics the functionally graded trabecular porous structure of a natural bone and to apply CFD modelling of non-Newtonian blood flow through a variety of scaffold geometries. It is accomplished by modulating the scaffold porosity and using the power law model and monotone streamline upwind FEM method to predict their fluid properties.

2. Materials and Methods

2.1. Design of Voronoi Lattice-Based Scaffolds

A 3D scanned (EinScan-SE V2 3D scanner, SHINNING 3D Tech, Hangzhou, China) zygomatic bone model (Figure 5) was obtained and was licensed under CC BY 4.0 from Edgars Edelmers, Institute of Anatomy and Anthropology, Riga Stradins University, Latvia (https://skfb.ly/owx6M, accessed on 12 February 2024). nTopology software (version 4.22.2) was used to design Voronoi scaffolds of porosities 90%, 85%, 80%, 75% and 70% based on a virtual fracture performed on the zygoma.

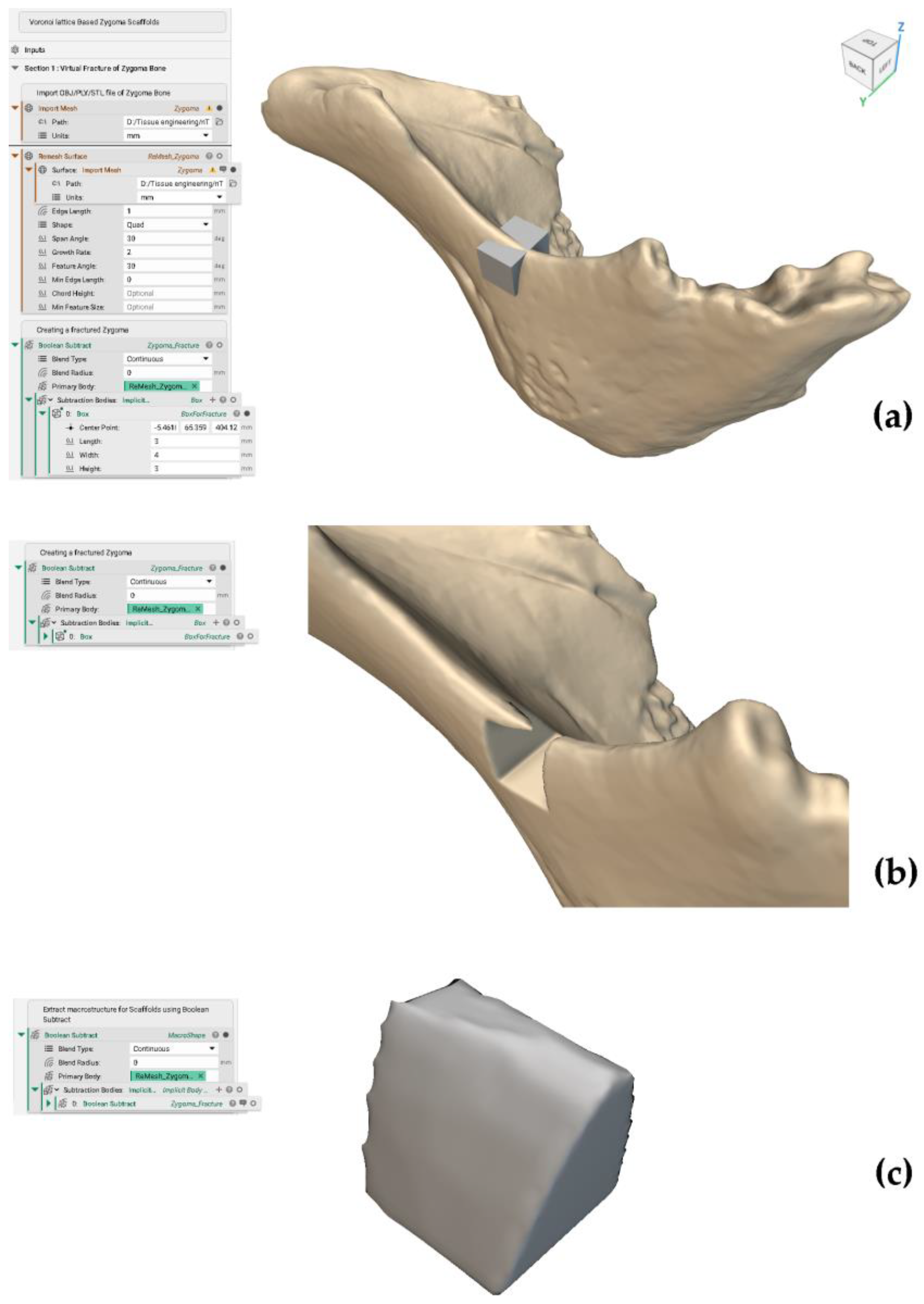
2.1.1. Extraction of Shape (Macrostructure) for Scaffolds

The zygoma model obtained from a 3D scanner was imported as a wavefront (.OBJ) file, which has the surface geometry of the given bone model in 3D format. A virtual fracture was performed using a box (3 × 4 × 3 mm³) in the Ju region of the zygoma to create the bone defect (Appendix A Figure A1). The fracture shape was obtained by a Boolean difference operation between the normal zygoma and the fractured zygoma (Figure 6). The extracted fracture shape acts as a shape or macrostructure for scaffolds.

2.1.2. Design of Voronoi Lattice (Microstructure) for Scaffolds

For generation of a Voronoi lattice, three things are required: (a) seed points, (b) boundary volume, and (c) strut (trabeculae) thickness.

(i.)

Creation of random seed points inside the implicit body of scaffold shape using point spacing.

The vital task in the design of the Voronoi lattice is generating random seed points within the implicit body. The shape of the scaffold, which was obtained from the defect region, is represented as an implicit body (Figure A1c). These seed points are cores for forming polyhedral Voronoi cells, and the combination of these cells with their edges and vertices creates a Voronoi diagram. The distance between the seed points is known as point spacing (PS), which influences the porosity (Figure 7) (Figure A2a). A random seed value of 10 was used to obtain the randomness of seed points. The larger point spacing gives large porosity and vice versa (Section 3.1).

(ii.)

Creation of a boundary volume from the shape of the scaffold

The bone defect region was obtained as a shape (macrostructure) of the scaffold. The shape obtained was converted to a surface mesh with a tolerance of 0.01 mm, and then it was converted to a volume mesh (tetrahedral element, edge length 2 mm and growth rate of 1.2). The created volume mesh became a boundary layer or a design volume, where the Voronoi cells were generated (Figure 8) (Figure A2b).

(iii.)

Creation of Voronoi lattice (microstructure) by adding strut thickness

By applying strut thickness (ST) to the Voronoi cells (Figure A3c), the Voronoi lattice-based scaffolds can be formed (Figure A2d). Therefore, PS and ST are essential specifications for altering the microarchitecture of scaffolds. In this research project, five Voronoi scaffolds of porosities 90% (V90), 85% (V85), 80% (V80), 75% (V75) and 70% (V70) were designed with constant strut thickness (ST) of 0.11 mm [16] and different PS values of 0.851 mm, 0.668 mm, 0.570 mm, 0.502 and 0.449 mm, respectively (Figure 9). The porosity of a scaffold is calculated by dividing its porous volume by the total volume.

2.1.3. Conversion of the Implicit Body (Voronoi Lattice) to CAD Body

The Voronoi lattice (implicit body) was converted to a Parasolid binary CAD file (.x_b) and exported to Autodesk Inventor Professional 2024 (version 28.0.153). In Inventor, the Parasolid file was converted to a lightweight Jupiter Tessellation (.JT) CAD file [74] (Figure 10). The JT file is smaller in size than the Parasolid binary file (as shown in Supplementary Table S1). The created JT file was then exported to Autodesk CFD 2024 (version 24.1) for CFD simulation.

2.2. CFD Modelling of Scaffolds

The CFD modelling in this research involves four steps: (a) geometry preparation (Import of CAD file and creation of fluid domain); (b) setting known values for CFD simulation (material properties, boundary conditions, and generation of volume mesh); (c) setting FEM-based solver; and (d) visualisation of results and analysis. All these steps were performed in Autodesk CFD 2024 (version 24.1) to inspect the flow properties of Voronoi scaffolds of distinct porosities. The CFD simulations were performed on a computer with 128 GB RAM and an i7-9700 CPU of 8 cores.

2.2.1. Geometry Preparation and Fluid Domain Generation for CFD Simulation

The CAD (.JT) file of the Voronoi lattice was imported into Autodesk CFD. A model assessment toolkit was used to assess the imported CAD model for any issues such as surface slivers, model slivers, edge lengths, part gaps, model gaps and interferences for assembly and part problems to improve the CAD geometry and ensure defectless mesh quality. A surface wrapping tool was used to create an external flow volume (fluid domain) of 3.5 × 4 × 3.5 mm³ surrounding the Voronoi lattice (Figure 11).

2.2.2. Setting Known Values for CFD Simulation

(i.)

Material Properties

In Newtonian fluids, which obey Newton’s viscosity law, the shear stress produced is directly proportional to the shear rate or the velocity gradient. The viscosity is constant for the Newtonian fluids for a given constant temperature.

$$\mathsf{\tau }=\mathrm{\mu }\left({\displaystyle \frac{\mathrm{d}\mathrm{u}}{\mathrm{d}\mathrm{y}}}\right)=\mathrm{\mu }\mathsf{\gamma }$$

(1)

where τ is the shear stress produced, µ is the dynamic viscosity of a given fluid, which is the ratio of viscosity of the given fluid and density of that fluid, and γ is the velocity gradient (or) the shear strain rate. However, biofluids such as blood do not obey Newton’s law due to the presence of hematocrit and other blood components, which lead to variable viscosity.

In this CFD simulation study, blood was considered as an incompressible non-Newtonian power law fluid material of variable dynamic viscosity for CFD simulation with the given parameters (Figure 12a): Density (ρ) = 1050 kg/m³, consistency index (K) = 0.017 Pa.s, and power law index (n) = 0.708 [70,71]. The formula for the non-Newtonian power law fluid model with shear rate (γ) dependence, which was applied to determine the dynamic viscosity (µ) of blood, is given here:

$$\mathsf{\tau }=\mathrm{K}{\left({\displaystyle \frac{\mathrm{d}\mathrm{u}}{\mathrm{d}\mathrm{y}}}\right)}^{\mathrm{n}}=\mathrm{K}{\mathsf{\gamma }}^{\mathrm{n}}$$

(2)

$$\mathrm{\mu }=\mathrm{K}{\mathsf{\gamma }}^{\mathrm{n}-1},\mathrm{where}{\mathrm{\mu }}_{\min }<\mathrm{\mu }<{\mathrm{\mu }}_{\max }$$

(3)

The scaffold material (solid domain) was assigned as PEEK (polyether ether ketone). It was considered a rigid material to ignore the effects of fluid–structure interaction (fsi).

(ii.)

Boundary Conditions

The boundary conditions designate the input conditions to the CFD models required for the simulation. The three steady state boundary conditions are an inlet fluid velocity, an outlet pressure and slip wall conditions. The applied inlet velocity was assigned 0.7 mm/s to analyse the fluid flow scenarios for different scaffolds [75]. The outlet pressure was 0 Pa, and a no-slip condition was applied to the walls of the scaffolds (Figure 12b).

(iii.)

Volume Mesh Generation

The given geometry domain must be divided into smaller elements to transform the given geometry model into a simulation model, and the process is known as meshing. In the case of CFD simulations, having a finer mesh may lead to better results. However, increasing the number of elements in a mesh leads to more computational time. So, a tradeoff is often required between the number of elements and the computational cost depending on the hardware of a given computer. A mesh independence test was performed to choose the optimal element size for getting a converged solution irrespective of mesh element size (Supplementary Figure S1). A volume mesh (Figure 13) with quadratic order tetrahedral elements (four-noded elements with every node having five degrees of freedom for laminar flow) was generated for CFD simulation with the parameters given in Supplementary Table S2.

2.2.3. Setting FEM-Based Solver for CFD Simulation

The applied governing equation to solve the CFD of the incompressible laminar flow of blood passing through scaffolds using FEM is the steady-state Navier–Stokes equation of mass conservation and momentum [76]. As the governing equations are represented in PDEs, FEM was used to reduce these PDEs to algebraic equations, which are achieved by meshing or discretisation of the given domain for solving them numerically with the required boundary conditions. A monotone streamline upwind-based FEM scheme was used to discretise the advection terms of the governing equations in this CFD simulation to accomplish numerical stability to avoid errors of numerical diffusion [50]. Advection is the transportation of a quantity, such as velocity, in a fluid domain. It is handled by upwind methods such as the monotone streamline method. In this method, the advection terms are modified to streamline coordinates. This method, whose order is between 1 and 2, is a more stable numerical method compared to other streamline methods such as Petrov–Galerkin and min-mod and is suitable for complex porous structures [77]. An absolute criteria value of 10⁻⁵ was set to check the convergence of continuity, x/y/z velocity components residuals and pressure residual (Supplementary Figure S2).

2.2.4. Visualisation of Results and Analysis

The main goal of the research work is to predict the permeability of the given Voronoi lattice-based scaffolds. Darcy law for calculating the permeability (k) of Newtonian fluid through porous scaffolds:

$$\mathrm{k}={\displaystyle \frac{\mathrm{u}\mathsf{\mu }\mathrm{L}}{∆\mathrm{p}}}$$

(4)

where k is the permeability through the given scaffold, µ is the dynamic viscosity, L is the length of the given scaffold, and ∆p is the pressure drop predicted from the CFD simulation and is the difference of pressures at inlet and outlet of the given fluid domain.

As the given fluid (blood) is considered a non-Newtonian power law material, an altered Darcy’s equation to estimate the permeability through porous scaffolds is given below:

$$\mathrm{k}=\mathrm{u}{\mathrm{K}\left({\displaystyle \frac{\mathrm{L}}{∆\mathrm{p}}}\right)}^{1/\mathrm{n}}$$

(5)

where k is the permeability through the given scaffold, L is the length of the scaffold (3.4217 mm), n is the power law exponent, and ∆p is the predicted pressure drop from CFD simulation.

The CFD simulation results were used in Autodesk CFD to determine the values of velocities and pressure variations inside the fluid domain. The velocity and pressure contours were plotted from the simulation results. The pressure drop values were obtained and applied to find the permeability of the fluid passing through the Voronoi scaffolds.

3. Results and Discussion

3.1. Design of Voronoi Lattice-Based Scaffolds

The architecture (pore dimensions and porosity) of the Voronoi scaffold can be varied by varying the strut thickness (ST) of the Voronoi volume lattice (or) point spacing (PS) of seed points inside the volume of the lattice. Different porous architectures in this research were obtained by varying the PS in the design of the Voronoi lattice with a constant strut thickness of 0.11 mm (Appendix B). By modifying the point spacing, the number of seed points varied, leading to a change in the number of Voronoi cells to have variations in the morphological parameters of scaffolds (

Table 1. Morphological parameters for Voronoi scaffold designs with constant ST of 0.11 mm.

Voronoi Scaffolds	Porosity (%)	Strut Thickness ST (mm)	Point Spacing PS (mm)	Voronoi Seed Points	Voronoi Cell Numbers	Surface Area * SA (mm2)	Surface Area/Volume SA: V (mm−1)
V90	90	0.11	0.851	65	11	70.5	2.29
V85	85	0.11	0.668	124	35	102	3.32
V80	80	0.11	0.570	206	70	131	4.26
V75	75	0.11	0.502	314	121	160	5.19
V70	70	0.11	0.449	433	180	185	6.01

* Computation of SA using mass properties block in nTopology; Bounding box Volume V = 30.82 mm³.

). The obtained porous structures are functionally graded, which implies that the scaffolds have different pore sizes.

3.1.1. Gradient Pore Size Distribution

Having a gradient porous structure is beneficial such that the larger pores help in the transfer of nutrients and cell infiltration for beneficial bone ingrowth, and smaller pores lead to cell attachment to the extracellular matrix [78]. It was reported that a mean pore size of 596 µm was beneficial for uniform Voronoi-based trabecular biomimetic scaffolds [3], while a pore size range of 458 µm to 989 µm was found to be optimal [72] for regenerating bone tissues (BT) in graded Voronoi scaffolds. In another study, it was found in an animal model that a pore size of 300 µm was required for BT regeneration in bone defects of zygoma [79]. The pore sizes of BT scaffolds between 20 µm and 1500 µm were reported in different research works about their effects on cell proliferation, cell attachment, blood vessel growth, osteogenic differentiation, increase of alkaline phosphate and calcium deposition [80,81,82].

In this research work, the given gradient Voronoi scaffolds have an extensive range of pore sizes from 19.8 µm to 923 µm, which can satisfy the requirements of bone regeneration (

Table 2. Range of pore sizes in the Voronoi scaffolds.

Voronoi Scaffolds	Number of Pores	Range of Pore Sizes (µm)
V90	216	22.2 to 923
V85	455	20.2 to 669
V80	668	20.7 to 618
V75	983	20.1 to 532
V70	1362	19.8 to 482

). Figure 14 shows the scalar point maps, which are the outputs of lattice pore size calculations of the diameter of the largest sphere fitting in each Voronoi cell. Every point map denotes the centre point and diameter of every sphere. The V90 scaffold has 216 pores, and the V70 scaffold has the largest number of pores, 1362.

3.1.2. Consequences of Surface Area and Surface Area to Volume Ratio

Figure 15a illustrates that as scaffold porosity increases for a given strut diameter, surface area decreases. Higher porosity (such as 90% in the V90 scaffold) enhances the mass transport of cells, nutrients, and oxygen. This increases scaffold permeability, promoting bone tissue growth by supporting more significant cell proliferation [83]. On the other hand, lower porosity results in a larger surface area, providing more sites for cell attachment but reducing permeability [84]. The V70 scaffold, with the largest surface area of 185 mm², supports better cell adhesion, facilitating bone matrix accumulation, osteogenic gene expression, and effective osseointegration [85]. The surface area is dependent on the size of the pores and the porosities of scaffolds. Scaffolds with heterogeneous pore sizes mimicking natural bone structures are essential in bone remodelling [86].

Apart from the surface area, the parameter surface area to volume ratio (SA: V), also known as specific surface area, is vital for bone growth. Figure 15b shows that the highest SA: V was observed in the scaffold (V70) of 70% porosity. It means that there is ample room for the transport of nourishment and oxygen for cell consumption due to increased collision with scaffold walls. An increase in SA: V leads more cells to adhere to the surface of scaffolds. Lower SA: V means that there is less growth of cells due to lower chances of oxygen collision with scaffold walls and less consumption of oxygen by the cells living on the surface [87].

3.2. CFD Simulation

A pressure drop is a decline in pressure when the fluid passes through scaffolds, and it is a decisive part of CFD for designing scaffolds, as it is involved in calculating permeability so that the performance of scaffolds is evaluated. As the fluid passes through the scaffolds, the scaffold walls restrict the flow, leading to energy loss, and ultimately, the pressure drop occurs. The main factors that contribute to pressure drop are viscosity, fluid velocity or flow rate, density, types of flow (laminar flow in this study), and flow obstructions. Pressure drops are calculated from the difference of pressures at inlet and outlet regions near scaffolds.

3.2.1. Reliability of CFD Models

Even though the inlet velocity of 0.7 mm/s was applied for this CFD simulation research (Section 2.2.2: (ii.)), the reliability of all CFD models and the accomplishment of given boundary conditions were tested using five inlet velocities 0.5, 0.6, 0.7, 0.75 and 0.8 mm/s [71]. Figure 16 depicts the variation of pressure drop for all Voronoi scaffolds based on the given inlet velocities. It is a noticeable fact that when the inlet velocity rises, the pressure drop also increases. The highest pressure drop is found in the V70 scaffold due to the high number of Voronoi cells found in the scaffold, which restrict the fluid flow. The lowest pressure drop was found in the V90 scaffold due to a smaller number of Voronoi cells.

3.2.2. Velocity and Pressure Distributions Within Voronoi Scaffolds

The cross-sectional velocity contours and the velocity streamlines of the given Voronoi scaffolds with different porosities are shown in Figure 17 and Figure 18. It was noticed that all Voronoi scaffolds exhibited higher velocities inside the scaffolds compared to the inlet velocity of 0.7 mm/s. The reason was the change in the internal architecture of scaffolds between the inlet and outlet zones, and the fluid flow was hindered, leading to the acceleration of the flow. Therefore, the fluid velocity inside the scaffolds is influenced by the inhomogeneous microarchitecture of the scaffolds. The 3D velocity streamlines show the travel of the fluid particles through the scaffolds. V90 scaffold showed a lower velocity change compared to other scaffolds. This phenomenon is helpful in determining how smoothly the cells and nutrients pass through the scaffold pores to achieve the goal of bone tissue regeneration. Even though the higher velocities are beneficial for the transport of nutrients, they do not help the attached cells on the surface of scaffolds absorb the nutrients. A similar trend of higher velocities in the central region of scaffold surfaces due to complex architectures was found in permeability simulation by Ali et al. [69].

Figure 19 depicts the pressure contours of Voronoi scaffolds at the inlet velocity of the fluid. It displays the difference in pressures at the inlet and outlet sections of both fluid domains and scaffolds. There was a gradual drop in pressure from the maximum value at the inlet to the minimal value of pressure at the outlet. This indistinguishable trend of pressure distribution was observed in all Voronoi scaffolds. The pressure drops of scaffolds decreased with an increase in porosity (Figure 20).

3.2.3. Permeability Evaluation

Knowing the pressure drop across the scaffold is vital for estimating permeability by applying the altered Darcy’s formula given in (5), as the given fluid blood is a non-Newtonian fluid. Permeability is an index for the transport of nutrients and removal of metabolic wastes required for bone growth through a porous network. Scaffolds with low permeability cannot deliver enough nutrients, and scaffolds with high permeability result in significant removal of cells, hindering the growth of bone tissues. Thus, designing scaffolds for bone tissue regeneration requires permeability values in scaffolds proximate to those values of trabecular bones. The highest permeability was found in the V90 scaffold, and the lowest value was found in the V70 scaffold (Figure 20) (

Table 3. Pressure drop and permeabilities of the Voronoi scaffolds.

Voronoi Scaffolds	Porosity (%)	Pressure Drop * (Pa)	Permeability (×10−9 m2)
V90	90	1.52	2.17
V85	85	2.42	1.13
V80	80	3.13	0.78
V75	75	4.73	0.44
V70	70	5.81	0.33

* Refer to pressure contours for visualisation: Figure 19.

). When the porosity value increases, the permeability value also increases. In V70 scaffolds, due to the increase of cells in the internal architecture, the resistance to the fluid flow is the largest, leading to the highest pressure drop and the lowest permeability.

In this study, the range of permeability was found to range from 0.33 × 10⁻⁹ m² to 2.17 × 10⁻⁹ m². The predicted permeability from CFD analysis of flow properties of scaffolds meets the permeability requirements of natural human trabecular bone, as shown in

Table 4. Comparison of predicted permeability of Voronoi scaffolds with other research works for trabecular (cancellous) bone applications.

Scaffolds/Bones	Permeability (×10−9 m2)	References
Voronoi scaffolds *	0.33 to 2.17	This study *
Human Trabecular bone	0.40 to 11	Grimm et al. [88]
Trabecular bone specimens	0.0268 to 20	Nauman et al. [89]
Gyroid scaffolds	0.29 to 3.91	Ma et al. [90]
Schwartz gyroid/diamond/primitive scaffolds	0.431 to 8.44	Santos et al. [91]
Sheet and skeletal gyroid scaffolds	0.61 to 3.34	Yanez et al. [28]
Diamond/Octet/Truncate-Octahedron/Double-Diamond/TPMS Scaffolds	1.85 to 5.62	Ali et al. [76]

* Refer to Table 3.

. Grimm et al. measured the permeabilities of human calcaneal trabecular bone specimens of 16 cadavers between 0.4 and 11 × 10⁻⁹ m². They found that permeability is a vital factor for modelling bones as poroelastic materials [88]. Nauman et al. found that the intertrabecular permeabilities of human and bovine bone specimens ranged from 2.68 × 10⁻¹¹ m² to 2 × 10⁻⁸ m². They inferred that the permeability, depending on the flow direction, is helpful for prosthesis and implant designs [89]. Our results of permeability values are in agreement with those values of bone specimens, as well as other research works on permeability studies of scaffolds (Table 4).

Porosity depends on pore size and pore network of scaffolds, and it influences the permeability to transfer required nutrients and oxygen, aiding cell growth and blood vessel formation. High porous scaffolds lead to an increase in mass transport, improvement in oxygen diffusion and a surge in the number and magnitude of osteoclasts, making room for osteoblasts to build new bone tissues by increasing vascularization [92]. High porosity is associated with drawbacks such as decreased mechanical strength, diminished cell seeding ability, and reduced surface area for cell adhesion. Low-porosity scaffolds have the advantages of increased mechanical strength, increased cell seeding ability and large surface area [93]. The cons of low porosity are decreased transport of materials, which leads to the deferred formation of blood vessels [94]. The Voronoi lattice designs are helpful in modifying the porosity of the scaffolds to reach the goal of bone remodelling by adjusting the seed points and strut thickness.

3.3. Validation of Non-Newtonian Power Law Models with Newtonian Models

When the power law index (n) of non-Newtonian power law models in Equations (2) and (3) becomes 1, the dynamic viscosity is equal to the consistency index, and this model becomes a Newtonian model which is given below:

$$\mathrm{\mu }=\mathrm{K}{\mathsf{\gamma }}^{\mathrm{n}-1}=\mathrm{K}{\mathsf{\gamma }}^0=\mathrm{K}$$

(6)

$$\mathsf{\tau }=\mathrm{K}{\left({\displaystyle \frac{\mathrm{d}\mathrm{u}}{\mathrm{d}\mathrm{y}}}\right)}^1=\mathrm{K}{\mathsf{\gamma }}^1=\mathrm{\mu }\mathsf{\gamma }$$

(7)

The above Equation (7) is Newton’s law of viscosity for a Newtonian fluid. This concept is applied to validate the power law models for a non-Newtonian fluid with a Newtonian fluid model by performing CFD simulations for both models (

Table 5. Validation of non-Newtonian power law models with Newtonian models.

Voronoi Scaffolds	Newtonian Model (µ = 0.0045 Pa.s)	Non-Newtonian Power Law Model (n = 1, K = 0.0045 Pa.s)	Non-Newtonian Power Law Model * (n = 0.708, K = 0.0017 Pa.s)
	Pressure Drop (Pa)	Pressure Drop (Pa)	Pressure Drop (Pa)
V90	0.726	0.726	1.52
V85	1.26	1.26	2.42
V80	1.75	1.75	3.13
V75	2.88	2.88	4.73
V70	3.76	3.76	5.81

* Refer to Table 3 and Figure 19.

). It is not surprising to see that the pressure drops for both models are identical, as the non-Newtonian models become Newtonian models at n = 1 (Figure 21). The pressure drop values of the non-Newtonian power law model with n = 0.708 are almost double the pressure drop of the Newtonian model and non-Newtonian model with n = 1. The viscosity nature of the non-Newtonian model provides defiance to the fluid flow; therefore, the pressure drop is higher.

3.4. Limitations and Future Directions

The power law model applied in this research requires two parameters (consistency index and power law index) to describe the connection between the fluid viscosity and the shear rate of the given fluid. This model works only for fluids with viscosities of a given range of shear rate values (Figure 22) and does not work for fluids with viscosities of lower and higher shear rates. Therefore, a focus on other non-Newtonian viscosity models, such as Casson, Herschel Bulkley, and Carreau–Yasuda, is needed to model viscosities across all shear rates. Non-Newtonian fluids require a yield stress to have a transition from a resting state to a flow state, which a power law model does not consider; therefore, a Casson model can be applied to define the non-Newtonian fluid with yield stress. For Newtonian models with yield stress and higher shear rates, the Herschel Bulkley model can be applied. Unfortunately, Casson and Herschel Bulkley do not work for lower shear rates. Therefore, the Carreau–Yasuda model can be utilised to model blood flow behaviour at both lower and higher shear rates, making it favourable for biomedical applications [95].

Moreover, the prediction of WSS was not included in the present research. WSS is one of the vital cues for the stimulation of MSCs to differentiate into functional tissues for BT regeneration. In future research, WSS estimation should be included. Turbulent flow models can be used at higher velocities to study the fluid–structure interactions between the fluid and the scaffolds in future research [96].

4. Conclusions

In this research study, five designs of Voronoi lattice-based scaffolds based on bone fractures to mimic trabecular bone microstructure were developed. Various scaffold porosities were achieved by adjusting the point spacing and strut thickness. The surface area and the surface-to-volume ratio of the given graded scaffolds were found to be decreasing with their increasing porosities. The fluid flow behaviour of all Voronoi scaffolds was analysed using FEM-based CFD simulations for a power law model of a non-Newtonian fluid (blood). These simulations were performed to assess the velocity and pressure profiles and to estimate the pressure drops and permeability of fluid passing through scaffolds of different porosities. The pressure drops were higher in scaffolds of lower porosities due to the increased number of Voronoi cells in the microstructure. Using altered Darcy’s formula, the permeability of fluid passing through the scaffolds was calculated. The permeability values were found to increase with increasing porosity. The predicted permeability values were in the range from 0.33 × 10⁻⁹ m² to 2.17 × 10⁻⁹ m², which is in good agreement with those values of human and bovine trabecular bones as well as that of scaffolds from other research works.