Asymptotic and Probabilistic Perturbation Analysis of Controllable Subspaces

Abstract

In this paper, we consider the sensitivity of the controllable subspaces of single-input linear control systems to small perturbations of the system matrices. The analysis is based on the strict component-wise asymptotic bounds for the matrix of the orthogonal transformation to canonical form derived by the method of the splitting operators. The asymptotic bounds are used to obtain probabilistic bounds on the angles between perturbed and unperturbed controllable subspaces implementing the Markoff inequality. It is demonstrated that the probability bounds allow us to obtain sensitivity estimates, which are much tighter than the usual deterministic bounds. The analysis is illustrated by a high-order example.

1. Introduction

The notion of controllable subspace plays an important role in linear control theory ([1], Ch. 1). This notion has several applications to differential algebraic systems [2], networks [3], time-varying systems [4], quantum dynamical systems [5], and switched linear systems [6], to name a few.

In this paper, we are interested in the sensitivity to small parameter perturbations of the controllable subspaces of single-input time-invariant linear control systems, described by the state equation

$$\dot{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right),$$

(1)

where $x\in {\mathbb{R}}^n$ is the state vector, $u\in {\mathbb{R}}^1$ is the control vector and $A\in {\mathbb{R}}^{n\times n},B\in {\mathbb{R}}^{n\times 1}$. The subspace

$${\mathcal{C}}_k=\sum _{j=1}^{k-1}{A}^j\mathcal{R}\left(B\right)=\mathcal{R}\left([B,AB,\dots ,A^{k-1}B]\right),k=1,2,\dots ,n$$

is said to be the kth controllable subspace of (1). Clearly,

$$\dim \left({\mathcal{C}}_k\right)=\mathrm{rank}\left([B,AB,\dots ,A^{k-1}B]\right).$$

We have that

$${\mathcal{C}}_1\subset {\mathcal{C}}_2\subset \cdots \subset {\mathcal{C}}_n.$$

The subspace ${\mathcal{C}}_n$ is said to be the controllable subspace of the pair $(A,B)$. If $\dim \left({\mathcal{C}}_n\right)=n$, i.e., ${\mathcal{C}}_n$ is the whole state space, then the system (1) and, respectively, the pair $(A,B)$ are called controllable. If the system is controllable, then for every vector $x_T\in {\mathcal{C}}_n$ and $T>0$ there exists a continuous control $u:[0,T]\to {\mathbb{R}}^1$, such that the state vector $x\left(t\right)$ of (1) with $x\left(0\right)\in {\mathcal{C}}_n$ satisfies $x\left(T\right)=x_T$, i.e., each $x_T\in {\mathcal{C}}_n$ may be reached starting from each initial state $x\left(0\right)\in {\mathcal{C}}_n$. If $\dim \left({\mathcal{C}}_n\right)<n$, the system is said to be uncontrollable. Note that the controllability of a system is not affected by non-singular transformations of the state or control vector. As it is well known ([1], Ch. 1), the controllability is a generic property that is open and dense in the parameter space. The genericity means that each uncontrollable pair $(A,B)$ can be made controllable by arbitrary small perturbations of A and B.

In case of some perturbations of the system matrices A and B, the controllable subspaces change, and for sufficiently large perturbations a controllable system may become an uncontrollable one. That is why the sensitivity of the controllable subspaces of a linear control system is closely related to the magnitude of the distance of a controllable system to an uncontrollable one, which is roughly defined as the size of the smallest perturbations in A, B that makes a controllable system an uncontrollable one [7,8,9]. Following the well-known paradigm in the numerical analysis [10], it is justified to expect that the sensitivity of the controllable subspaces is inversely proportional to the distance to an uncontrollable system. However, in contrast to the numerous papers devoted to the estimation of the distance to an uncontrollable system (see [11,12,13,14], to name a few), the sensitivity of the controllable subspaces has not been studied up to this moment.

In this paper, we consider the sensitivity of the controllable subspaces of single-input linear control systems to small perturbations of the system matrices that preserve the system controllability. The analysis is based on the new strict component-wise asymptotic bounds for the matrix of the orthogonal transformation to canonical form, derived by the method of the splitting operators [15]. The asymptotic bounds on the orthogonal transformation matrix entries are used to obtain probabilistic bounds on the angles between the perturbed and unperturbed controllable subspaces implementing the Markoff inequality. The analysis is illustrated by a high-order example. The analysis performed and the example given demonstrate that, in contrast to the deterministic bounds, the probabilistic bounds are much tighter with a sufficiently high probability. We note that the same approach of perturbation analysis is used in [16] to perform perturbation analysis of invariant, deflating and singular subspaces of matrices.

The paper is organised as follows. In Section 2, we show how to find orthonormal bases of the controllable subspaces using an appropriate system canonical form. Using the method of splitting operators, we derive asymptotic bounds on the orthonormal bases, which are then used in the perturbation analysis of controllable subspaces. In Section 3, we briefly present some results concerning the derivation of lower magnitude bounds on the entries of a random matrix using only their Frobenius norm. In the same section, we describe the application of this approach to derive probabilistic perturbation bounds for the controllable subspaces of a single-input system. A discussion on the advantages and disadvantages of the proposed new bounds is performed in Section 4. We illustrate the theoretical results with an example of a 100th-order system demonstrating that the probability bounds of the controllable subspaces are much tighter than the corresponding deterministic asymptotic bounds. Some conclusions are made in Section 6.

All computations in the paper are performed with MATLAB^® Version 9.9 (R2020b) [17] using IEEE double-precision arithmetic on a machine equipped with a 12th Gen Intel(R) Core(TM) i5-1240P CPU running at 1.70 GHz and with 32 GB of RAM. M-files implementing the perturbation bounds described in the paper can be obtained from the authors.

2. Asymptotic Perturbation Bounds for the Controllable Subspaces

The sensitivity of linear subspaces to perturbations is analysed by determining the angles between the perturbed and unperturbed subspaces [18,19]. For this aim, the best results from the numerical point of view are obtained if one uses orthonormal bases for these subspaces. Therefore, our first task is to find the controllable subspaces’ orthonormal bases. This can be done by reducing the system into some special form that reveals the controllable subspaces by using orthogonal similarity transformations.

2.1. Orthonormal Bases of the Controllable Subspaces

Using a sequence of $n-1$ orthogonal similarity transformations (plane rotations or Householder reflections)

$$x_{i+1}=Q_i{x}_i,i=1,2,\dots n-1,x_1=x,$$

the system (1) can be reduced to the form

$${\dot{x}}^c\left(t\right)=A^c{x}^c\left(t\right)+B^{c}u\left(t\right),$$

(2)

where $x^c=x_{n-1}$ and $A^c=U^{T}AU,B^c=U^{T}B$ and $U=Q_1{Q}_2\cdots Q_{n-1}$. For appropriately chosen orthogonal transformations, the matrices $A^c$ and $B^c$ are reduced to the form

$$A^c=\left[\begin{array}{ccccc}{a}_{11}& a_{12}& \cdots & a_{1,n-1}& a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2,n-1}& a_{2n}\\ & \ddots & \ddots & ⋮& ⋮\\ & & & a_{n-1,n-1}& a_{n-1,n}\\ & & & a_{n,n-1}& a_{n,n}\end{array}\right],B^c=\left[\begin{array}{c}{b}_1\\ 0\\ ⋮\\ 0\end{array}\right]$$

and we say that the system (2) is in the orthogonal canonical form [20] or Hessenberg form [21]. Details of the reduction can be found in the references above and [22]. The corresponding algorithm is proved to be numerically stable, and it requires approximately $8n^3/3$ floating point operations (flops).

Since

$$\begin{array}{ccc}\hfill [B,AB,\dots ,A^{k-1}B]& =& U[B^c,A^c{B}^c,\dots ,{A^c}^{k-1}B]\hfill \\ & =& U\left[\begin{array}{cccc}{b}_1& \ast & \dots & \ast \\ & b_1{a}_{21}& \dots & \ast \\ & & \ddots & \ast \\ & & & b_1{a}_{21}\dots a_{k,k-1}\end{array}\right],k=2,3,\dots ,n\hfill \end{array}$$

(3)

where * denotes an unspecified entry, it follows that the controllability of the system (1) ensures the fulfilment of the conditions

$$b_1\ne 0$$

and

$$a_{k,k-1}\ne 0,k=2,3,\dots ,n,$$

i.e., $A^c$ is an unreduced Hessenberg matrix [23]. Note that the expression (3) represents the QR decomposition of the controllability matrix $[B,AB,\dots ,A^{k-1}B]$, which makes it possible to determine immediately the orthonormal bases of the controllable subspaces ${\mathcal{C}}_1,{\mathcal{C}}_2,\dots ,{\mathcal{C}}_n$. Partitioning the orthogonal transformation matrix, U, by columns as

$$U=\left[U_1,U_2,\dots ,U_n\right]$$

we have that

$$\begin{array}{ccc}\hfill {\mathcal{C}}_1& =& \mathcal{R}\left(U_1\right),\hfill \\ \hfill {\mathcal{C}}_2& =& \mathcal{R}\left([U_1,U_2]\right),\hfill \\ \hfill ⋮& & \\ \hfill {\mathcal{C}}_n& =& \mathcal{R}\left([U_1,U_2,\dots U_n]\right).\hfill \end{array}$$

If the matrices A and B are subject to perturbation $\delta A$ and $\delta B$, respectively, then, instead of the decomposition (2), we have the decomposition

$${\dot{\tilde{x}}}^c\left(t\right)={\tilde{A}}^c{\tilde{x}}^c\left(t\right)+{\tilde{B}}^{c}u\left(t\right),$$

(4)

where the pair $({\tilde{A}}^c,{\tilde{B}}^c)$ with

$$\begin{array}{ccc}\hfill {\tilde{A}}^c& =& {\tilde{U}}^T\tilde{A}\tilde{U},\tilde{A}=A+\delta A,\hfill \\ \hfill {\tilde{B}}^c& =& {\tilde{U}}^T\tilde{B},\tilde{B}=B+\delta B\hfill \end{array}$$

is again in orthogonal canonical form and $\tilde{U}$ is orthogonal, i.e., ${\tilde{U}}^T\tilde{U}=I_n$. The columns of the perturbed matrix of the orthogonal transformation

$$\tilde{U}=[{\tilde{U}}_1,{\tilde{U}}_2,\dots ,{\tilde{U}}_n]$$

represent the basis vectors of the perturbed controllability subspaces

$$\begin{array}{ccc}\hfill {\tilde{\mathcal{C}}}_1& =& \mathcal{R}\left({\tilde{U}}_1\right),\hfill \\ \hfill {\tilde{\mathcal{C}}}_2& =& \mathcal{R}\left([{\tilde{U}}_1,{\tilde{U}}_2]\right),\hfill \\ \hfill ⋮& & \\ \hfill {\tilde{\mathcal{C}}}_n& =& \mathcal{R}\left([{\tilde{U}}_1,{\tilde{U}}_2,\dots {\tilde{U}}_n]\right).\hfill \end{array}$$

Further on, we shall assume that for small perturbations $\delta A$ and $\delta B$ the pair $({\tilde{A}}^c,{\tilde{B}}^c)$ preserves its controllability, i.e., $\dim \left({\tilde{\mathcal{C}}}_n\right)=n$. Note that in this case ${\tilde{\mathcal{C}}}_n={\mathcal{C}}_n$ and the perturbation analysis of the controllable subspace ${\mathcal{C}}_n$ does not represent interest.

The sensitivity of the canonical form $(A^c,B^c)$ without analyzing the sensitivity of the orthogonal transformation matrix, U, is studied by several authors [21,24,25].

Denote for brevity the controllable subspace of dimension k by $\mathcal{X}=\mathcal{R}\left(U_X\right)$ and its perturbed counterpart by $\tilde{\mathcal{X}}=\mathcal{R}\left({\tilde{U}}_X\right)$, where $\mathrm{rank}\left(U_X\right)=\mathrm{rank}\left({\tilde{U}}_X\right)=k$. The sensitivity of the controllable subspace $\mathcal{X}$ is measured by the canonical angles

$${\Theta }_1\ge {\Theta }_2\ge \cdots \ge {\Theta }_k\ge 0$$

between the perturbed and unperturbed subspaces. The maximum angle ${\Theta }_{max}={\Theta }_1$ between $\tilde{\mathcal{X}}$ and $\mathcal{X}$ can be computed efficiently from [18] (Ch. 4).

$${\Theta }_{max}(\tilde{\mathcal{X}},\mathcal{X})=arcsin(\parallel {U_X^{perp}}^T{\tilde{U}}_X{\parallel }_2),$$

(5)

where $U_X^{perp}$ is the orthogonal complement of $U_X,{U_X^{perp}}^T{U}_X=0$.

2.2. Perturbation Bounds by the Splitting Operator Method

Denote by

$$\begin{array}{ccc}\hfill \delta U& =& \tilde{U}-U=[\delta U_1,\delta U_2,\dots ,\delta U_n],\hfill \\ \hfill \delta A^c& =& {\tilde{A}}^c-A^c.\hfill \end{array}$$

According to the splitting operator method [15], it is possible to derive separately perturbation bounds on $\left|\delta U\right|$ and $|\delta A^c|$, which allows for obtaining tight bounds. For this aim, it is appropriate to use the matrix

$$\delta W=U^T\delta U=\left[\begin{array}{cccc}{U}_1^T\delta U_1& U_1^T\delta U_2& \dots & U_1^T\delta U_n\\ U_2^T\delta U_1& U_2^T\delta U_2& \dots & U_2^T\delta U_n\\ ⋮& ⋮& ⋮& ⋮\\ U_n^T\delta U_1& U_n^T\delta U_2& \dots & U_n^T\delta U_n\end{array}\right]\in {\mathbb{R}}^{n\times n}$$

which is orthogonally equivalent to the unknown matrix $\delta U$. Further on, we shall use the perturbation parameter vector

$$\begin{array}{ccc}\hfill x& =& \mathrm{vec}\left(\mathrm{Low}\right(\delta W\left)\right)\hfill \\ & =& {\left[U_2^T\delta U_1\dots U_n^T\delta U_1|U_3^T\delta U_2\dots U_n^T\delta U_2|\dots |U_n^T\delta U_{n-1}\right]}^T\in {\mathbb{R}}^p,p=n(n-1)/2,\hfill \end{array}$$

where the components of x are the entries of the strictly lower triangular part of $\delta W$. Using this vector, it is convenient to find bounds on various elements related to the orthogonal canonical form and the transformation matrix, U.

From the orthogonality of the matrix $\tilde{U}$, it follows that

$$\begin{array}{ccc}\hfill {(U_i+\delta U_i)}^T(U_i+\delta U_i)& =& 1,\hfill \\ \hfill {(U_i+\delta U_i)}^T(U_j+\delta U_j)& =& 0,i<j,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill U_i^T\delta U_i& =& -\delta U_i^T\delta U_i/2,\hfill \\ \hfill U_i^T\delta U_j& =& -U_j^T\delta U_i-\delta U_i^T\delta U_j.\hfill \end{array}$$

Hence, the matrix $\delta W$ can be represented as

$$\delta W=\delta V-\delta D-\delta Y,$$

(6)

where

$$\begin{array}{ccc}\hfill \delta V& =& \left[\begin{array}{ccccc}0& -x_1& -x_2& \dots & -x_{n-1}\\ x_1& 0& -x_n& \dots & -x_{2n-3}\\ x_2& x_n& 0& \dots & -x_{3n-6}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ x_{n-1}& x_{2n-3}& x_{3n-6}& \dots & x_p\end{array}\right]\in {\mathbb{R}}^{n\times n},\hfill \end{array}$$

and the matrices

$$\delta D=\left[\begin{array}{cccc}\delta U_1^T\delta U_1/2& 0& \dots & 0\\ 0& \delta U_2^T\delta U_2/2& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & \delta U_n^T\delta U_n/2\end{array}\right]\in {\mathbb{R}}^{n\times n},$$

$$\delta Y=\left[\begin{array}{ccccc}0& \delta U_1^T\delta U_2& \delta U_1^T\delta U_3& \dots & \delta U_1^T\delta U_n\\ 0& 0& \delta U_2^T\delta U_3& \dots & \delta U_2^T\delta U_n\\ 0& 0& 0& \dots & \delta U_3^T\delta U_n\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & \delta U_{n-1}^T\delta U_n\end{array}\right]\in {\mathbb{R}}^{n\times n},$$

contain second-order terms in $\delta U_j,j=1,2,\dots ,n$.

The vector x can be found from the perturbations $\delta A$ and $\delta B$ as follows. From the relationships

$$U^{T}AU=A^c,U^{T}B=B^c,$$

we have that

$$\begin{array}{ccc}\hfill U_i^{T}B& =& 0,i=2,3,\dots ,n,\hfill \\ \hfill U_i^{T}A{U}_j& =& 0,i=3,4,\dots ,n,j=1,2,\dots ,i-2.\hfill \end{array}$$

(7)

The corresponding perturbed quantities satisfy

$$\begin{array}{ccc}\hfill {\tilde{U}}_i^T(B+\delta B)& =& 0,i=2,3,\dots ,n,\hfill \\ \hfill {\tilde{U}}_i^T(A+\delta A){\tilde{U}}_j& =& 0,i=3,4,\dots ,n,j=1,2,\dots ,i-2.\hfill \end{array}$$

(8)

Assuming that the perturbations of the data are small, we can neglect the second-order term $\delta U_i^{T}A\delta U_j$, thus obtaining asymptotic estimates. From (7) and (8), we find that

$$\begin{array}{ccc}\hfill \delta U_i^{T}B& =& -{\tilde{U}}_i^T\delta B,i=2,3,\dots ,n.\hfill \\ \hfill U_i^{T}A\delta U_j+\delta U_i^{T}A{U}_j& =& -{\tilde{U}}_i^T\delta A{\tilde{U}}_j,\hfill \\ & & i=3,4,\dots ,n,j=1,2,\dots ,i-2,\hfill \end{array}$$

(9)

Exploiting the identities

$$U^{T}A=A^c{U}^T,AU=U{A}^c,U^{T}B=B^c,$$

the terms on the left-hand side of (9) are expressed as

$$\begin{array}{ccc}\hfill \delta U_i^{T}B& =& b_1{U}_1^T\delta U_i,i=2,3,\dots ,n\hfill \\ \hfill \delta U_i^{T}A{U}_j& =& \sum _{k=1}^{j+1}{a}_{kj}{U}_k^T\delta U_i,i=3,4,\dots ,n,j=1,2,\dots ,i-2,\hfill \\ \hfill U_i^{T}A\delta U_j& =& \sum _{k=i-1}^n{a}_{ik}{U}_k^T\delta U_j,i=3,4,\dots ,n,j=1,2,\dots ,i-2.\hfill \end{array}$$

Since ${\tilde{U}}_i^T{\tilde{U}}_j=0,i\ne j$, up to the first-order terms we obtain

$$\delta U_i^T{U}_j=-U_i^T\delta U_j,i\ne j.$$

(10)

In this way

$$\begin{array}{ccc}\hfill b_1{U}_1^T\delta U_i& =& -{\tilde{U}}_i^T\delta B,\hfill \\ \hfill \sum _{k=i-1}^n{a}_{ik}{U}_k^T\delta U_j+\sum _{k=1}^{j+1}{a}_{kj}{U}_k^T\delta U_i& =& -{\tilde{U}}_i^T\delta A{\tilde{U}}_j.\hfill \end{array}$$

(11)

Denote

$$F=-{\tilde{U}}^T\delta A\tilde{U},G={\tilde{U}}^T\delta B$$

and construct a vector, h, consisting of the columns of the strict lower part of the matrix $H=[G,F]$, i.e.,

$$\begin{array}{ccc}\hfill h& =& \mathrm{vec}\left(\mathrm{Low}\right([G,F]\left)\right)\hfill \\ & =& {\left[{\tilde{U}}_2^T\delta B,\dots ,{\tilde{U}}_n^T\delta B|-{\tilde{U}}_3^T\delta A{\tilde{U}}_1,\dots ,-{\tilde{U}}_n^T\delta A{\tilde{U}}_1|\dots |-{\tilde{U}}_n^T\delta A{\tilde{U}}_{n-1}\right]}^T\in {\mathbb{R}}^p.\hfill \end{array}$$

The system of equations (11) can be represented as the linear system of equations for the perturbation parameters,

$$Mx=h,$$

(12)

where $M\in {\mathbb{R}}^{p\times p}$ is a lower triangular matrix. The equation (12) describes the linear perturbation problem in respect to x, and the matrix $M^{-1}$ can be considered as the matrix of the linear perturbation operator, which maps the perturbation vector h into the perturbation parameter vector x. According to (11), the matrix M is determined from the entries of $A^c$ and $B^c$ as

For instance, if $n=5$, then

It is possible to show that the matrix M is determined from

$$M=M_1+M_2,$$

where

$$\begin{array}{ccc}\hfill M_1& =& \mathsf{\Omega }(C\otimes A^c){\mathsf{\Omega }}^T\in {\mathbb{R}}^{p\times p},\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill M_2& =& \mathsf{\Omega }({[B^c,-{A^c}_{1:n,1:n-1}]}^T\otimes I_n){\mathsf{\Omega }}^T\in {\mathbb{R}}^{p\times p},\hfill \end{array}$$

(14)

$$C=\left[\begin{array}{ccccc}0& & & & \\ 1& 0& & & \\ & 1& \ddots & & \\ & & \ddots & 0& \\ & & & 1\end{array}\right]$$

and

$$\begin{array}{ccc}\hfill \mathsf{\Omega }& :=& \left[\mathrm{diag}({\mathsf{\Omega }}_1,{\mathsf{\Omega }}_2,\dots ,{\mathsf{\Omega }}_{n-1}),0_{p\times n}\right]\in {\mathbb{R}}^{p\times n^2},\hfill \\ \hfill {\mathsf{\Omega }}_k& :=& \left[0_{(n-k)\times k},I_{n-k}\right]\in {\mathbb{R}}^{(n-k)\times n},k=1,2,\dots ,n-1.\hfill \end{array}$$

(15)

The triangular matrix M is non-singular since, due to the controllability of the system, the diagonal entries $b_1,a_{21},\dots a_{n-1,n-2}$ are different from zero. With the decreasing magnitude of these entries, the distance to the uncontrollable system decreases, and the matrix M becomes ill-conditioned. If some or several diagonal elements become zeros, the system becomes uncontrollable, and the matrix M becomes singular. This shows that there is a close connection between the singular values of M and the distance to the uncontrollable system. More specifically, for small perturbations $\delta A$ and $\delta B$, the smallest singular value of M can be considered as an asymptotic estimate of the distance to an uncontrollable system.

Since ${\parallel h\parallel }_2\le \sqrt{{\parallel \delta A\parallel }_F^2+{\parallel \delta B\parallel }_F^2}$, we have that

$$|x_{\ell }|⪯x_{\ell }^{lin},\ell =1,2,\dots ,p,$$

where

$$x_{\ell }^{lin}={\parallel M_{\ell ,1:p}^{-1}\parallel }_2\sqrt{{\parallel \delta A\parallel }_F^2+{\parallel \delta B\parallel }_F^2}$$

(16)

is the asymptotic (linear) bound on $|x_{\ell }|$.

According to (6), the matrix $\left|\delta W\right|$ can be estimated as

$$\left|\delta W\right|⪯\delta W^{lin}+{\Delta }^W,$$

(17)

where

$$\delta W^{lin}=\left[\begin{array}{ccccc}0& x_1^{lin}& x_2^{lin}& \dots & x_{n-1}^{lin}\\ x_1^{lin}& 0& x_n^{lin}& \dots & x_{2n-3}^{lin}\\ x_2& x_n^{lin}& 0& \dots & x_{3n-6}^{lin}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ x_{n-1^{lin}}& x_{2n-3}^{lin}& x_{3n-6}^{lin}& \dots & 0\end{array}\right]\in {\mathbb{R}}^{n\times n}$$

is a first-order approximation of $\left|\delta W\right|$ and ${\Delta }^W$ contains higher-order terms in x. Thus, an asymptotic (linear) approximation of the matrix $\left|\delta U\right|$ can be determined as

$$\left|\delta U\right|⪯\delta U^{lin}=\left|U\right||U^H\delta U|=|U|\delta W^{lin}.$$

(18)

The determination of an estimate of the basis vector perturbation $\delta U$ allows to find estimates of the angles between the perturbed and unperturbed controllability subspaces. Consider the sensitivity of a controllable subspace $\mathcal{X}=\mathcal{R}\left(U_X\right)$ of dimension k. Since

$${\tilde{U}}_X=U_X+\delta U_X,{U_X^{perp}}^T{U}_X=0,$$

we have that

$$sin\left({\Theta }_{max}(\tilde{\mathcal{X}},\mathcal{X})\right)=\parallel {U_X^{perp}}^T{\tilde{U}}_X{\parallel }_2=\parallel {U_X^{perp}}^T\delta U_X{\parallel }_2={\parallel \delta W_{k+1:n,1:k}\parallel }_2.$$

(19)

Equation (19) shows that the sensitivity of the controllable subspace $\mathcal{X}$ of dimension k is connected to the values of the perturbation parameters $x_{\ell }=U_i^T\delta U_j,\ell =i+(j-1)$$n-{\displaystyle \frac{j(j+1)}{2}},i>k,$$j=1,2,\dots ,k$. Consequently, if the perturbation parameters are known, it is possible to find at once sensitivity estimates for all controllable subspaces with dimension $k=1,2,\dots ,n-1$. More specifically, let

$$\delta W=\left[\begin{array}{ccccc}\ast & \ast & \ast & \dots & \ast \\ x_1& \ast & \ast & \dots & \ast \\ x_2& x_n& \ast & \dots & \\ ⋮& ⋮& ⋮& \ddots & ⋮\\ x_{n-1}& x_{2n-3}& x_{3n-6}& \dots & \ast \end{array}\right].$$

Then, the maximum angle between the perturbed and unperturbed controllable subspace of dimension k is given by

$${\Theta }_{max}(\tilde{\mathcal{X}},\mathcal{X})=arcsin(\parallel \delta W_{k+1:n,1:k}{\parallel }_2).$$

(20)

Thus, we obtain the following result.

Theorem 1. 

Let the system (1) be reduced into an orthogonal canonical form (2) and assume that the Frobenius norms of the perturbations $\delta A$ and $\delta B$ are known. Set

$$L=\left[\begin{array}{ccccc}\ast & \ast & \ast & \dots & \ast \\ M_{1,1:p}^{-1}& \ast & \ast & \dots & \ast \\ M_{2,1:p}^{-1}& M_{n,1:p}^{-1}& \ast & \dots & \ast \\ ⋮& ⋮& ⋮& \ddots & ⋮\\ M_{n-1,1:p}^{-1}& M_{2n-3,1:p}^{-1}& M_{3n-6,1:p}^{-1}& \dots & \ast \end{array}\right]\in {\mathbb{R}}^{n\times n.p},$$

where the matrix M is determined as in (12). Then, for the kth controllable subspace of (1), the following asymptotic perturbation bound holds,

$${\Theta }_{max}^{lin}(\tilde{\mathcal{X}},\mathcal{X})\le arcsin(\parallel L_{k+1:n,1:kp}{\parallel }_2{\parallel h\parallel }_2)\le arcsin\left(\parallel L_{k+1:n,1:kp}{\parallel }_2\sqrt{{\parallel \delta A\parallel }_F^2+{\parallel \delta B\parallel }_F^2}\right).$$

(21)

The proof of Theorem 1 follows directly from (20), replacing the matrix $\delta W$ by its linear approximation $\delta W^{lin}$ and substituting each $x_{\ell }^{lin}$ by its approximation (16). Note that, as always, in the case of perturbation bounds, the equality can be achieved only for specially constructed perturbation matrices $\delta A$ and $\delta B$.

Similarly to the component-wise sensitivity analysis of the orthogonal transformation matrix, it is possible to find perturbation bounds on the entries of the matrices $A^c$ and $B^c$.

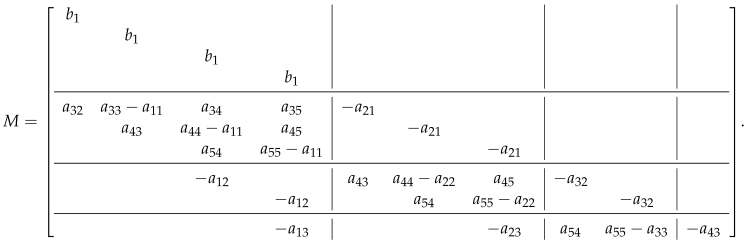
3. Probabilistic Perturbation Bounds for Controllable Subspaces

The asymptotic perturbation bounds for controllability subspaces are usually pessimistic, especially for high-order systems. The conservatism of these estimates can be substantially reduced if, instead of the quantities ${\parallel \delta A\parallel }_F$ and ${\parallel \delta B\parallel }_F$, producing the maximum possible (and unrealistic) perturbation bound (21), we use their estimates obtained for a specified probability. This can be achieved by exploiting the properties of perturbation matrices with random entries. For this aim, we use the Markoff inequality, which allows for a given probability to reduce substantially the magnitude estimates of the perturbation matrix entries. We note that our approach to the analysis of the random matrices is different from the random matrix analysis methods proposed by Edelman and Rao [26] and Stewart [27].

3.1. Probabilistic Bounds for Random Matrices

Assume we are given an $n\times m$ random matrix, $\delta A$, with uncorrelated elements. To bound the entries of this matrix in the perturbation analysis, we have to use the matrix bound $\Delta A=[\Delta a_{ij}],\Delta a_{ij}>0$, so that $\left|\delta A\right|⪯\Delta A$, i.e.,

$$|\delta a_{ij}|\le \Delta a_{ij},i=1,2,\dots ,n,j=1,2,\dots ,m,$$

(22)

where $\Delta a_{ij}=\parallel \delta A\parallel$ and $\parallel .\parallel$ is some matrix norm. If we use the Frobenius norm of $\delta A$, we have the deterministic bound $\Delta a_{ij}={\parallel \delta A\parallel }_F$ that guarantees the fulfilment of (22). However, for such a bound we have that

$${\parallel \Delta A\parallel }_F=\sqrt{mn}{\parallel \delta A\parallel }_F,$$

which yields very pessimistic results for large n and m. That is why to decrease ${\parallel \Delta A\parallel }_F$, we shall reduce the entries of $\Delta A$, taking a bound with $\Delta a_{ij}={\parallel \delta A\parallel }_F/\Xi$, where $\Xi >1$. Obviously, in the general case, such a bound may not satisfy (22) for all i and j. However, we can allow to exist some entries, $\delta a_{ij}$, of the perturbation $\delta A$ that exceed in magnitude with some prescribed probability the corresponding bound $\Delta a_{ij}$. The probability that $|\delta a_{ij}|>\Delta a_{ij}$ can be determined by the Markoff inequality [28] (Sect. 5-4)

$$\mathcal{P}\{\xi \ge a\}\le {\displaystyle \frac{E\left\{\xi \right\}}{a}},$$

(23)

where $\mathcal{P}\{\xi \ge a\}$ is the probability that the random variable $\xi$ is greater or equal to a given number, a, and $E\left\{\xi \right\}$ is the average (mean value) of $\xi$. We note that the Markoff inequality is valid for the arbitrary distribution of $\xi$, which makes it conservative for a specific probability distribution. Applying the Markoff inequality with $\xi$ equal to the entry $|\delta a_{ij}|$ and a equal to the corresponding bound $\Delta a_{ij}$, we obtain the following result [29].

Theorem 2. 

For an $n\times m$ random perturbation, $\delta A$, and a desired probability $0<{\mathcal{P}}^{ref}<1$, the estimate $\Delta A=[\Delta a_{ij}]$, where

$$\Delta a_{ij}={\displaystyle \frac{{\parallel \delta A\parallel }_F}{\Xi }},$$

(24)

and

$$\Xi =(1-{\mathcal{P}}^{ref})\sqrt{mn},$$

(25)

satisfies the inequality

$$\mathcal{P}\left\{\right|\delta a_{ij}|<\Delta a_{ij}\}\ge {\mathcal{P}}^{ref},i=1,2,\dots ,n,j=1,2,\dots ,m.$$

According to Theorem 2, the using of the scaling factor (25) guarantees that the inequality

$$|\delta a_{ij}|<\Delta a_{ij}$$

holds for each i and j with a probability no less than ${\mathcal{P}}^{ref}$.

Theorem 2 can be used to decrease the mean value of the bound $\Delta A$ and hence the magnitude of its entries by the quantity $\Xi$, choosing the desired probability, ${\mathcal{P}}^{ref}$, less than 1. The value ${\mathcal{P}}^{ref}=1$ corresponds to the case of the deterministic bound $\Delta A$, which fulfils (22). The value ${\mathcal{P}}^{ref}<1$ corresponds to $\Delta a_{ij}={\parallel \delta A\parallel }_F/\Xi$, where $\Xi >1$. We note that the probability bound produced by the Markoff inequality is very conservative, and the actual results are much better than the results predicted by the probability ${\mathcal{P}}^{ref}$.

In perturbation analysis, we frequently encounter the problem of determining a bound on the elements of the vector

$$x=Mf,$$

(26)

where M is given matrix and $f\in {\mathbb{R}}^p$ is a random vector with a known probabilistic bound on its elements. It may be shown that it is valid for the following deterministic linear component-wise bound

$$|x_{\ell }|\le x_{\ell }^{lin}:=\parallel M_{\ell ,1:p}{\parallel }_2{\parallel f\parallel }_2,\ell =1,2,\dots ,p.$$

(27)

A probability bound on $|x_{\ell }|,\ell =1,2,\dots ,p$ can be determined by the following theorem [29].

Theorem 3. 

If the estimate of the parameter vector x is chosen as $x^{est}=\left|Mf\right|/\Xi$, where Ξ is determined according to

$$\Xi =\sqrt{p}(1-{\mathcal{P}}^{ref}),$$

(28)

then

$$\mathcal{P}\left\{\right|x_{\ell }|\le \parallel x^{est}{\parallel }_2\}\le {\mathcal{P}}^{ref}.$$

(29)

Since

$$\parallel x^{est}{\parallel }_2\le {\parallel M\parallel }_2{\parallel f\parallel }_2/\Xi ,$$

the inequality (29) shows that the probability estimate of the component $|x_{\ell }|$ can be determined if in the linear estimate (27) we replace the perturbation norm ${\parallel f\parallel }_2$ by the probability estimate ${\parallel f\parallel }_2/\Xi$, where the scaling factor $\Xi$ is taken as in (28) for a specified probability, ${\mathcal{P}}^{ref}$. In this way, instead of the linear estimate, $x_{\ell }^{lin}$, we obtain the probabilistic estimate

$$x_{\ell }^{est}=x_{\ell }^{lin}/\Xi =\parallel M_{\ell ,1:p}{\parallel }_2{\parallel f\parallel }_2/\Xi ,\ell =1,2,\dots ,p.$$

Theorems 2 and 3 can be used to decrease the asymptotic bounds on the sensitivity of the controllable subspaces replacing for a given probability the quantities ${\parallel \delta A\parallel }_F\parallel$ and ${\parallel \delta B\parallel }_F$ by their probability estimates obtained by using (24). Due to the conservatism of the Markoff inequality, such probability bounds for controllable subspaces can produce reliable results, reducing the bound size significantly.

3.2. Probabilistic Sensitivity Analysis of Controllable Subspaces

To determine tighter perturbation bounds of the controllable subspaces, we replace the Frobenius norms of the matrix perturbations $\delta A$ and $\delta B$ in the linear estimate (21) by much smaller probabilistic estimates of the perturbations entries, determined by using Theorems 2 and 3. This makes it possible to decrease with a specified probability the perturbation bounds for the different subspaces, achieving realistic results for higher- dimensional problems. For this aim, we replace ${\parallel \delta A\parallel }_F$ and ${\parallel \delta B\parallel }_F$ in (21) by the ratios ${\parallel \delta A\parallel }_F/{\Xi }_A$ and ${\parallel \delta B\parallel }_F/{\Xi }_B$, where

$${\Xi }_A=n(1-{\mathcal{P}}^{ref}),{\Xi }_B=\sqrt{n}(1-{\mathcal{P}}^{ref}).$$

Using Theorem 3, the probabilistic perturbation bounds of x and $\delta U$ can be found from (16) and (18), replacing in (16) the perturbation norms ${\parallel \delta A\parallel }_F$ and and ${\parallel \delta B\parallel }_F$ by the quantities ${\parallel \delta A\parallel }_F/{\Xi }_A$ and $\parallel \delta B\parallel /{\Xi }_B$, respectively. In this way, we obtain the probabilistic asymptotic estimate

$${\Theta }_{max}^{est}(\tilde{\mathcal{X}},\mathcal{X})=arcsin(\parallel L_{k+1:n,1:kp}{\parallel }_2{\parallel \delta A\parallel }_F/\Xi )$$

(30)

of the maximum angle between the perturbed and unperturbed invariant subspace of dimension k. Comparing (30) and (21), we see that, for small angles, the probabilistic bound is approximately $\Xi$ times smaller than the deterministic one.

4. Discussion on the Results

The deterministic approach to the perturbation analysis of orthogonal canonical forms is already used in [24,25], but it is based on the implementation of the sensitivity estimates for the QR decomposition of a matrix, which does not allow us to find at once an estimate of the perturbation $\delta U$ and leads to conservative bounds. In this respect, the asymptotic bounds derived in Section 2 are strict, but they may also produce large overestimates in cases of high-order problems.

The proposed probabilistic perturbation bounds are slight modifications of the asymptotic bounds, which allows us to compute them simultaneously with the deterministic bounds. The probabilistic approach makes it possible to reduce the bounds considerably, producing realistic results with a high probability. This approach is justified in the case of high-order systems when the strict deterministic bounds are very conservative.

Consider briefly the numerical aspects of computing the asymptotic and probability estimates. The main computational operations in both cases are the reduction into the orthogonal canonical form, the computation of the matrix M and its inverse, and the calculation of the perturbation bounds. As mentioned above, the reduction into the canonical form is numerically stable due to the use of orthogonal transformations. As shown in [23], the lower triangular matrix M inversion is also stable. Finally, the perturbation bounds are computed by manipulating orthonormal vectors, which is always carried out with high precision. Hence, the asymptotic and probabilistic perturbation bounds are evaluated stably. A disadvantage of the method presented is the large number of operations for high-order systems due to the use of the Kronecker product. The inversion of a triangular matrix of order $p=n(n-1)/2$ requires $p^3/6\approx n^6/48$ flops, but this figure is largely overestimated since the matrix M is structured. The largest diagonal block of this matrix is of order $n-1$, and it is a strictly diagonal matrix whose inversion is straightforward.

5. A Numerical Example

In this example, we present the asymptotic deterministic perturbation bounds for the controllable subspaces, along with the probabilistic bounds obtained by using the Markoff inequality.

Example 1. 

Consider a single-input linear system with matrix A, taken as

$$A=Q_0{A}_0{Q}_0^{-1},B=Q_0{B}_0,$$

where

$$\begin{array}{ccc}\hfill A_0& =& \left[\begin{array}{ccccccc}p& 2p& 3p& 4p& \dots & (n-1)p& np\\ 5.0& (n+1)p& (n+2)p& (n+3)p& \dots & (2n-2)p& (2n-1)p\\ & 5.0& 2np& (2n+1)p& \dots & (3n-4)p& (3n-3)p\\ & & 5.0& (3n-1)p& \dots & (4n-6)p& (4n-6)p\\ & & & 5.0& \dots & ⋮& ⋮\\ & & & & \ddots & ((n^2+n)/2-2)p& ((n^2+n)/2-1)p\\ & & & & & 5.0& ((n^2+n)/2)p\end{array}\right],\hfill \\ \hfill p& =& 0.00001\hfill \\ \hfill B_0& =& {\left[\begin{array}{ccccccc}1& 0& 0& 0& \dots & 0& 0\end{array}\right]}^T,\hfill \end{array}$$

and the matrix $Q_0$ is constructed as [30]

$$\begin{array}{ccc}\hfill Q_0& =& H_2\mathsf{\Sigma }{H}_1,Q_0^{-1}=H_1{\mathsf{\Sigma }}^{-1}{H}_2,\hfill \\ \hfill H_1& =& I_n-2u{u}^T/n,H_2=I_n-2v{v}^T/n,\hfill \\ \hfill u& =& {[1,1,1,\dots ,1]}^T,v={[1,-1,1,\dots ,{(-1)}^{n-1}]}^T,\hfill \\ \hfill \mathsf{\Sigma }& =& \mathrm{diag}(1,\sigma ,{\sigma }^2,\dots ,{\sigma }^{n-1}),\hfill \end{array}$$

where $H_1,H_2$ are elementary reflections, σ is taken equal to $1.01$ and $\mathrm{cond}\left(Q_0\right)=2.678$. The parameter σ is used to change the conditioning of the matrix $Q_0$ and the parameter p is used to change the conditioning of the controllable subspaces.

The perturbation of A and B are taken as $\delta A={10}^{-8}{A}_r$, $\delta B={10}^{-8}{B}_r$, where $A_r$ and $B_r$ are matrices with random entries with normal distribution and ${\parallel \delta A\parallel }_F=9.91429\times {10}^{-7}$, ${\parallel \delta B\parallel }_F=9.50807\times {10}^{-8}$. The matrix M in (12) is of order $p=4950$ and its inverse satisfies $\parallel M^{-1}{\parallel }_2=1.88694\times {10}^4$. This shows that the problem for the sensitivity of the controllable subspaces is ill-conditioned since the perturbations of A and B can be magnified ${10}^4$ times in x and, consequently, in $\delta U$ and $\Theta (\tilde{\mathcal{X}},\mathcal{X})$. The minimum singular value of M equals $5.29957\times {10}^{-5}$, which shows that small perturbations may transform the given system into an uncontrollable one. The computation of the asymptotic estimate was carried out for approximately 15 s, of which 13 s were necessary to compute the matrix M and 1.45 s for its inversion. The computation of all 99 asymptotic bounds required 0.02 s.

In Figure 1, we show the mean value of the matrix $[\Delta a_{ij}/|\delta a_{ij}\left|\right]$ and the relative number $N\{\Delta a_{ij}\ge |\delta a_{ij}\left|\right\}/\left(n^2\right)$ of the entries of the matrix $\left|\delta A\right|$ for which $|\delta a_{ij}|\le |\Delta a_{ij}|$, and in Figure 2 the corresponding quantities for $\left|\delta B\right|$, obtained for the normal distribution of the entries of $\delta A$ and $\left|\delta B\right|$ and for different values of the desired probability, ${\mathcal{P}}^{ref}$. For the case of ${\mathcal{P}}^{ref}=90\%$, the size of the probability entry bound $\Delta a_{ij}$ decreases 10 times in comparison with the size of the entry bound ${\parallel \delta A\parallel }_F$, which allows us to decrease the mean value of the ratio $\Delta a_{ij}/\left|\delta a_{ij}\right|$ from $840.86$ to $84.086$ (

Table 1. The mean value of the ratios $[\Delta a_{ij}/|\delta a_{ij}\left|\right]$ and the relative number of entries for which $N\{\Delta a_{ij}>|\delta a_{ij}\left|\right\}/n^2$, obtained for different values of ${\mathcal{P}}^{ref}$, $n=100$.

${\mathcal{P}}^{\mathbf{ref}}$	$\mathbf{\Xi }$	$\mathit{E}\left\{\right[\mathbf{\Delta }{\mathit{a}}_{\mathbf{ij}}/|\mathit{\delta }{\mathit{a}}_{\mathbf{ij}}\left|\right]\}$	$\mathit{N}\{\mathbf{\Delta }{\mathit{a}}_{\mathbf{ij}}>|\mathit{\delta }{\mathit{a}}_{\mathbf{ij}}\left|\right\}/{\mathit{n}}^2$
%			%
$100.0$	$1.0000\times {10}^0$	$8.4086\times {10}^2$	$100.0000$
$90.0$	$1.0000\times {10}^1$	$8.4086\times {10}^1$	$100.0000$
$80.0$	$2.0000\times {10}^1$	$4.2043\times {10}^1$	$100.0000$
$70.0$	$3.0000\times {10}^1$	$2.8029\times {10}^1$	$99.8800$
$60.0$	$4.0000\times {10}^1$	$2.1022\times {10}^1$	$98.8200$
$50.0$	$5.0000\times {10}^1$	$1.6817\times {10}^1$	$98.8200$
$40.0$	$6.0000\times {10}^1$	$1.4014\times {10}^1$	$90.3400$

). For ${\mathcal{P}}^{ref}=40\%$, the probability bound $\Delta a_{ij}$ is 60 times smaller than the bound ${\parallel \delta A\parallel }_F$ and, even for this small, desired probability, the number of entries for which $|\delta a_{ij}|\le |\Delta a_{ij}|$ is still $90.34\%$. The corresponding quantities for $\delta B$ are shown in

Table 2. The mean value of the ratios $[\Delta b_{ij}/|\delta b_{ij}\left|\right]$ and the relative number of entries for which $N\{\Delta b_{ij}>|\delta b_{ij}\left|\right\}/n$, obtained for different values of ${\mathcal{P}}^{ref}$, $n=100$.

${\mathcal{P}}^{\mathbf{ref}}$	$\mathbf{\Xi }$	$\mathit{E}\left\{\right[\mathbf{\Delta }{\mathit{b}}_{\mathbf{ij}}/|\mathit{\delta }{\mathit{b}}_{\mathbf{ij}}\left|\right]\}$	$\mathit{N}\{\mathbf{\Delta }{\mathit{b}}_{\mathbf{ij}}>|\mathit{\delta }{\mathit{b}}_{\mathbf{ij}}\left|\right\}/{\mathit{n}}^2$
%			%
$100.0$	$1.0000\times {10}^0$	$4.3503\times {10}^1$	$100.0000$
$90.0$	$1.0000\times {10}^0$	$4.3503\times {10}^1$	$100.0000$
$80.0$	$2.0000\times {10}^0$	$2.1751\times {10}^1$	$100.0000$
$70.0$	$3.0000\times {10}^0$	$1.4501\times {10}^1$	$100.0000$
$60.0$	$4.0000\times {10}^0$	$1.0876\times {10}^1$	$97.0000$
$50.0$	$5.0000\times {10}^0$	$8.7005\times {10}^0$	$94.0000$
$40.0$	$6.0000\times {10}^0$	$7.2504\times {10}^0$	$88.0000$

.

In Figure 3, we compare the asymptotic bound $\delta U^{lin}$ and the probabilistic estimate $\delta U^{prob}$ with the actual component-wise perturbations $\left|\delta U\right|$ for normal distribution of perturbation entries and probabilities ${\mathcal{P}}^{ref}=90\%,80\%$ and $60\%$. The probabilistic bound $\delta U^{prob}$ is much tighter than the linear bound $\delta U^{lin}$ and the inequality $\left|\delta U\right|⪯\delta U^{prob}$ is satisfied for all entries and chosen probabilities. In particular, the size of the estimate $\delta U^{prob}$ is 10 times smaller than the linear estimate $\delta U^{lin}$ for ${\mathcal{P}}^{ref}=90\%$, 20 times for ${\mathcal{P}}^{ref}=80\%$ and 40 times for ${\mathcal{P}}^{ref}=60\%$. In Figure 4, we show the ratio $[\delta U_{ij}^{lin}/|\delta U_{ij}\left|\right]$ (left) and the ratio $[\delta U_{ij}^{prob}/|\delta U_{ij}\left|\right]$ (right) for ${\mathcal{P}}^{ref}=0.6$ for normal random distributions of the entries of the matrices A and B. Note that the mean value of the ratio for the probabilistic estimate is 40 times smaller than the mean value for the deterministic estimate, and its value for each i and j is greater than 1.

In Figure 5, we show the asymptotic bound $\delta {\Theta }_k^{lin}$ and the probabilistic estimate $\delta {\Theta }_k^{prob}$ along with the exact value $|\delta {\Theta }_k|$ of the maximum angle between the perturbed and unperturbed controllable subspace of dimension $k=1,2,\dots ,n-1$ for the same probabilities ${\mathcal{P}}^{ref}=90\%,80\%$ and $60\%$. The probability estimate satisfies $|\delta {\Theta }_k|<\delta {\Theta }_k^{est}$ for all $1\le k<100$. Note that the sensitivity of the controllable subspaces varies from ${10}^{-7}$ for $k=1$ to ${10}^{-4}$ for $k=75$.

6. Conclusions

In this paper, we present strict asymptotic perturbation bounds of the controllability subspaces of single-input linear systems implementing the splitting operator method. An advantage of the analysis is the possibility of determining the perturbation bounds of all controllability subspaces using a single matrix representing the linear approximation of the auxiliary matrix $\delta W=U^T\delta U$. Since the bounds obtained are overestimated, especially for high-order systems, we propose to use probabilistic bounds based on the Markoff inequality. The probabilistic bounds are found easily from the asymptotic bounds, allowing for a significant decrease in the sensitivity estimates with a guaranteed probability of near 1 in practice. This makes the probability bounds suitable for high-order problems. The analysis presented in this paper is also valid for linear discrete-time single-input systems with a state-space description

$$x_{k+1}=A{x}_k+B{u}_k.$$

By duality, the results of this paper can be also used to analyse the observability subspaces of linear single-input systems.

A possible extension of the presented results can be performed in the following directions. An important problem not treated in this paper is the sensitivity of the controllable subspaces of multi-input systems. The perturbation analysis of the orthogonal canonical form of such systems presented in [24,25], is concerned only with the changes in the form itself and does not deal with the changes in the corresponding orthogonal transformation matrix. A possible approach to the solution of this problem can be the use of component-wise estimates of the QR and SVD decomposition to find tight asymptotic estimates of the changes in the orthogonal transformation that can be applied to find perturbation bounds of the controllable subspaces. Since the evaluation of the new bounds requires a considerable volume of operations, it is appropriate to consider the implementation of parallel algorithms in the computation of the matrix M of the linear perturbation operator. Another possible research direction is to enhance the application of the probability perturbation estimates to solve other problems in control systems analysis.