Abstract
Global optimization is used in many practical and scientific problems. For this reason, various computational techniques have been developed. Particularly important are the evolutionary techniques, which simulate natural phenomena with the aim of detecting the global minimum in complex problems. A new evolutionary method is the Eel and Grouper Optimization (EGO) algorithm, inspired by the symbiotic relationship and foraging strategy of eels and groupers in marine ecosystems. In the present work, a series of improvements are proposed that aim both at the efficiency of the algorithm to discover the total minimum of multidimensional functions and at the reduction in the required execution time through the effective reduction in the number of functional evaluations. These modifications include the incorporation of a stochastic termination technique as well as an improvement sampling technique. The proposed modifications are tested on multidimensional functions available from the relevant literature and compared with other evolutionary methods.
1. Introduction
The goal of global optimization method is to discover the global minimum of a continuous multidimensional function, and it is defined as
with S as follows:
The function is defined as , and the set S denotes the bounds of x. In recent years, many researchers have published important reviews on global optimization [1,2,3]. Global optimization is a technique of vital importance in many fields of science and applications, as it allows us to find the optimal solution to problems with multiple local solutions. In mathematics [4,5,6,7], it is used to solve complex mathematical problems; in physics [8,9,10], it is used to analyze and improve models that describe natural phenomena; in chemistry [11,12,13], it analyzes and designs molecules and chemical diagnostic tools; and in medicine [14], it analyzes and designs therapeutic strategies and diagnostic tools.
The methods that aim to discover the global minimum has two main categories, deterministic [15,16,17] and stochastic [18,19,20]. In the first category, there are techniques aimed at identifying the total minimum with some certainty, such as interval methods [21,22], and they are usually distinguished by their complex implementation. The vast majority of global optimization algorithms belong to stochastic methods that have simpler implementation and can also be applied to large-scale problems. Recently, Sergeyev et al. [23] published a systematic comparison between deterministic and stochastic methods for global optimization problems.
An important branch of the stochastic methods are the evolutionary methods, that attempt to mimic a series of natural processes. Among these methods one can find the Differential Evolution method [24,25], Particle Swarm Optimization (PSO) methods [26,27,28], Ant Colony optimization methods [29,30], Genetic algorithms [31,32], the Exponential Distribution Optimizer [33], the Brain Storm Optimization method [34], etc. Additionally, since in recent years there has been an extremely widespread increase in parallel computing units, many research studies have proposed evolutionary methods that exploit modern parallel processing units [35,36,37].
Among the evolutionary techniques, one finds a large group of methods that have been explored intensively in recent years, the so-called swarm intelligence algorithms. These methods [38,39,40] are inspired by the collective behavior of swarms. These algorithms mimic systems in which candidate solutions interact locally and cooperate worldwide to discover the global minimum of any problem. These algorithms are very important tools for dealing with complex optimization problems in many applications.
In addition to the previously mentioned Particle Swarm Optimization and Ant Colony techniques that are also included in swarm intelligence algorithms, other methods that belong to this category are the Fast Bacterial Swarming Algorithm (FBSA) [41], the Fish Swarm Algorithm [42], the Dolphin Swarm Algorithm [43], the Whale Optimization Algorithm (WOA) algorithm [44,45,46,47], the Tunicate Swarm Algorithm [48], the Salp Swarm algorithm (SSA) algorithm [49,50,51,52], the Artificial Bee Colony algorithm [53], etc. These methods simulate a series of complex interactions between biological species [54], such as the following:
- 1.
- Naturalism, where two species can live without affecting each other.
- 2.
- Predation, where one creature dies by feeding another.
- 3.
- Parasitism, where one species can cause harm to another.
- 4.
- In competitive mode, the same or different organizations compete for resources.
- 5.
- Mutualism [55,56,57], when two organisms have a beneficial interaction.
Among swarm intelligence algorithms, one can find the Eel and Grouper (EGO) algorithm, which is inspired by the symbiotic interaction and foraging strategy of eels and groupers in marine ecosystems. Bshary et al. [58] consider that target ingestion, something observed in eels and groupers, is a necessary condition for interspecific cooperative hunting to occur. Intraspecific predation could increase the hunting efficiency of predators by mammals. According to Ali Mohammadzadeh and Seyedali Mirjalili the EGO optimization algorithm [59] generates a set of random answers, then stores the best answers found so far, allocates them to the target point, and changes the answers with them. As the number of iterations increases, the limits of the sine function are changed to enhance the phase of finding the best solution. This method stops the process when the iteration exceeds the maximum number. Because the EGO optimization algorithm generates and boosts a collection of random responses, it has the advantage of increased local optimum discovery and avoidance compared to individual methods. According to Ali Mohammadzadeh and Seyedali Mirjalili, the algorithm’s capabilities extend to NP-hard problems in wireless sensor networks [60], IoT [61], logistics [62], smart agriculture [63], bioinformatics [64], and machine learning [65] in various fields such as programming, image segmentation [66], electrical circuit design [67], feature selection, and 3D path planning in robotics [68].
This paper introduces some modifications to the EGO algorithm in order to improve its efficiency. The proposed amendments are presented below:
- The addition of a sampling technique based on the K-means method [69,70,71]. The sampling points facilitate finding the global minimum of the function in the most efficient way. Additionally, by applying this method, nearby points are discarded. The initialization of the population in evolutionary techniques is a crucial factor which can push these techniques to more efficiently locate the global minimum, and in this direction, a multitude of research works have been presented in recent years, such as the work of Maaranen et al. [72], where they apply quasi-random sequences to the initial population of a genetic algorithm. Likewise, Paul et al. [73] suggested a method for the initialization of the population of genetic algorithms using a Vari-begin and Vari-diversity (VV) seeding method. Ali et al. proposed a series of initialization methods for the Differential Evolution method [74]. A novel method that initializes the population of evolutionary algorithms using clustering and Cauchy deviates is suggested in the work of Bajer et al. [75]. A systematic review of initialization techniques for evolutionary algorithms can be found in the work of Kazimipour et al. [76].
- Using a termination technique that is developed with random measurements. Each time the algorithm is repeated, the minimum value is recorded. When this remains constant for a predefined number of iterations, the process is terminated. Therefore, the method terminates without wasting execution time in iterations, avoiding unnecessary consumption of computing resources. There are several methods found in the recent bibliography to terminate optimization methods. An overview of methods used to terminate evolutionary algorithms can be found in the work of Jain et al. [77]. Also, Zielinski et al. outlined some stopping rules used particularly in the Differential Evolution method [78]. Recently, Ghoreishi et al. published a literature study concerning various termination criteria on evolutionary algorithms [79]. Moreover, Ravber et al. performed extended research on the impact of the maximum number of iterations on the effectiveness of evolutionary algorithms [80].
- The application of randomness in the definition of the range of the positions of candidate solutions.
2. The Proposed Method
The main steps of the proposed algorithm are discussed in this section. Also, the mentioned modifications are fully described.
2.1. The Main Steps of the Algorithm
The EGO optimization algorithm starts by initializing a population consisting of “search agents” that search to find the optimal solution. At each iteration, the position of the “prey” (optimal solution) is calculated. Agent positions are adjusted based on random variables and their distance based on the optimal position. At the end of each iteration, the current solutions are compared, and it is decided whether the algorithm should continue or terminate. The steps of the proposed method are provided in Algorithm 1. Also, the algorithm is presented as a series of steps in the flowchart of Figure 1. Using a flowchart and algorithm simultaneously enhances visual perception and provides a detailed analysis of logic and processes.
| Algorithm 1 EGO algorithm |
|
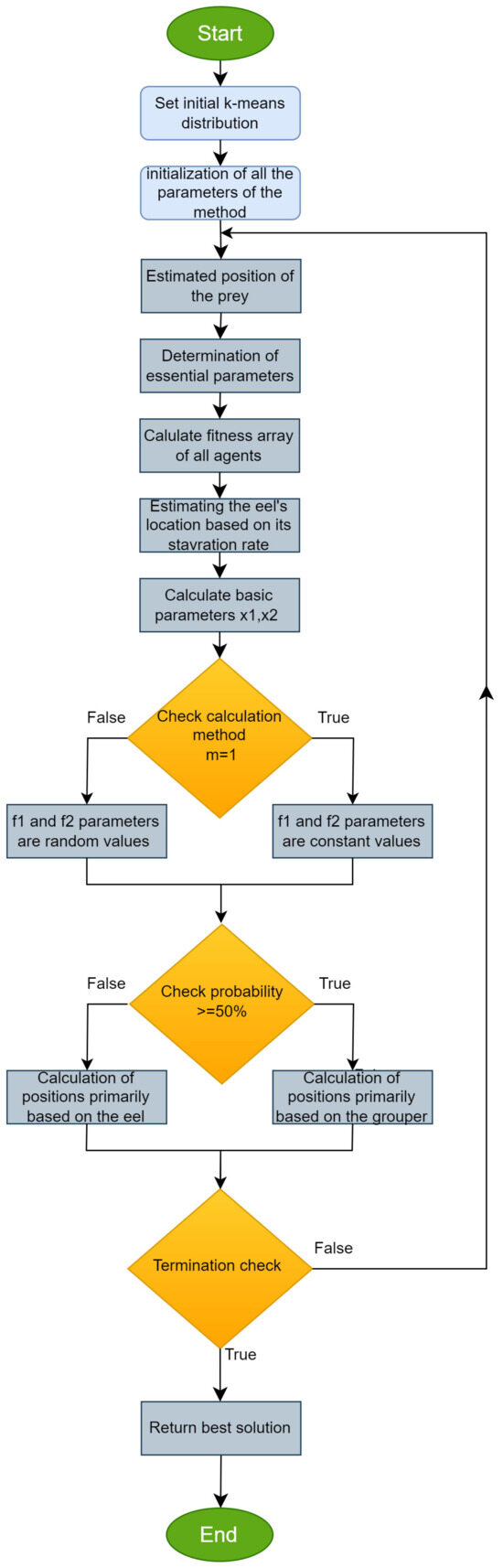
Figure 1.
Flowchart of the suggested global optimization procedure.
The main modifications introduced by the proposed algorithm are the following:
- 1.
- The members of the population are initialized using a procedure that incorporates the K-means algorithm. This procedure is fully described in Section 2.2. The purpose of this sampling technique is to produce points that are close to the local minima of the objective problem through systematic clustering. This potentially significantly reduces the time required to complete the technique. The samples used in the proposed algorithm are the calculated centers of the K-means algorithm. This sampling technique has also been utilized in some recent papers related to Global Optimization techniques, such as the extended version of the Optimal Foraging algorithm [82] or the new genetic algorithm proposed by Charilogis et al. [83].
- 2.
- The second modification proposed is the stopping rule invoked at every step of the algorithm. This rule measures the similarity between the best fitness values obtained between consecutive iterations of the algorithm. If this difference takes low values for a consecutive number of iterations, then the algorithm may not be able to find a lower value for the global minimum and should stop. This stopping rule has been applied in recent years in various methods such as in the work of Charilogis and Tsoulos, which presented an improved parallel PSO method [84], the work of Kyrou at al., which suggested an improved version of the Giant-Armadillo optimization method [85], or the recent work of Kyrou et al., which proposed an extended version of the Optimal Foraging Algorithm [82]. Of course, this method is general enough for application in any global optimization procedure.
- 3.
- The third modification is the m flag, which controls the randomness in the range of candidate solutions. When this value is set to 2, then the critical parameters are calculated using random numbers.
The overall procedure that outlines the basic steps of the method and the added modifications is shown in Algorithm 2.
| Algorithm 2 The basic steps of the algorithm accompanied with the proposed modifications |
|
2.2. The Used Sampling Procedure
The used sampling procedure incorporated in this work initially generates samples from the objective problem. Then, using the K-means method, only the estimated centers are selected as samples for the proposed algorithm. This technique, due to James MacQueen [71], is one of the best-known clustering algorithms in the broad research community, both in data analysis and in machine learning [86] and pattern recognition [87]. The algorithm aims to divide a data set into K clusters. The K-means algorithm tries to divide the data into groups in such a way that the internal points of each group are as close as possible to each other. At the same time, it tries to place the central points of each group in positions which are as representative as possible of the points of their group. Over the years, a series of variants of this algorithm have been proposed, such as the genetic K-means algorithm [88], the unsupervised K-means algorithm [89], the fixed-centered K-means algorithm [90], etc. A review of K-means clustering algorithms can be found in the work of Oti et al. [91]. Next, the basic steps of the algorithm are provided in Algorithm 3. A flowchart of the K-means procedure is also depicted in Figure 2.
| Algorithm 3 K-means algorithm |
|
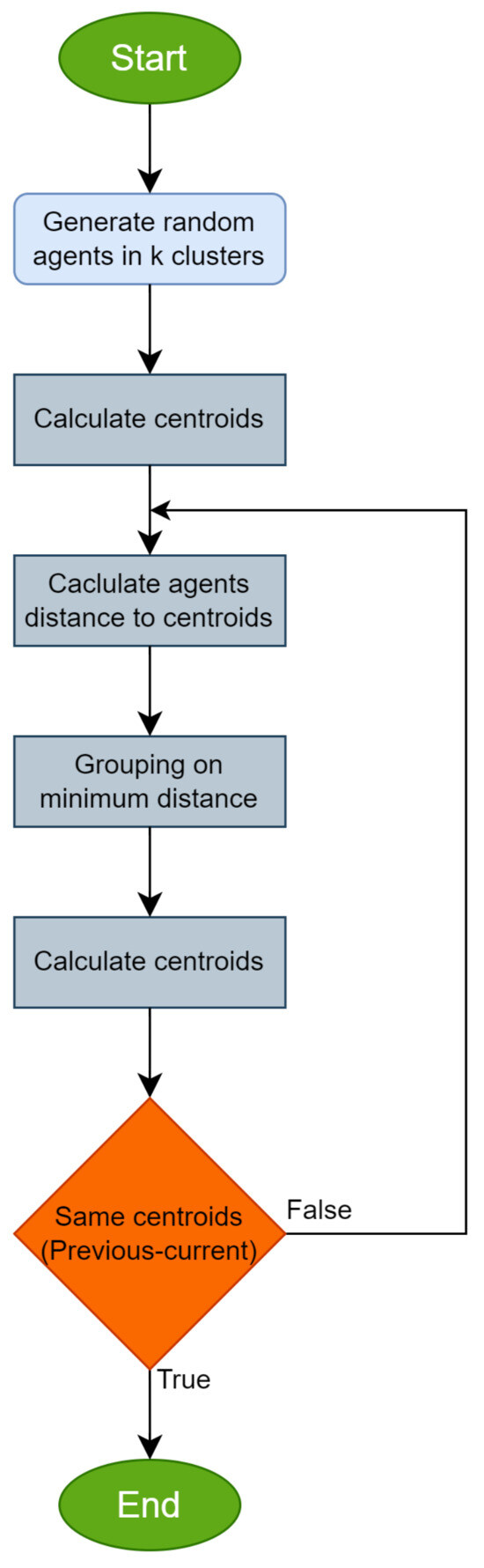
Figure 2.
The flowchart of the K-means procedure.
3. Results
This section begins with a detailed description of the functions that were used in the experiments, followed by an analysis of the experiments performed and comparisons with other global optimization techniques.
3.1. Test Functions
The test functions used in the experiments were suggested in a series of relative works [92,93] and they originated in a series of scientific fields. Also, these objective functions were studied in various publications [94,95,96,97,98]. Also, a series of function found in [99] were used as test functions. The used functions were defined as follows:
- Ackley’s function:with a = 20.0.
- Bf1 (Bohachevsky 1) function:
- Bf2 (Bohachevsky 2) function:
- Bf3 (Bohachevsky 3) function:
- Branin function:with .
- Camel function:
- Easom function:with
- Equal maxima function, defined as:
- Exponential function, with the following definition:The values were used in the conducted experiments.
- F9 test function:with
- Extended F10 function:
- F14 function:
- F15 function:
- F17 function:
- Five-uneven-peak trap function:
- Himmelblau’s function:with .
- Griewank2 function:
- Griewank10 function, given by the equationwith .
- Gkls function [100]: The function is a test function proposed in [100] with w local minima. The values , and were used in the conducted experiments.
- Goldstein and Price’s functionwith .
- Hansen’s function: , .
- Hartman 3 function:with and and
- Hartman 6 function:with and and
- Potential function: this function represents the energy of a molecular conformation of N atoms. The interaction of these atoms is determined by the Lennard–Jones potential [101]. The definition of this potential is:For the conducted experiments, the values were used.
- Rastrigin’s function.
- Rosenbrock function.The values were incorporated in the conducted experiments.
- Shekel 5 function.
with and
- Shekel 7 function.
with and .
- Shekel 10 function.
with and .
- Sinusoidal function, defined as:The values were incorporated in the conducted experiments.
- Schaffer’s function:
- Schwefel221 function:
- Schwefel222 function:
- Shubert function:with
- Sphere function:
- Test2N function:The values were incorporated for the conducted experiments.
- Test30N function:For the conducted experiments, the values were used.
- Uneven decreasing maxima function:
- Vincent’s function:with .
Also, the dimension for each problem, as used in the experiments, is shown in Table 1.

Table 1.
The dimension for every function used in the experiments.
3.2. Experimental Results
A series of global optimization methods were applied to the mentioned test functions. All experiments were performed 30 times using different seeds for the random generator and the average value of function calls was measured. The used software was coded in ANSI C++ using the freely available OPTIMUS optimization environment v1.0, available from https://github.com/itsoulos/OPTIMUS (accessed on 27 September 2024). The experiments were executed on a Debian Linux system with an AMD Ryzen 5950X processor and 128 GB of RAM. In all cases, the BFGS [102] local optimization method was used at the end of each global optimization technique to ensure that an actual minimum was discovered by the global optimization method. The values for all experimental parameters are shown in Table 2.

Table 2.
The values used for every parameter of the used algorithms.
The experimental results for the test functions and a series of optimization methods are shown in Table 3, where the following applies to this table:

Table 3.
Experimental results using the incorporated optimization methods. The numbers in parentheses denote the standard deviation for the number of function calls.
- The column function represents the used test function.
- The column genetic represents the usage of a genetic algorithm [31,32] into the test function. This genetic algorithm was equipped with chromosomes, and the maximum number of generations was set to . The modified version of Tsoulos [103] was used as a genetic algorithm here.
- The column PSO represents the incorporation of a Particle Swarm Optimizer [27,28] into each test function. This algorithm had particles, and the maximum number of allowed iterations was set to . For the conducted experiments, the improved PSO method proposed by Charilogis and Tsoulos was used [81].
- The column DE refers to the Differential Evolution method [24,25].
- The column EGO represents the initial method without the modifications suggested in this work.
- The column EEGO represents the usage of the proposed method. The corresponding settings are shown in Table 2.
- The row sum is used to measure the total function calls for all problems.
- If a method failed to find the global minimum over all runs, this was noted in the corresponding table with a percentage enclosed in parentheses next to the average function calls.
The same termination method, as detailed in Section 2.1, was used in all global optimization techniques in order to be able to evaluate all techniques fairly and with the same rules. In Figure 3, we present the total function calls of every optimization method graphically. The proposed method had excellent results compared to the other optimization techniques according to the experiments conducted. As we can observe, it had the least number of calls among all other techniques.
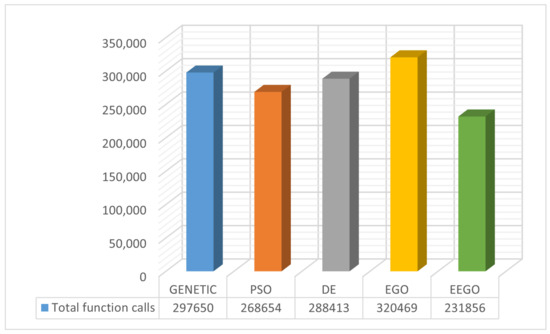
Figure 3.
Total function calls for the considered optimization methods. The numbers represent the sum of function calls for each mentioned method.
Furthermore, as the experimental results clearly indicate, the modified version outperformed the original EGO method in terms of average and function calls and this is depicted in Figure 4, which outlines box plots for the mentioned methods.
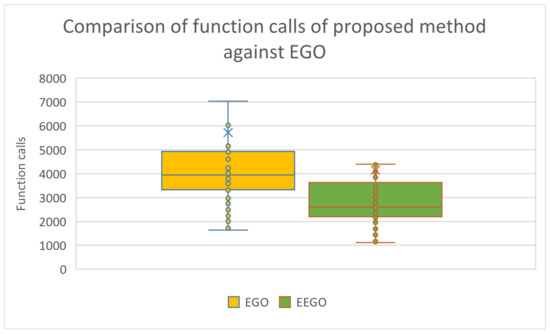
Figure 4.
Box plot used to compare the EGO method and the modified version as suggested in the current work.
A box plot between all the used methods is depicted in Figure 5.
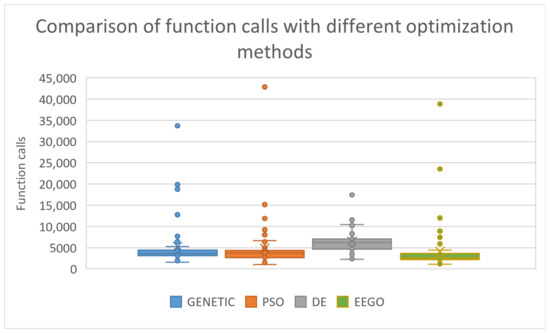
Figure 5.
Comparison of average function calls for the incorporated optimization methods, using the proposed initial distribution.
Moreover, a statistical comparison of all used methods is outlined in Figure 6.
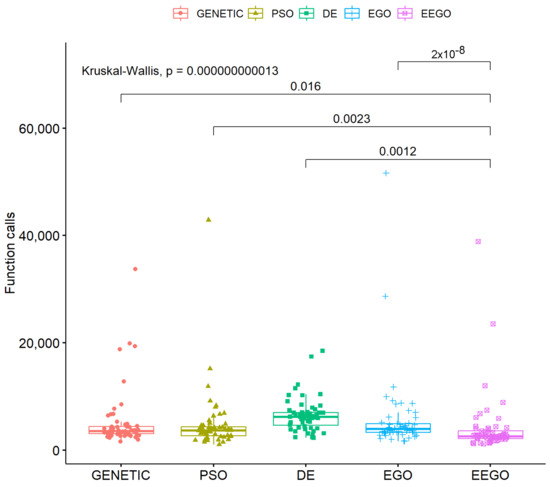
Figure 6.
Statistical comparison of all used methods.
According to Table 3 and Figure 6, the EEGO method proved to be more efficient, as it consistently required fewer function calls compared to the DE, PSO, genetic, and EGO methods, and these differences were statistically significant (p < 0.05). For example, in the Ackley function, EEGO required 4199 calls, while DE required 10.220, PSO 6885, and the genetic algorithm 6749, with a p-value < 0.05, showing that EEGO is significantly more efficient. Similar examples are observed in the BF1 function, where EEGO had 3228 calls, while DE required 8268 (p < 0.05), and in the Branin function, where EEGO required 1684 calls, compared to 4101 for DE (p < 0.05). Overall, EEGO showed the best performance in most cases, with statistically significant differences in function calls, as it effectively reduced the number of calls compared to the other methods. While PSO and the genetic algorithm performed better than DE in some instances, they still lagged significantly behind EEGO. The p-values confirmed that these differences were statistically significant, indicating that EEGO was the most efficient method overall.
One more experiment was performed with the ultimate goal of measuring the importance of K-means sampling in the proposed method. The results for this experiment are outlined in Table 4 and the following sampling methods were used:

Table 4.
A series of sampling techniques was used in the proposed method. The number in parentheses denotes the standard deviation for the number of function calls.
- 1.
- The column uniform represents the usage of uniform sampling in the current method.
- 2.
- The column triangular stands for the usage of the triangular distribution [104] for sampling.
- 3.
- The column Maxwell represents for the application of the Maxwell distribution [105] to produce initial samples for the used method.
- 4.
- The column K-means represents the usage of the method described in Section 2.2 to produce initial samples for the used method.
The initial distributions play a critical role in a wide range of applications, including optimization, statistical analysis, and machine learning. Table 4 presents the proposed distribution alongside other established distributions. The uniform distribution is widely used due to its ability to evenly cover the search space, making it suitable for initializing optimization algorithms [106]. The triangular distribution is applied in scenarios where there is knowledge of the bounds and the most probable value of a phenomenon, making it useful in risk management models [107]. The Maxwell distribution, although originating from physics, finds applications in simulating communication networks, where data transfer speeds can be modeled as random variables [108]. Finally, the K-means method is used for data clustering, with K-means++ initialization offering improved performance compared to random distributions, particularly in high-dimensional problems [109]. As observed in Table 4, the choice of an appropriate initial distribution can significantly affect the performance of the algorithms that utilize them.
In the scatter plot in Figure 7, the critical parameter “p” was found to be very small, leading to the rejection of the null hypothesis and indicating that the experimental results were highly significant.
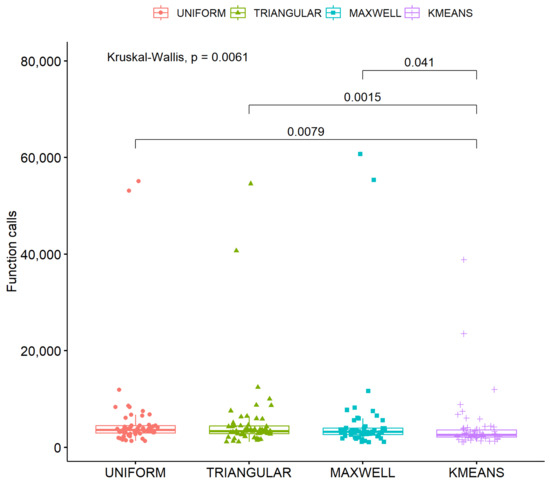
Figure 7.
Scatter plot for different initial distributions.
In addition, in order to investigate the impact that the choice of sampling method had on the optimization method, an additional experiment was performed, in which the execution time of the proposed method was recorded with different sampling techniques for the ELP function, whose dimension was varied between 5 and 50. This function is defined as:
where the parameter n defines the dimension of the function. The results from this experiment are graphically outlined in Figure 8.
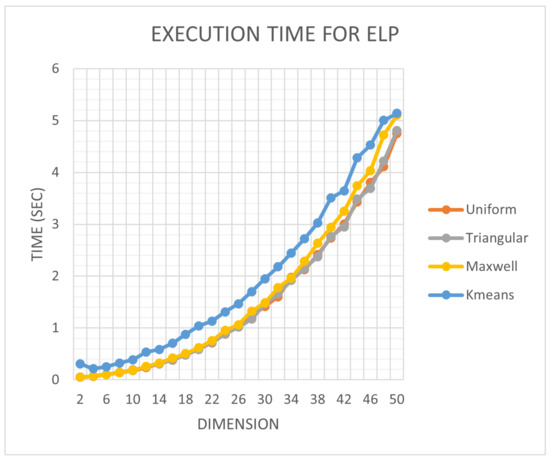
Figure 8.
Time comparison for the ELP function and the proposed optimization method using the four sampling techniques mentioned before. The time depicted in the figure is the sum of the execution times for 30 independent runs.
The proposed sampling method significantly increased the required execution time, since an iterative process was required before starting the algorithm. The next sampling procedure in required execution time appeared to be the Maxwell sampling, but it was not significantly different compared to uniform sampling.
4. Conclusions
The article proposed some modifications to the EEGO optimization method, aimed to improve the overall performance and reduce the needed function calls to discover the global minimum. The first modification concerned the application of a sampling technique based on the K-means method. This technique allowed us to significantly minimize the number of function calls to find the global minimum and further improved the accuracy with which it is located. In particular, the application of the K-means method accelerated the finding of a solution, as it more efficiently located the points of interest in the search space and led to the fastest convergence to the global minimum. Compared to other methods based on random distributions, the proposed technique proved its superiority, especially in multidimensional and complex functions.
The second proposed amendment concerned the termination rule based on the similarity of solutions during iterations. The main purpose of this rule was to stop the optimization process when the iterated solutions were too close to each other, thus preventing pointless iterations that did not provide any significant improvement. It therefore avoided wasting computing time in cases where the process was already very close to the desired result. The use of the termination rule significantly improved the efficiency of the algorithm.
Furthermore, one more improvement was suggested in this research paper. This optimization added randomness to the generation of new candidate solutions from the old ones aiming to better explore the search space of the objective problem in search of the global minimum.
To verify the effectiveness of the new method, a series of experiments were performed on a large group of objective problems from the recent literature. In these experiments both the efficiency and speed improvement of the original technique was measured, and a comparison of the speed of the new method was made in relation to other known techniques from the relevant literature. Furthermore, a series of extensive experiments were carried out to study the dynamics of the proposed initialization technique as well as the additional time required by its implementation. A number of useful conclusions were drawn from the execution of these experiments. First of all, the new method significantly improved the efficiency and speed of the original method. Furthermore, the experiments revealed that the new method required a significantly lower number of function calls on average than other global optimization methods. In addition, the sampling method proved to be highly efficient in finding the global minimum and significantly reduced the required number of function calls compared to other initialization techniques. The additional time required by the new initialization method was noticeable compared to other techniques, but the gains it brought were equally significant.
Future extensions of the proposed technique could be the use of parallel programming techniques to speed up the overall process, such as the MPI programming technique [110] or the integration of the OpenMP library [111], as well as the use of other termination techniques that could potentially speed up the termination of the method.
Author Contributions
G.K., V.C. and I.G.T. created the software. G.K. conducted the experiments, using a series of objective functions from various sources. V.C. conducted the needed statistical tests. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been financed by the European Union: Next Generation EU through the Program Greece 2.0 National Recovery and Resilience Plan, under the call RESEARCH–CREATE–INNOVATE, project name “iCREW: Intelligent small craft simulator for advanced crew training using Virtual Reality techniques” (project code: TAEDK-06195).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Törn, A.; Ali, M.M.; Viitanen, S. Stochastic global optimization: Problem classes and solution techniques. J. Glob. Optim. 1999, 14, 437–447. [Google Scholar] [CrossRef]
- Floudas, C.A.; Pardalos, P.M. (Eds.) State of the Art in Global Optimization: Computational Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Horst, R.; Pardalos, P.M. Handbook of Global Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 2. [Google Scholar]
- Intriligator, M.D. Mathematical Optimization and Economic Theory; Society for Industrial and Applied Mathematics, SIAM: New Delhi, India, 2002. [Google Scholar]
- Cánovas, M.J.; Kruger, A.; Phu, H.X.; Théra, M. Marco A. López, a Pioneer of Continuous Optimization in Spain. Vietnam. J. Math. 2020, 48, 211–219. [Google Scholar] [CrossRef]
- Mahmoodabadi, M.J.; Nemati, A.R. A novel adaptive genetic algorithm for global optimization of mathematical test functions and real-world problems. Eng. Sci. Technol. Int. J. 2016, 19, 2002–2021. [Google Scholar] [CrossRef]
- Li, J.; Xiao, X.; Boukouvala, F.; Floudas, C.A.; Zhao, B.; Du, G.; Su, X.; Liu, H. Data-driven mathematical modeling and global optimization framework for entire petrochemical planning operations. AIChE J. 2016, 62, 3020–3040. [Google Scholar] [CrossRef]
- Iuliano, E. Global optimization of benchmark aerodynamic cases using physics-based surrogate models. Aerosp. Sci. Technol. 2017, 67, 273–286. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Yang, L.; Robin, D.; Sannibale, F.; Steier, C.; Wan, W. Global optimization of an accelerator lattice using multiobjective genetic algorithms. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrom. Detect. Assoc. Equip. 2009, 609, 50–57. [Google Scholar] [CrossRef]
- Heiles, S.; Johnston, R.L. Global optimization of clusters using electronic structure methods. Int. J. Quantum Chem. 2013, 113, 2091–2109. [Google Scholar] [CrossRef]
- Shin, W.H.; Kim, J.K.; Kim, D.S.; Seok, C. GalaxyDock2: Protein–ligand docking using beta-complex and global optimization. J. Comput. Chem. 2013, 34, 2647–2656. [Google Scholar] [CrossRef] [PubMed]
- Liwo, A.; Lee, J.; Ripoll, D.R.; Pillardy, J.; Scheraga, H.A. Protein structure prediction by global optimization of a potential energy function. Proc. Natl. Acad. Sci. USA 1999, 96, 5482–5485. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hosney, M.E.; Mohamed, W.M.; Ali, A.A.; Younis, E.M. Fuzzy-based hunger games search algorithm for global optimization and feature selection using medical data. Neural Comput. Appl. 2023, 35, 5251–5275. [Google Scholar] [CrossRef]
- Ion, I.G.; Bontinck, Z.; Loukrezis, D.; Römer, U.; Lass, O.; Ulbrich, S.; Schöps, S.; De Gersem, H. Robust shape optimization of electric devices based on deterministic optimization methods and finite-element analysis with affine parametrization and design elements. Electr. Eng. 2018, 100, 2635–2647. [Google Scholar] [CrossRef]
- Cuevas-Velásquez, V.; Sordo-Ward, A.; García-Palacios, J.H.; Bianucci, P.; Garrote, L. Probabilistic model for real-time flood operation of a dam based on a deterministic optimization model. Water 2020, 12, 3206. [Google Scholar] [CrossRef]
- Pereyra, M.; Schniter, P.; Chouzenoux, E.; Pesquet, J.C.; Tourneret, J.Y.; Hero, A.O.; McLaughlin, S. A survey of stochastic simulation and optimization methods in signal processing. IEEE J. Sel. Top. Signal Process. 2015, 10, 224–241. [Google Scholar] [CrossRef]
- Hannah, L.A. Stochastic optimization. Int. Encycl. Soc. Behav. Sci. 2015, 2, 473–481. [Google Scholar]
- Kizielewicz, B.; Sałabun, W. A new approach to identifying a multi-criteria decision model based on stochastic optimization techniques. Symmetry 2020, 12, 1551. [Google Scholar] [CrossRef]
- Chen, T.; Sun, Y.; Yin, W. Solving stochastic compositional optimization is nearly as easy as solving stochastic optimization. IEEE Trans. Signal Process. 2021, 69, 4937–4948. [Google Scholar] [CrossRef]
- Wolfe, M.A. Interval methods for global optimization. Appl. Math. Comput. 1996, 75, 179–206. [Google Scholar]
- Csendes, T.; Ratz, D. Subdivision direction selection in interval methods for global optimization. SIAM J. Numer. Anal. 1997, 34, 922–938. [Google Scholar] [CrossRef]
- Sergeyev, Y.D.; Kvasov, D.E.; Mukhametzhanov, M.S. On the efficiency of nature-inspired metaheuristics in expensive global optimization with limited budget. Sci. Rep. 2018, 8, 453. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Liu, J.; Lampinen, J. A fuzzy adaptive differential evolution algorithm. Soft Comput. 2005, 9, 448–462. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, USA, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization: An overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Trelea, I.C. The particle swarm optimization algorithm: Convergence analysis and parameter selection. Inf. Process. Lett. 2003, 85, 317–325. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Socha, K.; Dorigo, M. Ant colony optimization for continuous domains. Eur. J. Oper. Res. 2008, 185, 1155–1173. [Google Scholar] [CrossRef]
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Publishing Company: Reading, MA, USA, 1989. [Google Scholar]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Abdel-Basset, M.; El-Shahat, D.; Jameel, M.; Abouhawwash, M. Exponential distribution optimizer (EDO): A novel math-inspired algorithm for global optimization and engineering problems. Artif. Intell. Rev. 2023, 56, 9329–9400. [Google Scholar] [CrossRef]
- Ma, L.; Cheng, S.; Shi, Y. Enhancing learning efficiency of brain storm optimization via orthogonal learning design. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6723–6742. [Google Scholar] [CrossRef]
- Zhou, Y.; Tan, Y. GPU-based parallel particle swarm optimization. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1493–1500. [Google Scholar]
- Dawson, L.; Stewart, I. Improving Ant Colony Optimization performance on the GPU using CUDA. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1901–1908. [Google Scholar]
- Barkalov, K.; Gergel, V. Parallel global optimization on GPU. J. Glob. Optim. 2016, 66, 3–20. [Google Scholar] [CrossRef]
- Hassanien, A.E.; Emary, E. Swarm Intelligence: Principles, Advances, and Applications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Tang, J.; Liu, G.; Pan, Q. A review on representative swarm intelligence algorithms for solving optimization problems: Applications and trends. IEEE/CAA J. Autom. Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Brezočnik, L.; Fister, I., Jr.; Podgorelec, V. Swarm intelligence algorithms for feature selection: A review. Appl. Sci. 2018, 8, 1521. [Google Scholar] [CrossRef]
- Chu, Y.; Mi, H.; Liao, H.; Ji, Z.; Wu, Q.H. A fast bacterial swarming algorithm for high-dimensional function optimization. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 3135–3140. [Google Scholar]
- Neshat, M.; Sepidnam, G.; Sargolzaei, M.; Toosi, A.N. Artificial fish swarm algorithm: A survey of the state-of-the-art, hybridization, combinatorial and indicative applications. Artif. Intell. Rev. 2014, 42, 965–997. [Google Scholar] [CrossRef]
- Wu, T.Q.; Yao, M.; Yang, J.H. Dolphin swarm algorithm. Front. Inf. Technol. Electron. Eng. 2016, 17, 717–729. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Nasiri, J.; Khiyabani, F.M. A whale optimization algorithm (WOA) approach for clustering. Cogent Math. Stat. 2018, 5, 1483565. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Gholizadeh, H. A comprehensive survey: Whale Optimization Algorithm and its applications. Swarm Evol. Comput. 2019, 48, 1–24. [Google Scholar] [CrossRef]
- Wang, J.; Bei, J.; Song, H.; Zhang, H.; Zhang, P. A whale optimization algorithm with combined mutation and removing similarity for global optimization and multilevel thresholding image segmentation. Appl. Soft Comput. 2023, 137, 110130. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.L.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Wan, Y.; Mao, M.; Zhou, L.; Zhang, Q.; Xi, X.; Zheng, C. A novel nature-inspired maximum power point tracking (MPPT) controller based on SSA-GWO algorithm for partially shaded photovoltaic systems. Electronics 2019, 8, 680. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Bairathi, D.; Gopalani, D. Salp swarm algorithm (SSA) for training feed-forward neural networks. In Proceedings of the Soft Computing for Problem Solving: SocProS, Bhubaneswar, India, 23–24 December 2017; Springer: Singapore, 2019; Volume 1, pp. 521–534. [Google Scholar]
- Abualigah, L.; Shehab, M.; Alshinwan, M.; Alabool, H. Salp swarm algorithm: A comprehensive survey. Neural Comput. Appl. 2020, 32, 11195–11215. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A comparative study of artificial bee colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Abdullahi, M.; Ngadi, M.A.; Dishing, S.I.; Abdulhamid, S.I.M.; Usman, M.J. A survey of symbiotic organisms search algorithms and applications. Neural Comput. Appl. 2020, 32, 547–566. [Google Scholar] [CrossRef]
- Wang, Y.; DeAngelis, D.L. A mutualism-parasitism system modeling host and parasite withmutualism at low density. Math. Biosci. Eng. 2012, 9, 431–444. [Google Scholar]
- Aubier, T.G.; Joron, M.; Sherratt, T.N. Mimicry among unequally defended prey should be mutualistic when predators sample optimally. Am. Nat. 2017, 189, 267–282. [Google Scholar] [CrossRef]
- Addicott, J.F. Competition in mutualistic systems. In The biology of Mutualism: Ecology and Evolution; Croom Helm: London, UK, 1985; pp. 217–247. [Google Scholar]
- Bshary, R.; Hohner, A.; Ait-el-Djoudi, K.; Fricke, H. Interspecific communicative and coordinated hunting between groupers and giant moray eels in the Red Sea. Plos Biol. 2006, 4, e431. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Mirjalili, S. Eel and Grouper Optimizer: A Nature-Inspired Optimization Algorithm; Springer Science+Business Media, LLC.: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Gogu, A.; Nace, D.; Dilo, A.; Meratnia, N.; Ortiz, J.H. Review of optimization problems in wireless sensor networks. In Telecommunications Networks—Current Status and Future Trends; BoD: Norderstedt, Germany, 2012; pp. 153–180. [Google Scholar]
- Goudos, S.K.; Boursianis, A.D.; Mohamed, A.W.; Wan, S.; Sarigiannidis, P.; Karagiannidis, G.K.; Suganthan, P.N. Large Scale Global Optimization Algorithms for IoT Networks: A Comparative Study. In Proceedings of the 2021 17th International Conference on Distributed Computing in Sensor Systems (DCOSS), Pafos, Cyprus, 14–16 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 272–279. [Google Scholar]
- Arayapan, K.; Warunyuwong, P. Logistics Optimization: Application of Optimization Modeling in Inbound Logistics. Master’s Thesis, Malardalen University, Västerås, Sweeden, 2009. [Google Scholar]
- Singh, S.P.; Dhiman, G.; Juneja, S.; Viriyasitavat, W.; Singal, G.; Kumar, N.; Johri, P. A New QoS Optimization in IoT-Smart Agriculture Using Rapid Adaption Based Nature-Inspired Approach. IEEE Internet Things J. 2023, 11, 5417–5426. [Google Scholar] [CrossRef]
- Wang, H.; Ersoy, O.K. A novel evolutionary global optimization algorithm and its application in bioinformatics. ECE Tech. Rep. 2005, 65. Available online: https://docs.lib.purdue.edu/cgi/viewcontent.cgi?article=1065&context=ecetr (accessed on 7 September 2024).
- Cassioli, A.; Di Lorenzo, D.; Locatelli, M.; Schoen, F.; Sciandrone, M. Machine learning for global optimization. Comput. Optim. Appl. 2012, 51, 279–303. [Google Scholar] [CrossRef]
- Houssein, E.H.; Helmy, B.E.D.; Elngar, A.A.; Abdelminaam, D.S.; Shaban, H. An improved tunicate swarm algorithm for global optimization and image segmentation. IEEE Access 2021, 9, 56066–56092. [Google Scholar] [CrossRef]
- Torun, H.M.; Swaminathan, M. High-dimensional global optimization method for high-frequency electronic design. IEEE Trans. Microw. Theory Tech. 2019, 67, 2128–2142. [Google Scholar] [CrossRef]
- Wang, L.; Kan, J.; Guo, J.; Wang, C. 3D path planning for the ground robot with improved ant colony optimization. Sensors 2019, 19, 815. [Google Scholar] [CrossRef] [PubMed]
- Arora, P.; Varshney, S. Analysis of k-means and k-medoids algorithm for big data. Procedia Comput. Sci. 2016, 78, 507–512. [Google Scholar] [CrossRef]
- Ahmed, M.; Seraj, R.; Islam, S.M.S. The k-means algorithm: A comprehensive survey and performance evaluation. Electronics 2020, 9, 1295. [Google Scholar] [CrossRef]
- MacQueen, J.B. Some Methods for classification and Analysis of Multivariate Observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 21 June–18 July 1967; pp. 281–297. [Google Scholar]
- Maaranen, H.; Miettinen, K.; Mäkelä, M.M. Quasi-random initial population for genetic algorithms. Comput. Math. Appl. 2004, 47, 1885–1895. [Google Scholar] [CrossRef]
- Paul, P.V.; Dhavachelvan, P.; Baskaran, R. A novel population initialization technique for genetic algorithm. In Proceedings of the 2013 International Conference on Circuits, Power and Computing Technologies (ICCPCT), Nagercoil, India, 20–21 March 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1235–1238. [Google Scholar]
- Ali, M.; Pant, M.; Abraham, A. Unconventional initialization methods for differential evolution. Appl. Math. Comput. 2013, 219, 4474–4494. [Google Scholar] [CrossRef]
- Bajer, D.; Martinović, G.; Brest, J. A population initialization method for evolutionary algorithms based on clustering and Cauchy deviates. Expert Syst. Appl. 2016, 60, 294–310. [Google Scholar] [CrossRef]
- Kazimipour, B.; Li, X.; Qin, A.K. A review of population initialization techniques for evolutionary algorithms. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2585–2592. [Google Scholar]
- Jain, B.J.; Pohlheim, H.; Wegener, J. On termination criteria of evolutionary algorithms. In Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation, Francisc, CA, USA, 7–11 July 2001; p. 768. [Google Scholar]
- Zielinski, K.; Weitkemper, P.; Laur, R.; Kammeyer, K.D. Examination of stopping criteria for differential evolution based on a power allocation problem. In Proceedings of the 10th International Conference on Optimization of Electrical and Electronic Equipment, Brasov, Romania, 18–20 May 2006; Volume 3, pp. 149–156. [Google Scholar]
- Ghoreishi, S.N.; Clausen, A.; Jørgensen, B.N. Termination Criteria in Evolutionary Algorithms: A Survey. In Proceedings of the IJCCI, Funchal, Portugal, 1–3 November 2017; pp. 373–384. [Google Scholar]
- Ravber, M.; Liu, S.H.; Mernik, M.; Črepinšek, M. Maximum number of generations as a stopping criterion considered harmful. Appl. Soft Comput. 2022, 128, 109478. [Google Scholar] [CrossRef]
- Charilogis, V.; Tsoulos, I.G. Toward an ideal particle swarm optimizer for multidimensional functions. Information 2022, 13, 217. [Google Scholar] [CrossRef]
- Kyrou, G.; Charilogis, V.; Tsoulos, I.G. EOFA: An Extended Version of the Optimal Foraging Algorithm for Global Optimization Problems. Computation 2024, 12, 158. [Google Scholar] [CrossRef]
- Charilogis, V.; Tsoulos, I.G.; Stavrou, V.N. An Intelligent Technique for Initial Distribution of Genetic Algorithms. Axioms 2023, 12, 980. [Google Scholar] [CrossRef]
- Charilogis, V.; Tsoulos, I.G.; Tzallas, A. An improved parallel particle swarm optimization. SN Comput. Sci. 2023, 4, 766. [Google Scholar] [CrossRef]
- Kyrou, G.; Charilogis, V.; Tsoulos, I.G. Improving the Giant-Armadillo Optimization Method. Analytics 2024, 3, 225–240. [Google Scholar] [CrossRef]
- Li, Y.; Wu, H. A clustering method based on K-means algorithm. Phys. Procedia 2012, 25, 1104–1109. [Google Scholar] [CrossRef]
- Ali, H.H.; Kadhum, L.E. K-means clustering algorithm applications in data mining and pattern recognition. Int. J. Sci. Res. (IJSR) 2017, 6, 1577–1584. [Google Scholar]
- Krishna, K.; Murty, M.N. Genetic K-means algorithm. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1999, 29, 433–439. [Google Scholar] [CrossRef]
- Sinaga, K.P.; Yang, M.S. Unsupervised K-means clustering algorithm. IEEE Access 2020, 8, 80716–80727. [Google Scholar] [CrossRef]
- Ay, M.; Özbakır, L.; Kulluk, S.; Gülmez, B.; Öztürk, G.; Özer, S. FC-Kmeans: Fixed-centered K-means algorithm. Expert Syst. Appl. 2023, 211, 118656. [Google Scholar] [CrossRef]
- Oti, E.U.; Olusola, M.O.; Eze, F.C.; Enogwe, S.U. Comprehensive review of K-Means clustering algorithms. Criterion 2021, 12, 22–23. [Google Scholar] [CrossRef]
- Ali, M.M.; Khompatraporn, C.; Zabinsky, Z.B. A numerical evaluation of several stochastic algorithms on selected continuous global optimization test problems. J. Glob. Optim. 2005, 31, 635–672. [Google Scholar] [CrossRef]
- Floudas, C.A.; Pardalos, P.M.; Adjiman, C.; Esposito, W.R.; Gümüs, Z.H.; Harding, S.T.; Klepeis, J.L.; Meyer, C.A.; Schweiger, C.A. Handbook of Test Problems in Local and Global Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 33. [Google Scholar]
- Ali, M.M.; Kaelo, P. Improved particle swarm algorithms for global optimization. Appl. Math. Comput. 2008, 196, 578–593. [Google Scholar] [CrossRef]
- Koyuncu, H.; Ceylan, R. A PSO based approach: Scout particle swarm algorithm for continuous global optimization problems. J. Comput. Des. Eng. 2019, 6, 129–142. [Google Scholar] [CrossRef]
- Siarry, P.; Berthiau, G.; Durdin, F.; Haussy, J. Enhanced simulated annealing for globally minimizing functions of many-continuous variables. ACM Trans. Math. Softw. (TOMS) 1997, 23, 209–228. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Lagaris, I.E. GenMin: An enhanced genetic algorithm for global optimization. Comput. Phys. Commun. 2008, 178, 843–851. [Google Scholar] [CrossRef]
- LaTorre, A.; Molina, D.; Osaba, E.; Poyatos, J.; Del Ser, J.; Herrera, F. A prescription of methodological guidelines for comparing bio-inspired optimization algorithms. Swarm Evol. Comput. 2021, 67, 100973. [Google Scholar] [CrossRef]
- Li, X.; Engelbrecht, A.; Epitropakis, M.G. Benchmark Functions for CEC’2013 Special Session and Competition on Niching Methods for Multimodal Function Optimization; Technology Report; RMIT University, Evolutionary Computation and Machine Learning Group: Melbourne, Australia, 2013. [Google Scholar]
- Gaviano, M.; Kvasov, D.E.; Lera, D.; Sergeyev, Y.D. Algorithm 829: Software for generation of classes of test functions with known local and global minima for global optimization. ACM Trans. Math. Softw. (TOMS) 2003, 29, 469–480. [Google Scholar] [CrossRef]
- Jones, J.E. On the Determination of Molecular Fields.—II. From the Equation of State of a Gas; Series A, Containing Papers of a Mathematical and Physical Character; Royal Society: London, UK, 1924; Volume 106, pp. 463–477. [Google Scholar]
- Powell, M.J.D. A Tolerant Algorithm for Linearly Constrained Optimization Calculations. Math. Program 1989, 45, 547–566. [Google Scholar] [CrossRef]
- Tsoulos, I.G. Modifications of real code genetic algorithm for global optimization. Appl. Math. Comput. 2008, 203, 598–607. [Google Scholar] [CrossRef]
- Stein, W.E.; Keblis, M.F. A new method to simulate the triangular distribution. Math. Comput. Model. 2009, 49, 1143–1147. [Google Scholar] [CrossRef]
- Sharma, V.K.; Bakouch, H.S.; Suthar, K. An extended Maxwell distribution: Properties and applications. Commun. Stat. Simul. Comput. 2017, 46, 6982–7007. [Google Scholar] [CrossRef]
- Sengupta, R.; Pal, M.; Saha, S.; Bandyopadhyay, S. Uniform distribution driven adaptive differential evolution. Appl. Intell. 2020, 50, 3638–3659. [Google Scholar] [CrossRef]
- Glickman, T.S.; Xu, F. Practical risk assessment with triangular distributions. Int. J. Risk Assess. Manag. 2009, 13, 313–327. [Google Scholar] [CrossRef]
- Ishaq, A.I.; Abiodun, A.A. The Maxwell–Weibull distribution in modeling lifetime datasets. Ann. Data Sci. 2020, 7, 639–662. [Google Scholar] [CrossRef]
- Beretta, L.; Cohen-Addad, V.; Lattanzi, S.; Parotsidis, N. Multi-swap k-means++. Adv. Neural Inf. Process. Syst. 2023, 36, 26069–26091. [Google Scholar]
- Gropp, W.; Lusk, E.; Doss, N.; Skjellum, A. A high-performance, portable implementation of the MPI message passing interface standard. Parallel Comput. 1996, 22, 789–828. [Google Scholar] [CrossRef]
- Chandra, R. Parallel Programming in OpenMP; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).