Networks Based on Graphs of Transient Intensities and Product Theorems in Their Modelling
Abstract
1. Introduction
2. Materials and Methods
2.1. Ergodicity Theorem
- (A)
- A system of equationswhich has at least one solution such that .
- (B)
- All process states are communicating, i.e., .
- (C)
- The regularity condition is met, i.e.,
2.2. Product Theorems
3. Results
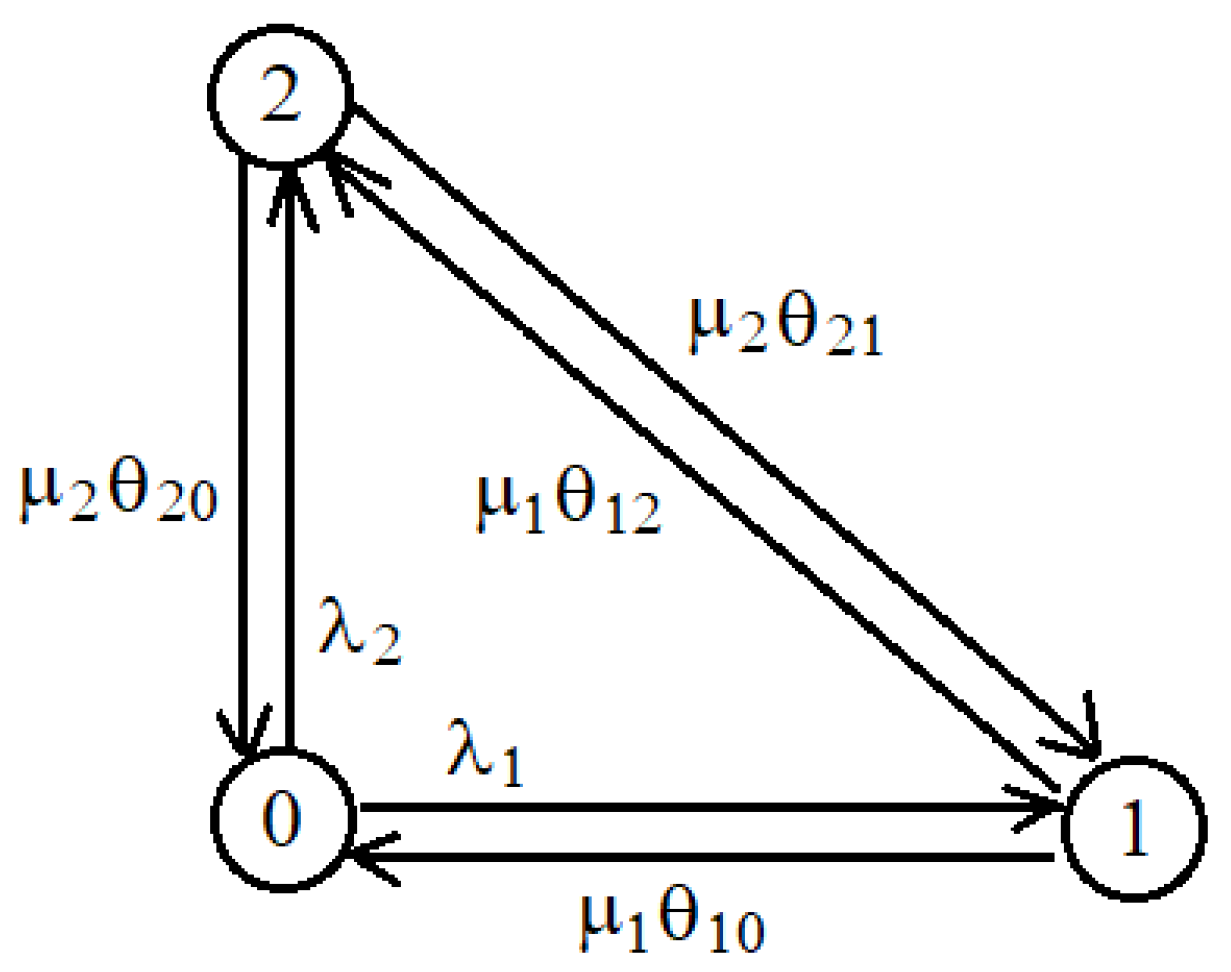
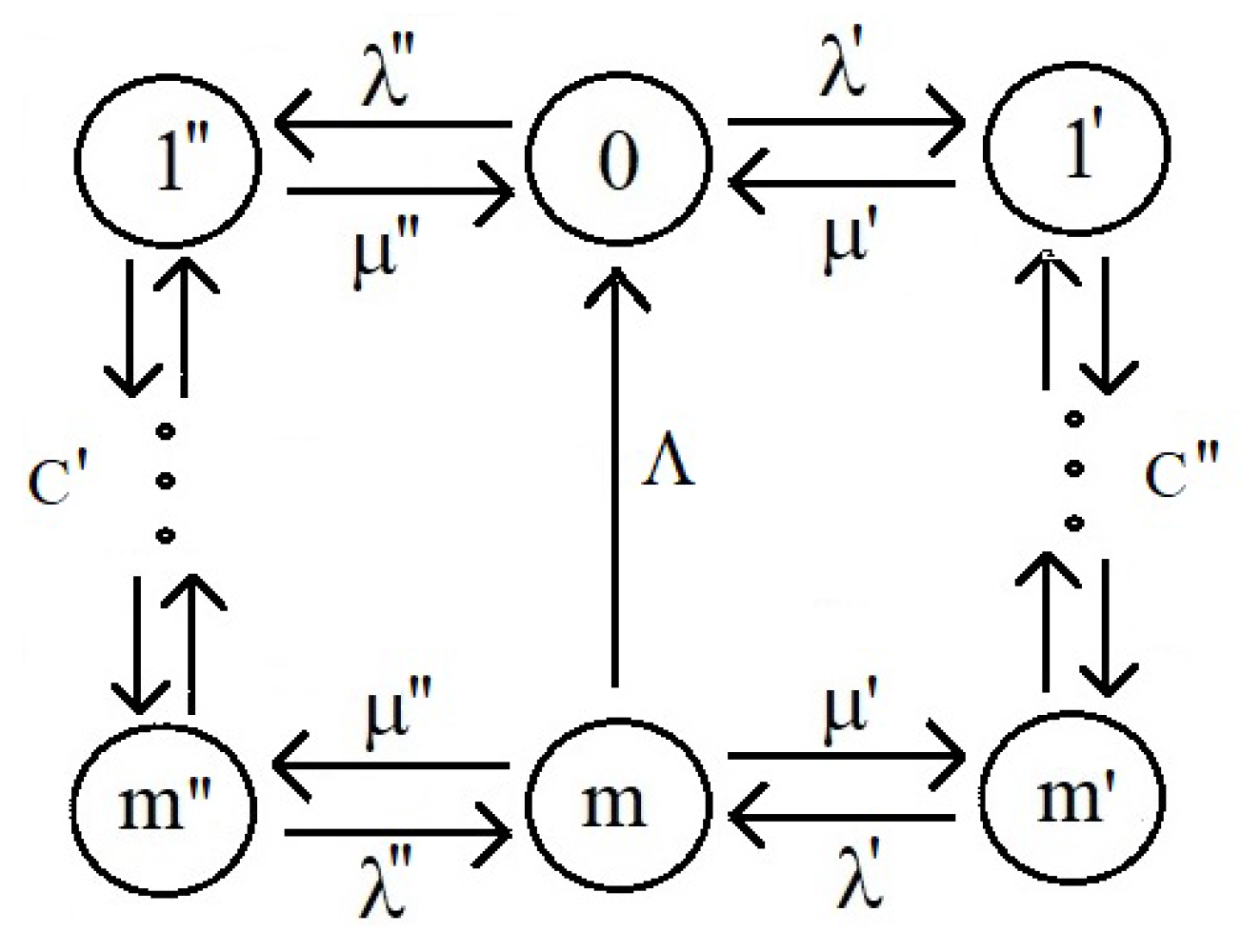
3.1. Queuing Networks with Varying Structure
Basic Theorems on Stationary Distributions of Markov Processes with Connecting Transient Intensities
3.2. Queuing Networks with Uniform Stationary Distributions
3.2.1. Main Balance Theorem
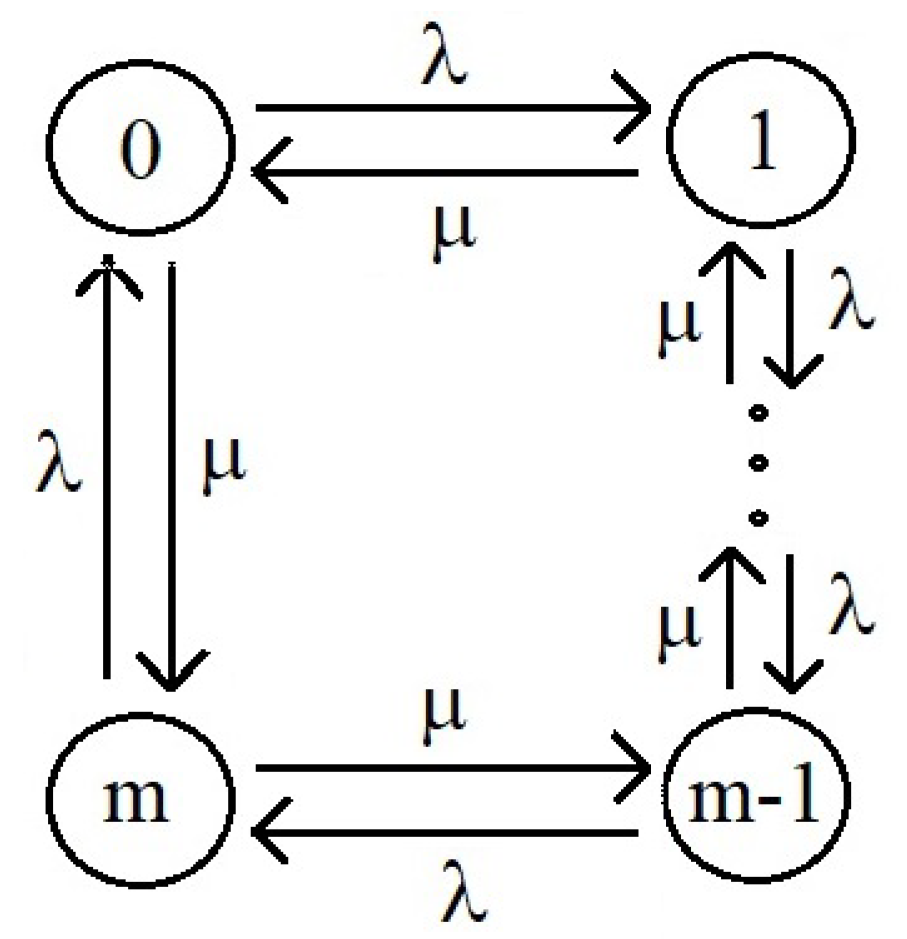
3.2.2. Queuing Network Formed from a Transportation Network
3.3. Some Generalizations of Product Theorems
3.3.1. Main Product Theorem
3.3.2. Closed Queuing Network
3.4. Open Queuing Networks with Finite Numbers of Customers
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grimmett, G. Probability on Graphs, 2nd ed.; Volume 8 of the IMS Textbooks Series; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Van der Hofstad, R. Random Graphs and Complex Networks; Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press: Cambridge, UK, 2017; Volume 1. [Google Scholar]
- Bet, G.; van der Hofstad, R.; van Leeuwaarden, J.S. Big jobs arrive early: From critical queues to random graphs. Stochastic Syst. 2020, 10, 310–334. [Google Scholar] [CrossRef]
- Kriz, P.; Szala, L. The Combined Estimator for Stochastic Equations on Graphs with Fractional Noise. Mathematics 2020, 8, 1766. [Google Scholar] [CrossRef]
- Overtona, C.E.; Broomb, M.; Hadjichrysanthouc, C.; Sharkeya, K.J. Methods for approximating stochastic evolutionary dynamics on graphs. J. Theor. Biol. 2019, 468, 45–59. [Google Scholar] [CrossRef] [PubMed]
- Legros, B.; Fransoo, J.C. Production, Manufacturing, Transportation and Logistics Admission and pricing optimization of on-street parking with delivery bays. Eur. J. Oper. Res. 2024, 312, 138–149. [Google Scholar] [CrossRef]
- Ning, R.; Wang, X.; Zhao, X.; Li, Z. Joint optimization of preventive maintenance and triggering mechanism for k-out-of-n: F systems with protective devices based on periodic inspection. Reliab. Eng. Syst. Saf. 2024, 251, 110396. [Google Scholar] [CrossRef]
- Feng, H.; Zhang, S.H.; Zhang, Y. Production, Manufacturing, Transportation and Logistics Managing production-inventory-maintenance systems with condition monitoring. Eur. J. Oper. Res. 2023, 310, 698–711. [Google Scholar] [CrossRef]
- Anokhin, P.K. Ideas and facts in the development of the theory of functional systems. Psychol. J. 1984, 5, 107–118. (In Russian) [Google Scholar]
- Redko, V.G.; Prokhorov, D.V.; Burtsev, M.S. Theory of Functional Systems, Adaptive Critics and Neural Networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; pp. 1787–1792. [Google Scholar]
- Vartanov, A.V.; Kozlovsky, S.A.; Skvortsova, V.B. Human memory and anatomical features of the hippocampus. Vestn. Moscow. Univ. Ser. 14. Psychol. 2009, 4, 3–16. (In Russian) [Google Scholar]
- Lye, T.C.; Grayson, D.A.; Creasey, H.; Piguet, O.; Bennett, H.P.; Ridley, L.J.; Kril, J.J.; Broe, G.A. Predicting memory performance in normal ageing using different measures of hippocampal size. Neuroradiology 2006, 48, 90–99. [Google Scholar] [CrossRef]
- Lupien, S.J.; Evans, A.; Lord, C.; Miles, J.; Pruessner, M.; Pike, B.; Pruessner, J.C. Hippocampal volume is as variable in young as in older adults: Implications for the notion of hippocampal atrophy in humans. Neuroimage 2007, 34, 479–485. [Google Scholar] [CrossRef]
- Squire, L.R. The legacy of patient H.M. for neuroscience. Neuron 2009, 61, 6–9. [Google Scholar] [CrossRef]
- Jackson, J.R. Networks of Waiting Lines. Oper. Res. 1957, 5, 518–521. [Google Scholar] [CrossRef]
- Gordon, K.D.; Newell, G.F. Closed Queuing Systems with Exponential Servers. Oper. Res. 1967, 15, 254–265. [Google Scholar] [CrossRef]
- Pathria, R.K.; Beale, P.D. Statistical Mechanics, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Gyenis, B. Maxwell and the normal distribution: A coloured story of probability, independence, and tendency toward equilibrium. Stud. Hist. Philos. Sci. Part Stud. Hist. Philos. Mod. Phys. 2017, 57, 53–65. [Google Scholar] [CrossRef]
- Ford, L.R.; Fulkerson, D.R. Maximal flow through a network. Can. J. Math. 1956, 8, 399–404. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Algorithms: Introduction to Second Edition; The MIT Press Cambridge: Cambridge, UK, 1990. [Google Scholar]
- Ghosh, S.; Hassin, R. Inefficiency in stochastic queueing systems with strategic customers. Eur. J. Oper. Res. 2021, 295, 1–11. [Google Scholar] [CrossRef]
- He, Q.M.; Bookbinder, J.H.; Cai, Q. Optimal policies for stochastic clearing systems with time-dependent delay penalties. Naval Res. Logist. 2020, 67, 487–502. [Google Scholar] [CrossRef]
- Kim, B.K.; Lee, D.H. The M/G/1 queue with disasters and working breakdowns. Appl. Math. Model. 2014, 38, 1788–1798. [Google Scholar] [CrossRef]
- Missbauer, H.; Stolletz, R.; Schneckenreither, M. Order release optimisation for time-dependent and stochastic manufacturing systems. Int. J. Prod. Res. 2023, 62, 2415–2434. [Google Scholar] [CrossRef]
- Tsitsiashvili, G.S.; Osipova, M.A. New multiplicative theorems for queuing networks. Probl. Inf. Transm. 2005, 41, 111–122. (In Russian) [Google Scholar] [CrossRef]
- Ivchenko, G.I.; Kashtanov, V.A.; Kovalenko, I.N. Theory of Queuing: A Textbook for Universities; Higher School: Moscow, Russia, 1982. (In Russian) [Google Scholar]
- Kovalenko, I.N.; Kuznetsov, N.Y.; Shurenkov, V.M. Random Processes; Naukova Dumka: Kiev, Ukraine, 1983. (In Russian) [Google Scholar]
- Mikosch, T.; Resnick, S.; Rootzen, H.; Stegeman, A. Is network traffic approximated by stable Levy motion or fractional Brownian motion? Ann. Appl. Probab. 2002, 12, 23–68. [Google Scholar] [CrossRef]
- Stillwell, J. Mathematics and Its History, 2nd ed.; Springer Science and Business Media Inc.: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Vilenkin, N.Y. Combinatorics; Nauka: Moscow, Russia, 1969. (In Russian) [Google Scholar]
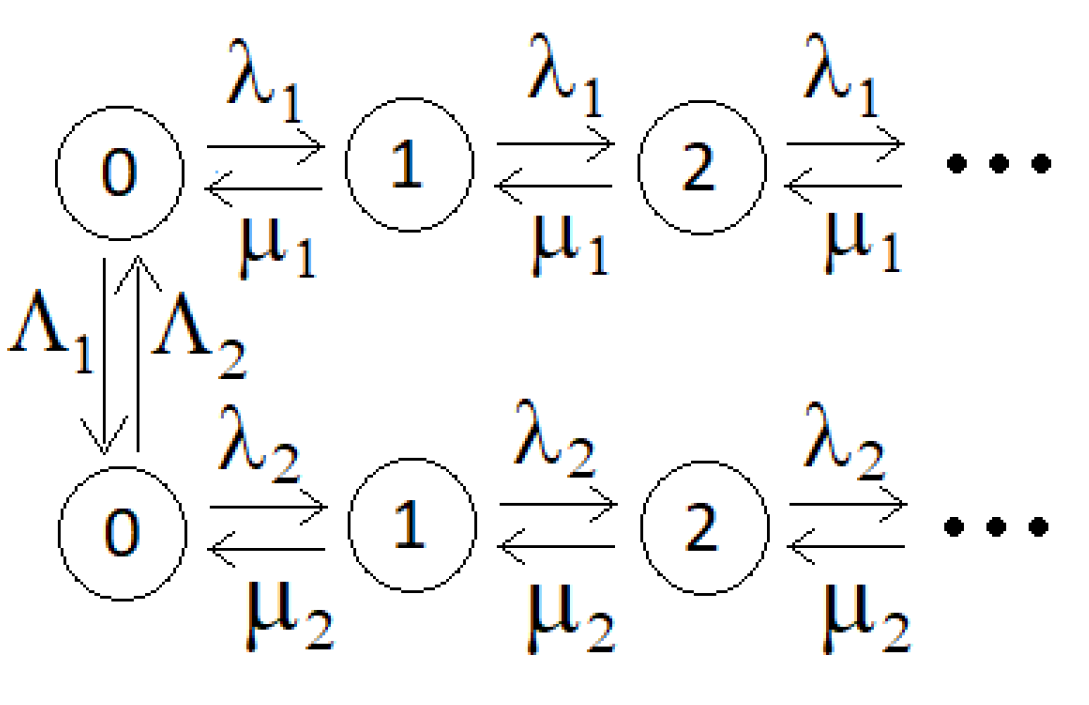
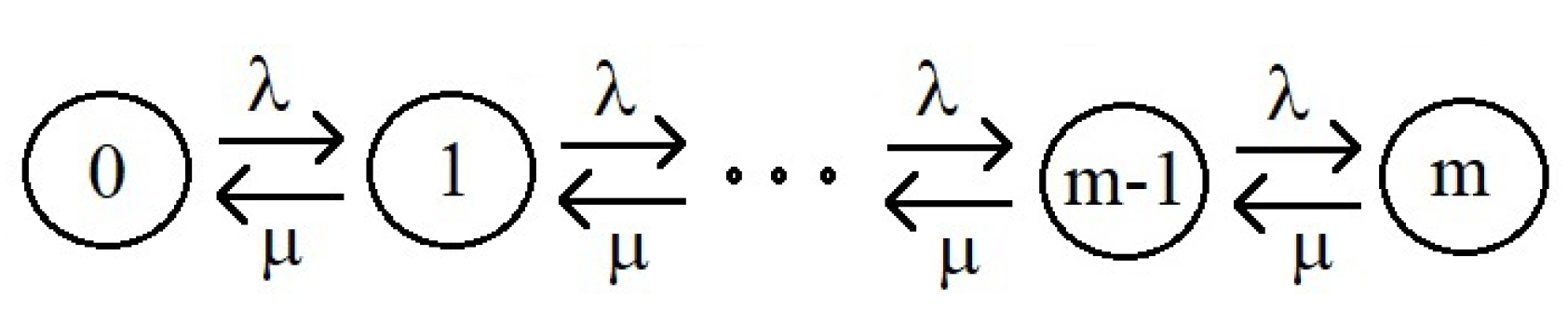


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsitsiashvili, G. Networks Based on Graphs of Transient Intensities and Product Theorems in Their Modelling. Computation 2024, 12, 195. https://doi.org/10.3390/computation12100195
Tsitsiashvili G. Networks Based on Graphs of Transient Intensities and Product Theorems in Their Modelling. Computation. 2024; 12(10):195. https://doi.org/10.3390/computation12100195
Chicago/Turabian StyleTsitsiashvili, Gurami. 2024. "Networks Based on Graphs of Transient Intensities and Product Theorems in Their Modelling" Computation 12, no. 10: 195. https://doi.org/10.3390/computation12100195
APA StyleTsitsiashvili, G. (2024). Networks Based on Graphs of Transient Intensities and Product Theorems in Their Modelling. Computation, 12(10), 195. https://doi.org/10.3390/computation12100195