Dynamics of Blood Flows in the Cardiocirculatory System

Abstract

Models and simulations of blood flow in vascular networks are useful to deepen knowledge of cardiovascular diseases. This paper considers a model based on partial differential equations that mimic the dynamics of vascular networks in terms of flow velocities and arterial pressures. Such quantities are found by using ad hoc numerical schemes to examine variations in the pressure and homeostatic conditions of a whole organism. Two different case studies are examined. The former uses 15 arteries—a network that shows the real oscillations in pressures and velocities due to variations in artery volume. The latter focuses on the 55 principal arteries, and blood flows are studied by using a model of a heart valve that opens and closes via the differences in the aortic and left ventricle pressures. This last case confirms the possibility of autonomously regulating blood pressure and velocity in arteries in general and when tilt tests are applied to patients.

1. Introduction

The need for accurate investigations into cardiovascular diseases has inspired the formulation of analytical and numerical models that are able to reproduce the evolution of blood flows in vascular networks and simulate the consequences of medical interventions. The common medical surgery that uses bypass for cardio-circulatory issues has a non-negligible failure probability. Hence, researchers deal with local hemodynamics that describe how different surgery solutions could affect blood circulation.

Various techniques [1,2] are already known and focus on blood evolution in arteries (edges) and at nodes, i.e., points where two or more edges intersect. A fundamental aspect is the role of organs because they represent the boundary conditions for a system of large arteries. Indeed, the description of different phenomena needs various models for networks: capillary systems [3,4] have a complex structure that is not tree-like, and their task is to irrigate all organs and tissues; venous systems [5] consist of collapsible tubes and venous valves with high fluid volume and low-pressure gradients. Finally, there are other effects [6] described by heart chambers, valves, and pulmonary circulation. Considering the variety of the structures involved, computational efforts for simulations are very expensive, and the overall presentation of dynamics is quite limited to specific cases that are not always useful for medical analyses. An example is hypertension, which needs models of wide portions of tissues and organs.

In order to describe the dynamics inside human systems, one remedy is the following: only some parts of a large network are studied in detail using fully three-dimensional (3D) models that describe the arterial systems or the vascularization of organs while other portions are modeled via reduced approaches, such as one-dimensional (1D) or zero-dimensional (0D) models (see [7,8] for pioneering exposures, [9] for a possible description of the whole circulatory system, [10] for the evolution of blood flows due to postural changes from sitting to standing and, finally, [11] for a complete overview about models in human physiology; [12,13] for some detailed reviews). In this case, the boundary and inflow/outflow conditions that mimic the dynamics of the network are removed from the model. These aspects are still under investigation. Some recent results dealing with real data can be found in [14]. In this direction, important aspects focus on networks of large arteries with auto-regulation mechanisms. Indeed, the physical systems to model are assumed in dynamic equilibrium, i.e., regular heartbeat and nominal pressure values with a quasi-periodic profile. In case of disturbances, such as blockage or release thereof, the system must return to its equilibrium (homeostasis). Equilibrium states are reached in a minimum time [15] via a suitable choice of boundary controls imposed at the root of a vascular network, i.e., the heart, and at the peripheral nodes, i.e., the ends of large arteries. Other approaches to control a vascular network need the peripheral resistance [16] that models micro circulations inside organs.

1.1. Adopted Model: Features, Limitations and Scientific Context

In this paper, we describe a 1D approach [17] for vascular networks. The model consists of partial differential equations (PDEs) and algebraic relations among cross-section area, average flow velocity, blood pressure, and friction force for arteries.

Some assumptions are considered: Arteries are seen as elastic, homogeneous, and thin tubes; blood behaves like a Newtonian fluid (a fluid that continues to flow despite any force being applied to it) with homogeneity and noncompressibility properties.

The assumption for blood seems to be limiting. In fact, blood is a non-Newtonian fluid because its viscosity depends on the shear rate applied to it. The non-Newtonian behavior of blood is essential to describe the flow through blood vessels, especially in regions with varying shear rates, such as some groups of arteries, the heart, and capillaries. Indeed, the hypothesis for blood as a Newtonian fluid is reasonable for the case studies that are proposed in the paper that deal with large blood vessels where non-Newtonian effects are less predominant than in other human tissues.

Various types of boundary conditions underline the possible differences in terms of biological behavior. The equations of the model are numerically solved by using a discontinuous Galerkin scheme [18,19] and an Adam-Bashfort two-step time integration approach with quadrature formulas [20]. The adopted numerical schemes are adequate for either the geometries of the proposed case studies or convergence and stability issues. These last features are also guaranteed by the assumption of Newtonian-type blood that assures a constant viscosity, avoiding the possibility of further equations that complicate the model itself.

Indeed, although the model presents some limitations, there are advantages from either a modeling or numerical point of view. However, better descriptions of blood flows should require not only 1D models but also higher-order approaches. Higher-dimension models allow for variations in parameters in a space with continuity, ensuring the adoption of convective terms, which are useful for describing further dynamics in vascular networks. Finally, the possible coupling of 1D and higher-order models might be suitable to reveal the real variations for pressures and velocities in specific areas that involve organs and tissues. Some analyses are actually under investigation, with an emphasis on computational resources. An example is [21], wherein the authors consider an analytical and numerical analysis that proves how flow velocities in blood vessels can not be flat or parabolic.

Despite the apparent simple analytical formulation, the presented model has been deeply studied and validated. For instance, the reader can refer to following: [22], where the main features of 1D modeling are proved via wave measurements; [23], where the pulse waveform is analyzed by using a peripheral component that deals with cardiac output and a conduit component that depends on the main arteries and the aortic valve; [24], which presents a real, first validation by considering the real human pressure and data of blood flows; [25], where a discontinuous Galerkin scheme and a Taylor-Galerkin formulation are used to model the evolution of blood flows; [26], which describes pressures and blood flows in arteries by using a visco-elastic and 1D model. Finally, in [27], a 1D model is used to capture some of the features of blood flows and, at the same time, 1D algorithms are used to guarantee fast simulations; in [28], the transmission and reflection of pulses at bifurcations in arterial systems are fully studied for validation purposes.

The captured physiological features describe the autonomous regulation of heartbeat (see [29], where a 0D model investigates the effects of the recent global pandemic on the cardiovascular system. In [30], a 3D-0D fluid dynamic model was used with the aim of simulating the evolution of blood flows in the left section of the human heart, and in [31], delays and increases in wall shear stresses in the left ventricle are described in pathological situations).

Other important works for the presented issue are [32,33]. The former presents a fast Fourier transform (FFT) approach to solve equations of a vascular network in case of variable properties and geometries. The latter considers a feedback optimal control for a 3D model of stationary flows of a non-Newtonian type. In this last case, possible advantages arise in terms of the generalized results for the proposed model of vascular networks. Moreover, to create personalized plans for medical treatments, the authors of [34] describe numerical algorithms for the dynamics between heart walls, valves, organs, and tissues.

Notice that the proposed approach for vascular networks is similar to other well-known models listed here: The authors of [35] deal with telecommunication networks modeled by a conservation law for packet density and a semi-linear equation for the functions that describe the packet paths. This allows for the possibility of fixing sources and destinations on a network. In [36], supply chains are modeled by using PDEs to obtain the densities of parts from suppliers and ordinary differential equations (ODEs) for the queues among consecutive arcs. The complete model is used to minimize (via a genetic algorithm) a cost functional that weighs the queues with respect to a predefined outflow. The authors of [37] describe a different overview of the issue in [36] by using numerical schemes for differential quadrature rules and a Picard-like recursion. Finally, the work [38] covers an approach to optimize the travel times of emergency vehicles on assigned paths in case of critical events. The complete evolution of traffic is studied by using a fluid dynamic model, and some simulations prove the usefulness of the model in real contexts. Indeed, the previous studies consider control approaches similar to those described in [39], where a variational inequality is analyzed by the anisotropic p-Laplacian.

1.2. Contribution and Structure of the Paper

The main contribution of the paper is described as follows. We focus on different scenarios for vascular networks with large blood vessels and underline some of the effects that are obtained when also using more complicated models. First, a test network with 15 edges is studied by using terminal conditions that focus on conservative effects. The presence of oscillations in pressures indicates a natural propensity for autonomic regulation. Finally, a complete network that consists of the fundamental arteries of the human body is analyzed. We assume dissipative and conservative effects due to organs, tissues, and a heart valve model that works through the differences in the left ventricle and aortic pressures. The last case confirms the possibility of regulation mechanisms under suitable external conditions. For this analyzed network, a tilt test, i.e., a diagnostic analysis for blood pressures and heartbeats due to patients transitioning from a horizontal to a semi-vertical position, is also considered. It is shown that the return of pressures and velocities to nominal conditions is strictly dependent on the duration of the test.

The paper is structured as follows: Section 2 introduces the equations of the model and the boundary conditions. Section 3 presents the numerical schemes for the used model. Section 4 shows some of the simulation results for the various discussed scenarios. Conclusions and future research activities are presented in Section 5. At the end of the paper, Appendix A presents all the notations and acronyms used, as well as data for the simulation of the network with main arteries.

2. Mathematical Model

This section presents a model for the analysis of flow and pressure waves in vascular networks. Although various approaches are commonly adopted (see, for instance [11,14,25]), we focus on a 1D model for pressure and flow velocities in arteries. First, we discuss a fundamental assumption about the features of blood flow. Then, we consider how to model the evolution along arteries and at the interfaces.

2.1. Newtonian Blood Flow

It is known that thromboembolism often occurs due to a prosthetic mechanical heart valve that provokes blood damage. A preventive diagnostic tool is useful for the health of patients, but a complete description of the hemodynamics of mechanical heart valves remains a hard task for the following reasons: the kinematics of the valves; the physiological inflow of blood; irregular arterial passage geometry; and turbulence due to the opening and closing of valves and the amplitude of flows, with the consequent formation of regions of high and low stresses.

Within this framework, a correct mathematical formulation of flows inside organs and tissues requires a careful analysis of some physiological characteristics. For this aim, we observe that blood is an inhomogeneous fluid that consists of plasma and red blood cells, and its viscosity depends on either the temperature or the hematocrit. In regions of low shear stresses (for instance, veins), blood cells often aggregate and form rouleaux with a consequent increment in viscosity. In this case, blood is well described by a non-Newtonian, shear-thinning model. The non-Newtonian features are essential for a complete and exhaustive description of the overall circulatory system. A recent and preliminary analysis in this direction is provided in [40].

On the other hand, blood could be considered a Newtonian flow in large blood vessels, such as the main arteries and veins. In these cases (an example is the aorta), the flow is quite fast, the viscosity tends to remain almost constant, the deformations of red blood cells are smaller than in smaller vessels, and non-Newtonian effects become less significant. In this work, in consideration of the proposed case studies, blood is assumed to be a homogeneous, incompressible, and Newtonian fluid. Hence, viscosity and density are considered constant or dependent only on the temperature, which is treated as a parameter without the necessity of introducing an energy equation or a thermodynamic state equation. Moreover, blood is assumed to be laminar (low Reynolds numbers); hence, it does not create turbulence.

2.2. Basic Equations

A vascular network is a graph defined by the couple $\left(\mathcal{I},\mathcal{J}\right)$, where $\mathcal{I}={\left\{I_k\right\}}_{k=1,\dots ,K}$ is the set of edges $I_k$, $k=1,\dots ,K$, each one represented by an interval $\left[a_k,b_k\right]\subset \mathbb{R}$, and $\mathcal{J}={\left\{j_m\right\}}_{m=1,\dots ,M}$ is the set of interfaces $j_m$, $m=1,\dots ,$ M. Precisely, for a generic artery (edge $I_k\in \mathcal{I}$ of the vascular network) studied at location x and at time t, by using $A_k=A_k\left(t,x\right)$, we denote the cross-section area; $P_k=P_k\left(t,x\right)$ denotes blood pressure; $U_k=U_k\left(t,x\right)$ denotes average flow velocity; and $f_k=f_k\left(t,x\right)$ denotes the friction force (for unit length). Assuming that ${\rho }_k$ is blood density, we obtain the following system ∀$k=1,\dots ,K$:

$$\left\{\begin{array}{c}{\left(A_k\right)}_t+{\left(A_k{U}_k\right)}_x=0,\hfill \\ {\left(U_k\right)}_t+U_k{\left(U_k\right)}_x+{\rho }_k^{-1}{\left(P_k\right)}_x=f_k,\hfill \end{array}\right.$$

(1)

where the first equation is the mass conservation inside the network, and the second is derived from the Navier–Stokes equations under some assumptions of the flow velocity profile across a cross-section. By assuming ${\mu }_k$ is fluid viscosity, we obtain $f_k=-22\pi {\mu }_k{U}_k{\rho }_k^{-1}{A}_k^{-1}$, as described in [41,42]. We deal with a velocity profile that is assumed to be parabolic. The reason is the following: The layers of laminar-flowing blood create a parabolic wave because the velocity of blood flow is highest in the central layers and lowest at the vessel wall. Indeed, various wave propagation models consider flat or parabolic velocity evolution to estimate nonlinear convection and diffusion terms. However, in a recent piece of work [21], some further analyses prove that the flow characteristics and velocity profile are in good agreement with some computational results; the axial velocity across the cross-section reveals neither flat nor parabolic profiles. In this work, we still assume parabolic velocity, but some further investigations are needed for possible refinements to the model.

Arteries are seen as fluid-filled tubes having elastic walls, and blood is assumed to be a Newtonian fluid. For the generic artery $I_k$, $k=1,\dots ,K$, we consider the Young modulus, $E_k$, wall density. ${\rho }_{k,w}$, wall thickness, $h_{k,w}$, and an unstressed radius, $r_{k,0}$. The hydrodynamic pressure, $P_k$, is taken to be constant across the vessel cross-section and is computed via ${\eta }_k={\eta }_k(t,x)$, which represents wall displacement. We consider a linear dependence of $P_k$ on ${\eta }_k$ given by

$$P_k=P_{k,ext}+{\beta }_k{\eta }_k{r}_{k,0}^{-2},$$

(2)

where $P_{k,ext}$ represents the external pressure, and ${\beta }_k$ is the coefficient of the arterial wall:

$${\beta }_k={\displaystyle \frac{E_k{h}_{k,w}\sqrt{\pi }}{1-{\sigma }_k^2}},$$

with ${\sigma }_k$ as the Poisson ratio, often taken as $0.5$. Finally, by denoting the unstressed cross-section area as $A_{k,0}=\pi r_{k,0}^2$, $P_k$ depends on $A_k$, as

$$P_k=P_{k,ext}+{\displaystyle \frac{{\beta }_k\left(\sqrt{A_k}-\sqrt{A_{k,0}}\right)}{A_{k,0}}}.$$

(3)

Remark 1.

In cases of visco-elasticity or wall inertia, Equations (2) and (3) can be modified by adding wall velocity and acceleration, ${\left({\eta }_k\right)}_t$ and ${\left({\eta }_k\right)}_{tt}$, respectively. Exhaustive descriptions of these cases can be found in [17], and details about the used rheological equation can be found in [22,23].

2.3. Interfaces

In order to define the dynamics at interfaces (nodes), we need some further assumptions. For a generic node of degree N (N is the total number of edges for the node), assume that $\left(A_i,U_i,P_i\right)$, $i=1,\dots ,n$ and $\left(A_j,U_j,P_j\right)$, $j=n+1,\dots N$, are the states at time t, respectively, for the n incoming edges $I_i$, $i=1,\dots ,n$ and the $N-n$ outgoing edges $I_j$, $j=n+1,\dots ,N-n$. Finally, for a generic edge $I_k$, $k=1,\dots ,N$, by using $\left(A_k^u,U_k^u,P_k^u\right)$, $k=1,\dots ,N$, we indicate the upwind states, i.e., the states at time $t+\Delta t$. Then, we define the following:

Definition 1.

A Riemann solver (RS) at an interface of degree N of a vascular network is a function that, when assuming $\left(A_k,U_k,P_k\right)$, $k=1,\dots ,N$, computes $\left(A_k^u,U_k^u,P_k^u\right)$, $k=1,\dots ,N$.

For this aim, the building block is the solution to the Riemann problem (RP) at the interface, i.e., the solution of Cauchy problems at an interface with constant states on the incoming and outgoing edges. From the solutions to the RPs at the interfaces, different boundary conditions are defined.

For simplicity, from now on, we consider that blood density is the same for all arteries, i.e., ${\rho }_k=\rho$∀$k=1,\dots ,K$.

2.3.1. Riemann Problem at the Interface

We describe the solution to the RP at an interface. Assume that $\left(A_L,U_L\right)$ and $\left(A_R,U_R\right)$ are the states on the left and on the right, respectively, of the interface at time t. Then, the upwind states $\left(A_L^u,U_L^u\right)$ and $\left(A_R^u,U_R^u\right)$ are found by solving the following system by using an iterative Newton-Raphson method:

$$\left\{\begin{array}{c}{W}_f\left(A_L,U_L\right)=W_f\left(A_L^u,U_L^u\right),\hfill \\ W_b\left(A_R,U_R\right)=W_b\left(A_R^u,U_R^u\right),\hfill \\ A_L^u{U}_L^u=A_R^u{U}_R^u,\hfill \\ 2P\left(A_L^u\right)+\rho {\left(U_L^u\right)}^2=2P\left(A_R^u\right)+\rho {\left(U_R^u\right)}^2.\hfill \end{array}\right.$$

(4)

The first two equations indicate the condition of inviscid flow between two initial states, and, for the generic artery $I_k$, the forward (resp. backward) characteristic information, $W_f$ (resp. $W_b$), is

$$W_x=U_k+4a\left(c_k-c_{k,0}\right),$$

where $\left(x,a\right)=\left(f,+1\right)$ or $\left(x,a\right)=\left(b,-1\right)$ and

$$c_k=\sqrt{{\displaystyle \frac{{\beta }_k\sqrt{A_k}}{2\rho A_{k,0}}}},c_{k,0}=\sqrt{{\displaystyle \frac{{\beta }_k}{2\rho \sqrt{A_{k,0}}}}}.$$

The remaining equations are due to the mass conservation and the continuity of the total pressure at the interface.

2.3.2. Inflow, Interface, and Terminal Boundary Conditions

As for inflow, different choices are possible. In particular, we can prescribe the following functions: $A_{bc}\left(t\right)$, $U_{bc}\left(t\right)$ or $Q_{bc}\left(t\right)$, namely an inflow time-dependent area, a velocity, or a flow rate, respectively. At the inlet of arteries, we could have

$$A_{bc}\left(t\right):=\left\{\begin{array}{c}{A}_L={\left(2\sqrt[4]{A_{bc}}-\sqrt[4]{A_R}\right)}^4,\hfill \\ U_L=U_R,\hfill \end{array}\right.$$

$$U_{bc}\left(t\right):=\left\{\begin{array}{c}{A}_L=A_R,\hfill \\ U_L=2U_{bc}-U_R,\hfill \end{array}\right.$$

$$Q_{bc}\left(t\right):=\left\{\begin{array}{c}{A}_L=A_R,\hfill \\ U_L={\displaystyle \frac{2Q_{bc}-A_R{U}_R}{A_R}}.\hfill \end{array}\right.$$

Considering the features of the real vascular networks, all different formulations are valid. Indeed, a possible discrimination depends on the heart model that is coupled to the equations of the network.

Now, we describe the interface boundary conditions. In considering the real nodes of the vascular network, we have quite large degrees, N. In what follows, we face only the situations $N=2$ and $N=3$, as the remaining cases are similar. If $N=2$, a node connects an incoming edge and an outgoing one; hence, the upwind states are found by solving Equation (4). If $N=3$, the nodes have two possible geometries: $1\times 2$, i.e., an incoming edge 1 and two outgoing ones, 2 and 3; and $2\times 1$, namely two incoming edges, 2 and 3, and one outgoing edge, 1. Assume that $\left(A_1,U_1,P_1\right)$, $\left(A_2,U_2,P_2\right)$ and $\left(A_3,U_3,P_3\right)$ are the initial states near the node. The upwind states $\left(A_i^u,U_i^u,P_i^u\right)$, $i=1,2,3,$ are found by solving

$$\left\{\begin{array}{c}{W}_f\left(A_1^u,U_1^u\right)=W_f\left(A_1,U_1\right),\hfill \\ W_b\left(A_{\psi }^u,U_{\psi }^u\right)=W_b\left(A_{\psi },U_{\psi }\right),\psi =2,3,\hfill \\ A_1^u{U}_1^u=A_2^u{U}_2^u+A_3^u{U}_3^u,\hfill \\ 2P_1\left(A_1^u\right)+\rho {\left(U_1^u\right)}^2=2P_{\psi }\left(A_{\psi }^u\right)+\rho {\left(U_{\psi }^u\right)}^2,\psi =2,3,\hfill \end{array}\right.$$

(5)

for nodes of $1\times 2$, and

$$\left\{\begin{array}{c}{W}_b\left(A_1^u,U_1^u\right)=W_b\left(A_1,U_1\right),\hfill \\ W_f\left(A_{\psi }^u,U_{\psi }^u\right)=W_f\left(A_{\psi },U_{\psi }\right),\psi =2,3\hfill \\ A_1^u{U}_1^u=A_2^u{U}_2^u+A_3^u{U}_3^u,\hfill \\ 2P_1\left(A_1^u\right)+\rho {\left(U_1^u\right)}^2=2P_{\psi }\left(A_{\psi }^u\right)+\rho {\left(U_{\psi }^u\right)}^2,\psi =2,3,\hfill \end{array}\right.$$

(6)

for nodes of $2\times 1$. Indeed, the real differences between Equations (5) and (6) are provided by the characteristic waves $W_f$ and $W_b$, respectively.

Now, we consider the terminal boundary conditions that can be used to analyse the effects of pulse wave propagations on the wall compliance, fluid resistance, and inertia of small arteries and capillaries. Such conditions are derived from analogies with electric circuits, and an exhaustive overview can be found in [18].

For a generic artery $I_k$, $k=1,\dots ,K$, the description is similar to the one that follows for RPs. In this case, $\left(A_L,U_L\right)$ represents the state at the end point of the arterial domain, while $\left(A_R,U_R\right)$ is used to generate the upwind state $\left(A^u,U^u\right)$. Notice that the values of ${\beta }_k$ and $A_{k,0}$ are easily indicated by ${\beta }_L$ and $A_{0_L}$ in $\left(A_L,U_L\right)$. We distinguish several cases.

• Case 1 (pure resistance). We assume that the power exchanges between the different parts of the human body involved in the network are mostly due to dissipative effects, described by the only terminal resistance, $R_t$. Such an assumption reads as

  $$W_b=-R_t{W}_f,-1\le R_t\le 1.$$
  Notice that $R_t=-1$ corresponds to a free terminal site, namely $c_k=c_{k,0}$, and we obtain

  $$A_R=A_L,U_R=W_b+W_f-U_L.$$
  Finally, $R_t=0$ means there are no reflected characteristics at the terminal site; $R_t=+1$ indicates a complete reflection, i.e., blockage condition, $U_k=0$.
• Case 2 (RC cell). This case deals with a typical RC cell, i.e., a simple circuit with a resistor and a capacitor. In analogy with other situations that involve more electric components, this situation obeys the need to provide suitable modeling for both the dissipative and conservative effects within the human body. A similar situation is not unusual considering that, especially in the cardiovascular system, the heart is used to suffering the effects of other tissues (dissipative phenomena) and radiating energy (conservative effect) to the individual organs of the body by pumping blood. From a mathematical point of view, without affecting the generality of the discussion, we consider the lumped parameter model that consists of only a resistance $R_{\mu }$ that, under suitable assumptions, refers to either dissipative or conservative effects. In this case, assuming that $P_{in}$ and $P_{out}$ are, respectively, the pressures at the inlet and at the end of the arterial domain, we have the following nonlinear equation for $A^u$:

  $$A^u\left(U_L+4\sqrt{{\displaystyle \frac{{\beta }_L\sqrt{A_L}}{2\rho A_{0_L}}}}\right)R_{\mu }-4R_{\mu }\sqrt[5]{{\left(A^u\right)}^4}\sqrt{{\displaystyle \frac{{\beta }_L}{2\rho A_{0_L}}}}+$$

  $$-P_{in}-{\displaystyle \frac{{\beta }_L}{A_{0_L}}}\left(\sqrt{A^u}-\sqrt{A_L}\right)+P_{out}=0.$$
  The last equation is easily solved (numerically) by using Newton’s method and assuming $A^u=A_L$ as a starting point. Finally, we have

  $$U^u={\displaystyle \frac{P\left(A^u\right)-P_{out}}{R_{\mu }{A}^u}},$$

  and the terminal conditions reduce to

  $$A_R=A_L,U_R=2U^u-U_L.$$
• Case 3 (compliance). As the previous case can generate oscillations for pressure and flow, a more complicated model that deals with compliance can be considered. Compliance is a capacitor, C, that models the stabilization of the pressure. In this case, it is necessary to compute $A^u=A_{in}^n$ by using a recursive equation of the following form:

  $$A_{in}^n=F\left(A_{in}^{n-1},R_{\mu },C,P_{in},P_{out}\right),$$

  where F is the suitable continuous function described in [18]. In this case, the terminal conditions are written as

  $$A_R=\sqrt[4]{2\sqrt[4]{{\left(A^u\right)}^n}-\sqrt[4]{A_L}},U_R=U_L.$$

3. Numerical Schemes

In order to find suitable approximations for Equation (1), for each artery, we use a discontinuous Galerkin and an Adams-Bashfort time-integration scheme. From now on, we present a description for a generic artery of the vascular network omitting, for simplicity, the pedex $k=1,\dots ,K$.

Equation (1) can be written as

$${\left(\mathbf{U}\right)}_t+{\left(\mathbf{F}\right)}_x=\mathbf{V},$$

(7)

with

$$\mathbf{U}=\left[\begin{array}{c}A\\ U\end{array}\right],\mathbf{F}\left(\mathbf{U}\right)=\left[\begin{array}{c}AU\\ {\displaystyle \frac{U^2}{2}}+{\displaystyle \frac{p}{\rho }}\end{array}\right],\mathbf{V}\left(\mathbf{U}\right)=\left[\begin{array}{c}0\\ {\displaystyle \frac{1}{\rho }}({\displaystyle \frac{f}{A}}-{\displaystyle \frac{\partial p}{\partial A_0}}{\displaystyle \frac{d{A}_0}{dx}}-{\displaystyle \frac{\partial p}{\partial \beta }}{\displaystyle \frac{d\beta }{dx}})\end{array}\right].$$

The domain $\mathsf{\Gamma }=[0,l]$ of each artery is discretized in a mesh of M non-overlapping elemental regions, ${\mathsf{\Gamma }}_h=[x_h^L,x_h^R]$, $h=1,\dots ,M$, such that $x_h^R=x_{h+1}^L$∀$h=1,\dots ,M-1$ and ${\cup }_{h=1}^M{\mathsf{\Gamma }}_h=\mathsf{\Gamma }$. Notice that the superscripts L and R refer to left and right boundaries, respectively, of each elemental region ${\mathsf{\Gamma }}_h$. If

$${(\mathbf{a},\mathbf{b})}_{\mathsf{\Gamma }}={\int }_{\mathsf{\Gamma }}\mathbf{ab}dx,$$

the weak form of Equation (7) is

$${\left({\displaystyle \frac{\partial \mathbf{U}}{\partial t}},\mathbf{\Phi }\right)}_{\mathsf{\Gamma }}+{\left({\displaystyle \frac{\partial \mathbf{F}}{\partial x}},\mathbf{\Phi }\right)}_{\mathsf{\Gamma }}={(\mathbf{V},\mathbf{\Phi })}_{\mathsf{\Gamma }},$$

(8)

where $\mathbf{\Phi }$ is a set of test functions. Assuming that $\mathbf{U}(x,t)$ and $\mathbf{\Phi }\left(x\right)$ are approximated by ${\mathbf{U}}^{\delta }(x,t)$ and ${\mathbf{\Phi }}^{\delta }\left(x\right)$, respectively, we obtain (see [18,25]):

$$\begin{array}{c}\sum _{h=1}^M\left({\left({\displaystyle \frac{\partial {\mathbf{U}}_h^{\delta }}{\partial t}},{\mathbf{\Phi }}_h^{\delta }\right)}_{{\mathsf{\Gamma }}_h}+{\left({\displaystyle \frac{\partial \mathbf{F}\left({\mathbf{U}}_h^{\delta }\right)}{\partial x}},{\mathbf{\Phi }}_h^{\delta }\right)}_{{\mathsf{\Gamma }}_h}+{[({\mathbf{F}}^u-\mathbf{F}\left({\mathbf{U}}_h^{\delta }\right))·{\mathbf{\Phi }}_h^{\delta }]}_{x_h^L}^{x_h^R}\right)=\\ =\sum _{h=1}^M{(\mathbf{V}\left({\mathbf{U}}_h^{\delta }\right),{\mathbf{\Phi }}_h^{\delta })}_{{\mathsf{\Gamma }}_h}.\end{array}$$

By introducing ${\mathsf{\Gamma }}_{st}=\{\alpha \in \mathbb{R}:-1\le \alpha \le 1\}$, we define the map:

$${\chi }_h\left(\alpha \right)=x_h^L{\displaystyle \frac{1-\alpha }{2}}+x_h^R{\displaystyle \frac{1+\alpha }{2}},\alpha \in {\mathsf{\Gamma }}_{st},$$

(9)

where

$$\alpha =2{\displaystyle \frac{x_h-x_h^L}{x_h^R-x_h^L}}-1,x_h\in {\mathsf{\Gamma }}_h.$$

(10)

As the expansion basis, we use the Legendre polynomials $L_k\left(\alpha \right)$, where k is the polynomial order, hence obtaining

$${\mathbf{U}}_h^{\delta }({\chi }_h\left(\alpha \right),t)=\sum _{k=0}^K{L}_k\left(\alpha \right)\widehat{{\mathbf{U}}_h^k}\left(t\right),$$

(11)

where $\widehat{{\mathbf{U}}_h^k}\left(t\right)$ represents the generic coefficient of the expansion.

By letting ${\mathbf{\Phi }}_h^{\delta }={\mathbf{U}}_h^{\delta }$, $2R$ differential equations are obtained, ∀${\mathsf{\Gamma }}_h,$ $h=1,\dots ,M:$

$${\left(\widehat{U_{i,h}^k}\right)}^{\prime }=\mathcal{G}\left({\mathbf{U}}_h^{\delta }\right),k=0,\dots ,R,i=1,2,$$

(12)

where $\widehat{U_{i,h}^k},i=1,2,$ is the generic component $\widehat{{\mathbf{U}}_h^k}\left(t\right)$, and

$$\mathcal{G}\left({\mathbf{U}}_h^{\delta }\right)=-{\left({\displaystyle \frac{\partial F_i}{\partial x}},L_k\right)}_{{\mathsf{\Gamma }}_h}-{\displaystyle \frac{2{\left[L_k(F_i^u-F_i\left({\mathbf{U}}_h^{\delta }\right))\right]}_{x_h^L}^{x_h^R}}{x_h^R-x_h^L}}+{(V_i\left({\mathbf{U}}_h^{\delta }\right),L_k)}_{{\mathsf{\Gamma }}_h}.$$

The scheme is completed by adopting a second-order Adams-Bashforth time-integration approach, i.e.,

$$\begin{array}{c}{\left(\widehat{U_{i,h}^k}\right)}^{n+1}={\left(\widehat{U_{i,h}^k}\right)}^n+{\displaystyle \frac{\Delta t}{2}}\left[3\mathcal{G}\left({\left({\mathbf{U}}_h^{\delta }\right)}^n\right)-\mathcal{G}\left({\left({\mathbf{U}}_h^{\delta }\right)}^{n-1}\right)\right],\\ k=0,\dots ,R,i=1,2,h=1,\dots ,M,\end{array}$$

(13)

where $\Delta t$ is the time step. Notice that the integrals are easily computed by using a Gauss quadrature formula of order $q\ge R+1$. Further details can be found in [18,25].

It is easy to prove that the computational effort of the two combined schemes is linearly dependent on the number of total arcs and nodes of the vascular network. Indeed, the computational time is not influenced by the topology of the considered network, with the consequent possibility of simulating systems of big dimensions. Moreover, the used approach is characterized by scalability. In fact, for each iteration of the simulation, the solutions to the RPs at interfaces are computed independently from the evolution on the edges. This suggests that the computational load could be redistributed; hence, multiprocessing programming is a good possibility for simulative aspects.

4. Simulation Results

This section deals with the simulation of different vascular networks. First, we consider the variations in pressures and velocities inside arteries for a system with 15 edges. Finally, we study a network that contains the main arteries (55 edges) of the human body. The described networks are shown in Figure 1.

The 15-edged network consists of the composition of several 3-edged trees. In particular, edges 1, 4, 5, 6, and 7 have lengths of 1 m and rays of 10 mm; for edges 2, 8, 10, 12, and 14, we have lengths and rays, respectively, of 0.9 m and 9 mm. Finally, edges 3, 9, 11, 13, and 15 have lengths of 0.8 m and rays equal to 8 mm. The 55-edged network is analyzed by following a similar scheme to those proposed in [18,22,23].

Notice that the 15-edged network is a test symmetric and is useful for introducing some phenomena that are still under investigation and are the objects of future research activities.

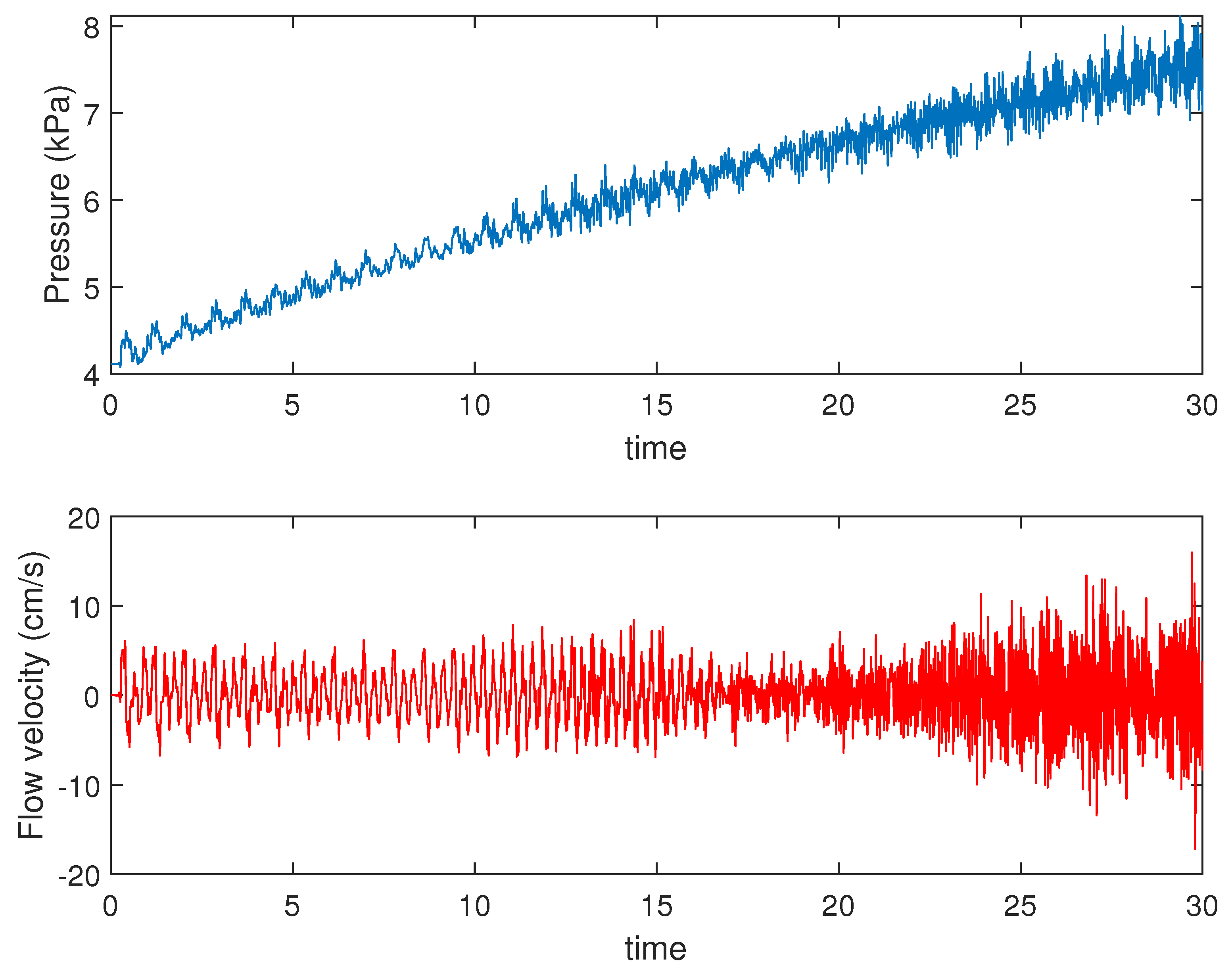
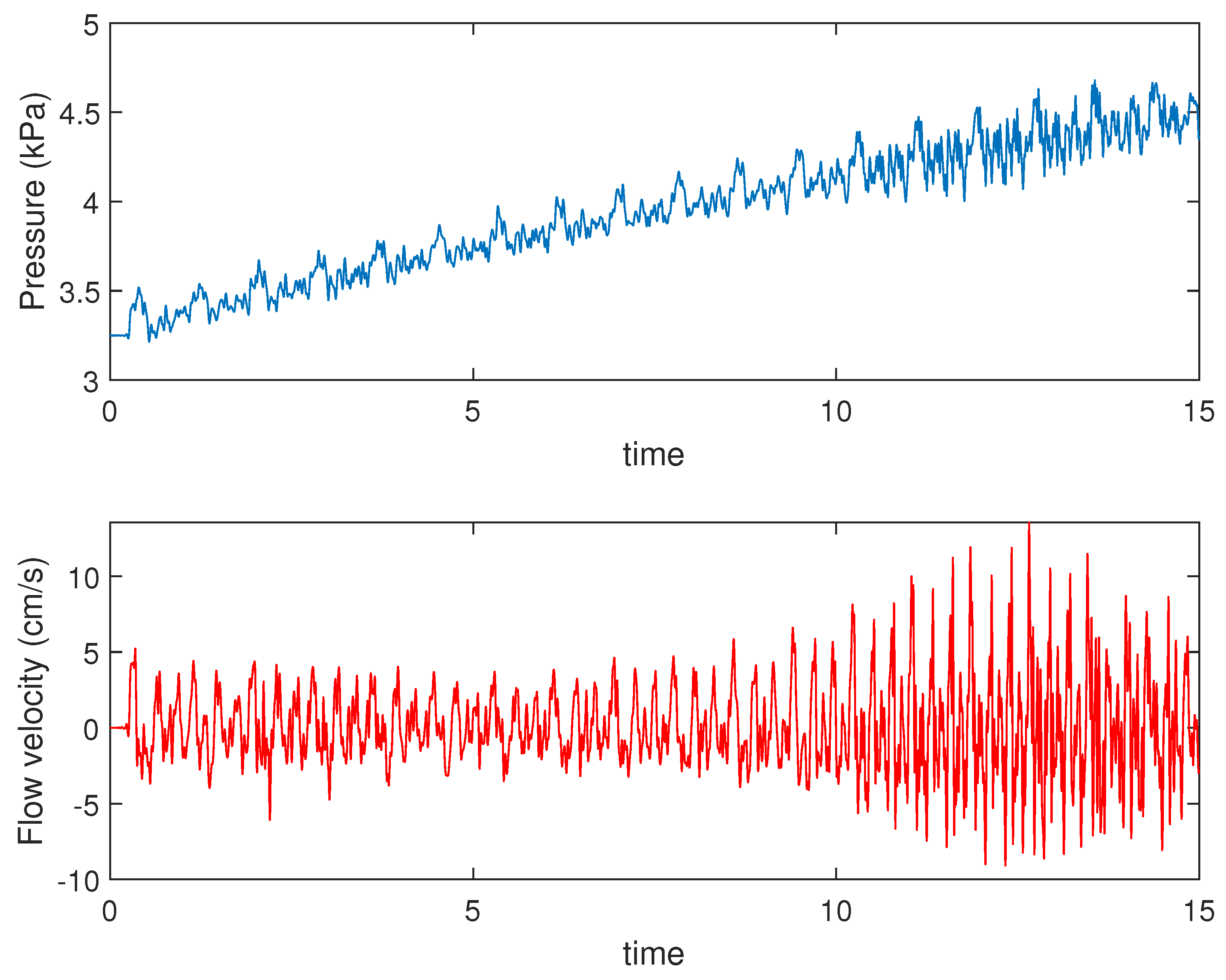
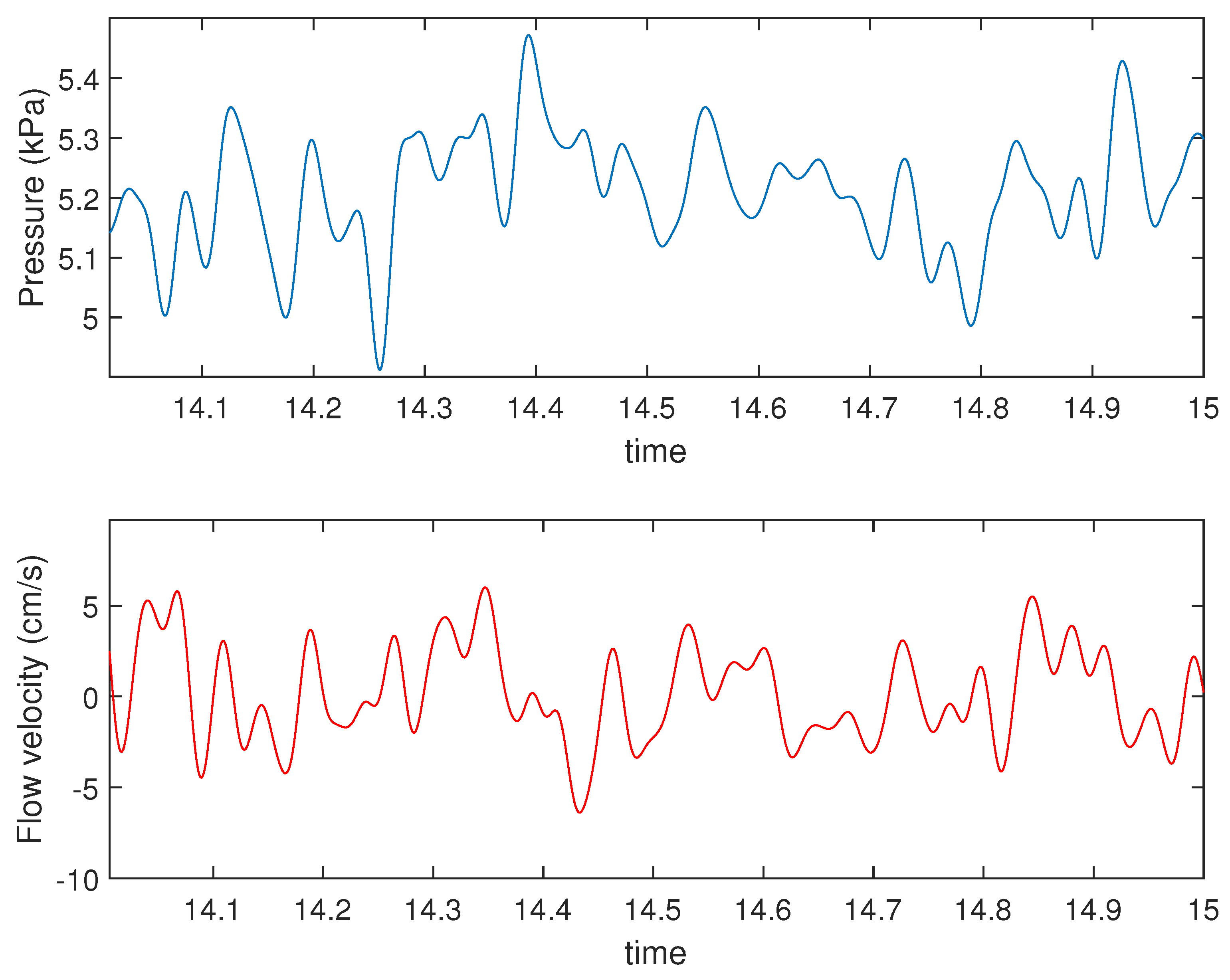
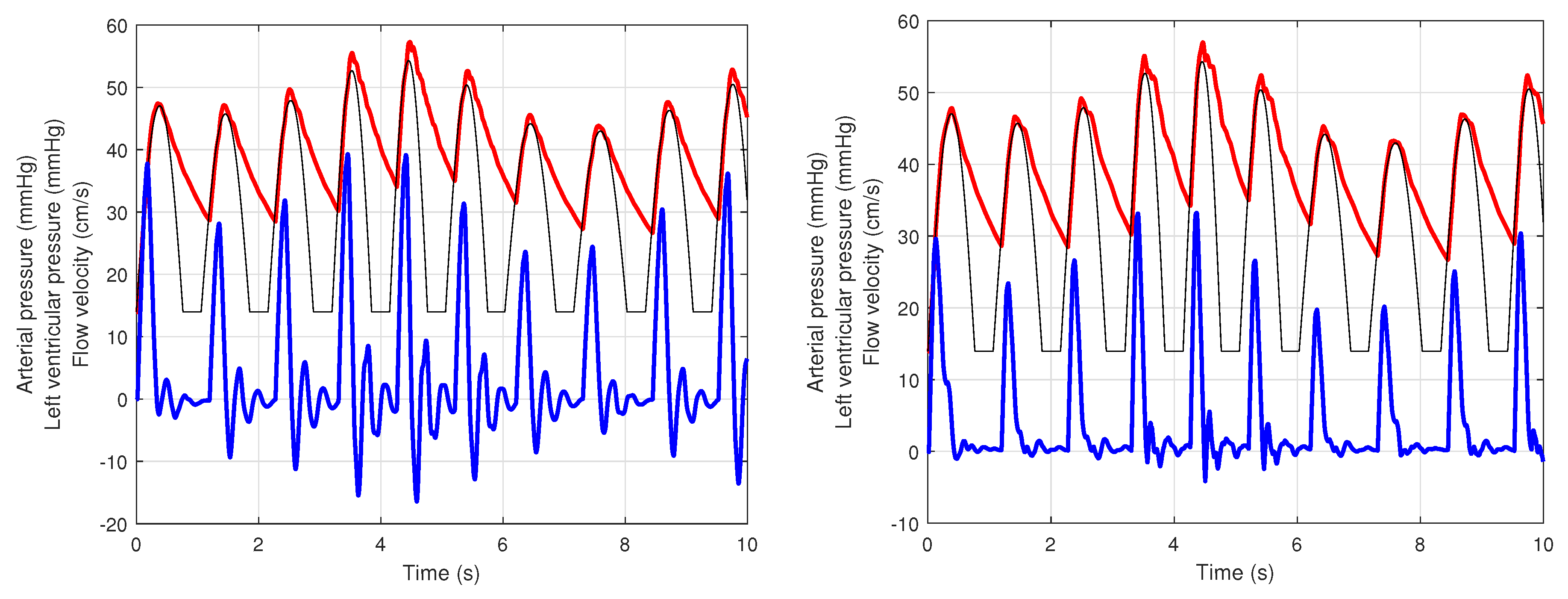
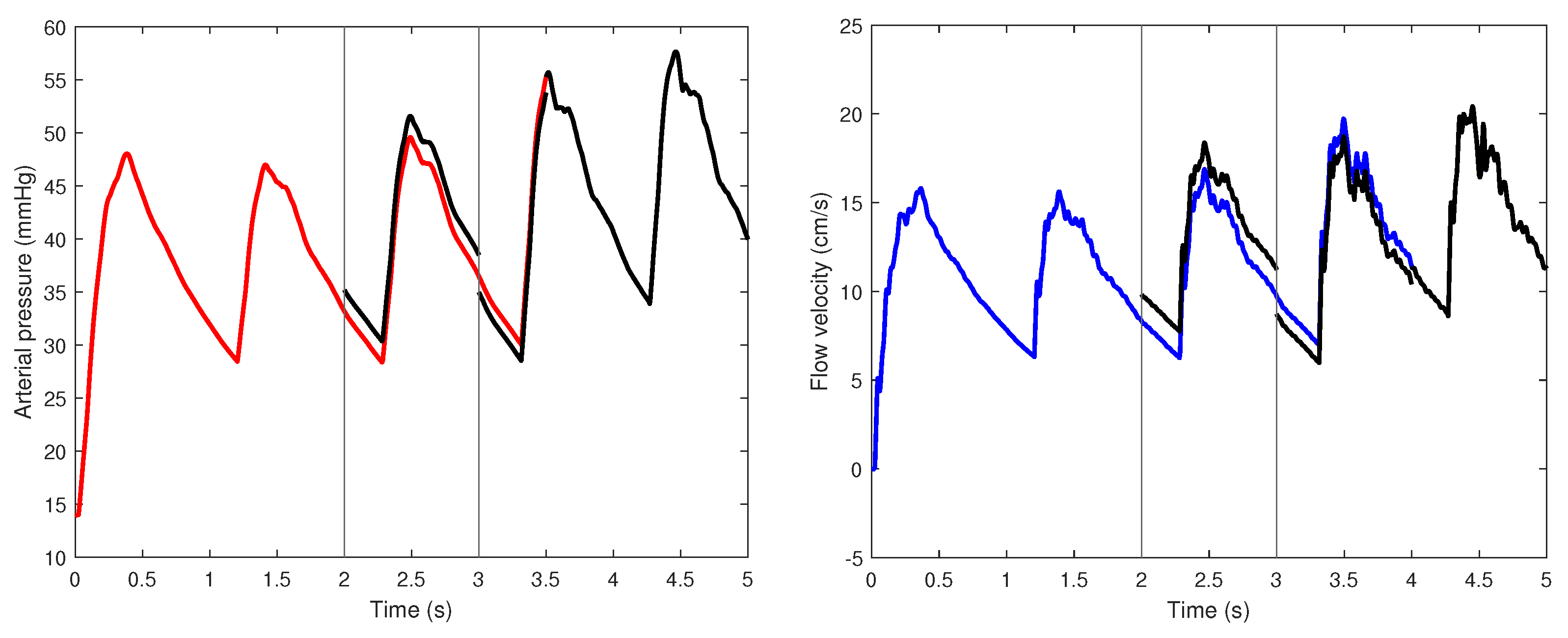
4.1. Presence of Mayer Waves

Focus on the network in Figure 1 (left). We assume that, for all arteries, namely for each edge $I_k$, $k=1,\dots ,K$, we have the same viscosity ${\mu }_k=$$\mu =4·{10}^{-3}$ Pa·s; the same blood density ${\rho }_k=$$\rho =1050$ kg/m³; and the same external pressure $P_{k,ext}=P_{ext}=1862$ Pa; ${\beta }_k=\beta =1418$ kg/s². Finally, at the root of the network, we prescribe a periodic flow rate $Q_{bc}\left(t\right)$, expressed in liters/sec, with period $T=62/HR$ (notice that $HR$ represents the heartbeat):

$$Q_{bc}\left(t\right)=\left\{\begin{array}{cc}7·{10}^{-4}sin{\displaystyle \frac{\pi }{\tau }}t,\hfill & 0\le t\le \tau \hfill \\ 0,\hfill & 0\le t\le T,\hfill \end{array}\right.$$

where $\tau =T/4$ and $HR=75$ beats per minute. The various cases are simulated assuming initial conditions of empty arteries and a compliance model, see Section 2.3.2, for the boundary conditions. The reason is as follows: As we deal with the interactions of the network with tissues and organs, more suitable results are obtained by using more complete assumptions that consider all the energy effects inside the human body.

For the peripheral edges of the network, we assume $C={10}^{-6}$, expressed in Farad, and analyze the cases $R_{\mu }=0.25$, $R_{\mu }=0.75$ and $R_{\mu }=1$. If $R_{\mu }=0.25$, no oscillations occur, as the steady state is reached quite quickly. This situation occurs for either the pressure or the flow velocity, which behave like limited functions. Such a phenomenon is not surprising, as we are dealing with an inflow rate that is a limited function. When high resistance values are used, some high oscillations are observed. In particular, if $R_{\mu }=0.75$, for edge 5, see Figure 2 and Figure 3 for the pressure and flow velocity, where the frequency is about 0.05 Hz; it becomes 0.12 Hz, see Figure 4, in the case $R_{\mu }=1$. Such a difference is reminiscent of the presence of Mayer waves inside vascular networks [15]. These waves, the frequency of which is slower than the usual heart rate, indicate the presence of a regulation mechanism that occurs autonomously within the human body. Indeed, the frequency values obtained in the two different simulations are not equal to one of the Mayer waves; hence, the values of $R_{\mu }$ help to tune the pressure that, in normal cases, should present slow and transitory oscillations. Some further remarks are necessary: Figure 2, Figure 3 and Figure 4 show an increasing evolution for pressure. This is a clear consequence of the boundary conditions that, following the compliance model, allow for the mimicking of the dissipative and conservative effects that involve the narrowing and widening of arteries. In the first instants of simulation, the pressure tends to explode because of the inflow rate, which implies abrupt changes; on the contrary, the flow velocity keeps itself quite limited. This exactly reflects what is observed in real phenomena: the pressure tends to recalibrate to bring the human body into equilibrium conditions for blood flows, and the flow velocity remains approximately stable. The evolution of pressure, indeed, also affects the radii of the various arteries. The pressure itself depends on the cross-section area that is continuously modulated. In this sense, by considering the appropriate scaling, the evolutions of the radii follow the pressure ones. It is also evident that a steady state is reached in each case. This is represented in Figure 5 and Figure 6, which refer, respectively, to edges 13 and 9 for different values of $R_{\mu }$. For different edges, the pressure becomes stable and limited, as does the flow velocity.

The described aspects are still under investigation and are the object of analysis for more complex, real scenarios. Indeed, the obtained results are different from those derived by terminal conditions with a pure resistance $R_t$. In this last case, the initial effects of a rise in pressure cannot be adequately modeled. Hence, the presented simulations prove the real oscillation phenomena due to volume variations of arteries, and this is not shown only in the presence of $R_t$. Such a situation confirms that modeling conservative effects indicates more realistic features for the dynamics of organs and tissues.

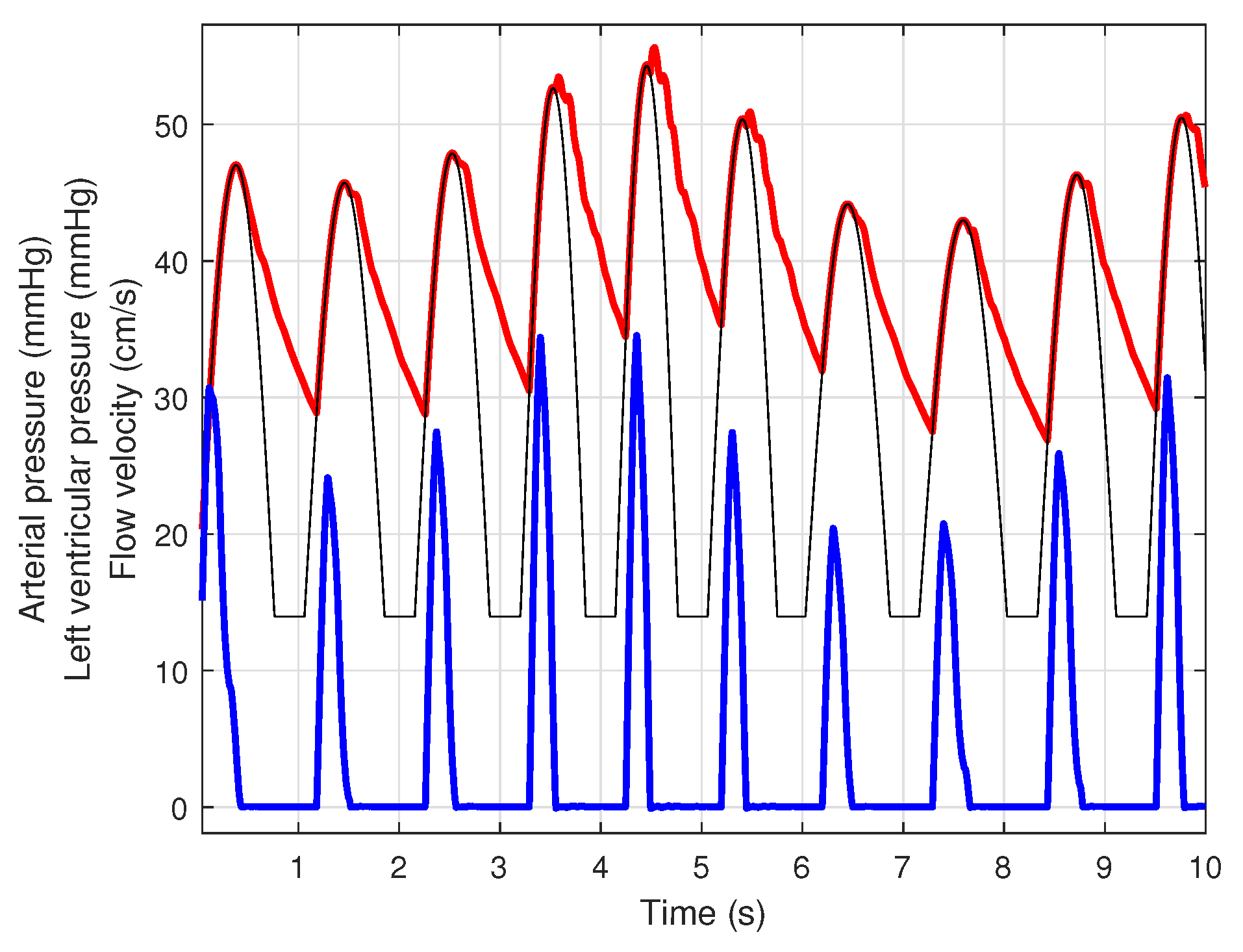
4.2. Principal Arteries

We present the analysis of the principal arteries shown in Figure 1 (right). The various conditions for the simulations are as follows.

The left ventricle pressure, $P_{LV}\left(t\right)$, is dependent on the heart rate, $HR$, as

$$P_{LV}\left(t\right)=P_{ext}+5·{10}^{-6}HRsin{\displaystyle \frac{\pi t}{\tau }},$$

where: $P_{ext}$ is the external pressure for a generic artery, and $\tau =15H{R}^{-1}$. In this case, we assume that viscosity, blood density, and external pressure, as well as heartbeat, are the same as those used in the previous subsection. Finally, if $P\left(t,0\right)$ and $U\left(t,0\right)$ represent, respectively, pressure and flow velocity at $x=0$, for the generic artery, we prescribe the following inflow conditions:

$$U\left(t,0\right)=0\mathrm{if}{P}_{LV}\left(t\right)<P\left(t,0\right),$$

(14)

$$P\left(t,0\right)=P_{LV}\left(t\right)\mathrm{if}U\left(t,0\right)>0.$$

(15)

Equations (14) and (15) simulate a valve model. Precisely, the opening and closing of the valve are determined by the differences in the left ventricle and aortic pressures; the valve closes in the case of Equation (14) and opens when Equation (15) holds. The input data for the simulations are reported in Appendix A. For terminal conditions, we use a compliance model with values of $R_{\mu }$, as in Appendix A, and all equal capacitors, expressed in Farad, $C={10}^{-6}$. The choice of such data obeys some features of the human body, and further details can be found in [8,18]. Notice that the adoption of a compliance model is justified by considering the simultaneous presence of dissipative and conservative effects due to organs.

In Figure 7 and Figure 8, for arteries 1 (ascending aorta), 26 (intercostal edge), and 49 (anterior tibial edge), respectively, we present flow velocity [cm/s] (in blue), arterial pressure [mmHg] (in red), and left ventricular pressure (in black) at the root edge. From Figure 7, we notice how the valve works; the flow is zero when the aortic pressure is higher than the left ventricular one. Indeed, the overall cardiac output strictly depends on the timing of valve opening, and the flow has quite high values, as the artery is directly connected to the heart. Figure 8 shows an expected outcome: As artery 49 is quite far from the heart, the flow is lower than the other quantities. However, the mechanism of tissue irrigation remains identical, as confirmed by the arterial pressure. Artery 26 presents the evolution of flow and pressure in an artery near the lungs. Notice that, in this case, the values of flow velocity are also not very high. Another interesting aspect is the presence of backflow, which is a physiological effect. This phenomenon occurs in middle arteries, such as edges 7 and 18, see Figure 9. For the former, the backflow is quite evident from the negative peaks; for the latter, there are some minimal negative variations.

We also focus on a tilt test, described as follows: Consider a body on a horizontal bed and assume that there are no differences in terms of orthostatic pressures in the vascular network. At a given time instant, a tilt of the table occurs, but the level of the heart remains the same, i.e., much of the body moves downward except the shoulders and head. This creates a variation in the orthostatic pressure in some parts of the vascular network. Such a phenomenon is simulated by changing the external pressure of the generic artery as follows (see [10] for details):

$$P_{ext}\left(t\right)=\rho g\Delta hsin{\displaystyle \frac{\pi t}{2}},$$

where g is the gravity acceleration, and $\Delta h$ is (in the case where a person is upright) the elevation change between the heart and the middle of the edge. The possible variations in aortic pressure and flow velocity at edge 26 (intercostal artery) are presented in Figure 10. The tilt has a duration, T, of just 1 s, and it occurs between seconds 2 and 3 of the simulation process. We present (in black) the variations in arterial pressure and flow velocity. For such quantities, the recovery times, which indicate the autoregulation mechanisms, are different, i.e., about 0.5 s for pressure and about 1 s for flow velocity. Notice that we observe different recovery times for the various edges. Finally, we discuss the numerical optimization for the value of the tilt duration, T, to minimize, either for pressure or flow velocity, the average recovery time in all arteries. By using the MATLAB (version R2023B) routine fminsearch, we found that the optimal value is $T_{opt}\simeq 0.8$. This outcome is meaningful, considering that the tilt test allows for the diagnosis of syncope or dysautonomia. Hence, $T_{opt}$ indicates the duration that avoids meaningful drops in blood pressure or heart rate, with the consequence of becoming unconscious.

5. Conclusions

In this paper, a theoretical model for blood flow in vascular networks is considered. The approach, based on PDEs, describes arterial pressures and flow velocities. Numerical solutions are found by using ad hoc approximation schemes that reveal the details of pressures and velocities in segments of vascular networks. Indeed, the presented results are obtained using some limited assumptions (for instance, blood is seen as a Newtonian fluid); however, the analysis is quite realistic due to the considered case studies. This assumption allows for the investigation of phenomena that are often described by different and more complicated models and numerical approaches.

First, a 15-edged network is presented. The corresponding simulations prove that pressures and velocities have oscillations, which results in consequent volume variations in arteries. This context also relies on the presence of Mayer waves in the human body. Finally, another situation is presented for the principal arteries, and some results were obtained via modeling the heart valve. This last case shows the mechanism of autonomous regulation for blood pressures and flow velocities in general and also in the presence of tilt tests that cause high variations in equilibrium conditions for blood flows.

For future research activities, the primary aim is to study other vascular networks by using models that remove some of the hypotheses of the presented approach. Notice that the adoption of new models implies further numerical methods that are more suitable for the dimension of the studied domains. Then, optimization issues that involve either heart rates or oxygenation caused by the pulmonary system will be faced.