Cutting-Edge Computational Approaches for Approximating Nonlocal Variable-Order Operators
Abstract
1. Introduction
2. Theoretical Results
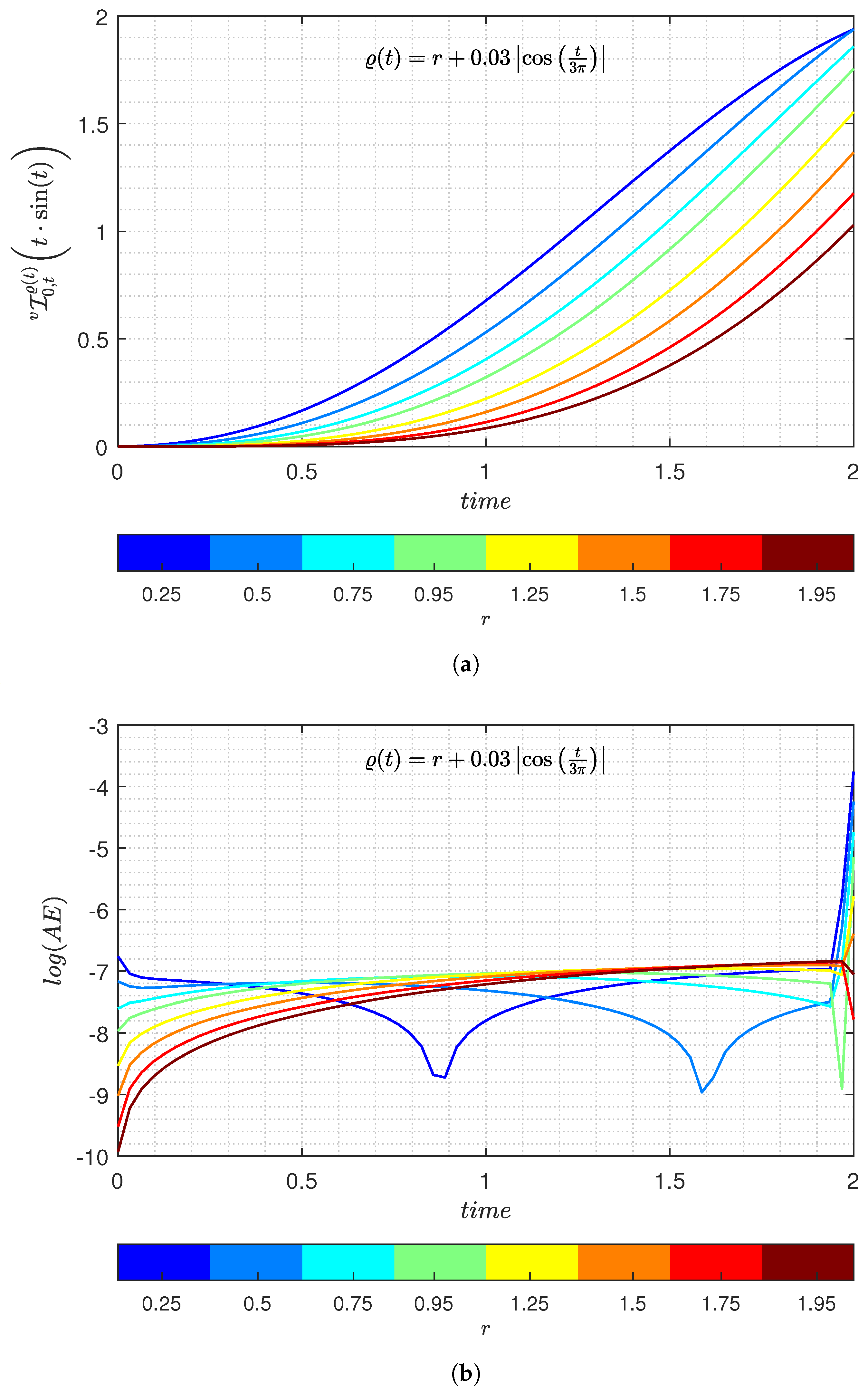
3. Numerical Demonstrations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moniri, Z.; Moghaddam, B.P.; Roudbaraki, M.Z. An Efficient and Robust Numerical Solver for Impulsive Control of Fractional Chaotic Systems. J. Funct. Spaces 2023, 2023, 9077924. [Google Scholar] [CrossRef]
- Babaei, A.; Ahmadi, M.; Jafari, H.; Liya, A. A Mathematical Model to Examine the Effect of Quarantine on the Spread of Coronavirus. Chaos Solitons Fractals 2021, 142, 110418. [Google Scholar] [CrossRef] [PubMed]
- Dabiri, A.; Butcher, E.A. Numerical solution of multi-order fractional differential equations with multiple delays via spectral collocation methods. Appl. Math. Model. 2018, 56, 424–448. [Google Scholar] [CrossRef]
- Moghaddam, B.P.; Dabiri, A.; Mostaghim, Z.S.; Moniri, Z. Numerical solution of fractional dynamical systems with impulsive effects. Int. J. Mod. Phys. C 2023, 34, 2350013. [Google Scholar] [CrossRef]
- Zahra, W.K.; Ouf, W.A.; El-Azab, M.S. A robust uniform B-spline collocation method for solving the generalized PHI-four equation. Appl. Appl. Math. Int. J. (AAM) 2016, 11, 24. [Google Scholar]
- Zahra, W.K.; Ouf, W.A.; El-Azab, M.S. Cubic B-spline collocation algorithm for the numerical solution of Newell Whitehead Segel type equations. Electron. J. Math. Anal. Appl. 2014, 2, 81–100. [Google Scholar]
- Behforooz, H. Approximation by integro cubic splines. Appl. Math. Comput. 2006, 175, 8–15. [Google Scholar] [CrossRef]
- Zhanlav, T.; Mijiddorj, R. Integro cubic splines and their approximation properties. Appl. Math. Ser. Tver State Univ. Russ. 2008, 26, 65–77. [Google Scholar] [CrossRef]
- Behforooz, H. Interpolation by integro quintic splines. Appl. Math. Comput. 2010, 216, 364–367. [Google Scholar] [CrossRef]
- Zhanlav, T.; Mijiddorj, R. The local integro cubic splines and their approximation properties. Appl. Math. Comput. 2010, 216, 2215–2219. [Google Scholar] [CrossRef]
- Lang, F.G.; Xu, X.P. On integro quartic spline interpolation. J. Comput. Appl. Math. 2012, 236, 4214–4226. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, X. Integro sextic spline interpolation and its super convergence. Appl. Math. Comput. 2013, 219, 6431–6436. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, X. Integro quadratic spline interpolation. Appl. Math. Model. 2015, 39, 2973–2980. [Google Scholar] [CrossRef]
- Lang, F.G.; Xu, X.P. On the superconvergence of some quadratic integro-splines at the mid-knots of a uniform partition. Appl. Math. Comput. 2018, 338, 507–514. [Google Scholar] [CrossRef]
- Wu, J.; Shan, T.; Chungang, Z. Integro quadratic spline quasi-interpolants. J. Syst. Sci. Math. Sci. 2018, 38, 1407. [Google Scholar]
- Wu, J.; Ge, W.; Zhang, X. Integro spline quasi-interpolants and their super convergence. Comput. Appl. Math. 2020, 39, 1–11. [Google Scholar] [CrossRef]
- Lang, F.G.; Xu, X.P. Some new super convergence of a quartic integro-spline at the mid-knots of a uniform partition. ScienceAsia 2022, 48, 479. [Google Scholar] [CrossRef]
- Samko, S. Fractional integration and differentiation of variable order: An overview. Nonlinear Dyn. 2012, 71, 653–662. [Google Scholar] [CrossRef]
- Hao, W.K.; Wang, J.S.; Li, X.D.; Song, H.M.; Bao, Y.Y. Probability distribution arithmetic optimization algorithm based on variable order penalty functions to solve combined economic emission dispatch problem. Appl. Energy 2022, 316, 119061. [Google Scholar] [CrossRef]
- Zhang, Q.; Shang, Y.; Li, Y.; Cui, N.; Duan, B.; Zhang, C. A novel fractional variable-order equivalent circuit model and parameter identification of electric vehicle Li-ion batteries. ISA Trans. 2020, 97, 448–457. [Google Scholar] [CrossRef]
- Mehta, P.P.; Pang, G.; Song, F.; Karniadakis, G.E. Discovering a universal variable-order fractional model for turbulent Couette flow using a physics-informed neural network. Fract. Calc. Appl. Anal. 2019, 22, 1675–1688. [Google Scholar] [CrossRef]
- Zhang, S. The uniqueness result of solutions to initial value problems of differential equations of variable-order. Rev. Real Acad. Cienc. Exactas FíSicas y Naturales. Serie A. MatemáTicas 2017, 112, 407–423. [Google Scholar] [CrossRef]
- Sarwar, S. On the Existence and Stability of Variable Order Caputo Type Fractional Differential Equations. Fractal Fract. 2022, 6, 51. [Google Scholar] [CrossRef]
- Telli, B.; Souid, M.S.; Alzabut, J.; Khan, H. Existence and Uniqueness Theorems for a Variable-Order Fractional Differential Equation with Delay. Axioms 2023, 12, 339. [Google Scholar] [CrossRef]
- Moghaddam, B.P.; Yaghoobi, S.; Machado, J.A.T. An Extended Predictor–Corrector Algorithm for Variable-Order Fractional Delay Differential Equations. J. Comput. Nonlinear Dyn. 2016, 11, 061001. [Google Scholar] [CrossRef]
- Zhao, T.; Wu, Y. Hermite Cubic Spline Collocation Method for Nonlinear Fractional Differential Equations with Variable-Order. Symmetry 2021, 13, 872. [Google Scholar] [CrossRef]
- Sun, L.Y.; Lei, S.L.; Sun, H.W. Efficient Finite Difference Scheme for a Hidden-Memory Variable-Order Time-Fractional Diffusion Equation. Comp. Appl. Math. 2023, 42, 362. [Google Scholar] [CrossRef]
- Sun, H.G.; Chang, A.; Zhang, Y.; Chen, W. A Review on Variable-Order Fractional Differential Equations: Mathematical Foundations, Physical Models, Numerical Methods and Applications. Fract. Calc. Appl. Anal. 2019, 22, 27–59. [Google Scholar] [CrossRef]
- Shah, K.; Naz, H.; Sarwar, M.; Abdeljawad, T. On spectral numerical method for variable-order partial differential equations. AIMS Math. 2022, 7, 10422–10438. [Google Scholar] [CrossRef]
- Kadkhoda, N. A numerical approach for solving variable order differential equations using Bernstein polynomials. Alex. Eng. J. 2020, 59, 3041–3047. [Google Scholar] [CrossRef]
- Tural-Polat, S.N.; Dincel, A.T. Numerical solution method for multi-term variable order fractional differential equations by shifted Chebyshev polynomials of the third kind. Alex. Eng. J. 2022, 61, 5145–5153. [Google Scholar] [CrossRef]
- Samko, S.G.; Ross, B. Integration and Differentiation to a Variable Fractional Order. Integral Transform. Spec. Funct. 1993, 1, 277–300. [Google Scholar] [CrossRef]
- Samko, S.G. Fractional Integration and Differentiation of Variable Order. Ann. Math. 1995, 21, 213–236. [Google Scholar] [CrossRef]
- Moghaddam, B.P.; Machado, J.A.T. Extended Algorithms for Approximating Variable Order Fractional Derivatives with Applications. J. Sci. Comput. 2016, 71, 1351–1374. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Dover Publications: Mineola, NY, USA, 1964. [Google Scholar]
- Moghaddam, B.P.; Machado, J.A.T.; Behforooz, H. An integro quadratic spline approach for a class of variable-order fractional initial value problems. Chaos Solitons Fractals 2017, 102, 354–360. [Google Scholar] [CrossRef]
- Keshi, F.K.; Moghaddam, B.P.; Aghili, A. A numerical approach for solving a class of variable-order fractional functional integral equations. Comput. Appl. Math. 2018, 37, 4821–4834. [Google Scholar] [CrossRef]




| IQS Algorithm | Developed Algorithm | ||||||
|---|---|---|---|---|---|---|---|
| 2.02 | 0.719 | 2.64 | 5.310 | ||||
| 1.93 | 2.672 | 2.53 | 8.216 | ||||
| 1.87 | 9.563 | 2.45 | 14.203 | ||||
| 1.83 | 36.954 | 2.39 | 28.765 | ||||
| 1.18 | 0.640 | 2.53 | 5.281 | ||||
| 1.18 | 2.344 | 2.44 | 8.187 | ||||
| 1.18 | 8.313 | 2.38 | 14.109 | ||||
| 1.18 | 31.344 | 2.34 | 28.562 | ||||
| 1.71 | 0.703 | 3.35 | 6.297 | ||||
| 1.68 | 2.688 | 3.21 | 8.297 | ||||
| 1.66 | 10.047 | 3.11 | 14.375 | ||||
| 1.64 | 39.328 | 3.04 | 29.578 | ||||
| 0.86 | 0.688 | 2.75 | 6.297 | ||||
| 0.92 | 2.516 | 2.63 | 8.172 | ||||
| 0.96 | 8.172 | 2.56 | 14.250 | ||||
| 0.99 | 30.203 | 2.50 | 28.921 | ||||
| B-Spline Algorithm | Developed Algorithm | ||||||
|---|---|---|---|---|---|---|---|
| 2.94 | 0.328 | 4.15 | 5.719 | ||||
| 2.74 | 0.672 | 3.83 | 8.625 | ||||
| 2.61 | 2.594 | 3.59 | 15.328 | ||||
| 2.40 | 8.610 | 3.42 | 29.391 | ||||
| 2.94 | 0.297 | 4.60 | 5.921 | ||||
| 2.75 | 0.657 | 4.35 | 8.734 | ||||
| 2.63 | 2.047 | 4.13 | 14.687 | ||||
| 2.54 | 7.938 | 3.96 | 29.359 | ||||
| 2.90 | 0.313 | 4.85 | 5.906 | ||||
| 2.72 | 0.672 | 4.69 | 9.266 | ||||
| 2.39 | 10.047 | 4.56 | 14.828 | ||||
| 2.42 | 9.594 | 4.46 | 29.390 | ||||
| 2.91 | 0.312 | 4.90 | 5.731 | ||||
| 2.73 | 0.641 | 4.76 | 8.781 | ||||
| 2.61 | 2.532 | 4.65 | 14.859 | ||||
| 2.53 | 7.390 | 4.56 | 29.406 | ||||
| Finite Difference Algorithm | Developed Algorithm | ||||||
|---|---|---|---|---|---|---|---|
| 2.39 | 0.297 | 4.22 | 7.047 | ||||
| 2.12 | 0.829 | 3.78 | 11.796 | ||||
| 1.93 | 3.141 | 3.49 | 23.265 | ||||
| 1.80 | 12.485 | 3.28 | 40.703 | ||||
| 2.36 | 0.172 | 4.21 | 6.984 | ||||
| 2.09 | 0.797 | 3.77 | 11.906 | ||||
| 1.92 | 3.125 | 3.47 | 23.156 | ||||
| 1.79 | 12.656 | 3.26 | 40.609 | ||||
| 2.33 | 0.313 | 4.27 | 6.953 | ||||
| 2.07 | 0.844 | 3.83 | 11.781 | ||||
| 1.90 | 2.203 | 3.53 | 23.312 | ||||
| 1.77 | 12.375 | 3.32 | 40.671 | ||||
| 2.32 | 0.281 | 4.27 | 7.062 | ||||
| 2.06 | 0.797 | 3.82 | 11.765 | ||||
| 1.89 | 3.156 | 3.53 | 23.406 | ||||
| 1.77 | 12.266 | 3.31 | 40.781 | ||||
| IQS Algorithm | Developed Algorithm | ||||||
|---|---|---|---|---|---|---|---|
| 1.55 | 1.687 | 4.32 | 1.968 | ||||
| 1.46 | 5.765 | 3.94 | 1.765 | ||||
| 1.40 | 21.641 | 3.68 | 2.062 | ||||
| 1.35 | 86.219 | 3.50 | 3.281 | ||||
| 2.19 | 1.234 | 4.00 | 1.828 | ||||
| 2.05 | 6.328 | 3.63 | 1.796 | ||||
| 1.95 | 22.703 | 3.39 | 2.125 | ||||
| 1.87 | 90.031 | 3.21 | 3.437 | ||||
| 3.26 | 1.625 | 5.01 | 1.656 | ||||
| 2.97 | 5.844 | 4.59 | 1.828 | ||||
| 2.77 | 21.125 | 4.31 | 2.156 | ||||
| 2.64 | 84.600 | 4.10 | 3.515 | ||||
| 3.35 | 1.703 | 5.04 | 1.687 | ||||
| 3.05 | 5.750 | 4.61 | 1.760 | ||||
| 2.84 | 21.125 | 4.33 | 2.156 | ||||
| 2.70 | 85.344 | 4.13 | 3.453 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanha, N.; Parsa Moghaddam, B.; Ilie, M. Cutting-Edge Computational Approaches for Approximating Nonlocal Variable-Order Operators. Computation 2024, 12, 14. https://doi.org/10.3390/computation12010014
Tanha N, Parsa Moghaddam B, Ilie M. Cutting-Edge Computational Approaches for Approximating Nonlocal Variable-Order Operators. Computation. 2024; 12(1):14. https://doi.org/10.3390/computation12010014
Chicago/Turabian StyleTanha, Nayereh, Behrouz Parsa Moghaddam, and Mousa Ilie. 2024. "Cutting-Edge Computational Approaches for Approximating Nonlocal Variable-Order Operators" Computation 12, no. 1: 14. https://doi.org/10.3390/computation12010014
APA StyleTanha, N., Parsa Moghaddam, B., & Ilie, M. (2024). Cutting-Edge Computational Approaches for Approximating Nonlocal Variable-Order Operators. Computation, 12(1), 14. https://doi.org/10.3390/computation12010014








