Enhancing the Hardware Pipelining Optimization Technique of the SHA-3 via FPGA

Abstract

Information is transmitted between multiple insecure routing hops in text, image, video, and audio. Thus, this multi-hop digital data transfer makes secure transmission with confidentiality and integrity imperative. This protection of the transmitted data can be achieved via hashing algorithms. Furthermore, data integrity must be ensured, which is feasible using hashing algorithms. The advanced cryptographic Secure Hashing Algorithm 3 (SHA-3) is not sensitive to a cryptanalysis attack and is widely preferred due to its long-term security in various applications. However, due to the ever-increasing size of the data to be transmitted, an effective improvement is required to fulfill real-time computations with multiple types of optimization. The use of FPGAs is the ideal mechanism to improve algorithm performance and other metrics, such as throughput (Gbps), frequency (MHz), efficiency (Mbps/slices), reduction of area (slices), and power consumption. Providing upgraded computer architectures for SHA-3 is an active area of research, with continuous performance improvements. In this article, we have focused on enhancing the hardware performance metrics of throughput and efficiency by reducing the area cost of the SHA-3 for all output size lengths (224, 256, 384, and 512 bits). Our approach introduces a novel architectural design based on pipelining, which is combined with a simplified format for the round constant (RC) generator in the Iota ($\iota$) step only consisting of 7 bits rather than the standard 64 bits. By reducing hardware resource utilization in the area and minimizing the amount of computation required at the Iota ($\iota$) step, our design achieves the highest levels of throughput and efficiency. Through extensive experimentation, we have demonstrated the remarkable performance of our approach. Our results showcase an impressive throughput rate of 22.94 Gbps and an efficiency rate of 19.95 Mbps/slices. Our work contributes to advancing computer architectures tailored for SHA-3, therefore unlocking new possibilities for secure and high-performance data transmission.

1. Introduction

The transmission of sensitive data in a highly dependable, highly secure, and highly reliable way has become urgent in the last few years. Cryptography is an important technique used to store information, protect it, and secure it against unauthorized access while it is being transmitted. These three goals may all be accomplished using cryptography. For example, the healthcare sector, the military, the government, industry, educational institutions, and private businesses collect a vast amount of personally identifiable digital information stored in a network environment. Therefore, cryptographic algorithms have seen an increased amount of application in recent years due to their ability to ensure a high level of security for various digital media formats, such as photos, text, video, and audio [1,2,3].

A binding domain of cryptography consists of hashing. Hashing is computing a fixed-length string using a standard algorithm, regardless of the input size. The output string will be the same length for the same hashing algorithm, no matter the input size. Each output string is unique for a specific input, and vice versa; even one byte altered results in a very different output. This property makes hashing a cornerstone in our ICT infrastructure, and algorithms have become essential in every aspect of our lives [4,5,6]. Hashing is used in every authentication scheme, from our local operating system to cloud banking or web email services. Hashing is also used in integrity verification, from the local file system like Zettabyte File System (ZFS) [7], which stores a hash for every block, to the operating system that keeps hashes for every critical file. Windows, Linux, FreeBSD, and other popular file systems keep a database with hashes for core components, up to the intrusion detection systems that inspect every file and compute its hash compared to a golden reference. Hashing is also used in data transmission to guarantee integrity, from the IP protocol up to the secure web browsing of the HTTPS/TLS protocol. Hashing is also used in indexing databases, allowing queries to execute faster, which is essential in our modern era with the humongous amounts of data created and processed. Everyone interacts with multiple hashing techniques, even if they do not know it. For this reason, it is a lucrative target for malicious individuals to exploit. They are utilizing, implementing, and accelerating new, more robust, and secure hashing algorithms [8].

Today, old standards of hash functions are vulnerable to attacks. Up today, many successful attacks have been recorded against the SHA-1 [9] and the SHA-2 hashing algorithms [10,11,12]. Thus, the National Institute of Standards and Technology (NIST) decided to investigate new, more secure hashing algorithms and adopted the SHA-3 (Keccak), which offers a higher level of security [13,14,15]. These new hash functions use larger hash values and more complex algorithms, making it much more difficult for attackers to find collisions or other vulnerabilities. Hash functions are widely used in the Hashed Message Authentication Code (HMAC) [16], network security [17], in the Digital Signatures [18], in Secure Electronic Transactions (SET) [19], and in Public Key Infrastructure (PKI) [20].

The new SHA-3 emerged during a competition organized by NIST in 2011 for the new Secure Hash Algorithm (SHA). Open competitions have been used as methods of selection for cryptographic standards worldwide. Therefore, in 2012, NIST announced that the Keccak hash function would represent SHA-3. The new hashing algorithm, SHA-3, provides high efficiency and throughput in hardware, both in Graphics Processing Unit (GPU) and in Field-Programmable Gate Array (FPGA) [21]. The FPGA-based embedded processing systems provide significant computing resources as security requirements grow [22]. FPGAs are also well-known for their high-performance capabilities and low energy consumption, making them ideal for embedded applications where space and power are limited [23,24]. With the growing need for secure systems, FPGAs have become attractive for implementing security features such as encryption, authentication, and intrusion detection. Therefore, the cryptography community concentrates on the SHA-3 (Keccak algorithm), which provides high performance in hardware and flexibility [25,26].

The following is a summary of the contributions given in this article:

• We propose a new method optimization technique based on pipelining for the algorithm SHA-3. This method places the additional register after step Theta ($\theta$) in the function f. The newly presented optimization technique can operate as the policy for the hardware optimization technique of the SHA-3. Our design performs significant advancements in performance metrics and reduces the area cost of FPGA devices.
• We suggest a novel format for the RC generator that is more straightforward to increase performance (throughput and efficiency) while simultaneously decreasing the amount of hardware resources available in the area. The new, more straightforward structure RC generator only consists of 7-bits rather than the previous 64-bits, which helps minimize the amount of computation required at the Iota ($\iota$) step, where the number of necessary XORs is decreased to 7.
• We confirmed the accuracy of the whole design with reliable examples provided by NIST. At the same time, we performed extensive evaluation and analysis to compare the proposed architecture’s area (slices), throughput (Gbps), frequency (MHz), and efficiency (Mbps/slices) to other similar methods in the published literature.

The rest of the article is organized as follows: In the following Section 2, we briefly introduce the SHA-3 overview. In Section 3, we present the related works in the literature. Section 4 defines our new proposed hardware optimization techniques of the SHA-3 algorithm on FPGA. In Section 5, we show the experimental outcomes of our study. In Section 6, we discuss the effects of our optimization technique and the comparisons with other relevant studies. Finally, Section 7 summarizes our article’s conclusions and future work.

2. The SHA-3 Overview

In 2012, after a contest conducted by the NIST, the Keccak hash function was the next SHA-3 standard. However, unlike the SHA-1 and SHA-2 standards, SHA-3 primarily depends on the sponge functions (absorb/squeeze), as presented in Figure 1.

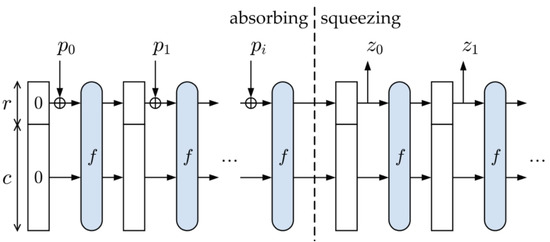
Figure 1. Sponge function of the SHA-3.

The sponge procedure is a state matrix of $b=r+c$ bits, where c bits is the capacity and r bits are the bit rate. In the beginning, this state matrix is initialized from zero values. Keccak hash function manages the state b as a three-dimensional matrix $5\times 5\times (word-size)$. An input message is padded to form its total size, a multiple of r bits. Then the padded message is split into blocks of equal size Pi. At the absorbing step, r bits $XOR$ with each block and permutation function f. The f function is the central processing part and includes 24 rounds with procedures. The five distinct steps of the function f are Theta ($\theta$), Rho ($\rho$), P_i ($\pi$), Chi ($\chi$) and Iota ($\iota$) on a 1600-bit state matrix A [27].

The process’s Theta ($\theta$) step includes a parity computation, rotated by one position, then bitwise XOR. The Rho ($\rho$) step rotates by an offset that depends on the word assignment, and the P_i ($\pi$) step is a permutation. The Chi ($\chi$) step operates bitwise XOR, NOT, and AND gates to modify the process. Lastly, the Iota ($\iota$) step involves adding a constant value to the sequence at each round. The steps Theta ($\theta$), Rho ($\rho$), P_i ($\pi$), Chi ($\chi$) and Iota ($\iota$) are detailed in Equations (1)–(4).

Step Theta ($\theta$):

$$\begin{array}{c}C\left[x\right]=A[x,0]\oplus A[x,1]\oplus A[x,2]\oplus A[x,3]\oplus A[x,4],\hfill \\ x=0,1,2,3,4\hfill \\ D\left[x\right]=C[x-1]\oplus ROT\left(C\right[x+1],1),\hfill \\ x=0,1,2,3,4\hfill \\ A[x,y]=A[x,y]\oplus D\left[x\right],\hfill \\ x=0,1,2,3,4\hfill \end{array}$$

(1)

The state array A is also used to calculate a serviceable $5\times 5$ array B in the following two steps. Interestingly, the array $B[i,j]$ describes a bit stream with w bits.

Steps Rho ($\rho$) and Pi ($\pi$):

$$\begin{array}{c}B[y,2x+3y]=ROT\left(A\right[x,y],r[x,y\left]\right),\hfill \\ (x,y)=0,1,2,3,4\hfill \end{array}$$

(2)

Step Chi ($\chi$):

$$\begin{array}{c}A[x,y]=B[x,y]\oplus \left(NOTB\right[x+1,y\left]\right)AND\left(B\right[x+2,y\left]\right),\hfill \\ (x,y)=0,1,2,3,4\hfill \end{array}$$

(3)

Step Iota ($\iota$):

$$A[0,0]=A[0,0]\oplus RC\left[i\right]$$

(4)

The round constants are produced by the RC generator that is used in Iota ($\iota$) step. The $R{C}_i$ function is present in Table 1, and it is made up of 24 different value permutations that may assign 64-bit data to the SHA-3 function [15].

Table 1. The $R{C}_i$ generator in Iota ($\iota$) step.

$\mathit{R}{\mathit{C}}_0$	0000000000000001	$\mathit{R}{\mathit{C}}_8$	000000000000008A	$\mathit{R}{\mathit{C}}_{16}$	8000000000008002
$R{C}_1$	0000000000008082	$R{C}_9$	0000000000000088	$R{C}_{17}$	8000000000000080
$R{C}_2$	800000000000808A	$R{C}_{10}$	0000000080008009	$R{C}_{18}$	000000000000800A
$R{C}_3$	8000000080008000	$R{C}_{11}$	000000008000000A	$R{C}_{19}$	800000008000000A
$R{C}_4$	000000000000808B	$R{C}_{12}$	000000008000808B	$R{C}_{20}$	8000000080008081
$R{C}_5$	0000000080000001	$R{C}_{13}$	800000000000008B	$R{C}_{21}$	8000000000008080
$R{C}_6$	8000000080008081	$R{C}_{14}$	8000000000008089	$R{C}_{22}$	0000000080000001
$R{C}_7$	8000000000008009	$R{C}_{15}$	8000000000008003	$R{C}_{23}$	8000000080008008

According to Table 2, the NIST has determined four different variants of the SHA-3 hashing algorithm based on the message M and the output length size d.

Table 2. The four forms of the SHA-3.

Message (M)	Output Length Size (d)	Rate (r) (Block Size)	Capacity (c)
224	224	1152	448
256	256	1088	512
384	384	832	768
512	512	576	1024

3. Related Work

The community of cryptography has done substantial research on optimizing models and techniques for the SHA-3 in FPGA devices [28]. Each of these models aims to improve the throughput of the FPGA while simultaneously decreasing the amount of area and the amount of power it needs [29,30,31,32]. Despite this, there is still an urgent need to increase performance measures related to throughput and area reduction. In this part, we will discuss other research studies comparable to ours.

The paper’s authors [33], suggested a pipelining technique for the SHA-3 512 bits. The proposed design was implemented in the FPGA Virtex-5. The proposed architecture needs 2.326 slices (area), achieves the highest frequency rate of 306 MHz, and demonstrates a throughput rate of 5.56 Gbps and a rate of efficiency of 2.40 Mbps/slices. In [34], the authors proposed a two-staged pipelined technique for the SHA-3 256. The proposed design was implemented in FPGA Virtex-5. They achieved a maximum frequency of 317.11 MHz, throughput of 12.68 Gbps, area (slices) of 4.793, and efficiency of 2.71 Mbps/slices.

The authors [35] suggested a pipelining design for the SHA-3 512. The proposed method was implemented in the FPGA Virtex-5. The proposed architecture achieves the highest frequency rate of 273 MHz, needs 1.163 slices (area), demonstrates a throughput rate of 7.80 Gbps, and an efficiency rate of 6.06 Mbps/slices. In [36], the writers proposed a two-stage pipelined design for the SHA-3 512 on three FPGA devices. The proposed architecture was implemented in FPGA boards, Virtex-4, Virtex-5, and Virtex-6. The outcomes demonstrate that the suggested method for the SHA-3 512 performs more promising effects with Virtex-6. They reached a maximum frequency rate of 391 MHz, throughput rate of 18.76 Gbps, area (slices) of 2.296, and efficiency of 8.17 Mbps/slices.

In a study by [37], the authors proposed a two-staged pipelined technique for the SHA-3 256. The VHDL programing language is used and implemented in the Virtex-5, Virtex-6, and Virtex-7 FPGA boards. Outcomes indicate that the suggested design achieves better results with Virtex-7. They gained a throughput rate of 20.8 Gbps, the highest frequency rate of 434 MHz, an area rate of 1618 slices, and an efficiency of 12.90 Mbps/slices. The authors [38] suggested a pipelining design for the SHA-3 256 and SHA-3 512. The proposed method was implemented in the Virtex-5 and Virtex-6 FPGA boards. The proposed method for SHA-3 256 needs 1.456 slices (area) and demonstrates a throughput rate of 14.942 Gbps and an efficiency rate of 10.26 Mbps/slices with Virtex-6, and for SHA-3 512 needs 1.263 slices (area) and demonstrates a throughput rate of 8.114 Gbps and an efficiency rate of 6.42 Mbps/slices with Virtex-6.

In [39] they proposed an architecture that supports all output size lengths (224, 256, 384, and 512 bits) of the SHA2 and SHA-3 cryptographic hash functions. The proposed design was implemented and verified on a Stratix IV FPGA, utilizing the NIOS II processor. The proposed architecture for the SHA-3 needs 5.363 slices (area) and achieves the highest frequency rate of 110 MHz. The authors of [40] presented a design for the SHA-3 512 algorithm. This design was implemented in the Virtex-5 FPGA boards. In Virtex-5, the proposed architecture required 1.680 slices and a frequency of 387 MHz. The proposed architecture achieves a throughput of 8.06 Gbps and 4.91 Mbps/slices efficiency.

Table 3 summarizes the techniques thought with the two-staged pipelined method for the SHA-3 algorithm. Most of the study has focused on the register’s placement after the Pi step ($\pi$) and used the classic RC generator with 64 bits. This work aims to compare the performance metrics efficiency (Mbps/slices) and throughput (Gbps) when we insert the register after step Pi ($\pi$) or step Theta ($\theta$) in the hash permutation f function with the new format of the RC generator with 7-bits for all output lengths 224, 256, 384 and 512 bits. Our extensive experiments reveal that the outcomes obtained are directly affected by the critical path of the f function, which decreases significantly when the register is inserted after step Theta ($\theta$) with the new simplified structure RC generator. The proposed optimization technique surpasses previous investigations in performance measures and can be applied as a strategy for FPGA boards.

Table 3. Summary of the approaches in the publications of pipelined technique for the SHA-3 algorithm.

Work	Output Length	Register’s Placement	RC Generator
Provelengios et al. [33]	SHA-3 512	-	64-bit
Mestiri et al. [34]	SHA-3 256	after step Pi ($\pi$)	64-bit
Sunda et al. [35]	SHA-3 512	after step Pi ($\pi$)	64-bit
Ioannou et al. [36]	SHA-3 512	after step Pi ($\pi$)	64-bit
Athanasiou et al. [37]	SHA-3 256	after step Pi ($\pi$)	64-bit
Gaj et al. [38]	SHA-3 256	after step Pi ($\pi$)	64-bit
Gaj et al. [38]	SHA-3 512	after step Pi ($\pi$)	64-bit
Nannipieri et al. [39]	SHA-3	-	64-bit
Mestiri et al. [40]	SHA-3 512	-	64-bit

4. Proposed Pipelining Optimization Technique of the SHA-3

The main goal of our work is to attain a higher rate of throughput (Gbps) and efficiency (Mbps/slices) in our system without further hardware resources. This objective is achieved by introducing the register after the Theta ($\theta$) step and with the new simplified format of the proposed RC generator.

In Figure 2, we present the system design of the proposed pipelining optimization technique. The first unit is the padding unit, which pads the input message to ensure that it is of the appropriate length. Next, the mapping unit maps the input message into a state array that is compatible with the Keccak round. The Keccak round is the core of the design and performs the bulk of the processing. It is responsible for executing the sponge function, which converts the input message into a hash value. The truncating unit is then responsible for truncating the hash value to the desired output length. The control unit is an essential system component as it manages and coordinates data flow throughout the architecture. The input message to our system is 64 bits, and the selected output length can be varied according to the requirements. The possible values for the select output length are presented in Table 4.

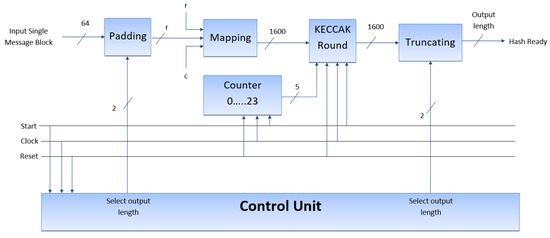
Figure 2. The proposed approach of the SHA-3.

Table 4. Select output length.

Value	00	01	10	11
Hash Output	224	256	384	512

The padding scheme ensures that the input message has a fixed size and is processable by the algorithm. In the case of SHA-3, the padding scheme involves appending the input message with a certain number of bits such that the total message size is a multiple of a fixed number of bits denoted by r (576, 832, 1088, or 1152). To achieve this, the input message of 64-bits is first appended with a “1”-bit, followed by as many “0”-bits as necessary to bring the total message size to $r-64$-bits, and then appended with a “1”-bit. This ensures that the final message size is a multiple of r-bits [41].

The padding scheme used in SHA-3 consists of a 4-to-1 multiplexer. The output length of the algorithm determines which padding scheme is used. For example, if the output length is set to 224 bits, then the padding scheme for $r=1152$ bits is used. The padding scheme is shown in Figure 3.

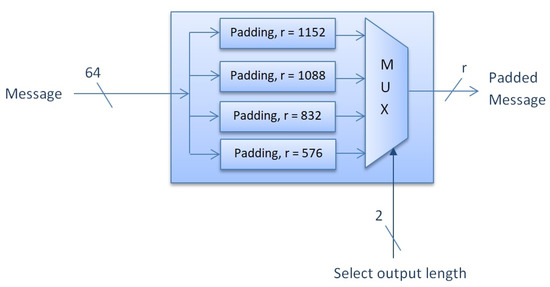
Figure 3. Padding scheme of the SHA-3.

Once the message has been padded, it is passed to the mapping scheme, which is XORed with the initial r-bits. This ensures that the padded message is different from the initial message. The result is then appended with the initial c-bits, where c is a constant value that depends on the value of r. This completes the padding scheme and prepares the message for processing by the hashing algorithm.

A data transformation that includes truncating the digits of a state depending on the desired output length is shown in Equation (5). The specific digits chosen depend on the output length selected (576, 832, 1088, or 1152). This process is achieved using a truncating unit consisting of a 4-to-1 multiplexer.

$$\mathrm{State}[x,y,z]=\left((\mathrm{Padded}\mathrm{data}r\oplus r)\right|\left|c\right)\ast \left[64\ast (5\ast y+x)+z\right]$$

(5)

In addition, the Iota ($\iota$) step includes modifying a few bits of the state array A, as shown in Equation (6).

$$A^{\prime }[x,y,z]=A[x,y,z]\oplus RC\left[i_w\right]$$

(6)

The RC is calculated as shown in Equation (7), which can be found in the SHA-3 specifications [15] and all other values of $RC\left[i_{\mathrm{w}}\right]\left[x\right]\left[y\right]\left[z\right]$ are set to zero. It can be seen from Equation (7) that only 7 of the 64 bits may have the value 1.

$$RC\left[i_{\mathrm{w}}\right]\left[0\right]\left[0\right]\left[2^q-1\right]=wc\left[q+7i_{\mathrm{w}}\right]\mathrm{for}\mathrm{all}0\le q\le m$$

(7)

In accordance with the specifications of the SHA-3, Table 5 details the precise placements of the 7 bits when the value of m = 6. Therefore, the only bit locations with the value “1” are 0, 1, 3, 7, 15, 31, and 63; all other bit places have the value “0”.

Table 5. The places for each of the 7-bits where have the value 1.

q	0	1	2	3	4	5	6
[z]	0	1	3	7	15	31	63

Table 6 shows an example of the simplified format that was used for RC[6] of Table 7. As a result, the $XOR$ gate in state array A can have 7 particular bits set.

Table 6. Example of the new format of the RC[6] in Iota ($\iota$) step.

Hexadecimal	Binary				Places with Value 1
8081	1000	0000	1000	0001	0th = 1 1st = 0 3rd = 0 7th = 1 15th = 1
8000	1000	0000	0000	0000	31st = 1
0000	0000	0000	0000	0000	-
8000	1000	1000	1000	1000	63th = 1

Table 7. The new format of the $R{C}_i$ in Iota ($\iota$) step.

$\mathit{R}{\mathit{C}}_0$	1000000	$\mathit{R}{\mathit{C}}_8$	0111000	$\mathit{R}{\mathit{C}}_{16}$	0100101
$R{C}_1$	0101100	$R{C}_9$	0011000	$R{C}_{17}$	0001001
$R{C}_2$	0111101	$R{C}_{10}$	1010110	$R{C}_{18}$	0110100
$R{C}_3$	0000111	$R{C}_{11}$	0110010	$R{C}_{19}$	0110011
$R{C}_4$	1111100	$R{C}_{12}$	1111110	$R{C}_{20}$	1001111
$R{C}_5$	1000010	$R{C}_{13}$	1111001	$R{C}_{21}$	0001101
$R{C}_6$	1001111	$R{C}_{14}$	1011101	$R{C}_{22}$	1000010
$R{C}_7$	1010101	$R{C}_{15}$	1100101	$R{C}_{23}$	0010101

The pipelined architecture is a popular design approach for achieving low power consumption, high security, and increased performance [42]. In our system, we aim to optimize the two-stage pipelined architecture to achieve higher frequency (MHz), efficiency (Mbps/slices), and throughput (Gbps) for all output lengths. We designed two strategies for optimizing a two-stage pipelined architecture to achieve that goal. Improving performance is directly related to reducing the crucial path of the f operation. The f operation consists of a total of 24 rounds and five special operations: Theta ($\theta$), Rho ($\rho$), P_i ($\pi$), Chi ($\chi$) and Iota ($\iota$). Therefore, the registry pipeline must be appropriately positioned to decrease the crucial path to the f procedure.

The first proposed pipelined architectural design of the Keccak is shown in Figure 4. In this architecture, the first pipeline is placed between the P_i ($\pi$) and Chi ($\chi$) steps, while the second is at the end of the round. The second proposed pipelined architectural design of the Keccak round is presented in Figure 5. In this design, the first pipeline is placed between the Theta ($\theta$) and Rho ($\rho$) steps, while the second is at the end of the round. In both proposed pipelined architectures (Figure 4 and Figure 5), the control signs of the two registers are the reset and the clock. The component counter provides the control signal of the round constant.

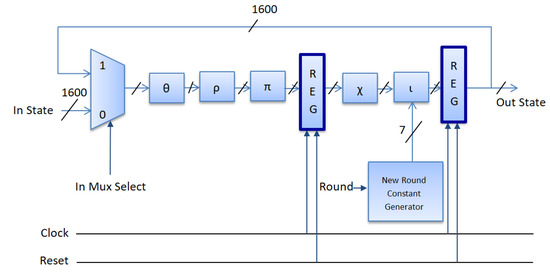
Figure 4. First proposed pipelined (dark blue) optimization technique where the first pipeline is placed after step P_i ($\pi$).

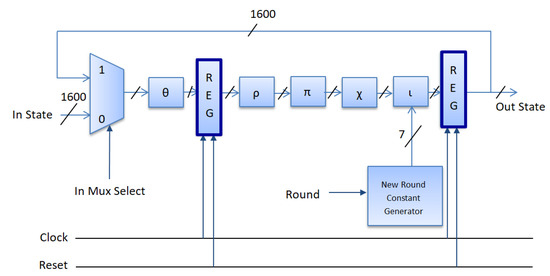
Figure 5. Second proposed pipelined (dark blue) optimization technique where the first pipeline is placed after step Theta ($\theta$).

5. Experimental Results

We use the Virtex-5, Virtex-6, and Virtex-7 FPGA boards to compare the suggested strategy to other existing studies fairly. The methods were implemented in the Virtex-5/Virtex-6 using Xilinx ISE, and the designs in the Virtex-7 using Xilinx Vivado.

5.1. Validating the Modified Construction

The modified construction is based on the SHA-3 specifications [15], especially Equation (7). According to Equation (7), only 7 of the 64 bits in the RC format can have the value 1; by strictly adhering to the SHA-3 specification and relying on the established security properties of SHA-3, the modified construction benefits from the security guarantees provided by SHA-3. Simulation examples provided by NIST [43], a reputable source for cryptographic standards, are employed to validate the modified construction’s implementation further and ensure its correct functioning. This validation process ensures that the modified construction behaves as intended and consistently produces the expected results when tested against valid examples. Therefore, the combination of adhering to the SHA-3 specification and validating the modified construction through simulation using NIST-provided examples collectively contributes to confidence in the system’s security.

5.2. Efficiency and Throughput Performance Measures

Standard evaluation measures, such as efficiency and throughput, are used to conduct the metrics of SHA-3 when implemented on FPGA [28,44]. The term “throughput” refers to the number of bits that are processed in a certain amount of time and may be expressed in either Gbps or Mbps. The throughput is determined with Equation (8).

$$Throughpu{t}_{pipeline}=\frac{\mathrm{A}\mathrm{message}\mathrm{block}’\mathrm{s}\mathrm{bits}}{\mathrm{Cycles}\mathrm{of}\mathrm{the}\mathrm{clock}\mathrm{for}\mathrm{each}\mathrm{message}\mathrm{block}}\times \mathrm{Frequency}$$

(8)

In Equation (8), a message block’s bits are the bitrate size r (576, 832, 1088, 1152), frequency is the maximum clock periodicity, and cycles of the clock for each message block characterize the number of resumptions needed for the five unique processes: Theta ($\theta$), Rho ($\rho$), P_i ($\pi$), Chi ($\chi$) and Iota ($\iota$) to generate the hash value. The efficiency is determined with Equation (9).

$${\mathit{Efficiency}}_{\mathit{pipeline}}=\frac{{\mathit{Throughput}}_{\mathit{pipeline}}}{{\mathit{Area}}_{\mathit{pipeline}}}$$

(9)

5.3. Results of Our Two Architectures

To enhance the performance of the algorithm SHA-3, it is crucial to identify the most computationally costly steps in the algorithm and focus on optimizing those steps. In traditional construction, the computation of parity bits across the columns of the state array requires accessing the entire array, resulting in significant data movement and computational overhead. This increases resource utilization and hinders the algorithm’s overall throughput and efficiency. We introduce a register immediately after the Theta ($\theta$) step to address this challenge because this step is the most computation-costly in the permutation function, consuming over 50% of the total computation time. This register is a temporary storage element that retains the computed parity bits, eliminating the need to access the entire state array repeatedly. By storing the parity bits in the register, subsequent steps within the algorithm can directly access these data without requiring extensive data movement or recomputation. Therefore, introducing the register significantly reduces the computation load and resource requirements in subsequent steps, improving throughput and efficiency. Second, it streamlines the data flow within the algorithm, enabling faster and more efficient processing. Last, it minimizes the overall area cost of the SHA-3 implementation by optimizing resource utilization.

On the other hand, inserting a pipeline after the Pi ($\pi$) step may also improve the throughput of the algorithm, but to a lesser extent. The Pi ($\pi$) step is mainly responsible for rearranging the order of the bits in the state array, and its computation is less intensive than that of the Theta ($\theta$) step. Therefore, inserting a pipeline after the Theta ($\theta$) step has a more significant improvement in the throughput of the SHA-3 algorithm than inserting a pipeline after the Pi ($\pi$) step.

Table 8 displays the results of our two pipelined optimization techniques with Virtex-5, Virtex-6, and Virtex-7 FPGA boards. The proposed design with the first pipelined optimization technique requires 1102 slices operating at 374 MHz, while the second pipelined design requires 998 slices operating at 402 MHz in Virtex-5. On the FPGA board Virtex-6, the proposed design with the first pipelined architecture requires 1146 slices operating at 392 MHz, while the second pipelined optimization technique requires 1042 slices operating at 422 MHz. Finally, on the FPGA board Virtex-7, the proposed design with the first pipelined optimization technique requires 1288 slices operating at 446 MHz, while the second pipelined design requires 1150 slices operating at 478 MHz.

Table 8. Metrics on the performance of our two pipelined optimization techniques for SHA-3 when implemented on the Virtex-5, Virtex-6, and Virtex-7 FPGA.

Design	Length	First Proposed Pipelined Optimization Technique Where the First Pipeline Is Placed after Step Pi ($\mathit{\pi }$)			Second Proposed Pipelined Optimization Technique Where the First Pipeline Is Placed after Step Theta ($\mathit{\theta }$)
FPGA		Virtex-5	Virtex-6	Virtex-7	Virtex-5	Virtex-6	Virtex-7
Area (slices)		1102	1146	1288	998	1042	1150
Frequency (MHz)		374	392	446	402	422	478
Throughput (Gbps)	r = 1152	17.952	18.816	21.408	19.296	20.256	22.944
	r = 1088	16.955	17.771	20.219	18.224	19.131	21.669
	r = 832	12.965	13.589	15.461	13.936	14.629	16.571
	r = 576	8.976	9.408	10.704	9.648	10.128	11.472
Efficiency (Mbps/slices)	r = 1152	16.29	16.42	16.62	19.33	19.44	19.95
	r = 1088	15.39	15.51	15.70	18.26	18.36	18.84
	r = 832	11.77	11.86	12.00	13.96	14.04	14.41
	r = 576	8.15	8.21	8.31	9.67	9.72	9.98

The power consumption of our proposed designs is evaluated using the Xilinx XPower Analysis tool [45]. Table 9 displays the power consumption results of our two pipelined optimization techniques with Virtex-5, Virtex-6, and Virtex-7 FPGA boards. In the first proposed pipelined optimization technique, the power consumption on Virtex-5, Virtex-6, and Virtex-7 FPGAs, was 267 mW, 222 mW, and 179 mW, respectively. In the second proposed pipelined optimization technique, the power consumption on Virtex-5, Virtex-6, and Virtex-7 FPGAs was 242 mW, 198 mW, and 157 mW, respectively. Across all FPGA models, the second proposed pipelined optimization technique (after step Theta ($\theta$)) exhibits lower power consumption than the first proposed technique (after step Pi ($\pi$)). Among the Virtex FPGA models, Virtex-7 consistently demonstrates the lowest power consumption for both optimization techniques. Virtex-6 generally exhibits lower power consumption than Virtex-5 in both cases. Therefore, the second proposed pipelined optimization technique, with the first pipeline placed after step Theta ($\theta$), is more power-efficient across the evaluated FPGA models.

Table 9. The power consumption of our two pipelined optimization techniques for SHA-3 when implemented on the Virtex-5, Virtex-6, and Virtex-7 FPGA.

Design	FPGA	Power (mW)
First proposed pipelined optimization technique where the first pipeline is placed after step Pi ($\pi$)	Virtex-5	267
	Virtex-6	222
	Virtex-7	179
Second proposed pipelined optimization technique where the first pipeline is placed after step Theta ($\theta$)	Virtex-5	242
	Virtex-6	198
	Virtex-7	157

6. Result in Discussion

The main target of our work is to attain a higher rate of throughput (Gbps) and efficiency (Mbps/slices) in our system. The experimental procedure showed that the obtained results are directly affected by the critical path of the function f, which is significantly reduced when the register is inserted after step Theta ($\theta$) than when the register is inserted after step Pi ($\pi$). Table 10 and Table 11 present the comparison with other similar architectures for all output lengths (224, 256, 384, and 512 bits) of the measures of throughput (Gbps), frequency (MHz) and efficiency (Mbps/slices) for the SHA-3 (Keccak) algorithm. Most authors experiment only with output lengths of 256 or 512 bits. All results are reported for single-block messages.

Table 10. Results and comparisons of throughput for the SHA-3 algorithm for each of the output lengths (224, 256, 384, and 512 bits).

Design	FPGA	Area (Slices)	Frequency (MHz)	Throughput (Gbps) r = 1152	Throughput (Gbps) r = 1088	Throughput (Gbps) r = 832	Throughput (Gbps) r = 576
Provelengios et al. [33]	Virtex-5	2326	306	-	-	-	5.56
Mestiri et al. [34]	Virtex-5	4793	317.11	-	12.68	-	-
Sunda et al. [35]	Virtex-5	1163	273	-	-	-	7.80
Ioannou et al. [36]	Virtex-5	2652	352	-	-	-	8.44
	Virtex-6	2296	391	-	-	-	9.38
Athanasiou et al. [37]	Virtex-5	1702	389	-	18.07	-	-
	Virtex-6	1649	397	-	19.01	-	-
	Virtex-7	1618	434	-	20.80	-	-
Gaj et al. [38]	Virtex-5	2123	-	-	12.523	-	7.380
	Virtex-6	1456	-	-	14.942	-	8.114
Nannipieri et al. [39]	Stratix IV	5363	110	-	-	-	-
Mestiri et al. [40]	Virtex-5	1680	387	-	-	-	8.06
Second proposed pipelined optimization technique where the first pipeline is placed after step Theta ($\theta$)	Virtex-5	998	402	19.29	18.22	13.93	9.64
Second proposed pipelined optimization technique where the first pipeline is placed after step Theta ($\theta$)	Virtex-6	1042	422	20.25	19.13	14.62	10.12
Second proposed pipelined optimization technique where the first pipeline is placed after step Theta ($\theta$)	Virtex-7	1150	478	22.94	21.66	16.57	11.47

Table 11. Results and comparisons of the SHA-3’s efficiency for each output length (224, 256, 384, and 512 bits).

Design	FPGA	Area (Slices)	Frequency (MHz)	Efficiency (Mbps/Slices) r = 1152	Efficiency (Mbps/Slices) r = 1088	Efficiency (Mbps/Slices) r = 832	Efficiency (Mbps/Slices) r = 576
Provelengios et al. [33]	Virtex-5	2326	306	-	-	-	2.40
Mestiri et al. [34]	Virtex-5	4793	317.11	-	2.71	-	-
Sunda et al. [35]	Virtex-5	1163	273	-	-	-	6.06
Ioannou et al. [36]	Virtex-5	2652	352	-	-	-	6.37
	Virtex-6	2296	391	-	-	-	8.17
Athanasiou et al. [37]	Virtex-5	1702	389	-	10.98	-	-
	Virtex-6	1649	397	-	11.60	-	-
	Virtex-7	1618	434	-	12.90	-	-
Gaj et al. [38]	Virtex-5	2123	-	-	5.90	-	4.16
	Virtex-6	1456	-	-	10.26	-	6.42
Nannipieri et al. [39]	Stratix IV	5363	110	-	-	-	-
Mestiri et al. [40]	Virtex-5	1680	387	-	-	-	4.91
Second proposed pipelined optimization technique where the first pipeline is placed after step Theta ($\theta$)	Virtex-5	998	402	19.33	18.26	13.96	9.67
Second proposed pipelined optimization technique where the first pipeline is placed after step Theta ($\theta$)	Virtex-6	1042	422	19.44	18.36	14.04	9.72
Second proposed pipelined optimization technique where the first pipeline is placed after step Theta ($\theta$)	Virtex-7	1150	478	19.95	18.84	14.41	9.98

The researchers in the works [33,34,35,36,38,40] with the Virtex-5 FPGA board show a high area in comparison to our implementations, and the frequency which they achieved is lower than our practical applications. Furthermore, in the works of [36,37] with the Virtex-6 FPGA board, there is a lower frequency than we accomplished, showing significant growth in the area. Yet, in the work of [37] with the Virtex-7 FPGA board, the investigators display a more extensive area and frequency than we achieved with our optimization techniques. Finally, in the work of [39] with the Stratix IV FPGA board, the investigators depict a more extensive area and poor frequency than we achieved with our optimization techniques.

With our method in the new simplified format of the RC generator for the output length of 256-bits with Virtex-7 FPGA, our architecture achieves better throughput, over 10%, efficiency over 14%, frequency over 11%, and reduction in the area over 14%, compared to the immediately better implementation of [37]. Finally, for the output length of 512-bits with Virtex-6 FPGA, our architecture achieves higher throughput, over 10%, efficiency of over 11%, frequency of over 10%, and reduction in the area of over 22% compared to the immediately better implementation of [36].

7. Conclusions and Future Work

In today’s digital age, information is transmitted in various forms, such as image, text, video, and audio; therefore, transmissions must be carried out with safety, confidentiality, and integrity to avoid unauthorized access. Cryptography algorithms are widely used to provide high security in digital media. Aggressions against SHA-1 and SHA-2 directed NIST to embrace a new and more secure algorithm, SHA-3. The SHA-3 (Keccak) algorithm offers a high level of security and shows strong resistance to cryptanalysis attacks. Additionally, it provides us with a suitable combination of acceleration, performance and safety.

In this article, we concentrate our study on the optimal performance of the throughput and efficiency measures of the SHA-3 for all output lengths (224, 256, 384, and 512 bits) on the Virtex-5, Virtex-6, and Virtex-7 FPGA boards. We compare the innovative method we propose to similar designs and show that our suggested method has the highest performance in the standard evaluation criteria throughput (Gbps) and efficiency (Mbps/slices). We achieved a throughput rate of 22.94 Gbps and an efficiency rate of 19.95 Mbps/slices with Virtex-7. The suggested architecture works correctly with single-block messages.

In future work, we will analyze the architectural technique of more in-depth pipelines to reduce the crucial path and enhance throughput and efficiency performance metrics per round. Also, we intend to propose more practical experiments implementing FPGA and entire systems-on-chip.