On the Time Frequency Compactness of the Slepian Basis of Order Zero for Engineering Applications
Abstract
1. Introduction
2. Materials and Methods
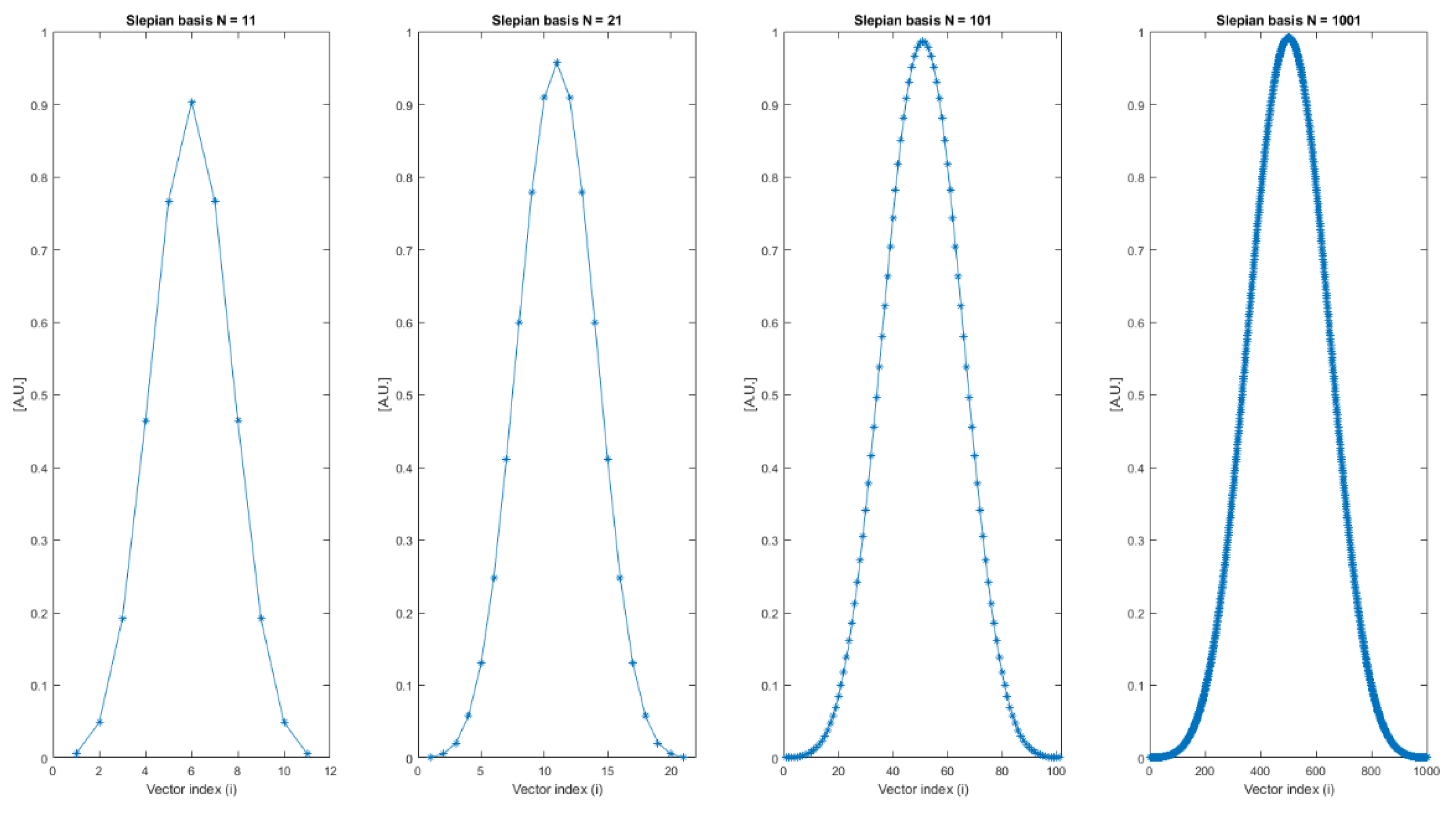
2.1. Slepian Basis
2.2. Compactness
3. Results and Discussion
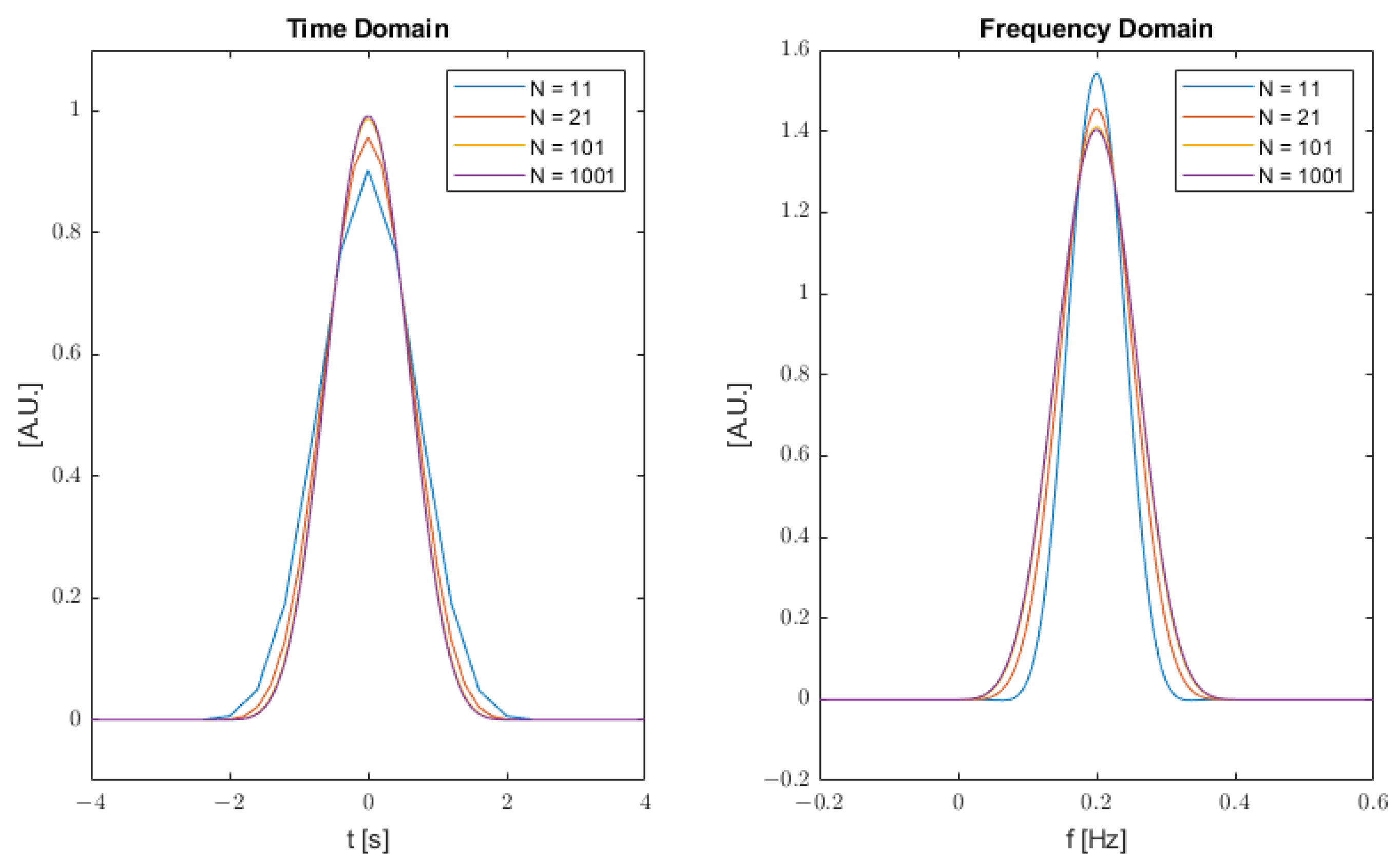
3.1. Mapping to Time Domain
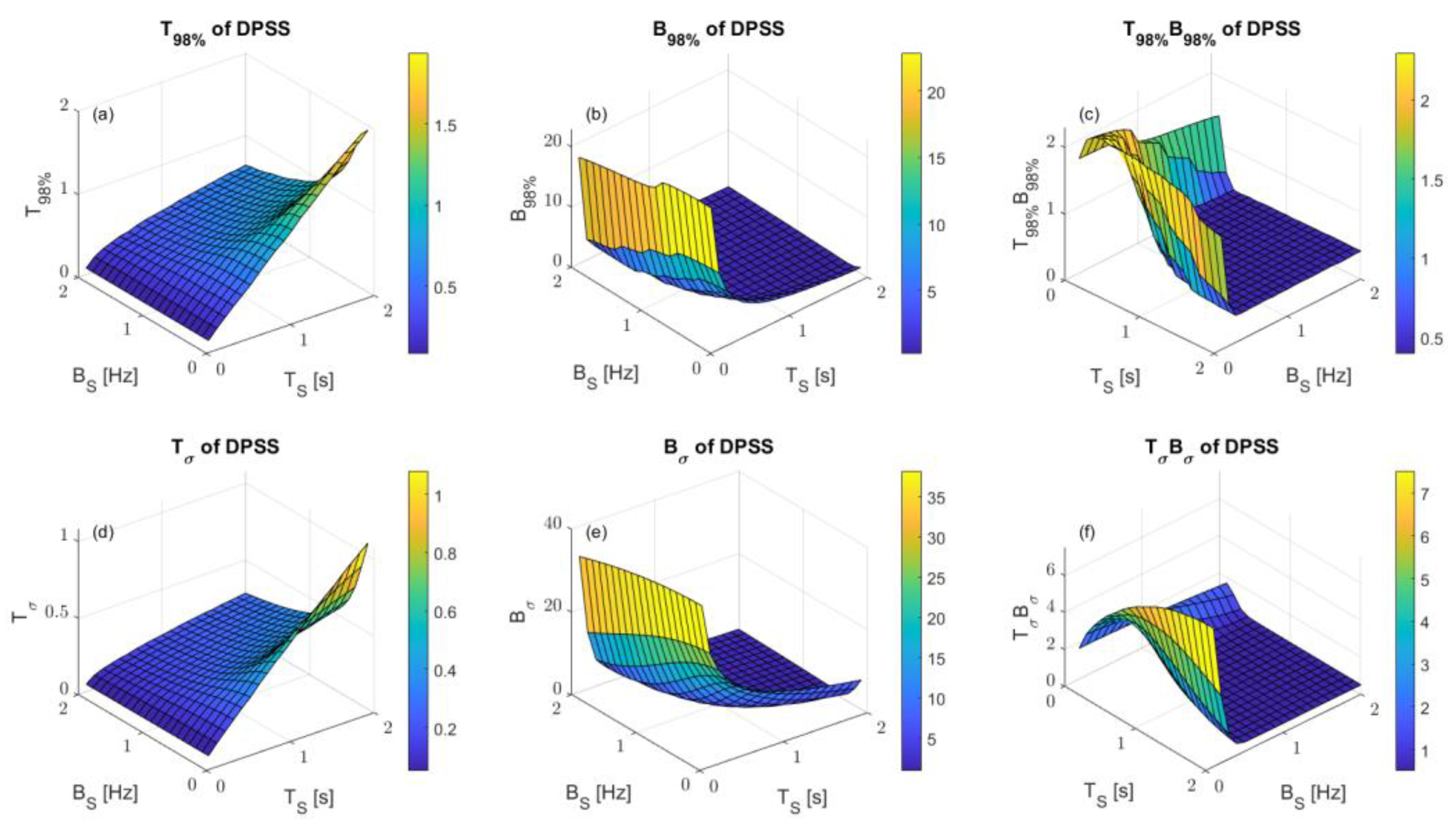
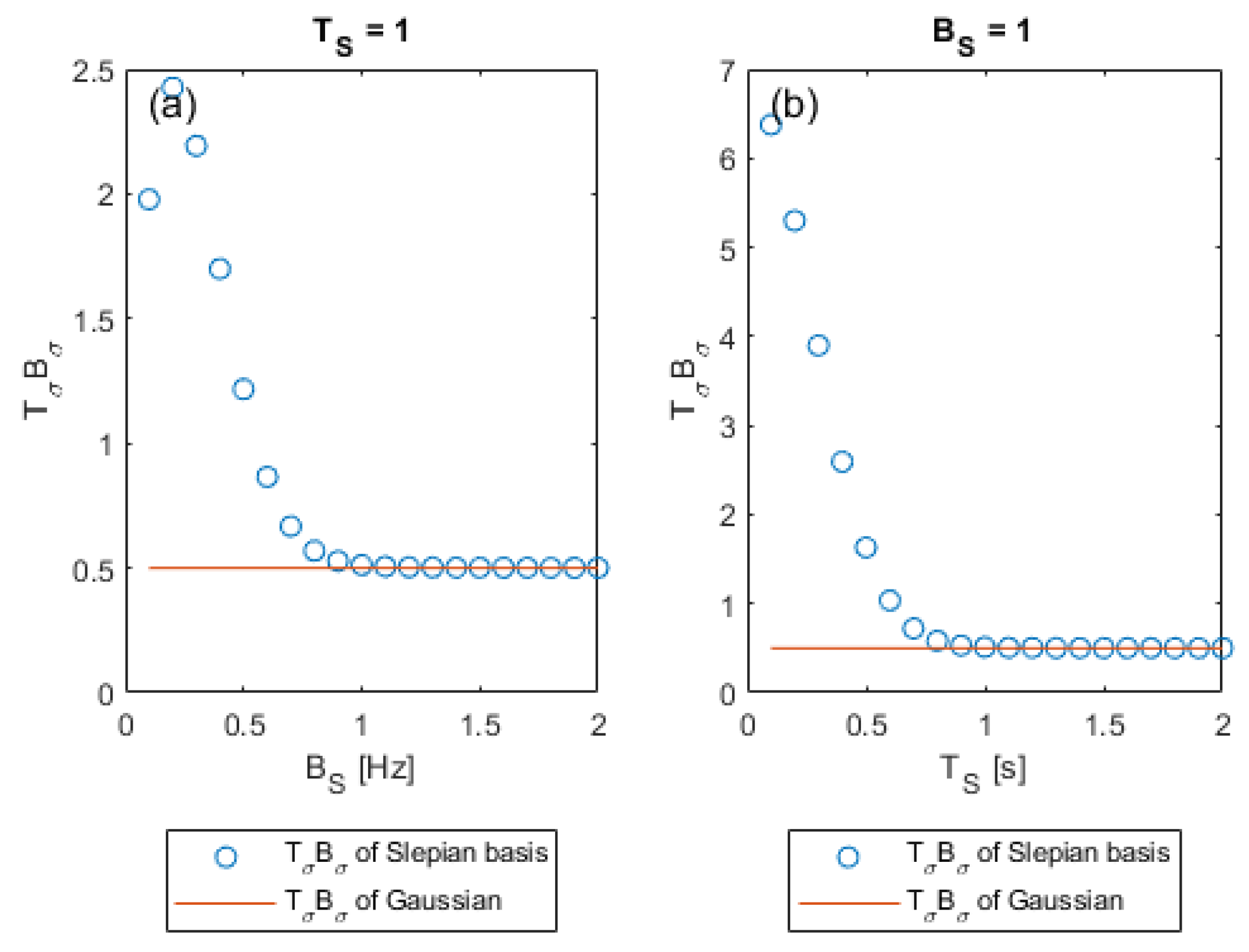
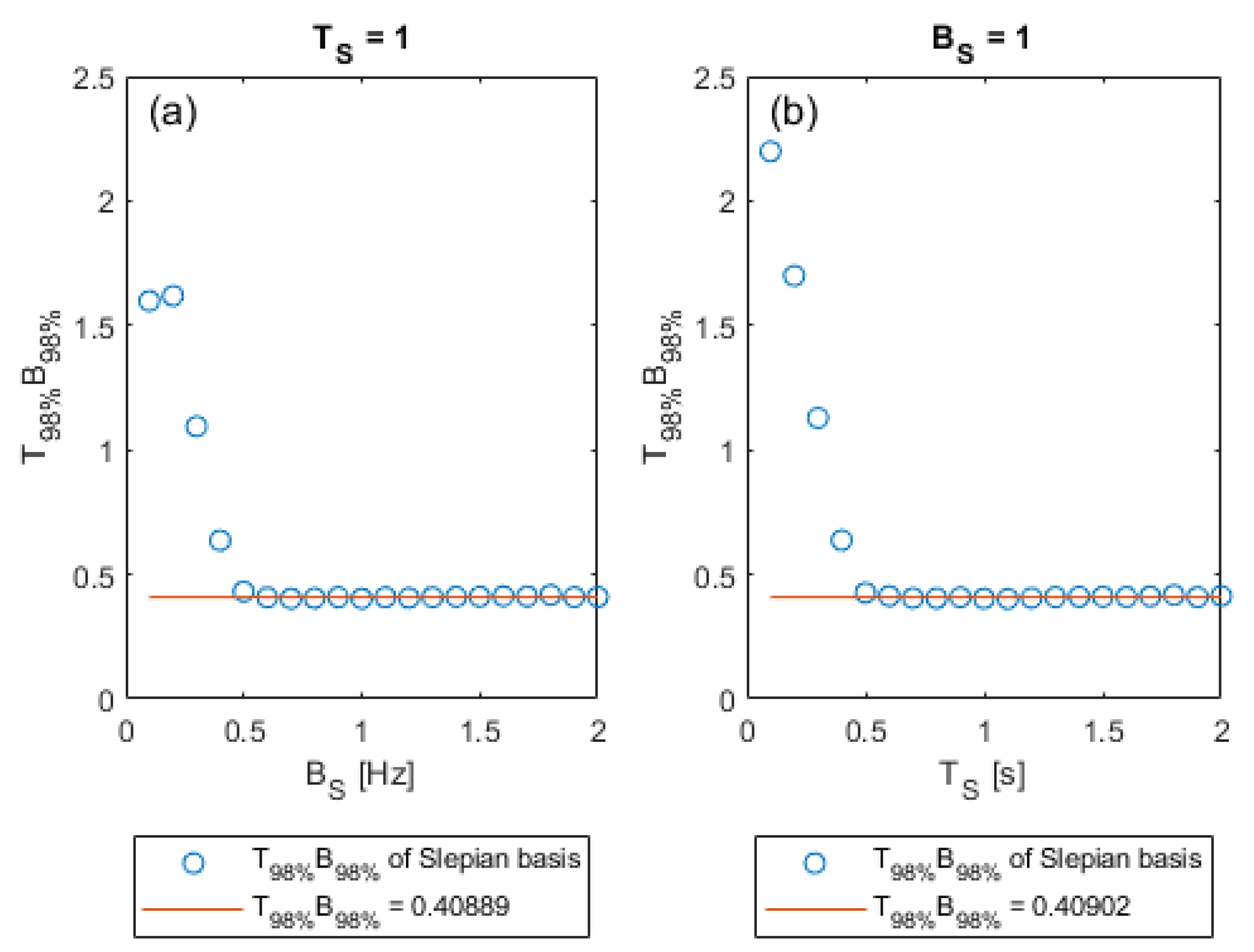
3.2. Time Frequency Characteristics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

Appendix B

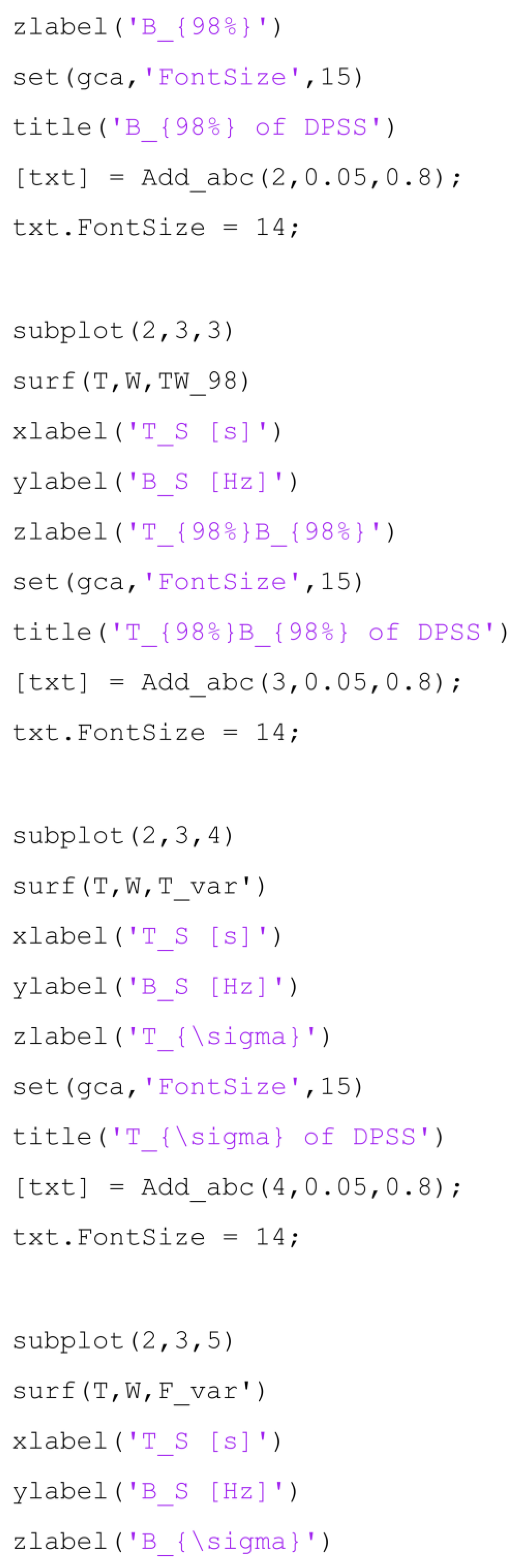
Appendix C






References
- Hague, D.A. Adaptive Transmit Waveform Design Using Multitone Sinusoidal Frequency Modulation. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1274–1287. [Google Scholar] [CrossRef]
- Lo Conte, L.R.; Merletti, R.; Sandri, G.V. Hermite Expansions of Compact Support Waveforms: Applications to Myoelectric Signals. IEEE Trans. Biomed. Eng. 1994, 41, 1147–1159. [Google Scholar] [CrossRef] [PubMed]
- Cheng, S.; Wang, W.-Q.; Shao, H. Large Time-Bandwidth Product OFDM Chirp Waveform Diversity Using for MIMO Radar. Multidimens. Syst. Signal Process. 2016, 27, 145–158. [Google Scholar] [CrossRef]
- Moazzeni, T.; Al Hasani, S.A.; Memon, M.I.; Hussaini, S.J. On the Effect of Compactness of Pulse Shaping Function on Inter-Symbol Interference. IEEE Commun. Lett. 2022, 26, 828–832. [Google Scholar] [CrossRef]
- Parhizkar, R.; Barbotin, Y.; Vetterli, M. Sequences with Minimal Time–Frequency Uncertainty. Appl. Comput. Harmon. Anal. 2015, 38, 452–468. [Google Scholar] [CrossRef]
- Rihaczek, A. Signal Energy Distribution in Time and Frequency. IEEE Trans. Inf. Theory 1968, 14, 369–374. [Google Scholar] [CrossRef]
- Baddour, N.; Sun, Z. Photoacoustics Waveform Design for Optimal Signal to Noise Ratio. Symmetry 2022, 14, 2233. [Google Scholar] [CrossRef]
- Slepian, D.; Pollak, H.O. Prolate Spheroidal Wave Functions, Fourier analysis and Uncertainty—I. Bell Syst. Tech. J. 1961, 40, 43–63. [Google Scholar] [CrossRef]
- Landau, H.J.; Pollak, H.O. Prolate Spheroidal Wave Functions, Fourier analysis and Uncertainty—II. Bell Syst. Tech. J. 1961, 40, 65–84. [Google Scholar] [CrossRef]
- Landau, H.J.; Pollak, H.O. Prolate Spheroidal Wave Functions, Fourier analysis and Uncertainty—III: The Dimension of the Space of Essentially Time- and Band-Limited Signals. Bell Syst. Tech. J. 1962, 41, 1295–1336. [Google Scholar] [CrossRef]
- Slepian, D. Prolate Spheroidal Wave Functions, Fourier analysis and Uncertainty—IV: Extensions to Many Dimensions; Generalized Prolate Spheroidal Functions. Bell Syst. Tech. J. 1964, 43, 3009–3057. [Google Scholar] [CrossRef]
- Slepian, D. Prolate Spheroidal Wave Functions, Fourier analysis, and Uncertainty—V: The Discrete Case. Bell Syst. Tech. J. 1978, 57, 1371–1430. [Google Scholar] [CrossRef]
- Karnik, S.; Romberg, J.; Davenport, M.A. Improved Bounds for the Eigenvalues of Prolate Spheroidal Wave Functions and Discrete Prolate Spheroidal Sequences. Appl. Comput. Harmon. Anal. 2021, 55, 97–128. [Google Scholar] [CrossRef]
- Donoho, D.L.; Stark, P.B. Uncertainty Principles and Signal Recovery. SIAM J. Appl. Math. 1989, 49, 906–931. [Google Scholar] [CrossRef]
- Varah, J.M. The Prolate Matrix. Linear Algebra Its Appl. 1993, 187, 269–278. [Google Scholar] [CrossRef]
- Breitenberger, E. SSA Matlab Implementation; 1995. [Google Scholar]
- Singh, N.; Pradhan, P.M. Achievable Simultaneous Time and Frequency Domain Energy Concentration for Finite Length Sequences. IET Signal Process. 2019, 13, 736–746. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Baddour, N. On the Time Frequency Compactness of the Slepian Basis of Order Zero for Engineering Applications. Computation 2023, 11, 116. https://doi.org/10.3390/computation11060116
Sun Z, Baddour N. On the Time Frequency Compactness of the Slepian Basis of Order Zero for Engineering Applications. Computation. 2023; 11(6):116. https://doi.org/10.3390/computation11060116
Chicago/Turabian StyleSun, Zuwen, and Natalie Baddour. 2023. "On the Time Frequency Compactness of the Slepian Basis of Order Zero for Engineering Applications" Computation 11, no. 6: 116. https://doi.org/10.3390/computation11060116
APA StyleSun, Z., & Baddour, N. (2023). On the Time Frequency Compactness of the Slepian Basis of Order Zero for Engineering Applications. Computation, 11(6), 116. https://doi.org/10.3390/computation11060116





