Abstract
In the radio telemetry systems of spacecraft, various data compression methods are used for data processing. When using any compression methods, the data obtained as a result of compression is formed randomly, and transmission over radio communication channels should be carried out evenly over time. This leads to the need to use special buffer storage devices. In addition, existing spacecraft radio telemetry systems require grouping of compressed data streams by certain characteristics. This leads to the need to sort compressed data by streams. Therefore, it is advisable to use associative buffer storage devices in such systems. This article is devoted to the analysis of the processes of formation of output streams of compressed data generated at the output of an associative storage device (ASD). Since the output stream of compressed data is random, queue theory and probability theory are used for analysis. At the same time, associative memory is represented as a queue system. Writing and reading in an ASD can be interpreted as servicing orders in a queue system. The purpose of the analysis is to determine the characteristics of an associative storage device (ASD). Such characteristics are the queue length M{N} in the ASD, the deviation of the queue length D{N} in the ASD and the probability of a given volume of compressed data in the ASD (including the probability of emptying and the probability of memory overflow). The results obtained are of great practical importance, since they can be used to select the amount of memory of an associative storage device (ASD) when designing compression devices for telemetry systems of spacecraft.
1. Introduction
In recent years, in the field of information and computing systems, there has been a need for a significant increase in the performance of computers and systems [1]. This trend is especially relevant in on-board spacecraft systems, since such systems are designed in conditions of restrictions on the weight and size characteristics and energy consumption [2]. The large role is played at the same time by improvement of technical means, in particular the memory devices (MD). Not only is the performance of such devices improved, but also the range of functions they perform is expanded. The process of increasing on-board computer performance is accompanied by the fact that the equipment begins to perform a significant number of functions previously performed by software. In this regard, the task of developing and using associative processing and storage of information becomes especially important. Therefore, research on the use of associative storage devices (ASD) in information computing systems, especially in radio telemetry systems of spacecraft, is extremely relevant.
The principles of associative addressing and hardware implementation of associative storage devices are devoted to the well-known Kohonen T. book [3]. This book describes the basis of the theory and technique of associative memory devices. The general principles of operation of associative storage devices, methods of searching and sampling information and extracting a multi-valued response from the device are considered. Some of the most interesting elements and circuits of associative memory devices are described, as well as their applications in modern computer engineering.
Recently, associative storage devices have also received a great deal of attention. Some works are devoted to the use of associative storage devices in neural networks. For example, [4] discusses relational–indeterminate computing for associative memory modeling. The work in [5] is devoted to the study of the functions of associative memory using three-level quantum elements. The work in [6] relates to the study of the methods of using associative storage devices in the construction of deep neural networks in the field of image classification. Finally, [7] discusses the architecture of distributed associative memory.
Unlike the above-mentioned works, this article addresses the use of associative memory devices in radio telemetry systems of spacecraft.
The transmitting part of the radio telemetry system with data compression may be represented by the flowchart of Figure 1 [8].

Figure 1.
Transmitting part of the radio telemetry system with data compression.
The source of the message is the sensor of the telemetry system. The data compression device generates a random compressed data stream in accordance with the compression algorithm [9]. Data generated at the output of a data compression device, in radio telemetry systems of spacecraft, are commonly called significant counts (SC). The device for transmission to a communication channel is designed to convert a random compressed data stream (significant counts) into a time-uniform output data stream.
In accordance with the principles of formation of radio telemetry systems with data compression, the following types of data streams can generally be formed on the transmitting side [10,11,12,13]:
- Data streams with different accuracies of message recovery at the receiving side.
- Data streams with different priorities (multi-priority generation).
- Data streams with different addresses of information consumers (multicast generation).
- Data streams with a different combination of the above-mentioned methods of generation (multi-purpose generation).
For spacecraft radio telemetry systems, as a rule, multi-purpose generation of output streams is required. The combination of the first and third types of streams is the subject of a great interest: together with the generation of several compressed data streams from all sources, it is necessary to form several compressed data streams from different message source groups for different recipients. The combinations of streams of the first and second types and the second type with the third are of not smaller interest: in any of the compressed data streams, it is necessary to transmit compressed data from the most important parameters for operational control.
At the same time, each of the streams can be both uniform in structure and heterogeneous (data with different errors, with different priority rank and different consumer addresses may be present in one stream). However, an analytical study of such combined streams is not yet possible. Therefore, we will limit ourselves to considering only homogeneous streams in the future.
In the data compression device (Figure 1), in accordance with the accepted compression algorithm, the significant samples that are to be transmitted to the communication channel are determined. The second device is designed to convert a random compressed data stream into a time-uniform output data stream. This is due to the fact that the data obtained as a result of compression is formed randomly, but transmission over radio channels should be carried out evenly over time. The implementation of the device for transmission to the communication channel is the main difficulty in view of the need to use buffer memory devices [14].
At the output of the data compression device, as shown above, compressed data streams of several types may be generated, i.e., not one, but several compressed data (significant counts) streams are generated. The requirement to generate multiple compressed data streams at the output of the compression device results in the need to sort the compressed data into streams. To generate several compressed data streams at the output of the compression device, it is necessary to use associative storage devices, in which information is written and read in accordance with some associative feature [1,2,15], i.e., not at addresses. This property of the associative memories determines the ability to perform information processing in parallel across all message sources, which leads to a decrease in the requirements for the fast operation of the on-board computer system that is almost inversely proportional to the number of processed signals.
The stream of compressed data (significant samples) coming to the input of the matching device with the communication channel is a random process, and the service process in general is also random. For this reason, when analyzing the device for generating several streams of compressed data, it can be considered as a queue system [16]. A compression system with the associative formation of several compressed data streams is a large system. It is advisable to carry out an experimental study of it by methods of mathematical modeling on a computer [17]. The analytical apparatus is used to obtain the most general dependencies characterizing the formation processes while limiting itself to tasks that do not lead to excessively cumbersome expressions, which are almost impossible to bring to numerical results. To obtain more specific results, and with the excessive complexity of analytical methods, mathematical modeling is used [18].
The task of analyzing the process of formation of compressed data streams is to obtain the performance characteristics of the associative memory device with the output stream generation scheme. These characteristics are the mean of queue length , the queue length variance and the probability of a predetermined number of compressed data (significant counts) in the memory (including emptying probability and the probability of overflow in the memory register [19]). The determination of these characteristics allows for optimizing the memory capacity of the associative storage device. This is very important, since there are restrictions on the weight, size and energy consumption of on-board systems. In [20], the functioning of a device for transmission to a communication channel with buffer memory, with adaptive, asynchronous–cyclic and priority commutation, was investigated. In this case, the theory of queues was used. A matching device using the buffer memory was presented as a system with a limited-length queue and ordinary service without priorities and—for a matching device without the buffer memory—as a system with failures and ordinary service with priorities.
Based on the above, the result of the research conducted in this article is the determination of the characteristics of the associative memory device with the output stream generation scheme. Such characteristics, in terms of queue theory, are the mean of queue length , the queue length variance and the probability of a predetermined number of compressed data (significant counts) in the memory. To obtain these characteristics, the article used probability theory and queue theory. At the same time, for the study of the queue system, we justified the use of embedded Markov chains, for which the Chapman–Kolmogorov equation is valid. This equation allows for determination of the states of the queue system at arbitrary points in time. To carry out the necessary transformations, we have justified and proposed the use of the method of producing functions. The article shows the entire sequence of mathematical transformations leading to the final result. The results obtained are of great practical importance, since they can be used to select the amount of memory of an associative storage device when designing compression devices for telemetry systems of spacecraft.
2. Material and Methods
The analysis of the device is limited to the process of formation of the − stream, the sorting process for which is described by a system with a limited queue length for group services without prioritization [21,22]. This system is much more complicated than systems with ordinary maintenance and limited queue length or a system with failures (adaptive commutation) and is their generalization [23,24]. Indeed, at = 1 ( is the number of compressed data in the group), the generation of the stream is reduced to processes with buffer memory; at = 1 and ( is the memory capacity of the associative memory device), the generation of the − stream is reduced to the adaptive switching process [25].
Since compressed data (significant counts) is served by groups that do not exceed a certain number of , a single-channel system model with group service can be used for consideration [26,27]. According to this model, the probability density of data service time of orders is determined by the formula
In this formula, is the service intensity of one order and is the Erlangian distribution parameter [28]. The mean of the Erlangian distribution is , and the variance is With , the Erlangian distribution becomes exponential, and with regular [29].
Thus, we are dealing with a network of queues with a Poisson incoming stream, service in batches and an Erlangian distribution of service interval. For such a network, the foundations of the theory were developed in the works of N. Bailey and F. Downton, a concise presentation of which is given in the book [30]. In these works, the values of the mean and variance of the number of data in the system are obtained for two system load values (0.8 and 0.9), several values of in the group and the coefficient of Erlang’s law. Some theoretical provisions are also available in the book [31,32]. In an analytical study of the process of forming the stream of compressed data, these works were taken as a basis, verified theoretically and experimentally and significantly developed. In this case, analytical expressions are obtained to determine the probability of emptying and overflow of the associative memory.
The method of obtaining numerical characteristics of the delay time value is discussed in sufficient detail in [33,34]. Therefore, we will limit ourselves only to mathematical modeling. As such, as a result of the analytical study of the process of forming the stream, it is necessary to obtain the characteristics and .
3. Theory/Calculation
Our objective is to derive the equation of state of the system for forming the compressed data streams. As is known, the state of the network of queues with an arbitrary distribution of the time in service does not form the Markov chain [35]. Therefore, to determine the probabilistic characteristics of the stream formation process, it is impossible to use the Chapman—Kolmogorov equations, and so more complex methods have to be used. We use Kendall’s method, called the method of embedded Markov chains [36]. Kendall showed that, at times immediately preceding the end of servicing of a group of orders of the states of the network of queues with the Poisson incoming stream and the arbitrary distribution of service time form the Markov chain (regeneration points), and the system can be described by the Chapman—Kolmogorov equations. Such points are the moments of time immediately preceding the beginning of sampling of pieces of the compressed data (significant counts) from the associative memory and their direction to the path.
Consider two adjacent cycles of the output streams formation (Figure 2).
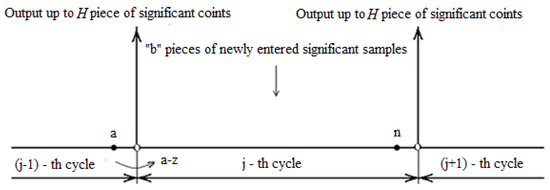
Figure 2.
Output stream generation cycles.
We say that, at time j (where j—the cycle number), the system is in state n if the number of the compressed data (significant counts) in the associate memory is equal to n. Accordingly, the probability of such a state of the system will be denoted by . Let, at the end of the cycle, the system be in state a. As a result of sampling pieces of the compressed data, the system jumps into state at or to state 0 at During the cycle, in addition to the available of the compressed data, b pieces of the compressed data are again entered into the associative memory, as a result of which the system passes into state n.
At the points of the embedded Markov chain, the Chapman—Kolmogorov equation is valid [37]:
where is the probability of the system transition from state a to state n; is the probability that, at the end of the j cycle, the system will be in state n and is the probability that, at the end of the () cycle, the system was in state .
Let be the probability that, in the cycle, the number of newly entered compressed data will be . Obviously, if if then and at does not determine the state of the system by the end of the cycle, i.e.,
If 0 ≤ ≤ ; if H ≤ ; if The last ones can be determined as the probability of combining two events:
where —is the probability of entering the exactly n data at the interval t (Poisson’s probability [38]) and λ = is the intensity of the incoming stream of the compressed data.
is the probability of service [39], determined in accordance with expression (1).
Taking into account the above dependencies, Equation (2) can be written as follows:
The state probabilities obey the normalization condition [40]:
For the steady state (), the system of equations will have the form
To solve this system of equations, the method of producing functions is proposed in the literature [41,42]. The essence of the method of producing functions is that the producing functions of this form are introduced into consideration:
where z is an independent variable.
Substituting the value from the system of Equation (4) into the expression (5) after the transformations, we get
With the Erlang distribution of the service duration, expression (6) takes the following form:
where is the load determined by the formula
is the parameter of the Erlang distribution, λ is the intensity of the incoming flow, is the number of SC in the group and is the service intensity of one data.
Substituting (5) into the system of Equation (4) after some transformations and taking into account (8), we get
After simplifications, the expression for the producing function is
where is the roots of the denominator (10) outside the unit circle. To find the probabilities of the states of the system, we will use the method of decomposing the expression (11) into simple fractions:
where the expansion coefficients are , determined from the expression
Changing the within and substituting the corresponding expressions for (13) in (12), we get the expression for the probabilities of the states as coefficients with the corresponding powers of .
Thus
If is the smallest root outside the unit circle, then the approximate expression for will be
The average number (mean) of orders in the system and the variance of the number of orders are determined from (11) as follows:
It is difficult to directly calculate the mean and variance of formulas (16) and (17). A significant simplification gives the application of dependencies between these values and semi-invariants expressed through the producing function. The simplification is caused by the fact that semi-invariants are associated with the logarithmic dependence of the producing function. Therefore, the products in expression (11) are converted to sums.
Assuming in expression (5), we get the following expression for the producing function:
After transformations [43,44], we get
where the coefficients are called semi-invariants (cumulants) of the random variable N, where N is the queue length, i.e., the number of SC in the ASD.
Function
is called the semi-invariants producing function or the sequence producing function [45,46].
From expression (18), we get
Since
We then get the final expressions for calculating the average value and variance of the queue length N:
Substituting in expression (11) for , we get the following:
Logarithmically, we get the expression for the producing function of the semi-invariants
According to (22) and (23), we get
The obtained relations are dependencies on the values, which are the roots of the equations of the corresponding producing functions. Calculating the roots of is a separate problem, and we will not give all the necessary transformations here. Note only that, for the solution, an iterative method [47] was used to determine the roots of the polynomial of degree (H + k) according to the standard program for the Muller method. The equations were solved for the following parameter values: θ = 0.5; 0.1; 0.2; 0.4; 0.6; 0.7; 0.8; 0.9; H = 1, 2, 3, 6, 12, 24; k = 1, 2, 10.
4. Discussion and Results
In various radio telemetry systems of spacecraft, there are different laws for the distribution of a random τ value—the duration of the transmission cycle of pieces of significant samples. When using synchronous communication channels in radio telemetry systems and without taking into account auxiliary information, the random τ variable turns into a deterministic one [48]; there is a constant cycle duration. In the Erlang distribution, this corresponds to the value of the parameter. With some degree of consideration of auxiliary information and with an asynchronous communication channel, the value of the parameter of the Erlang distribution greatly changes [49,50,51], and, in the limit, the value of has an exponential distribution. In the Erlang distribution, this case corresponds to the value of the parameter . Thus, for the analytical study of real systems, it is necessary to obtain appropriate characteristics in the range of values; in other words, in order to estimate the limit characteristics, it is advantageous to determine these characteristics for the limit cases of the Erlang distribution corresponding to the values and . Along with this, the choice of the parameter —the number of significant counts transmitted in one cycle—is very important for calculating real systems. Obviously, the limit values of the parameter are = 1 and . Without giving intermediate calculations, we will give the final results for some limiting cases of the Erlang distribution.
- Group service. The service interval is distributed by exponential law;
- 2.
- Group service. The service interval is constant;
- 3.
- Ordinary service.
In a case :
In a case :
- 4.
- Group service with an infinite number of orders.
For the case of , we get the following relations.
For the case of , we get the following relations.
Calculations were made on a computer using formulas obtained above. Various combinations of the Erlang distribution parameter , group service parameter and queue system load were used. The parameter values were selected as follows:
For these values, the dependencies of the system state probability distributions (Figure 3) were calculated, as well as the mean of the queue length M {N} (Figure 4) and the variance of the queue length D {N} (Figure 5).
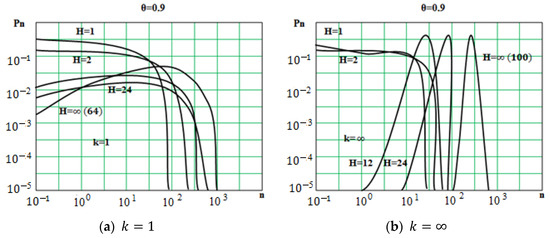
Figure 3.
Dependencies of system state probability distributions.
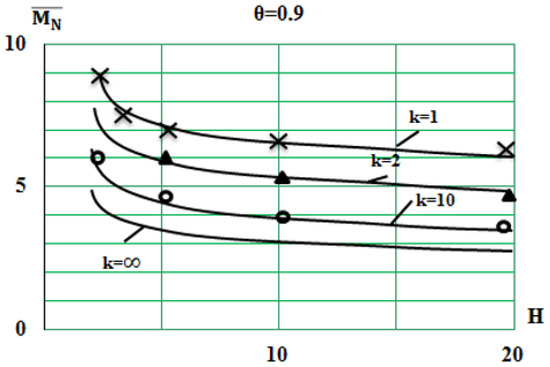
Figure 4.
Mean of the queue length in associative memory.
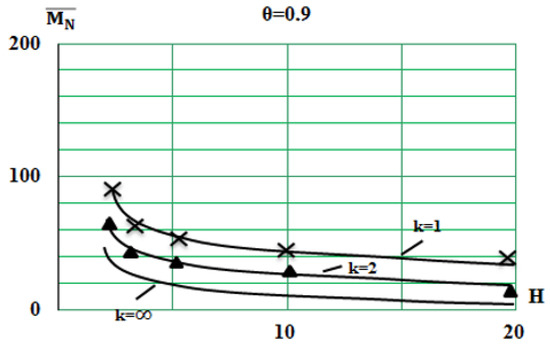
Figure 5.
Variance of the queue length in associative memory.
To emphasize the behavior of the mean and the variance of the length of the queue, they are led to a dimensionless shape in the graphs.
From the analysis of the resulting constraints, you can draw the following conclusions.
1. The following conclusions can be drawn from Figure 3. With large load values ( = 0.9 0.95), the distribution of probabilities of the state of the system and the relative average length of the queue and its variance significantly depend on the nature of the service time distribution law determined by the parameters and of simultaneously serviced compressed data. The strongest dependence occurs at small values of and ; with an increase in and , the dependence decreases, and, at →∞ (almost at > 20), constant values are set. With small values of the system load ( = 0.1 0.3), this dependence is weak.
2. With an increase in the number of orders in the group, the relative length of the queue and its variance quickly tend to their asymptotic values. Thus, extreme queue lengths are reached at the boundary of the function modification area and (Figure 4 and Figure 5).
3. With a system load of 0.95, regular service improves the system performance by 5–20 times compared to exponential service.
4. With an increase in the number of compressed data in the group of more than 10, the characteristics of the system are almost the same for any laws of service time distribution.
5. The variance of the queue lengths when the system is loaded at = 0.3 and = 0.95 differ by almost an order of magnitude. This follows the advantage of associative stream shaping over other compression methods, since it easily implements the control of system load amount.
In conclusion, we note that the results obtained are of great practical importance. The dependencies shown in Figure 3, Figure 4 and Figure 5 can be used to select the memory size of the associative memory when designing spacecraft telemetry compression devices.
This article discusses the issue of formation of output streams of compressed data in radio telemetry systems of spacecraft. Radio telemetry systems of spacecraft differ in a number of features that are not inherent in other radio communication systems. These features, firstly, include the need to process and transmit data to Earth at a real pace. Secondly, on-board radio telemetry systems are subject to restrictions on mass and overall characteristics and power consumption. Since, in radio telemetry systems of spacecraft, it is necessary to process huge amounts of data in a short time, this leads to the need to optimize the characteristics of on-board computing systems. Such characteristics include, but are not limited to, the amount of onboard memory.
Various data compression techniques are typically used to process data in spacecraft radio telemetry systems. This causes the output data transmitted to the radio communication channel to be generated randomly depending on the compression algorithm used. In this case, transmission via radio communication channels should be carried out uniformly in time. This leads to the need to use special buffer memories, the input of which receives a random data stream, and, at the output, a uniform output data stream is formed. In addition, in existing radio telemetry systems of spacecraft, grouping of compressed data streams according to some features is required. This makes it necessary to sort the compressed data into streams. Therefore, it is advantageous to use associative-type buffer memories in radio telemetry systems of spacecraft. Optimizing the parameters of the associative storage device is an urgent task in view of the restrictions on mass-dimensional characteristics and power consumption.
Since the compressed data stream arriving at the input of the channel matcher is a random process, and the service process is generally also random, we considered the associated storage device as a queue system in an analytical study. At the same time, we considered a queue system with Poisson incoming flow, group service and an Erlang service interval distribution.
In the article, the tasks of analyzing the process of formation of compressed data streams are to obtain performance characteristics of an associative memory with an output stream formation circuit and to determine the parameters of the output streams of compressed data. Such characteristics are the average value of the queue length in the ASD, the variance of the queue length in the ASD and the probability of given a number of compressed data in the associative memory (including the probability of emptying and the probability of memory overflow).
The procedure for analyzing the queue system is well developed for Markov circuits. In this case, the basic equation for analysis is the Chapman–Kolmogorov equation. As is known, the state of the queue system in arbitrary service time allocation does not form a Markov chain. Therefore, it is impossible to use the known Chapman–Kolmogorov equations to determine the probabilistic characteristics of the flow formation process. Therefore, we used the Kendall method, called the nested Markov chain method. In the article, we show that, at the moments of time immediately preceding the end of service of a group of orders, the states of the queue system with Poisson incoming flow and arbitrary distribution of service time form a Markov chain (regeneration points), and the system can be described by Chapman–Kolmogorov equations. This steady-state equation is converted into a set of equations describing the state of the queue system. To solve this system of equations, we used the method of producing functions. The resulting relations are dependencies on the values of some variable , which are the roots of the equations of the corresponding producing functions. The calculation of the roots of was carried out iteratively according to a standard program.
The article presents the final results for some marginal Erlang distribution cases. These limit cases are as follows: 1. Group service. The service interval is distributed by exponential law. 2. Group service. The service interval is constant. 3. Ordinary service. 4. Group service with an infinite number of orders.
5. Conclusions
The article obtained the necessary dependencies to determine the parameters of the associative storage device: the average value of the queue length in the associative storage device, the variance of the queue length and the probability of given a number of compressed data in the associative storage device.
Author Contributions
Conceptualization, B.-B.Y.; methodology, B.-B.Y. and N.A.; software, M.B. and A.I.; validation, B.-B.Y., A.A. and K.K.; formal analysis, A.I. and K.K.; investigation, B.-B.Y. and K.A.; writing—original draft preparation, A.M. and A.A.; writing—review and editing, B.-B.Y., N.A. and A.M.; visualization, K.A. and M.B.; supervision, B.-B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The team of authors of the article expresses sincere gratitude to the scientists and specialists of the chairs “Radio-electronic systems and devices” and “Information systems and telecommunications” of N. Bauman Moscow State Technical University, whose consultations and advices were taken into account when performing scientific research.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MD | memory device |
| ASD | associative storage device |
| SC | significant counts |
References
- Naderi-Gavareshki, Y.; Khani, H.; Rahiminejad, E. Improved coded/uncoded monobit receiver for transmit-reference UWB communication systems: Performance evaluation and digital circuit design. Int. J. Electron. Commun. 2020, 127, 153460. [Google Scholar] [CrossRef]
- Cal, B. Lead-Free Soldering Risks and Reliability Problems in Space Electronics. In Proceedings of the 3rd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 11–13 October 2019. [Google Scholar] [CrossRef]
- Kohonen, T. Associative Memories; Translation from English; Mir: Moscow, Russia, 1982; 384p. [Google Scholar]
- Pineda, L.A.; Fuentes, G.; Morales, R. An entropic associative memory. Sci. Rep. 2021, 11, 6948. [Google Scholar] [CrossRef] [PubMed]
- Zobov, V.; Pichkovskiy, I. Associative memory on qutrits by means of quantum. Quantum Inf. Process. 2020, 19, 342. [Google Scholar] [CrossRef]
- Yang, G.; Ding, F. Associative memory optimized method on deep neural networks for image classification. Inf. Sci. 2020, 533, 108–119. [Google Scholar] [CrossRef]
- Park, T.; Choi, I.; Lee, M. Distributed associative memory network with memory refreshing loss. Neural Netw. 2021, 144, 33–48. [Google Scholar] [CrossRef]
- Nazarov, A.V.; Kozyrev, G.I.; Shitov, I.V.; Obruchenkov, V.P.; Drevin, A.V.; Kruskin, V.B.; Kudryakov, S.G.; Petrov, A.I.; Sokolov, S.M.; Yakimov, V.L.; et al. Modern Telemetry in Theory and Practice; Training Course; Science and Technology: St. Petersburg, Russia, 2007; 667p. [Google Scholar]
- Nahar, N.; Haque, M.J. Data Compression Methods and Analysis; Communications on Applied Electronics (CAE); Foundation of Computer Science FCS: New York, NY, USA, 2017; Volume 7. [Google Scholar] [CrossRef]
- Mamchev, G.V. The Radio Communication and Television Bases; The Manual for High Schools; The Hot line—A Telecom: Moscow, Russia, 2007; 416p. [Google Scholar]
- Salomon, D. Compression of Data, Images and a Sound; A Technosphere: Moscow, Russia, 2004; 368p. [Google Scholar]
- Yesmagambetov, B.-B.S.; Inkov, A.M.; Ajmenov, Z.T. Definition of characteristics of output streams of the random data in radio telemetering systems with compression. In Proceedings of the Second International Conference on Analysis and Applied Mathematics ICAAM 2014, Shymkent, Kazakhstan, 11–13 September 2014; p. 125. [Google Scholar]
- Ivanov, V.G.; Lomonosov, U.B.; Lyubarsky, M.G. Analiz and classification of methods of compression of the information. Bulletin NTU HPI. Thematic issue: Information science and modelling. Kharkov NTU KhPI 2008, 49, 78–86. [Google Scholar]
- Yesmagambetov, B.-B.S. Control of buffer memory filling in data compression systems. KazATK Bull. Almaty 2007, 1, 161–163. [Google Scholar]
- Yesmagambetov, B.-B.S.; Utepbergenov, I.T.; Sagjndjkova, S.N. Generate compressed message streams. Sci. News Kazakhstan. Almaty 2006, 4, 143–149. [Google Scholar]
- Yesmagambetov, B.-B.S. Optimization of parameters of associative data compression device. Bulletin of the Committee for Supervision and Certification in the Sphere of Education and Science of the Ministry of Education and Science of the Republic of Kazakhstan. Astana 2006, 2, 130–135. [Google Scholar]
- Yudanova, V.V. Imitating modeling of mass service systems. Russ. J. Resour. Conserv. Recycl. 2019, 4, 1–13. [Google Scholar] [CrossRef]
- Vasquez-Toledo, L.A.; Borja-Benítez, B.; Marcelin-Jiménez, R.; Rodríguez-Colina, E.; Tirado-Mendez, J.A. Mathematical analysis of highly scalable cognitive radio systems using hybrid game and queuing theory. AEU Int. J. Electron. Commun. 2020, 127, 153406. [Google Scholar] [CrossRef]
- Baccelli, F.; Machiraju, S.; Veitch, D.; Bolot, J. On optimal probing for delay and loss measurement. In Proceedings of the ACM Sigcomm Internet Measurement Conference, San Diego, CA, USA, 24–26 October 2007; pp. 291–302. [Google Scholar]
- Bailey, N.T.Y. On queuing processing with bulk service. J. R. Stat. Sos. 1954, B16, 80–87. [Google Scholar]
- Solnyshkina, I.V. Theory of Mass Service. Tutorial; Komsomolsk-on-Amur: Federal State Budgetary Educational Institution of Higher Professional Education; Komsomolsky-on-Amur State Technical University: Komsomolsk-on-Amur, Russia, 2015; 76p. [Google Scholar]
- Belyi, E.K. Introduction to Mass Service Theory. Tutorial; Publishing House of Petrozavodsk State University: Petrozavodsk, Russia, 2014; 76p. [Google Scholar]
- Taylor, P.G. Insensitivity in stochastic models. Chapter 3. In Queueing Networks; van Dijk, N., Boucherie, R., Eds.; A Fundamental Approach; Springer: Berlin, NY, USA, 2010; pp. 121–140. [Google Scholar]
- Chen, J.; Bhatia, H.; Addie, R.G.; Zukerman, M. Statistical Characteristics of Queue with Fractional Brownian Motion Input. IET Electron. Lett. 2015, 51, 699–701. [Google Scholar] [CrossRef]
- Wang, M.; Li, S.; Eric, W.; Wong, M.; Zukerman, M. Performance Analysis of Circuit Switched Multi-service Multi-rate Networks with Alternative Routing. J. Light. Technol. 2014, 32, 179–200. [Google Scholar] [CrossRef]
- Zhernovyi, Y. Creating Models of Queueing Systems Using GPSS World: Programs, Detailed Explanations and Analysis of Results; LAP Lambert Academic Publishing: Saarbrücken, Germany, 2015; 220p. [Google Scholar]
- Zhernovyi, Y. Invariance of Service System Characteristics; LAP Lambert Academic Publishing: Saarbrücken, Germany, 2014; p. 108. [Google Scholar]
- Kingman, J.F.C. The First Erlang Century—And the Next; Queueing Syst 63; Springer Science+Business Media: Bristol, UK, 2009. [Google Scholar] [CrossRef]
- Downton, F. Waiting time in Bulk service queuses. J. R. Stat. Sos. 1955, 17, 256–261. [Google Scholar]
- Saati, T.L. Elements of the Theory of Queuing and Its Applications; Soviet Radio: Moscow, Russia, 1971; 520p. [Google Scholar]
- Pirogova, I.; Skachkov, P.; Philippova, E. Queuing Theory: Study Guide; Ural State University of Communication Paths: Ekaterinburg, Russia, 2017; p. 84. [Google Scholar]
- Musaev, M.U.; Manshurov, S.T.; Yuldashev, L.T. Mathematical model of a single-loop control computer system and analysis of information exchange systems using stochastic graphs. Univers. Electron. Sci. J. Tech. Sci. 2020, 1, 62/64+66/69. [Google Scholar] [CrossRef]
- Kashtanov, V.; Enatskaya, N. Random Processes: A Textbook and a Workshop for Applied Undergraduate Studies; Yurite Publishing House: Moscow, Russia, 2017; 156p. [Google Scholar]
- Popov, A.M. Probability Theory and Mathematical Statistics: A Textbook for Secondary Vocational Education; Yurite Publishing House: Moscow, Russia, 2019; 434p. [Google Scholar]
- Kendall, D.C. Same problems in the theory of queens. J. R. Stat. Sos. 1951, 13, 151–173. [Google Scholar]
- Zorin, A.V.; Zorin, V.A.; Prokhodakova, E.V.; Fedotkin, M.A. Introduction to Common Markov Chains. Educational and Methodological Manual; Nizhny Novgorod State University: Nizhny Novgorod, Russia, 2013; 51p. [Google Scholar]
- Grigorios, A.P. Markov Processes and the Chapman–Kolmogorov Equation; Stochastic Processes and Applications; Springer: New York, NY, USA, 2014; pp. 33–38. [Google Scholar]
- Addie, R.G.; Neame, T.D.; Zukerman, M. Performance analysis of a Poisson–Pareto queue over the full range of system parameters. Comput. Netw. 2009, 53, 1099–1113. [Google Scholar] [CrossRef]
- Pleskunov, M.A. Mass Service Theory. Tutorial; Publishing House of Ural University: Yekaterinburg, Russia, 2022; 264p. [Google Scholar]
- Hajek, B. Random Processes for Engineers; Cambridge University Press: Cambridge, UK, 2015; 448p. [Google Scholar]
- Lando, S.K. Lectures on Producing Functions, 3rd ed.; Publishing House of the Moscow Center for Continuing Mathematical Education: Moscow, Russia, 2007; 144p. [Google Scholar]
- Pavsky, V.A. Theory of Mass Service; Kemerovo Technological Institute of the Food Industry: Kemerovo, Russia, 2008; 116p. [Google Scholar]
- Kophman, A.; Kryuon, P. Mass Service. Theory and Application; Mir: Moscow, Russia, 1965; 302p. [Google Scholar]
- Aliev, T.I. Discrete Systems Design Tasks and Methods; Study Guide; ITMO: St. Petersburg, Russia, 2015; 127p. [Google Scholar]
- Pheller, V. Introduction to Probability Theory and Its Application; Mir: Moscow, Russia, 1967; Volume 2, 752p. [Google Scholar]
- Trophimova, E.; Kisliak, N.; Giliov, D. Probability Theory and Mathematical Statistics: Study Guide; Ural University Publishing House: Ekaterinburg, Russia, 2018; 160p. [Google Scholar]
- He, X. Probabilistic Quality-of-Service Constrained Robust Transceiver Design in Multiple Antenna Systems; The University of Hong Kong: Hong Kong, China, 2012. [Google Scholar] [CrossRef]
- Berber, S. Designing Discrete and Digital Communication Systems. In Discrete Communication Systems; Oxford Academic: Oxford, UK, 2021; pp. 542–561. [Google Scholar] [CrossRef]
- Fiedler, M.; Hossfeld, T.; Tran-Gia, P. A generic quantitative relationship between quality of experience and quality of service. IEEE Netw. 2010, 24, 36–41. [Google Scholar] [CrossRef]
- Chen, J.; Addie, R.G.; Zukerman, M.; Neame, T.D. Performance evaluation of a queue fed by a Poisson Lomax burst process. IEEE Commun. Lett. 2015, 19, 367–370. [Google Scholar] [CrossRef]
- Chen, J.; Addie, R.G.; Zukerman, M. Performance Evaluation and Service Rate Provisioning for a Queue with Fractional Brownian Input. Perform. Eval. 2013, 70, 1028–1045. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).