Exploring Polygonal Number Sieves through Computational Triangulation

Abstract

The paper deals with the exploration of subsequences of polygonal numbers of different sides derived through step-by-step elimination of terms of the original sequences. Eliminations are based on special rules similarly to how the classic sieve of Eratosthenes was developed through the elimination of multiples of primes. These elementary number theory activities, appropriate for technology-enhanced secondary mathematics education courses, are supported by a spreadsheet, Wolfram Alpha, Maple, and the Online Encyclopedia of Integer Sequences. General formulas for subsequences of polygonal numbers referred to in the paper as polygonal number sieves of order k, that include base-two exponential functions of k, have been developed. Different problem-solving approaches to the derivation of such and other sieves based on the technology-immune/technology-enabled framework have been used. The accuracy of computations and mathematical reasoning is confirmed through the technique of computational triangulation enabled by using more than one digital tool. A few relevant excerpts from the history of mathematics are briefly featured.

1. Introduction

The title of this paper includes several terms that need to be explained as to why they were put together. The term triangulation (with origin in the ancient mathematical technique of using triangles when estimating distances) was introduced in social sciences research in the second part of the 20th century [1] toward overcoming the deficiency of rigor in qualitative research grounded in typically subjective interviews. In other words, triangulation allows for looking at the same point from different angles; thereby, making the domain more rigorous. In the age of technology, with the ubiquity of computational thinking [2] in diverse disciplines, the methodology of triangulation became integrated with advances in digital technology, allowing for scientific experiments to be supported and validated by more than one computational instrument. In particular, the pragmatism of independent computational experiments enhances the credibility of quantitative problem solving [3].

Computational triangulation is a new term [4] that grew out of the author’s experience using computers with future K-12 teachers of mathematics and interest in learning how social sciences research was enriched by the triangulation approach to sociology [5]. The use of sophisticated software tools in modern-day education enables prospective teachers of school mathematics to appreciate the intrinsic complexity of various learning management systems that abolish geographical boundaries of interpersonal collaboration in the rigorous study of school mathematics. Furthermore, computational triangulation of solutions to certain problems used in mathematics teacher education may be seen as a replacement of “the traditional social process of proof” [6] (p. 1402) to avoid both subtle and unsubtle errors in problem solving in the digital era. Furthermore, Van Bendegem’s [7] perspective on a mathematical experiment as integration of digital computation and physical manipulation makes it possible, by using concrete materials to enhance the visual component of mathematics education, including the mathematical preparation of schoolteachers.

The term polygonal number is probably best known in mathematics from the conjecture by Pierre de Fermat (1607–1665) that every natural number is a sum of at most m polygonal numbers of side m. When m = 3, we have triangular numbers, known from the time of Pythagoras (570–490 B.C.) as partial sums of consecutive natural numbers [8]. The term triangular number is familiar to mathematicians from the theorem proved in 1796 by Carl Friedrich Gauss (1777–1855) that any natural number is a sum of at most three triangular numbers [9]. The general case, known as the polygonal number theorem, was proved by Augustin-Louis Cauchy (1789–1857) some fifteen years later [10]. In other words, triangular and, in general, m-gonal numbers form an additive basis of orders three and m, respectively, for natural numbers [11]. In mathematics education, triangular numbers connect arithmetic to geometry, as such sums can be represented in the form of evolving equilateral triangles representing a special case of the partial sums of arithmetic sequences. In the United States, Principles and Standards for School Mathematics introduce triangular numbers as a context that “illustrates what reasoning and proof can look like in the middle grades” [12] (p. 264).

Finally, the word sieve is borrowed from the context of prime numbers when, in the 3rd century B.C., the method of separating primes from natural numbers, commonly referred to as the sieve of Eratosthenes, was devised by the Greek scholar Eratosthenes (c.276 B.C–c.195 B.C.) to whom Archimedes (287–212 B.C.) wrote: “Certain things first became clear to me by a mechanical method, although they had to be demonstrated by geometry afterwards because their investigation by the said mechanical method did not furnish an actual demonstration. But it is of course easier, when the method has previously given us some knowledge of the questions, to supply the proof than it is to find it without any previous knowledge” [13] (p. 13). Nowadays, what Archimedes called a mechanical method is the use of digital tools that are capable of initiating the interplay between computations and mathematics. This interplay is in the duality of mathematical and computational methods in the sense that whereas computations facilitate access to mathematical knowledge, mathematics itself is used to improve the efficiency of computations, which, in turn, enable advancements in various applications of mathematics, including education, engineering and science. In the modern-day discourse, the reference to geometry by Archimedes as a rigorous demonstration can be substituted by computational triangulation supported by more than one digital instrument capable of symbolic computations and more than one problem-solving approach that structures the algebraic symbolism of computations. In the context of triangular (or, more generally, polygonal) numbers, the activity of developing sieves of such numbers means crossing out every other term from the original number sequence, then every other term from the so-developed subsequence, and so on, thus arriving in the k-th step of this elimination process to the sieve of order k. Other, more complicated types of sieves will be considered also.

The paper’s focus is predominantly didactic, and it is written to connect all of the concepts described above into a single exploratory milieu for an education-oriented inquiry into the behavior of subsequences of polygonal numbers using the sieve approach. Within this milieu, two objectives of the paper can be identified. The primary objective is to use the context of elementary number theory and commonly available computational tools as an appropriate research-like experience for future teachers of pre-college mathematics. The secondary objective is to demonstrate how the modern-day computational experiment can be put into historically rich context of the subject matter of mathematics as an enrichment of teacher education pedagogy.

2. Materials and Methods

Two types of materials were used by the author when working on this paper. The first type included what the National Council of Teachers of Mathematics [14] called “mathematical action technologies”—the computational knowledge engine Wolfram Alpha developed by Wolfram Research (www.woframalpha.com accessed on 12 November 2023), Maple [15]—mathematics software (Maple 2023.1) for education and STEM fields, and an electronic spreadsheet conceptualized by its inventor as a combination of an electronic blackboard and electronic chalk in a classroom [16]. The tools are called action technologies because their appropriate use enables learners of mathematics to take action by implementing certain computational problem-solving algorithms and, in the true spirit of action learning methodology [17,18], to reflect on the results. In some cases, such reflection will be supported by the Online Encyclopedia of Integer Sequences (OEIS^®, https://oeis.org/, accessed on 12 November 2023).

The second type of materials used by the author included teaching and learning mathematics standards [12,19] and recommendations for mathematics teacher preparation in the United States [20,21]. These materials argue for the appropriate use of technology by the learners and teachers of mathematics, provide expectations for both groups, and offer ideas for mathematics education courses. In full agreement with the above-mentioned documents, methods specific for mathematics education used in this paper include computer-based instruction, standards-based mathematics, and problem solving. In particular, those methods are conducive to enabling teacher candidates’ professional development as they “use number-theory to justify relationships involving whole numbers” [12] (p. 290) and “connect the mathematical practices to mathematical content in mathematics instruction” [19] (p. 8). Through such development, one can provide evidence of how “the proper use of technology make[s] complex ideas tractable” [20] (p. 57) in the context of secondary mathematics teacher education courses.

Four problem-solving techniques will be implemented in this paper to mathematise computationally inquiries into the sieves of polygonal numbers. The first technique will begin with demonstrating the use of Wolfram Alpha in making a transition from the first few terms of a number sequence to its possible algebraic identification and numeric continuation. The next step within this technique will be in generating closed-form formulas for numeric sequences in order to have a single formula for the entire family of numeric sequences called the polygonal (in particular, triangular) number sieve of order k. The process of generalization will be based on the technology-immune/technology-enabled (TITE) framework [22], which can be briefly described as a combination of computational thinking [2], the resulting digital computations, and epistemic-oriented interpretation of those pragmatically obtained results. Such combination of the tool use of its epistemology allows for Wolfram Alpha, being an element of the instrumental act [23], to be inserted between a problem solver (a subject) and a problem (an object) in order to act bi-directionally. On the one hand, the tool acts primarily toward solving a problem through computation. On the other hand, the tool’s adaptation is not always straightforward, as it requires various intellectual efforts of the subject, thereby acting toward their cognitive development. In the words of Vygotsky [23], “Mental processes…are directed toward the solution of a problem posed by the object, and the tool dictates their coordination and course. They form a new whole—the instrumental act…What makes the instrumental act particularly unique is the simultaneous presence of stimuli of both kinds, i.e., of object and tool at the same time, each of which plays a qualitatively and functionally distinct role”.

The second technique to be used in the development of algebraic formulas for polygonal number sieves of order k, consists of the study of ranks of polygonal numbers that constitute the specific sieve. Through this technique, one can develop an alternative form of a second-degree polynomial representing the polygonal number sieve of order k and then use another digital tool—Maple—for proving computationally that different formulas developed for the sieve are identical in the sense that they generate the same integers as those delivered by Wolfram Alpha. This computational and analytical triangulation provides rigor for the development of symbolic representations of polygonal number sieves.

The third problem-solving technique is to use a spreadsheet in generating triangular number sieves of different orders and using computational triangulation in verifying the accuracy of symbolic computations provided by Wolfram Alpha and Maple. This technique enables another generalization and the development of a closed-form formula for a polygonal number sieve of order k that includes triangular, square, pentagonal, hexagonal, and other sieves of polygonal numbers.

Finally, the fourth problem-solving technique begins with a mathematical interpretation of numerical modeling of polygonal number sieves that leads to the discovery of a special type of sequence by recourse to OEIS^®. This new sequence structures a new polygonal number sieve, the terms of which grow fast due to an exponential growth of numbers to be eliminated at each step. Commonalities among new sieves of different sides are explained in the context of the fourth technique through computational triangulation.

3. Triangular Number Sieves: The First Approach

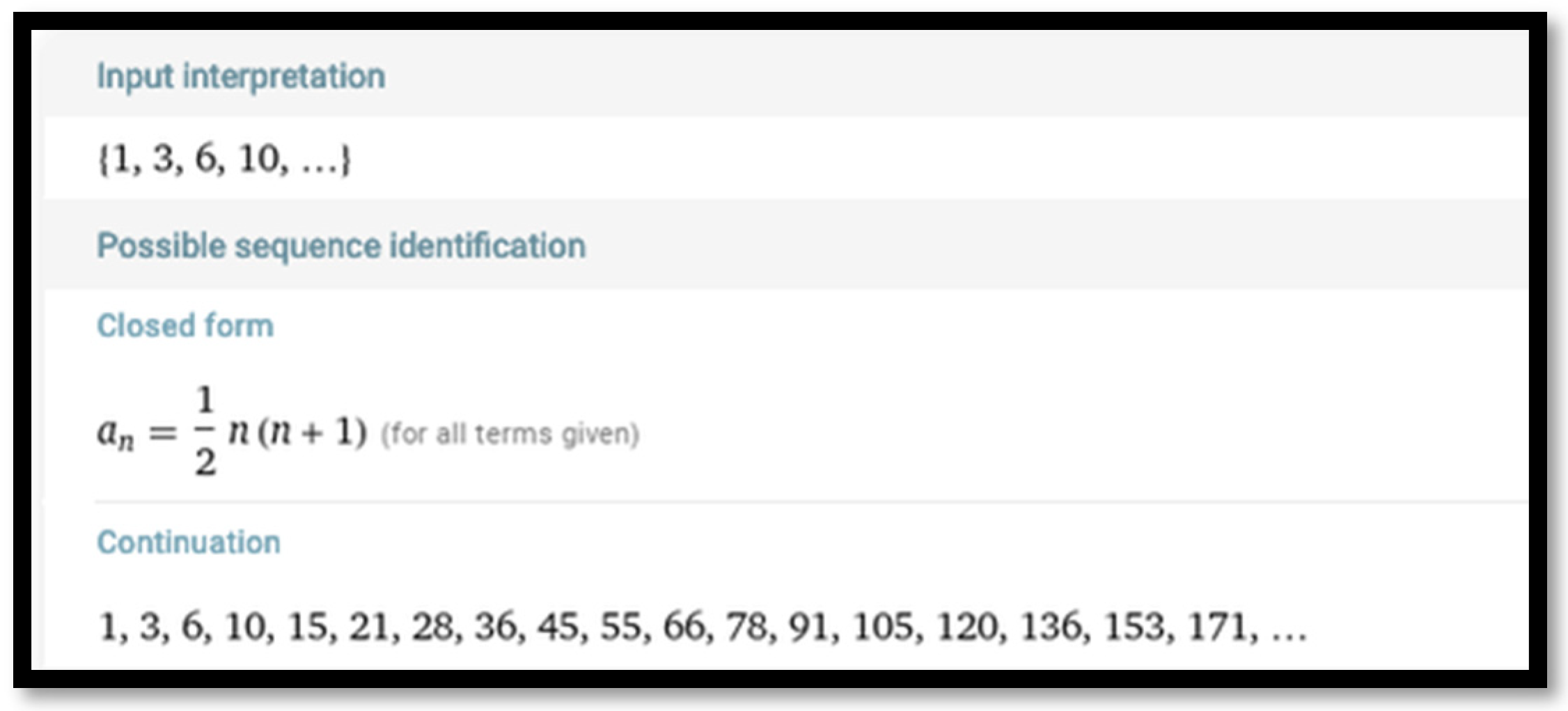
Consider the sequence of triangular numbers 1, 3, 6, 10, 15, 21, …, which are the partial sums of consecutive natural numbers 1, 1 + 2 = 3, 1 + 2 + 3 = 6, and so on. In order to find a closed-form formula for triangular numbers, one can enter their first four terms into the input box of Wolfram Alpha to obtain (Figure 1) $a_n=\frac{n\left(n+1\right)}{2}$, which, for consistency with the notation that follows, can be written as

$$t_{n,0}=\frac{1}{2}{n}^2+\frac{1}{2}n$$

(1)

It is known that every other triangular number is a hexagonal number.

1, 6, 15, 28, 45, …

(2)

The closed-form formula for sequence (2), generated by Wolfram Alpha (Figure 2), is

$$t_{n,1}=2n^2-n$$

(3)

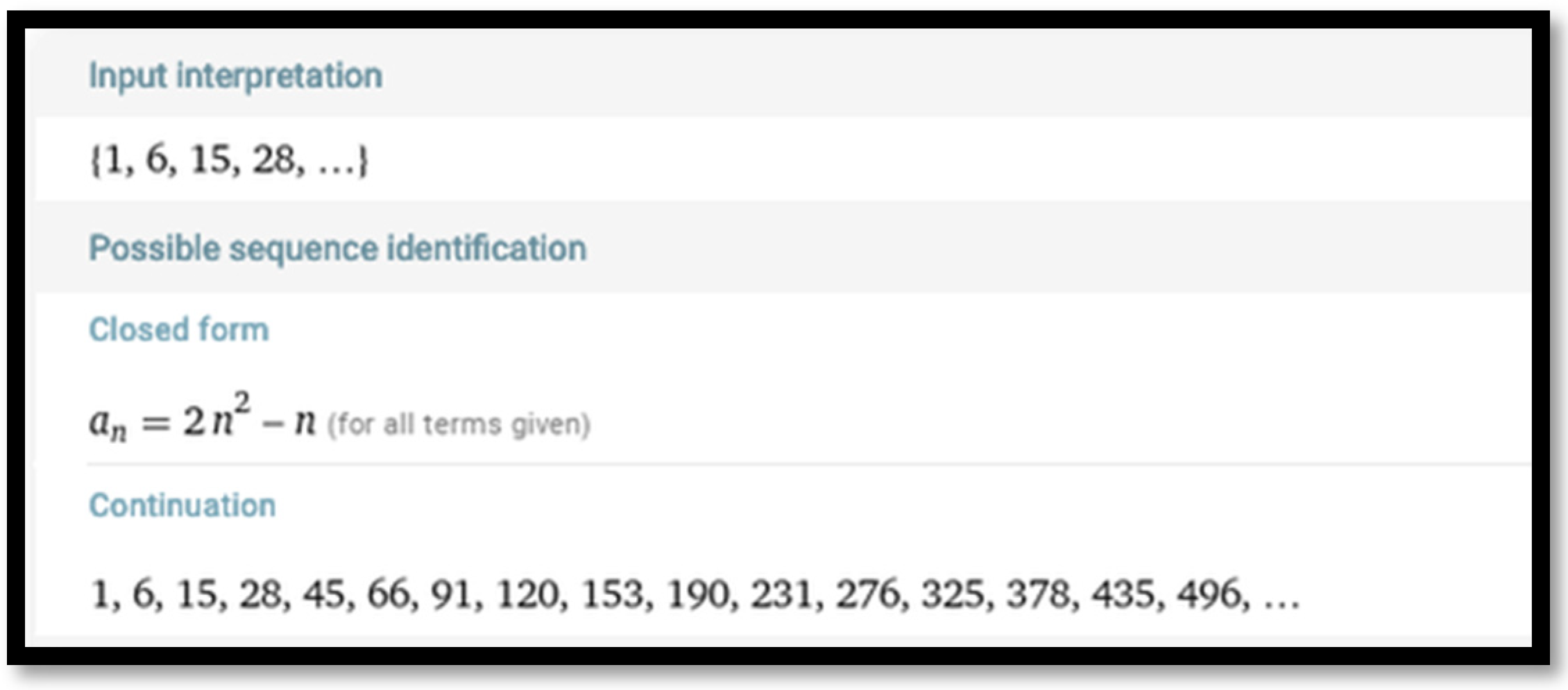
The sequence of hexagonal numbers can be called the triangular number sieve of order one. Triangular numbers (1) and hexagonal numbers (3) can be called the triangular number sieves of orders zero and one, respectively. In order to develop the triangular number sieve of order two, one has to leave out every other number from sequence (2) to obtain the sequence

1, 15, 45, 91, 153, …

(4)

In order to find a closed-form formula for sequence (4), one can enter its first four terms into the input box of Wolfram Alpha to obtain (Figure 3)

$$t_{n,2}=8n^2-10n+3$$

(5)

Continuation of the sequence defined by formula (5) can be verified over the corresponding sequences generated by Wolfram Alpha through the second approach (Section 4) and by a spreadsheet through the third approach (Section 5).

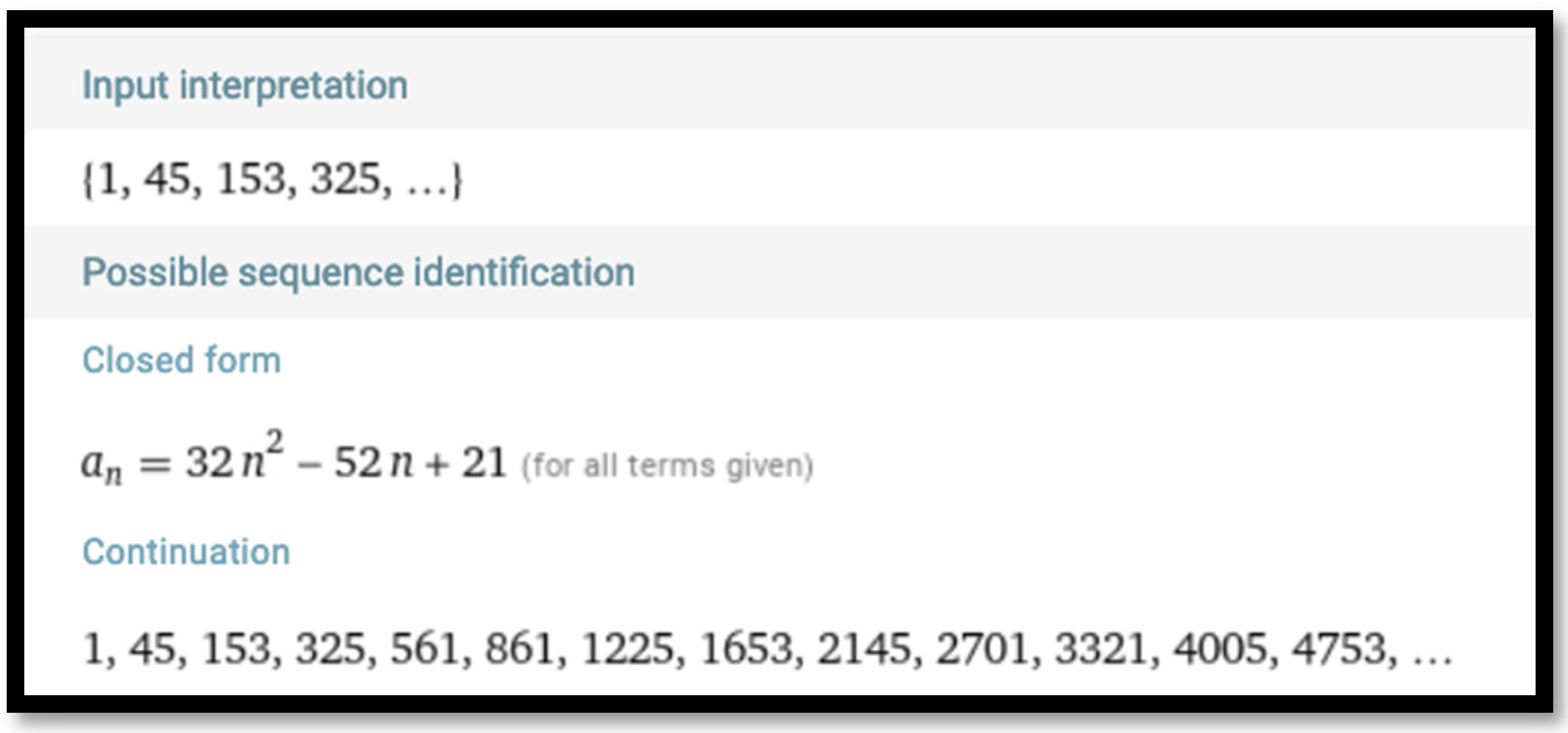
In turn, by crossing out every other number from sequence (4), one develops the triangular number sieve of order three,

1, 45, 153, 325, 561, …,

(6)

the closed-form formula of which can be generated by Wolfram Alpha (Figure 4) in the form

$$t_{n,3}=32n^2-52n+21$$

(7)

Continuation of the sequence defined by formula (7) can be verified over the corresponding sequences generated by Wolfram Alpha through the second approach (Section 4) and by a spreadsheet through the third approach (Section 5).

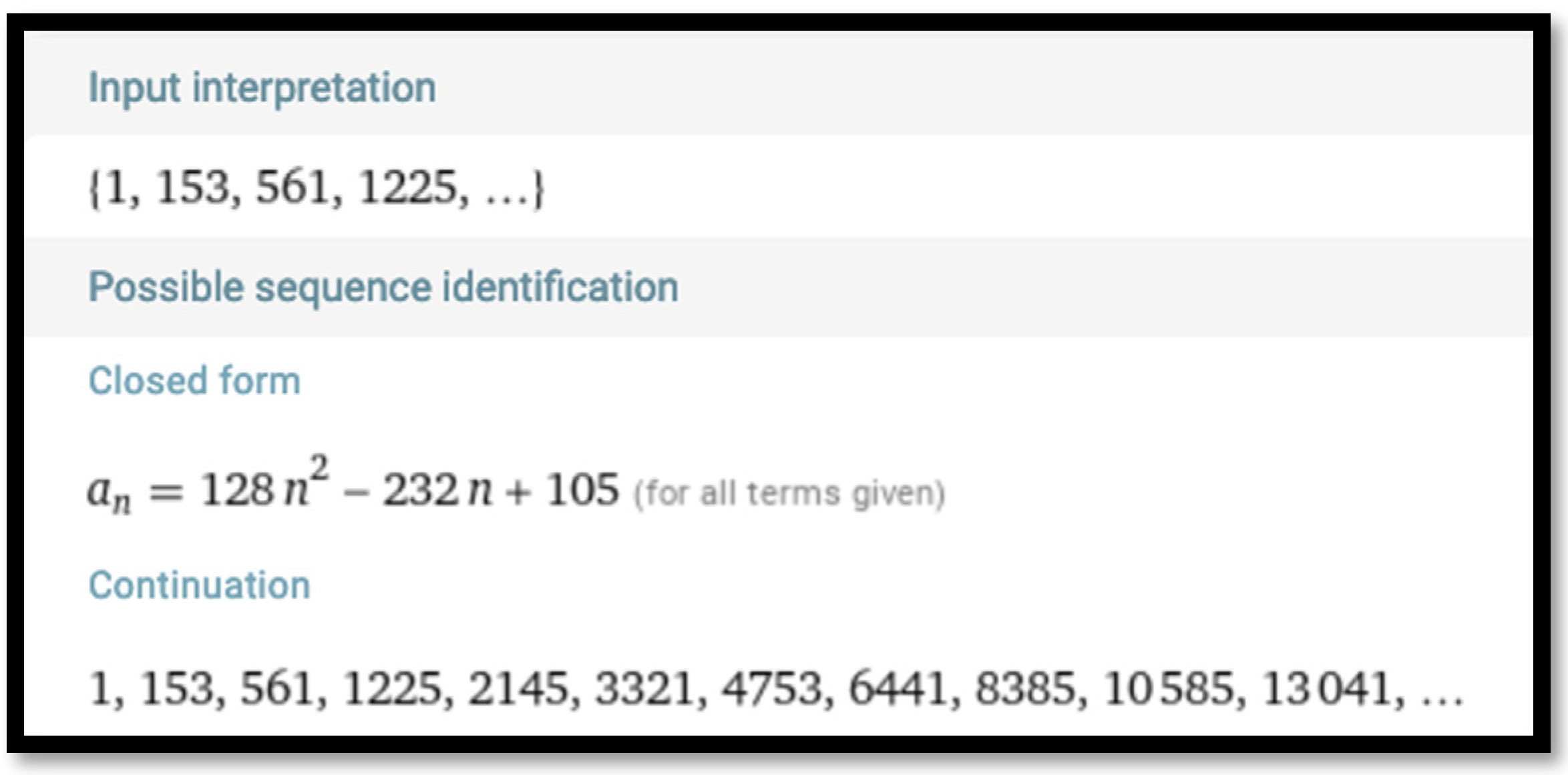
Deleting every other number from sequence (6) yields the triangular number sieve of order four,

1, 153, 561, 1225, 2145, …

(8)

with the closed-form formula (generated by Wolfram Alpha as shown in Figure 5)

$$t_{n,4}=128n^2-232n+105$$

(9)

Continuation of the sequence defined by formula (9) can be verified over the corresponding sequences generated by Wolfram Alpha through the second approach (Section 4) and by a spreadsheet through the third approach (Section 5).

Likewise, the formula

$$t_{n,5}=512n^2-976n+465$$

(10)

can be developed for the triangular number sieve of order five (Figure 6).

Continuation of the sequence defined by formula (10) can be verified over the corresponding sequences generated by Wolfram Alpha through the second approach (Section 4) and by a spreadsheet through the third approach (Section 5).

Observing formulas (1), (3), (5), (7), (9) and (10), one can note that the coefficients in n² are $2^{-1}, 2^1, 2^3, 2^5, 2^7, 2^9$. The sequence of exponents −1, 1, 3, 5, 7, 9, … can be written in the form $a_k=2k-1,$ where k = 0, 1, 2, 3, … are the values of the order of a sieve. The sequence of the coefficients in n¹ is 1/2, −1, −10, −52, −976, …. Using Wolfram Alpha (Figure 7), one obtains the formula $b_k=2^{2k}-3\times 2^{k-1}$. 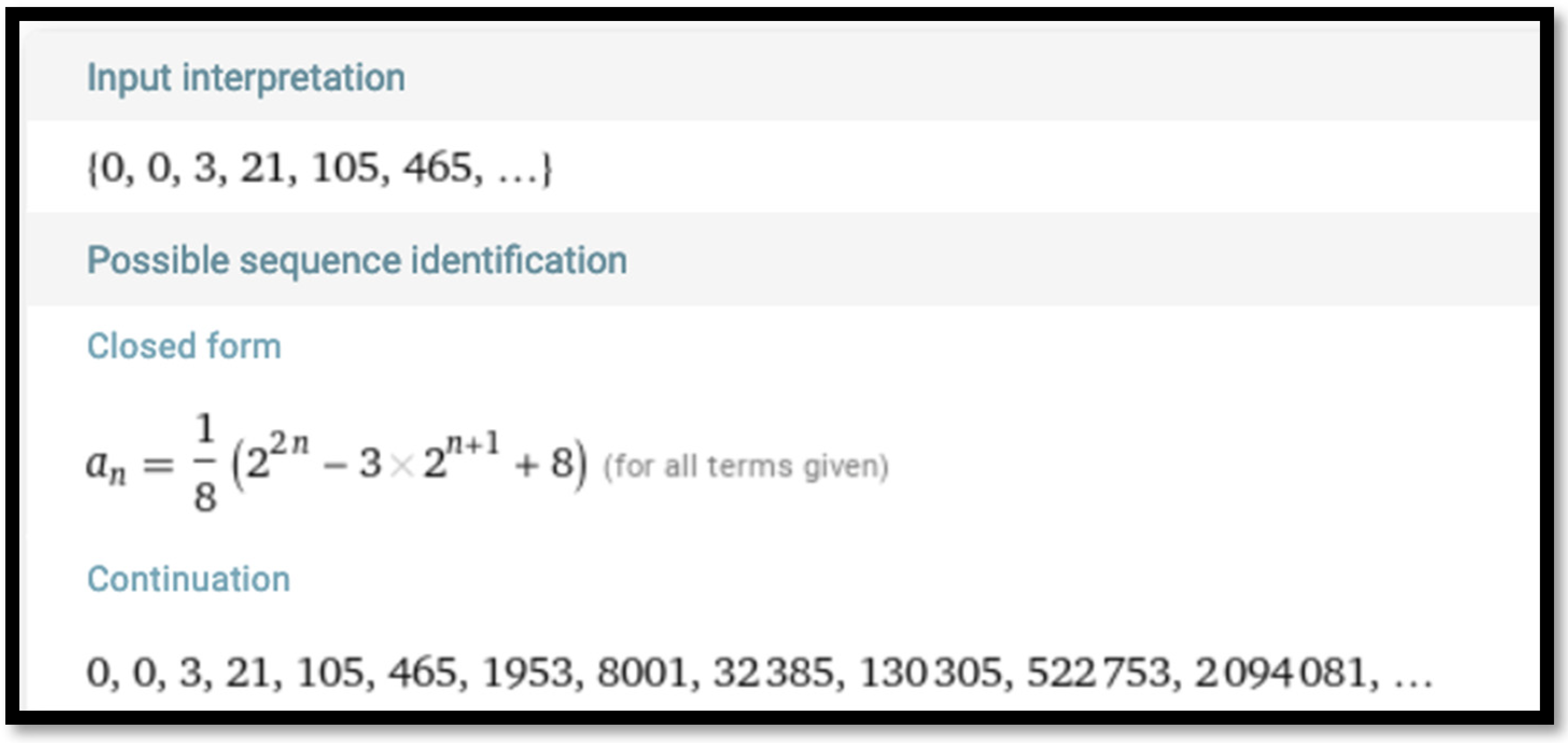The sequence of the coefficients in n⁰ is 0, 0, 3, 21, 105, 465, …. Using Wolfram Alpha (Figure 8), one obtains the formula

$$c_k=\frac{2^{2k}-3\times 2^{k+1}+8}{8}=\frac{(2^k-4)\times (2^k-2)}{8}$$

These computations prompt generalization to have a closed-form formula for the triangular number sieve of order k:

$$t_{n,k}=2^{2k-1}{n}^2-(2^{2k}-3\times 2^{k-1})n+(2^k-1)(2^{k-1}-1)$$

(11)

Remark 1.

One can use the OEIS^® to obtain closed-form formulas for triangular number sieves of different orders by entering the first few terms of sequences (5), (7), (9), (10) into the input box of this online source of information. It turns out that sequence (5) is included in OEIS^®, yet the tool offers the quadratics $8n^2+6n+1,$ rather than $8n^2-10n+3$ defined by relation (6). Note that the former turns into the latter after substituting n − 1 for n. Indeed, $8{(n-1)}^2+6\left(n-1\right)+1=8n^2-10n+3$. At the same time, whereas triangular number sieves defined by (6), and (7), are parts of the OEIS^®, the tool offers their closed-form identical to what is offered by Wolfram Alpha.

Remark 2.

One can use Maple (Figure 9) to replace closed-form formula (11) by recursive formula for the triangular number sieve of order k. This formula and its initial condition are

$$t_{n+1,k}=t_{n,k}+\frac{4^k\left(2n-1\right)+3·2^k}{2},t_{0,k}=\left(2^k-1\right)\left(2^{k-1}-1\right)$$

(12)

In particular, when k = 0, we have $t_{n+1,0}=t_{n,0}+\left(n+1\right)$, and when n = k = 0, we have $t_{1,0}=t_{0,0}+1=1$.

4. Triangular Number Sieves: The Second Approach

One may wonder: where did exponents with the base two come from? Of course, whereas the elements of the triangular number sieves as triangular numbers are the second powers of their ranks within a sieve, it is due to the coefficients that the growth of the elements of the sieve takes place. Another approach to developing a closed-form formula for the elements of the triangular number sieve of order k is to look for the ranks of triangular numbers that form the sieves of order k, k = 0, 1, 2, 3, ….

The ranks of the elements of the triangular sieve of order zero, that is, of the sequence of triangular numbers, are 1, 2, 3, 4, 5, …, which can be defined as

$$r_{n,0}=2^0\left(n-1\right)+1,n=1,2,3,\dots$$

(13)

The ranks of the elements of the sieve of order one, that is, the ranks of the triangular numbers 1, 6, 15, 28, 45, … are 1, 3, 5, 7, 9,…, which can be defined as

$$r_{n,1}=2^1\left(n-1\right)+1,n=1,2,3,\dots$$

(14)

The ranks of the elements of the sieve of order two, that is, the ranks of the triangular numbers 1, 15, 45, 91, 153, … are 1, 5, 9, 13, 17, …, which can be defined as

$$r_{n,2}=2^2\left(n-1\right)+1,n=1,2,3,\dots$$

(15)

The ranks of the elements of the sieve of order three, that is, the ranks of the triangular numbers 1, 45, 153, 325, 561 are 1, 9, 17, 25, 33, and the latter numbers can be defined as

$$r_{n,3}=2^3\left(n-1\right)+1,n=1,2,3,\dots$$

(16)

Generalizing from formulas (13)–(16) to the ranks of the elements of the triangular number sieve of order k yields the sequence of the ranks

$$r_{n,k}=2^k\left(n-1\right)+1,n=1,2,3,\dots ,k=0,1,2,\dots$$

(17)

Therefore, the n-th element of the triangular number sieve of order k has the form

$$t_{n,k}=\frac{1}{2}[2^k\left(n-1\right)+1][2^k\left(n-1\right)+2],n=1,2,3,\dots ,k=0,1,2,\dots$$

(18)

This explains where the powers of two came from and provides triangulation for the approach based on the use of Wolfram Alpha (Figure 10), yielding formula (11), by using Maple (Figure 11).

5. Triangular Number Sieves: The Third Approach

One can also use a spreadsheet to generate triangular number sieves by using formulas describing the ranks of the terms of the sieves developed in the previous section. The general form of the n-th rank of the term of the sieve of order k is given by formula (17). This formula can be applied to other polygonal number sieves using formulas that define a polygonal number through its rank. 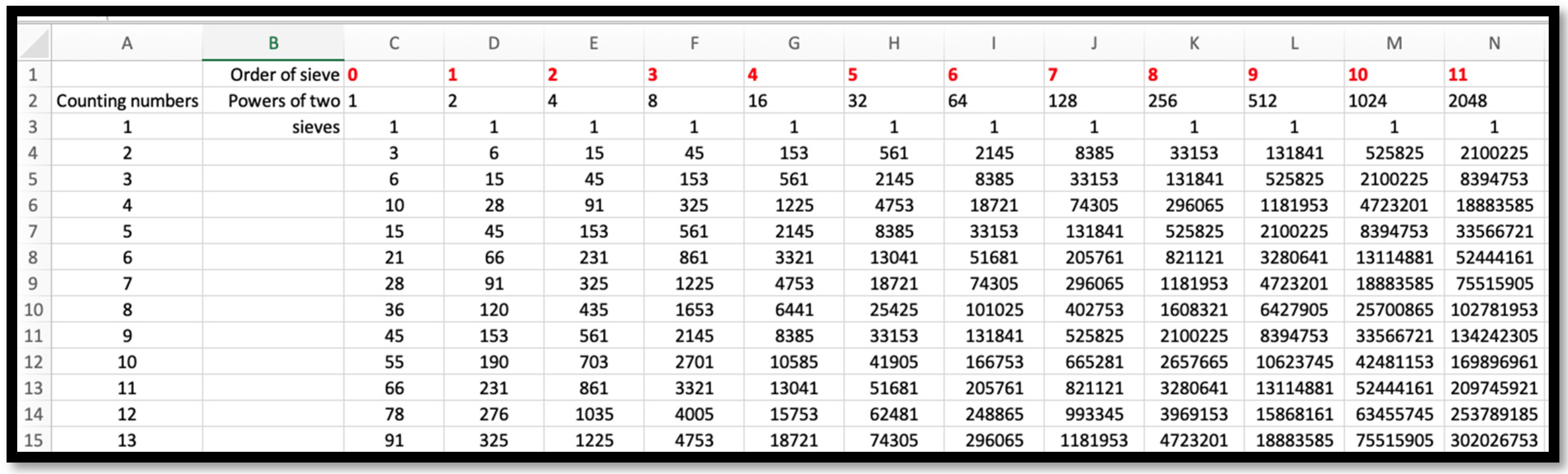For example, formula (18) defines the n-th term of the triangular sieve of order k. The spreadsheet that generates triangular number sieves of orders zero through eight is shown in Figure 12. 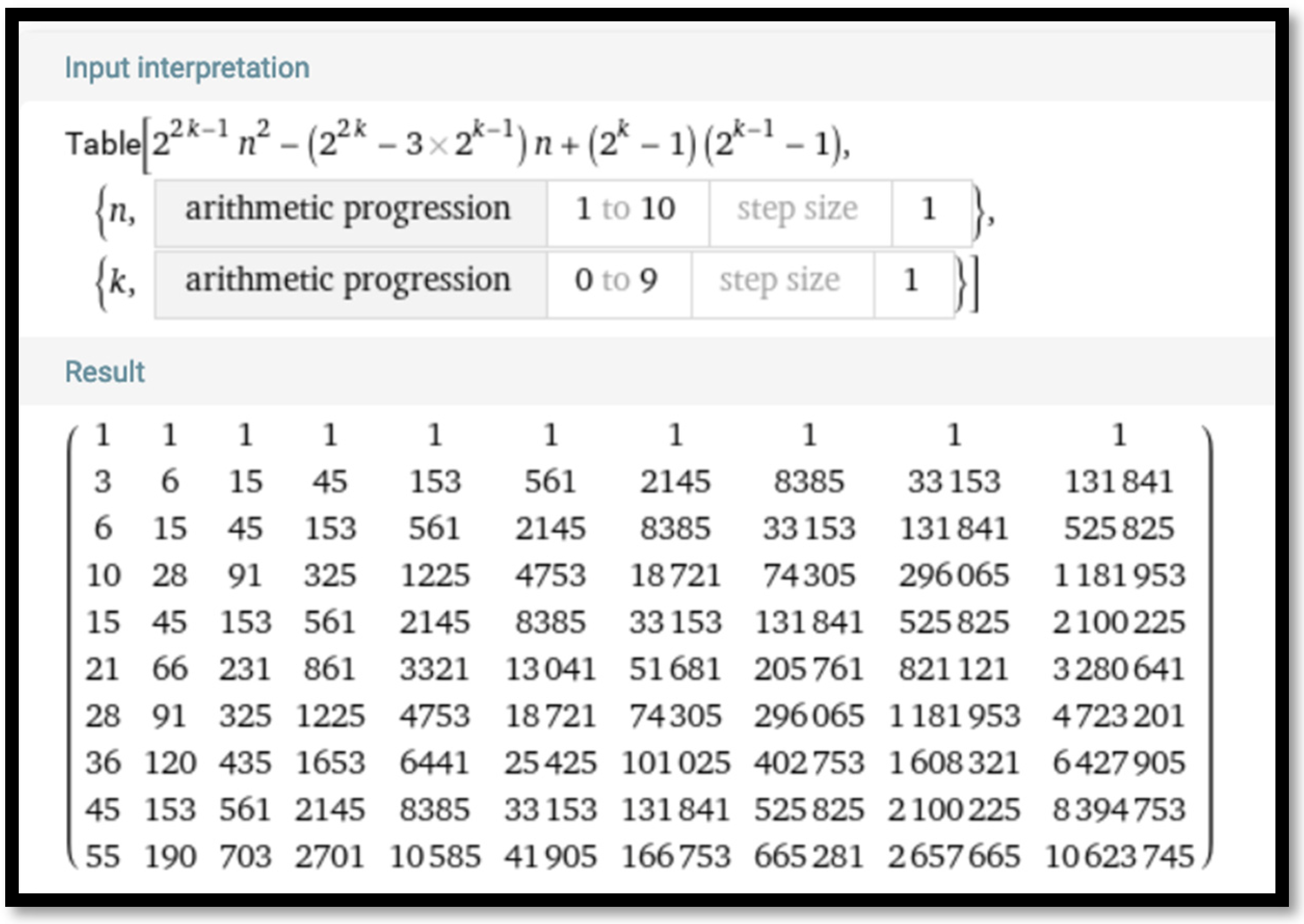The third approach makes it possible to generalize the spreadsheet-based triangular number sieve of order k to an m-gonal number sieve of order k using the formula $P\left(m,n\right)=\frac{n\left(n-1\right)\left(m-2\right)}{2}+n$ representing an m-gonal number. In that way, the formula

$$p_{n,m,k}=\frac{2^k\left(n-1\right)[2^k\left(n-1\right)+1]\left(m-2\right)}{2}+2^k\left(n-1\right)+1$$

(19)

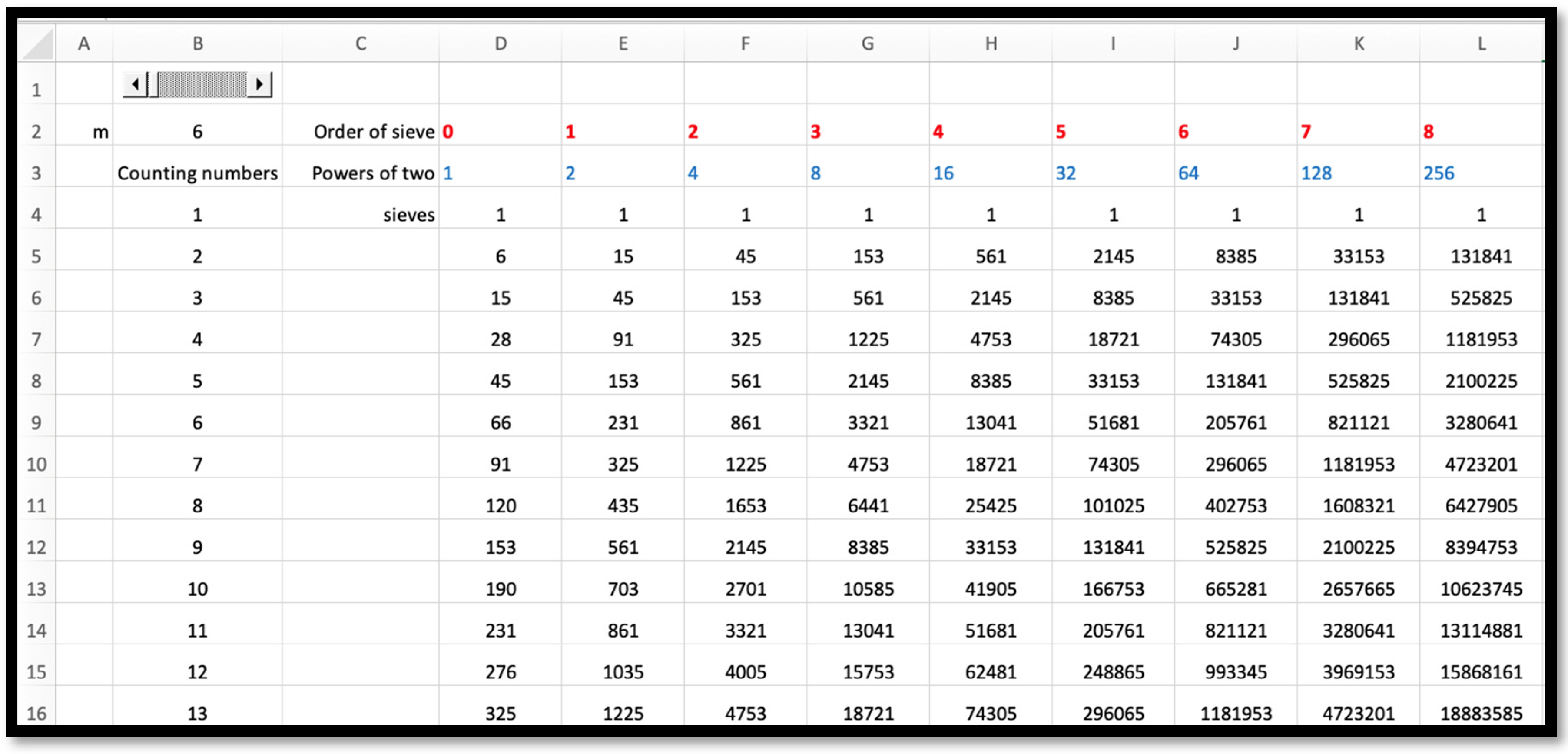
entered in cell D4 and replicated to cell L16 with the value of m displayed in cell B2 (Figure 13) makes it possible to have a single spreadsheet that displays m-gonal number sieves of different orders. In particular, the spreadsheet of Figure 13 shows hexagonal (m = 6) number sieves of orders zero through eight. One can check to see that every other triangular number is a hexagonal number.

Formula (19) represents the polygonal number sieve of order k and side m, the rank of which is equal to $2^k\left(n-1\right)+1$. Using the spreadsheet of Figure 13, one can generate polygonal number sieves of different orders by changing the value of m in cell B2. In that way, formula (19) may be considered as a family of two-dimensional formulas depending on m. 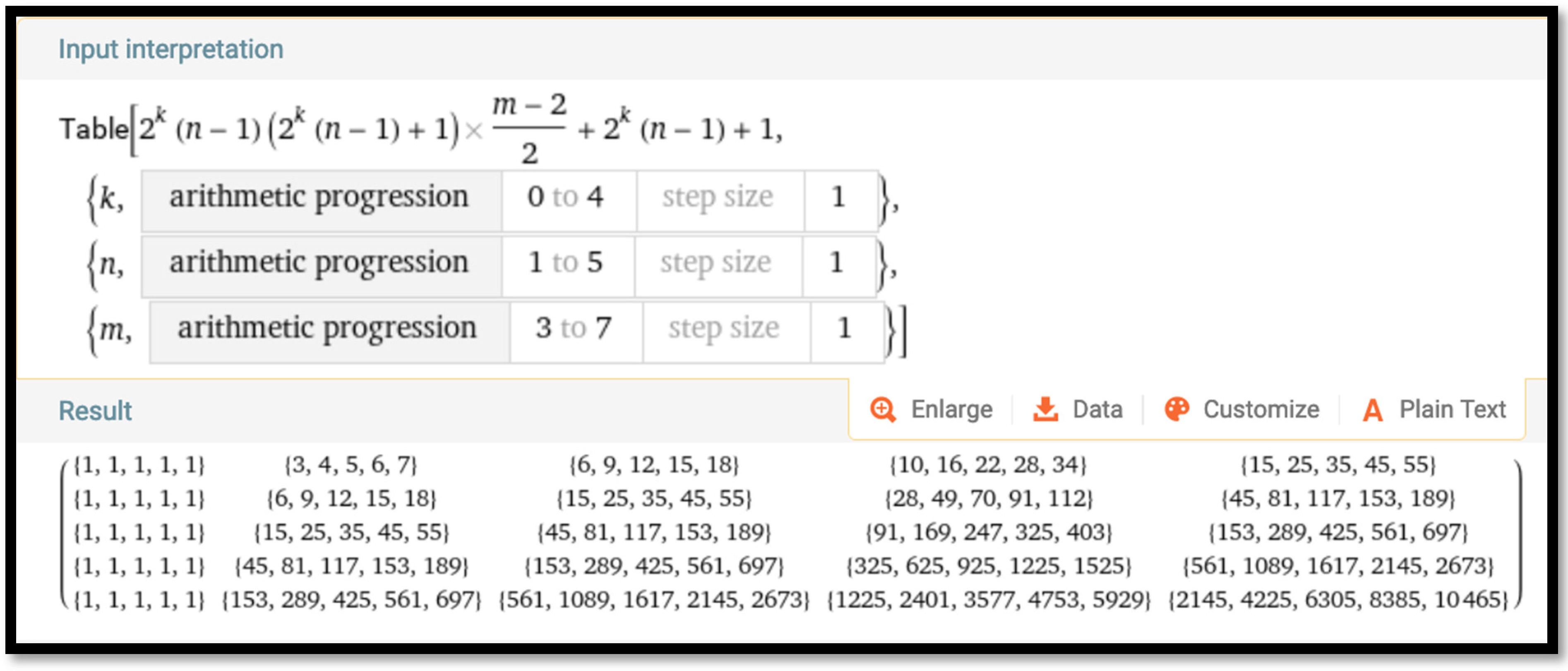At the same time, the use of Wolfram Alpha makes it possible to use formula (19) as a three-dimensional modeling tool by creating a table of the elements of the corresponding polygonal number sieves for different values of m. Such a table is shown in the bottom part of Figure 14 generating the first five elements of the five sieves for $n\in \left[1,5\right], k\in \left[0,4\right], m\in \left[3,7\right].$ In this table, horizontally, the first position in each row contains numbers that belong to the triangular number sieves of orders zero through four. For example, the first element in the second bracket of the fifth row of the Wolfram Alpha table is 153. This number can be found in cell G4 of the spreadsheet of Figure 12—the second element of the triangular number sieve of order four. Likewise, the second, third, fourth and fifth positions in each row contain numbers that belong, respectively, to square, pentagonal, hexagonal, and heptagonal number sieves of orders zero through four. For example, the fourth element in the third bracket of the fifth row of the Wolfram Alpha table is 2145. This number can be found in cell H6 of the spreadsheet of Figure 13—the third element of the hexagonal number sieve of order four. In that way, the joint use of Wolfram Alpha and a spreadsheet provides computational triangulation in the context of constructing polygonal number sieves of different sides and orders. Furthermore, as will be discussed in the next section, the table developed by Wolfram Alpha prompts the development of other types of sieves of polygonal numbers.

6. Exploring Cullen-Type Polygonal Number Sieves as a TITE Exploration

Explorations begin with interpreting the results of computations in mathematical terms. However, while a TI part of explorations follows the TE part provided by a spreadsheet and Wolfram Alpha, the former part is not totally independent of technology by seeking information available online and carrying out the very basic computation of products and exponents as a verification of formal reasoning through falling back on the results of digital computations. Consider the numbers 1, 6, 45, 325, 2145, which, according to the table of Figure 14, represent the 1st, 2nd, 3rd, 4th, and 5th elements of triangular number sieves of orders 0, 1, 2, 3, and 4, respectively. In particular, the number 2145 can be found in cell G7 of the spreadsheet of Figure 12 as the 5th element of the triangular number sieve of order 4 (alternatively, the 5th sieve, if the sieve of order zero is considered the 1st sieve). The ranks of the above five numbers are 1, 3, 9, 25, 65, the general form of which, $r\left(n\right)=\left(n-1\right)·2^{n-1}+1, n=1,2,3,\dots ,$ can be found in OEIS^® (A002064) and referred to as Cullen numbers, named after James Cullen (1867–1933), an Irish mathematician and Jesuit priest. One can check to see that r(6) = 161 so that the 6th element of the 6th triangular number sieve (assigning n = 1 to the sieve of order zero) is $\frac{161·162}{2}=13041$ (see cell H8 in the spreadsheet of Figure 12). Also, r(7) = 385, and the 7th element of the 7th triangular number sieve is $\frac{385·386}{2}=74305$ (see cell I9 in the spreadsheet of Figure 12). In order to define the sequence of triangular numbers 1, 6, 45, 325, 2145, 13041, 74,305, …, (which can be interpreted as a Cullen-type triangular number sieve), one has to use the formula

$$t_{r\left(n\right)}=\frac{\left[\left(n-1\right)·2^{n-1}+1\right]\left[\left(n-1\right)·2^{n-1}+2\right]}{2},n=1,2,3\dots$$

(20)

For example, $t_{r\left(6\right)}=\frac{\left(5·2^5+1\right)\left(5·2^5+2\right)}{2}=\frac{161·162}{2}=13041$.

Alternatively, the sequence $t_{r\left(n\right)}$ defined by formula (20) can be described through the following action. To move along the triangular number sieve from 1 to 6, one skips 1 triangular number; to move from 6 to 45 one has to skip 5 triangular numbers; to move from 45 to 325, one has to skip 15 triangular numbers; to move from 325 to 2145, one has to skip 39 triangular numbers; to move from 2145 to 13,041, one has to skip 95 triangular numbers, to move from 13,041 to 74,305, one has to skip 225 triangular numbers. The general form of the sequence 1, 5, 15, 39, 95, 225 is $a\left(n\right)=\left(n+1\right)·2^{n-1}-1, n=1,2,3,\dots$, and it can be found in OEIS^® under the number A099035. That is, the triangular number sieve 1, 6, 45, 325, 2145, 13,041 can be defined as the step-by-step elimination of $\left(n+1\right)·2^{n-1}-1$ triangular numbers, n ≥ 1.

Likewise, one can consider the numbers 1, 15, 153, 1225, 8385, which, according to the table of Figure 14, represent the 1st, 2nd, 3rd, 4th, and 5th elements of hexagonal number sieves of orders 0, 1, 2, 3, and 4, respectively. In particular, the number 8385 can be found in cell H8 of the spreadsheet of Figure 13 as the 5th element of the 5th hexagonal number sieve. The ranks of the above five numbers are also Cullen numbers $r\left(n\right)=\left(n-1\right)·2^{n-1}+1, n=1,2,3,\dots .$ Thus, as r(6) = 161, the 6th element of the 6th hexagonal number sieve is $161·\left(2·161-1\right)=51681$ (see cell I9 in the spreadsheet of Figure 13). In order to define the sequence of hexagonal numbers 1, 15, 153, 1225, 8385, 51,681, …, which can be interpreted as the Cullen-type hexagonal number sieve, one has to use the formula

$$h_{r\left(n\right)}=\left[\left(n-1\right)·2^{n-1}+1\right]·\left[2·\left(\left(n-1)·2^{n-1}+1\right)\right)-1\right],n=1,2,3\dots .$$

(21)

For example, $h_{r\left(6\right)}=\left(5·2^5+1\right)·\left(2·\left(5·2^5+1\right)-1\right)=161·321=51,681$ (see cell I9 in the spreadsheet of Figure 13).

Generalizing from formulas (20) and (21), the following formula

$$P_{r\left(n\right),m}=\left(n-1\right)·2^{n-2}·\left[\left(n-1\right)·2^{n-1}+1\right]·\left(m-2\right)+\left(n-1\right)·2^{n-1}+1,$$

(22)

where n ≥ 1, m ≥ 3, for the Cullen-type polygonal number sieve can be derived.

The table in Figure 15 created by Wolfram Alpha allows one to write down the first three terms of the Cullen-type number sieves after the second elimination for triangular numbers (1, 45, 2,100,225), square numbers (1, 81, 4,198,401), pentagonal numbers (1, 117, 6,296,577), hexagonal numbers (1, 153, 8,394,752), and so on. One can check to see that the third element in each of the four triples has rank 2049 on the original list of the corresponding polygonal numbers. For example, the original ranks of triangular and square numbers prior to any elimination are $\frac{-1+\sqrt{1+8·2100225}}{2}=2049$ and $\sqrt{4,198,401}=2049$, respectively. Furthermore, those third elements, respectively, have rank nine on the list of the corresponding triangular, square, pentagonal, and hexagonal number sieves of order eight (alternatively, the 9th sieves, counting the sieve of order zero as the 1st sieve). Likewise, the triangular number 45 and the hexagonal number 153 appear in cells F4 and G5 of the spreadsheets of Figure 11 and Figure 12, respectively, both having rank 2 on the lists of the corresponding 4th sieves (including sieves of order zero). The same is true for the square, 81, and pentagonal, 117, numbers. That is, regardless of the side of polygonal numbers, the Cullen-type elimination process provides the same place within a sieve for the same-rank survivors.

To explain a mathematical meaning of such connections, note that among the first n natural numbers (n > 0), there are $INT\left(\frac{n}{2}\right)$ even numbers and, because $n-INT\left(\frac{n}{2}\right)=\{\begin{array}{c}2l-INT\left(\frac{2l}{2}\right)=l\\ 2l+1-INT\left(\frac{2l+1}{2}\right)=l+1\end{array}$, there are $INT\left(\frac{n}{2}\right)+1$ numbers that survive elimination of every other number from a polygonal number sieve (whatever its number). In other words, if a polygonal number in a sieve has rank n, on the next elimination step, when n = 2l, it has the rank l, and it has the rank l + 1 when n = 2l + 1. That is, if a number survives elimination, its rank decreases. Therefore, the rank 2049 of a polygonal number on the original list (e.g., $2,100,225=\frac{2049·\left(2049+1\right)}{2}$ on the list of triangular numbers) would follow the following transformations before this number appears on the 5th sieve: $2049\to 1025\to 513\to 257\to 129\to 65\to 33\to 17\to 9\to 5$. One can also start from the rank 2049 and move up to determine ranks of the polygonal numbers and their corresponding values by increasing by one the double of each rank to obtain the following chain of ranks: $2049\leftarrow 4097\leftarrow 8193\leftarrow 16,385\leftarrow 32,769\leftarrow 65,537\leftarrow 131,073\leftarrow 262,145\leftarrow 524,289$. Using formulas connecting polygonal numbers to their ranks, the corresponding polygonal numbers can be found. For example, $t_{4097}=8,394,753$ and $t_{8193}=33,566,721$. These two triangular numbers can be seen in cells L11 and M11 of the spreadsheet of Figure 12—they both have rank nine, but belong to the 9th and the 10th sieves, respectively.

One can see how computations provide learners of mathematics with numeric evidence for recognizing patterns which require explanations that are independent from the use of technology (i.e., technology-immune). At the same time, when mathematical results are driven by computations (i.e., technology-enabled), formal reasoning may not be entirely detached from computing, as reasoning constantly resorts to the results of digital computations for the verification of the absence of possible errors. In other words, computation is the primary instrument used to trigger, amplify, and verify mathematical argument.

7. Conclusions

The paper demonstrated how digital computations in elementary number theory can support educational activities with triangular, hexagonal, and, in general, polygonal numbers. The computations were based on the classic idea, known from the time when Eratosthenes found a way to separate prime numbers from natural numbers, of creating a whole number sieve by eliminating certain integers from the original sequence. The activities, designed for future teachers of secondary mathematics, followed the TITE framework [22] demonstrating how mathematical explorations, providing research-like experience for the teachers, may be both dependent on and independent of technology. For example, the construction of quadratic trinomials as analytic representations of triangular number sieves was enabled by Wolfram Alpha, yet to demonstrate that coefficients in those quadratics are, in fact, base-two exponents of the order (i.e., the step) of elimination required using formal reasoning, pattern recognition, and recourse to an online source of information, the use of which is free from computation. This was followed by using Maple in turning a closed-form formula into a recursive formula, thereby providing two forms of representation for a triangular number sieve of order k. When an alternative analytic closed-form representation of the triangular number sieve of order k was obtained through a different approach, Maple was used again to confirm algebraic identicity of two representations, thus enriching activities with computational triangulation [4].

Furthermore, it was shown how the triangular and the hexagonal number sieves of order k can be generalized to the polygonal number sieve of side m, rank n and order k to be used within a spreadsheet and to allow for the value of m to serve as a slider-controlled parameter on which a family of two-dimensional number sieves depends. By changing the value of m, such a spreadsheet immediately recalculates a large amount of modeling data. The accuracy of spreadsheet modeling was confirmed by Wolfram Alpha, which enabled one to tabulate the above-mentioned family of polygonal number sieves for different values of m at once. This made it possible not only to observe the development of polygonal number sieves in three dimensions, but to pinpoint identical elements appearing in arrays of different dimensions.

Through a combination of the TITE framework and computational triangulation, another elimination procedure was developed, resulting in what was called the Cullen-type polygonal number sieves. In such sieves, the number of integers to be eliminated at a certain step was also a base-two exponent of the step number (a Cullen number). Using the three-dimensional table provided by Wolfram Alpha, the first three elements of the Cullen-type sieves of the second order were identified, located within the corresponding spreadsheets, and connections between two types of modeling were mathematically explained. In that way, the paper, emphasizing the value of the notion of computational triangulation [4], can serve as a bridge to earlier writings on the TITE framework [24,25] by offering a new domain for using technology in mathematics education.

A brief history of major developments in the mathematics of polygonal numbers was featured as a way of presenting “mathematics as a living and evolving subject” [20], p. 61, an important aspect of any mathematics education course designed for future teachers of secondary mathematics. To this end, the paper prompted that evolution of ideas about the properties of polygonal numbers, on the path from distinguishing them among those used just to count to recognition of their properties in the form of the additive number theory conjectures to formal demonstration of the correctness of the conjectures, was associated with several of the most famous contributors to mathematics in the history of humankind. The paper showed how the terms triangulation and sieve, associated with classic ideas of mathematics, can be extended, respectively, for using multiple methods in the study of the same phenomenon in social sciences and for novel explorations in mathematics teacher education. All things considered, digital computations allow for ancient and classic mathematical ideas to be revisited in mathematics education through the lens of the modern-day instrumental method, which, in general, as Vygotsky [23] put it, “immensely extends the possibilities of behavior by making the results of the work of geniuses available to everyone”.