Correlations of the Electronic, Elastic and Thermo-Electric Properties of Alpha Copper Sulphide and Selenide
Abstract
:1. Introduction
2. Computational Details
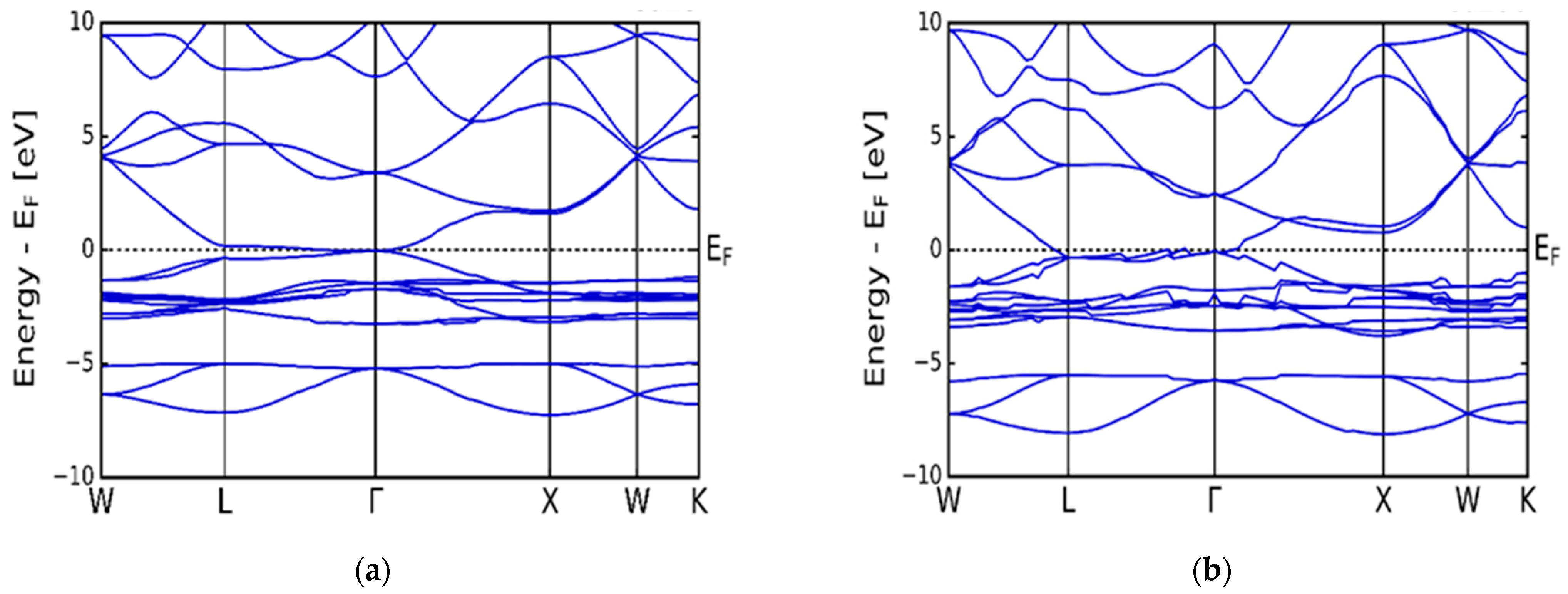
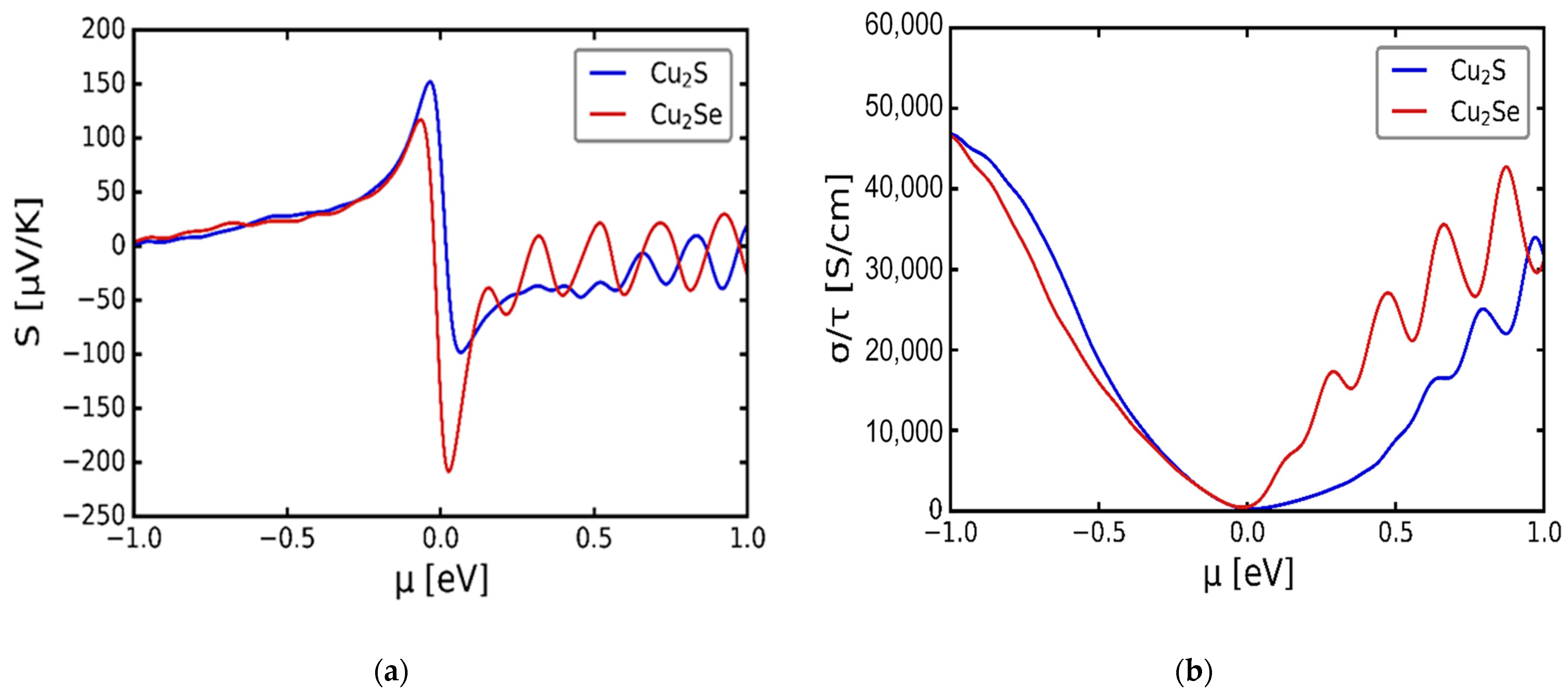
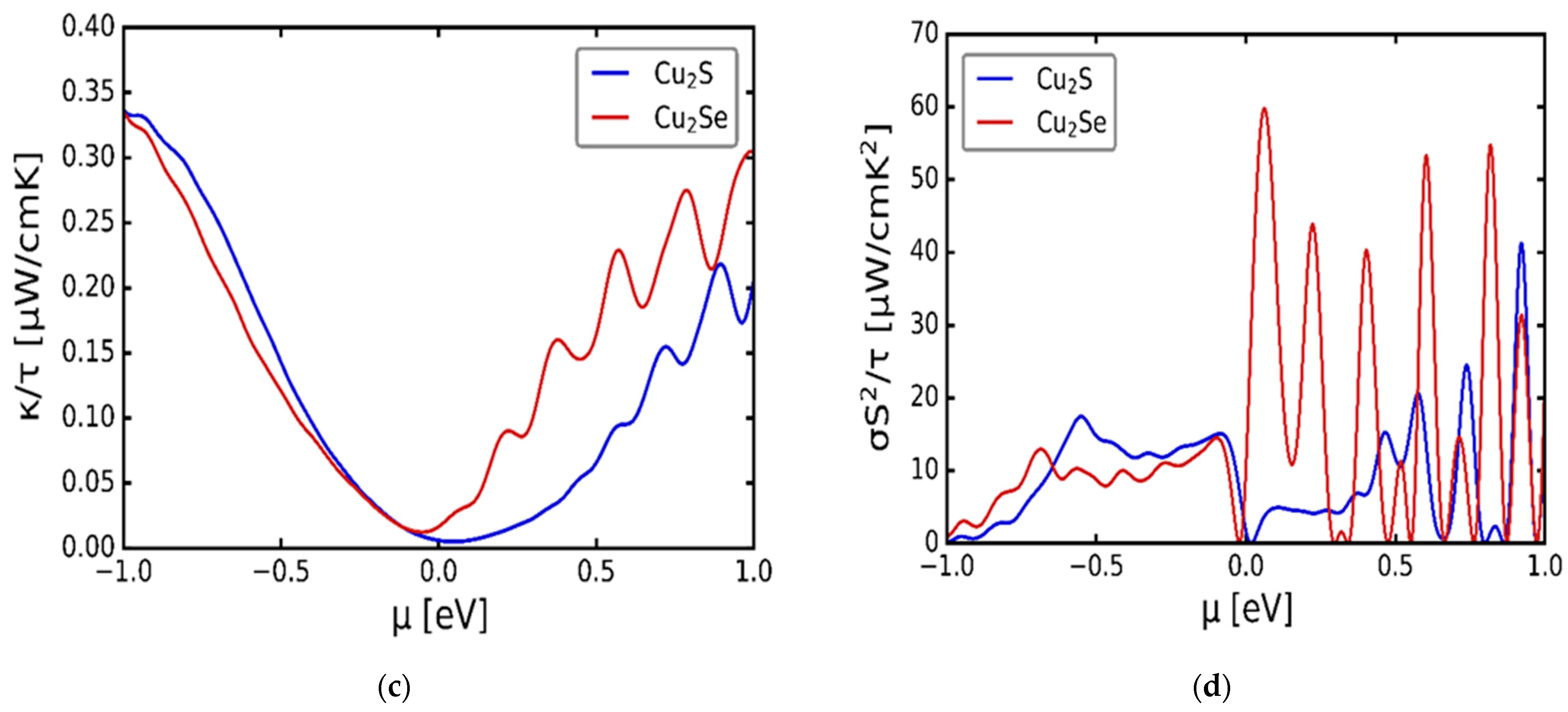
3. Results and Discussion
3.1. Electronic Properties
3.2. Elastic Properties
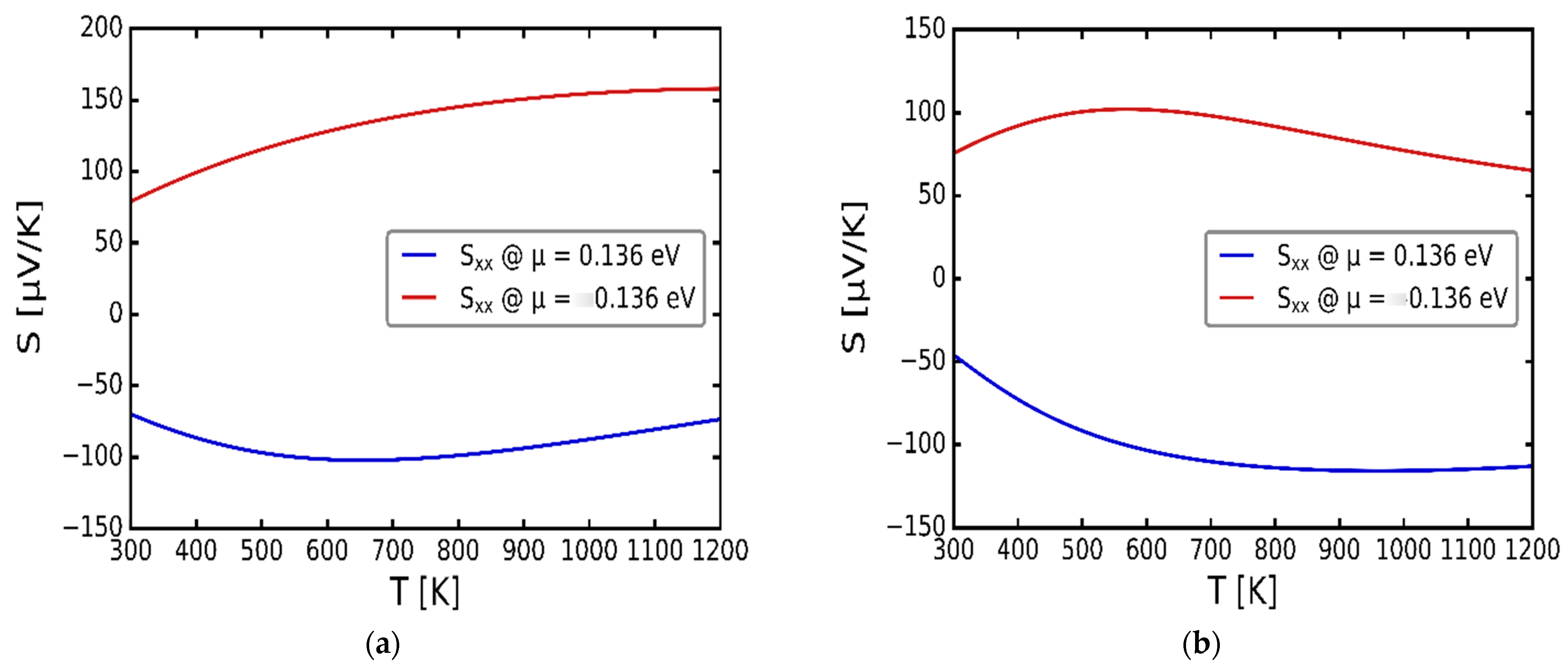
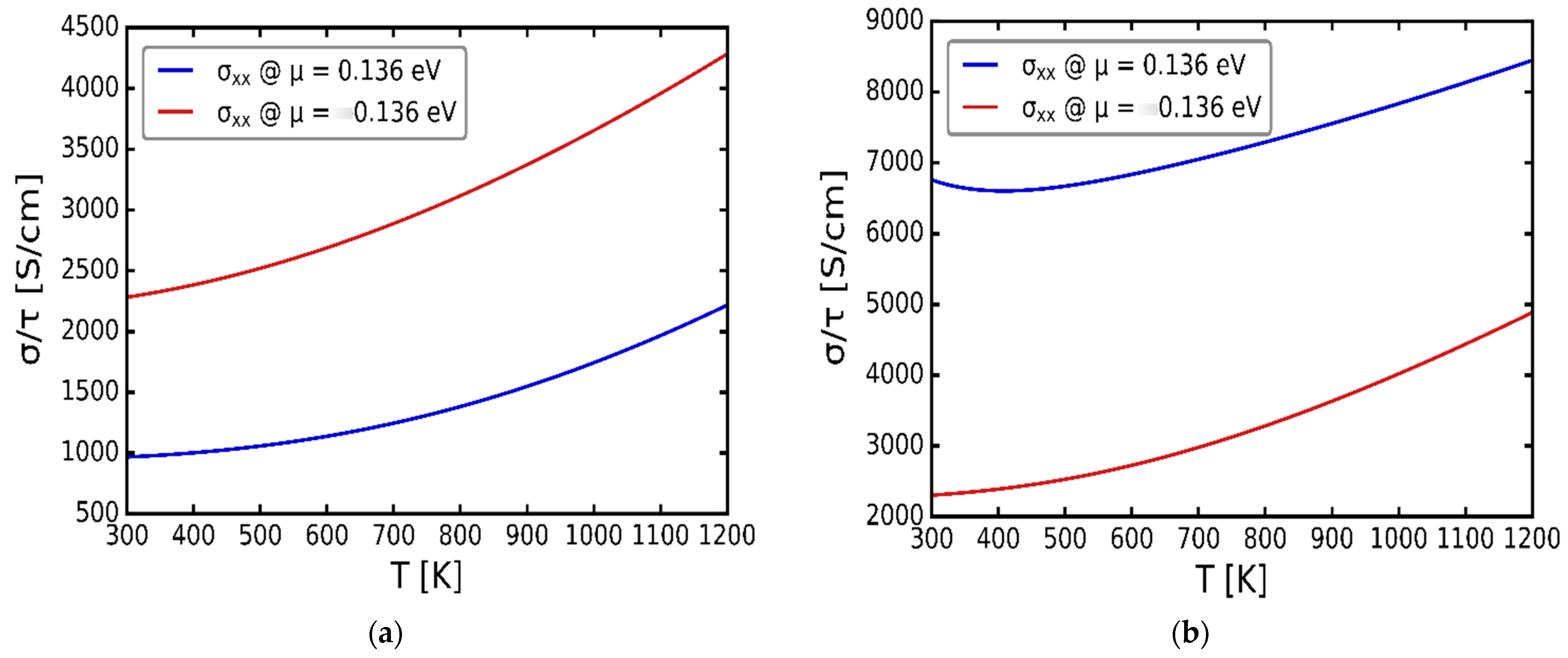
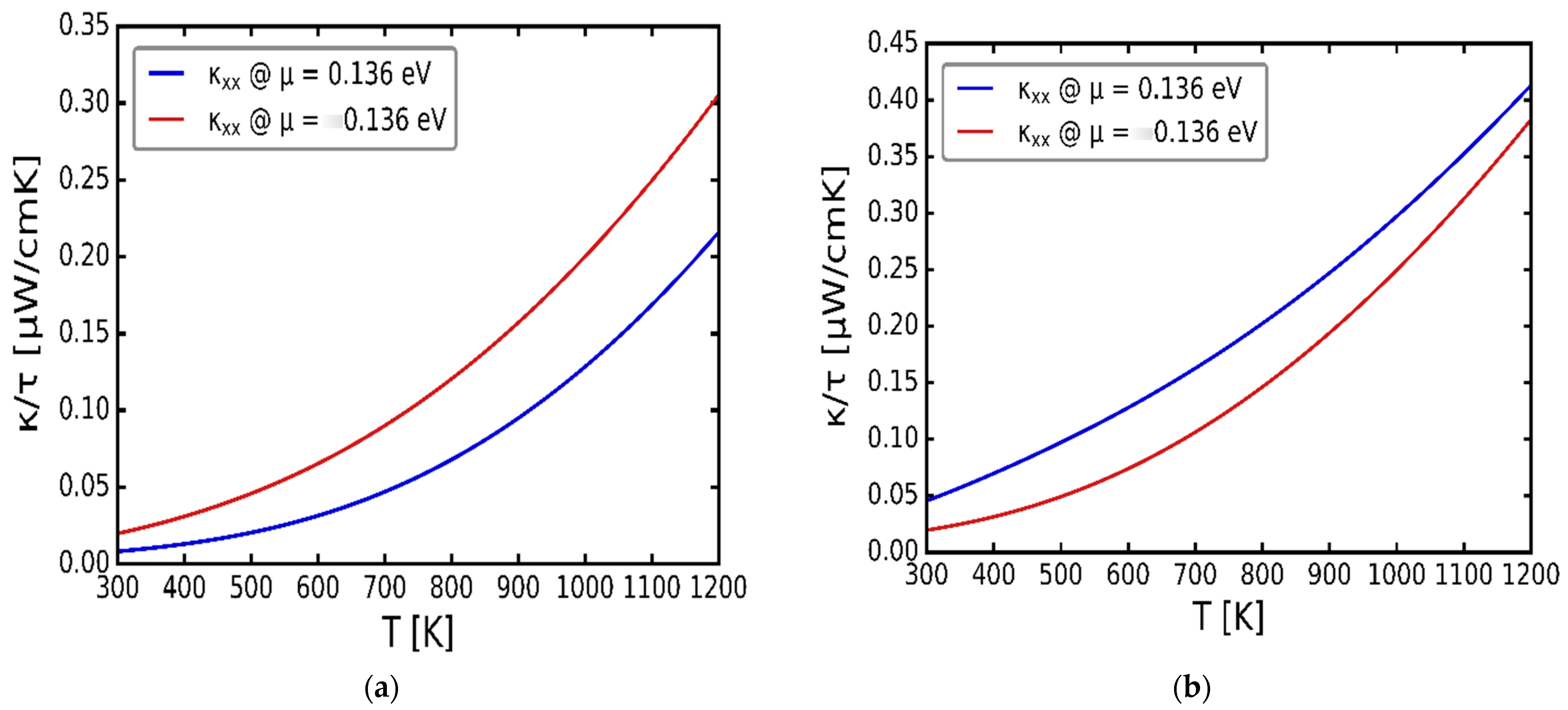
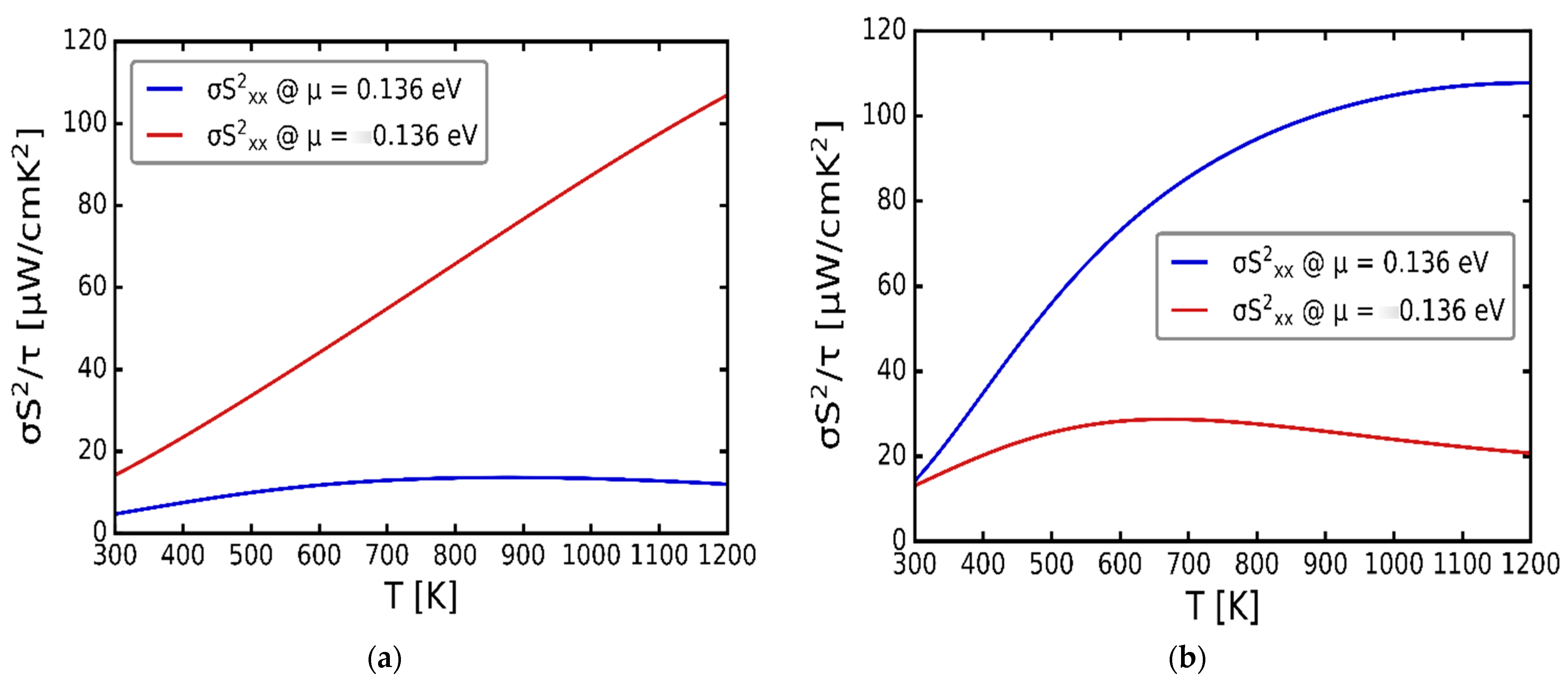
3.3. Transport Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ashfaq, A.; Tahir, S.; ur Rehman, U.; Ali, A.; Ashfaq, H.F.; Ahmad, W.; Mushtaq, S.; Saeed, R.; Haneef, M.; Khan, K.M.; et al. Structural, morphological and thermoelectric properties of copper deficient and excessive Cu2−xS nanoparticles with (x = 0–0.3). Surf. Interfaces 2022, 30, 101965. [Google Scholar] [CrossRef]
- Dioum, A.; Diakite, Y.I.; Malozovsky, Y.; Ayirizia, B.A.; Beye, A.C.; Bagayoko, D. First-principles investigation of electronic and related properties of cubic magnesium silicide (Mg2Si). Computation 2023, 11, 40. [Google Scholar] [CrossRef]
- Namsani, S.; Gahtori, B.; Auluck, S.; Singh, J.K. An interaction potential to study the thermal structure evolution of a thermoelectric material: β-Cu2Se. J. Comput. Chem. 2017, 38, 2161–2170. [Google Scholar] [CrossRef]
- Potter, R.W. An electrochemical investigation of the system copper-sulfur. Econ. Geol. 1977, 72, 1524–1542. [Google Scholar] [CrossRef]
- Will, G.; Hinze, E.; Abdelrahman, A.R.M. Crystal structure analysis and refinement of digenite, Cu1.8S, in the temperature range 20 to 500 °C under controlled sulfur partial pressure. Eur. J. Mineral. 2002, 14, 591–598. [Google Scholar] [CrossRef]
- Kim, H.; Ballikaya, S.; Chi, H.; Ahn, J.P.; Ahn, K.; Uher, C.; Kaviany, M. Ultralow thermal conductivity of β-Cu2Se by atomic fluidity and structure distortion. Acta Mater. 2015, 86, 247–253. [Google Scholar] [CrossRef]
- Tyagi, K.; Gahtori, B.; Bathula, S.; Auluck, S.; Dhar, A. Band structure and transport studies of copper selenide: An efficient thermoelectric material. Appl. Phys. Lett. 2014, 105, 173905. [Google Scholar] [CrossRef]
- Nelson, H.D.; Li, X.; Gamelin, D.R. Computational studies of the electronic structures of copper-doped CdSe nanocrystals: Oxidation states, Jahn-Teller distortions, Vibronic bandshapes, and Singlet-triplet splittings. J. Phys. Chem. C 2016, 120, 5714–5723. [Google Scholar] [CrossRef]
- He, Y.; Day, T.; Zhang, T.; Liu, H.; Shi, X.; Chen, L.; Snyder, G.J. High thermoelectric performance in non-toxic earth-abundant copper sulfide. Adv. Mater. 2014, 26, 3974–3978. [Google Scholar] [CrossRef]
- Arora, S.; Kabra, K.; Joshi, K.B.; Sharma, B.K.; Sharma, G. Structural, elastic, thermodynamic and electronic properties of covellite, CuS. Phys. B Condens. Matter 2020, 582, 311142. [Google Scholar] [CrossRef]
- Lv, Z.; Cui, H.; Huang, H.; Li, X.; Wang, H.; Ji, G. Study of the electronic, bonding, elastic and acoustic properties of covellite via first principles. J. Alloys Compd. 2017, 692, 440–447. [Google Scholar] [CrossRef]
- Tang, Y.Q.; Ge, Z.H.; Feng, J. Synthesis and thermoelectric properties of copper sulfides via solution phase methods and spark plasma sintering. Crystals 2017, 7, 141. [Google Scholar] [CrossRef]
- Gulans, A.; Kontur, S.; Meisenbichler, C.; Nabok, D.; Pavone, P.; Rigamonti, S.; Sagmeister, S.; Werner, U.; Draxl, C. Exciting: A full-potential all-electron package implementing density-functional theory and many-body perturbation theory. J. Phys. Condens. Matter 2014, 26, 363202. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. arXiv 2007, arXiv:0707.2088v2. [Google Scholar] [CrossRef]
- Mahan, G.D.; Sofo, J.O. The best thermoelectric. Proc. Natl. Acad. Sci. USA 1996, 93, 7436–7439. [Google Scholar] [CrossRef]
- Aroyo, M.I.; Perez-Mato, J.M.; Capillas, C.; Kroumova, E.; Ivantchev, S.; Madariaga, G.; Kirov, A.; Wondratschek, H. Bilbao crystallogarphic server I: Databases and crystallographic computing programs. Z. Krist. 2006, 221, 15–27. [Google Scholar]
- Bharathi, B.; Thanikaikarasan, S.; Ramesh, K. Structural, compositional, and optical properties of electrochemically deposited Cu2S thin films. Int. J. ChemTech Res. 2014, 6, 1907–1909. [Google Scholar]
- Sakuma, T.; Sugiyama, K.; Matsubara, E.; Waseda, Y. Determination of the Crystal Structure of Superionic Phase of Cu2Se. Mater. Trans. JIM 1989, 30, 365–369. [Google Scholar] [CrossRef]
- Råsander, M.; Bergqvist, L.; Delin, A. Density functional theory study of the electronic structure of fluorite Cu2Se. J. Phys. Condens. Matter 2013, 25, 125503. [Google Scholar] [CrossRef]
- Garba, E.J.D.; Jacobs, R.L. The electronic structure of Cu2−xSe. Phys. B+C 1986, 138, 253–260. [Google Scholar] [CrossRef]
- Zeng, X.; Peng, R.; Yu, Y.; Hu, Z.; Wen, Y.; Song, L. Pressure effect on elastic constants and related properties of Ti3Al intermetallic compound: A first-principles study. Materials 2018, 11, 2015. [Google Scholar] [CrossRef] [PubMed]
- Stadler, R.; Wolf, W.; Podloucky, R.; Kresse, G.; Furthmuller, J.; Hafner, J. Ab initio calculations of cohesive, elastic, and dynamical properties of CoSi2 by pseudopotential and all-electrons techniques. Phys. Rev. B 1996, 54, 1729–1734. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, O.H.; Martin, R.M. First-principles calculation of stress. Phys. Rev. Lett. 1983, 50, 697–700. [Google Scholar] [CrossRef]
- Jamal, M.; Asadabadi, S.J.; Ahmad, I.; Aliabad, H.R. Elastic constants of cubic crystals. Comput. Mater. Sci. 2014, 95, 592–599. [Google Scholar] [CrossRef]
- Hasan, S.; Baral, K.; Ching, W.Y. Total bond order density as a quantum mechanical metric for materials design: Application to chalcogenide crystals. Preprints 2019, 2019060199. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, C.; Zhu, T.; Yan, Y.; Su, X.; Tang, X. Mechanical properties and thermal stability of the high-thermoelectric-performance Cu2Se compound. ACS Appl. Mater. Interfaces 2021, 13, 45736–45743. [Google Scholar] [CrossRef]
- Mott, P.H.; Dorgan, J.R.; Roland, C.M. The bulk modulus and Poisson’s ratio of “incompressible” materials. J. Sound Vib. 2008, 312, 572–575. [Google Scholar] [CrossRef]
- Byeon, D.; Sobota, R.; Delime-Codrin, K.; Choi, S.; Hirata, K.; Adachi, M.; Kiyama, M.; Matsuura, T.; Yamamoto, Y.; Matsunami, M.; et al. Discovery of colossal Seebeck effect in metallic Cu2Se. Nat. Commun. 2019, 10, 72. [Google Scholar] [CrossRef]
- Hasan, S.; San, S.; Baral, K.; Li, N.; Rulis, P.; Ching, W.Y. First-Principles Calculations of Thermoelectric Transport Properties of Quaternary and Ternary Bulk Chalcogenide Crystals. Materials 2022, 15, 2843. [Google Scholar] [CrossRef]
- Scheidemantel, T.J.; Ambrosch-Draxl, C.; Thonhauser, T.; Badding, J.V.; Sofo, J.O. Transport coefficients from first-principles calculations. Phys. Rev. B 2003, 68, 125210. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, H.; Khaliq, J.; Shen, Y.; Simpson, K.; Reece, M.J. Enhancement of thermoelectric properties by atomic-scale percolation in digenite CuxS. J. Mater. Chem. A 2014, 2, 9486–9489. [Google Scholar] [CrossRef]
- Narjis, A.; Outzourhit, A.; Aberkouks, A.; El Hasnaoui, M.; Nkhaili, L. Structural and thermoelectric properties of copper sulphide powders. J. Semicond. 2018, 39, 122001. [Google Scholar] [CrossRef]
- Zhao, L.D.; Berardan, D.; Pei, Y.L.; Byl, C.; Pinsard-Gaudart, L.; Dragoe, N. Bi1−xSrxCuSeO oxyselenides as promising thermoelectric materials. Appl. Phys. Lett. 2010, 97, 092118. [Google Scholar] [CrossRef]
- Yang, D.; Su, X.; Yan, Y.; He, J.; Uher, C.; Tang, X. Mechanochemical synthesis of high thermoelectric performance bulk Cu2X (X = S, Se) materials. APL Mater. 2016, 4, 116110. [Google Scholar] [CrossRef]
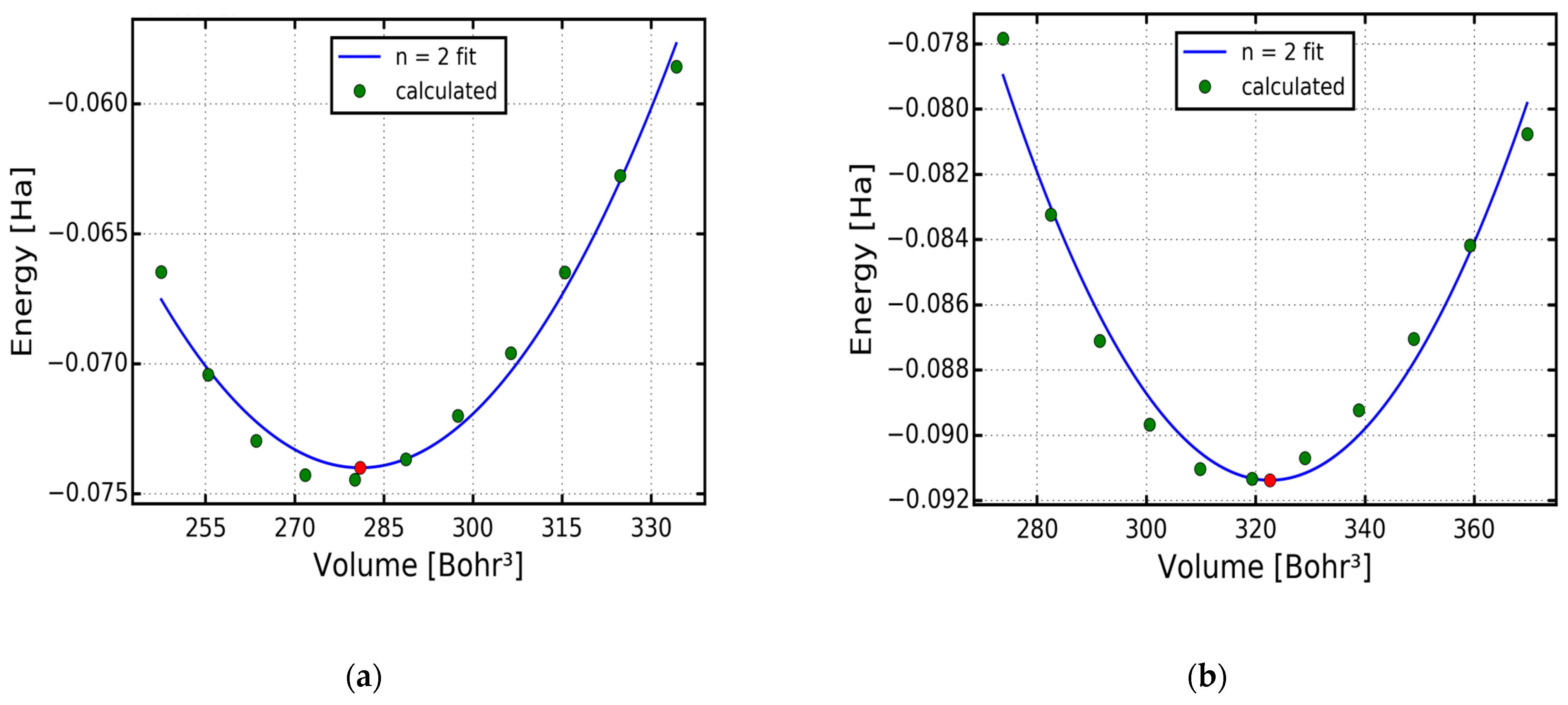

| Cu2S | Cu2Se | |
| (Bohr3) | 281.02 | 322.57 |
| (Bohr) | 10.39 | 10.89 |
| (eV) | −3705.95 | −5735.90 |
| α-Cu2S | C11 | C12 | C44 | B0 | Y | G | |
| This work (GPa) | 105.940 | 54.680 | 23.442 | 71.767 | 63.421 | 23.442 | 0.3530 |
| Computational (GPa) | - | 80.70 a | 65.413 a | 23.692 a | 0.360 a |
| α-Cu2Se | C11 | C12 | C44 | B0 | Y | G | |
| This work (GPa) | 120.11 | 110.49 | 16.540 | 113.70 | 47.320 | 16.540 | 0.4400 |
| Computational (GPa) | 121.298 b | 73.419 b | 74.101 b | 89.276 b | 53.57 c | 20.58 b | 0.300 b |
| Experimental (GPa) | 72.80 c | - | - | 45.70 c | 34.20 c | 13.60 c | 0.390 c |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramoshaba, M.; Mosuang, T. Correlations of the Electronic, Elastic and Thermo-Electric Properties of Alpha Copper Sulphide and Selenide. Computation 2023, 11, 233. https://doi.org/10.3390/computation11110233
Ramoshaba M, Mosuang T. Correlations of the Electronic, Elastic and Thermo-Electric Properties of Alpha Copper Sulphide and Selenide. Computation. 2023; 11(11):233. https://doi.org/10.3390/computation11110233
Chicago/Turabian StyleRamoshaba, Moshibudi, and Thuto Mosuang. 2023. "Correlations of the Electronic, Elastic and Thermo-Electric Properties of Alpha Copper Sulphide and Selenide" Computation 11, no. 11: 233. https://doi.org/10.3390/computation11110233
APA StyleRamoshaba, M., & Mosuang, T. (2023). Correlations of the Electronic, Elastic and Thermo-Electric Properties of Alpha Copper Sulphide and Selenide. Computation, 11(11), 233. https://doi.org/10.3390/computation11110233







