Numerical Approximations of Diblock Copolymer Model Using a Modified Leapfrog Time-Marching Scheme
Abstract
1. Introduction
2. Phase Field Models for Diblock Copolymers
3. Numerical Schemes
3.1. Temporal Discretization
- Solve for using the following schemeThe system can have either periodic boundary conditions or the following the physical boundary conditions:where
3.2. Spatial Discretization
- We solve for and using the following scheme:with periodic boundary conditions.
4. Numerical Examples for the Diblock Copolymer Model
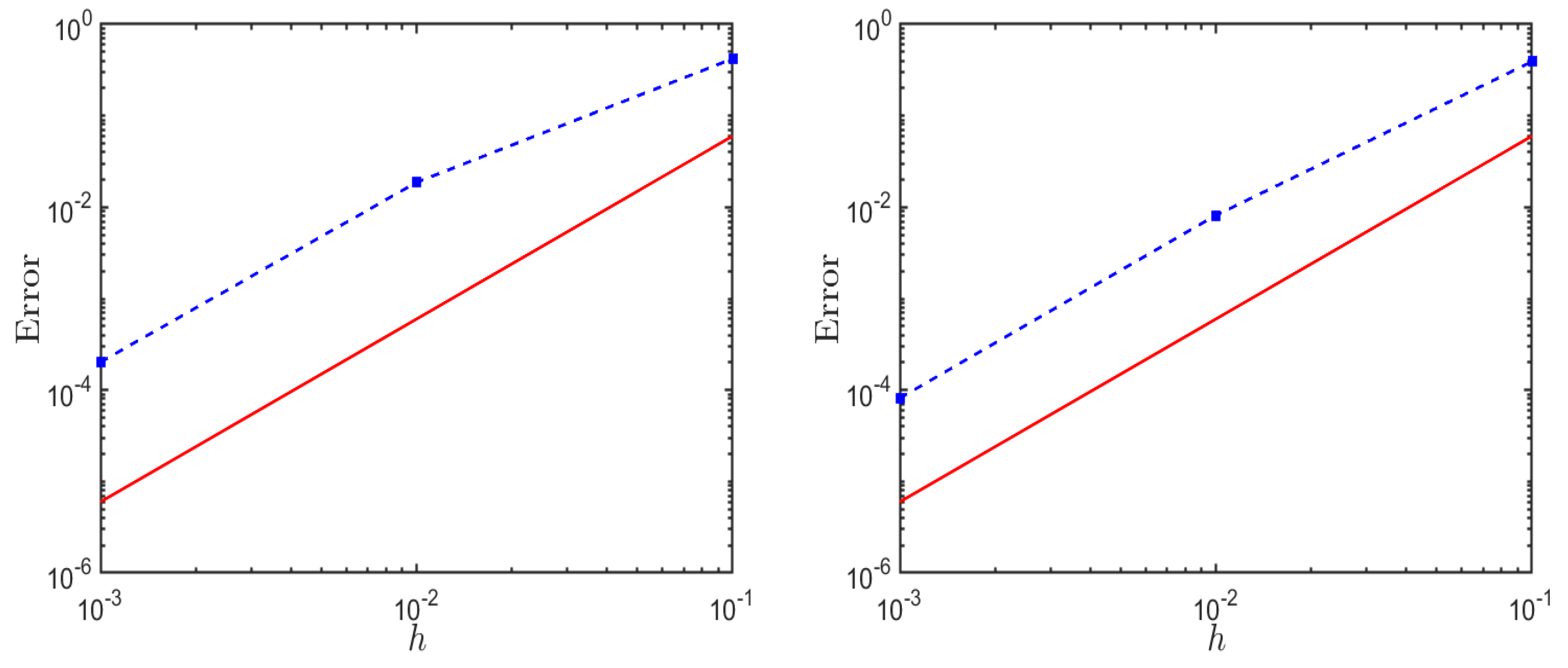
4.1. Accuracy Test
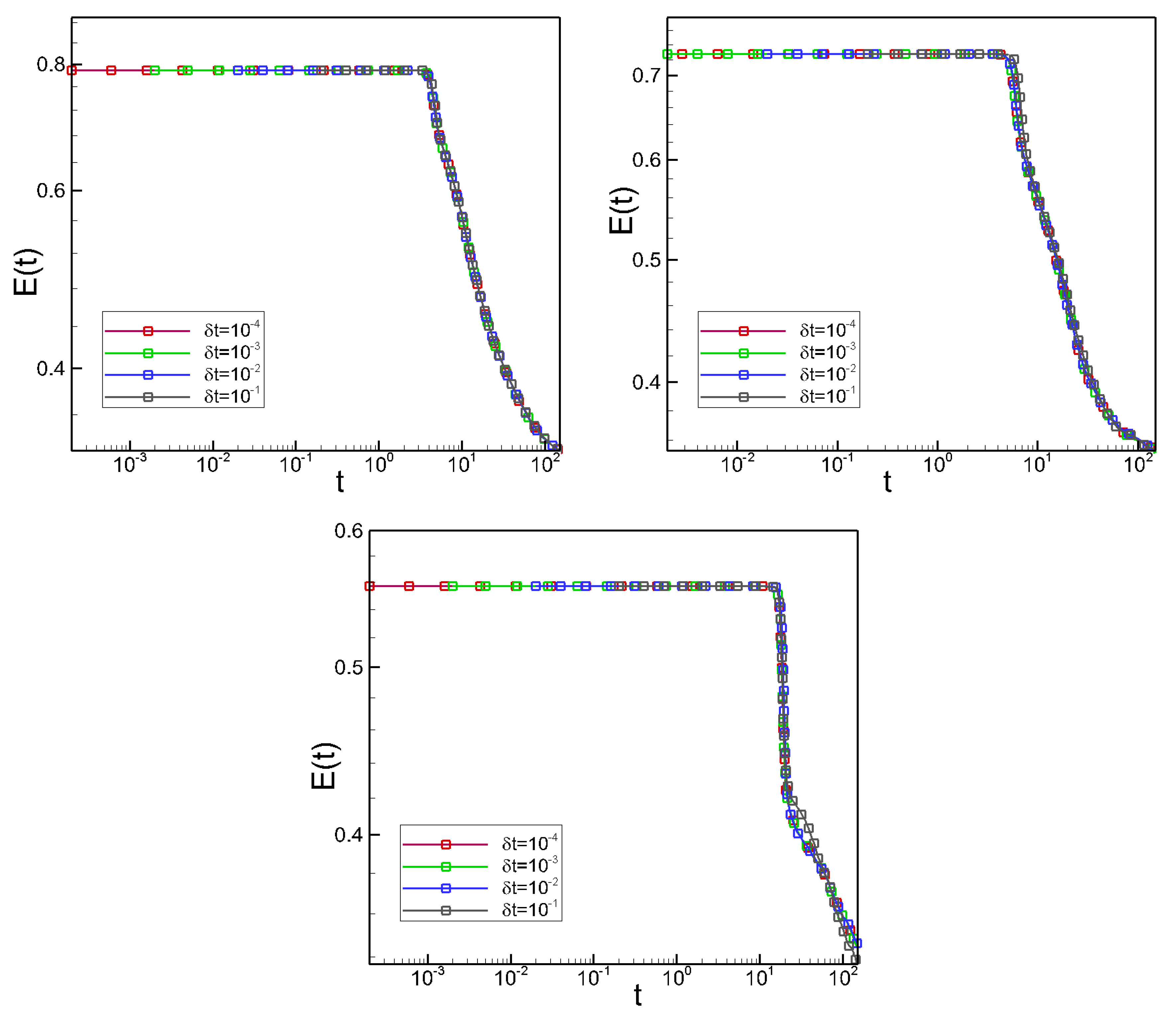
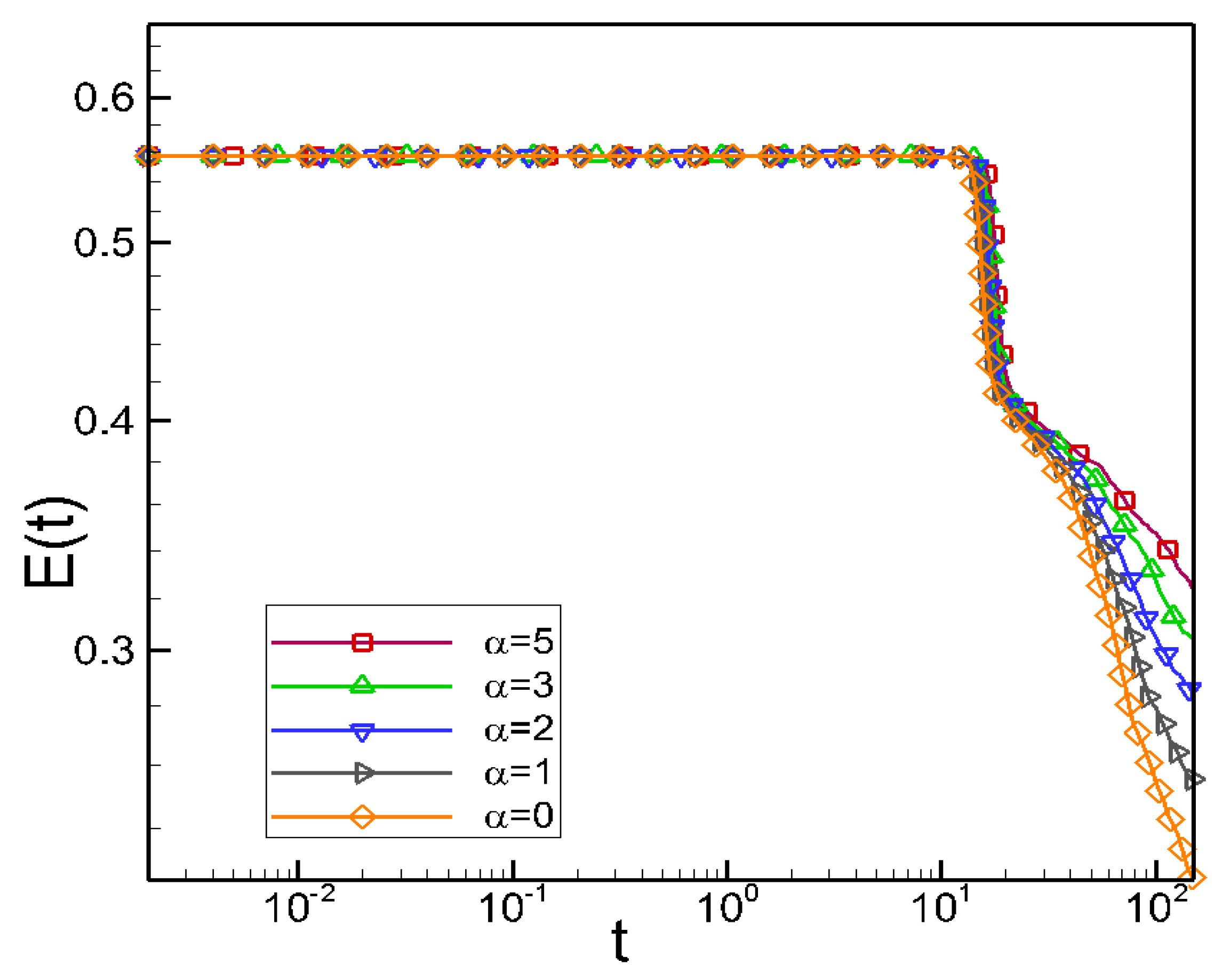
4.2. Phase Separations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Olszowka, V.; Hund, M.; Kuntermann, V.; Scherdel, S.; Tsarkova, L.; Böker, A.; Krausch, G. Large scale alignment of a lamellar block copolymer thin film viaelectric fields: A time-resolved sfm study. Soft Matter 2006, 2, 1089–1094. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.-F.; Dzenis, Y.A. Phase-field modeling of the formation of lamellar nanostructures in diblock copolymer thin films under inplanar electric fields. Phys. Rev. E 2008, 77, 031807. [Google Scholar] [CrossRef] [PubMed]
- Hamley, I.W. The physics of block copolymers. Surf. Interfacial Asp. Biomed. Appl. 1998, 19, 114–125. [Google Scholar]
- Fasolka, M.J.; Mayes, A.M. Block copolymer thin films: Physics and applications. Annu. Rev. Mater. Res. 2001, 31, 323–355. [Google Scholar] [CrossRef]
- Hadjichristidis, N.; Pispas, S.; Floudas, G. Block Copolymers: Synthetic Strategies, Physical Properties, and Applications; John Wiley and Sons: Hoboken, NJ, USA, 2003; pp. 114–125. [Google Scholar]
- Boyer, F.; Minjeaud, S. Numerical schemes for a three component cahn-hilliard model. Math. Model. Numer. Anal. 2011, 45, 697–738. [Google Scholar] [CrossRef]
- Feng, X.; Prol, A. Numerical analysis of the allen-cahn equation and approximation for mean curvature flows. Numer. Math. 2003, 94, 33–65. [Google Scholar] [CrossRef]
- Shen, J.; Yang, X. Numerical approximations of allen-cahn and cahn-hilliard equations. Discret. Contin. Dyn. Syst. A 2010, 28, 1669–1691. [Google Scholar] [CrossRef]
- Aristotelous, A.; Karakashian, O.; Wise, S.M. A mixed discontinuous galerkin, convex splitting scheme for a modified cahn-hilliard equation and an efficient nonlinear multigrid solver. Discret. Contin. Dyn. Syst. B 2013, 18, 2211–2238. [Google Scholar] [CrossRef]
- Jeong, D.; Shin, J.; Li, Y.; Choi, Y.; Jung, J.; Lee, S.; Kim, J. Numerical analysis of energy-minimizing wavelengths of equilibrium states for diblock copolymers. Curr. Appl. Phys. 2014, 14, 1263–1272. [Google Scholar] [CrossRef]
- Eyre, D. Unconditionally gradient stable time marching the cahn-hilliard equation. J. Comput. Phys. 1998, 529, 39–46. [Google Scholar] [CrossRef]
- Liu, C.; Shen, J.; Yang, X. Decoupled energy stable schemes for a phase-field model of two-phase incompressible flows with variable density. J. Sci. Comput. 2015, 62, 601–622. [Google Scholar] [CrossRef]
- Shen, J.; Yang, X.; Yu, H. Efficient energy stable numerical schemes for a phase field moving contact line model. J. Comput. Phys. 2015, 284, 617–630. [Google Scholar] [CrossRef]
- Shen, J.; Yang, X.; Wang, Q. On mass conservation in phase field models for binary fluids. Comm. Compt. Phys. 2012, 13, 1045–1065. [Google Scholar] [CrossRef]
- Zhao, J.; Li, H.; Wang, Q.; Yang, X. A linearly decoupled energy stable scheme for phase-field models of three-phase incompressible flows. J. Sci. Comput. 2017, 70, 1367–1389. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, X.; Li, J.; Wang, Q. Energy stable numerical schemes for a hydrodynamic model of nematic liquid crystals. SIAM J. Sci. Comput. 2016, 38, A3264–A3290. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, X.; Shen, J.; Wang, Q. A decoupled energy stable scheme for a hydrodynamic phase-field model of mixtures of nematic liquid crystals and viscous fluids. J. Comput. Phys. 2016, 305, 539–556. [Google Scholar] [CrossRef]
- Ma, L.; Chen, R.; Yang, X.; Zhang, H. Numerical approximations for allen-cahn type phase field model of two-phase incompressible fluids with moving contact lines. Comm. Comput. Phys. 2017, 21, 867–889. [Google Scholar] [CrossRef]
- Chen, R.; Ji, G.; Yang, X.; Zhang, H. Decoupled energy stable schemes for phase-field vesicle membrane model. J. Comput. Phys. 2015, 302, 509–523. [Google Scholar] [CrossRef]
- Yang, X.; Feng, J.J.; Liu, C.; Shen, J. Numerical simulations of jet pinching-off and drop formation using an energetic variational phase-field method. J. Comput. Phys. 2006, 218, 417–428. [Google Scholar] [CrossRef]
- Yang, X.; Forest, M.G.; Li, H.; Liu, C.; Shen, J.; Wang, Q.; Chen, F. Modeling and simulations of drop pinch-off from liquid crystal filaments and the leaky liquid crystal faucet immersed in viscous fluids. J. Comput. Phys. 2013, 236, 1–14. [Google Scholar] [CrossRef]
- Xu, C.; Tang, T. Stability analysis of large time-stepping methods for epitaxial growth models. SIAM J. Numer. Anal. 2006, 44, 1759–1779. [Google Scholar] [CrossRef]
- Yang, X. Error analysis of stabilized semi-implicit method of allen-cahn equation. Discret. Contin. Dyn. Syst. B 2009, 11, 1057–1070. [Google Scholar] [CrossRef]
- Yu, H.; Yang, X. Decoupled energy stable schemes for phase field model with contact lines and variable densities. J. Comput. Phys. 2017, 334, 665–686. [Google Scholar] [CrossRef]
- Cheng, Q.; Yang, X.F.; Shen, J. Efficient and accurate numerical schemes for a hydro-dynamically coupled phase field diblock copolymer model. J. Comput. Phys. 2017, 341, 44–60. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, C.J.; Yang, X.F. Efficient and energy stable method for the cahn-hilliard phase-field model for diblock copolymers. Appl. Numer. Math. 2020, 151, 263–281. [Google Scholar] [CrossRef]
- Chen, L.Z.; Zhang, Z.Y.; Zhao, J. Numerical approximations of phase field models using a general class of linear time-integration schemes. Commun. Comput. Phys. 2021, 30, 1290–1322. [Google Scholar] [CrossRef]
- Chen, L.Z.; Zhao, J. A novel second-order linear scheme for the cahn-hilliard-navier-stokes equations. J. Comput. Phys. 2020, 423, 109782. [Google Scholar] [CrossRef]
- Chen, L.Z.; Zhao, J.; Gong, Y.Z. A novel second-order scheme for the molecular beam epitaxy model with slope selection. Appl. Numer. Math. 2020, 25, 1024–1044. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, X.; Gong, Y.; Zhao, X.; Yang, X.; Li, J.; Wang, Q. A general strategy for numerical approximations of non-equilibrium models? Part i: Thermo-dynamical systems. Int. J. Numer. Anal. Model. 2018, 15, 884–918. [Google Scholar]
- Shen, J.; Xu, J.; Yang, J. The scalar auxiliary variable (sav) approach for gradient flows. J. Comput. Phys. 2018, 353, 407–416. [Google Scholar] [CrossRef]
- Han, D.; Wang, X. A second order in time, uniquely solvable, unconditionally stable numerical scheme for cahn-hilliard-navier-stokes equation. J. Commput. Phys. 2015, 290, 139–156. [Google Scholar] [CrossRef]
- Han, D.; Brylev, A.; Yang, X.; Tan, Z. Numerical analysis of second order, fully discrete energy stable schemes for phase field models of two phase incompressible flows. J. Sci. Comput. 2017, 70, 965–989. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Ma, Y.; Ren, B.; Zhang, G. Numerical Approximations of Diblock Copolymer Model Using a Modified Leapfrog Time-Marching Scheme. Computation 2023, 11, 215. https://doi.org/10.3390/computation11110215
Chen L, Ma Y, Ren B, Zhang G. Numerical Approximations of Diblock Copolymer Model Using a Modified Leapfrog Time-Marching Scheme. Computation. 2023; 11(11):215. https://doi.org/10.3390/computation11110215
Chicago/Turabian StyleChen, Lizhen, Ying Ma, Bo Ren, and Guohui Zhang. 2023. "Numerical Approximations of Diblock Copolymer Model Using a Modified Leapfrog Time-Marching Scheme" Computation 11, no. 11: 215. https://doi.org/10.3390/computation11110215
APA StyleChen, L., Ma, Y., Ren, B., & Zhang, G. (2023). Numerical Approximations of Diblock Copolymer Model Using a Modified Leapfrog Time-Marching Scheme. Computation, 11(11), 215. https://doi.org/10.3390/computation11110215




