Abstract
Electromembrane processes underlie the functioning of electrodialysis devices and nano- and microfluidic devices, the scope of which is steadily expanding. One of the main aspects that determine the effectiveness of membrane systems is the choice of the optimal electrical mode. The solution of this problem, along with experimental studies, requires tools for the theoretical analysis of ion-transport processes in various electrical modes. The system of Nernst–Planck–Poisson and Navier–Stokes (NPP–NS) equations is widely used to describe the overlimiting mass transfer associated with the development of electroconvection. This paper proposes a new approach to describe the electrical mode in a membrane system using the displacement current equation. The equation for the displacement current makes it possible to simulate the galvanodynamic mode, in which the electric field is determined by the given current density. On the basis of the system of Nernst–Planck, displacement current and Navier–Stokes (NPD–NS) equations, a model of the electroconvective overlimiting mass transfer in the diffusion layer at the surface of the ion-exchange membrane in the DC current mode was constructed. Mathematical models based on the NPP–NS and NPD–NS equations, formulated to describe the same physical situation of mass transfer in the membrane system, differ in the peculiarities of numerical solution. At overlimiting currents, the required accuracy of the numerical solution is achieved in the approach based on the NPP–NS equations with a smaller time step than the NPD–NS equation approach. The accuracy of calculating the current density at the boundaries parallel to the membrane surface is higher for the model based on the NPD–NS equations compared to the model based on the NPP–NS equations.
1. Introduction
Electromembrane processes underlie the functioning of electrodialysis devices and nano- and microfluidic devices, the scope of which is steadily expanding [1,2,3,4]. The key principle of the operation of these systems is the selective transport of ion-exchange membranes, that is, high permeability for counterions and obstruction of the movement of co-ions [5]. The current–voltage characteristic (CVC) of a system with an ion-exchange membrane has a non-linear shape, mainly due to the phenomena of concentration polarization, current-induced convection and water dissociation [6,7]. The following modes are typically distinguished on the CVC of the membrane system (Figure 1) [8,9,10,11,12,13]:
- Underlimiting current: at low current densities, the concentration of ions in the near-membrane region is quite high, and the CVC is in a linear shape in this region. The selective transfer of counterions in the membrane during the flow of the electric current through the ion-exchange membrane reduces the concentration of ions on one side of the membrane and increases on the other (the phenomenon of concentration polarization). As the current density increases, almost complete depletion of ions in the region near the membrane surface and the transition of the system to the limiting state are observed [14,15].
- Limiting current: almost complete depletion of ions near the membrane surface is reflected by the current saturation, and the CVC in this area has the form of a plateau with a slight slope [16,17].
- Overlimiting current: a secondary increase in current indicates an increase in the conductivity of the depleted region. For the diluted electrolyte solutions considered in this work, the main mechanism that destroys the depleted region and provides an overlimiting mass transfer is electroconvection, which is confirmed by many theoretical [18,19,20,21] and experimental [8,9,10,11,12,13] studies. Electroconvection is the entrainment of liquid molecules by ions that form the space charge at the ion-selective surface under the action of the electric force [22]. During the passage of the overlimiting current, when a macroscopic space charge region (SCR) is formed at the solution/membrane interface, the intensity of electroconvection increases [23].
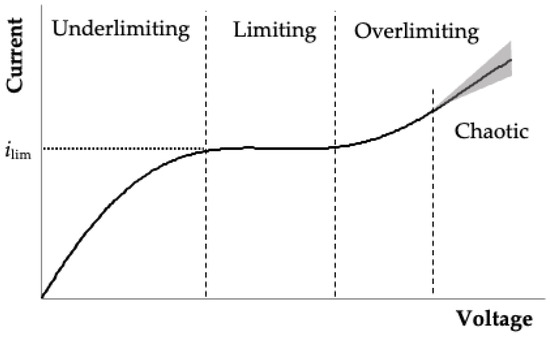
Figure 1.
Schematic typical CVC of a system with an ion-exchange membrane. The dashed lines show the changes in the CVC modes: underlimiting, limiting current (ilim) plateau, overlimiting and overlimiting with chaotic current oscillations (grey color schematically shows the range of oscillations).
Thus, one of the main aspects that determine the effectiveness of the use of membrane systems is the choice of the optimal electrical mode. The solution for this problem, along with experimental studies, requires tools for the theoretical analysis of ion-transport processes in various electrical modes.
To model mass transfer processes in electromembrane systems, the system of Nernst–Planck–Poisson and Navier–Stokes (NPP–NS) equations is widely used, which provides a comprehensive description of the problem [22,24,25,26]. The Nernst–Planck equations describe the transport of ions in an electrolyte solution through diffusion, migration and convection. The Nernst–Planck equation was derived for dilute solutions and requires the diffusion coefficient and ion mobility to be specified, which are assumed to be constant. A detailed review of other limitations of the Nernst–Planck equations can be found in [27]. The Poisson equation describes the distribution of the electric field, taking into account the violation of the electrical neutrality of the solution and the formation of SCR near the membrane surface due to its permselectivity [23,28]. The flow velocity of the electrolyte solution is determined by the Navier–Stokes equation in the assumption of the constant density and viscosity of the liquid. The Navier–Stokes equations take into account the action of pressure changes, viscous forces and a force acting on a fluid element [29].
Numerical modeling of overlimiting mass transfer based on the NPP–NS equations made it possible to obtain detailed information on the development of electroconvection in systems with ion-exchange membranes: the influence of forced flow on the height [21,30], speed [31] and state [32,33,34] of the electroconvective vortex; the calculation of the CVC of the flow-through electrodialysis membrane cells, taking into account overlimiting mass transfer caused by electroconvection [20]; the influence of the potential drop on the mode of electrokinetic instability [35]; statistical analysis of electroconvective flow [36]; the calculation of the trajectory of particles that visualize the dynamics of electroconvective flow [37]; development of electroconvection during pulsed electric field electrodialysis [38]; the study of the coupling between buoyancy forces and electroconvective instability [39]; and many others results.
The electrical mode in membrane systems can be determined either by setting the current density (galvanodynamic mode) or by setting the potential drop (potentiodynamic mode). When modeling the potentiodynamic mode, to solve the Poisson equation, the potential drop is set at the boundaries of the region under consideration (parallel to the membrane surface), which are assumed to be equipotential [18,19,20,21,30,31,32,33,34,35,36,37,38,39,40,41,42]. When modeling the galvanodynamic mode, one of these boundaries is assumed to be equipotential (usually a zero potential is fixed on it), and on the other, a boundary condition is set that relates the normal derivative (to the membrane surface) of the potential and the given current density [28,43,44,45,46,47,48,49,50].
J. Manzanares et al. [28], in order to numerically simulate ion transport in a system including an ion-exchange membrane and two adjacent diffusion layers, built a 1D model using a system of NPP equations with a boundary condition connecting the mixed derivative of the electric potential and the specified current density. This relation was obtained by expressing the displacement current term from the equation for the total current. Based on the solution of the NPP equations using this boundary condition, studies of the evolution of the structure of diffusion layers adjacent to the ion-exchange membrane [28], the impedance of the membrane system [43], and other problems for the galvanodynamic mode were successfully carried out.
In [44], a similar boundary condition was proposed for modeling the galvanodynamic mode, also obtained from the equation for the total current, but the spatial derivative of the potential was expressed from the conduction current term. This boundary condition directly connects the normal derivative of the potential and the specified current density. Using a 1D mathematical model based on the NPP equations and this boundary condition, the ion concentrations, potential, space charge density and chronopotentiogram of the depleted diffusion layer at the surface of the ion-exchange membrane were calculated, taking into account the formation of an extended SCR at overlimiting DC currents [44]. In [49], the model of ion transport in a 1D section of a desalination channel formed between anion- (AEM) and cation-exchange (CEM) membranes is formulated and implemented on the basis of the NPP equations and the galvanodynamic boundary condition. This model made it possible to study the dynamics of the extended SCRs formed at the AEM and CEM under the action of the DC current [49]. Due to the simplicity of the implementation of this form of galvanodynamic boundary condition, 2D models were built on its basis in the form of a boundary value problem for the NPP–NS system of equations, which made it possible to theoretically study the chronopotentiograms of homogeneous [45,47] and heterogeneous [46] membranes, taking into account the development of electroconvection, as well as to study the structure of the electroconvective flow developing near the surfaces AEM and CEM in the electrodialysis desalting channel under the action of overlimiting DC currents [50].
Y. Green in [48] performed 1D modeling of ion transport in the diffusion layer at the membrane surface using the NPP equations and galvanodynamic boundary condition. The boundary condition applied in this work is similar to the boundary condition from [44] but is formulated for a symmetric binary electrolyte solution with identical diffusion coefficients. In [48], the galvanodynamic boundary condition is set at the boundary of the diffusion layer with the bulk of the solution; therefore, the terms of the boundary condition associated with ion concentration gradients are discarded (they are negligible when the diffusion coefficients are equal).
In this case, the error in calculating the gradients of the concentration and potential fields at the boundary at which the condition that determines the current density is specified significantly affects the accuracy of calculating the distribution of the electric field.
In the Poisson equation, a small parameter stands at the highest spatial derivative and determines the appearance of the boundary layer at the solution/membrane interface, which is characterized by a large electric potential gradient. The thickness of the boundary layer is of the order of the Debye length [18], which is several orders of magnitude smaller than the typical size of electromembrane systems. The multiscale nature of the problem of ion transport in electromembrane systems determines its significant numerical complexity. Therefore, the solution of the transport problem in the boundary layer is expensive and requires proper mesh refinement.
Another approach to modeling the galvanodynamic mode in problems of ion transport in membrane systems is to determine the electric field strength based on the equation for the total current, that is, the Nernst–Planck equations are solved together with the equation for the displacement current (NPD). Replacing the Poisson equation with the equation for the displacement current was first performed by Cohen and Cooley [51] in order to calculate the problem of ion transport at a given current density in a completely mechanically permeable membrane, without describing its other physical properties. Later, Brumleve and Buck [52] calculated the frequency characteristics of the impedance of a permselective membrane at a DC underlimiting current based on the system NPD equations. Urtenov M.Kh. et al. [53,54,55] used the equation for the electric field strength in the decomposition of the non-stationary system of NPP equations; the decomposition system of equations is convenient for deriving various simplified models and applying asymptotic methods [54,55].
In recent work [56], based on the mathematical model in the form of the boundary value problem for the system of NPD equations, concentration profiles and electric field strengths were calculated in a depleted diffusion layer near the surface of an ion-exchange membrane, as well as in the cross-section of a desalination channel under the action of an overlimiting DC current. It was shown that this approach allows one to describe the formation of the extended SCR, as well as the approach based on the NPP equations. The equation for the displacement current contains only the time derivative and does not require the determination of boundary conditions [51,52,56]. In the equation for the displacement current, the small parameter stands at the time derivative of the electric field strengths. For this reason, numerical calculations based on the NPD equations differ from those based on the NPP equations by a longer calculation time and less error for the same values of the parameters [56]. In [51,52,56], 1D cases of model geometry are considered; the flow of an electrolyte solution is either not considered or is assumed to be laminar.
The aim of this work is to develop a 2D mathematical model of mass transfer based on the Nernst–Planck, displacement current and Navier–Stokes (NPD–NS) equations, which take into account the development of the electroconvective flow under the action of overlimiting currents. Also, the work is devoted to the study of the possibility of calculating with high accuracy the characteristics of mass transfer using this model.
The paper is organized as follows. The Methods section describes the mathematical formulation of the 2D model of electroconvective overlimiting mass transfer in the depleted diffusion layer near the surface of the ion-exchange membrane based on the NPD–NS system of equations, and it provides an implementation of the model. The Results and Discussion section presents the results of a series of calculations of mass transfer characteristics for the underlimiting, limiting and overlimiting current densities based on the NPD–NS models; validation of the NPD–NS model is performed by comparing the modeling results with the results of the model known in the literature based on the NPP–NS equations; estimates of the error and calculation time for the NPD–NS and NPP–NS models are given. The conclusion contains the conclusions and prospects for the development of the proposed approach.
2. Methods
2.1. Modeling Assumptions
The main subject of this study is the methods of mathematical description of overlimiting mass transfer, taking into account the formation of SCR and the development of electroconvection in the electrolyte layer near the membrane surface under the action of an overlimiting DC current; therefore, we consider a depleted diffusion layer that is formed near the CEM surface in an electrodialysis desalination channel. The membrane is assumed to be homogeneous with a smooth surface and a uniform distribution of the concentration of fixed charges. The ion-selective properties of the membrane, to which the diffusion layer adjoins, are specified by the boundary conditions. The transfer of water across the membrane is not taken into account. Assume that the channel is short enough so that the diffusion layer thickness is small compared to the intermembrane distance and approximately constant in the tangential direction [27]. The density, temperature and dielectric constant of the solution are assumed to be constant; chemical reactions are not considered.
2.2. Model Formulation
Figure 2 shows the geometry of the considered diffusion layer with thickness δ and length L. The electrical mode is determined by the current density .
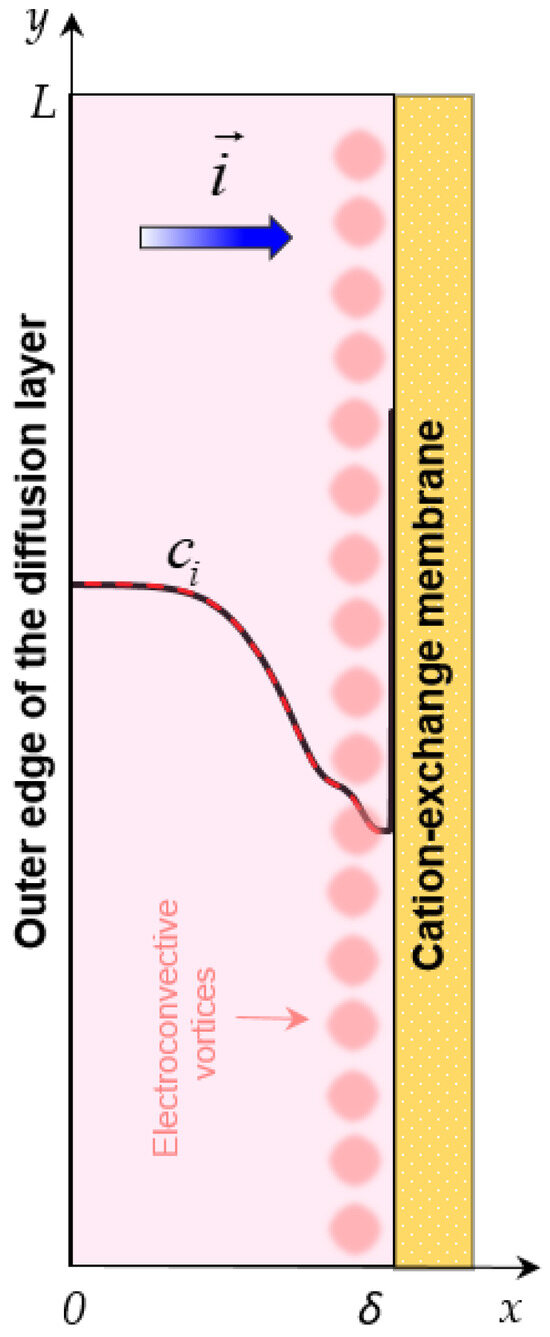
Figure 2.
Geometry of the model of mass transfer in a depleted diffusion layer near the surface of a cation-exchange membrane (CEM). Electroconvective vortices and concentration profiles (cations, , and anions, ) are schematically shown. A current of density flows in the system.
The system of NPP–NS equations for a binary electrolyte solution is written as follows [18,20]:
where is the solution flow rate; is the pressure; is the density of the solution; is the kinematic viscosity; are the flow, the molar concentration, the diffusion coefficient and the charge number of the n-ion, respectively; is the electric potential; is the electrical constant; is the relative permittivity of the electrolyte solution; is Faraday’s constant; is the gas constant; and is the absolute temperature. In the system of Equations (1)–(5), are functions of coordinates and time t.
Equation (1) is the Navier–Stokes equation, which describes the fluid flow velocity, taking into account the action of the electric field force ; Equation (2) is the continuity equation for the incompressible fluid. The Nernst–Planck equations, Equation (3), and material balance, Equation (4), describe the transfer of ions. The Poisson Equation (5) is necessary for calculating the electric field.
The density of the total current is described by Equation (6) [51,52,53]:
where the term determines the density of the Faraday current (or conduction current), and is the density of the displacement current (or charging current) associated with the change in the space charge.
Differentiating the Poisson Equation (5) with respect to time and substituting the material balance, Equation (4), gives , that is . Therefore, to calculate the density distribution of the total current density in the 2D diffusion layer, an electric current stream function can be introduced analogous to the flat flow of the incompressible liquid (for which the conditions , are satisfied [57]):
where is the electric current stream function [45,46,55,58,59]. Differentiating the components of the current density and by the coordinates y and x, respectively, and determining their difference gives the equation for the rotor of the total current density vector:
For the galvanodynamic mode in the 2D case, the normal component of the total current density at the boundaries and is a function of the tangential coordinate y, but its average value must be equal to the given current density [58]:
Fulfillment of the conditions of the galvanodynamic mode, Equation (9), is provided by setting the following boundary conditions for the electric current stream function [58]:
The calculation of the current density using the equation for the electric current stream function, Equation (8), allows one to derive the equations of the electric field strength. Thus, Equation (7) can be written in the following form:
or
The substitution of Nernst–Planck Equation (3) into material balance, Equation (4), and the displacement current, Equations (13) and (14), gives a closed system of equations with respect to the components of velocity, ; pressure, ; ion concentrations, , ; and electric field strength , :
Thus, the system of Equations (15)–(20) is the system of NPD–NS equations for the binary electrolyte solution.
To solve the system of NPD–NS equations, initial boundary conditions for Equations (15)–(17) and (20) are required; equations for the electric field strength components (18) and (19) include only time derivative and require only initial conditions.
The boundary conditions for the flow velocity assume the no-slip condition at the solution/membrane interface and zero normal velocity at the other boundaries:
At the solution/membrane interface, the counterion concentration, , is set as a constant value times greater than the initial solution concentration, , Equation (22), and continuous flow of co-ions, Equation (23), [23]; at the outer boundary of the diffusion layer, the concentrations of ions of both signs are equal to , Equation (24); at the lower and upper boundaries, the tangential diffusion components of the ion fluxes are equal to zero, Equation (25), which, together with the assumption of zero tangential migratory components of the fluxes, provides a zero normal current through the boundaries:
where is the effective transport number of anion in the CEM, that is, the fraction of the Faraday current carried by ions of this type [60]. Due to the fact that the Faraday current is realized by ions of both types, the relations are fulfilled.
Assume that at the initial time t = 0 at all points of the region under consideration the solution is at rest; the condition of electrical neutrality is satisfied, and the concentrations of cations and anions are equal to the initial concentration of the electrolyte, ; the electric field strength is zero:
In order to validate the model based on the NPD–NS equations, its results are compared with the results of modeling using the NPP–NS equations [45]. When modeling a galvanodynamic mode using the system of NPP–NS equations, the boundary conditions (10) and (21)–(26) must be supplemented by the conditions for the electric potential:
Condition (27) assumes that the outer boundary of the diffusion layer is equipotential; at the solution/membrane interface, the condition is established according to which the derivative of the potential normal to the membrane surface is determined as the function of the electric current density [45]; at the upper and lower boundaries, as noted above, there is a zero normal migration flux of ions.
2.3. System Parameters
Calculations are performed for NaCl electrolyte solution with concentration mol/m3; temperature K; electrolyte solution density ; viscosity ; diffusion coefficients and ; cation transport number in the CEM and in solution ; ion charge numbers . The diffusion layer thickness is estimated by the formula [61] for the following parameters of membrane system: intermembrane distance ; channel length ; and average solution velocity . To simplify the numerical solution, the ratio of the cation concentration at to (used in the boundary condition (22)) was taken to be . This value is less than in real systems [23]; however, it is shown in [62,63] that for , the value of does not significantly affect the solution of the problem in the extended SCR. The constant current density was set as , where is the limiting current density determined by the Leveque formula [61] and where is the electrolyte diffusion coefficient.
As noted above, the computational complexity of the problem under consideration is associated with large gradients of ion concentrations and potential at the solution/membrane interface. The complexity of the calculations increases with decreasing thickness of the region of large gradients, the order of which is estimated by the Debye length [18]. Therefore, to reduce the computational complexity of the problem and the calculation time, the concentration value was chosen at several orders of magnitude less than in real systems.
Detailed studies of the influence of the dimensionless Debye number (that is, the concentration of the electrolyte in the solution) were carried out in the literature [40,45,62]. With increasing electrolyte concentration in the solution, the size of the SCR in the depleted solution at the membrane surface decreases, but the charge density and the tangential component of the bulk electric force increase [62]. These two factors have opposite effects on the development of electroconvection in the depleted solution near the membrane surface. The results of numerical calculations show that the dominant factor is the reduction in the size of the SCR: with increasing concentration, the intensity of overlimiting transfer, measured by the ratio i/ilim, decreases at a fixed potential drop [62]. Therefore, although the structure of chronopotentiograms does not change with increasing concentration, a higher concentration corresponds to a larger average value of the potential drop in the quasi-stationary state [45]. The work of P. Shi [40] shows that reducing the thickness of a thin Debye layer enhances small-scale vortices and promotes its onset, which is attributable to the increase in the driving force to the layer of extended SCR.
2.4. Estimation of Calculation Error
The accuracy of the numerical solution of boundary value problems of mass transfer models in the DC current mode (both based on the NPP–NS and based on the NPD–NS) can be assessed from the error in fulfilling the condition of equality of the average current density at and to the given value of the current density , Equation (9). Therefore, the calculation error was determined by the following values for and :
where is the time of stopping the calculations; in the considered calculations, this is the time of establishing a stationary (or quasi-stationary) state.
2.5. Model Implementation
The boundary value problems of the considered mathematical models were solved by the finite element method using the commercial package Comsol Multiphysics 6.1 (COMSOL AB, Stockholm, Sweden). All calculations were performed using an Intel(R) Core(TM) i9-10900K CPU (10 cores @ 3.70GHz), 64 GB of RAM.
The Navier–Stokes equation and continuity equation for the incompressible fluid, Equations (15) and (16), are implemented using the “Laminar Flow” module; the equations for the ion concentration (17) and the electric current stream function (20) are built on the basis of the “General Form PDE” modules; and the equations for the electric field strength components (18) and (19) involve the “Domain ODEs and DAEs” modules. Spatial discretization of the fields of concentration, electric field strength and electric current stream function uses quadratic Lagrange interpolation functions. The discretization of the “Laminar Flow” module is “P2 + P1”, which means the use of second-order elements for the velocity components and linear elements for the pressure field [64]. Time-dependent computations are implemented using the segregated node with an implicit BDF (backward differentiation formula) time step-selection method [64]. Each segregated iteration involves performing three separate steps: the first step is to calculate the concentration and electric stream function; at the second step, the velocity and pressure are calculated; and the third step calculates the electric field strength. The built-in solver determines the time step so that the requirement for the relative tolerance is met (is set to 10−3). In addition, when solving the boundary value problems of the models, a limit was set on the maximum time step so that the error in calculating the current density at the boundaries was less than 1%. The implementation of the boundary value problem based on the NPP–NS equations is similar to that described for the NPD–NS equations, with the difference being that the equation for the electric field strength is replaced by the Poisson equation for the potential.
Large gradients of ion concentrations and electric field strength near the solution/membrane interface (Figure 2) cause significant computational complexity of the problem under consideration. Therefore, in order to simplify the numerical solution of the problem, a non-uniform computational mesh was constructed, in which 25 boundary layers with a stretching factor of 1.23, the first layer thickness of 0.0005 µm, and 30 layers of the same thickness of 0.05 µm are defined near the boundary. For the computational mesh in the rest of the area, the “Mapped” option is used, and the maximum element size constraint is set to 1.5 µm (Figure 3). In general, the grid consists of 92,713 domain elements and 2279 boundary elements. The described structure of the computational mesh is determined by the following procedure: calculations are performed for a certain computational mesh (consisting of k1 elements) and the chronopotentiogram is calculated for the current density in the time interval from 0 to the establishment of a stationary state (t′). Then, the mesh is refined (k2 elements), the calculations are performed again, and the values of are calculated. The maximum relative error of the calculation of the potential drop is determined by the following formula: . The procedure was repeated until the condition was met.
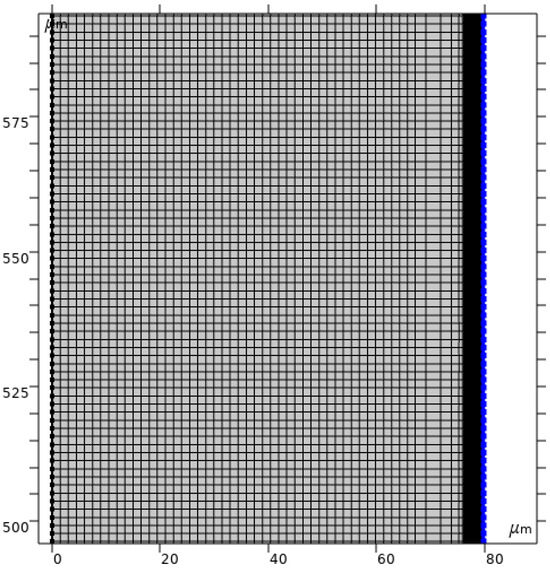
Figure 3.
Spatial discretization (computational mesh) of the model geometry fragment.
3. Results and Discussion
3.1. Model Validation
3.1.1. Comparison of Chronopotentiograms Calculated on the Basis of NPP–NS and NPD–NS Approaches
Based on the NPP–NS and NPD–NS approaches, the characteristics of mass transfer in the diffusion layer are calculated for the underlimiting (), limiting (), and overlimiting (, ) current densities. The chronopotentiogram (ChP) of the system was calculated based on the values of the potential drop averaged over the channel length, that is, for the NPP–NS model:
and for the NPD–NS model:
The ChPs calculated based on both approaches at the same values of the given current density coincide quite well (Figure 4a). At the current density equal to and , the difference in the potential drop over the entire considered time interval (from 0 to 9 s) does not exceed 2% (the maximum difference is 1.6% and 1.4%, respectively). At overlimiting values of and , the difference does not exceed 5% in the same time period, except for the moments of time of a sharp decrease in the potential drop at and , respectively. This difference is due to the fact that a rapid decrease in the potential drop in the two approaches occurs with a small time difference of 0.02 s.
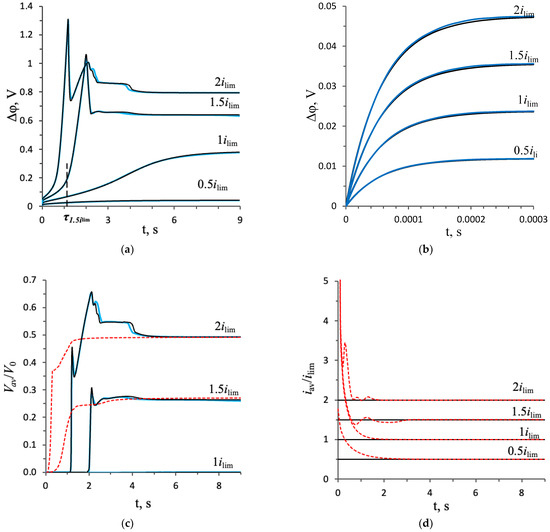
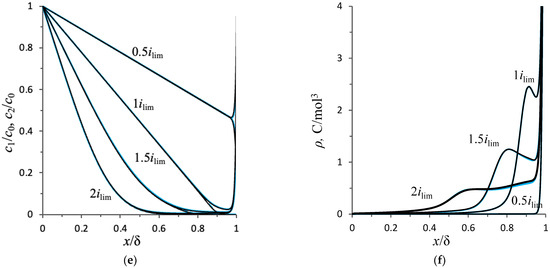
Figure 4.
(a) Chronopotentiograms; (b) enlargement fragment of (a); (c) average value of the flow velocity of the electrolyte solution; (d) dependencies of the average current density on time; (e) concentration profiles; (f) charge density distribution in the section y = 0.5 L of the diffusion layer in the steady state at t = 9 s. Calculation results based on the NPP–NS (blue lines) and NPD–NS (black lines) approaches at current densities of i = 0.5 ilim, ilim, 1.5 ilim, and 2 ilim. The red dotted lines are the calculation results for the constant potential drop mode. The dashed line in Figure 4a denotes the transition time for the current density 1.5 ilim, .
Consider the structure of the calculated ChPs and estimate the intensity of the developing electroconvection for each of the indicated values of the current density. To quantify the intensity of electroconvection, the average value of the electrolyte solution flow velocity (normalized by the value ) was calculated (Figure 4c):
For all ChPs at , a sharp increase in the potential drop from zero to a value determined by the initial ohmic resistance of the solution is observed [44]. Further, at a current density of and , a monotonic increase in the potential drop is observed, which is associated with electrodiffusion desalination of the solution near the membrane surface (Figure 4e). At , stationary states are established. At the current density of in the steady state, the potential drop is and the average velocity is , that is, there is no electroconvective flow (Figure 5a). At the current density of , the solution at the membrane surface is depleted almost to zero (Figure 4e) and the potential drop increases to . A space charge begins to form (Figure 4f), but it is very close to the solution/membrane interface, on which the no-slip condition is accepted, so the electroconvective flow is negligibly small: (Figure 5b). Since there is no forced flow in the system under consideration and at the current density of and , the electroconvective flow is negligible, and the distribution of the ion concentration in the cross-section (Figure 4e,f) is typical for the entire length of the diffusion layer (Figure 5a,b).
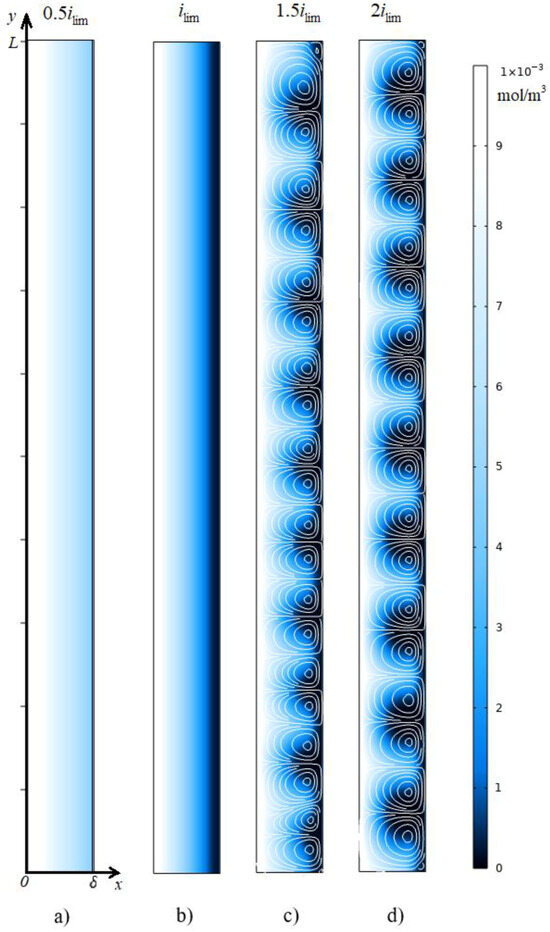
Figure 5.
Cation concentration distribution (shown in color) and streamlines of the electrolyte solution (white lines) at the time (stationary state). The calculation results at the current density: i = 0.5 ilim (a), i lim (b), 1.5 ilim (c), 2 ilim (d).
At the overlimiting current density (, ), the ChP structure becomes more complicated, and effects associated with the development of electroconvection are observed.
In the calculation for the current density equal to at the time moment , the tangent to the concentration profiles in the electroneutral region near the membrane surface passes through 0 at . After this point in time, the formation of the extended SCR begins, and a rapid increase in the potential drop is noted on the ChPs (Figure 4a). As a result, in the time interval from 2.02 s to 2.08 s, a rapid increase in the average velocity from 0 to 0.28 is observed, which is associated with the appearance of electroconvective vortices. The vortices mix the depleted solution near the membrane surface with the more concentrated solution in the volume of the diffusion layer (Figure 5c). The movement of the fresh solution to the membrane surface causes a decrease in the potential drop. As a result, the ChPs show a slowdown in the growth of the potential drop at t = 2.02 s and a rapid decrease by 0.43 V in the time interval from 2.05 s to 2.27 s. This decrease in the potential drop causes a decrease in the average velocity by 0.04 at time from 2.14 s to 2.3 s. This is followed by an almost simultaneous weak increase, a slight decrease, and a transition to a stationary state of the potential drop and average velocity. The flow structure in the steady state is shown in Figure 5c.
In the calculation for the current density of , the desalination of the solution proceeds faster, so the appearance of the electroconvective flow occurs earlier (at t ≈ 1.15 s, Figure 6a) at a larger potential drop. As with a current density of , in this case, a rapid increase in the average flow velocity causes a decrease in the potential drop (≈0.56 V, at t ≈ 1.18 s), which causes a slowdown in the growth of the average velocity. But then, at a current of , there is a significant increase in the average flow velocity and potential drop at times between 1.33 s and 2.07 s. In this time range, the size and velocity of the electroconvective vortices increases (Figure 6b,c), then at the moments of 2.17 s, 2.31 s, and 4.5 s, neighboring vortices merge into one larger one (Figure 6d–f), which is expressed by a decrease in the potential drop (Figure 4a).
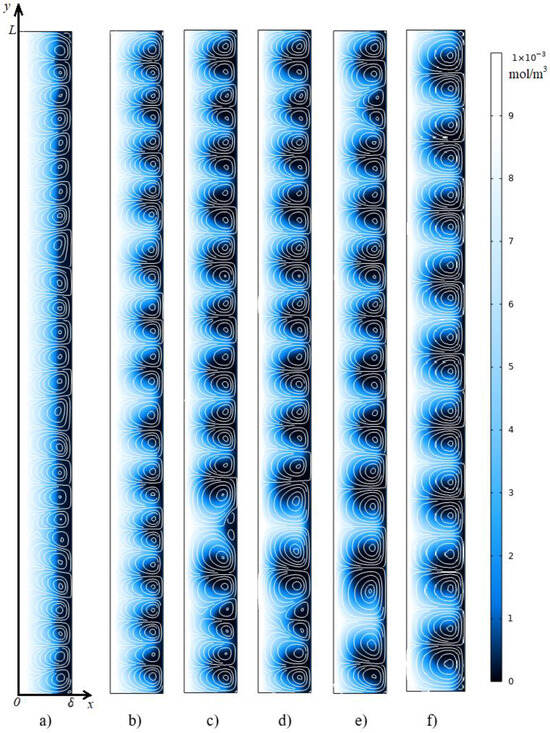
Figure 6.
Cation concentration distribution (shown in color) and streamlines of the electrolyte solution (white lines) at a current density of i = 2 ilim. The calculation results at time t = 1.15 s (a), 1.33 s (b), 2.07 s (c), 2.17 s (d), 2.31 s (e), 4.5 s (f).
In experimental measurements of the ChPs of the CEM [65,66], the moment of time preceding the rapid growth of the potential drop is defined as the transition time. For an analytical estimate of the transition time, Equation (32) is used:
Equation (32) was obtained by Sand on the basis of a theoretical analysis of an infinite diffusion layer [67].
The transition time values calculated by the proposed model for current density equal to and differ from Sand’s analytical estimate by less than 5%.
Thus, on the ChPs, calculated for the overlimiting currents, the following sections are distinguished:
- the initial fast ohmic growth of the potential drop;
- the section of monotonic growth of the potential drop caused by electrodiffusion desalination of the solution. The growth rate of the potential drop increases rapidly after the depletion of the concentration at the solution/membrane interface;
- the transitional section associated with the development of electroconvection;
- the stationary section characterized by both a constant potential drop and a constant average velocity of the electroconvective flow.
This structure of the calculated ChPs qualitatively coincides with those observed in experimental [6,65,66,68,69] and theoretical [45,46] studies. However, the shape of the transitional part corresponding to the development of an electroconvective flow differs from that observed in experiments. It should be noted, however, that this section of ChPs differs significantly for different ion-exchange membranes and current mode also in experimental measurements [6,65,66,69]. For example, in the experiment measuring the ChPs of CEM (Neosepta CMX) and a 10 mM CuSO4 electrolyte by de Valenca et al. [65] at the time of electroconvection development on the ChP, a decrease in the potential drop of a small value (about 0.1 V) is recorded; in the experimental study of AEM (MA-40-13 membrane specially treated by NPO “Vladipor”) and a 5 mM NaCl solution performed by Belova et al. [6], this value is up to 0.5 V. This makes it possible to explain the difference in the transitional section of the ChPs by an essential connection between the development of electroconvection and the properties of the membrane (surface inhomogeneity, electrical inhomogeneity, and others).
3.1.2. Comparison of Mass Transfer Characteristics Calculated for Galvanostatic and Potentiostatic Modes
Comparison of the modeling results for the galvanostatic mode (at the constant current density) based on the NPD–NS equations and for the potentiostatic mode (at the constant potential drop) based on the NPP–NS equations showed a good agreement between the ion-transport characteristics after the establishment of the stationary state (Figure 4c,d). In the potentiostatic mode, the Poisson equation was solved with the following boundary conditions:
where is the value of the potential drop in the stationary state, obtained in the calculation for the galvanostatic mode at the current density . Figure 4d shows the dependences of the average current density on time, calculated for the potentiostatic mode using the formula . The average current density for the potentiostatic mode, , differs from the corresponding value of the current density, i/ilim = 0.5, 1, 1.5, 2, by less than 1% (see Table 1).

Table 1.
Current density and potential drop after the stationary state establishment in the galvanostatic and potentiostatic modes.
The values of the average velocity, , after the stationary state establishment, calculated in the galvanostatic and potentiostatic modes, also agree well (the difference is less than 3%) (Figure 4c). Note that in the potentiostatic mode, the electroconvective flow develops earlier than in the galvanostatic mode, since the potential drop and current density are higher in the initial period in this mode (Figure 4a,d).
3.2. Assessment of the Computational Complexity of the Model
To assess the computational complexity of the proposed model based on the NPD–NS equations, the calculation time of the time period equal to 0.1 s after the establishment of the stationary state, , was fixed. Also, the calculation time, , was fixed for the model based on the NPP–NS equations. Calculations based on NPD–NS and NPP–NS were performed on the same computational mesh (described in Section 2.5), and the accuracy of discretization in time was controlled using a parameter that limits the maximum time step. The iterative calculations of the corresponding boundary value problems were performed for the values of the maximum time step decreasing (in the series of values 0.01 s, 0.005 s, 0.002 s, 0.001 s, 0.0005 s, and 0.0002 s) until the error and is less than 1%.
In the approach of modeling ion transport in the galvanodynamic mode based on the NPP–NS equations, the boundary condition on the derivative of the potential (which determines the given current density) can also be specified at the outer boundary of the diffusion layer, that is:
When the conditions of zero tangential components of the current density, Equation (10), are accepted at boundaries and , these boundaries become equipotential. Therefore, the position of the boundary condition on the derivative of the potential (the variant of the boundary conditions (27) or conditions (34)) does not affect the solution of the NPP–NS equations, but it may affect the computational complexity of obtaining a numerical solution. Compare the calculation time, , for the model based on NPD–NS and two variants based on the NPP–NS system, when the galvanodynamic boundary condition is specified at the outer boundary of the diffusion layer (Equation (34), denoted briefly as NPPL–NS) and at the solution/membrane interface (Equation (27), NPPR–NS).
For calculations based on the NSN–PPδ approach, the required accuracy for all considered current density values () was obtained with the same maximum time step equal to 0.001 s (see Table 2 and Table 3). Therefore, for calculations for the considered values of the current density on the same computational mesh, the calculation time, , and the amount of required memory approximately coincide (average 15.8 GB).

Table 2.
Maximum time step and calculation time for the NPPR–NS, NPPL–NS, and NPD–NS approaches.

Table 3.
Calculation errors and for the NPPR–NS, NPPL–NS, and NPD–NS approaches (with the limitation on the maximum time step, according to Table 2).
At the solution/membrane interface, , the gradients of the ion concentration and potential fields are higher than at the outer boundary of the diffusion layer, . For this reason, in the calculation using the NPPL–NS approach (when the galvanodynamic boundary condition is set at the boundary ), the required calculation errors (see Table 3) were achieved at a larger value of the maximum time step equal to 0.002 s. The calculation time based on the NPPL–NS approach is less (by 13% on average) than that based on the NPPR–NS approach, and the required memory differs little—16.2 GB.
For calculations based on the NPD–NS equations, the maximum time step, providing the error of less than 1%, at the underlimiting current density () coincides with the value of this parameter for calculations based on NPPR–NS. Therefore, the calculation time of these approaches at the current density equal to is comparable (Table 2). At the limiting () and overlimiting ( and ) current densities, the value of the maximum time step for the NPD–NS approach is five times less than for the underlimiting one. As a result, the calculation time for the NPD–NS approach for the current density equal to , , and exceeds, on average, three times the calculation time based on the NPPR–NS approach. The amount of memory used in the solution based on the NPD–NS approach is approximately 12.8 GB.
Thus, the numerical solution based on the NPD–NS approach is more demanding on the accuracy of discretization in time compared to the solution of the NPP–NS equations with the other parameters being the same.
In order to evaluate the relationship between the error of the considered modeling approaches and the quality of the computational mesh, it is necessary to exclude the influence of the time discretization accuracy. For this purpose, calculations were performed for the approaches of NPPR–NS, NPPL–NS, and NPD–NS with the same and rather small value of the time step. Table 4 shows the errors of calculations, and , based on the NPPR–NS, NPPL–NS, and NPD–NS approaches for the same system parameters, computational mesh, and the maximum time step equal to 0.0002 s. In calculations based on the NPPR–NS approach, the decrease in the maximum time step led to the decrease in the calculation error by at least two times and by at least 21 times. In calculations based on the NPPL–NS approach, a decrease in the time step affects the calculation error and is not significant. For all considered approaches, it is characteristic that the higher current density corresponds to the large error in the calculation of and (Table 4). For each value of the current density, the calculation error of the NPD–NS approach is less than the calculation error of the NPPR–NS approach, which, in turn, is smaller than for calculations based on the NPPL–NS approach. Thus, the calculation error of the approaches increases in the series NPD–NS, NPPR–NS, and NPPL–NS.

Table 4.
Calculation errors and for the NPPR–NS, NPPL–NS, and NPD–NS approaches (with the limitation on the maximum time step equal to 0.0002 s).
4. Conclusions
A 2D mathematical model of mass transfer in the depleted diffusion layer near the surface of the ion-exchange membrane in the galvanodynamic mode is constructed based on the NPD–NS equations. The model is able to describe the process of mass transfer in a binary electrolyte solution in a wide range of the current density values, including both underlimiting and overlimiting modes. For the overlimiting current densities, the model takes into account the violation of the electrical neutrality of the solution, the formation of the extended SCR, and the development of electroconvection.
Comparison of the modeling results using the proposed model based on the NPD–NS equations and the previously published model based on the NPP–NS equations for the same current density and system parameters showed the following:
- (1)
- Good quantitative coincidence of ChPs in all characteristic sections, including the initial sharp ohmic growth, monotonic slow electrodiffusion growth, the transition region of the development of electroconvection and the establishment of a stationary state;
- (2)
- Good agreement between the characteristics of mass transfer after the establishment of the stationary state, calculated for the galvanostatic and potentiostatic modes.
The Poisson equation for the electric potential and the equation for the electric field strength based on the expression for the displacement current have a common physical basis. The differences in the equations manifest themselves when constructing mathematical models of mass transfer.
When modeling mass transfer in the galvanodynamic mode based on the NPP–NS equations, it is necessary to specify one of the boundaries parallel to the membrane surface as equipotential. Then, the galvanodynamic boundary condition can be specified at another of these boundaries. The NPD–NS-equations-based mass transfer modeling does not require the introduction into the problem statement assumptions about the potential distribution at the boundaries of the region under consideration. At the same time, both of these approaches require calculation of the current density distribution. To solve this problem, the electric current stream function method is used. The boundary conditions for the electric current stream function at the boundaries parallel to the membrane surface are formulated using the assumption of a zero tangential current component. Therefore, in the calculations based on the NPD–NS equations, the tangential component of the electric field strength is negligible (the range of variation of Ey is approximately five orders of magnitude smaller than the range of variation in Ex), which is equivalent to specifying an equipotential boundary. Therefore, models based on the NPP–NS and NPD–NS equations in the above formulations describe the single physical situation but differ in the numerical solution procedures. At overlimiting currents, the required accuracy of the numerical solution is achieved in the approach based on the NPP–NS equations with a smaller time step than the NPD–NS equation approach. The accuracy of calculating the current density at the boundaries parallel to the membrane surface is higher for the model based on the NPD–NS equations compared to the model based on the NPP–NS equations. Future research will be devoted to constructing a mathematical model of mass transfer in a membrane system without using the assumption that the tangential component of the current density is zero.
The proposed mathematical model can be easily extended in future works for electrolyte solutions with an arbitrary number of ions. The next step is to take into account the forced flow of the electrolyte solution and consider the processes in the electrodialysis channel of desalination. In addition, the proposed NPD–NS approach, modified for the case without setting a zero tangential current density at the system boundaries, will provide new information on the effect of geometric and electrical inhomogeneity of the membrane surface on mass transfer processes.
Funding
The study was funded by the Russian Science Foundation grant No. 23-29-00534, https://rscf.ru/en/project/23-29-00534/ (accessed on 17 August 2023).
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
| 1D | one dimensional |
| 2D | two dimensional |
| AEM | anion-exchange membrane |
| CEM | cation-exchange membrane |
| ChP | chronopotentiogram |
| CVC | current–voltage characteristic |
| NPD | Nernst–Planck and displacement current system of equations |
| NPD–NS | Nernst–Planck, displacement current and Navier–Stokes system of equations |
| NPP | Nernst–Planck–Poisson system of equations |
| NPP–NS | Nernst–Planck–Poisson and Navier–Stokes system of equations |
| SCR | space charge region |
| Symbols | |
| c0 | concentration of electrolyte, mol/m3 |
| cn | molar concentration of ion n, mol/m3 |
| D | diffusion coefficient of electrolyte, m2/s |
| Dn | diffusion coefficient of ion n, m2/s |
| E | electric strength, V/m |
| F | Faraday constant, C/mol |
| H | intermembrane distance, m |
| i | current density, A/m2 |
| ilim | limiting current density, A/m2 |
| jn | flux density of ion n, mol/(m2·s) |
| L | length of the channel, m |
| Nc | ratio of the concentration of cations to the initial concentration of the solution |
| P | pressure, Pa |
| R | universal gas constant, J/(mol·K) |
| r0 | calculation error at x = 0 |
| rδ | calculation error at x= δ |
| T | absolute temperature, K |
| t | time, s |
| tn | transport number of ion n in electrolyte solution |
| TnC | transport number of ion n in cation-exchange membrane |
| velocity of the solution, m/s | |
| x | normal to membrane coordinate, m |
| y | tangential coordinate, m |
| zn | charge number of ion n |
| Greek symbols | |
| γ | maximum relative error of the calculation of the potential drop |
| δ | depleted diffusion layer thickness, m |
| ε0 | electric constant, F/m |
| εr | relative permittivity of the electrolyte solution |
| η | electric current stream function, A/m |
| ν | kinematic viscosity, m2/s |
| ρ0 | solution density, kg/m3 |
| φ | electric potential, V |
| Subscripts | |
| 1 | cation |
| 2 | anion |
| av | average |
| lim | limiting |
| pot | potentiostatic mode |
| tot | total |
| R | right |
| L | left |
References
- Kim, S.J.; Song, Y.-A.; Han, J. Nanofluidic concentration devices for biomolecules utilizing ion concentration polarization: Theory, fabrication, and applications. Chem. Soc. Rev. 2010, 39, 912–922. [Google Scholar] [CrossRef]
- Elimelech, M.; Phillip, W.A. The Future of Seawater Desalination: Energy, Technology, and the Environment. Science 2011, 333, 712–717. [Google Scholar] [CrossRef] [PubMed]
- Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G. Electrodialysis Applications in Wastewater Treatment for Environmen-tal Protection and Resources Recovery: A Systematic Review on Progress and Perspectives. Membranes 2020, 10, 146. [Google Scholar] [CrossRef]
- Strathmann, H. Ion-Exchange Membrane Processes in Water Treatment. Sustain. Sci. Eng. 2010, 2, 141–199. [Google Scholar] [CrossRef]
- Wilson, J.R. Demineralization by Electrodialysis; Butterworths Scientific Publications: London, UK, 1960. [Google Scholar]
- Belova, E.I.; Lopatkova, G.Y.; Pismenskaya, N.D.; Nikonenko, V.V.; Larchet, C.; Pourcelly, G. Effect of anion-exchange membrane surface properties on mechanisms of overlimiting mass transfer. J. Phys. Chem. B 2006, 110, 13458–13469. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Kovalenko, A.V.; Urtenov, M.K.; Pismenskaya, N.D.; Han, J.; Sistat, P.; Pourcelly, G. Desalination at overlimiting currents: State-of-the-art and perspectives. Desalination 2014, 342, 85–106. [Google Scholar] [CrossRef]
- Maletzki, F.; Rosler, H.W.; Staude, E. Ion transfer across electrodialysis membranes in the overlimiting current range: Stationary voltage current characteristics and current noise power spectra under different conditions of free convection. J. Membr. Sci. 1992, 71, 105–116. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V.; Pismenskaya, N.D.; Laktionov, E.V.; Urtenov, M.K.; Strathmann, H.; Wessling, M.; Koops, G.H. Coupled transport phenomena in overlimiting current electrodialysis. Sep. Purif. Technol. 1998, 14, 255–267. [Google Scholar] [CrossRef]
- Rubinshtein, I.; Zaltzman, B.; Pretz, J.; Linder, C. Experimental Verification of the Electroosmotic Mechanism of Overlimiting Conductance Through a Cation Exchange Electrodialysis Membrane. Russ. J. Electrochem. 2002, 38, 853–863. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Nikonenko, V.V.; Belova, E.I.; Lopatkova, G.Y.; Sistat, P.; Pourcelly, G.; Larshet, C. Coupled convection of solution near the surface of ion-exchange membranes in intensive current regimes. Russ. J. Electrochem. 2007, 43, 307–327. [Google Scholar] [CrossRef]
- Rubinstein, S.M.; Manukyan, G.; Staicu, A.; Rubinstein, I.; Zaltzman, B.; Lammertink, R.G.H. Direct Observation of a Nonequilibrium Electro-Osmotic Instability. Phys. Rev. Lett. 2008, 101, 236101. [Google Scholar] [CrossRef] [PubMed]
- Kwak, R.; Guan, G.; Peng, W.K.; Han, J. Microscale electrodialysis: Concentration profiling and vortex visualization. Desalination 2013, 308, 138–146. [Google Scholar] [CrossRef]
- Shaposhnik, V.A.; Vasileva, V.I.; Praslov, D.B. Concentration Fields of Solutions under Electrodialysis with Ion-Exchange Membranes. J. Membr. Sci. 1995, 101, 23–30. [Google Scholar] [CrossRef]
- Shaposhnik, V.A.; Vasil’eva, V.I.; Grigorchuk, O.V. The interferometric investigations of electromembrane processes. Adv. Colloid Interf. Sci. 2008, 139, 74–82. [Google Scholar] [CrossRef]
- Frilette, V.J. Electrogravitational Transport at Synthetic Ion Exchange Membrane Surfaces. J. Phys. Chem. 1957, 61, 168–174. [Google Scholar] [CrossRef]
- Balster, J.; Yildirim, M.H.; Stamatialis, D.F.; Ibanez, R.; Lammertink, R.G.H.; Jordan, V.; Wessling, M. Morphology and microtopology of cation-exchange polymers and the origin of the overlimiting current. J. Phys. Chem. B 2007, 111, 2152–2165. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Electro-osmotically induced convection at a permselective membrane. Phys. Rev. E 2000, 62, 2238–2251. [Google Scholar] [CrossRef]
- Demekhin, E.A.; Shelistov, V.S.; Polyanskikh, S.V. Linear and nonlinear evolution and diffusion layer selection in electrokinetic instability. Phys. Rev. E 2011, 84, 036318. [Google Scholar] [CrossRef]
- Urtenov, M.K.; Uzdenova, A.M.; Kovalenko, A.V.; Nikonenko, V.V.; Pismenskaya, N.D.; Vasil’eva, V.I.; Sistat, P.; Pourcelly, G. Basic mathematical model of overlimiting transfer enhanced by electroconvection in flow-through electrodialysis membrane cells. J. Membr. Sci. 2013, 447, 190–202. [Google Scholar] [CrossRef]
- Kwak, R.; Pham, V.S.; Lim, K.M.; Han, J. Shear Flow of an Electrically Charged Fluid by Ion Concentration Polarization: Scaling Laws for Electroconvective Vortices. Phys. Rev. Lett. 2013, 110, 114501. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Mareev, S.A.; Pis’menskaya, N.D.; Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Pourcelly, G. Effect of Electroconvection and Its Use in Intensifying the Mass Transfer in Electrodialysis (Review). Russ. J. Electrochem. 2017, 53, 1122–1144. [Google Scholar] [CrossRef]
- Rubinstein, I.; Shtilman, L. Voltage against current curves of cation exchange membranes. J. Chem. Soc. Faraday Trans. 1979, 75, 231–246. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V. Ion Transport in Membranes; (In Russian). Nauka: Moscow, Russia, 1996. [Google Scholar]
- Newman, J.; Balsara, N.P. Electrochemical Systems, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Mani, A.; Wang, K.M. Electroconvection Near Electrochemical Interfaces: Experiments, Modeling, and Computation. Annu. Rev. Fluid Mech. 2020, 52, 509–529. [Google Scholar] [CrossRef]
- Yaroslavtsev, A.B.; Nikonenko, V.V.; Zabolotsky, V.I. Ion transfer in ion-exchange and membrane materials. Russ. Chem. Rev. 2003, 72, 393–421. [Google Scholar] [CrossRef]
- Manzanares, J.A.; Murphy, W.D.; Mafe, S.; Reiss, H. Numerical Simulation of the Nonequilibrium Diffuse Double Layer in Ion-Exchange Membranes. J. Phys. Chem. 1993, 97, 8524–8530. [Google Scholar] [CrossRef]
- Levich, V.G. Physicochemical Hydrodynamics; Prentice Hall: New York, NY, USA, 1962. [Google Scholar]
- Liu, W.; Zhou, Y.; Shi, P. Shear electroconvective instability in electrodialysis channel under extreme depletion and its scaling laws. Phys. Rev. E 2020, 101, 043105. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, Y.; Shi, P. Scaling relations in shear electroconvective vortices. Phys. Fluids 2020, 32, 072009. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, Y.; Shi, P. Critical selection of shear sheltering in electroconvective flow from chaotic to steady state. J. Fluid Mech. 2022, 946, A3. [Google Scholar] [CrossRef]
- Kwak, R.; Pham, V.; Han, J. Sheltering the perturbed vortical layer of electroconvection under shear flow. J. Fluid Mech. 2017, 813, 799–823. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, Y.; Shi, P. Sheltering electroconvective instability in a weak electrolyte. Phys. Fluids 2021, 33, 072011. [Google Scholar] [CrossRef]
- Demekhin, E.A.; Nikitin, N.V.; Shelistov, V.S. Direct Numerical Simulation of Electrokinetic Instability and Transition to Chaotic Motion. Phys. Fluids 2013, 25, 122001. [Google Scholar] [CrossRef]
- Druzgalski, C.; Mani, A. Statistical analysis of electroconvection near an ion-selective membrane in the fully chaotic regime. Phys. Rev. Fluids 2016, 1, 073601. [Google Scholar] [CrossRef]
- Magnico, P. Electro-Kinetic Instability in a Laminar Boundary Layer Next to an Ion Exchange Membrane. Int. J. Mol. Sci. 2019, 20, 2393. [Google Scholar] [CrossRef] [PubMed]
- Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Nikonenko, V.V. Effect of electroconvection during pulsed electric field electrodialysis: Numerical experiments. Electrochem. Commun. 2015, 51, 1–5. [Google Scholar] [CrossRef]
- Karatay, E.; Andersen, M.B.; Wessling, M.; Mani, A. On the coupling between buoyancy forces and electroconvective instability near ion-selective surfaces. Phys. Rev. Lett. 2016, 116, 194501. [Google Scholar] [CrossRef]
- Shi, P. Direct numerical simulation of electroconvection with thin Debye layer matching canonical experiments. Phys. Fluids 2021, 33, 032015. [Google Scholar] [CrossRef]
- Kovalenko, A.V.; Nikonenko, V.V.; Chubyr, N.O.; Urtenov, M.K. Mathematical modeling of electrodialysis of a dilute solution with accounting for water dissociation-recombination reactions. Desalination 2023, 550, 116398. [Google Scholar] [CrossRef]
- Leon, T.; Lopez, J.; Torres, R.; Grau, J.; Jofre, L.; Cortina, J.-L. Describing ion transport and water splitting in an electrodialysis stack with bipolar membranes by a 2-D model: Experimental validation. J. Membr. Sci. 2022, 660, 120835. [Google Scholar] [CrossRef]
- Moya, A.A. Electrochemical impedance of ion-exchange systems with weakly charged membranes. Ionics 2013, 19, 1271–1283. [Google Scholar] [CrossRef]
- Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Nikonenko, V.V. 1D Mathematical Modelling of Non-Stationary Ion Transfer in the Diffusion Layer Adjacent to an Ion-Exchange Membrane in Galvanostatic Mode. Membranes 2018, 8, 84. [Google Scholar] [CrossRef]
- Uzdenova, A. 2D mathematical modelling of overlimiting transfer enhanced by electroconvection in flow-through electrodialysis membrane cells in galvanodynamic mode. Membranes 2019, 9, 39. [Google Scholar] [CrossRef]
- Mareev, S.A.; Nebavskiy, A.V.; Nichka, V.S.; Urtenov, M.K.; Nikonenko, V.V. The nature of two transition times on chronopotentiograms of heterogeneous ion exchange membranes: 2D modelling. J. Membr. Sci. 2019, 575, 179–190. [Google Scholar] [CrossRef]
- Uzdenova, A.; Urtenov, M. Potentiodynamic and Galvanodynamic Regimes of Mass Transfer in Flow-Through Electrodialysis Membrane Systems: Numerical Simulation of Electroconvection and Current-Voltage Curve. Membranes 2020, 10, 49. [Google Scholar] [CrossRef] [PubMed]
- Green, Y. Approximate time-dependent current-voltage relations for currents exceeding the diffusion limit. Phys. Rev. E 2020, 101, 043113. [Google Scholar] [CrossRef] [PubMed]
- Uzdenova, A.; Urtenov, M. Mathematical Modeling of the Phenomenon of Space-Charge Breakdown in the Galvanostatic Mode in the Section of the Electromembrane Desalination Channel. Membranes 2021, 11, 873. [Google Scholar] [CrossRef]
- Uzdenova, A.; Kovalenko, A.; Urtenov, M. Theoretical Analysis of Electroconvection in the Electrodialysis Desalination Channel under the Action of Direct Current. Membranes 2022, 12, 1125. [Google Scholar] [CrossRef] [PubMed]
- Cohen, H.; Cooley, J.W. The Numerical Solution of the Time-Dependent Nernst–Planck Equations. Biophys. J. 1965, 5, 145. [Google Scholar] [CrossRef]
- Brumleve, T.R.; Buck, R.P. Numerical solution of the Nernst–Planck and Poisson equation system with applications to membrane electrochemistry and solid state physics. J. Electroanal. Chem. 1978, 90, 1–31. [Google Scholar] [CrossRef]
- Urtenov, M.A.K. Boundary Value Problems for Systems of Nernst–Planck-Poisson Equations (Factorization, Decomposition, Models, Numerical Analysis); Universervis: Krasnodar, Russia, 1998. (In Russian) [Google Scholar]
- Lavrentyev, A.V.; Pismensky, A.V.; Urtenov, M.K. Mathematical Modeling of Transport in Electromembrane Systems Taking into Account Convective Flows; KubSTU: Krasnodar, Russia, 2006. (In Russian) [Google Scholar]
- Kovalenko, A.V.; Khromykh, A.A.; Urtenov, M.K. Decomposition of a two-dimensional system of equations Nernst–Planck–Poisson for ternary electrolyte. Bull. Russ. Acad. Sci. 2014, 458, 526. [Google Scholar] [CrossRef]
- Uzdenova, A.M. Ion Transport in Electromembrane Systems under the Passage of Direct Current: 1D Modelling Approaches. Membranes 2023, 13, 421. [Google Scholar] [CrossRef]
- Roache, P.J. Computational Fluid Dynamics; Hermosa Publishers: Albuquerque, NM, USA, 1976. [Google Scholar]
- Pismensky, A.V.; Urtenov, M.K.; Nikonenko, V.V.; Sistat, P.; Pismenskaya, N.D.; Kovalenko, A.V. Model and Experimental Studies of Gravitational Convection in an Electromembrane Cell. Russ. J. Electrochem. 2012, 48, 756–766. [Google Scholar] [CrossRef]
- Mareev, S.A.; Nichka, V.S.; Butylskii, D.Y.; Urtenov, M.K.; Pismenskaya, N.D.; Apel, P.Y.; Nikonenko, V.V. Chronopotentiometric Response of Electrically Heterogeneous Permselective Surface: 3D Modeling of Transition Time and Experiment. J. Phys. Chem. C 2016, 120, 13113–13119. [Google Scholar] [CrossRef]
- Larchet, C.; Nouri, S.; Auclair, B.; Dammak, L.; Nikonenko, V. Application of chronopotentiometry to determine the thickness of diffusion layer adjacent to an ion-exchange membrane under natural convection. Adv. Colloid Interface Sci. 2008, 139, 45–61. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Vasil’eva, V.I.; Akberova, E.M.; Uzdenova, A.M.; Urtenov, M.K.; Kovalenko, A.V.; Pismenskaya, N.D.; Mareev, S.A.; Pourcelly, G. Competition between diffusion and electroconvection at an ion-selective surface in intensive current regimes. Adv. Colloid Interface Sci. 2016, 235, 233–246. [Google Scholar] [CrossRef]
- Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Nikonenko, V.V. Theoretical analysis of the effect of ion concentration in solution bulk and at membrane surface on the mass transfer at overlimiting currents. Russ. J. Electrochem. 2017, 53, 1254–1265. [Google Scholar] [CrossRef]
- Urtenov, M.A.K.; Kirillova, E.V.; Seidova, N.M.; Nikonenko, V.V. Decoupling of the Nernst–Planck and Poisson equations, Application to a membrane system at overlimiting currents. J. Phys. Chem. B 2007, 11151, 14208–14222. [Google Scholar] [CrossRef] [PubMed]
- Comsol Multiphysics Reference Manual. Available online: https://doc.comsol.com/6.1/doc/com.comsol.help.comsol/COMSOL_ReferenceManual.pdf (accessed on 10 June 2023).
- de Valenca, J.C.; Wagterveld, R.M.; Lammertink, R.G.H.; Tsai, P.A. Dynamics of microvortices induced by ion concentration polarization. Phys. Rev. E 2015, 92, 031003. [Google Scholar] [CrossRef]
- Valenca, J.; Jogi, M.; Wagterveld, R.M.; Karatay, E.; Wood, J.A.; Lammertink, R.G.H. Confined electroconvective vortices at structured ion exchange membranes. Langmuir 2018, 34, 2455–2463. [Google Scholar] [CrossRef] [PubMed]
- Krol, J.J.; Wessling, M.; Strathmann, H. Chronopotentiometry and overlimiting ion transport through monopolar ion exchange membranes. J. Membr. Sci. 1999, 162, 155–164. [Google Scholar] [CrossRef]
- Titorova, V.D.; Mareev, S.A.; Gorobchenko, A.D.; Gil, V.V.; Nikonenko, V.V.; Sabbatovskii, K.G.; Pismenskaya, N.D. Effect of current-induced coion transfer on the shape of chronopotentiograms of cation-exchange membranes. J. Membr. Sci. 2021, 624, 119036. [Google Scholar] [CrossRef]
- Barros, K.S.; Martí-Calatayud, M.C.; Scarazzato, T.; Bernardes, A.M.; Espinosa, D.C.R.; Pérez-Herranz, V. Investigation of ion-exchange membranes by means of chronopotentiometry: A comprehensive review on this highly informative and multipurpose technique. Adv. Colloid Interface Sci. 2021, 293, 102439. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).