Sparse Reconstruction Using Hyperbolic Tangent as Smooth l1-Norm Approximation
Abstract
1. Introduction
2. Materials and Methods
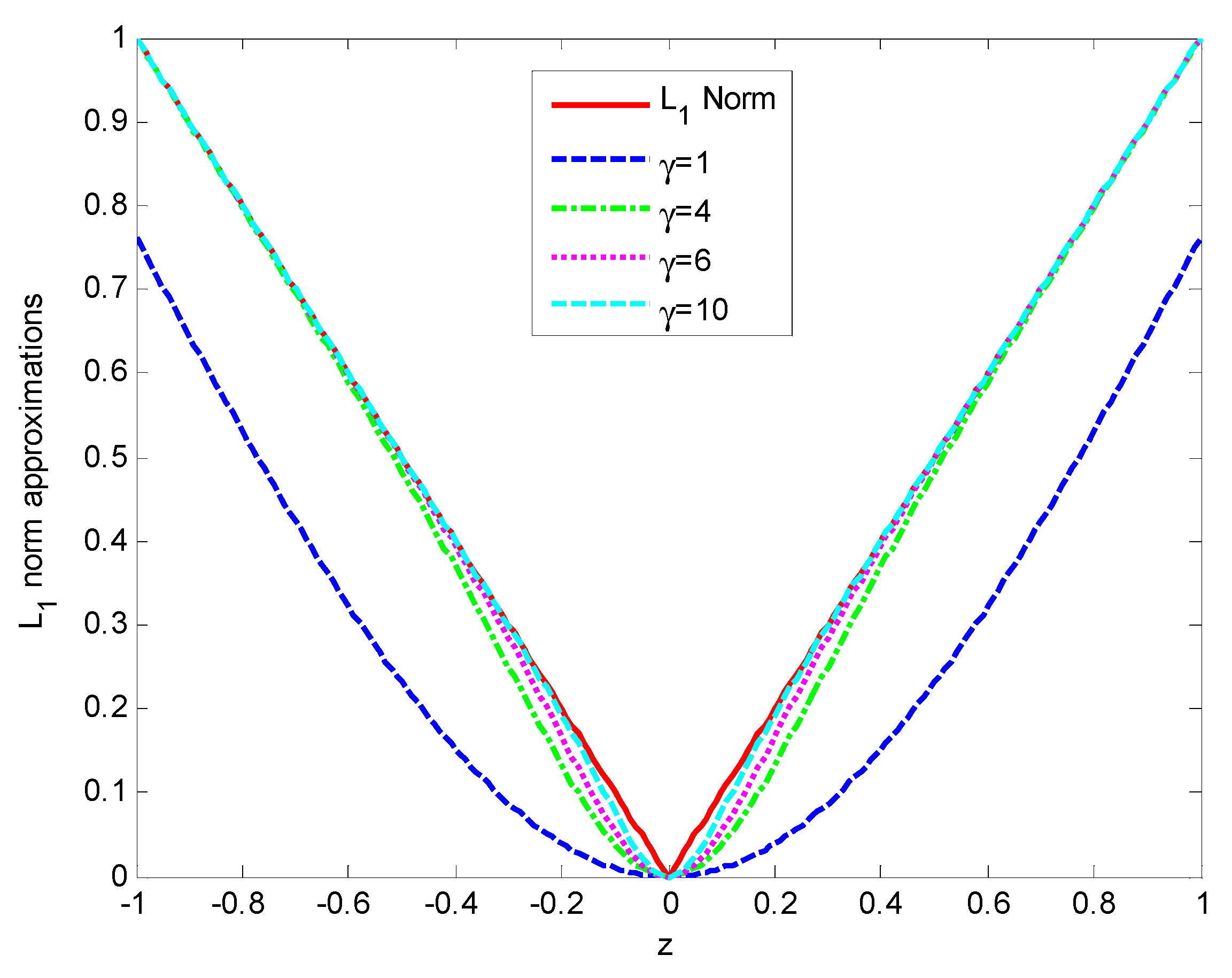
2.1. Proposed Method
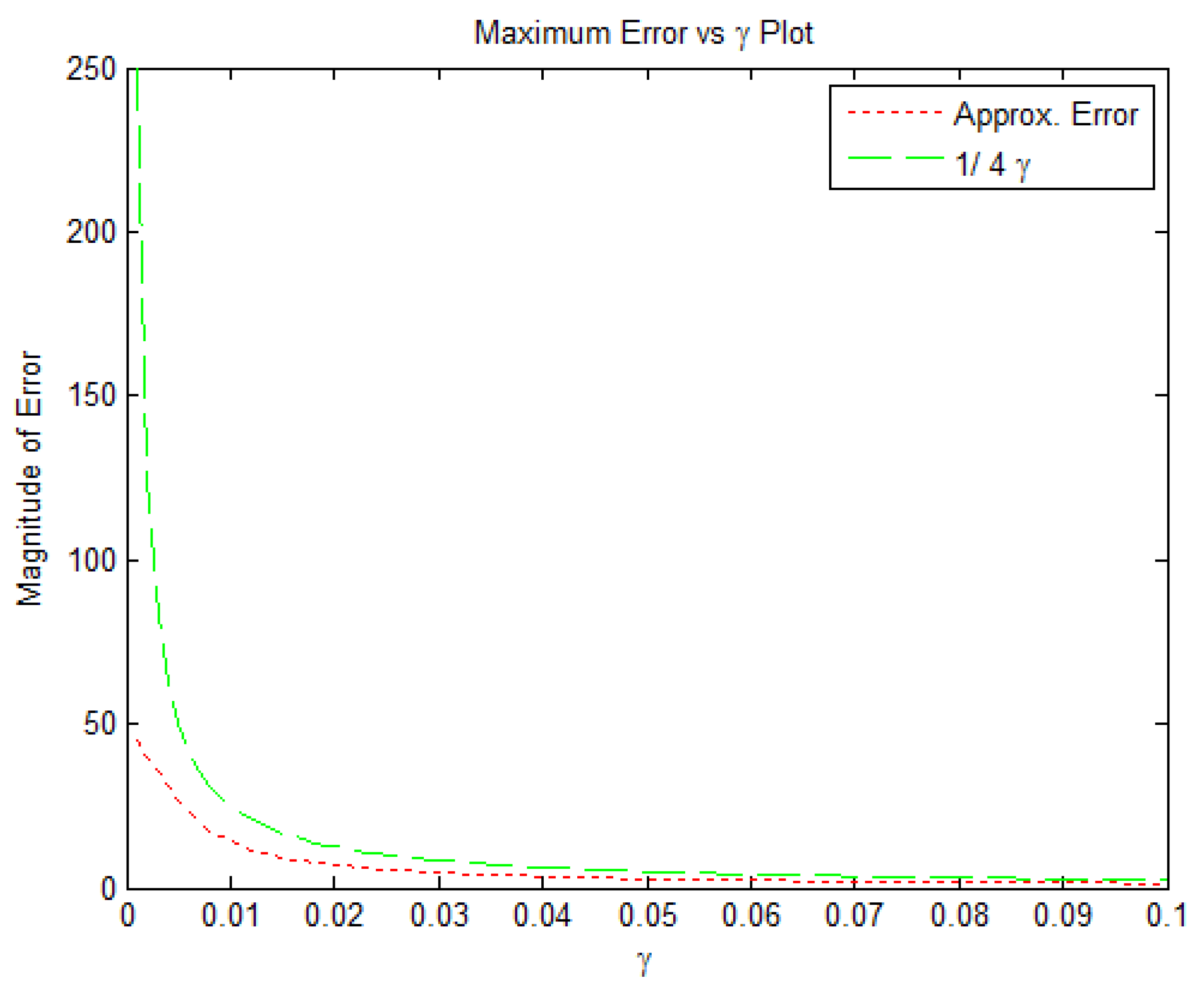
2.2. Error Bounds for Proposed Smooth -Norm
- , where is the plus function;
- This plus function can be smoothly approximated as:
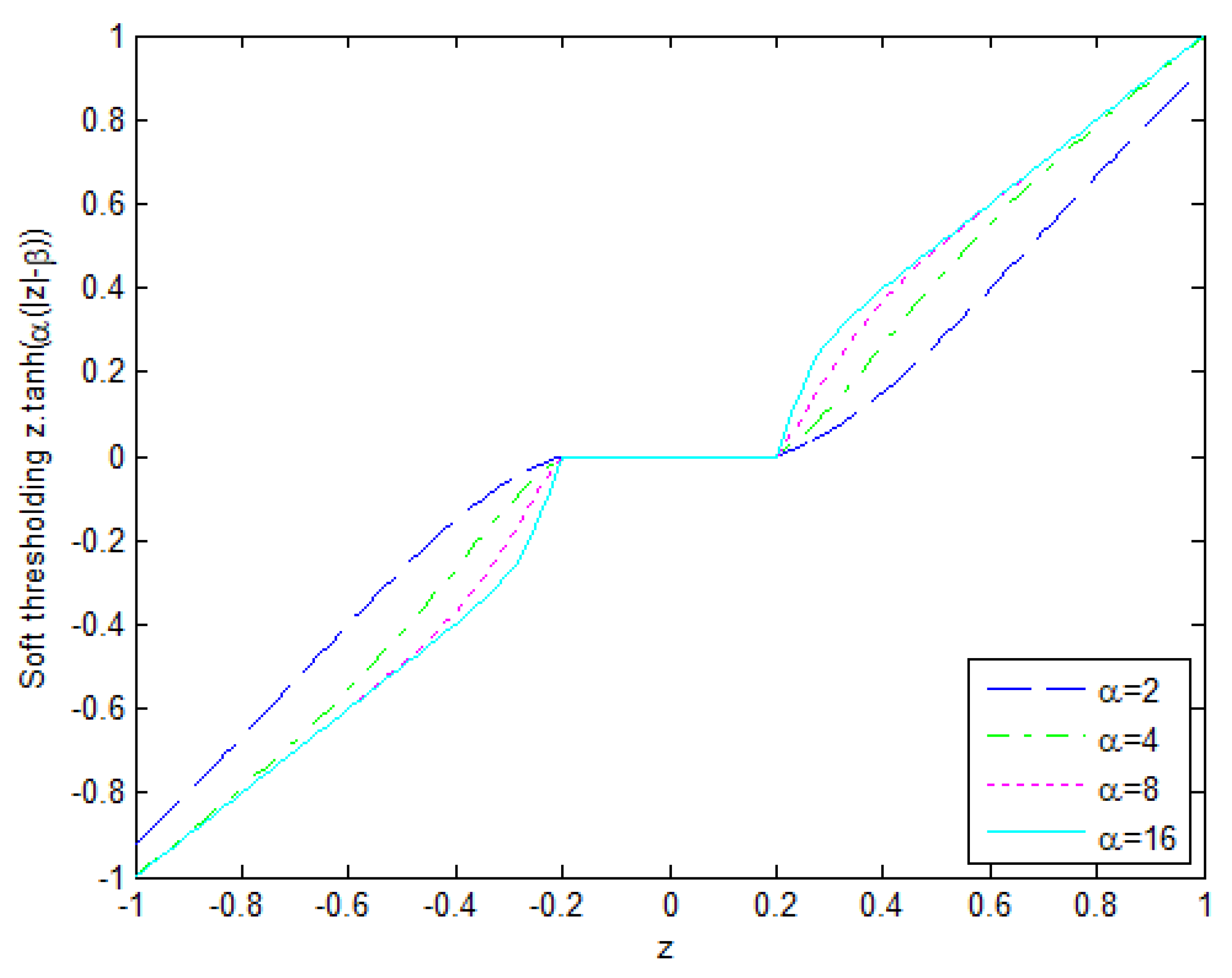
3. The Map Estimator and Proposed Thresholding Mechanism
| Algorithm 1. Proposed Algorithms. |
| Inputs: |
| Sensing matrix , measurement vector , parameters , , |
| Output: |
| A k-sparse vector |
| Initialization: Initialize , Index |
| Step-1 (Sparse Representation): |
| Step-1 (Gradient Computation): Find using Equation (5) |
| Step-2 (Solution Update): Compute the update using Equations (6) and (7). |
| Step-3 (Shrinkage): Estimate Solution using Equation (38), i.e., |
| Step-4 (Repeat): If stopping criterion is not met, & go to step 1 |
| Output: |
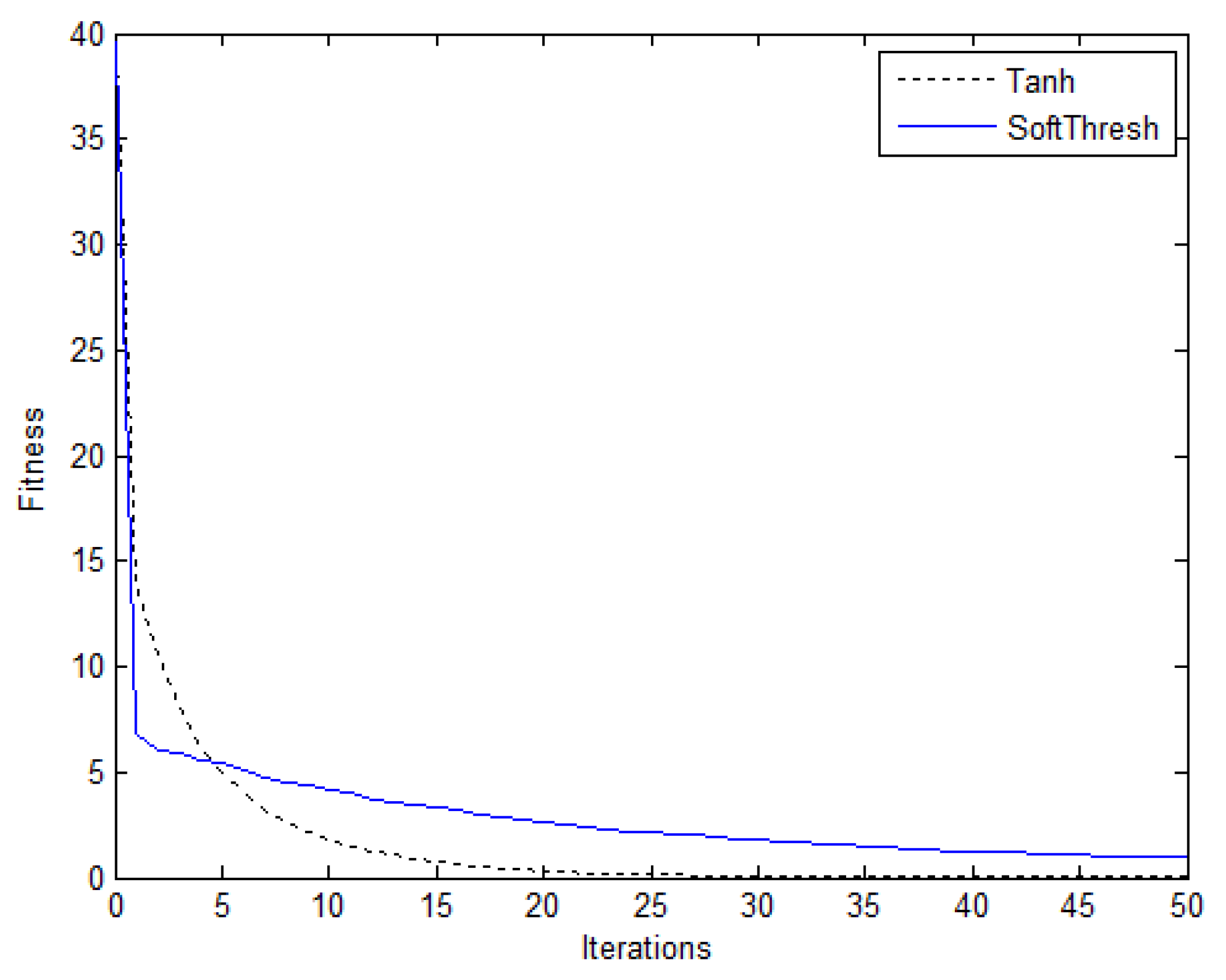
4. Results and Discussions
4.1. 1-D Sparse Signal Recovery
4.2. 2-D Compressively Sampled MR Image Recovery
4.3. Cardiac Cine Magnetic Resonance Imaging Recovery
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An Introduction To Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Near-Optimal Signal Recovery From Random Projections: Universal Encoding Strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.; Pauly, J.M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007, 58, 1182–1195. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.L.; Santos, J.M.; Pauly, J.M. Compressed Sensing MRI. IEEE Signal Process. Mag. 2008, 25, 72–82. [Google Scholar] [CrossRef]
- Auger, D.A.; Bilchick, K.C.; Gonzalez, J.A.; Cui, S.X.; Holmes, J.W.; Kramer, C.M.; Salerno, M.; Epstein, F.H. Imaging left-ventricular mechanical activation in heart failure patients using cine DENSE MRI: Validation and implications for cardiac resynchronization therapy. J. Magn. Reson. Imaging 2017, 46, 887–896. [Google Scholar] [CrossRef]
- Liu, J.; Feng, L.; Shen, H.-W.; Zhu, C.; Wang, Y.; Mukai, K.; Brooks, G.C.; Ordovas, K.; Saloner, D. Highly-accelerated self-gated free-breathing 3D cardiac cine MRI: Validation in assessment of left ventricular function. Magn. Reson. Mater. Phys. Biol. Med. 2017, 30, 337–346. [Google Scholar] [CrossRef]
- van Amerom, J.F.P.; Lloyd, D.F.A.; Price, A.N.; Kuklisova Murgasova, M.; Aljabar, P.; Malik, S.J.; Lohezic, M.; Rutherford, M.A.; Pushparajah, K.; Razavi, R.; et al. Fetal cardiac cine imaging using highly accelerated dynamic MRI with retrospective motion correction and outlier rejection. Magn. Reson. Med. 2018, 79, 327–338. [Google Scholar] [CrossRef]
- Paulus, W.J.; Tschöpe, C.; Sanderson, J.E.; Rusconi, C.; Flachskampf, F.A.; Rademakers, F.E.; Marino, P.; Smiseth, O.A.; De Keulenaer, G.; Leite-Moreira, A.F.; et al. How to diagnose diastolic heart failure: A consensus statement on the diagnosis of heart failure with normal left ventricular ejection fraction by the Heart Failure and Echocardiography Associations of the European Society of Cardiology. Eur. Heart J. 2007, 28, 2539–2550. [Google Scholar] [CrossRef]
- Yerly, J.; Gubian, D.; Knebel, J.-F.; Schenk, A.; Chaptinel, J.; Ginami, G.; Stuber, M. A phantom study to determine the theoretical accuracy and precision of radial MRI to measure cross-sectional area differences for the application of coronary endothelial function assessment. Magn. Reson. Med. 2018, 79, 108–120. [Google Scholar] [CrossRef]
- Ahmed, A.H.; Qureshi, I.M.; Shah, J.A.; Zaheer, M. Motion correction based reconstruction method for compressively sampled cardiac MR imaging. Magn. Reson. Imaging 2017, 36, 159–166. [Google Scholar] [CrossRef]
- Gamper, U.; Boesiger, P.; Kozerke, S. Compressed sensing in dynamic MRI. Magn. Reson. Med. 2008, 59, 365–373. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Iterative hard thresholding for compressed sensing. Appl. Comput. Harmon. Anal. 2009, 27, 265–274. [Google Scholar] [CrossRef]
- Tropp, J.A.; Wakin, M.B.; Duarte, M.F.; Baron, D.; Baraniuk, R.G. Random Filters for Compressive Sampling and Reconstruction. In Proceedings of the 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 14–19 May 2006. [Google Scholar]
- Yin, W.; Osher, S.; Goldfarb, D.; Darbon, J. Bregman Iterative Algorithms for $\ell_1$-Minimization with Applications to Compressed Sensing. SIAM J. Imaging Sci. 2008, 1, 143–168. [Google Scholar] [CrossRef]
- Khajehnejad, M.A.; Xu, W.; Avestimehr, A.S.; Hassibi, B. Weighted ℓ<inf>1</inf>minimization for sparse recovery with prior information. In Proceedings of the 2009 IEEE International Symposium on Information Theory, Seoul, Korea, 28 June–3 July 2009; pp. 483–487. [Google Scholar]
- Shah, J.; Qureshi, I.; Omer, H.; Khaliq, A. A modified POCS-based reconstruction method for compressively sampled MR imaging. Int. J. Imaging Syst. Technol. 2014, 24, 203–207. [Google Scholar] [CrossRef]
- Shah, J.A.; Qureshi, I.M.; Omer, H.; Khaliq, A.A.; Deng, Y. Compressively sampled magnetic resonance image reconstruction using separable surrogate functional method. Concepts Magn. Reson. Part A 2014, 43, 157–165. [Google Scholar] [CrossRef]
- Bilal, M.; Shah, J.A.; Qureshi, I.M.; Kadir, K. Respiratory Motion Correction for Compressively Sampled Free Breathing Cardiac MRI Using Smooth l(1)-Norm Approximation. Int. J. Biomed. Imaging 2018, 2018, 7803067. [Google Scholar] [CrossRef]
- Shah, J.; Qureshi, I.M.; Deng, Y.; Kadir, K. Reconstruction of Sparse Signals and Compressively Sampled Images Based on Smooth l1-Norm Approximation. J. Signal Process. Syst. 2017, 88, 333–344. [Google Scholar] [CrossRef]
- He, C.; Xing, J.; Li, J.; Yang, Q.; Wang, R. A New Wavelet Thresholding Function Based on Hyperbolic Tangent Function. Math. Probl. Eng. 2015, 2015, 528656. [Google Scholar] [CrossRef]
- Lu, J.-y.; Lin, H.; Ye, D.; Zhang, Y.-s. A New Wavelet Threshold Function and Denoising Application. Math. Probl. Eng. 2016, 2016, 3195492. [Google Scholar] [CrossRef]
- Schmidt, M.; Fung, G.; Rosales, R. Fast Optimization Methods for L1 Regularization: A Comparative Study and Two New Approaches. In Proceedings of the Machine Learning: ECML 2007, Berlin/Heidelberg, Germany, 17–21 September 2007; pp. 286–297. [Google Scholar]
- Chang, S.G.; Bin, Y.; Vetterli, M. Spatially adaptive wavelet thresholding with context modeling for image denoising. IEEE Trans. Image Process. 2000, 9, 1522–1531. [Google Scholar] [CrossRef]
- Sendur, L.; Selesnick, I.W. Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency. IEEE Trans. Signal Process. 2002, 50, 2744–2756. [Google Scholar] [CrossRef]
- Nasri, M.; Nezamabadi-Pour, H. Image denoising in the wavelet domain using a new adaptive thresholding function. Neurocomputing 2009, 72, 1012–1025. [Google Scholar] [CrossRef]
- Prinosil, J.; Smekal, Z.; Bartusek, K. Wavelet Thresholding Techniques in MRI Domain. In Proceedings of the 2010 International Conference on Biosciences, Online, 7–13 March 2010; pp. 58–63. [Google Scholar]
- Jin, J.; Yang, B.; Liang, K.; Wang, X. General image denoising framework based on compressive sensing theory. Comput. Graph. 2014, 38, 382–391. [Google Scholar] [CrossRef]


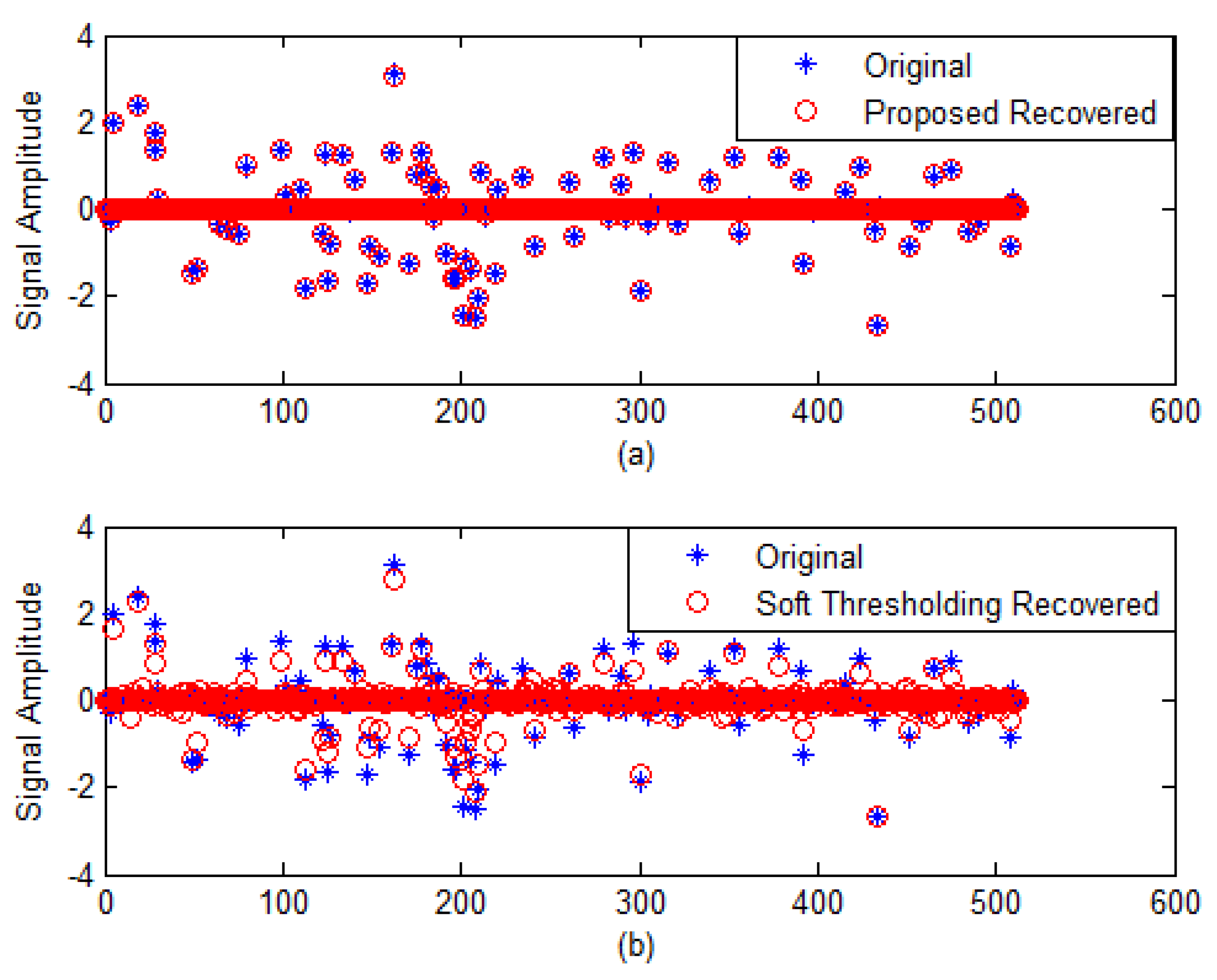

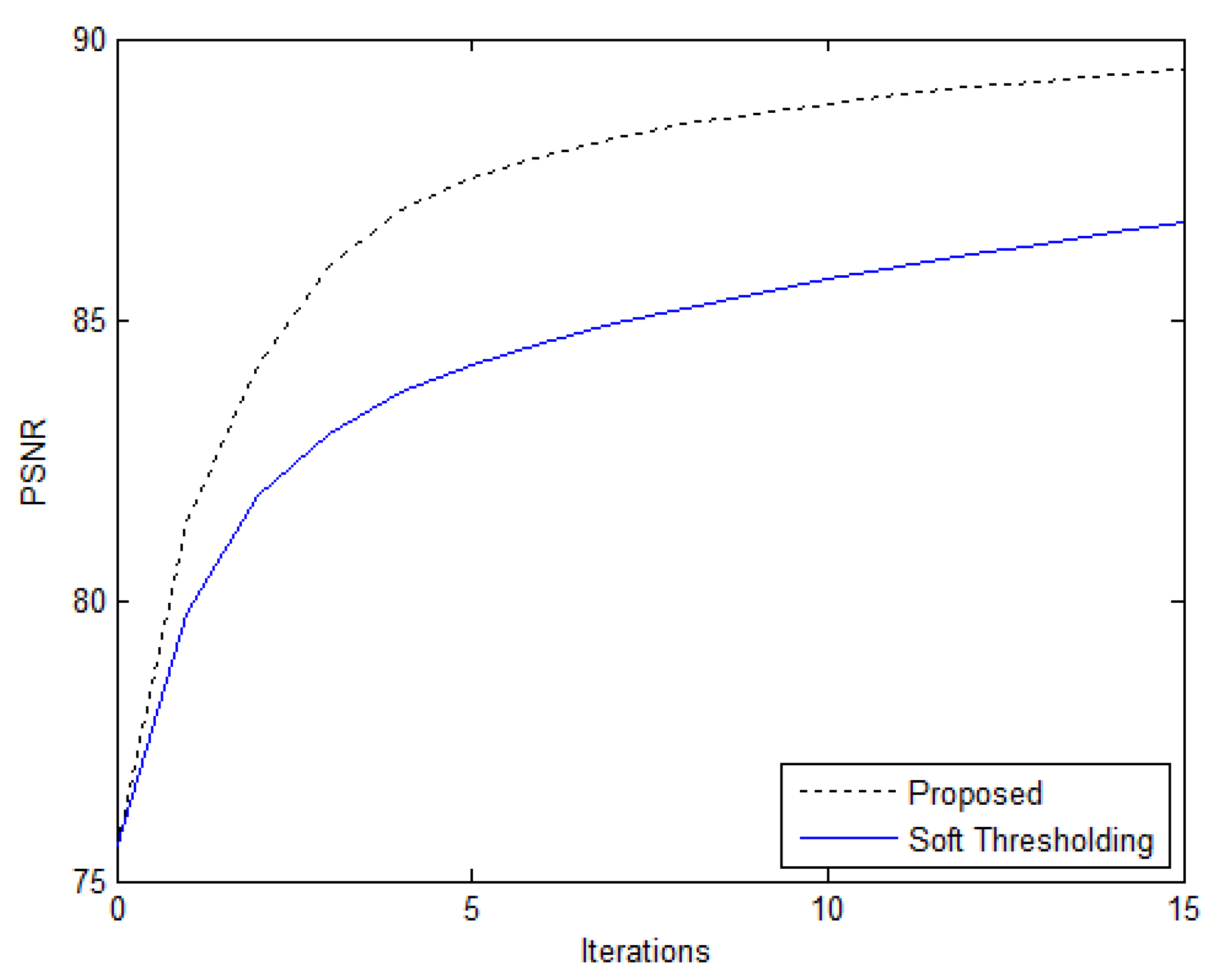
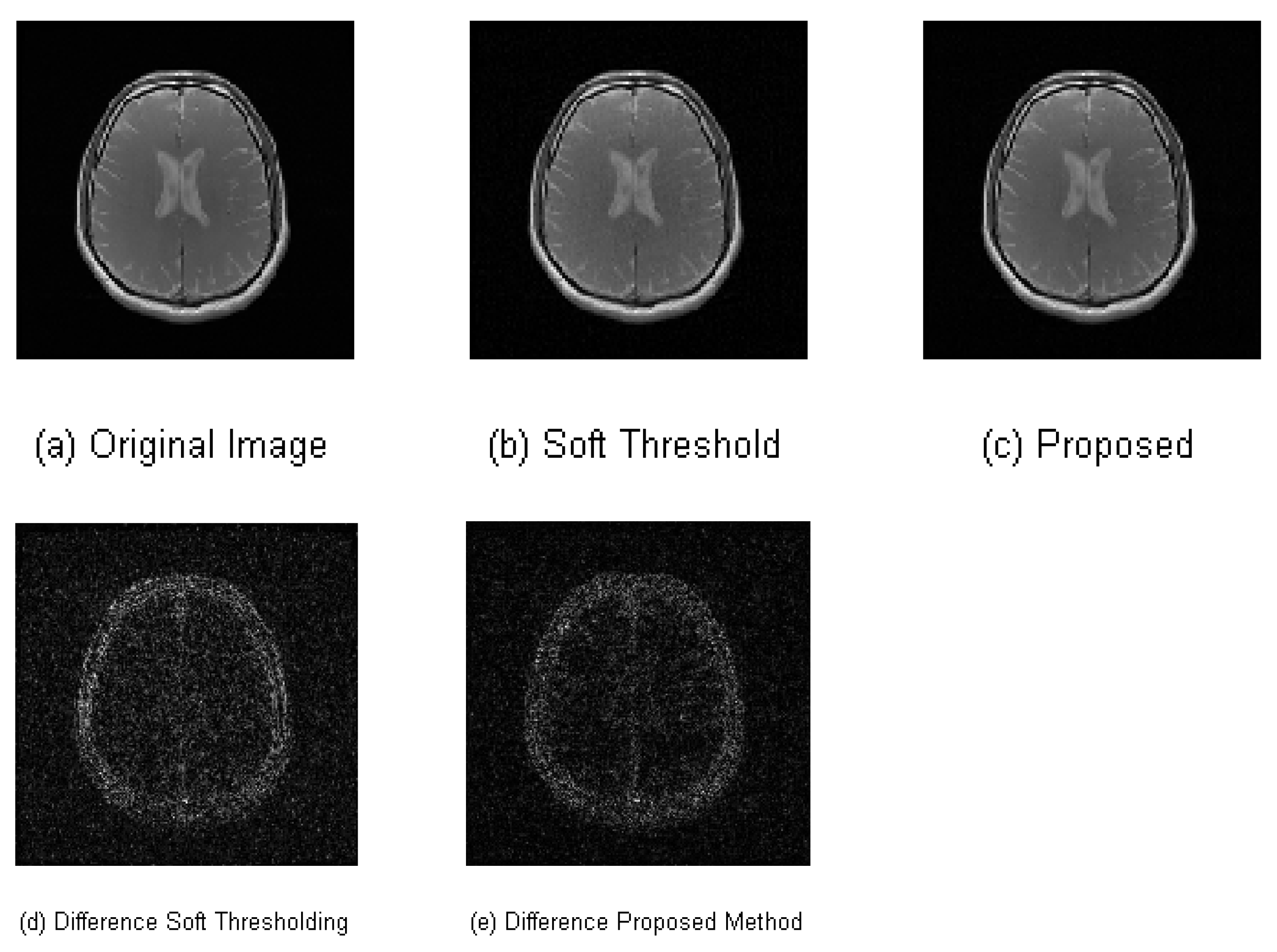



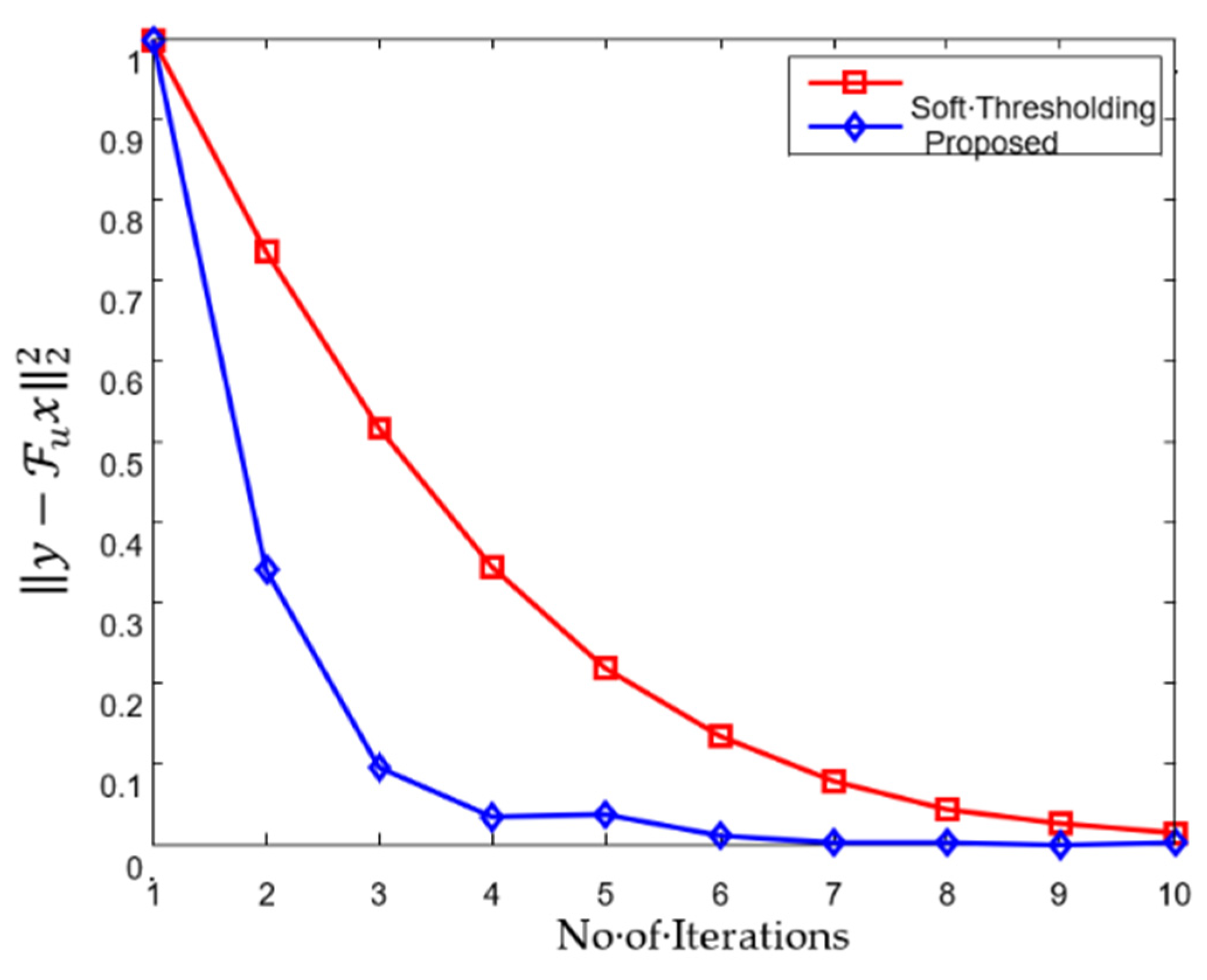


| Performance Metrics | Soft Thresholding | Proposed Algorithm |
|---|---|---|
| MSE | 1.00 × 10−2 | 1.61 × 10−4 |
| Fitness | 0.8664 | 0.0224 |
| SNR | 12.6712 | 30.6259 |
| Correlation | 0.9787 | 0.9995 |
| Compression Ratio | Soft Thresholding | Proposed Algorithm | ||
|---|---|---|---|---|
| SSIM | PSNR | SSIM | PSNR | |
| 5 % | 0.6843 | 75.9056 | 0.7048 | 76.1609 |
| 10% | 0.7786 | 78.9320 | 0.8175 | 79.6580 |
| 20% | 0.8994 | 82.0316 | 0.8472 | 83.7628 |
| 30% | 0.9407 | 87.3535 | 0.9790 | 91.1620 |
| 40% | 0.9724 | 91.2540 | 0.9920 | 96.1281 |
| 50% | 0.9884 | 95.4245 | 0.9955 | 99.5496 |
| Performance Metrics | Soft Thresholding | Proposed Algorithm |
|---|---|---|
| MSE | 1.38 × 10−4 | 0.73 × 10−4 |
| PSNR | 86.7195 | 89.4497 |
| ISNR | 28.3832 | 31.1135 |
| SSIM | 0.9346 | 0.9711 |
| SNR | 26.0298 | 28.7491 |
| Correlation | 0.9980 | 0.9989 |
| Acceleration Rates | Spatial Domain | Total Variation | Temporal FFT |
|---|---|---|---|
| 2 | 0.1096 | 0.1123 | 0.0728 |
| 4 | 0.2321 | 0.1849 | 0.0848 |
| 8 | 0.2810 | 0.2438 | 0.0948 |
| 12 | 0.3533 | 0.2684 | 0.1043 |
| 20 | 0.4756 | 0.2982 | 0.1150 |
| Acceleration Rates | Undersampled Image | Iterative Soft Thresholding | Proposed Method | |
|---|---|---|---|---|
| Simulated Data | 2 | 0.081 | 0.0365 | 0.0353 |
| 4 | 0.1218 | 0.0472 | 0.0372 | |
| 8 | 0.1498 | 0.0702 | 0.0419 | |
| 12 | 0.1583 | 0.0775 | 0.0485 | |
| 20 | 0.1782 | 0.0941 | 0.0606 | |
| In vivo Data | 2 | 0.085 | 0.0099 | 0.0056 |
| 4 | 0.106 | 0.0241 | 0.0172 | |
| 8 | 0.1170 | 0.0495 | 0.0206 | |
| 12 | 0.120 | 0.0567 | 0.0338 | |
| 20 | 0.1398 | 0.0585 | 0.0551 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haider, H.; Shah, J.A.; Kadir, K.; Khan, N. Sparse Reconstruction Using Hyperbolic Tangent as Smooth l1-Norm Approximation. Computation 2023, 11, 7. https://doi.org/10.3390/computation11010007
Haider H, Shah JA, Kadir K, Khan N. Sparse Reconstruction Using Hyperbolic Tangent as Smooth l1-Norm Approximation. Computation. 2023; 11(1):7. https://doi.org/10.3390/computation11010007
Chicago/Turabian StyleHaider, Hassaan, Jawad Ali Shah, Kushsairy Kadir, and Najeeb Khan. 2023. "Sparse Reconstruction Using Hyperbolic Tangent as Smooth l1-Norm Approximation" Computation 11, no. 1: 7. https://doi.org/10.3390/computation11010007
APA StyleHaider, H., Shah, J. A., Kadir, K., & Khan, N. (2023). Sparse Reconstruction Using Hyperbolic Tangent as Smooth l1-Norm Approximation. Computation, 11(1), 7. https://doi.org/10.3390/computation11010007






