Modified Kleene Star Algorithm Using Max-Plus Algebra and Its Application in the Railroad Scheduling Graphical User Interface
Abstract
1. Introduction
2. Research Methods
2.1. Max-Plus Algebra
- , and is normal addition operation.
2.2. Matrices in Max-Plus Algebra
- is a weighted directed graph.
- The number of vertices of is .
- If , then edge .
- Element is the weight of edge . In other words, .
2.3. Eigenvalues and Eigenvectors in Max-Plus Algebra
2.4. Model of a Railroad Network System in Max-Plus Algebra
3. Results and Discussion
3.1. Eigenvector Calculation Algorithm in Max-Plus Algebra
3.1.1. Steps and Time Complexity of the Kleene Star Algorithm
- Determine as the eigenvalues of , where is the maximum circuit average weight of the matrix .
- Determine .
- Determine
- The eigenvectors of which correspond to are the columns of , where is a critical circuit of , or .
- 1st step:
- 2nd step:
- 3rd step:
- 4th step:
3.1.2. Steps and Time Complexity of the Modified Kleene Star Algorithm
- Determine the eigenvalue by formula:
- Determine and , where .
- Determine a critical vertex of the graph ; that is, when , then is a critical vertex of the graph .
- Determine the eigenvectors of which correspond to ; that is the- of matrix .
- 1st step:
- 2nd step:
- 3rd step:
- 4th step:
3.1.3. Steps and Time Complexity of the Power Algorithm
- Choose an initial , with .
- Iterate , until there are integers and a real number , which satisfy .
- Determine the eigenvalue
- Determine eigenvector
3.1.4. Comparison of Kleene Star Algorithm, Modified Kleene Star Algorithm, and Power Algorithm
3.2. Max-Plus Algebra and Its Application in Railroad Network System
- : represents the th—departure time of all trains.
- : represents the th—departure schedule of all trains.
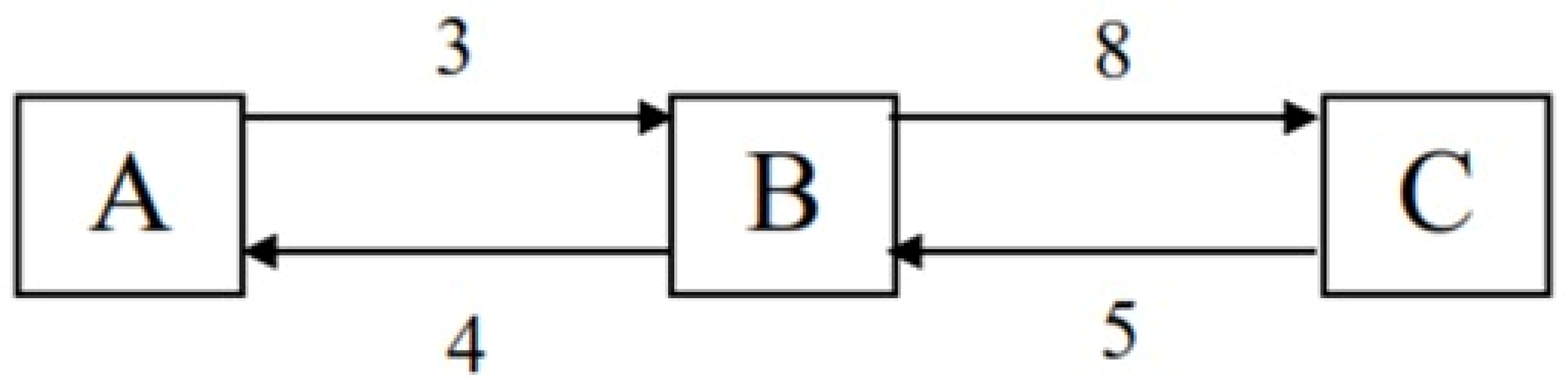
- The first route starts from station A. Each time a train departs on this route, it runs from station A to station B.
- The second route starts from station B. Each time a train departs on this route, it runs from station B to station C.
- The third route starts from station C. Each time a train departs on this route, it runs from station C to station B.
- The fourth route starts from station B. Each time a train departs on this route, it runs from station B to station A.
- The travel time for each train is fixed.
- The time for arrival, passenger drop-off, passenger boarding, and departure is considered 0.
- The train departures must wait for the arrival of the train from the previous departure. For example, a train departing from station A to station B must wait for the arrival of a train from station B to station A.
- Each train departure has a schedule. Trains that arrived earlier than the scheduled departure must wait for the current schedule to depart.
- : th departure time on the route from station A to B.
- : th departure time on the route from station B to C.
- : th departure time on the route from station C to B.
- : th departure time on the route from station B to A.
3.3. Graphical User Interface on Scilab for Railway Network System Scheduling
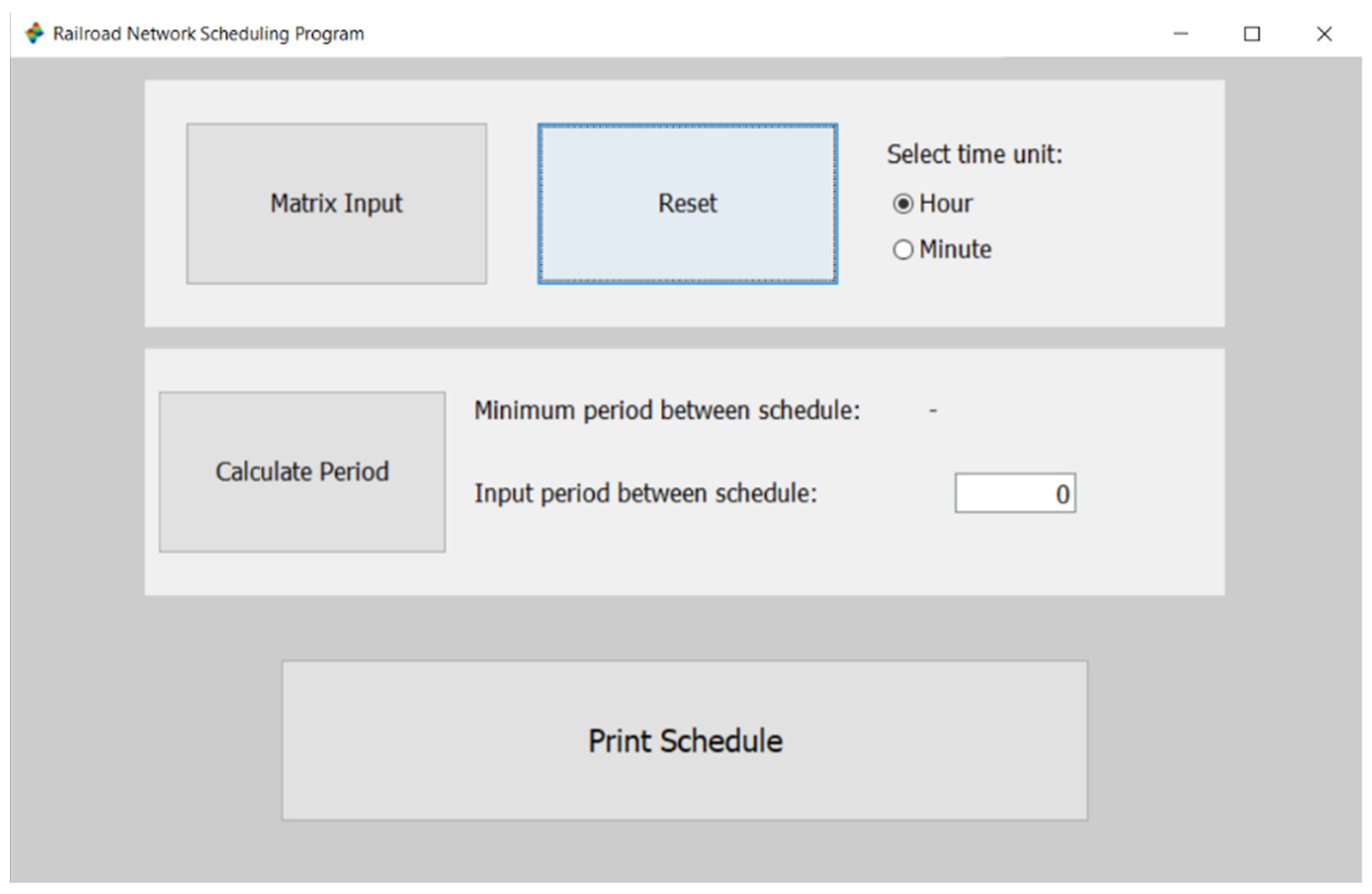
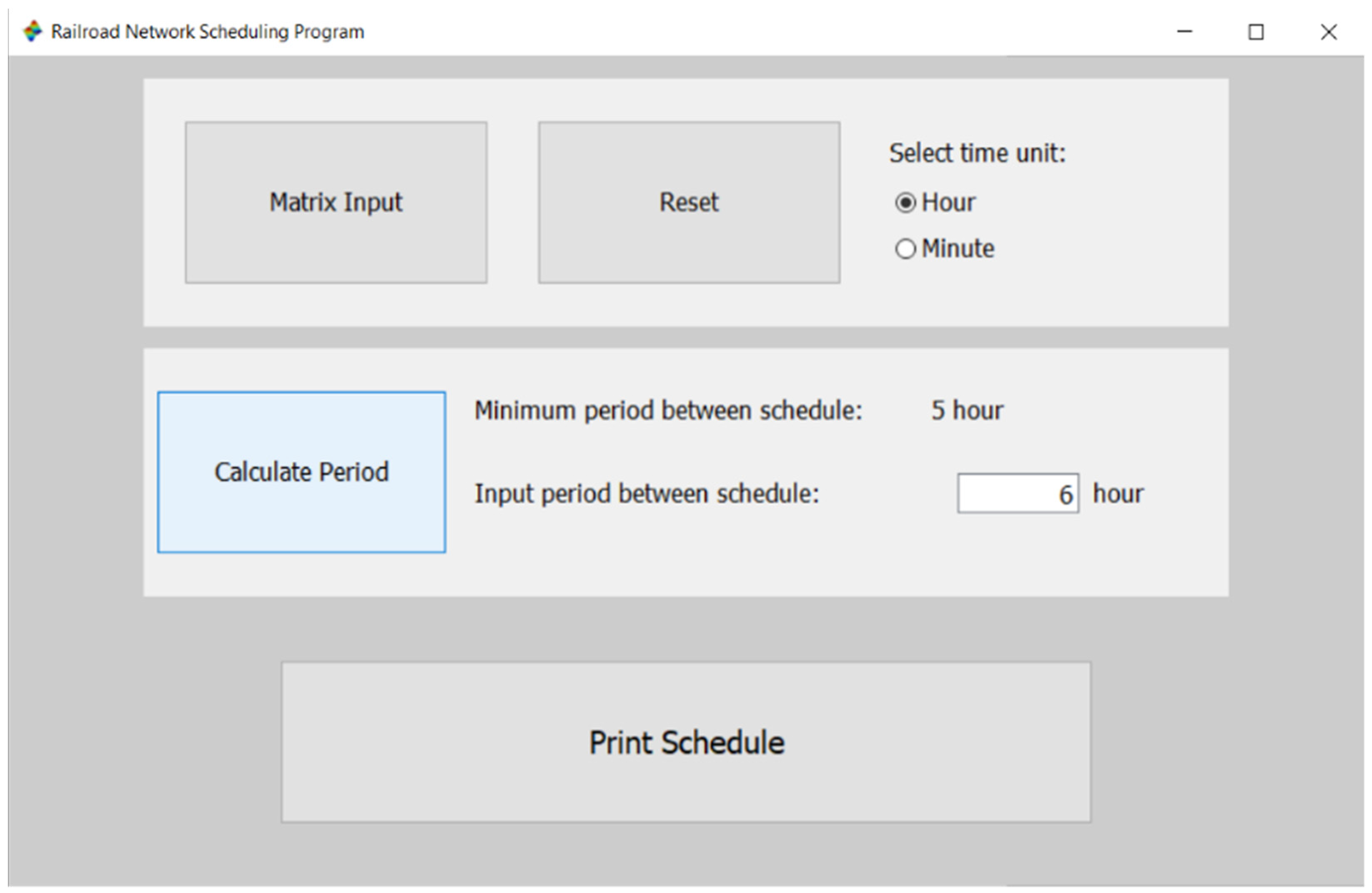
- Matrix Input: opens the “Variable Editor” window to enter the matrix of the railroad system model.
- Reset: restores the program to its original state and deletes the previously entered matrix.
- Select Time Unit: opens the menu to select the unit of time used by the model railroad matrix. There are two options: hours and minutes.
- Calculate Period: shows the minimum period between departures scheduled. In the space provided, the user then enters a period between schedules that is greater than the minimum schedule period.
- Print Schedule: shows the departure schedule on the Scilab console.
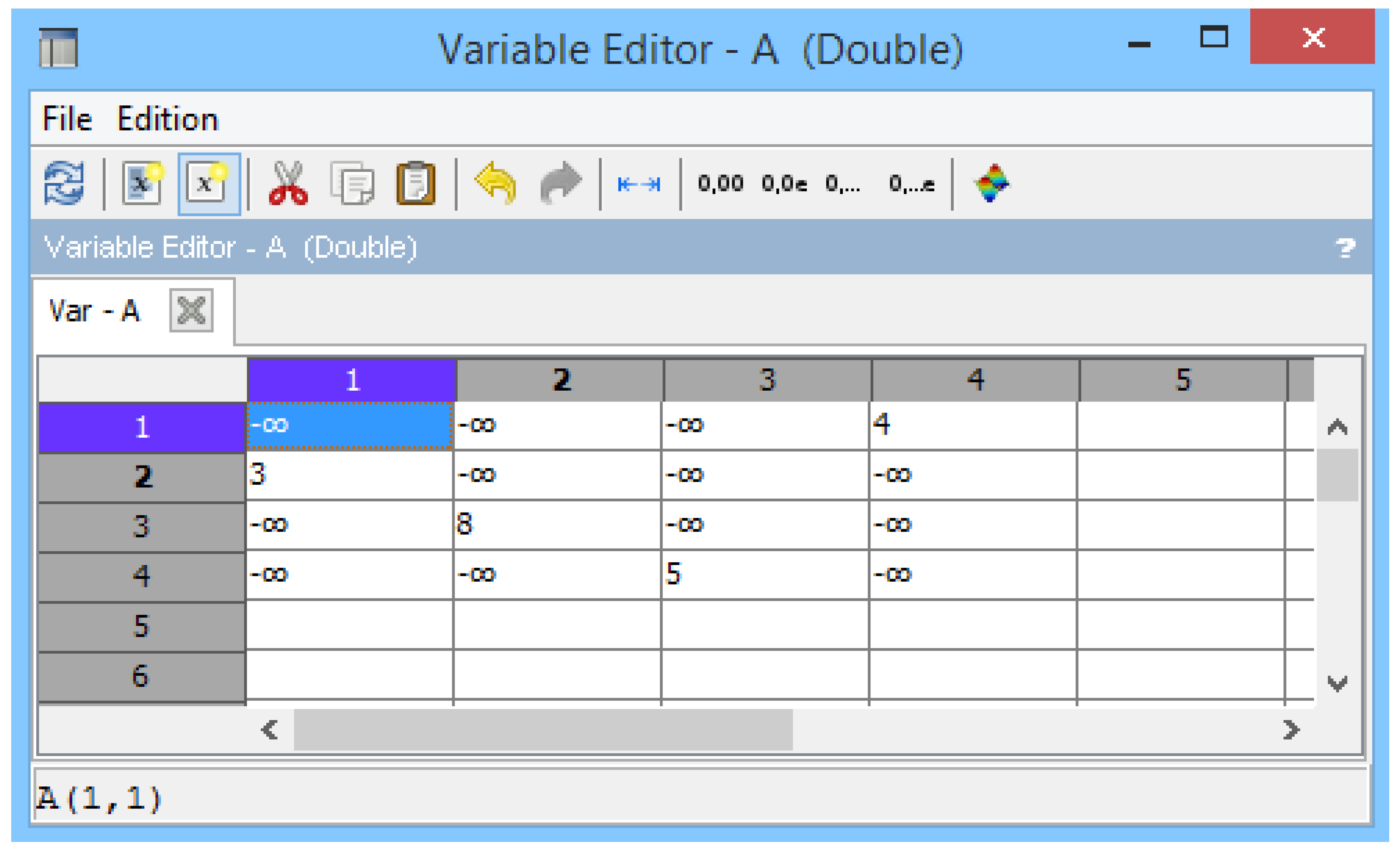
- Press the “Input Matrix” button to bring up the “Variable Editor” window and enter the input matrix. Note: the syntax to input on Scilab 6.02 is ‘-%inf,’ without quotes.
- Close the “Variable Editor” window and select the appropriate time unit. In this case, the unit of time is hours.
- Press the “Calculate Period” button to bring up the minimum period between schedules and enter the desired period between schedules.
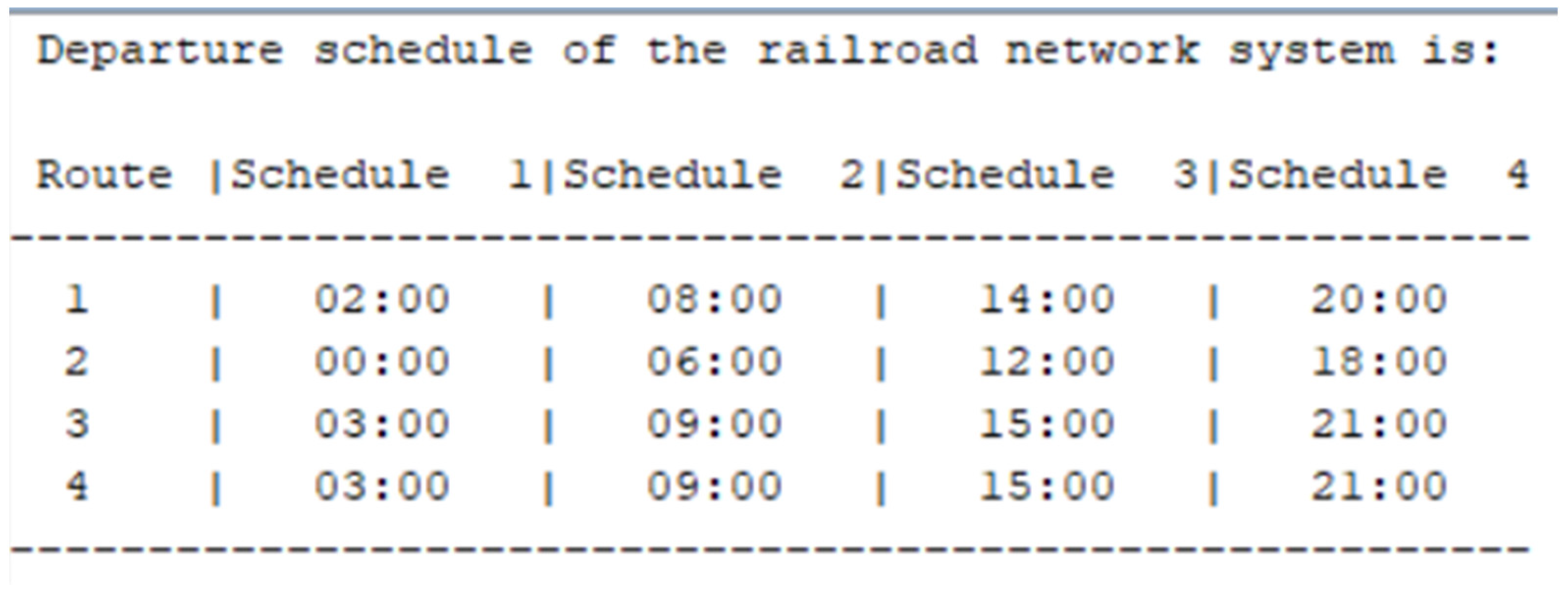
- Press the “Print Schedule” button to bring up the schedule in the Scilab console window.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farlow, K.G. Max-Plus Algebra; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2009. [Google Scholar]
- Krivulin, N.K. The Max-Plus Algebra Approach in Modelling of Queueing Networks. Available online: http://arxiv.org/abs/1212.0895 (accessed on 1 December 2012).
- Olsder, G.J.; Subiono. On Large Scale Max-Plus Algebra Models in Railway Systems. IFAC Proc. Vol. 1998, 31, 649–653. [Google Scholar] [CrossRef]
- Elmahi, I.; Grunder, O.; Elmoudni, A. A Max Plus Algebra Approach for Modelling and Control a Supply Chain. In Proceedings of the 2003 IEEE Conference on Control Applications, Istanbul, Turkey, 23–25 June 2003; Volume 2. [Google Scholar] [CrossRef]
- Imaev, A.; Judd, R.P. Block diagram-based modeling of manufacturing systems using. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 July 2009. [Google Scholar] [CrossRef]
- Becker, B.A.; Lastovetsky, A. Max-Plus Algebra and Discrete Event Simulation on Parallel Hierarchical Heterogeneous Platforms. In Proceedings of the 2010 Conference on Parallel Processing, San Diego, CA, USA, 13–16 September 2010; pp. 63–70. [Google Scholar] [CrossRef]
- Olsder, G.J. Eigenvalues of dynamic max-min systems. Discret. Event Dyn. Syst. Theory Appl. 1991, 1, 177–207. [Google Scholar] [CrossRef]
- Braker, J.G. Algorithms and Applications in Timed Discrete Event Systems; Delft University of Technology: Delft, The Netherlands, 1993. [Google Scholar]
- Subiono. Aljabar Min-Max Plus dan Terapannya. 2015. Available online: https://docplayer.info/68251215-Aljabar-min-max-plus-dan-terapannya.html (accessed on 1 December 2021).
- Fahim, K.; Subiono; van der Woude, J. On a generalization of power algorithms over max-plus algebra. Discret. Event Dyn. Syst. 2017, 27, 181–203. [Google Scholar] [CrossRef]
- Baccelli, F.; Cohen, G.; Olsder, G.J.; Quadrat, J.-P. Quadrat, Synchronization and Linearity: An Algebra for Discrete Event Systems; John Wiley & Sons: New York, NY, USA, 1992; Volume 7. [Google Scholar]
- Furche, T.; Gottlob, G.; Grasso, G.; Schallhart, C.; Sellers, A. OXPath: A language for scalable data extraction, automation, and crawling on the deep web. VLDB J. 2013, 22, 47–72. [Google Scholar] [CrossRef]
- Ernawati; Carnia, E.; Supriatna, A.K. Eigenvectors determination of the ribosome dynamics model during mRNA translation using the Kleene Star algorithm. IOP Conf. Ser. Mater. Sci. Eng. 2018, 332, 012019. [Google Scholar] [CrossRef]
- Krivulin, N. Tropical optimization technique in bi-objective project scheduling under temporal constraints. Comput. Manag. Sci. 2020, 17, 437–464. [Google Scholar] [CrossRef]
- Trunk, J.; Cottenceau, B.; Hardouin, L.; Raisch, J. Modelling and control of periodic time-variant event graphs in dioids. Discret. Event Dyn. Syst. 2020, 30, 269–300. [Google Scholar] [CrossRef]
- Rudhito, M.A. Aljabar Max-Plus Dan Penerapannya; Sanata Dharma University Press: Daerah Istimewa Yogyakarta, Indonesia, 2016. [Google Scholar]
- Tunisa, K.; Wijayanti, K.; Veronica, R.B. Nilai Eigen Dan Vektor Eigen Matriks Atas Aljabar Max-Plus. UJM 2017, 6, 189–197. [Google Scholar] [CrossRef]
- Alfiah, S. Pemodelan Jaringan Kereta Rel Listrik (KRL) Menggunakan Aljabar Max-Plu. Master’s Thesis, Institut Teknologi Sepuluh Nopember, Surabaya, Indonesia, 2011. [Google Scholar]
- Johnson, D.B. Finding All the Elementary Circuits of a Directed Graph. SIAM J. Comput. 1975, 4, 77–84. [Google Scholar] [CrossRef]
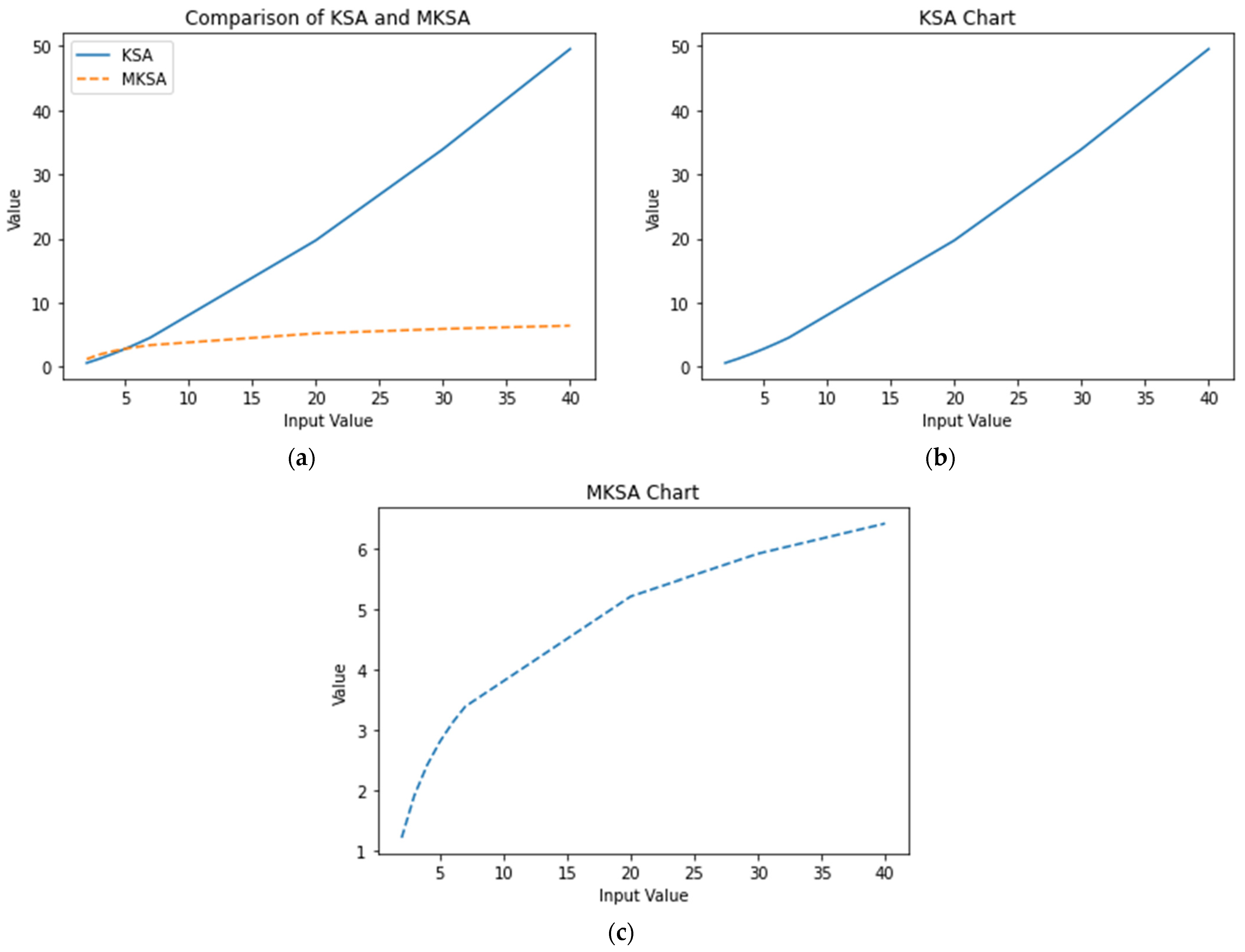
| Input Value (n) | ||
|---|---|---|
| 2 | 4 | 16 |
| 3 | 18 | 81 |
| 4 | 96 | 256 |
| 5 | 600 | 625 |
| 6 | 4320 | 1296 |
| 7 | 35,280 | 2401 |
| 20 | 4.86 | 160,000 |
| 30 | 7.95 | 810,000 |
| 40 | 3.26 | 2,560,000 |
| Departure Station | Arrival Station | Available Departure Hours | |||
|---|---|---|---|---|---|
| A | B | 02:00 | 08:00 | 14:00 | 20:00 |
| B | C | 00:00 | 06:00 | 12:00 | 18:00 |
| C | B | 03:00 | 09:00 | 15:00 | 21:00 |
| B | A | 03:00 | 09:00 | 15:00 | 21:00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carnia, E.; Wilopo, R.; Napitupulu, H.; Anggriani, N.; Supriatna, A.K. Modified Kleene Star Algorithm Using Max-Plus Algebra and Its Application in the Railroad Scheduling Graphical User Interface. Computation 2023, 11, 11. https://doi.org/10.3390/computation11010011
Carnia E, Wilopo R, Napitupulu H, Anggriani N, Supriatna AK. Modified Kleene Star Algorithm Using Max-Plus Algebra and Its Application in the Railroad Scheduling Graphical User Interface. Computation. 2023; 11(1):11. https://doi.org/10.3390/computation11010011
Chicago/Turabian StyleCarnia, Ema, Rinaldi Wilopo, Herlina Napitupulu, Nursanti Anggriani, and Asep K. Supriatna. 2023. "Modified Kleene Star Algorithm Using Max-Plus Algebra and Its Application in the Railroad Scheduling Graphical User Interface" Computation 11, no. 1: 11. https://doi.org/10.3390/computation11010011
APA StyleCarnia, E., Wilopo, R., Napitupulu, H., Anggriani, N., & Supriatna, A. K. (2023). Modified Kleene Star Algorithm Using Max-Plus Algebra and Its Application in the Railroad Scheduling Graphical User Interface. Computation, 11(1), 11. https://doi.org/10.3390/computation11010011







