BER Aided Energy and Spectral Efficiency Estimation in a Heterogeneous Network

Abstract

In this work, we adopt the analysis of a heterogeneous cellular network by means of stochastic geometry, to estimate energy and spectral network efficiency. More specifically, it has been the widely spread experience that practical field assessment of the Signal-to-Noise and Interference Ratio (SINR), being the key physical-layer performance indicator, involves quite sophisticated test instrumentation that is not always available outside the lab environment. So, in this regard, we present here a simpler test model coming out of the much easier-to-measure Bit Error Rate (BER), as the latter can deteriorate due to various impairments regarded here as equivalent with additive white Gaussian noise (AWGN) abstracting (in terms of equal BER degradation) any actual non-AWGN impairment. We validated the derived analytical model for heterogeneous two-tier networks by means of an ns3 simulator, as it provided the test results that fit well to the analytically estimated corresponding ones, both indicating that small cells enable better energy and spectral efficiencies than the larger-cell networks.

1. Introduction

It has been a considerable time since it has become evident that homogeneous cellular network architecture cannot adequately fulfill the fast-growing users’ demand for capacity and Quality of Service (QoS) [1], as well as for efficient spectrum and energy consumption.

Starting with the fourth generation (4G) mobile networks, it has become evident that smaller cells enhance network performance and off-load the macro network from excessive traffic. So, for example, simple plug-and-play installed femtocells are more profitable than macro cells, due to the reduced backhaul costs and less transmitted power required in small cells. Specifically, state-of-the-art Radio Access Systems (RAS) encompass cells of different classes to make up a Heterogeneous Cellular Network (HetNet), which includes at least two same-class groups—tiers [2,3]. The actual explosive growth of data traffic implies severe demand on energy efficiency (EE), so with the 4G Long-Term Evolution (LTE) and its extended version LTE Advanced (LTE-A), as well as with the incoming 5G HetNets, transmission performance enhancements include a reduction in the distance between the transmitting and the receiving antennas.

With respect to the EE of wireless access networks, the metrics are focused [4,5,6] on the energy per information [J/b], enriched by some QoS-related features [7] to improve HetNet’s capacity and coverage, which both depend on the Signal-to-Interference-and-Noise Ratio (SINR).

However, the SINR value is not always available and is not easily measurable. Therefore, we introduce here a novel approach by merging the link abstraction principle into the test scheme, to enable investigating various HetNet performance scenarios using Bit Error Rate (BER) rather than SINR at each User Equipment (UE) [8] within the serving tier area of a BS and a candidate-serving BS. This drastic simplification greatly improves the field availability of various HetNet performance tests and, so far, has not been used in such an environment.

We will pursue BER analysis towards network spectral efficiency (SE) and EE. Concretely, instead of the classic hexagonal-grid based cellular network composition with a BS-centered each cell [9,10], we use stochastic geometry to capture randomness in network topology [9,10,11,12,13].

In this regard, the HetNet topology is modeled through the Poisson Point Process (PPP) [8], which describes a non-regular positioning of BSs in a real network, better than the classic hexagonal-grid model [9]. Although the PPP-based analysis of topology is not new [10,11,14], it was not long ago when the PPP-distributed BSs were introduced in various HetNets [12,15,16,17,18] and MIMO-inclusive network scenarios [19].

In Section 2, we firstly provide a short basic theoretical review, specifically considering the performance limits and related trade-off between SE and EE. The short-term BER-, SE-, and EE-based analytical model is presented as applicable for large HetNets with serving and candidate-serving BSs that have random distribution in the actual serving tier area. Finally, the analytical model is verified in Section 3, by presenting the test results obtained using an ns3 simulation tool that provided the short-term BER values for all UEs of the network under test. Conclusions are summarized in Section 4.

2. Analysis

Complex relationship between SE and EE of multiuser radio networks is determined by compromising the involved throughput, overall system energy, frequency resources distribution, traffic flow patterns, acceptable erroneous protocol data unit rates, and achieved vs. target QoS level.

Generally, the SE of wireless communication networks is the ratio of the data rate R [b/s] to the bandwidth B [Hz] that is needed to achieve R [13].

Moreover, the radio channel EE [b/J] is the ratio of bit energy E_b to the noise spectral density N₀, i.e., EE expresses the count of information bits per energy unit.

So, the Shannon formula for radio channel capacity C [b/s], originally depending on channel bandwidth B and mean power P_s, can be expressed by SE and EE as follows [13]:

$$C=B·lo{g}_2\left(1+\frac{P_s}{P_N}\right)=B·lo{g}_2\left(1+\frac{E_b}{N_0}·\frac{R}{B}\right)=B·lo{g}_2\left(1+SE·EE\right)$$

(1)

Specifically, for the case of the Additive White Gaussian Noise (AWGN) channel, having given P_s and B, where we consider EE as the ratio C/B, (1) implies that:

$$SE={\log }_2\left(1+SE·EE\right)$$

(2)

Thus, we can explicitly express EE as a function of SE:

$$EE=\frac{2^{SE}-1}{SE}$$

(3)

In the simplest case of a single-BS and a single-UE wireless network, Equation (3) enables the analysis of the SE vs. EE relationship in linear and non-linear power and energy regions, thus aiming to enable considerably enlargements of throughput and data rate [13].

From these considerations, it is obvious that increasing the data rate requires a significantly larger power of the received signal. This implies BS-to-UE distances of the order of several times 10 m, but still in the linear region that tolerates considerably larger values (at the price of smaller SE, due to EE reduction by propagation impairments).

In the non-linear region of (3), however, a considerably larger EE can be achieved, as stronger received signals enable lower cell dimensions down to 10 m, with the variety of cell classes comprising micro-, nano-, pico-, and femtocells. These enable statistical distribution of EE that is close to the uniform one, with significantly larger SE, and, thus, the throughput and rationally distributed coverage still have good enough EE (even in such areas crowded with active users) and considerably lower electromagnetic radiation [13].

So far, the HetNet’s overall efficiency was analyzed by considering both SE and EE and determining the SINR for each UE within the k-tier of HetNet having N_T tiers overall.

Each tier (e.g., k-th) is modeled by a homogeneous PPP Φ_k, with the transmit power of P_k, BSs density of λ_k, and the SINR threshold of τ_k (often referenced as “bias”) at UE, respectively.

2.1. BER-Based SINR Estimation by AWGN Abstraction of Radio Interference

Degraded SINR usually implies constellation symbol errors, and, thereby, SINR is often tested, which requires complex equipment to measure the noise and inter-symbol interference (ISI) [20]. Instead, estimating BER can be an alternative, i.e., an easy-to-measure performance trade-off “currency”, rather than SINR (where, by “easiness”, we consider the possibility to estimate BER in-service, simply by counting the retransmissions at the physical/MAC layer [21] with a count that determines the Block Error ratio (BLER). Then, an appropriate model can be applied to estimate BER from BLER [20].

This could be useful in practice encompassing the various phases of product-related research, development, manufacturing, and, finally, exploitation of a product in the LTE and 5G New Radio Environment.

Note the classical expression for BER determined by the Signal-to-Noise Ratio (SNR), for the M-QAM signal transmission over the AWGN channel [22]:

$$BER=\frac{4}{{\log }_{2}M}\cdot Q\left(\sqrt{\frac{3\cdot SNR}{M-1}}\right)$$

(4)

where Q(·) stands for the Gaussian tail function, represented by the “waterfall”—steep curves in Figure 1, which visualize the threshold effect that is immanent to digital radio receivers.

Specifically, in very small cells, it is quite justifiable to presume strong received signals (i.e., high SNR), as well as that the base-band inter-symbol interference (ISI) due to channel time dispersion, is, usually, to the large extent, eliminated by a (long-enough) standard cyclic prefix (CP) [20], though some (mostly equipment-related) non-AWGN impairments can still remain.

Furthermore, it is also fairly justifiable to consider radio interference a dominant impairment, which itself (being a sum of enough many mutually independent RF interfering signals and according to the Central Limit Theorem) can be reliably considered a Gaussian random variable.

In this case, SINR practically reduces to SNR, so Equation (4) implies that:

$$SINR\approx SNR=\frac{M-1}{3}{\left[Q^{-1}\left(\frac{BER\cdot {\log }_{2}M}{4}\right)\right]}^2$$

(5)

where $Q^{-1}$(·) denotes the inverse function of the Gaussian tail.

Applying link abstraction, any distortion, be it additive Gaussian or not, can be considered equivalent to that much additive Gaussian noise that would result with equal BER degradation, i.e., shift the BER(SNR) curves to the right for the adequate SNR degradation. This is shown in Figure 2, as the non-AWGN degradation of the 16 QAM modulation symbols (visible on the part of the constellation on the left) is modeled by the carrier-to-noise (C/N) degradation for the same BER value.

As an illustrative example, let us derive a simplified model of radio interference by superposing a narrow-band interfering signal (such as, e.g., dominantly from an adjacent channel) to the information-carrying one, thus reducing the effective noise margin, as shown in Figure 3.

As reducing noise margin implies increased probability of a symbol error, let us consider the probability of the in-phase signal overpassing a single decision boundary.

In Figure 4, it can be seen that the effective (now reduced) noise margin, equal to d–I cosθ, where I denotes the interfering signal amplitude, with the phase θ taking any value, uniformly distributed between 0 and 2π.

As the noise margin is normalized to the noise effective value σ, the probability of in-phase signal overpassing a single decision boundary is:

$$P(e)=Q\left(\frac{d-I\cos \vartheta }{\sigma }\right)$$

(6)

where Q(·) can be developed by expressing the phase θ as the multiple of n arbitrarily small intervals Δθ, obtained by dividing 2π into N equal parts:

$$\vartheta =\left(n-\frac{1}{2}\right)\cdot \Delta \vartheta ;\begin{array}{c}\end{array}\Delta \vartheta =\frac{2\mathsf{\pi }}{N}$$

(7)

Furthermore, we consider that for enough large N, Q(·) does not vary significantly within any Δθ, so by substituting Equation (7) into Equation (6) we can approximate the latter by:

$$P(e)\approx \frac{1}{N}\cdot {\displaystyle \sum _{n=1}^{N}Q\left[\frac{d-I\cos \left(2\mathsf{\pi }\cdot \frac{n-1/2}{N}\right)}{\sigma }\right]}$$

(8)

where I and σ are expressed by their related ratios S/I and SNR, respectively:

$$I=\sqrt{2}d\cdot {10}^{\frac{-\left(S/I-K\right)}{20}}$$

(9)

$$\sigma =d\cdot {10}^{\frac{-\left(SNR-K\right)}{20}}$$

(10)

while the factor K (expressed in dB units) relates the signal power to the relevant modulation scheme (so, e.g., for QPSK it is K = 0 and for 16 QAM it is K = 10 log 5 = 6.99).

Besides, in front of the sum in Equation (8), weighting factors are to be inserted reflecting the average number of possible transitions over the symbol boundaries, in a particular modulation of interest. For example, for the in-phase component and 16 QAM modulation, there are two boundaries for the inner symbols and a single one for the outer symbols. This implies that K= 1.5, whereas for 4 QAM and 64 QAM, K equals 2 and 1.75, respectively.

Graphical presentation of Equation (8) for 16 QAM is shown in Figure 5, where adequate trade-off between the non-AWGN radio interference and the AWGN, represented by S/I and SNR, respectively, can be identified to determine the goodness of abstracting a non-AWGN distortion by equivalent AWGN producing the same BER degradation.

Specifically, moving to the right along the red horizontal line of constant BER = 10⁻² from the middle curve for S/I = 30 dB, to the line crossing with the utmost right curve for S/I = 20 dB (i.e., increasing the interference for 10 dB), is tracked by almost equal increase in the SNR value.

Moreover, if this quite balanced trade-off between S/I and SNR is evident even for the simple non-AWGN interfering signal of the AWGN modeled above, then we can justifiably expect even more conformance if, instead of the narrowband radio interference, we deal with an almost-AWGN interference (as a sum of a number of mutually independent interferers), which we consider here as the real AWGN.

On the other hand, for certain interference (characterized by certain S/I ratio) and at any SNR point of its corresponding BER curve, the equivalent interference—free SNR can be obtained by drawing a vertical line (the turquoise one in Figure 5) down to the crossing with the curve with S/I = ∞ (representing the no-interference case).

So, e.g., the (middle) curve in Figure 5, representing the non-AWGN interference (with S/I = 30 dB) and having BER = 10⁻² at S/N = 20 dB, can be AWGN-abstracted by the utmost left AWGN curve (with S/I = ∞), if we consider BER degradation from 2 + 10⁻⁴ to 10⁻², upwards the vertical turquoise line.

Consequently, Equations (1)–(3), i.e., the simple SE vs. EE relationship, continue to apply for the AWGN-abstracted non-AWGN radio interference, and SINR can be approximated by the AWGN-equivalent SNR, which can be estimated from easy-to-measure BER.

2.2. Spectral and Energy Efficiency Model

The tiers are sorted in ascending order according to the access points’ density: λ₁ ≤ λ₂ … λ_k−1 ≤ λ_k. For a certain λ_k, the count of tier k_i (i = 1,2,…,N_T) access points within the covered area $\mathcal{A}$ [m²] is a Poisson random variable with mean value of $\mathcal{A}·{\lambda }_k$, being independent of other tiers. Furthermore, all k-tier access points transmit with power P_k.

Each downlink is modeled by Rayleigh fading channel, with the BS-transmitted power $P_i^{tx}$ and the UE-received power $P_i^{rx}$ at R_i distance from BS.

In this model, we have chosen the path-loss exponent to be equal to 4 [2], while macro BSs do not transmit during the Almost Blank Subframes (ABS) [3].

For each tier, we consider the frequency reuse factor of unity, and the RF band of one channel skipped between the two same-standard tiers, which implies that for a particular UE being connected to tier k, all of the interfering BSs are within that tier (k), with the exception of the serving one.

In the considered scenario, each UE is granted access only to the specific BSs in tiers 1, 2, …, K_open from Open Access (OA) macro-/femtocells, while the Closed Subscriber Group (CSG) femtocells normally do not provide service to the considered users [8]. So, a certain HetNet is represented by the counts of tiers: N_T = 3 and OA tiers: N_open = 2, respectively, where tier 1, tier 2, and tier 3 represent the macro cells, the OA femtocells, and the CSG femtocells, respectively.

Moreover, we presume the maximal allowed BS-transmitted power (for the actual tier).

Now, let us analyze the above-explored relation of the network SE to the total power, so that the distribution of BSs within each tier follows the PPP model.

In addition, we suppose that any particular BS b_k of a serving tier k_i transmits only the users’ subset U_b served by b_k ∈ Φ_k.

Now, consider the SINR $\Gamma \left(u_b\right)$ for the specific user u_b ∊ U_b, expressed by BER, according to Equation (5). Then, the spectral efficiency SE_k of the link from b_k to any target u_b is:

$$S{E}_k=\mathrm{E}\left\{{\log }_2\cdot \left[1+\Gamma (u_b)\right]\right\}\approx \mathrm{E}\left\{{\log }_2\cdot \left[1+\frac{M-1}{3}\cdot \left(Q^{-1}{\left(\frac{BER\cdot {\log }_{2}M}{4}\right)}^2\right)\right]\right\}$$

(11)

$$b\in \mathsf{\Phi }, P\left\{U_b=u_b\right\}=\frac{1}{\left|U_b\right|},u_b\in U_b$$

The analytical model derived here presents the spectral efficiencies SE_k and SE_TOT for individual tiers (k = 1…N_T) and for the whole HetNet, respectively. Furthermore, the selection of serving or candidate-serving cells according to the LTE-A standard is mostly centered around the picocell BSs range extension that enables traffic load balancing, preventing inter-cell radio interference in those areas with evident or expected signal overlapping coverage [13]. The mean levels of the UE-received pilot, originating by the candidate-serving macro and pico BSs, were used for selecting the optimal small-cell tier, which is to serve a particular UE, following two schemes:

Firstly, we consider the macro tier i to be the serving tier, and the pico tier j to be the candidate-serving tier, otherwise it is the pico tier j to serve the UE, whereas the macro tier i is the candidate-serving tier [8].

In the following, with R_i and R_j, we denoted the distances of the UE to the candidate-serving (i.e., the nearest) macro BS and the femto BS, respectively. As we plan to simply model the HetNet SE, we adopt that the power of the instantaneous transmitted signal of any macro BS is considered a random variable close to zero during the ABS state or to $P_1^{\mathrm{tx}}$ otherwise. Furthermore, we denote the instantaneous transmit power of the serving BS by $P_2^{\mathrm{tx}}$.

Firstly, we adopt that a certain UE of an arbitrary location is being served by the micro tier i, with a SINR Γ_i that is greater than the threshold γ with the probability ${\mathcal{P}}_i$.

Secondly, we consider that a certain UE is being served by the micro tier i, whereas ${\mathcal{P}}_j$ is the probability of the UE being served by the pico tier with appropriate SINR.

Thereby, from Equations (1) and (2), SE_i and SE_j can be found from:

$${\mathcal{P}}_i=\mathcal{P}\left\{{\Gamma }_i>\gamma \parallel {\mathcal{R}}_i=r_i,{\mathcal{R}}_j=r_j\right\}$$

(12)

$${\mathcal{P}}_j=\mathcal{P}\left\{{\Gamma }_j>\gamma \parallel {\mathcal{R}}_i=r_i,{\mathcal{R}}_j=r_j\right\}$$

(13)

Integrating the (exponential) probability density functions of distances between the UE and the serving tier i, as well as from the candidate-serving tier j, provides $S{E}_i$, and $S{E}_i$, and, finally, the overall HetNet spectral efficiency, as follows:

$$S{E}_{\mathrm{TOT}}=S{E}_i+S{E}_j$$

(14)

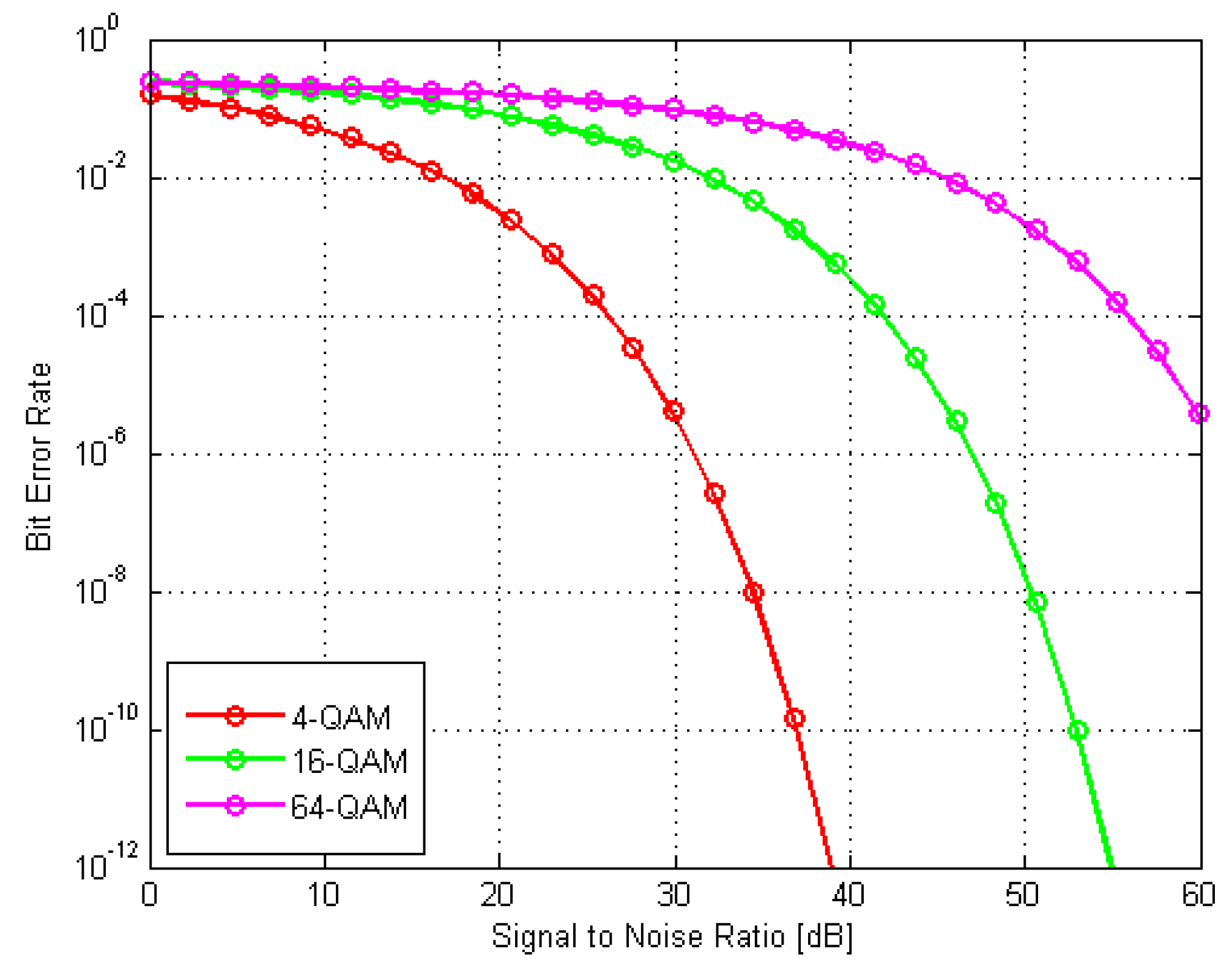
3. Test Results

The above presented analytical model is implemented in software by using an ns3 network simulator. The goal of the preliminary tests’ results is just the verification of the presented concept, whereas the comprehensive follow-up tests can be repeated as many times as needed. Five rounds of according simulations were made, with the BER results, in particular, enhanced by statistical data averaging. Both “native” SINR and the BER-based one were estimated by simulation.

The three considered scenarios were tested, with the following parameters each:

-

single-tier, 5 macro BSs, BS power: 40 W;

-

single-tier 250 pico BSs, BS power: 0.25 W;

-

two-tier 5 macro and 250 pico BSs.

The set-up data for the simulation are presented in

Table 1. Parameters in ns3 simulations.

Parameter	Value
Maximal size (L) of LTE code-block	6144 Bytes
Count of macro cell BSs	5
Maximal output transmit power of macro-cell BS	40 W
Maximal output transmit power of small-cell BS	250 mW
Count of small-cell BSs	250
Population density per m2	3.8·10−4
Maximal distance between BSs in macro cell	500 m
Maximal distance between BSs in small cell	50 m
Count of resource blocks with LTE 5 MHz channel bandwidth	25
Center of frequency operating band	2.1 GHz
LTE channel bandwidth	5 MHz

.

The obtained simulation results for BER, SINR, SE, and EE are presented in

Table 2. Simulation results (after averaging).

BER	SINR	SE [b/s/Hz]	EE [b/J]
0.0378	11.98	17.28	0.53
0.0550	11.06	15.96	1.04
0.0659	10.55	15.22	1.65
0.0813	9.86	14.22	3.09
0.0921	9.45	13.63	4.45
0.0996	9.16	13.22	5.75

, giving rise to the SE graphs presented in Figure 6 as a function of the instantaneous transmit powers $P_1^{\mathrm{tx}}$ and $P_2^{\mathrm{tx}}$ ratio for the various exemplar scenarios considered here.

Coming out of the presented curves, it is evident that the SE of the entire HetNet of interest grows exponentially with the transmit power ratio, when small cells are implemented surrounding a typical macro cell.

However, it is quite different when a single macro tier is to be considered, where the SE is not affected by the transmitting power ratio. Therefore, more picocells in the network necessarily imply higher spectral efficiency, which complies to the expected values coming out of the proposed analytical model.

Accordingly, the diagrams in Figure 7a,b represent SE and EE, respectively, resulting from simulations of the three above-reviewed scenarios and parameters’ values in Table 1.

In both the above diagrams, it can be seen that the two-tier setup scenario yielded the top efficiencies.

Furthermore, the small-cell scenario (250 pico BSs) came out to be more efficient than what was achieved with macro cells (5 BSs), while still with an unchanged users’ layout and count.

Finally, considering various transmit power values within the pico tier with constant macro-tier transmit power, SE exhibits a rising trend with regard to the transmit powers.

4. Conclusions

Instead of SINR, we proposed the simpler-to-measure BER as the key performance indicator, by abstracting the performance degradation due to various (generally non-AWGN) impairments, by the according AWGN ones, which have the same effect on BER as any specific distortion.

It emerged that inserting small cells into HetNets of any distribution of BSs significantly improved both the energy and spectral efficiency. So, with smaller distances in between the BSs and UEs of contemporary networks—e.g., LTE and LTE-A, the trend is the rationalization and optimization of the signal coverage, by reinforcing it in the areas of increased traffic.

Such a strategy seems to be appropriate in the tested exemplar environments, but it needs to be enhanced and fine-tuned with other sophisticated tests, taking into account other impairments, e.g., RF interference, traffic patterns, bandwidth and channel allocation, etc., with management that is aimed to enable the projected QoS level, complexity reduction, and fair distribution.

This work was aimed at analyzing and verifying the simplifyied real-life HetNet performance testing, by focusing the BER rather than analog values such as SINR. This paves the way for the following R&D and field tests, while also taking into account various design and deployment issues, by using sophisticated test hardware and dedicated software simulation tools.