Abstract
Generating dynamic operators are constructed here from the cumulative case function to recover all state dynamics of a Susceptible–Exposed–Infectious–Recovered (SEIR) model for COVID-19 transmission. In this study, recorded and unrecorded EIRs and a time-dependent infection rate are taken into account to accommodate immeasurable control and intervention processes. Generating dynamic operators are built and implemented on the cumulative cases. All infection processes, which are hidden in this cumulative function, can be recovered entirely by implementing the generating operators. Direct implementation of the operators on the cumulative function gives all recorded state dynamics. Further, the unrecorded daily infection rate is estimated from the ratio between IFR and CFR. The remaining dynamics of unrecorded states are directly obtained from the generating operators. The simulations are conducted using infection data provided by Worldometers from ten selected countries. It is shown that the higher number of daily PCR tests contributed directly to reducing the effective reproduction ratio. The simulations of all state dynamics, infection rates, and effective reproduction ratios for several countries in the first and second waves of transmissions are presented. This method directly measures daily transmission indicators, which can be effectively used for the day-to-day control of the epidemic.
1. Introduction
The COVID-19 pandemic is an ongoing global disease caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). The virus was reported to be first identified in December 2019 in Wuhan, China [1]. It was suspected that the original infection came from animals in the Wuhan Animal Market [2]. The number of cases grew exponentially, with more evidence of newly infected people who had never been visiting the market. This fact provided evidence that human-to-human transmission was the primary source of the fast transmission [3]. Immediately, the cases spread throughout all provinces in the country and even passed the borders through the neighboring countries. At the end of January 2020, the government of Wuhan imposed a total lockdown, preventing people from entering and leaving the city of Wuhan. The strict lockdown was also extended in response to the rapid spread of the virus [4].
Effort to predict the progress of COVID-19 transmission was made using the early data to obtain insight into infection characteristics. Zhang et al. used the stochastic model of the SEIR (Susceptible–Exposed–Infected–Recovery) model and provided the forecasts on the number of cases in several provinces in China, i.e., Shanghai, Beijing, Guangdong, Zhejiang, Chongqing, and Hunan using [5]. It was estimated that the virus transmission would be significantly disappearing in those regions in March 2020. The compartmental model-based predictions on COVID-19 figures were also conducted by Bertozzi et al. [6], who used the generic SIR (Susceptible–Infected–Recovery) model. They studied the COVID-19 spread in California and predicted the end of the first outbreak in August 2020. Not limited to that, other work utilized the Richard’s Curve to yield the extrapolated figure of the infection trajectories. The work conducted by Nuraini et al. predicted that the spread would reach the peak in late March 2020 and soon decrease significantly until totally vanishing in April 2020 [7].
Learning from the experience of many countries during the first wave of transmission, the detection of infected persons was a crucial aspect. The availability of a sufficient amount of diagnostic tests was necessary. In the early phase of the pandemic, many developing countries were struggling to provide the proper amount of specimens to detect COVID-19. During the first wave transmission, as a non-manufacturer of Polymerase Chain Reaction (PCR) Reagents for real-time COVID-19 detection and due to the limitations of world supply, health authorities in Indonesia could not fulfill the daily PCR testing target as was recommended by the WHO ([8,9]). The lack of testing capacity certainly implies the low recorded cases as compared to total infections. Consequently, as many countries were already able to contain the disease within two months, other countries, including Indonesia, were still facing the outbreaks for a more extended period.
The complication of COVID-19 transmission is mainly related to the inability of the authorities to record all infected people and people’s behavior toward the disease. It is a challenge for epidemiologists to construct simple models that can accommodate the most important phenomena. Compartmental models are very widely used in the construction of the disease transmission [10]. The simplest compartmental model for direct transmission is known as the SIR model, which contains susceptible (S), infectious (I), and recovered (R) compartments. Ross already applied this model in the early 20th century [11]. SIR-type models for COVID-19 transmission were used extensively in the early phase of the pandemic. Typical observations in the early transmission focused on predicting the outbreak’s peak and the disappearance of the disease by exploiting the daily COVID-19 data. Yang et al. predicted the epidemic’s future using the modified SEIR model linked with artificial intelligence. For daily progress, Susanto et al. estimated the effective reproduction ratio using the transmission data in Italy [12]. We have constructed, in Section 2, the basic formulation of the generating operators for the simple SEIR dynamics, which are then generalized to accommodate both recorded and unrecorded cases, as given in Section 3. Using the cumulative infections data provided by Worldometers, the simulations are conducted for country comparisons, i.e., Brazil, China, Germany, India, Indonesia, Islamic Republic of Iran, Italy, Japan, Republic of Korea, and Singapore.
2. Generating Operator in a Simple SEIR Model
During the early transmission of COVID-19, there was pressure in each affecting country to measure the daily reproduction ratio and predict the time when the outbreak was slowing and disappearing. With limited data and information, the simple SEIR model was used extensively. We formulate the concept of a generating operator to extract all states, which was first introduced in [13].
2.1. Model Formulation
We start the SEIR transmission model of COVID-19 with susceptible compartment S, exposed compartment under incubation period E, infected and infectious compartment I, and recovered compartment R. The overall process of infections is shown in Figure 1.
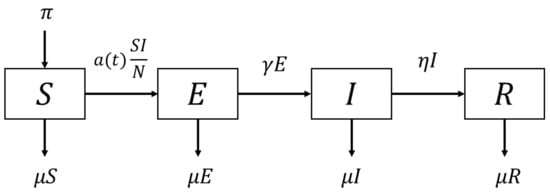
Figure 1.
Flow diagram of the simple SEIR model.
The governing equations of the simple SEIR model are formulated as:
where the parameters , , , , are the recruitment rate, the natural death rate, the inverse of the incubation period, and the inverse of the recovery period, respectively. The infection rate is given as a time-dependent parameter to accommodate the intervention process, which is not measurable in the field. In this model, the total population is assumed constant, i.e., . When it comes to the interaction process, we assume that the population is well-mixed, which can be physically analogous to ‘well-stirred’ individuals that force infected and susceptible to all-to-all interaction at all times. This assumption simplifies the mathematics evolutionary processes, which makes the analytical solutions possible [14].
Note that those being labeled with ‘estimated’ in Table 1 will be evaluated using the generating operator, while the others will be adjusted to specific regions. The transition rate exists in the generalized model, the values of which will be further explained in the next section.
In the case of constant infection rate , the basic reproduction ratio , representing the average number of secondary infections caused by one infected person in the early pandemic [19], is given as
As time evolves, the basic reproduction ratio is no longer appropriate to measure the progress of the transmission. The corresponding effective reproduction ratio, denoted with , is intended for tracking in the progress of transmission, which is given as:
The effective reproduction ratio is basically a basic reproduction ratio but with the time-dependent transmission rate and additional term of . This formula is obtained by implementing the NGM method without substituting the Disease Free Equilibrium [12].
In the following subsection, the state generating operator and a method for estimating the transmission rate will be constructed. This construction gives a more adaptable estimate to track the progress of transmission involving intervention in the field.
2.2. Cumulative Case Data for Constructing the Generating Operator
The inability of the timely and accurate collection of COVID-19 data in daily case reports occurs in many countries. Discrepancies of confirmed official COVID-19 data were reported from many countries, such as Bangladesh [20], India [21], and the USA ([22,23]). The quality of the COVID-19 data certainly contributes to the consistency of the model and the accuracy of prediction.
The fluctuation of the daily cases also contributes to the prediction bias due to errors in data fitting. The choice of cumulative data for generating strategic indicators is mainly due to the smooth profile of the data to allow accurate fitting. Detail transmission behavior is kept within the cumulative case data, which can be recovered by identifying the proper generating operator. The S-curve shape of the cumulative data is best fitted with (one of them) Richard’s curve.
We start with data fitting of cumulative cases using the Generalized Linear Growth Model (GLGM), widely known as Richard’s Curve ([24,25]). The model comprises four parameters, denoted by . The value of acts as the final epidemic size, with , whereas represents the intrinsic growth rate. The higher this value, the steeper the curve at the early outbreak. The other two values are and , which both act as the adjuster. While the former adjusts the lag phase of the curve, the latter is strongly related to the adjustment of the initial value at [26]. The general form of Richard’s Curve is given by Equation (4) as follows:
All the parameters that exist in the explicit formula of Richard’s Curve are extracted by applying the optimization scheme to obtain the minimum deviation between the data and the fitted formula . The optimization problem on parameter estimation can be written as
where is the search domain of the parameters and N represents the length of cumulative data.
The construction of the generating operator starts with the definition of the additional compartment , representing the cumulative cases at time t, which is given as follows.
Take the first derivative of K, then we have
Solving for , then we have
From the result above, we can express as a function of as follows
Further, by taking the derivative of , the we obtain the daily new exposed
Let depicting the dynamics of active infections and total recovery simultaneously. Thus, the third and fourth equation in system (1) can be rewritten as:
where With initial value , the solution of a system can be obtained by applied the integration factor.
Then, we have the solution for and as follows
where and is given by the data of initial active cases and total recovery. Substituting Equation (13) to Equation (14), the -related formula of is given by
Assuming that the number of population, N, is constant, we have the dynamics of susceptible individuals written as follows.
Now, consider an equation of E in (1). We can find by manipulating the equation. We have that
where S and I can be written as Equations (13) and (16), respectively. By that, the estimation of all states, as well as the transmission rate, can be generated using the information of cumulative infections. Summarizing the above construction, we formulate the generating operator
for the SEIR dynamics is given as follows
where
and A is given in (31). Hence, we have
Figure 2 this illustrates the flow of how this dynamics generator works on the estimation of all state dynamics, including the time-dependent rate of transmission by means of the empirical fit to Richard’s Curve.
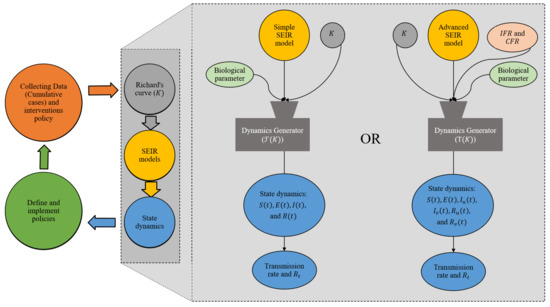
Figure 2.
Diagram of the approach for estimating all state dynamics of the SEIR models using the dynamics generator.
3. Generalized SEIR for Second Wave Transmission of COVID-19
Many countries suffered badly during the second wave of COVID-19, which came unexpectedly after the period of relaxation at the end of the first wave ([27,28,29]). The phenomena of hospitals filling up, beds becoming scarce, and death rates exploding became constant daily news. Most countries implemented massive PCR testing as recommended by the WHO to isolate the positive cases in the population. Naturally, the simple SEIR model will not be realistic in representing the transmission.
3.1. Model Construction
We generalize the model (1) to accommodate for the intervention effect of COVID-19. The consequence of the COVID-19 testing capacity is also taken into account by distinguishing the recorded and unrecorded infections. It is assumed that the recorded infected people will have the self-awareness to lessen the contact with others than those who are not recorded. The mathematical model of the advanced SEIR is given as follows
with the assumption of the constant total population, we have
and .
The two compartments I and R are split into two, with indexes n and s, which stand for unrecorded and recorded (and isolated for treatment), respectively. In the previous assumptions, people in the compartment do not have a chance to infect the susceptible individuals due to the isolation and hospitalization. In addition, people in the can cause infections by making contact with people in the S compartment. Depicted in Figure 3, people will be either identified as an unrecorded or recorded infected person once they leave the E compartment. Infected individuals will recover after a period of time and become immune to the virus. No difference is assumed in the infection period, which implies the same value for the recovery rate for both recorded and unrecorded infections. More details about the parameters of the generalized model are given in Table 1.
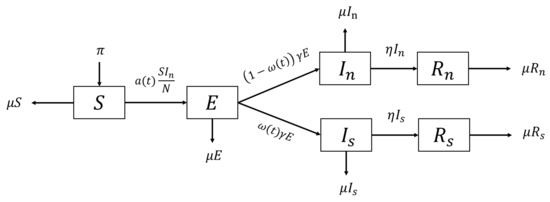
Figure 3.
Flow diagram of the generalized SEIR Model.
In the case of constant infection rate and transition rate , we have the formulation of basic reproduction number given, as follows
for zero transition rate, , reduces to . Following the same derivation in the previous section, we construct the effective reproduction ratio
Following the similar construction in Section 2, we define a new cumulative compartment as in (6)
from the first derivative of K,
we obtain the daily new recorded cases , in the form
Let depict the dynamics of active infections and total recovery simultaneously. Thus, the fourth and sixth equations in system (24) can be rewritten as
where With the initial value , the solution of a system can be obtained by applying the integration factor as follows
The explicit form of , , , and can be given as:
and
and
Assuming the number of population, N, is constant, then
from the first equation of S in (24), we can find
with S and given as in the previous derivation.
Summarizing from the above derivation, we generalize the construction (18)
with for the generalized SEIR dynamics as follows
where
and A is given in (31). The five states , and are produced by these operators as follows
3.2. Estimation of
Referring to Figure 3, new infections are separated into recorded and unrecorded cases. While the former will be immediately quarantined and treated and hence unable to infect susceptible individuals, the latter remains unidentified and then will spread the virus. From the daily new infected persons, , the portion is recorded through testing, which will enter the compartment. The rest of the portion, will remain unrecorded and enter the unrecorded . By that, , depicts the share of the recorded newly infected population against its total. This parameter represents the ability of the “random” selection of the test target to capture the positive cases.
The capacity of some countries to cover all infections is strongly related to their ability to provide the testing kits [30]. In the early pandemic, many countries struggled to fulfill the demand for COVID-19 testing kits, resulting in the low value of . Nevertheless, in early 2021, several countries were able to conduct more massive daily testings [31], making the figure of testing capacity change dramatically. In response, it is reasonable to set the value of to vary over time (time-dependent) and hence denoted with . The dynamics of will be estimated using the Infection Fatality Ratio (IFR) and Case Fatality Ratio (CFR).
In epidemiology, a CFR is the proportion of deaths from a certain disease compared to the total number of people diagnosed/confirmed with the disease for a particular period [32]. Similarly, the IFR also applies to infectious disease transmission to represent the proportion of deaths among all infected individuals, including all recorded and unrecorded subjects [33]. This quantity is closely related to the CFR but with additional accounts for unapparent infections among healthy people. The observed CFR in time t is defined by the total number of deaths, , divided by the total number of confirmed cases at time t, , i.e., , whereas the IFR is defined based on the total number of infections. Formally, , where and denote the median of total deaths and estimated total infections considered from the early pandemic until a certain specified time. The will be estimated by involving the data of total tests. The total number of infections is estimated by assuming that each person is only tested once, and the distribution of infections among the entire population is equal. The total infections, , for each country follow the definition introduced in [34], which is defined by dividing the total confirmed cases with the total tests conducted and multiplying it with its population size, i.e.,
where is the total tests performed until a certain specified time. Note that this method estimates the constant value of IFR. This argument should confirm that this parameter is a virus-related parameter, which assumes that no significant mutation affecting the virulence will lead to a constant value of IFR [35]. The estimated constant CFR for related diseases in some countries can be seen in [36].
Dividing the estimated IFR by the observed time-dependent CFR depicts the share of infected individuals that were recorded. By that, the time-dependent reporting rate is defined as follows
the value of IFR is always less than that of CFR, resulting in the values . The greater the value , the more the infectious persons were isolated.
4. Numerical Simulations
4.1. Simple SEIR Model
In this section, the numerical simulations for Model (1) that resulted from implementing the generating operator on the fitted cumulative function are shown. COVID-19 data are selected from ten countries representing different population sizes: Brazil, China, Germany, India, Indonesia, Islamic Republic of Iran, Italy, Japan, Singapore, and South Korea. The COVID-19 data are taken from the official website of Worldometer [37], consisting of the daily number of active cases and total recovery. The data were taken during the early transmission period ranges from late February until September 2021. In these simulations, only the first 60 days after the initial transmission will be used and analyzed. The interval for each country may vary depending on the initial transmission.
All biological parameters for the selected countries are chosen as the same. The natural death rate, denoted by , was assumed to be , referring to the average human life expectancy. As of December 2020, Our World in Data claimed that the life expectancy of humans was about 70 years [16]. The remaining biological parameters are listed in Table 1.
4.1.1. Fitted Cumulative Data
The simulation began by estimating the closest GLGM dynamics to the provided data. All the parameters were obtained by solving the optimization problem (5). The calculation was conducted numerically using the built-in function in MATLAB. Notice that the global minimizer is difficult to obtain using the numerical method. Thus, the initial guess was varied following the Sobol sequence in 4-D so that the result would be close to the global minimizer. The estimated parameters for the ten observed countries are given in Table 2. The second and third columns in the Table indicate the time interval of the data used in the calculation. The interval varies among all countries depending on the initial transmission of the virus. The last four columns provide the estimated for each country. These values depict the characteristics of the virus spread in each country and, hence, may differ from one country to another, though it was the same virus that spreads. For instance, the data fitting suggests that the value of for India is significantly higher compared to that for Indonesia. This result indicates that the spread of the virus in India is more significant compared to that in Indonesia. This fact can be seen in Figure 4, where the graph for India is much steeper than that for Indonesia.

Table 2.
Parameter estimation of the cumulative dynamics using GLGM and the early pandemic data.
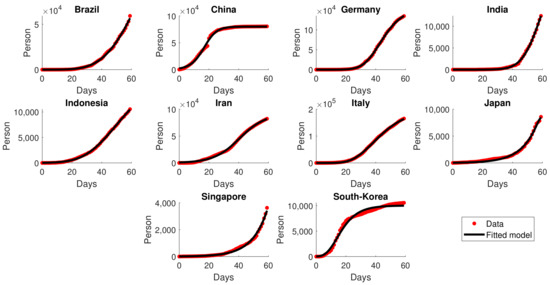
Figure 4.
Fitting results of cumulative data for several countries in the early pandemic. The red dots represent the actual data, and the solid black lines represent the fitted model .
Figure 4 illustrates the estimated models of cumulative infections together with the data for the first 60 days after the initial transmission. Overall, the general behavior of the data was well-fitted by the rendered S-curve Richard’s model. For instance, in China and South Korea, the cumulative infections started to ramp up rapidly in the early pandemic yet began to decline within the first 60 days of transmission, giving us the perfect S-curve models. The countries China, Germany, Iran, Italy, Japan, and South Korea underwent a sharp increase in transmission and start to bend down before the end of the 60-day period. For the rest of the countries, the total infections were stagnantly increasing and there was no sign of sloping down within the first 60 days.
With the direct substitution of on the right-hand side of (8), we obtain the estimate of the daily new cases . Figure 5 illustrates the estimation of daily new cases compared to the actual data for the ten observed countries. In general, the estimated dynamics resemble the real data of daily new cases. The model can also identify the peak time of the daily new cases.
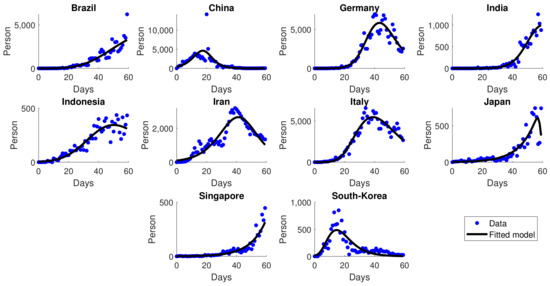
Figure 5.
Simulation results of daily new cases for several countries in the early pandemic. Blue dots represent the actual data, and the solid black lines represent the simulation.
4.1.2. Simulation of SEIR Dynamics
Simulation of E, I and R are obtained directly from substituting into and , respectively. For the ten observed countries, the dynamics of (Exposed–Infected–Recovery) are given in Figure 6, omitting the S compartment form visualization due to its scale problem.
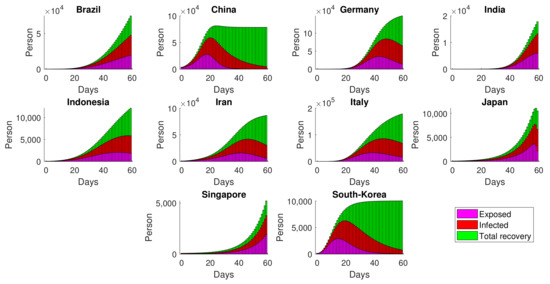
Figure 6.
Simulation of estimated SEIR in several countries by implementing the generating operator.
Given in Figure 6, the number of exposed cases dropped significantly in China and South Korea within the first 60 days, leaving no exposed cases in the late simulation. The success of the two countries in controlling the disease was the result of mobility restriction across the country [38], as well as the public participation in the implementation of COVID-19 protocols [39]. In other countries, such as Brazil and Singapore, the virus seems to not be rapidly spreading. However, the exposed cases gradually increased and had no sign of significant decrease within two months. Although Model (1) does not explicitly accommodate various interventions in the field, the time-dependent infection rate could represent the daily measure of infection due to the unmeasurable intervention and control.
4.1.3. Dynamics of the Effective Reproduction Number
The basic reproduction numbers of the observed countries are given in Table 3 using Equation (2). Since the basic reproduction number calculation only applies to the autonomous system, we drop the time dependency of the transmission rate. Thus, we use the average number of the 60-day transmission rate. In comparison, the time-dependent effective reproduction ratio is depicted in Figure 7 as a measure of the daily performance of virus transmission. It is shown in Figure 7 that, except for China and South Korea, other countries took much longer to reduce the effective reproduction ratio to below one.

Table 3.
Estimated basic reproduction number for the simple model.
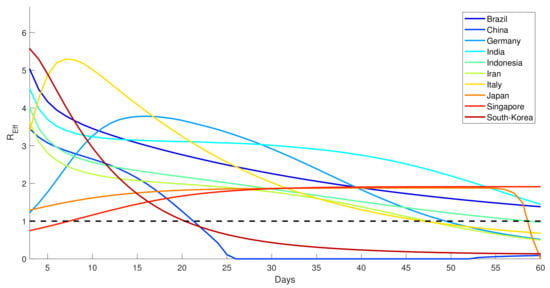
Figure 7.
Dynamics of the effective reproduction number () for several countries.
In general, the estimated models depict the behavior of the pandemic over time. Furthermore, the estimated parameters can be used to conduct the prediction of how the pandemic behaves in each country. The short-term prediction can be an option since parameters would change over time as the new data are retrieved. Moreover, extension beyond the period of observation could not be expected for the forecast [40].
4.2. Generalized SEIR Model
This section emphasizes the implementation of the operators described in Section 3 for the generalized SEIR model, which involves the recorded and unrecorded infections. The cumulative data were taken from [37] during the 60-day second wave period of transmission of each of the ten selected countries. The same parameters in Table 1 were used for simulations, and the values of were estimated using the information of and .
4.2.1. Fitted Cumulative Data
The same construction of cumulative dynamics using GLGM as performed in Section 2.2 is used for the second wave period. Table 4 shows the selected time interval for each country in which the second wave transmission is believed to occur, together with its estimated parameters for the GLGM. Given in Figure 8, the figures for cumulative infections were significantly increasing in the observed time intervals, which indicate the resurgence of the pandemic. In addition, it is shown that the rendered model fits the provided data well.

Table 4.
Parameter estimation of the cumulative dynamics using GLGM for the second transmission.
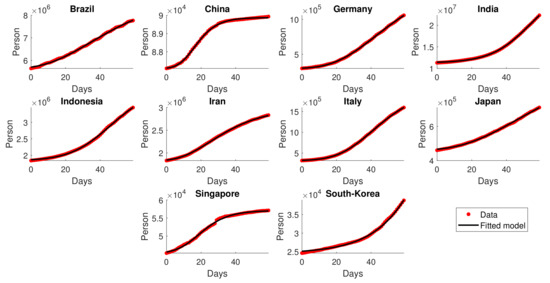
Figure 8.
Fitting results of cumulative data for the second wave transmission.
Figure 9 shows good agreement between the simulations and the data of daily new cases. All the depicted figures are considered to be the resurgence of cases after the first hit ends, e.g., China [41], Germany [42], Italy [43], and India [44].
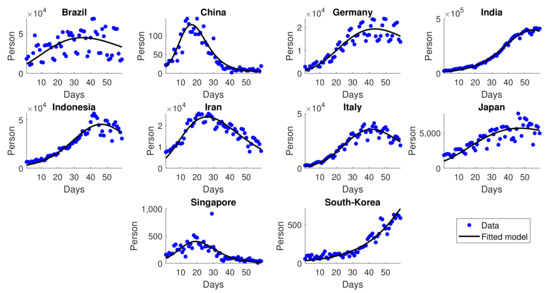
Figure 9.
Simulation results of daily new cases for the second wave transmission.
4.2.2. Estimated
The estimation of starts with the estimation of both and . As stated earlier in Section 3.2, the estimated value of is assumed to be constant over time, yet the depends on time. The observed time-dependent , which is defined as , is evaluated by utilizing the data retrieved from Worldometer [37]. On the other hand, the estimation of is obtained by first estimating the number of total infections using Equation (45), implementing the data of total tests performed by each country that is publicly provided by OurWorldinData [31].
Figure 10 shows the estimation of for the ten countries. Italy and Germany have higher values than other regions, while Singapore is considered the lowest. This result shows that even though the simple formula was claimed to underestimate the true [45], the general pattern for the observed ten countries resulted in consistent results [34].
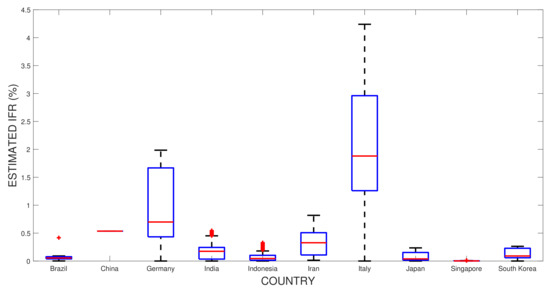
Figure 10.
Estimated for the ten observed countries. The blue boxes represents the range from the lower to upper quartiles, with the median (red line) was chosen to represent the single point estimated . The black add signs depicts its maximum and minimum values of the estimated IFR.
Utilizing the observed and estimated given in Figure 10, the dynamics of in each country’s time interval are evaluated by dividing the observed by the estimated . The dynamics of for each country are depicted in Figure 11.
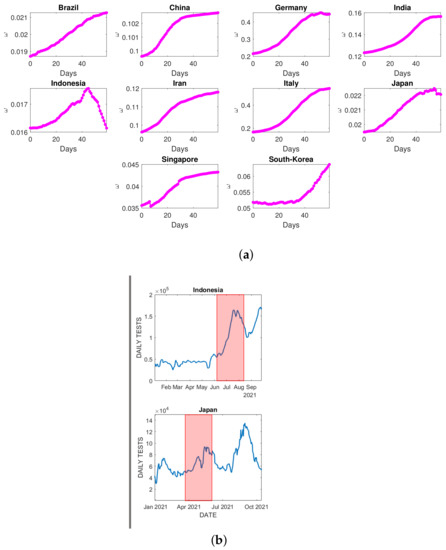
Figure 11.
(a) Dynamics of estimated , 60 days after the initial second wave emerged; (b) the daily test experienced a significant drop in Indonesia and Japan during the simulation interval (in the red-shaded area).
Overall, other than Indonesia and Japan, the share of those being reported against the total number of infections increased. According to ([46,47]), the number of deaths in Indonesia was rapidly increasing from April to May 2021, making the observed CFR increase as well [48]. Since the estimated IFR remains constant, the dynamics were significantly declining. The increasing CFR indicates that the total deaths increase more significantly than the total recorded infections. Assuming those total deaths are linearly dependent on the total infections, then the increasing CFR also indicates the number of total unapparent infected individuals. The unrecorded infections should be increasing once the daily test decreases. Indonesia experienced a significant decline in daily testing in August 2021, from about 160,000 to only 100,000 specimens a day, confirming the substantial drop in transition rate in this country. The same argument holds for explaining the slight decline in the transition rate for Japan in the late simulation. Figure 11a,b shows how the daily test in both countries experienced a significant decline in mid-August 2021 and May 2021, respectively. For the rest of the countries, the daily test delivered to the population is relatively increasing, making no significant increase in the unapparent infected individuals and decreasing the observed CFR.
4.2.3. Dynamics of the Generalized SEIR Model
Given the estimation of and the provided cumulative data, the number of exposed populations at time-t can be estimated by means of the generating operators for the advanced model, namely . In addition, the other unobservable compartments are obtained by implementing , resulting in an estimation of unrecorded active cases and the total recovered. The numerical simulation comparing the figures of infected people being recorded or not is depicted in Figure 12. In general, the number of unapparent cases is estimated to be way higher compared to that of being identified. These results are strongly related to the calculated values of for each country, which are identified as very low (around 10%), on average. On the other hand, the opposite results are found in Germany and Italy, which is a result of the relatively higher share of recorded infections.
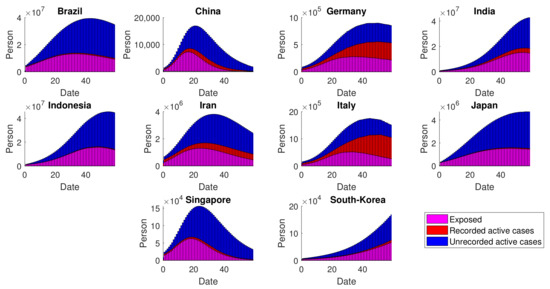
Figure 12.
Dynamics of exposed and infected individuals: both recorded and unrecorded cases. Some recorded cases may not be visible due to the higher figures of exposed and unrecorded infected individuals.
The performance of is related to the ratio between the recorded and unrecorded recovery. Figure 13 shows that other than China and Germany, the proportions of unrecorded recovery are much higher than the recorded recovery. This finding is consistent with the fact that the lower the values of for certain countries, the higher the share of unrecorded total recovery.
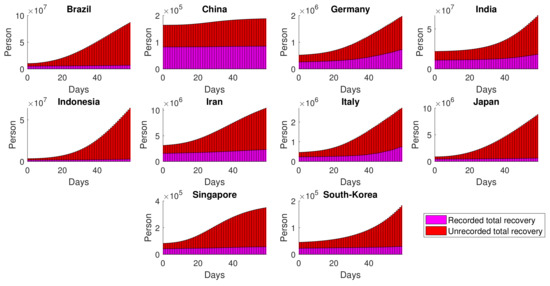
Figure 13.
Estimated dynamics of total recovery resulted from both recorded and unrecorded cases.
Finally, the estimated effective reproductive ratio is shown in Figure 14. It is shown that in the case of second-wave transmission, the effective reproductive ratios decreased to a level one much faster than those in the first-wave transmission. This evidence justifies that the role of massive testing played a significant role in controlling the transmission. Since early 2020, the evaluation of the effective reproductive ratio played a vital role in regulating proper interventions related to COVID-19. Germany, Italy and other European countries have been using the calculation of since the early pandemic [49], which was also followed by other countries such as Indonesia [50] and India [51].
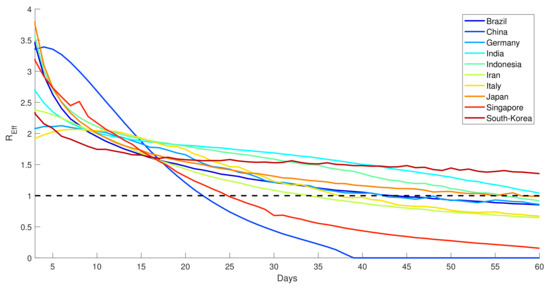
Figure 14.
Effective reproduction number of countries, 60 days from the initial second wave of COVID-19 first identified.
4.3. More about the Effective Reproduction Number
Specifically, in the second transmission, it is intriguing to learn how the countries’ intervention-related parameters, i.e., and , evolve over time. Depicted in Figure 15 is the countries’ profile situated in the contour plot, which is representing the effective reproduction number but omitting the term , i.e., . This formula is nothing but the effective reproduction number, which has not taken the dynamics of the susceptible populations into account. On day 1 of the second transmission, it is indicated that all countries experienced significant transmission of COVID-19 with a relatively low transition rate . As time evolved, all countries simultaneously moved to the left with lower reproduction numbers, and we ended up with five countries that were assigned with reproduction numbers higher than one at day 60. To be compared with that depicted in Figure 14, there were only two countries that had effective reproduction numbers higher than one at day 60. Since the reproduction numbers depicted in Figure 15 are omitting the role of , there are three countries that had a significant effect of susceptible population size on suppressing the effective reproduction number, i.e., Indonesia, Japan, and Brazil. In other words, the three mentioned countries have passed below one in regards to because of the significant deviation of compared to N. Since the dynamics of S at every time point are dependent on all other variables, this indicates that the unrecorded infections and recovery have had a significant effect on these countries. Acknowledging that these three are densely populated countries, the high estimated number of unrecorded infections and recovery has resulted in an of below one at day 60.
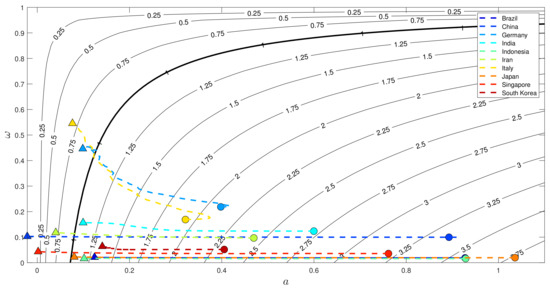
Figure 15.
Evolution of the reproduction number in the 60-day simulation of the second transmission. The solid black lines are the level sets of taken from (27) for constant and a. The evolution starts from circle-shaped graphs and ends with triangular-shaped graphs.
Lastly, the depiction of transmission given in Figure 15 also gives us insight into how countries handle the second wave. Germany and Italy are two European countries with high total tests. As time evolves, the snippets move to the left with a higher transition rate . On the 60th day, it is clear that these two countries are separated from the rest of the countries due to their high testing capacity. The snippets move to the left for China, Singapore, and Iran, with the transition rate leveling off. These results are expected to confirm the fact that the number of tests conducted was not high, but the large-scale intervention could be more effective [52]. The rest of the countries are dominated by the densely populated countries that were not really strict with lockdown and COVID-19 testing [53]. However, the fact that the estimated unrecorded infections and recovery are relatively high causes the to pass below one even though the transition rate remains low or the transmission rate remains high.
5. Conclusions
This study proposes a new approach to obtain the explicit solutions for each state’s dynamics in the SEIR models, or the so-called dynamics generator. There are three crucial components in the construction of the dynamics generator; cumulative data, Richard’s Curve, and the proposed compartmental models. The idea of this approach is to fit the cumulative empirical data to Richard’s Curve (K) and then define the relations between K and other state dynamics in the SEIR models. Using basic knowledge of linear algebra and calculus, the generator can be constructed to generate all state dynamics in terms of K. In other words, we have constructed a method that generates all state dynamics by means of the empirical data of cumulative cases. Cumulative recorded data was chosen due to its monotonic profile, which has the advantage of choosing a satisfactory fitted cumulative function.
In terms of the compartmental models, we have demonstrated the derivation of the dynamics generator for both simple and advanced models. The constructed dynamics generator produces all state dynamics of the SEIR model, including the figures of the hidden infections using the advanced model. One of the perks of using this approach is to also evaluate the time-dependent rate of transmission, which summarizes all individuals or governmental interventions.
Specifically for the advanced model, we estimated the rate of unrecorded cases using the Case Fatality Rate (CFR) and the estimated Infections Fatality Rate (IFR), which is constructed from the daily Polymerase Chain Reaction (PCR) test. The remaining unrecorded states are then generated directly from the dynamics generator. It is shown that the increase in the number of daily PCR tests significantly reduces the effective reproduction ratio and quickly lowers the ratio to a controllable level. This method gives an important indicator that could be used for daily control of the epidemic, even though it is hard to measure the effect of specific interventions such as mask covering.
Eventually, we have seen that the approach is well-used to generate all state dynamics of the SEIR models, given the cumulative data in a particular period that follows the general S-curve. Once the data does not follow the general S-curve, such as a double S-curved-like data, the standard Richard’s Curve will no longer be relevant. Hence, this study highlights room for improvement by considering other explicit functions other than Richard’s Curve that can be relevant for the non-S-curved empirical data.
Author Contributions
Conceptualization, E.S. and N.N.; methodology, E.S., K.K.S., A.L.L., M.V. and M.F.; software, K.K.S., A.L.L., M.V., R.K. and M.F.; validation, E.S., N.N., K.K.S. and M.F.; formal analysis, K.K.S., A.L.L. and M.V.; investigation, K.K.S., A.L.L. and M.V.; resources, E.S. and N.N.; data curation, K.K.S., A.L.L., M.V. and R.K.; writing—original draft preparation, K.K.S., A.L.L. and M.V.; writing—review and editing, E.S., M.F., R.K. and N.N.; visualization, K.K.S., A.L.L. and M.V.; supervision, E.S. and N.N.; project administration, E.S., N.N. and M.F.; funding acquisition, E.S. All authors have read and agreed to the published version of the manuscript.
Funding
Part of the research by E.S. is funded by the Indonesian RistekBrin Competitive Grant No. 120I/IT1.C02/TA.00/2021.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The initial data were openly accessible at: https://www.worldometers.info/coronavirus/#countries (accessed on 1 June 2021).
Conflicts of Interest
The authors declare there is no conflict of interest.
References
- Novel Coronavirus (2019-nCoV)—Situation Report 1. Available online: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200121-sitrep-1-2019-ncov.pdf (accessed on 5 April 2021).
- Andersen, K.G.; Rambaut, A.; Lipkin, W.I.; Holmes, E.C.; Garry, R.F. The proximal origin of SARS-CoV-2. Nat. Med. 2020, 26, 450–452. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef] [Green Version]
- Singhal, T. A review of coronavirus disease-2019 (COVID-19). Indian J. Pediatr. 2020, 87, 281–286. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; You, C.; Cai, Z.; Sun, J.; Hu, W.; Zhou, X.H. Prediction of the COVID-19 outbreak in China based on a new stochastic dynamic model. Sci. Rep. 2020, 10, 21522. [Google Scholar] [CrossRef]
- Bertozzi, A.; Franco, E.; Mohler, G.; Short, M.; Sledge, D. The challenges of modeling and forecasting the spread of COVID-19. Proc. Natl. Acad. Sci. USA 2020, 117, 16732–26738. [Google Scholar] [CrossRef]
- Nuraini, N.; Khairudin, K.; Apri, M. Modeling simulation of COVID-19 in Indonesia based on early endemic data. Commun. Biomath. Sci. 2020, 3, 1–8. [Google Scholar] [CrossRef]
- Sucahya, P.K. Barriers to COVID-19 RT-PCR Testing in Indonesia: A Health Policy Perspective. J. Indones. Health Policy Adm. 2020, 5, 36–42. [Google Scholar] [CrossRef]
- Indonesia’s Lab Problems Persist, Testing Rate Remains Below 1%. Available online: https://www.thejakartapost.com/news/2020/10/22/ri-lab-problems-persist-testing-rate-remains-below-1.html (accessed on 2 May 2021).
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165. [Google Scholar] [CrossRef]
- Ross, R. An application of the theory of probabilities to the study of a priori pathometry—Part I. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1916, 92, 204–230. [Google Scholar]
- Susanto, H.; Tjahjono, V.; Hasan, A.; Kasim, M.; Nuraini, N.; Putri, E.; Kusdiantara, R.; Kurniawan, H. How many can you infect? Simple (and naive) methods of estimating the reproduction number. Commun. Biomath. Sci. 2020, 3, 28–36. [Google Scholar] [CrossRef]
- Soewono, E. On the analysis of COVID-19 transmission in Wuhan, Diamond Princess and Jakarta-cluster. Commun. Biomath. Sci. 2020, 3, 9–18. [Google Scholar] [CrossRef]
- Azque-Herrerias, F.; Munuzuri-Perez, V.; Galla, T. Stirring does not make populations well mixed. Sci. Rep. 2018, 8, 4068. [Google Scholar] [CrossRef] [Green Version]
- World Population by Countries. Available online: https://www.worldometers.info/world-population/#density (accessed on 9 July 2021).
- Human Life Expectancy. Available online: https://www.worldometers.info/world-population/indonesia-population/ (accessed on 7 March 2021).
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Ann. Intern. Med. 2020, 172, 577–582. [Google Scholar] [CrossRef] [Green Version]
- Transmission of SARS-CoV-2: Implications for Infection Prevention Precautions. Available online: https://www.who.int/news-room/commentaries/detail/transmission-of-sars-cov-2-implications-for-infection-prevention-precautions (accessed on 6 April 2021).
- Diekmann, O.; Heesterbeek, J.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef] [Green Version]
- Ahamad, M.G.; Tanin, F.; Talukder, B.; Ahmed, M.U. Officially Confirmed COVID-19 and Unreported COVID-19—Like Illness Death Counts: An Assessment of Reporting Discrepancy in Bangladesh. Am. J. Trop. Med. Hyg. 2021, 104, 546. [Google Scholar] [CrossRef]
- Vasudevan, V.; Gnanasekaran, A.; Sankar, V.; Vasudevan, S.A.; Zou, J. Disparity in the quality of COVID-19 data reporting across India. BMC Public Health 2021, 21, 1211. [Google Scholar] [CrossRef]
- Woolf, S.H.; Chapman, D.A.; Sabo, R.T.; Weinberger, D.M.; Hill, L. Excess deaths from COVID-19 and other causes, March-April 2020. J. Am. Med. Assoc. 2020, 324, 510–513. [Google Scholar] [CrossRef]
- Ioannidis, J.P.; Cripps, S.; Tanner, M.A. Forecasting for COVID-19 has failed. Int. J. Forecast. 2020, 38, 423–438. [Google Scholar] [CrossRef]
- Richards, F. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–301. [Google Scholar] [CrossRef]
- Lei, Y.; Zhang, S. Features and partial derivatives of Bertalanffy-Richards growth model in forestry. Nonlinear Anal. Model. Control 2004, 9, 65–73. [Google Scholar] [CrossRef]
- Lee, S.Y.; Lei, B.; Mallick, B. Estimation of COVID-19 spread curves integrating global data and borrowing information. PLoS ONE 2020, 15, e0236860. [Google Scholar] [CrossRef]
- Germany Is Poised to Tighten Lockdown as COVID-19 Cases Surge Again. Available online: https://www.wsj.com/livecoverage/covid-2021-03-22/card/h7nDLKXUj1H0yZJsgeoI (accessed on 2 August 2021).
- S. Korea Sees Rise in Cases after Relaxing Social Distancing Rules. Available online: http://www.koreaherald.com/view.php?ud=20201102000137 (accessed on 4 July 2021).
- ‘The Perfect Storm’: Lax Social Distancing Fuelled a Coronavirus Variant’s Brazilian Surge. Available online: https://www.nature.com/articles/d41586-021-01480-3 (accessed on 4 July 2021).
- Fiore, V.G.; DeFelice, N.; Glicksberg, B.S.; Perl, O.; Shuster, A.; Kulkarni, K.; O’Brien, M.; Pisauro, M.A.; Chung, D.; Gu, X. Containment of COVID-19: Simulating the impact of different policies and testing capacities for contact tracing, testing, and isolation. PLoS ONE 2021, 16, e0247614. [Google Scholar] [CrossRef]
- Daily COVID-19 Tests. Available online: https://ourworldindata.org/grapher/daily-COVID-19-tests-smoothed-7-day (accessed on 7 September 2021).
- Case Fatality Rate. Available online: https://www.britannica.com/science/case-fatality-rate (accessed on 23 August 2021).
- Streeck, H.; Schulte, B.; Kümmerer, B.M.; Richter, E.; Höller, T.; Fuhrmann, C.; Bartok, E.; Dolscheid-Pommerich, R.; Berger, M.; Wessendorf, L.; et al. Infection fatality rate of SARS-CoV2 in a super-spreading event in Germany. Nat. Commun. 2020, 11, 5829. [Google Scholar] [CrossRef]
- Teppone, M. One Year of COVID-19 Pandemic: Case Fatality Ratio and Infection Fatality Ratio. A Systematic Analysis of 219 Countries and Territories. Preprints 2021, 1–13. [Google Scholar] [CrossRef]
- Ioannidis, J.P. Infection fatality rate of COVID-19 inferred from seroprevalence data. Bull. World Health Organ. 2021, 99, 19. [Google Scholar] [CrossRef]
- Mallapaty, S. How deadly is the coronavirus? Scientists are close to an answer. Nature 2020, 582, 467–469. [Google Scholar] [CrossRef]
- Reported Cases and Deaths by Country or Territory. Available online: https://www.worldometers.info/coronavirus/#countries (accessed on 21 March 2021).
- Kraemer, M.U.; Yang, C.H.; Gutierrez, B.; Wu, C.H.; Klein, B.; Pigott, D.M.; Open COVID-19 Data Working Group; du Plessis, L.; Faria, N.R.; Li, R.; et al. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science 2020, 368, 493–497. [Google Scholar] [CrossRef] [Green Version]
- Choi, S.; Ki, M. Estimating the reproductive number and the outbreak size of COVID-19 in Korea. Epidemiol. Health 2020, 42, e2020011. [Google Scholar] [CrossRef]
- Chowell, G. Fitting dynamic models to epidemic outbreaks with quantified uncertainty: A primer for parameter uncertainty, identifiability, and forecasts. Infect. Dis. Model. 2017, 2, 379–398. [Google Scholar] [CrossRef]
- China Reports Most New COVID-19 Cases Since January amid Delta Surge. Available online: https://www.reuters.com/world/china/china-reports-96-new-coronavirus-cases-aug-3-vs-90-day-ago-2021-08-04/ (accessed on 5 August 2021).
- Coronavirus Digest: Germany Cases Surge to New Record. Available online: https://www.dw.com/en/coronavirus-digest-germany-cases-surge-to-new-record/a-55292392 (accessed on 5 August 2021).
- Lai, A.; Bergna, A.; Menzo, S.; Zehender, G.; Caucci, S.; Ghisetti, V.; Rizzo, F.; Maggi, F.; Cerutti, F.; Giurato, G.; et al. Circulating SARS-CoV-2 Variants in Italy, October 2020–March 2021. Virol. J. 2021, 18, 168. [Google Scholar] [CrossRef]
- Visaria, A.; Dharamdasani, T. The complex causes of India’s 2021 COVID-19 surge. Lancet 2021, 397, 2464. [Google Scholar] [CrossRef]
- Luo, G.; Zhang, X.; Zheng, H.; He, D. Infection fatality ratio and case fatality ratio of COVID-19. Int. J. Infect. Dis. 2021, 113, 43–46. [Google Scholar] [CrossRef] [PubMed]
- Epidemiologist Urges Evaluation as Indonesia’s COVID-19 Deaths Increase. Available online: https://www.ugm.ac.id/en/news/21140-epidemiologist-urges-evaluation-as-indonesia-s-COVID-19-deaths-increase (accessed on 5 August 2021).
- COVID-19 in Southeast Asia: All Eyes on Indonesia. Available online: https://theconversation.com/COVID-19-in-southeast-asia-all-eyes-on-indonesia-164244 (accessed on 10 August 2021).
- Novel Coronavirus (2019-nCoV)—Situation Report 60. Available online: https://cdn.who.int/media/docs/default-source/searo/indonesia/covid19/external-situation-report-60_23-june-2021.pdf?sfvrsn=15d6c3ad_5 (accessed on 1 July 2021).
- Germany: Infection R-Rate Still Above 1, but Restrictions Still Lifted. Available online: https://www.dw.com/en/germany-infection-r-rate-still-above-1-but-restrictions-still-lifted/a-53383279 (accessed on 14 June 2022).
- Indonesia’s R0, Explained. Available online: https://www.thejakartapost.com/news/2020/06/01/indonesias-r0-explained.html (accessed on 14 June 2022).
- India’s Omicron Surge Explained: Reproduction Number up, Doubling Time down. Available online: https://www.business-standard.com/article/current-affairs/india-s-omicron-surge-explained-reproduction-number-up-doubling-time-down-122010900082_1.html (accessed on 14 June 2022).
- Liu, S.; Ermolieva, T.; Cao, G.; Chen, G.; Zheng, X. Analyzing the effectiveness of COVID-19 lockdown policies using the time-dependent reproduction number and the regression discontinuity framework: Comparison between countries. Eng. Proc. 2021, 5, 8. [Google Scholar]
- Andriani, H. Effectiveness of large-scale social restrictions (PSBB) toward the new normal era during COVID-19 outbreak: A mini policy review. J. Indones. Health Policy Adm. 2020, 5, 61–65. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).