Abstract
The growing importance of regional units in national economies gives rise to the objective need to improve the tools of spatial management. The construction of realistic development scenarios and forecasts is possible on the basis of the DSGE models’ tools. At the same time, models of a similar class that describe socio-economic processes at the level of the regional economy are practically not represented in modern studies. The purpose of the paper is to build a model of the regional economy based on DSGE tools. A feature of the proposed model is the consideration of spatial features through budget expenditures on the digitalization of such areas as healthcare and education. The high importance of these costs became evident during the COVID-19 crisis, when the consequences of underfunding IT costs in education and healthcare led to slowing economic growth. We have allocated health and education expenses in the standard budget limit of the regional government. On the basis of the developed model, response functions for shocks of exogenous variables for 20 periods were built. The result of the simulation is the response functions of endogenous variables in response to the fading growth in the share of spending on human capital in the region, as well as the obtained values of elasticities for a single change in shocks.
1. Introduction
The growing importance of the regions of the Russian Federation as the leading economic entities competing for financial and labor resources necessitates the development of adequate scenarios for their socio-economic development, taking into account fiscal and monetary destabilizing factors. Mismatched business cycles in various constituent entities of the Russian Federation and inflationary differentials [1], partly due to industry specifics, barriers to the redistribution of resources between heterogeneous regions, as well as imperfect mechanisms for adjusting relative prices that do not allow the economic agents of the territories to optimally respond to shocks [2], lead to losses in the welfare of the regions.
The construction of realistic development scenarios that take into account regional characteristics is possible on the basis of the tools of dynamic stochastic general equilibrium models (DSGE models), which form the foundation of modern macroeconomics and are widely used to study the aggregate parameters of the development of national economies. As Argentiero et al. objectively notes, “DSGE models can help to identify sources of fluctuations, answer questions about structural changes, forecast the effect of policy changes, etc.” [3] (p. 2).
Despite the fact that the level of criticism of the DSGE models’ quality by scientists is quite high, the work [4] provides an objective justification that this type of model is the most preferable one from the point of view of macroeconomic analysis. At the same time, “the elimination of shortcomings associated with poor justification at the micro level, as well as an unsatisfactory description of financial imperfections” is an important condition for the use of DSGE models [4] (p. 24).
Microeconomic justifications are used there as the theoretical basis of an analysis in DSGE models, in which the dynamics of the economic system is the result of some optimization activity of economic agents. At the same time, as Kenichi Tamegawa quite objectively notes, “In most of these models, the unit considered is a ‘country,’ and the country usually consists of a single region. However, in reality, most countries are divided into many regions with different economic structure” [5]. From this quote, we highlight two important points that determine the relevance of this study.
Firstly, despite the widespread use of the DSGE model toolkit by central banks and governments of many countries of the world when developing monetary and fiscal policy directions, in the scientific literature, there are practically no works on the description of the economies of the territorial units (regions) of the country using DSGE models. Thus, a similar class of models, which constitutes the theoretical foundation of modern macroeconomics, is mainly used in relation to the study of the national economy.
Secondly, the construction of DSGE models for large economies as a single whole homogeneous territory does not allow consideration of regional features. As a rule, in the scientific literature, heterogeneity in relation to territorial systems is understood as the differentiation of territories by income. Scientists identify various factors of economic growth as the reasons for differentiation. One of the key works devoted to the analysis of factors of the economic growth of territories is the study of P. Krugman [6]. The main idea is that the centers of economic activity are determined not only by the geographical location of the territory, but also by the results of human activity. The high importance of the contribution of human capital and, in particular, social capital to economic growth is a generally recognized fact, proven in the empirical data of many countries [7,8,9,10,11]. Gary Becker, one of the founders of the human capital concept, notes that the level of human capital is determined by the investment of resources in people. At the same time, he refers to education, training, migration, and health as the main areas of investment [12] (p. 42). According to Becker, it is these areas of spending that determine the inequality in income among people.
Continuing the discussion about the factors of the economic growth of territories, it is necessary to note such an important factor in the competitiveness of territories as digitalization. The Fourth Industrial Revolution led to the integration of digital technologies into production processes based on “smart machines”. The change in the order of organization of production processes, in turn, led to the emergence of new factors in the competitiveness of territories. Our research has confirmed that the introduction of modern digital solutions in various sectors of the economy and spheres of public life objectively has a positive impact on the indicators of spatial development [13]. In this regard, building a modern digital infrastructure and a system of Internet platforms, including in such important sectors of human capital formation as education and healthcare, is of strategic importance both in national and regional agendas.
The importance of these costs was especially evident during the COVID-19 crisis. In lockdown conditions, the costs of computer equipment and servers, Internet channels and special software are necessary for remote education in schools and universities. Underfunding of IT expenses in the field of education in a number of countries and regions has led to the impossibility of obtaining educational services. Similarly, spending on ICT in the health sector is necessary for the functioning of telemedicine, for the diagnosis of diseases and the development of individual treatment programs using artificial intelligence systems, the use of robotics during operations, including remote ones, in the development of new drugs and vaccines, etc. The low attention of a number of governments to the digitalization of education and healthcare eventually led to the loss of human capital and the growth of inequality.
The foregoing motivates our paper, the purpose of which is to model the regional economy based on DSGE tools in the conditions of digitalization. Heterogeneity of regions (territorial differences) is represented in the model by taking into account the institutional component represented by human capital.
The paper is structured as follows. The first section reviews the related literature. Section 2 constructs the dynamic stochastic general equilibrium (DSGE) model considering the institutional features of territorial development. Section 3 estimates the parameters. In particular, a system of linearized equations is presented and parameters are calibrated. Section 4 presents the simulation results obtained in the course of scenario calculations: visualization of the response function of endogenous variables in response to a damped growth in the share of spending on human capital, calculations of elasticity for a single change in other shocks, and the effects of tax measures. Section 5 concludes the paper.
2. Literature Review
2.1. DSGE Method in Regional Development Research
Recently, economic research, synthesizing the approaches of mathematical modeling of complex systems and a systematic analysis of the country’s economy in order to obtain a quantitative assessment of macroeconomic decisions made by the authorities, has gained the greatest relevance. At the same time, most economic models at the regional level are currently either econometric or balanced [14]. The weakness of econometric models is that they only state the existence of a relation between variables, and are not able to explain it. The weak side of the balance models is the inability to express relations between economic agents with their help. Therefore, balance models are often unable to fully take into account actual problems in the field of economic development.
More advanced tools for studying economics include computable general equilibrium models (CGE models), which describe economic processes as a result of the interaction of agents of various types and allow evaluation of the multiplicative effect of the influence of the estimated factor. This class of economic and mathematical models combines the advantages of information technology and the possibility of modeling complex systems. General equilibrium models are complex because they represent a group of nonlinear problems of agent behavior optimization. The strength of these models is a sufficient degree of detail in the description of the economy.
The weakness of the CGE models is a rather schematic description of the system of economic relations between agents. These relations are described as completely competitive relations between the owner—the consumer—and the company—the producer—against the background of state regulation. It should be noted that all of the above models do not take into account the expectations of economic agents. In addition, the parameters of these models do not have a microeconomic justification and do not take into account the preferences of individual agents.
The shortcomings listed above are eliminated in dynamic stochastic general equilibrium models (DSGE models), which currently constitute the theoretical foundation of modern economics. DSGE models describe the processes affecting the change in the aggregated parameters of the development of national economies as a result of fiscal and monetary policy [15,16,17,18,19], the influence of the shadow sector of the economy [20], technology [21,22,23,24], and energy and oil supply shocks [25,26,27].
Despite the widespread use of DSGE models tools in relation to national economic systems, there are practically no works in the scientific literature describing the economies of the territorial units (regions) of the country using DSGE models. Note, in this regard, a number of works devoted to the construction of regional DSGE models and which influenced the present study. Thus, let us highlight the work by Margarida Duarte and Alexander L. Wolman [28], which actualizes the need to use DSGE models in regional economies. An important conclusion of this paper is that regional fiscal policies can have substantial spill-over effects on the volatility of union-wide and foreign inflation. However, this study has no practical value. Further, the studies of Kenichi Tamegawa [5,29] can be noted. We should underline the following important result of the study: “the fiscal multiplier depends on which government (local or central) implements the fiscal policy and where the policy is implemented” [5] (p. 249). However, the models built in the works do not take into account the interaction and mutual influence of regions (territorial units) within one country, which is the most important factor in their spatial and economic development.
The work by Leonid Serkov, devoted to the development of multisectoral regional DSGE models for the analysis of the effects of economic policy, is also of interest for this study. The advantage of the study is, firstly, taking into account the peculiarities of the sectoral structure of the regions. The structure of the real sector of the economy is represented by the following sectors: raw materials, manufacturing, the sector of non-tradable goods and services, the sector of importing enterprises, and the sector of production of final goods and services [30]. Secondly, the parametrization of the model was carried out based on panel data of the economy of a particular region (Sverdlovsk region of Russia). At the same time, the work does not reflect the institutional specifics of the regions. As the author notes, “this issue is an interesting topic for future research in the field of modeling regional socio-economic systems” [30] (p. 248).
2.2. Accounting for Heterogeneity of Regions
Abstracting from regional features when building DSGE models for economies as a homogeneous territory can lead to a bias in the estimates obtained. This, in turn, may lead to obtaining not quite correct scenarios for the development of the analyzed economies. Territorial differences are taken into account in this work by introducing such spheres of human capital formation as healthcare and education into the model of budget expenditures for digitalization.
As noted in the Introduction, the role of human capital is one of the main research topics in relation to the study of the economic growth theory. It has been proven that human capital directly affects growth rates [31,32]. It should be noted that most of the issues we have studied in the field of human capital focus on the contribution of education to economic growth [33,34,35,36]. Along with education, healthcare is an integral part of human capital, an expense that stipulates economic growth [37,38]. Bloom and Malani [39], Bhargava et al. [40], and Kelly [41] et al. have shown that healthcare is an important factor in economic growth because it increases the life expectancy of the working population. Gradually, it was recognized that healthy workers are more productive than sick ones; since healthy workers have a minimum number of days of incapacity for work, this allows the employer to reduce labor turnover, which increases labor productivity and justifies higher wages [42]. Recently, many works have appeared that assess the impact of healthcare on economic growth [43,44,45]. On the one hand, such interest in investing in healthcare is due to the unfavorable epidemiological situation caused by COVID-19. Many modern studies have been devoted to the study of this problem [46,47]. On the other hand, the lockdown that followed the epidemic actualized the importance of financing modern digital infrastructure and Internet platform systems in the main sectors of human capital formation: education and healthcare.
Summing up our short review of research carried out in the field of human capital and its role in the digital economy, we note that, through the difference in this parameter in the regions, expressed by the differential levels of healthcare and education, one can objectively assess the heterogeneity of regions.
Since the formation of human capital is a long-term process, our model focuses on the dynamics of variables in the long run. Therefore, we abstract from such elements of short-term DSGE models as inflexible prices and inflation, consumption inertia and capital investment costs, and monetary policy that smooths short-term deviations from a long-term trend. In fact, our model belongs to the class of RBC models that describe the dynamics of real indicators, not nominal ones, in the long run.
Within the framework of the model presented in this study, each region consists of the household sector, firms (the real sector), and the public sector. At the same time, households form the supply of production factors (labor and capital), as well as demand for goods and services. Firms produce goods and services using labor and capital.
In the public sector, the main tax revenues of the constituent entities of the Russian Federation are income from personal income tax, income tax, as well as taxes on the property of individuals and legal entities. Therefore, the model takes into account taxes on household income, as well as receipts directly related to GRP and fixed capital. In turn, expenditures on the formation of human capital (education and healthcare) are the main expenditures of regional budgets. Therefore, in the model, we distinguish two types of expenditures: for the economy (in terms of public procurement) and for the public sector (in terms of the human capital formation). To simplify, we model the interaction between two regions (territorial units of the country). At the same time, they are interconnected by commodity flows, as well as by flows of labor and capital resources.
2.3. Innovations
The innovations of this article are as follows. We propose an approach in which budget spending on the human capital formation affects the following variables: labor supply; household consumption; total factor productivity.
As is known, the features of the DSGE approach are the following. Firstly, the foundation is a microfundament. That is, at the first step, a mathematical model is constructed that describes the behavior of representative economic agents with the help of dynamic problems of optimizing the utility of household goods and the profits of firms. To solve optimization problems, we used the standard method of Lagrange multipliers. The result is nonlinear supply and demand functions of economic agents.
Secondly, as a rule, DSGE models operate with variables—deviations around its steady state. To translate the model to a linear form, we used the log-linearizing method proposed by Uhlig [48].
Thirdly, either their calibration or estimation methods (maximum likelihood method, generalized method of moments, Bayesian methods, etc. [49]) are used to set models’ parameters. We calibrated the coefficients of the model based on previous regional DSGE models of Russia, as well as on the basis of statistical data on territorial units of the Russian Federation.
Finally, it is assumed that economic agents behave rationally; that is, they use all available information in the most optimal way. Mathematically, this means that the DSGE model is a system of difference equations with rational expectations. There are many numerical ways to solve such models: Blanchard, Kahn [50], Klein [51], Sims [52] and others. We used the methods built into the standard Dynare package.
3. DSGE Model Method
3.1. Household sector
A representative household of each region maximizes the expected total discounted utility
where is the rational expectations operator; —consumption of goods and services; —employment; —the rate of intertemporal substitution of consumption (elasticity of consumption at the real interest rate); —a parameter inverse to the elasticity of labor supply with respect to real wages. The parameter is responsible for the preference of households between work (leisure) and consumption.
The budget constraint of a representative household can be represented in the following way:
where is the stock of fixed assets that bring real returns ; —real wage; —personal income tax rate.
The optimization problem (1) under constraint (2) is solved by the following functions. The consumer demand function is described as follows:
The labor supply function can be written in the following way:
That is, the supply of labor depends positively on real wages and negatively on consumption and income tax.
If there are households in the economy, then aggregate consumption and labor supply are and , respectively. The stock of fixed assets (buildings and structures, machinery, and equipment) does not depend on the number of households . For example, excess mortality resulting from underfunded healthcare does not affect the capital stock.
3.2. Real Sector
Firms in each region maximize their real net profit:
where is the corporate income tax rate; is the property tax rate. At the same time, the volume of production (GRP) is given by a two-factor Cobb–Douglas production function:
where is the total factor productivity; is the labor elasticity coefficient of output. The dynamics of capital is determined by the equation:
where is the rate of disposal of fixed assets; is investment in fixed capital.
Accordingly, the demand for labor is expressed by the following equation:
Optimal stock of fixed assets:
Thus, the income tax negatively affects the demand for labor and for capital (investment).
Aggregate demand in each region consists of household consumption, investment, budget purchases, and net exports:
where is the import of goods and services from another region; is the export of goods and services to other regions.
3.3. Budget Sector
We assume that the regional budget should be balanced in the long run. Then, budget expenditures are equal to tax revenues:
Budget expenditures are allocated to public procurement , as well as to human potential development , i.e., healthcare and education. The latter can increase:
- labor supply and consumption by increasing the number of households (by reducing mortality, including those of working age), as well as by reducing morbidity and increasing their life expectancy;
- total factor productivity . In particular, labor productivity increases with the development of education and science, and the growth of acquired knowledge, skills, and abilities.
3.4. Relationship between Regions
Under the condition of flexible prices and their rapid equalization between regions, the consumption of imported goods and services depends only on the total consumption:
where is a parameter reflecting the propensity of the population to diversify the consumer basket; is a parameter that takes into account the share of imports in the consumer basket and the ratio of prices for imported goods to the cost of the consumer basket [53] (pp. 362–364), [54] (p. 121).
The flows of labor and fixed assets between regions are modeled on the basis of equations—analogues of the gravity model:
where and are coefficients reflecting the scales of two regions; and are elasticity coefficients reflecting the mobility of labor and capital between regions.
4. Linearization and Calibration
4.1. System of Linearized Equations
Linearized equations written in terms of percentage deviations of variables from their equilibrium values for each i-th region are written in the following form.
Household consumption (3) taking into account the impact of budget expenditures on the number of households:
where is the elasticity of consumption and employment with respect to budget expenditures for the human development sectors.
The export of the i-th region is the import of the j-th region and in percentage deviation coincides with consumption (12):
Labor supply (4) is expressed in the following way, also taking into account the impact of health spending on the number of households and labor migration:
Aggregate demand (10) in deviation variables takes the following form:
where is the share of household consumption in GRP, is the share of investments in GRP, is the share of budget expenditures in GRP, is the share of exports in GRP, and is the share of imports in GRP.
Aggregate supply (production function) (6):
The demand for labor (8) and the optimal stock of capital (9) after linearization have taken the following form:
where is the ratio of firms’ payments for interest payments and for property taxes.
Dynamics of fixed assets (7) taking into account the flow of capital between regions:
Revenues (expenditures) of the regional budget (11) after replacing the profit variable with the GRP proxy variable:
where is the share of personal income tax in the regional budget, is the share of property taxes in the regional budget, and is the share of income tax in the regional budget.
Budget expenditures for the purchase of goods and services and for the human capital sectors:
where is the average share of budget spending on human capital; is the percentage deviation of the share of budget spending from the equilibrium value.
Equations (15)–(25) are the same for both regions. The following equations describe interregional links (in addition to (16)).
Migration of labor resources:
Capital flow between regions:
Total factor productivity is usually set exogenously and is described by a first-order autoregressive equation. In our model, since investment in human capital sectors affects productivity, it is modeled as a function of budget spending:
where is the persistence of total factor productivity, is the elasticity of total factor productivity with respect to budget expenditures for human development sectors, and is the exogenous productivity shock.
Thus, in a two-region model, the dynamics of 26 variables is described with the corresponding number of equations.
4.2. Calibration Parameters
The calibration of the parameters of regional DSGE models differs from the calibration of country DSGE models. When calibrating the parameters of our model, we relied on well-known regional DSGE models of Russian regions (primarily [1,31], as well as statistical data of the territorial units (regions) of Russia.
The discount rate parameter is calibrated from the relation . We will take the long-term interest rate equal to 8%, based on the estimates of the productivity of physical capital from [53]. Following A. Polbin [55], we will take the share of depreciation deductions equal to per year.
The Russian labor market is characterized by significant inertia. Thus, our own estimates of the parameter inverse to the elasticity of labor supply for real wages, , are from 3.6 and higher. Other authors [56,57,58] calibrate and estimate the parameter in the range from 1 to 3. In this work, we will take the value .
The consumption elasticity parameter at the real interest rate and labor elasticity of output following [27] will be taken as 1 and 0.55, respectively.
We estimated the labor mobility parameter using Equation (26), which is an analogue of the gravity model. As is known, the gravity model takes into account the interaction and mutual influence of regions. Therefore, for an empirical assessment of the parameter , the authors used the migration matrix and the matrix of the difference in wages between Russian regions for 2019. The migration matrix was built on the basis of data on the number of people who left region i for region j [59]. The matrix of the difference in wages between regions was obtained on the basis of data on the average monthly nominal accrued wages of employees for a full range of organizations in the constituent entities of the Russian Federation in 2019 [60]. At the same time, the element of the wage difference matrix is equal to the ratio of wages in region i to the wages of region j.
Since fixed assets are much less mobile than labor resources, but it is not possible to estimate the capital elasticity parameter using statistical data, we took it equal to half of the staff mobility coefficient ().
The contribution of public spending on health and education to total factor productivity was estimated econometrically by modifying the Solow model in intensive form. The data sample included indicators of 78 Russian regions for 2010–2019, a total of 6240 observations. The per capita output of regional economies was used as productivity; as capital–labor ratio, we used the volume of investment in fixed assets per capita. Further, the parameters of panel data models with fixed and random effects were evaluated, taking into account different indicators for assessing the contributions of health indicators (the number of doctors, the number of hospital beds, healthcare costs) and education (expenditures on education, the share of students, the number of personnel engaged in scientific research). The selection of the best models was carried out on the basis of the Breusch–Pagan, Hausman, and F-test tests, as well as using the Akaike and Schwarz information criteria. According to the evaluation results, on average, the share of the contribution of budget expenditures on healthcare to total factor productivity was 0.3, education—0.1, which is in line with similar studies [9,35,61,62,63].
Since regional statistics in the Russian Federation give the structure of GRP only by the production method, the average structure of the Russian GDP [64] for the period 2011–2020 was taken as a representative structure of GRP by expenditures. At the same time, household consumption was combined with the expenditures of non-profit organizations, and gross capital formation was combined with the change in stocks.
The parameters of the representative structure of regional budgets were calibrated on the basis of the study [65]. At the same time, income tax, excises, and tax on total income were combined.
The final values of the parameters are presented in the table below (Table 1).

Table 1.
Calibrated parameter values.
The persistence coefficients in the autoregressive equations of exogenous shocks are assumed to be 0.7.
5. Simulation Results
Scenario calculations were carried out for 20 periods (years). Below, we present the response functions of endogenous variables in response to the fading growth in the share of digitalization expenditures in healthcare and education in the first region (Figure 1).
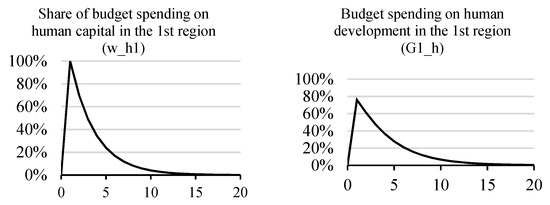
Figure 1.
Growth of the share of budget spending on human capital in the first region and the total budget spending on human capital.
When allocating the regional budget in favor of spending on human capital, current purchases of goods and services are being displaced (Figure 2). This effect is enhanced by a decrease in tax revenues due to a reduction in GRP in the first region (see below).
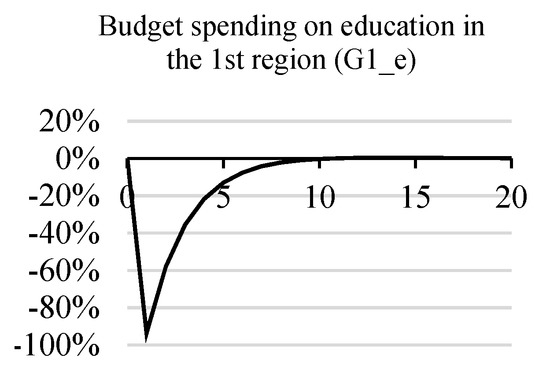
Figure 2.
Reduction in budget spending in the first region.
A consequence of the reduction in current budget spending is a decrease in regional product, employment, and investment (Figure 3).
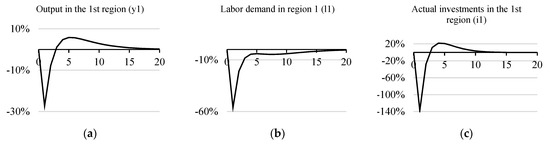
Figure 3.
Decrease in GRP, employment, and investment in the first region.
At the same time, the growth in aggregate factor productivity increases real wages and consumption (Figure 4). These effects smooth out the decrease in GRP in the first region.
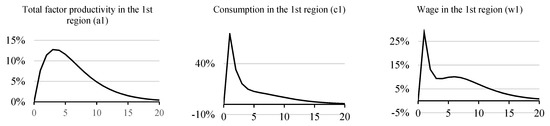
Figure 4.
Decrease in total factor productivity, consumption, and wages in the first region.
The interest rate (Figure 5) initially decreases (which also supports consumption) against the background of a decrease in demand for fixed assets. However, then, as investment activity recovers and aggregate factor productivity increases, it grows above the equilibrium level.
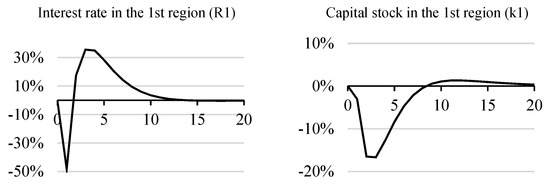
Figure 5.
Interest rate fluctuations and loss of fixed assets in the first region.
As a result of the growth of wages in the first region and a decrease in the second, labor resources flow from the second region to the first. Capital, on the contrary, first moves from the first region to the second, and then reverses (Figure 6).

Figure 6.
Net flows of factors of production from the first to the second region.
Exports of goods from the first region to the second are declining against the background of a decrease in consumer activity in the latter, which contributes to the decline in the first region. Conversely, the growth of consumer spending in the first region stimulates the import of goods from the second region and economic activity within it (Figure 7).
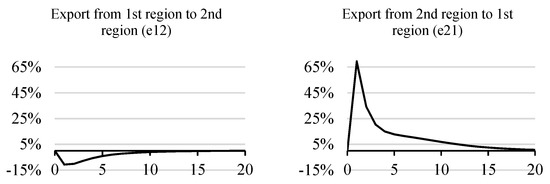
Figure 7.
Export from first to second region and export from second to first region.
Output in the second region is growing primarily due to the growth of exports to the first region (Figure 8).
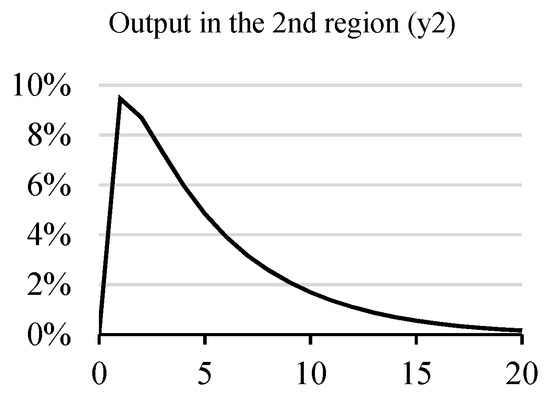
Figure 8.
Output growth in the second region.
A positive output gap in the second region triggers the following chain of budget effects—tax revenues increase, which proportionally increases both current budget purchases and human capital expenditures (Figure 9).
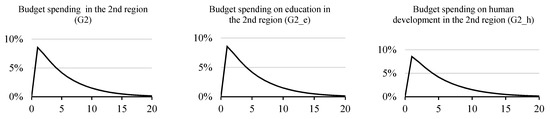
Figure 9.
Growth of budget revenues and expenditures in the second region.
The growth of current budget purchases reinforces the positive output gap. Moreover, the growth of human capital expenditures raises the aggregate factor productivity (Figure 10).
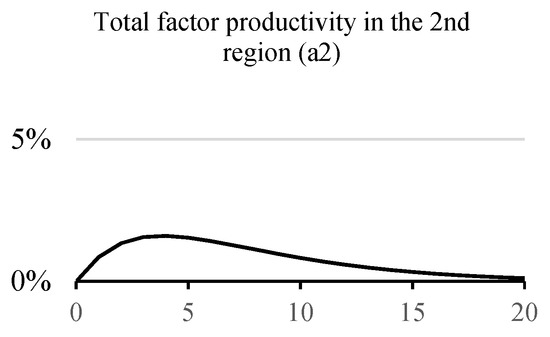
Figure 10.
Growth of budget revenues and expenditures in the second region.
In the labor market (Figure 11), there is simultaneously an increase in the demand for labor against the background of the expansion of production and an increase in the supply of labor due to an increase in healthcare costs. The second effect outweighs the first; as a result, wages are reduced. Consumption is declining as a result of a reduction in wages and an increase in the interest rate (see below).
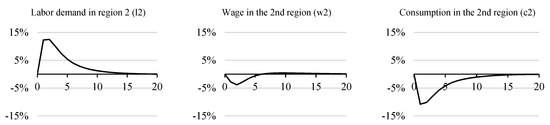
Figure 11.
Employment growth, reduction in wages, and consumption in the second region.
Finally, the capital market of the second region (Figure 12) shows a “displacement effect”—the growth of budget purchases increases the interest rate and reduces investment. The increased need for capital at first is covered by its import from the first region due to interest arbitration (in the second region, the percentage increases, while in the first region, it initially decreases).
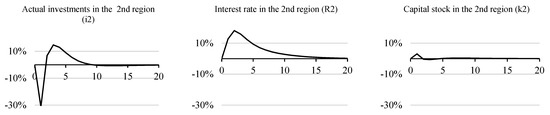
Figure 12.
Fluctuations in investment and capital, interest rate growth in the second region.
Elasticities (maximum) per unit change of other shocks are presented in Table 2.

Table 2.
Elasticities (maximum) per unit change in shocks.
From the calculations carried out, the following conclusions can be drawn. First, the multiplier of budget expenditures is less than 1 (more precisely, 0.56). This is partly due to the crowding out effect—an increase in government purchases increases the interest rate, which reduces investment (−1.25) and household consumption (−0.6). At the same time, the indirect impact on other regions is very small (0.005).
Secondly, it draws attention to the difference in the effects of budget purchases and investments in human capital. In the latter case, there is a negative impact on GRP (−0.27) and employment (−0.6). This is due to the fact that the redistribution of budget expenditures from current budget expenditures in favor of long-term ones creates a negative output gap in the short run, due to the fact that the effects of education are weaker in the short term than the effects of healthcare (0.1 vs. 0.3—see Table 1). Moreover, the positive impact on productivity results in lower demand for labor (−0.6) and investment (−1.3) in the short run. This is partly offset by an increase in real wages (0.3), which softens the decline in output. Thus, this scenario calculation clearly demonstrates the choice facing the authorities—the choice between short- and long-term development goals.
Let us turn to the analysis of the effects of tax measures. In general, the growth of the tax burden has a negative impact on economic activity, employment, and investment. This is because, in the case of income and property taxes, higher marginal rates reduce tax revenues. In other words, the model parameters presented in Table 1 reflect an economy that is on the right (downward) section of the Laffer curve. Thus, with an increase in the tax burden, there is not only a negative primary effect on the economy, but also a secondary one—a reduction in budget revenues leads to a decrease in budget expenditures on current purchases and on the sphere of human capital. The latter destimulates factor productivity.
The effects are somewhat different from the increase in income tax—there is a near-zero effect on output. That is, with an increase in the tax burden on households, the supply of labor decreases (−0.15) and real wages grow (0.1). At the same time, due to large marginal rates, budget revenues increase (0.36). That is, for income tax, the calibrated parameters reflect an economy that is on the left (increasing) section of the Laffer curve. As a result, the growth of budget expenditures smooths out the decline in GRP due to budget purchases of goods and services, as well as due to budget investments in human capital sectors, which increases productivity.
It is also noteworthy that under any of the three scenarios for the growth of the tax burden in the first region, the reaction of the second region is similar. For example, with an increase in income tax in the first region, positive gaps in output are formed in both regions. Of course, the reaction of the second region, in which the parameters of the tax policy do not change, turns out to be much weaker.
6. Discussion
The paper presents an extended version of the dynamic stochastic general equilibrium model for the conditions of the regional economy. Interaction modeling was carried out between the two regions. At the same time, the links between interregional commodity flows and flows of labor and capital resources were taken into account. The model takes into account the institutional features of the regions by including human capital in the form of education and healthcare in the parameters. The levels of sensitivity of the response functions to the parameters of the economies of specific regions and their dependence on each other in terms of the mobility of labor and capital, as well as the intensity of trade, were assessed.
We came to the following conclusion: in order to achieve short-term effects, economic policy should focus on current budget spendings. Money spent on education and healthcare has a greater impact on the stock of human capital and long-term economic growth. At the same time, estimates of the effects of investments in human capital can be underestimated if they are expressed in terms of variable deviations and do not take into account the shift in the course of potential economic growth.
In reality, the economic system of any country includes a wide variety of regions and links between them. Accordingly, the transition to a multi-regional-multi-sectoral model with asymmetric regions and costs for the movement of goods, labor, and capital could be the direction for further research. The calibration of the capital movement rate between regions of the same country is an another topic for econometric research. Most of the available data and built models are suitable for the evaluation of the movement of capital between countries.
In addition, the presentation of interacting economic agents as “fully-informed-optimising Muth-rational agents” [3] (p. 1) is a significant limitation of DSGE models. Moreover, in further assessments, it is important to take into account the correlation between the effects of the COVID-19 pandemic and the COVID-19 global crisis. In particular, these relationships can significantly change the level of public health spending’s contribution to total factor productivity. Overcoming these limiting prerequisites will allow the transformation of the objective features of the regions into the corresponding behavior of economic agents. The solution of this problem is expected to be carried out in the future based on the integration of regional DSGE models with agent-based models to take into account the heterogeneity of agents based on real data of Russian regions.
Author Contributions
Conceptualization, J.D. and E.K.; Methodology, D.S. and J.D.; Formal Analysis, D.S. and E.K.; Investigation, D.S. and J.D.; Data Curation, D.S. and E.K.; Writing—Original Draft Preparation, D.S. and J.D.; Visualization, E.K.; Supervision, J.D. All authors have read and agreed to the published version of the manuscript.
Funding
The research was carried out at the expense of the Russian Science Foundation, project no. 21-78-10134, https://rscf.ru/en/project/21-78-10134/ (accessed on 16 May 2022).
Data Availability Statement
The statistical data stored on the following websites were used: https://rosstat.gov.ru/storage/mediabank/tab2_zpl.xlsx (accessed on 20 February 2022); https://www.fedstat.ru/indicator/43513 (accessed on 10 February 2022).
Acknowledgments
The authors are grateful to A. Shulgin and L. Serkov for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Serkov, L.A. Inter-Regional Inflation Differential as a Consequence of Heterogeneity of the Russian Economic Space. Econ. Reg. 2020, 16, 325–339. [Google Scholar] [CrossRef]
- Napalkov, V.V.; Novak, A.E.; Shul’gin, A.G. Razlichija v jeffektah edinoj denezhno-kreditnoj politiki: Sluchaj regio-nov Rossii. Money Financ. 2021, 80, 3–45. [Google Scholar] [CrossRef]
- Over Consumption. A Horse Race of Bayesian DSGE Models. Available online: https://www.researchgate.net/publication/281548845_Over_consumption_A_horse_race_of_Bayesian_DSGE_models (accessed on 5 May 2022).
- Andreyev, M.Y.; Polbin, A.V. Trends of macroeconomic models. Adm. Consult. 2019, 2, 24–33. [Google Scholar] [CrossRef]
- Two-Region DSGE Analysis of Regionally Targeted Fiscal Policy. Available online: https://www.researchgate.net/publication/287552300_Two-Region_DSGE_Analysis_of_Regionally_Targeted_Fiscal_Policy (accessed on 17 February 2022).
- Krugman, P. First nature, second nature, and metropolitan location. J. Reg. Sci. 1993, 33, 129–144. [Google Scholar] [CrossRef]
- Pede, V.O.; Florax, R.J.G.M.; de Groot, H.L.F.; Barboza, G. Technological leadership and sectorial employment growth: A spatial econometric analysis for U.S. counties. Econ. Notes 2021, 50, 1–19. Available online: https://research.vu.nl/ws/files/123661099/Technological_leadership_and_sectorial_employment_growth.pdf (accessed on 5 May 2022). [CrossRef]
- Benhabib, J.; Spiegel, M. The role of human capital in economic development: Evidence from aggregate cross- country data. J. Monet. Econ. 1994, 34, 143–173. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, C. The Role of the Composition of the Human Capital on the Economic Growth: With the Spatial Effect among Provinces in China. Mod. Econ. 2015, 6, 770–781. [Google Scholar] [CrossRef][Green Version]
- Argentiero, A.; Cerqueti, R.; Sabatini, F. Does social capital explain the Solow residual? A DSGE approach. MPRA Pap. 2018, 87100, 1–31. Available online: https://mpra.ub.uni-muenchen.de/87100/ (accessed on 5 May 2022). [CrossRef]
- Felice, E. Regional convergence in Italy, 1891–2001: Testing human and social capital. Cliometrica 2012, 6, 267–306. [Google Scholar] [CrossRef]
- Becker, G.S. Investment in Human Capital: A Theoretical Analysis. J. Political Econ. 1962, 5, 9–49. [Google Scholar] [CrossRef]
- Dubrovskaya, J.V. Analysis of heterogeneity of economic development of territories in the conditions of digitalization. Her. Omsk. University. Ser. «ECONOMICS» 2020, 2, 102–113. [Google Scholar] [CrossRef]
- Granberg, A.R. Osnovy Regional’noi Ekonomiki; HSE Publishing House: Moscow, Russian, 2001. [Google Scholar]
- Adolfson, M.; Lassen, S.; Linde, J.; Villani, M. RAMSES—A new general equilibrium model for monetary policy analysis. Sver. Riksbank Econ. Rev. 2007, 2, 5–40. [Google Scholar]
- Harrison, R.; Nikolov, K.; Quinn, M.; Ramsay, G.; Scott, A.; Thomas, R. The Bank of England Quarterly Model; Bank of England: London, UK, 2005; p. 244. [Google Scholar]
- Murchison, S.; Rennison, A. ToTEM: The Bank of Canada’s New Quarterly Projection Model; Technical Report 97; Bank of Canada: Ottawa, ON, Canada, 2006; p. 120. [Google Scholar]
- Andreyev, M.Y.; Polbin, A.V. The Impact of Fiscal Policy on Macroeconomic Indicators in DSGE-models. Financ. J. 2018, 3, 21–33. [Google Scholar] [CrossRef]
- Rui, W. Evaluating the Unconventional Monetary Policy of the Bank of Japan: A DSGE Approach. J. Risk Financ. Manag. 2021, 14, 253. [Google Scholar] [CrossRef]
- Serkov, L.A.; Krasnykh, S.S. Combining the agent approach and the general equilibrium approach to analyze the influence of the shadow sector on the Russian economy. Comput. Res. Modeling 2020, 12, 669–684. [Google Scholar] [CrossRef]
- Sun, D.; Wang, F.; Chen, N.; Chen, J. The Impacts of Technology Shocks on Sustainable Development from the Perspective of Energy Structure—A DSGE Model Approach. Sustainability 2021, 13, 8665. [Google Scholar] [CrossRef]
- Chan, Y.T. The Environmental Impacts and Optimal Environmental Policies of Macroeconomic Uncertainty Shocks: A Dynamic Model Approach. Sustainability 2019, 11, 4993. [Google Scholar] [CrossRef]
- Niu, T.; Yao, X.; Shao, S.; Li, D.; Wang, W. Environmental tax shocks and carbon emissions: An estimated DSGE model. Struct. Change Econ. Dyn. 2018, 47, 9–17. [Google Scholar] [CrossRef]
- Xiao, B.; Fan, Y.; Guo, X. Exploring the macroeconomic fluctuations under different environmental policies in China: A DSGE approach. Energy Econ. 2018, 76, 439–456. [Google Scholar] [CrossRef]
- Argentiero, A.; Atalla, T.; Bigerna, S.; Micheli, S.; Polinori, P. Comparing Renewable Energy Policies in EU-15, US and China: A Bayesian DSGE Model. Energy J. 2017, 38, 77–96. [Google Scholar] [CrossRef]
- Balke, N.S.; Brown, S.P.A. Oil supply shocks and the US economy: An estimated DSGE model. Energy Policy 2018, 116, 357–372. [Google Scholar] [CrossRef]
- Baluta, V.I.; Shul’ts, D.N.; Lavrinenko, P.A. Assessing the Impact of Global Hydrocarbon Prices on the Russian Economy Based on the DSGE Model with Capital-Owning Firms. Stud. Russ. Econ. Dev. 2022, 33, 107–117. [Google Scholar] [CrossRef]
- Duarte, M.; Wolman, A.L. Fiscal policy and regional inflation in a currency Union. J. Int. Econ. 2008, 74, 384–401. [Google Scholar] [CrossRef][Green Version]
- Tamegawa, K. Constructing a Small-Region DSGE Model. ISRN Econ. 2013, 2013, 825862. [Google Scholar] [CrossRef]
- Serkov, L.A. Regional dynamic stochastic general equilibrium model as a tool for analysis of fiscal policy. Perm Univ. Her. Econ. 2019, 2, 248–267. [Google Scholar]
- Gurgand, M. Capital humain et croissance: La littérature empirique à un tournant? Public Econ. 2000, 2, 71–93. [Google Scholar] [CrossRef]
- Barro, R.J.; Sala-i-Martin, X. Economic Growth, 2nd ed.; MIT Press: Cambridge, MA, USA, 2004; p. 654. [Google Scholar]
- Koritskiy, A.V.; Karelin, I.N.; Semenikhina, V.A. Estimating state financial benefits of education in Russia. Vestn. NSUEM 2017, 1, 64–82. [Google Scholar]
- Berezovskaya, A.G.; Koritsky, A.V. Assessment of the impact of workers’ education in the regions of Russia on volumes of production of gross regional product. World Econ. Manag. 2018, 18, 42–54. [Google Scholar] [CrossRef]
- Shtercer, T.A. Rol’ chelovecheskogo kapitala v jekonomicheskom razvitii regionov RF. Mir Jekonomiki I Upr.-Nija 2006, 6, 37–51. [Google Scholar]
- Popescu, C. Measuring Progress towards the Sustainable Development Goals: Creativity, Intellectual Capital, and Innovation. In Handbook of Research on Novel Practices and Current Successes in Achieving the Sustainable Development Goals; Popescu, C., Ed.; IGI Global: Hershey, PA, USA, 2021; pp. 125–136. [Google Scholar] [CrossRef]
- Tarasova, O.V. Infrastructure of Spatial Development of the Russian Federation: Transport, Energy, Innovative System, Life Support; IEIE SB RAS: Novosibirsk, Russia, 2020; p. 456. [Google Scholar]
- Bykova, A.V.; Solodukhin, K.S. The Origination and Development of the Public Health Concept as an Investee: Theoretical Forerunners. Natl. Interests Priorities Secur. 2020, 16, 1765–1779. [Google Scholar] [CrossRef]
- Bloom, D.E.; Malaney, P.N. Macroeconomic consequences of the Russian mortality crisis. World Dev. 1998, 26, 2073–2085. [Google Scholar] [CrossRef]
- Bhargava, A.; Jamison, D.T.; Lau, L.J.; Murray, C.J.L. Modeling the effects of health on economic growth. J. Health Econ. 2001, 20, 423–440. [Google Scholar] [CrossRef]
- Kelly, M. Health capital accumulation, health insurance, and aggregate outcomes: A neoclassical approach. J. Macroecon. 2017, 52, 1–22. [Google Scholar] [CrossRef]
- Russell, K.C. Two Years Later: A Qualitative Assessment of Youth Well-Being and the Role of Aftercare in Outdoor Behavioral Healthcare Treatment. Child Youth Care Forum 2005, 34, 209–239. [Google Scholar] [CrossRef]
- Demidova, O.A.; Kajasheva, E.V.; Dem’janenko, A.V. Gosudarstvennye rashody na zdravoohranenie i jekonomicheskij rost v Rossii: Regional’nyj aspect. Prostranstvennaja Jekonomika 2021, 1, 97–122. [Google Scholar]
- Kaneva, M.A. Vlijanie kapitala zdorov’ja naselenija na jekonomicheskoj rost regionov RF. Reg. Econ. Sociol. 2019, 1, 47–70. [Google Scholar]
- Barro, R. Health and Economic Growth. Ann. Econ. Financ. 2013, 14, 329–366. [Google Scholar]
- Zhou, D.; Zhou, M. Mathematical Model and Optimization Methods of Wide-Scale Pooled Sample Testing for COVID-19. Mathematics 2022, 10, 1183. [Google Scholar] [CrossRef]
- Popescu, C.R.G. COVID-19 Pandemic Impact on New Economy Development and Societal Change; IGI Global: Hershey, PA, USA, 2021. [Google Scholar] [CrossRef]
- Uhlig, H.A. Toolkit for Analysing Nonlinear Dynamic Stochastic Models Easily. In Computational Methods for the Study of Dynamic Economies; Marion, R., Scott, A., Eds.; Oxford University Press: New York, NY, USA, 1999; pp. 30–61. [Google Scholar]
- DeJong, D.; Dave, C. Structural Macroeconometrics, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Blanchard, O.J.; Kahn, C.M. The solution of linear difference models under rational expectations. Econometrica 1980, 48, 1305–1312. [Google Scholar] [CrossRef]
- Klein, P. Using the generalized Schur form to solve a multivariate linear rational expectations model. J. Econ. Dyn. Control. 2000, 24, 1405–1423. [Google Scholar] [CrossRef]
- Sims, C.A. Solving Linear Rational Expectations Models. Available online: http://sims.princeton.edu/yftp/gensys/LINRE3A.pdf (accessed on 5 May 2022).
- Heijdra Ben, J.; Van Der Ploeg, F. The Foundations of Modern Macroeconomics; University Press: Oxford, UK, 2002; p. 751. [Google Scholar]
- Baluta, V.I.; Shults, D.N. A version of dynamic stochastic general equilibrium model for open economy. Matem. Mod. 2019, 31, 117–131. [Google Scholar] [CrossRef]
- Polbin, A.V. Teoreticheskie i Metodologicheskie Osnovy Dlja Razrabotki Dinamicheskoj Stohasticheskoj Modeli Ob-Shhego Ravnovesija Dlja Rossijskoj Jekonomiki. Ph.D. Thesis, RANEPA, Moscow, Russian, 2015. [Google Scholar]
- Andreyev, M. Adding a fiscal rule into a DSGE model: How much does it change the forecasts? Bank Russ. 2020, 64, 54. [Google Scholar]
- Kreptsev, D.; Seleznev, S. Forecasting for the Russian Economy Using Small-Scale DSGE Models. Money Financ. 2018, 2, 77. [Google Scholar] [CrossRef]
- Novak, A.; Shul’gin, A. Denezhno-Kreditnaja Politika v Jekonomike s Regional’noj Neodnorodnost’ju: Podhody na Osnove Agregirovannoj i Regional’noj Informacii. Available online: https://cbr.ru/Content/Document/File/108035/wp_2003.pdf (accessed on 3 April 2022).
- Chislo Vybyvshikh. Available online: https://www.fedstat.ru/indicator/43513 (accessed on 3 April 2022).
- Srednemesiachnaia Nominal’naia Nachislennaia Zarabotnaia Plata Rabotnikov po Polnomu Krugu Organizatsii po Sub”ektam Rossiiskoi Federatsii s 2019 Goda. Available online: https://rosstat.gov.ru/storage/mediabank/tab2_zpl.xlsx (accessed on 3 April 2022).
- Komarova, A.V.; Kritsyna, E.A. On the proportion human capital in GRP of Russian Regions. Vestn. NGU. Seriia Sotsial’no-Ekon. Nauk. 2012, 12, 5–14. [Google Scholar]
- Zemtsov, S.P.; Smelov, Y.A. Factors of Regional Development in Russia: Geography, Human Capital and Regional Policies. JNEA 2018, 40, 84–108. [Google Scholar] [CrossRef]
- Komarova, A.V.; Pavshok, P.O. Otsenka Vklada Chelovecheskogo Kapitala v Ekonomicheskii Rost Regionov Rossii (na os-nove modeli Menk’iu—Romera—Ueila). Vestn. NGU. Seriia Sotsial’no-Eknomicheskie Nauk. 2007, 7, 191–201. [Google Scholar]
- Elementy Ispol’zovaniia Valovogo Vnutrennego Produkta. Available online: https://rosstat.gov.ru/storage/mediabank/GDP-years-of-use-1995.xls (accessed on 3 April 2022).
- Analiz Tendentsii v Biudzhetno-Nalogovoi Sfere Rossii. Available online: https://www.rea.ru/Documents/%D0%91%D1%8E%D0%B4%D0%B6%D0%B5%D1%82_%D0%B8%D1%82%D0%BE%D0%B3_2020_2.pdf (accessed on 3 April 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).