Esoteric Pull and Esoteric Push: Two Simple In-Place Streaming Schemes for the Lattice Boltzmann Method on GPUs
Abstract
:1. Introduction
2. Naive Implementation—One-Step Pull and One-Step Push
3. State-of-the-Art Methods for In-Place Streaming on GPUs
3.1. AA-Pattern
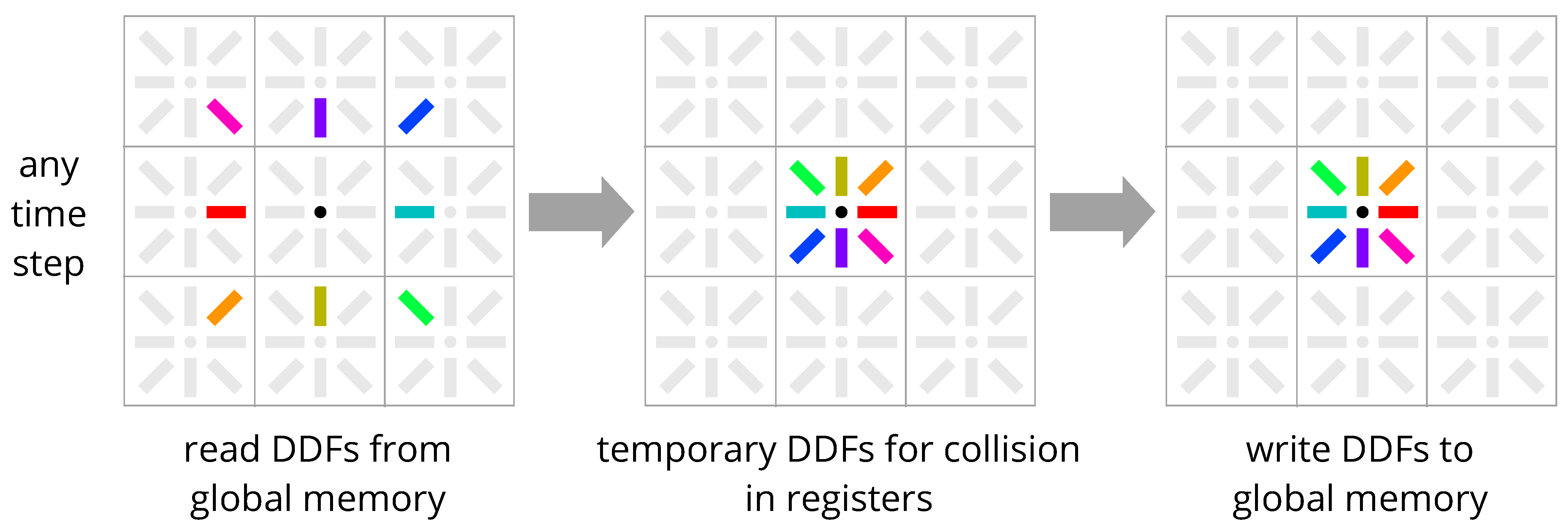
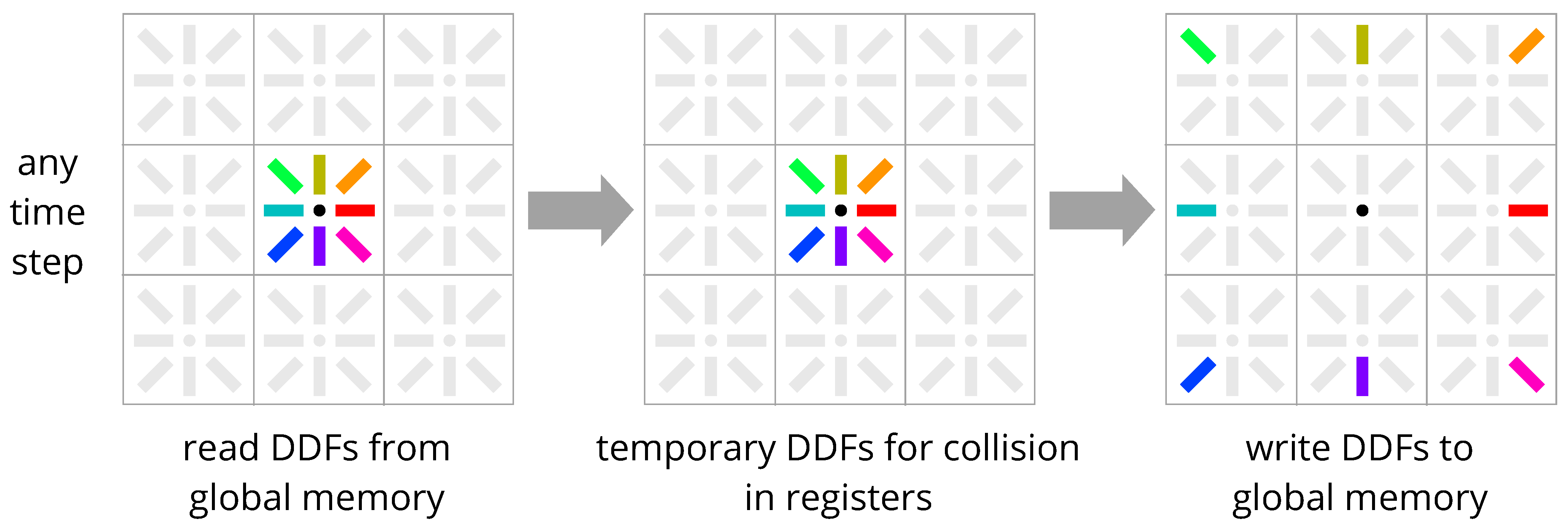
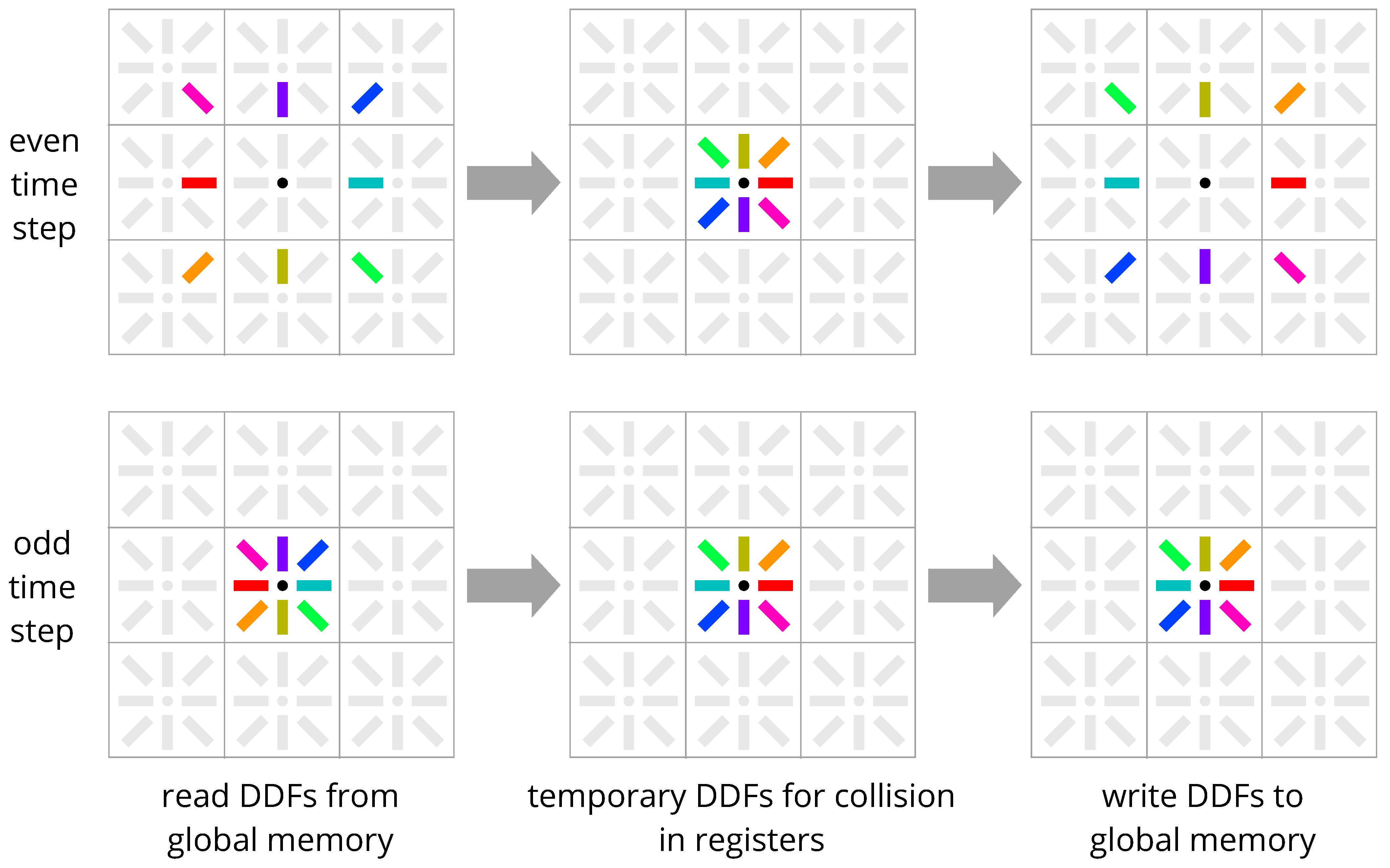
3.2. Esoteric Twist
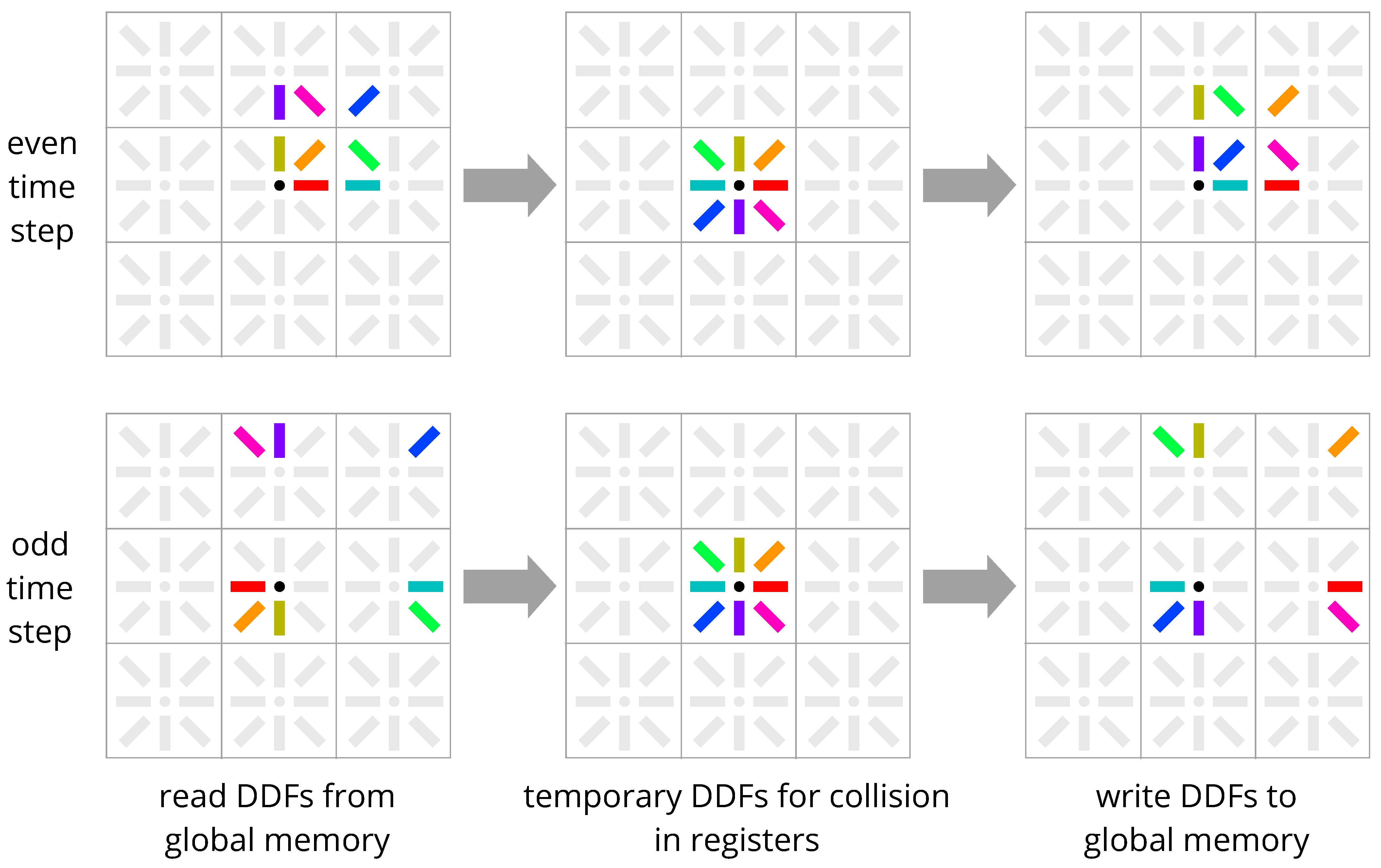
4. New Methods: Esoteric Pull and Esoteric Push
4.1. Implicit Bounce-Back
4.2. Comparison with Existing Streaming Schemes
5. Esoteric Pull for Free Surface LBM on GPUs
- stream_collide: Immediately return for G nodes. Stream in DDFs from neighbors, but for F and I nodes also load outgoing DDFs from the center node to compute the mass transfer for Volume-of-Fluid [67]. Apply excess mass for F or I nodes by summing it from all neighboring F and I nodes. Compute the local surface curvature with PLIC [26] and reconstruct DDFs from neighboring G nodes. After collision, compare mass m and post-collision density ; along with neighboring flags, mark whether the center node should remain I or change to IF or IG. Store post-collision DDFs at the local node.
- surface_1: Prevent neighbors of IF nodes from becoming/being G nodes; update flags of such neighbors to either I (from IF) or GI (from G).
- surface_2: For GI nodes, reconstruct and store DDFs based on the average density and velocity of all neighboring F, I, or IF nodes. For IG nodes, turn all neighboring F or IF nodes to I.
- surface_3: Change IF nodes to F, IG nodes to G, and GI nodes to I. Compute excess mass for each case separately as well as for F, I, and G nodes, then divide the local excess mass by the number of neighboring F, I, IF, and GI nodes and store the excess mass on the local node.
- surface_0: Immediately return for G nodes. Stream in DDFs as in Figure 5 (incoming DDFs), but also load outgoing DDFs in opposite directions to compute the mass transfer for Volume-of-Fluid. For I nodes, compute the local surface curvature with PLIC and reconstruct DDFs for neighboring G nodes; store these reconstructed DDFs in the locations at the neighbors from which they will be streamed in in the following stream_collide kernel. Apply excess mass for F or I nodes by summing from all neighboring F and I nodes.
- surface_1, surface_2, surface_3: unchanged
6. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LBM | lattice Boltzmann method |
| DDF | density distribution function |
| GPU | graphics processing unit |
| CPU | central processing unit |
| SRT | single-relaxation-time |
| OSP | One-Step Pull/Push |
| AA | AA-Pattern |
| ET | Esoteric Twist |
| EP | Esoteric Pull/Push |
Appendix A. OpenCL C Implementation of the Different Streaming Schemes
Appendix A.1. One-Step Pull

Appendix A.2. One-Step Push


Appendix A.3. AA-Pattern

Appendix A.4. Esoteric Twist

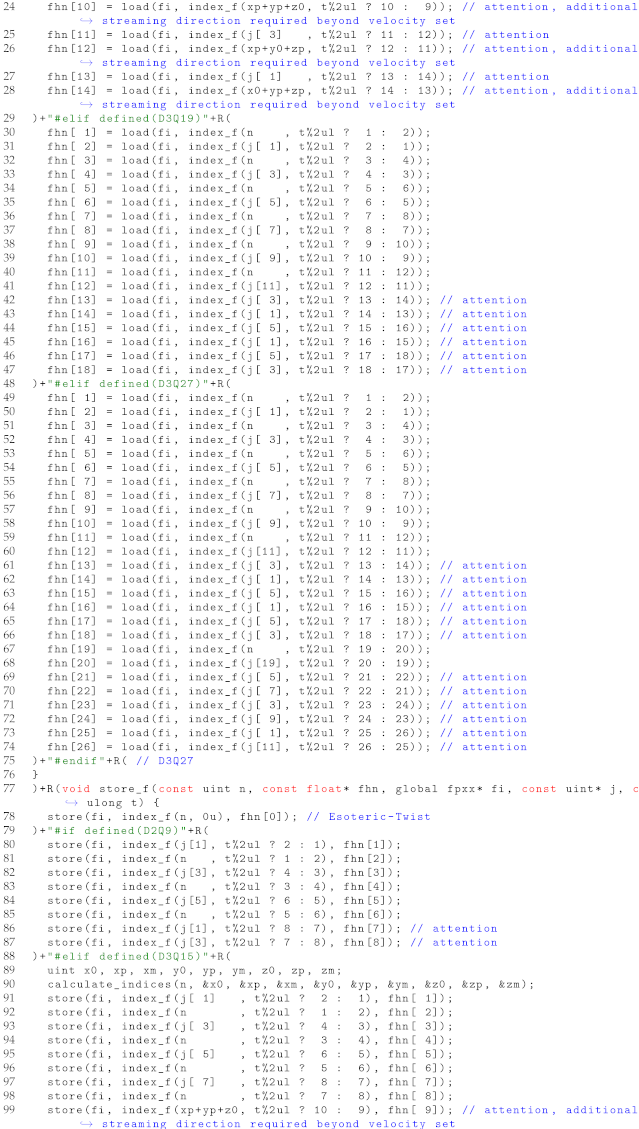

Appendix A.5. Esoteric Pull

Appendix A.6. Esoteric Push

Appendix B. OpenCL C Implementation of the FSLBM with Esoteric Pull
Appendix C. Setup Script for the Raindrop Impact Simulation


References
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method; Springer International Publishing: Cham, Switzerland, 2017; Volume 10, pp. 978–983. [Google Scholar]
- Geier, M.; Schönherr, M. Esoteric twist: An efficient in-place streaming algorithmus for the lattice Boltzmann method on massively parallel hardware. Computation 2017, 5, 19. [Google Scholar] [CrossRef]
- Bailey, P.; Myre, J.; Walsh, S.D.; Lilja, D.J.; Saar, M.O. Accelerating lattice Boltzmann fluid flow simulations using graphics processors. In Proceedings of the 2009 International Conference on Parallel Processing, Vienna, Austria, 22–25 September 2009; pp. 550–557. [Google Scholar]
- Mohrhard, M.; Thäter, G.; Bludau, J.; Horvat, B.; Krause, M. An Auto-Vecotorization Friendly Parallel Lattice Boltzmann Streaming Scheme for Direct Addressing. Comput. Fluids 2019, 181, 1–7. [Google Scholar] [CrossRef]
- Kummerländer, A.; Dorn, M.; Frank, M.; Krause, M.J. Implicit Propagation of Directly Addressed Grids in Lattice Boltzmann Methods. Comput. Fluids 2021. [Google Scholar] [CrossRef]
- Schreiber, M.; Neumann, P.; Zimmer, S.; Bungartz, H.J. Free-surface lattice-Boltzmann simulation on many-core architectures. Procedia Comput. Sci. 2011, 4, 984–993. [Google Scholar] [CrossRef] [Green Version]
- Riesinger, C.; Bakhtiari, A.; Schreiber, M.; Neumann, P.; Bungartz, H.J. A holistic scalable implementation approach of the lattice Boltzmann method for CPU/GPU heterogeneous clusters. Computation 2017, 5, 48. [Google Scholar] [CrossRef] [Green Version]
- Aksnes, E.O.; Elster, A.C. Porous rock simulations and lattice Boltzmann on GPUs. In Parallel Computing: From Multicores and GPU’s to Petascale; IOS Press: Amsterdam, The Netherlands, 2010; pp. 536–545. [Google Scholar]
- Holzer, M.; Bauer, M.; Rüde, U. Highly Efficient Lattice-Boltzmann Multiphase Simulations of Immiscible Fluids at High-Density Ratios on CPUs and GPUs through Code Generation. arXiv 2020, arXiv:2012.06144. [Google Scholar] [CrossRef]
- Duchateau, J.; Rousselle, F.; Maquignon, N.; Roussel, G.; Renaud, C. Accelerating physical simulations from a multicomponent Lattice Boltzmann method on a single-node multi-GPU architecture. In Proceedings of the 2015 10th International Conference on P2P, Parallel, Grid, Cloud and Internet Computing (3PGCIC), Krakow, Poland, 4–6 November 2015; pp. 315–322. [Google Scholar]
- Li, W.; Ma, Y.; Liu, X.; Desbrun, M. Efficient Kinetic Simulation of Two-Phase Flows. ACM Trans. Graph. 2022, 41, 114. [Google Scholar]
- Walsh, S.D.; Saar, M.O.; Bailey, P.; Lilja, D.J. Accelerating geoscience and engineering system simulations on graphics hardware. Comput. Geosci. 2009, 35, 2353–2364. [Google Scholar] [CrossRef]
- Lehmann, M.; Krause, M.J.; Amati, G.; Sega, M.; Harting, J.; Gekle, S. On the accuracy and performance of the lattice Boltzmann method with 64-bit, 32-bit and novel 16-bit number formats. arXiv 2021, arXiv:2112.08926. [Google Scholar]
- Lehmann, M. High Performance Free Surface LBM on GPUs. Master’s Thesis, University of Bayreuth, Bayreuth, Germany, 2019. [Google Scholar]
- Takáč, M.; Petráš, I. Cross-Platform GPU-Based Implementation of Lattice Boltzmann Method Solver Using ArrayFire Library. Mathematics 2021, 9, 1793. [Google Scholar] [CrossRef]
- Mawson, M.J.; Revell, A.J. Memory transfer optimization for a lattice Boltzmann solver on Kepler architecture nVidia GPUs. Comput. Phys. Commun. 2014, 185, 2566–2574. [Google Scholar] [CrossRef] [Green Version]
- Delbosc, N.; Summers, J.L.; Khan, A.; Kapur, N.; Noakes, C.J. Optimized implementation of the Lattice Boltzmann Method on a graphics processing unit towards real-time fluid simulation. Comput. Math. Appl. 2014, 67, 462–475. [Google Scholar] [CrossRef]
- Tran, N.P.; Lee, M.; Hong, S. Performance optimization of 3D lattice Boltzmann flow solver on a GPU. Sci. Program. 2017, 1205892. [Google Scholar] [CrossRef] [Green Version]
- Obrecht, C.; Kuznik, F.; Tourancheau, B.; Roux, J.J. Multi-GPU implementation of the lattice Boltzmann method. Comput. Math. Appl. 2013, 65, 252–261. [Google Scholar] [CrossRef]
- Obrecht, C.; Kuznik, F.; Tourancheau, B.; Roux, J.J. A new approach to the lattice Boltzmann method for graphics processing units. Comput. Math. Appl. 2011, 61, 3628–3638. [Google Scholar] [CrossRef] [Green Version]
- Feichtinger, C.; Habich, J.; Köstler, H.; Hager, G.; Rüde, U.; Wellein, G. A flexible Patch-based lattice Boltzmann parallelization approach for heterogeneous GPU–CPU clusters. Parallel Comput. 2011, 37, 536–549. [Google Scholar] [CrossRef] [Green Version]
- Calore, E.; Gabbana, A.; Kraus, J.; Pellegrini, E.; Schifano, S.F.; Tripiccione, R. Massively parallel lattice–Boltzmann codes on large GPU clusters. Parallel Comput. 2016, 58, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Obrecht, C.; Kuznik, F.; Tourancheau, B.; Roux, J.J. Global memory access modelling for efficient implementation of the lattice Boltzmann method on graphics processing units. In Proceedings of the International Conference on High Performance Computing for Computational Science, Berkeley, CA, USA, 22–25 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 151–161. [Google Scholar]
- Lehmann, M.; Oehlschlägel, L.M.; Häusl, F.P.; Held, A.; Gekle, S. Ejection of marine microplastics by raindrops: A computational and experimental study. Microplastics Nanoplastics 2021, 1, 18. [Google Scholar] [CrossRef]
- Laermanns, H.; Lehmann, M.; Klee, M.; Löder, M.G.; Gekle, S.; Bogner, C. Tracing the horizontal transport of microplastics on rough surfaces. Microplastics Nanoplastics 2021, 1, 11. [Google Scholar] [CrossRef]
- Lehmann, M.; Gekle, S. Analytic Solution to the Piecewise Linear Interface Construction Problem and Its Application in Curvature Calculation for Volume-of-Fluid Simulation Codes. Computation 2022, 10, 21. [Google Scholar] [CrossRef]
- Häusl, F. MPI-Based Multi-GPU Extension of the Lattice Boltzmann Method. Bachelor’s Thesis, University of Bayreuth, Bayreuth, Germay, 2019. [Google Scholar]
- Häusl, F. Soft Objects in Newtonian and Non-Newtonian Fluids: A Computational Study of Bubbles and Capsules in Flow. Master’s Thesis, University of Bayreuth, Bayreuth, Germay, 2021. [Google Scholar]
- Limbach, H.J.; Arnold, A.; Mann, B.A.; Holm, C. ESPResSo—An extensible simulation package for research on soft matter systems. Comput. Phys. Commun. 2006, 174, 704–727. [Google Scholar] [CrossRef]
- Institute for Computational Physics, Universität Stuttgart. ESPResSo User’s Guide. 2016. Available online: http://espressomd.org/wordpress/wp-content/uploads/2016/07/ug_07_2016.pdf (accessed on 15 June 2018).
- Hong, P.Y.; Huang, L.M.; Lin, L.S.; Lin, C.A. Scalable multi-relaxation-time lattice Boltzmann simulations on multi-GPU cluster. Comput. Fluids 2015, 110, 1–8. [Google Scholar] [CrossRef]
- Xian, W.; Takayuki, A. Multi-GPU performance of incompressible flow computation by lattice Boltzmann method on GPU cluster. Parallel Comput. 2011, 37, 521–535. [Google Scholar] [CrossRef]
- Ho, M.Q.; Obrecht, C.; Tourancheau, B.; de Dinechin, B.D.; Hascoet, J. Improving 3D Lattice Boltzmann Method stencil with asynchronous transfers on many-core processors. In Proceedings of the 2017 IEEE 36th International Performance Computing and Communications Conference (IPCCC), San Diego, CA, USA, 10–12 December 2017; pp. 1–9. [Google Scholar]
- Habich, J.; Feichtinger, C.; Köstler, H.; Hager, G.; Wellein, G. Performance engineering for the lattice Boltzmann method on GPGPUs: Architectural requirements and performance results. Comput. Fluids 2013, 80, 276–282. [Google Scholar] [CrossRef] [Green Version]
- Tölke, J.; Krafczyk, M. TeraFLOP computing on a desktop PC with GPUs for 3D CFD. Int. J. Comput. Fluid Dyn. 2008, 22, 443–456. [Google Scholar] [CrossRef]
- Herschlag, G.; Lee, S.; Vetter, J.S.; Randles, A. GPU data access on complex geometries for D3Q19 lattice Boltzmann method. In Proceedings of the 2018 IEEE International Parallel and Distributed Processing Symposium (IPDPS), Vancouver, BC, Canada, 21–25 May 2018; pp. 825–834. [Google Scholar]
- de Oliveira, W.B., Jr.; Lugarini, A.; Franco, A.T. Performance analysis of the lattice Boltzmann method implementation on GPU. In Proceedings of the XL Ibero-Latin-American Congress on Computational Methods in Engineering, ABMEC, Natal, Brazil, 11–14 November 2019. [Google Scholar]
- Rinaldi, P.R.; Dari, E.; Vénere, M.J.; Clausse, A. A Lattice-Boltzmann solver for 3D fluid simulation on GPU. Simul. Model. Pract. Theory 2012, 25, 163–171. [Google Scholar] [CrossRef]
- Rinaldi, P.R.; Dari, E.A.; Vénere, M.J.; Clausse, A. Fluid Simulation with Lattice Boltzmann Methods Implemented on GPUs Using CUDA. In Proceedings of the HPCLatAm 2009, Buenos Aires, Argentina, 26–27 August 2009. [Google Scholar]
- Ames, J.; Puleri, D.F.; Balogh, P.; Gounley, J.; Draeger, E.W.; Randles, A. Multi-GPU immersed boundary method hemodynamics simulations. J. Comput. Sci. 2020, 44, 101153. [Google Scholar] [CrossRef]
- Xiong, Q.; Li, B.; Xu, J.; Fang, X.; Wang, X.; Wang, L.; He, X.; Ge, W. Efficient parallel implementation of the lattice Boltzmann method on large clusters of graphic processing units. Chin. Sci. Bull. 2012, 57, 707–715. [Google Scholar] [CrossRef] [Green Version]
- Zhu, H.; Xu, X.; Huang, G.; Qin, Z.; Wen, B. An Efficient Graphics Processing Unit Scheme for Complex Geometry Simulations Using the Lattice Boltzmann Method. IEEE Access 2020, 8, 185158–185168. [Google Scholar] [CrossRef]
- Kuznik, F.; Obrecht, C.; Rusaouen, G.; Roux, J.J. LBM based flow simulation using GPU computing processor. Comput. Math. Appl. 2010, 59, 2380–2392. [Google Scholar] [CrossRef] [Green Version]
- Horga, A. With Lattice Boltzmann Models Using CUDA Enabled GPGPUs. Master’s Thesis, University of Timsoara, Timsoara, Romania, 2013. [Google Scholar]
- Geveler, M.; Ribbrock, D.; Göddeke, D.; Turek, S. Lattice-Boltzmann simulation of the shallow-water equations with fluid-structure interaction on multi-and manycore processors. In Facing the Multicore-Challenge; Springer: Wiesbaden, Germany, 2010; pp. 92–104. [Google Scholar]
- Beny, J.; Latt, J. Efficient LBM on GPUs for dense moving objects using immersed boundary condition. arXiv 2019, arXiv:1904.02108. [Google Scholar]
- Tekic, P.M.; Radjenovic, J.B.; Rackovic, M. Implementation of the Lattice Boltzmann method on heterogeneous hardware and platforms using OpenCL. Adv. Electr. Comput. Eng. 2012, 12, 51–56. [Google Scholar] [CrossRef]
- Bény, J.; Kotsalos, C.; Latt, J. Toward full GPU implementation of fluid-structure interaction. In Proceedings of the 2019 18th International Symposium on Parallel and Distributed Computing (ISPDC), Amsterdam, The Netherlands, 3–7 June 2019; pp. 16–22. [Google Scholar]
- Boroni, G.; Dottori, J.; Rinaldi, P. FULL GPU implementation of lattice-Boltzmann methods with immersed boundary conditions for fast fluid simulations. Int. J. Multiphysics 2017, 11, 1–14. [Google Scholar]
- Griebel, M.; Schweitzer, M.A. Meshfree Methods for Partial Differential Equations II; Springer: Cham, Switzerland, 2005. [Google Scholar]
- Zitz, S.; Scagliarini, A.; Harting, J. Lattice Boltzmann simulations of stochastic thin film dewetting. Phys. Rev. E 2021, 104, 034801. [Google Scholar] [CrossRef] [PubMed]
- Janßen, C.F.; Mierke, D.; Überrück, M.; Gralher, S.; Rung, T. Validation of the GPU-accelerated CFD solver ELBE for free surface flow problems in civil and environmental engineering. Computation 2015, 3, 354–385. [Google Scholar] [CrossRef] [Green Version]
- Habich, J.; Zeiser, T.; Hager, G.; Wellein, G. Performance analysis and optimization strategies for a D3Q19 lattice Boltzmann kernel on nVIDIA GPUs using CUDA. Adv. Eng. Softw. 2011, 42, 266–272. [Google Scholar] [CrossRef]
- Calore, E.; Marchi, D.; Schifano, S.F.; Tripiccione, R. Optimizing communications in multi-GPU Lattice Boltzmann simulations. In Proceedings of the 2015 International Conference on High Performance Computing & Simulation (HPCS), Amsterdam, The Netherlands, 20–24 July 2015; pp. 55–62. [Google Scholar]
- Onodera, N.; Idomura, Y.; Uesawa, S.; Yamashita, S.; Yoshida, H. Locally mesh-refined lattice Boltzmann method for fuel debris air cooling analysis on GPU supercomputer. Mech. Eng. J. 2020, 7, 19–00531. [Google Scholar] [CrossRef] [Green Version]
- Falcucci, G.; Amati, G.; Fanelli, P.; Krastev, V.K.; Polverino, G.; Porfiri, M.; Succi, S. Extreme flow simulations reveal skeletal adaptations of deep-sea sponges. Nature 2021, 595, 537–541. [Google Scholar] [CrossRef]
- Zitz, S.; Scagliarini, A.; Maddu, S.; Darhuber, A.A.; Harting, J. Lattice Boltzmann method for thin-liquid-film hydrodynamics. Phys. Rev. E 2019, 100, 033313. [Google Scholar] [CrossRef] [Green Version]
- Wei, C.; Zhenghua, W.; Zongzhe, L.; Lu, Y.; Yongxian, W. An improved LBM approach for heterogeneous GPU-CPU clusters. In Proceedings of the 2011 4th International Conference on Biomedical Engineering and Informatics (BMEI), Shanghai, China, 15–17 October 2011; Volume 4, pp. 2095–2098. [Google Scholar]
- Gray, F.; Boek, E. Enhancing computational precision for lattice Boltzmann schemes in porous media flows. Computation 2016, 4, 11. [Google Scholar] [CrossRef] [Green Version]
- Wellein, G.; Lammers, P.; Hager, G.; Donath, S.; Zeiser, T. Towards optimal performance for lattice Boltzmann applications on terascale computers. In Parallel Computational Fluid Dynamics 2005; Elsevier: Amsterdam, The Netherlands, 2006; pp. 31–40. [Google Scholar]
- Wittmann, M.; Zeiser, T.; Hager, G.; Wellein, G. Comparison of different propagation steps for lattice Boltzmann methods. Comput. Math. Appl. 2013, 65, 924–935. [Google Scholar] [CrossRef]
- Wittmann, M. Hardware-effiziente, hochparallele Implementierungen von Lattice-Boltzmann-Verfahren für komplexe Geometrien. Ph.D. Thesis, Friedrich-Alexander-Universität, Erlangen, Germany, 2016. [Google Scholar]
- Krause, M. Fluid Flow Simulation and Optimisation with Lattice Boltzmann Methods on High Performance Computers: Application to the Human Respiratory System. Ph.D. Thesis, Karlsruhe Institute of Technology (KIT), Universität Karlsruhe (TH), Karlsruhe, Germany, 2010. Available online: https://publikationen.bibliothek.kit.edu/1000019768 (accessed on 20 February 2019).
- Succi, S.; Amati, G.; Bernaschi, M.; Falcucci, G.; Lauricella, M.; Montessori, A. Towards exascale lattice Boltzmann computing. Comput. Fluids 2019, 181, 107–115. [Google Scholar] [CrossRef]
- D’Humières, D. Multiple–relaxation–time lattice Boltzmann models in three dimensions. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar] [CrossRef]
- Latt, J. Technical Report: How to Implement Your DdQq Dynamics with Only q Variables per Node (Instead of 2q); Tufts University: Medford, MA, USA, 2007; pp. 1–8. [Google Scholar]
- Bogner, S.; Rüde, U.; Harting, J. Curvature estimation from a volume-of-fluid indicator function for the simulation of surface tension and wetting with a free-surface lattice Boltzmann method. Phys. Rev. E 2016, 93, 043302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crane, K.; Llamas, I.; Tariq, S. Real-Time Simulation and Rendering of 3d Fluids; GPU gems 3.1, Addison-Wesley Professional: Boston, MA, USA, 2007; Volume 3. [Google Scholar]
- Gerace, S. A Model Integrated Meshless Solver (MIMS) for Fluid Flow and Heat Transfer. Ph.D. Thesis, University of Central Florida, Orlando, FL, USA, 2010. [Google Scholar]
- Lynch, C.E. Advanced CFD Methods for Wind Turbine Analysis; Georgia Institute of Technology: Atlanta, GA, USA, 2011. [Google Scholar]
- Keßler, A. Matrix-Free Voxel-Based Finite Element Method for Materials with Heterogeneous Microstructures. Ph.D. Thesis, der Bauhaus-Universität Weimar, Weimar, Germnay, 2019. [Google Scholar]




| Algorithm | Storage | Bandwidth |
|---|---|---|
| One-Step Pull | ||
| One-Step Push | ||
| AA-Pattern | ||
| Esoteric Twist | ||
| Esoteric Pull | ||
| Esoteric Push | ||
| OSP + FP32/16-bit | ||
| AA + FP32/16-bit | ||
| ET/EP + FP32/16-bit |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lehmann, M. Esoteric Pull and Esoteric Push: Two Simple In-Place Streaming Schemes for the Lattice Boltzmann Method on GPUs. Computation 2022, 10, 92. https://doi.org/10.3390/computation10060092
Lehmann M. Esoteric Pull and Esoteric Push: Two Simple In-Place Streaming Schemes for the Lattice Boltzmann Method on GPUs. Computation. 2022; 10(6):92. https://doi.org/10.3390/computation10060092
Chicago/Turabian StyleLehmann, Moritz. 2022. "Esoteric Pull and Esoteric Push: Two Simple In-Place Streaming Schemes for the Lattice Boltzmann Method on GPUs" Computation 10, no. 6: 92. https://doi.org/10.3390/computation10060092
APA StyleLehmann, M. (2022). Esoteric Pull and Esoteric Push: Two Simple In-Place Streaming Schemes for the Lattice Boltzmann Method on GPUs. Computation, 10(6), 92. https://doi.org/10.3390/computation10060092













