Abstract
Innumerable industries now use multi-agent systems (MASs) in various contexts, including healthcare, security, and commercial deployments. It is challenging to select reliable business protocols for critically important safety-related systems (e.g., in healthcare). The verification and validation of business applications is increasingly explored concerning multi-agent systems’ group social commitments. This study explains a novel extended reduction verification method to model-check business applications’ critical specification rules using action restricted computation tree logic (ARCTL). In particular, we aim to conduct the verification process for the CTLGC logic using a reduction algorithm and show its effectiveness to handle MASs with huge models, thus, showing its importance and applicability in large real-world applications. To do so, we need to transform the CTLGC model to an ARCTL model and the CTLGC formulas into ARCTL formulas. Thus, the developed method was verified with the model-checker new symbolic model verifier (NuSMV), and it demonstrated effectiveness in the safety-critical specification rule support provision. The proposed method can verify up to 2.43462 × 1014 states MASs, which shows its effectiveness when applied to real-world applications.
1. Introduction
Innumerable industries now use multi-agent systems (MASs) in various contexts, including healthcare, security, and commercial deployments [1,2,3]. Researchers have extensively undertaken highly structured modeling approaches for MASs to determine required specifications, considering the multifarious dimensions that must be technically accommodated within complex systems for synchronicity in modeling [4]. Model-checking verifies whether MASs perform as required in relation to their specifications [5]. This highly challenging context is inevitable for such modeling, and it presents a formidable challenge when modeling and verifying MASs [6,7]. This paper presents a model-checking tool to automatically investigate group commitment-related features. Investigating the problem of verifying MASs in the presence of single and group social commitments and their fulfillment is rarely addressed, specifically, the cases of specifying and verifying group-to-one and one-to-group social commitments. In our work in [8], we addressed group social commitments in MASs from semantics perspectives. In this work, we plan to enrich the literature of MASs by investigating group social commitment from a verification perspective (i.e., model-checking perspective). To do so, we extend our work in [8] by proposing a model-checking algorithm using the reduction approach, thus, providing an effective and consistent framework that can handle MASs with huge models. In particular, in this study, we investigate an MAS model that reaches 2.43462 × 1014 states before reaching a state explosion problem.
The following examples illustrate the rationale for undertaking specifying MASs using group social commitments.
Example 1.
Consider an employer who promises his employees a 5% salary raise if they complete a task over one month. This is a “one-to-group” commitment, whereby the single employer must remunerate each employee within the group if the group carried out the task.
Example 2.
Employees promise the employer that they will complete their task in two weeks; this relationship is a “group-to-one” commitment.
The analysis and determination of group and single commitments require commensurate tools and solutions. The expressive power of the logic developed by a previous study [9] was restricted to the reasoning and representation of single social commitments within MASs. More recent work has explored novel temporal logic for single and group social commitment reasoning in MASs in terms of verification and formal semantics [8]. In [8], computation tree logic group commitments (CTLGC) logic extended CTL [10,11] to fulfil single and group commitments with appropriate modalities, with a comprehensive logic able to process both commitment types simultaneously within the same architecture. The study also revised and developed the previous system of [12], with a formal CTLGC model for formula interpretation. The developed extension enables the modeling of interactions between groups and single agents.
The current study seeks to present a significant model-checking algorithm for the CTLGC logic [8] that can effectively verify large MASs with huge state space by introducing a reduction-based model-checker algorithm. The proposed algorithm transforms the CTLGC logic into the ARCTL logic [13], in order to use its model-checker [14] the NuSMV. The problem of model-checking the CTLGC logic has not been addressed before, which gives a novelty to our work.
Figure 1 is given as an overview of the developed approach, which comprises three phases. In phase 1, the CTLGC logic [8], which has modalities to reason about group and single commitments, was recalled. In phase 2, reduction/transformation was used for a formal verification algorithm, converting the model-checking CTLGC logic problem into an ARCTL-model checking problem [13]. In phase 3, the effectiveness of this approach was tested by application with the extended NuSMV model-checker [14], reporting the verification results.
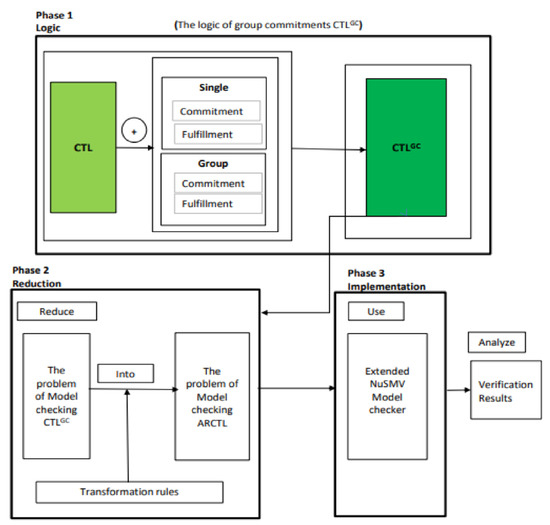
Figure 1.
Schematic diagram of new approach.
1.1. Paper Contributions
In this paper, we aim to enrich the literature of group social commitments in MASs from verification perspectives. In particular, we aim to address the following:
We aim to develop a reduction-based model-checking algorithm for the CTLGC group commitments logic, by transforming the CTLGC model-checking problem into an ARCTL model-checking problem using transformation rules. By doing so, we can use the extended NuSMV model-checker.
We aim to prove the soundness of the proposed reduction model-checking algorithm.
We aim to investigate the effectiveness and applicability of the proposed algorithm by implementing a real case study from the business domain (i.e., the NetBill protocol [15]).
1.2. Paper Organization
The remainder of this study is arranged as follows. Section 2 explores modeling development in terms of reasoning and verifying with regard to group and single MAS commitments. Subsequently, the formalism and effectiveness of interpreted systems (ISs) are explained for MAS modeling. Finally, the paradigm of symbolic model-checking is presented. Section 3 contains the semantics and syntax of the CTLGC logic, whose problem model-checking is analyzed in Section 4. Section 5 describes the implementation of the novel technique and the verification outcomes. Section 6 concludes the study.
2. Preliminaries
2.1. Commitments in Multi-Agent Systems (MASs)
A major aspect of multi-agent systems (MASs) is communication. Through communication, the agents do plan their behaviors and actions so as to achieve their predetermined goals [16]. In addition, autonomous, heterogeneous agents use agent communication languages (ACLs) in order to interact with each other and interchange messages [17,18,19,20]. Accordingly, there is significant need for the development of formal and coherent semantics for these ACLs [21,22].
A review of the published literature spotlights that numerous frameworks have been developed in the effort to find effective standards for the agent communications [22,23,24,25,26,27,28]. Within this context, Searle’s speech acts theory [29] represents the first endeavor to formulate standard semantic for the ACLs, namely, the mental approach. This semantic tries to analyze the tradeoffs among certain aspects of agent communications such as the belief-desire-intention (BDI) aspects, and provide a rational tradeoff between them [30]. This approach handles the communications as actions that ought to be performed by agents so as to achieve their goals. However, the mental methods focus on the minds of the interacting agents. Actually, they presume that the agents can guess how the others think [25]. As a consequence, these methods fail to determine if a certain agent does, or does not, behave on the basis of distinct semantics. Accordingly, these methods suffer from the well-known problem of semantics verification [31]. Besides this problem, these methods suffer from the lack of interoperability among the heterogeneous systems [25].
To fix these two problems of the ACL semantics, the MAS community made a substantial switch to social approaches [15,25]. Indeed, novel formal semantics for the ACLs were developed by adopting social approaches [15,32,33,34,35]. These approaches used the social commitments in order to produce robust frameworks which model the interactions among the agents in the MASs [2,21,26,36,37,38]. Manipulation and negotiation of commitments impart to the commitment-based techniques high flexibility and the capability to reason about the interactions among the agents in the MASs [39,40].
The social commitments have so far been successfully employed in numerous real applications, such as verification of the security protocols [41]; specification, modeling, and verification of multi-agent interaction protocols [42,43,44]; identification and verification of contracts of service composition [45]; development of Web-based applications [46,47]; modeling of the business processes [48]; introduction of artificial institutions [49]; and development of programming languages [50,51] and blockchain applications [52].
Varying frameworks were developed in order to formalize group commitments [53,54,55,56,57]. However, not one of those frameworks has the ability to classify the groups of agents. Additionally, not one of them can address the group-to-one social commitments and their fulfillment. Castelfranchi [58] categorized the commitments into three types: social, internal, and collective commitments. He has defined the internal commitment as a relation between a certain agent and its action. Moreover, he considered the social commitment as a relation between two agents. Furthermore, he stated that in the group (or collective) commitments “a set of agents is internally committed to a certain intention and (usually) there is mutual knowledge about that.” This conception of group commitment is very close to the conception of the previously-explained mental approaches. The rest of the frameworks followed a similar method to that of Castelfranchi [58] in formalizing the collective commitments.
Additionally, Wozna-Szczesniak and Szczesniak [31] expanded the work presented in [59] and presented new, real-time, unconditional, and conditional social commitment logic, referred to as RTCTLC. These researchers [31] defined their semantics over the duration communication interpreted system (DCIS), which is actually a system in which transitions have integer duration. These transitions enabled them to model numerous levels of deadlines and reduce further verification works because of using unit measure steps. The RTCTLC has the capability to figure out the unconditional, conditional, and group commitments and their associated fulfillments and real-time restraints, and to express them. For figuring out group commitments, these researchers examined only the one-to-group unconditional and conditional commitments and their fulfillment. Furthermore, they did not touch upon completeness and soundness of the RTCTLC. Moreover, they did not address the RTCTLC model-checking problem.
Sultan [60] examined MASs in which the agents have knowledge and communicate by manipulation of uncertain social commitments, particularly when the scope of the commitment steps is beyond the popular agent-to-agent plan or route. He proposed a method for model-checking that aims at verifying these systems and capitalizing not only on interactions between individuals, but also on one-to-group communicative commitments and knowledge under the condition of the presence of uncertainty. The effectiveness of this approach was assessed by implementing it atop of the PRISM model-checker. However, Sultan [60] did not address group-to-one commitments.
Lastly, we presented the CTLGC logic in [8]. It is a temporal logic of group commitments for the agent communications that extends the computation tree logic (CTL) in such a way as to simultaneously reason about and specify the group social commitments and their fulfillment. For this purpose, we categorized the groups of the communicating agents into indivisible and divisible communicating groups. Then, we classified the group commitments into two categories: group-to-one commitments and one-to-group commitments. Afterwards, we identified the social accessibility relationships that are necessary for capturing the semantics of every type of commitment group. Then, we adopted Benthem’s correspondence theory for the modal logics, so as to prove soundness and completeness of the CTLGC logic. However, we did not investigate the model-checking problem of CTLGC. Thus, in this study, we aim to address the model-checking problem of the CTLGC logic using reduction / transformation.
Revising the related research in the literature, we can summarize the gaps in the following:
- -
- Mental approaches in [22,23,24,25,27,52] suffer from a semantics verification problem [31]. Moreover, these methods suffer from the lack of interoperability among the heterogeneous systems [25].
- -
- Social approaches in [2,21,36,37,39,40,52] addressed only single commitment. None of them investigated group commitment.
- -
- Social approaches in [54,55,56,57,58] addressed group commitment using mental approaches. Therefore, none of them classified the groups of agents. Additionally, none of them addressed group-to-one social commitments and their fulfillment.
- -
- Wozna-Szczesniak and Szczesniak [27] did not address the RTCTLC model-checking problem.
- -
- Sultan [60] did not address group-to-one commitments and only investigated one-to-group commitments in the presence of uncertainty.
- -
- Our work in [8] classified a group of agents into divisible and indivisible, addressed one-to-group and group-to-one commitments, and proved the soundness and completeness of the CTLGC logic. However, model-checking CTLGC was not investigated.
Consequently, to close the gaps in the literature and extend our work in [8], we aim to address the verification problem of CTLGC by proposing a reduction-based model-checking algorithm and building more effective and consistent MASs.
2.2. Modeling MASs by Using Interpreted Systems
Formalism of the interpreted systems (ISs) was first developed by Fagin et al. [12], in an effort to model the temporal evolution of a MASs so as to infer the knowledge and associated temporal properties. Formalism of the ISs does model differing classes of the MASs such as the asynchronous and the synchronous systems. In addition, it is broadly employed for local modeling of the heterogeneous and autonomous agents interacting within a global system via message sending and receiving [21].
ISs formalism consists of:
- “Set of n agents; A = {1, …, n}, such that every single agent i is defined by:
- —
- Non-empty set of local states, Li. Local state of the agent i is described by li ∈ Li. Every local state of the agent holds complete information about the system which this agent has at a specified moment.
- —
- Set of local actions (Acti) in order to demonstrate the evolution of the system with time, i.e., the temporal evolution.
- —
- Function for local protocol (Pi: Li → 2Acti) in order to define the set of enabled actions which can be implemented in a certain local state.
- —
- Function for local evolution, τi, that specifies transitions for agent i between its local states. This function is defined as τi: Li × Acti → Li.
- Set of the entire global states in the system G ⊆ L1 ×⋯× Ln is a sub-set of the Cartesian product of the whole local states of the n agents such that:
- —
- Global state g ∈ G is tuple; g = (l1, …, ln), that corresponds to a snapshot of the system.
- —
- Local state of the agent i in global state g is denoted as li (g).
- I ⊆ G is the set of the initial global states for the system.
- Global transition function. This function can be defined as τ: G × ACT → G, where ACT = Act1 ×⋯× Actn and every constituent, a ∈ ACT, is a joint action; that is, a tuple of actions, one only for every single agent.
- Set of atomic presumptions, Φp, and valuation function, V, for these presumptions, V: G → 2Φp”.
For the provision of intuitive semantics for the social commitments which are established via communications among the interacting agents, Bentahar et al. [61] and El-Menshawy et al. [21] outspread formalism of the interpreted systems using shared and unshared variables.
In this paper, much like the case in telecommunications, we base our work on the assumption of asynchronous communication; that is, the creditor and debtor, both, function independent of one the other. Stated otherwise, the sender (i.e., the debtor) does not need to wait for acknowledgment of the sent message by the recipient (i.e., the creditor). Therefore, the debtor can send other messages or more to the creditor without knowing when those messages are received and processed by her/him. The idea of the herein designed model is similar to the communication architecture in the distributed systems, in that for any two agents, i and j, to communicate, they must have a shared channel for communication, which is exemplified by variables shared between these two agents: i and j [61].
2.3. Symbolic Model-Checking
Model-checking is an automatic, formal method that is employed for verification of finite state concurrent systems [11]. The process of model-checking is intended to answer the question: given certain model M and specific property φ that corresponds to specification in certain temporal logic, does this model fulfill this property? If the model does not fulfill this property, that is, M ⊭ φ, then the process returns a counterexample message that shows the steps wherein the error state was reached. However, if the model satisfies this property, namely, M ⊨ φ, then the process returns a true message.
Approaches to symbolic model-checking proved to be efficient in automatically verifying the soundness of MASs [62,63] as they, in general, utilize less memory than the automata-based methods because algorithms of the former methods are actually applied on Boolean functions (Bfs) rather than on explicit Kripke structures as is the case in the latter methods. In practice, the space requirements of the Bfs that can be expressed by employing ordered binary decision diagrams (OBDDs) [58] are exponentially smaller than the corresponding space requirements of an explicit representation. Accordingly, the symbolic model-checking techniques reduce the state explosion problem. In this study, we develop a model-checking method that belongs to the symbolic class of methods and apply our method on top of the expanded symbolic model-checker NuSMV [14].
3. The CTLGC Logic
This section recalls the syntax and semantics of the CTLGC logic which we earlier presented in [8]. The syntax of the CTLGC is an extension of the CTL [11], with modalities for both group and single commitments and associated fulfillments. It is defined as follows [8]:
Definition 1.
Syntax of the CTLGC.
“φ ::= p |¬φ | φ∨φ | EXφ | E(φUφ) | EG |C| Fu
C ::= Ci→jφ | Ci→Ωφ| CΩ→jφ
Fu ::= Fu(Ci→jφ) | Fu(Ci→Ωφ) | Fu(CΩ→jφ)”
Such that
- p, ¬,∨, E, X, U andG are similar CTL modalities [11].
- The formulae of social commitmentC are formulae for special state in the CTLGC that grab social characteristics by employing theCi→jφ,Ci→Ω, andCΩ→j modal connectives, which stand for ‘commitment’, ‘commitment to divisible group’, and ‘commitment from divisible group’, respectively.
The expression Ci→jφ means ”agent i commits to agent j that is φ” [61]. The term Ci→Ωφ implies that agent i commits to everyone in Ω that is φ. Meanwhile, the expression CΩ→jφ indicates that everyone in Ω commits to j that is φ.
In this study, we only recall semantics of the group and the single commitments and their associated fulfillments because the chief part of the CTLGC logic is the CTL logic [11].
Definition 2.
Satisfaction of the CTLGC [8].
By using modelM, satisfaction of the formula of CTLGC,, that is, φ, in some global statew described by (M,w) |= φ is defined repeatedly as follows:
- (M,w) |= Ci→jφ iff the condition of(M,w′) |= φ is satisfied for all the global statesw′∈W such thatw∼i→jw′;
- (M,w) |= Ci→Ωφ iff the condition of(M,w′) |= φ is satisfied for all the global statesw′∈W such thatw∼i→Ω w′;
- (M,w) |= CΩ→jφ iff the condition of(M,w′) |= φ is satisfied for all the global statesw′∈W such thatw∼Ω→jw′;
- (M,w) |= Fu(Ci→jφ) iff there isw′∈W such thatw′∼i→jw and(M,w′) |= Ci→jφ;
- (M,w) |= Fu(Ci→Ωφ) iff there isw′∈W such thatw′∼i→Ω w and(M,w′) |= Ci→Ωφ;
- (M,w) |= Fu(CΩ→jφ) iff there isw′∈W such thatw′∼Ω→jw and(M,w′) |= CΩ→jφ.
The semantics of the formulae of the CTLGC state are defined in model M such as the semantics of standard CTL [11] with modalities for specifying single social commitments, group social commitments, fulfillment, and group fulfillment. More details about the semantic of CTLGC can be found in [8].
4. Symbolic Model-Checking Algorithm for CTLGC
This section introduces a new method for model-checking of the CTLGC. The technical formulation of the problem of model-checking the CTLGC can be summarized as follows:
Given an MAS that is represented as an interpreted system model M and formula φ in the CTLGC that describes certain property, the model-checking problem can be described as determining whether or not ‘M ⊨ φ, i.e., ∀ s ∈ I M,s) ⊨ φ [8].
Checking the logic of the CTLGC can be conducted in either of the two methods, direct method or formal transformation (reduction) method, as follows:
- The direct method can be performed by either developing an appropriate model-checker from scratch or extending an already existent model-checker by using new algorithms for the due modalities as was made in [61,64,65,66].
- Formal transformation entails transforming a method into an existent model-checker as was made in [14,21,46,67]. In this study, we adopt this approach and, accordingly, transform the CTLGC model-checking problem into a problem of ARCTL model- checking [13].
4.1. Transforming the CTLGC into ARCTL
This section briefly reviews the ARCTL logic [13], and then illustrates how the CTLGC model-checking problem can be transformed, that is, reduced, to an ARCTL model-checking problem. The major advantage of employing this reduction (transformation) is benefiting from the procedure of efficient model-checking that is already incorporated into the extended NuSMV model-checker [68]. Figure 2 presents the workflow of such a transformation method that comprises three subsequent processes. Firstly, we reduce the CTLGC model M into the ARCTL model. Secondly, we reduce the CTLGC formulae into the ARCTL formulae. Then, both the ARCTL model and ARCTL formulae are inputted to the extended NuSMV model-checker so as to obtain the model verification outcomes.
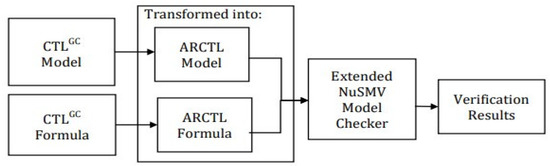
Figure 2.
Workflow of the proposed reduction technique.
Syntax of the ARCTL is defined by BNF grammar [13] as follows:
- “φ ::= p |¬φ | φ∨φ | EαXφ | Eα(φ U φ) | EαGφ
- α ::= b |¬α | α∨α”
where φ expresses state formula, α represents action formula, p ∈ Φp denotes atomic proposition, and b ∈ Φa stands for proposition of atomic action. The ARCTL logic integrates the action formulae and state formulae by means of confining the path formulae to the particular paths whose actions fulfill certain action formula.
Definition 3.
ARCTL Model.
A modelMAR = (SAR, IAR, ACAR, TAR, VSAR, VAAR) is tuple, whereSAR is non-empty set of states;IAR⊆SAR is set of initial states;ACAR is set of actions;TAR⊆SAR × ACAR × SAR is labeled transition relationship;VSAR : SAR → 2Φp is interpretation for the atomic propositions; andVAAR : ACAR → 2Φa is interpretation for atomic action propositions.
The semantics of this logic [13] are obtained by defining α-restriction of MAR as follows:
MαAR =(SAR, IAR, ACAR, TαAR, VS AR, VAAR), where TαAR is the transition relationship such that (s, a, s’) ∈ TαAR iff (s, a, s′) ∈ TAR and a |= α, in which |= is defined according to the subsequent equations:
- a |= b iff b ∈ VAAR(a);
- a |= ¬α iff not (a |= α) and;
- a |= α ∨ α′ iff a |= α or a |= α′.
The α-restriction stimulates us to always focus on distinctive transitions whose labels fulfill a certain action formula. Subsequently, when some formula needs to be checked, the relevant transitions only should be taken into consideration. For defining the semantics of the ARCTL, we just take into account the general case of the infinite paths.
Πα(s) is a set of the paths (referred to as the α-paths) whose actions fulfill a certain action formula α and start at s. The relationship of satisfaction (MαAR,s) |= φ is defined according to [13], with the omission of semantics of the propositional atoms and Boolean connectives:
- (MαAR,s) |= EαXφ iff there is path π ∈ Πα(s) and π(1) |= φ;
- (MαAR,s) |= Eα(φ U ψ) iff there is path π ∈ Πα(s) such that for certain k ≥ 0,π(k) |= ψ and π(j) |= φ for all 0 ≤ j < k;
- (MαAR,s) |= EαGφ iff there is path π ∈ Πα(s) such that π(k) |= φ for all k ≥ 0.
The transformation process is defined in this study as follows:
Considering a CTLGC model M, where M = (S, I, Rt,{∼i→j |(i, j) ∈A2},V) and CTLGC formula φ, we need to define α-restricted ARCTL model MαAR, where MαAR = T(M), and ARCTL formula φ, where φ = T(φ) by use of transformation function T such that M |= φ iff T(M) |= T(φ). The T(M) model is defined as ARCTL model MαAR = (SAR, IAR, ACAR, TAα, VSAR, VAAR) according to the following notions:
- SAR = S;
- IAR = I;
- VSAR = V.
- The set of propositions of the atomic action Φa is then defined as follows:
Every relationship in M is transformed into a labeled transition in T(M), that is, MαAR. Doing so allows us three sorts of actions: an action for the relationship of transition which is already present in the model; an action for the relationship of social accessibility ∼i→j to obtain the semantics of group and the single commitments; and an action from symmetric closure of the ∼i→j t in order to gain the fulfillment semantics. Hence,
Φa = {ϵ, α1→1, α1→2, ..., αn→n, αi→Ω, αΩ→j,} ∪ {β1→1, β1→2, ..., βn→n, βi→Ω, βΩ→j}
In consequence, we define the ACAR set of actions as follows:
where αo, αij, αiΩ, and αΩj are the actions that label the transitions which are defined, respectively, from the transition relationship Rt; and the relationships of the social accessibility ∼i→j, ∼i→Ω, and ∼Ω→j. In the meantime, the βij, βiΩ, and βΩj are the actions that denote the symmetric transitions which are added when there are transitions labeled with αij, αiΩ, and αΩj, which are actually needed for defining the transformation of the three formulae Fu(Ci→jφ), Fu(Ci→Ωφ), and Fu(CΩ→jφ).
ACAR = {αo, α11, α12, ..., αnn, αiΩ, αΩj}∪{β11, β12, ..., βnn, βiΩ, βΩj}
- The VAAR function is defined according to the following equations:
- If αo∈ACAR, thenVAAR(αo) = {ϵ};
- VAAR(αij) = {αi→j} for1 ≤ i ≤ n and1 ≤ j ≤ n;
- VAAR(αiΩ) = {αi→Ω} for1 ≤ i ≤ n andΩ = {1...n};
- VAAR(αΩj) = {αΩ→j} forΩ = {1...n} and1 ≤ j ≤ n;
- VAAR(βij) = {βi→j} for1 ≤ i ≤ n and1 ≤ j ≤ n;
- VAAR(βiΩ) = {βi→Ω} for1 ≤ i ≤ n andΩ = {1...n};
- VAAR(βΩj) = {βΩ→j} forΩ = {1...n} and1 ≤ j ≤ n.
- The labeled relationship of transition joins the temporal labeled transition Rt, accessibility relationships ∼i→j and ∼i→Ω, ∼Ω→i, and the symmetric closure of the relationships of social accessibility ∼i→j, ∼i→Ω, and ∼Ω→i under the sequent conditions for the states s and s′ ∈ S
- (s, αo, s′) ∈ TARϵ if (s, s′) ∈ Rt;
- (s, αij, s′) ∈ T AR αi→j if s ∼i→j s’;
- (s, αiΩ, s′) ∈ T AR Ω i→ Ω if s ∼i→ Ω s’;
- (s, αΩj, s′) ∈ T AR αΩ→j if s ∼ Ω → j s’;
- (s, βij, s′) ∈ TARβi→j if (s′, αij, s) ∈ TARαi→j;
- (s, βiΩ, s′) ∈ TARβi→Ω if (s′, αiΩ, s) ∈ TARαi→Ω;
- (s, βΩj, s′) ∈ TARβ Ω →j if (s′, αΩj, s) ∈ TARα Ω →j.
Henceforth, we define T (φ) by an induction on the form of formula φ of the CTLGC:- T (p) = p, if p is atomic proposition;
- T (¬φ) = ¬T (φ);
- T (φ ∨ ψ) = T (φ) ∨ T (ψ);
- T (EXφ) = Eϵ(XT (φ));
- T (E(φ U ψ)) = Eϵ(T (φ) U T (ψ));
- T (EGφ) = Eϵ(GT (φ));
- T (Ci→jφ) = Aαi→jXT (φ);
- T (Ci→Ωφ) = Aαi→ΩXT (φ);
- T (CΩ→jφ) = AαΩ→jXT (φ);
- T (Fu(Ci→jφ)) = Eβi→j(XT (Ci→jφ));
- T (Fu(Ci→Ωφ)) = Eβi→Ω(XT (Ci→Ωφ));
- T (Fu(CΩ→jφ)) = EβΩ→j(XT (CΩ→jφ)).
Thus, this transformation enables us to check the formulae of the CTLGC model via reducing them into ARCTL by employing the extended NuSMV tool [14]. Figure 3 gives an example that explains the transformation function T.
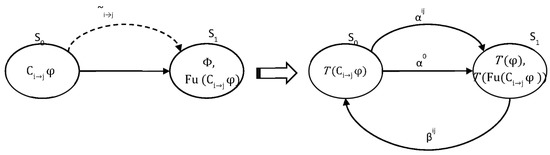
Figure 3.
Example of the transformation function T.
The CTLGC model M, which is located on the left side of Figure 3, will be transformed into ARCTL model MαAR, which is shown on the right of this figure. Model M comprises two global states: s0 and s1. The s1 state is accessible socially from the s0 state (that is, s0 ∼i→j s1). Moreover, φ holds on the s1 state, namely, (M, s1) |= φ. On this account, and based on semantics, we obtain (M, s0) |= Ci→jφ. Since the commitment modality applies to s0, i.e., (M, s0) |= Ci→jφ, and s1 is accessible socially from s0, that is, s0 ∼i→j s1, then, based on semantics, the fulfillment modality will apply to s1, namely, (M, s1) |= Fu(Ci→jφ). By using the aforementioned transformation method, model M will be reduced to MαAR according to the following steps. The transition relationship (that is, (s0, s1) ∈ Rt) is transformed into a labeled transition (s0, αo, s1). Additionally, the relationship of social accessibility (∼i→j) between s0 and s1 is transformed into a labeled transition (s0, αij, s1). The symmetric closure of the relationship of social accessibility (∼i→j) between these two states is also transformed into a labeled transition (s1, βij, s0). Lastly, every formula of state in the CTLGC will be transformed into the corresponding ARCTL formula through the use of the transformation function T. Indeed, the three formulae φ, Ci→jφ, and Fu(Ci→jφ) are due to be transformed, respectively, into T (φ), T (Ci→jφ), and T (Fu(Ci→jφ)).
The next theorem confirms the soundness of the herein conducted transformation algorithm the CTLGC to the ARCTL.
Theorem 1.
Soundness ofT.
Assume thatφ and M are a CTLGC formula and model, respectively, and assume thatT (φ) and T (M) are the corresponding formula and model in the ARCTL. We, then, haveM |= φ iffT (M) |= T (φ).
Proof.
This theorem is proven here by an induction on structure of the φ formula. The entire cases are direct cases, except the subsequent six cases:
- φ = Ci→jψ. We have (M, s) |= Ci→jψ iff (M, s′) |= ψ for each s′∈ S such that s∼i→j s′. Accordingly, (M, s) |= Ci→jψ iff (T (M), s′) |= T (ψ) for each s′∈ SAR such that (s, αij, s′)∈.TARαi→j. By using semantics of A and X, we get (T (M), s) |= Aαi→j(XT (ψ).
- φ = Ci→Ωψ. We have (M, s) |= Ci→Ωψ iff (M, s′) |= ψ for each s′∈ S such that s∼i→Ω s′. Thereupon, (M, s) |= Ci→Ωψ iff (T (M), s′) |= T (ψ) for each s′∈ SAR such that (s, αiΩ, s′)∈ TARαi→Ω. By using semantics of A and X, we end up with (T (M), s) |= Aαi→Ω(XT (ψ).
- φ = CΩ→jψ. We have (M, s) |= CΩ→jψ iff (M, s′) |= ψ for each s′∈ S such that s∼Ω→j s′. Thus, (M, s) |= CΩ→jψ iff (T (M), s′) |= T (ψ) for each s′∈ SAR such that(s, αΩj, s’)∈TARα Ω →j. By use of semantics of A and X, we get (T (M), s) |= AαΩ→j(XT (ψ).
- φ = Fu(Ci→jψ). We have (M, s) |= Fu(Ci→jψ) iff (M, s1) |= Ci→jψ for the state s1∈ S such that s1∼i→j s. Hence, (M, s) |= Fu(Ci→jψ) iff (T (M), s1) |= T (Ci→jψ) for s1∈ SAR such that (s, βij, s1)∈ TARαi→j. By using semantics of E and X, we end up with (T (M), s) |= Eβi→j(XT (Ci→jψ)).
- φ = Fu(Ci→Ωψ). We have (M, s) |= Fu(Ci→Ωψ) iff (M, s1) |= Ci→Ωψ for the state s1∈ S such that s1∼i→Ω s. So, (M, s) |= Fu(Ci→Ωψ) iff (T (M), s1) |= T (Ci→Ωψ) for s1∈ SAR such that(s, βiΩ, s′)∈TARβi→Ω. By use of the semantics of E and X, we get (M), s) |= Eβi→Ω(XT (Ci→Ωψ)).
- φ = Fu(CΩ→jψ). We have (M, s) |= Fu(CΩ→jψ) iff (M, s1) |= CΩ→jψ for the state s1∈ S such that s1∼Ω→j s. In consequence, (M, s) |= Fu(CΩ→jψ) iff (T (M), s1) |= T (CΩ→jψ) for s1∈ SAR such that(s, βΩj, s′)∈TARβΩ →j. Through use of the semantics of E and X, we get (M), s) |= EβΩ→j(XT (CΩ→jψ)).
Therefore, the theorem is confirmed. □
5. Case Study
One of the key motivations of this study is the need for checking the effectiveness of the herein proposed transformation algorithm. We applied the reduction method that was discussed in Section 4.1 atop of the extended NuSMV [14], in order to reason about, and verify, the single commitments, the group commitments, and their fulfillment in the MASs (phase 3 in Figure 1). The case study on which we were capable of responding to this motivation is the NetBill protocol [69], which is a protocol that was developed for the buying and selling of encrypted software on the Internet [69,70]. It consists of two interacting agents: the merchant and the customer [71,72]. A description of this protocol has been provided by [69].
In brief, the NetBill payment protocol consists of eight steps. In the first step, the first message demands a quote on the basis of identity of the customer (e.g., support for the subscriptions or volume discounts) so as to allow for a customized per user pricing. If the quote (step two) has been accepted (step three), then the merchant passes the relating digital information to the customer (step four) but encrypts it and keeps the key. The software of the customer creates an electronic payment order (EPO) that describes the transaction and includes a cryptographic checksum of the received goods. The order is then signed with the private key of the customer and passed to the merchant who verifies its contents, appends the key to it for decryption of the related goods, and approves the EPO with digital signature and passes it to the NetBill server. After that, the NetBill server verifies the funds in the NetBill account of the customer, debits the customer, and credits the merchant. Thereafter, the digitally-signed receipt, including the key for decryption of the goods, is first sent to the merchant, and then, to the customer. The software of the customer can, by that time, decrypt the bought information and present it to her/him. Figure 4 depicts the NetBill payment protocol.
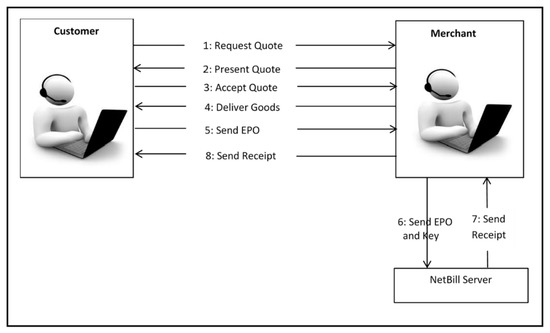
Figure 4.
The NetBill payment protocol [18].
Encoding the NetBill Protocol
The new symbolic model verifier (NuSMV) [68] is a symbolic model-checker for the branching temporal logics (CTLs) and the linear temporal logics (LTLs). Thus far, it has been used in an effective way in checking models of business, web service composition, and multi-agent interaction protocols [54]. However, the original NuSMV version does not support the action of model-checking and the cognitive characteristics in the system of agents. For overcoming this shortcoming, the extended version of the NuSMV is usually used to first support checking the ARCTL model, and then, transform the cognitive formulae to the ARCTL formulae [14]. The extended NuSMV employs symbolic methods that are based on ordered binary decision diagrams (OBDDs). In these methods, the formulae and states of the model to be tested are represented by Boolean functions (Bfs), which can be represented easily by using OBDDs. Likewise, the set of model states that fulfill the ARCTL formula is presented as Bfs. By holding comparisons between the set of states that fulfill the ARCTL formula with the set of the initial states, it becomes possible to find out whether or not a specific formula applies to the model under consideration. Therefore, the problem of checking the ARCTL model is reduced to a comparison of Bfs. In the extended NuSMV, the models are described using modular language that is known as the extended symbolic model verifier, i.e., extended SMV [13].
For the purpose of modeling the actions of the ARCTL, Lomuscio et al. [14] and Pecheur et al. [13] proposed the use of the existent input variables of the NuSMV. In addition, they made extensions to the NuSMV code in an attempt to enable the verification of these operators. Further details on ARCTL action modeling can be found in [13]. For the verification of the NetBill protocol by using the extended NuSMV, we carried out 15 experiments and had up to 22 agents.
6. Conclusions and Future Work
In this study, verification was conducted by using a DELL computer with Intel® CoreTM i3 CPU, a clock speed of 2.59 GHz, and RAM of 4GB RAM that operates on the Windows 10 64-bit operating system. We used the extended NuSMV (NuSVM-ARCTL-TLACE http://lvl.info.ucl.ac.be/Tools/NuSMV-ARCTL-TLACE (accessed on 1 January 2022)), which is based on the modified version of NuSMV 2.2.2 that can check the formulae of the ARCTL model. Figure 5 shows the verification workflow. The verification process starts by inserting the CTLGC model and specifications into the reduction algorithm. The reduction algorithm transforms the CTLGC model into the ARCTL model, and CTLGC specification into ARCTL specification. The ARCTL model and specification are inserted into the extended NuSMV model-checker and verification results are then obtained.
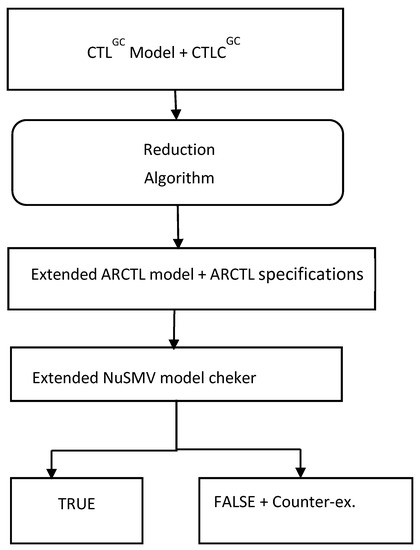
Figure 5.
Verification process workflow.
The results of 15 experiments are shown in Table 1. We began the experiments with two agents only: the merchant and the customer, who interact in an MAS so as to simultaneously determine their single commitments, group commitments, and fulfillment. In the second experiment, we added another customer. In the remainder of the experiments, we added up to 22 agents.

Table 1.
Results of verification of the NetBill protocol using the extended NuSMV.
Table 1 lists the numbers of agents (Agents), numbers of achievable states (States), execution times (Time (s)), and the memory use for constructing the data structure of the OBDD (Memory (MB)). We observed that the state space grows exponentially with the number of the agents. However, the memory use grows polynomially with the same number of agents. This supports the efficiency of our approach to model-checking under the condition of scaling up of the system (nearly 2.43462 × 1014 states).
Another noteworthy motivation of this study was the use of the CTLGC to verify the characteristics of the protocols that encompass single social commitments, group social commitments, and associated fulfillment. Usually, these characteristics express certain protocol requirements that need to be satisfied. In effect, varying properties are proposed in the related literature [36,43,64,67,73,74,75].
In this section, we examine the Liveness, Reachability, and Safety properties of the NetBill protocol because they are examples of common protocol characteristics.
- Safety
The safety property means that something that is not good will never take place. Generally, safety can be connoted in the CTL by AG¬φ, where φ points to a bad (i.e., non-desirable) situation. Bad situations encircle, for example, the case when the customer (cust) sends payment (Pay) to the merchant (mer); that is, the customer satisfies her/his commitment, but the merchant does not deliver the goods (Deliver). It is possible to avoid such a situation by using the CTLGC as follows:
φ1 = AG ¬(Fu(Ccust→merPay)∧ AG ¬(Cmer→custDeliver)).
It is possible to generalize this situation if a group of customers fulfill their commitments to a specific merchant via making their due payments, but the merchant does not deliver the due goods:
φ2 = AG ¬(Fu(CΩcust→merPay)∧ AG ¬(Cmer→ΩcustDeliver)).
- Liveness
This property refers to the case when eventually something good will occur, e.g., if the merchant commits to deliver goods to the customer, then it will eventually fulfill this commitment. This situation can be expressed as follows:
φ3 = AG(Cmer→custDeliver → EF Fu(Cmer→custDeliver)).
This property can be generalized in such a way as to express the commitment of a merchant to delivering the due goods to all her/his customers and the merchant eventually fulfilling her/his commitment. This situation can be expressed as follows:
φ4 = AG(Cmer→ΩcustDeliver → EF Fu(Cmer→ΩcustDeliver)).
- Reachability
The reachability property indicates that a specific situation can be reached. It is expressed as EFφ, where φ is the situation to be reached, e.g., the commitment of the merchant to deliver the due goods to all her/his customers, which is a situation that ought to be reached from the early state. This situation is expressed as follows:
φ5 = EF Cmer→ΩcustDeliver
One more example of reachability is the case when a group of customers commit to send the due payments for the required goods to a certain merchant. This situation can be expressed as:
φ6 = EF CΩcust→merDeliver
We note that the different formulae are true in the model as illustrated in Table 2.

Table 2.
Outcomes of verification of the NetBill protocol properties.
This means that our proposed method is successful in expressing the properties of the protocol by using CTLGC, and that our transformation-based method of model-checking works effectively.
In this paper, we presented a new method for model-checking the logic of single and group commitments, CTLGC. In this method, we developed a set of transformation rules so as to formally reduce the CTLGC model-checking problem to a problem of ARCTL model-checking. We experimentally proved the soundness of this proposed reduction method.
The effectiveness of this proposed method was assessed empirically by applying it on a real case study drawn from the e-business domain, which is the NetBill protocol, and then running the transformation algorithm atop of the extended NuSMV model-checker. We could successfully check some desirable properties of this protocol expressed in the CTLGC. In addition, we confirmed that this model is scalable since we could test 2.43462 × 1014 states. These appealing results support the capability of the CTLGC to capture interactions among the concepts of the single and the group commitments, not only in small and medium systems but also in large systems.
As future directions of this work, we plan to devise dedicated algorithms for checking the CTLGC model logic and apply them atop of the model checker for multi-agent systems (MCMAS) symbolic model-checker [61]. By doing so, we will become able to compare the outcomes of verification of the two algorithms, namely, the reduction/transformation algorithms and the model-checking algorithms. As well, we plan to investigate the single and the group social commitments under the condition of the presence of uncertainty. Moreover, we plan to investigate group conditional commitments (i.e., developing group conditional social commitments that handle one-to-group and group-to-one conditional commitment and their fulfillment), and address the verification problem of the proposed logic.
Author Contributions
Conceptualization, B.M.A., F.A.-S. and A.A.-S.; methodology, B.M.A., F.A.-S. and A.A.-S.; software, B.M.A., F.A.-S. and A.A.-S.; validation, B.M.A., F.A.-S. and A.A.-S.; formal analysis, B.M.A., F.A.-S. and A.A.-S.; investigation, B.M.A., F.A.-S. and A.A.-S.; resources, B.M.A.; data curation, B.M.A., F.A.-S. and A.A.-S.; writing—original draft preparation, B.M.A., F.A.-S. and A.A.-S.; writing—review and editing, B.M.A., F.A.-S. and A.A.-S.; visualization, B.M.A., F.A.-S. and A.A.-S.; supervision, B.M.A.; project administration, B.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Meignan, D.; Simonin, O.; Koukam, A. Simulation and evaluation of urban bus-networks using a multiagent approach. Simul. Model. Pr. Theory 2007, 15, 659–671. [Google Scholar] [CrossRef]
- Jennings, N.R.; Wooldridge, M.J. (Eds.) Applications of intelligent agents. In Agent Technology: Foundations, Applications, and Markets; Springer: Heidelberg, Germany, 1998; pp. 3–28. [Google Scholar]
- Wang, F.; Yang, M.; Yang, R. Simulation of Multi-Agent based Cybernetic Transportation System. Simul. Model. Pract. Theory 2008, 16, 1606–1614. [Google Scholar] [CrossRef]
- Paletta, M.; Herrero, P. Simulating collaborative systems by means of awareness of interaction among intelligent agents. Simul. Model. Prat. Theory 2011, 19, 17–29. [Google Scholar] [CrossRef]
- Bentahar, J.; Meyer, J.-J.; Wan, W. Model checking communicative agent-based system. In Specification and Verification of Multi-Agent Systems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 67–102. [Google Scholar]
- Béhé, F.; Galland, S.; Gaud, N.; Nicolle, C.; Koukam, A. An ontology-based metamodel for multiagent-based simulations. Simul. Model. Pract. Theory 2014, 40, 64–85. [Google Scholar] [CrossRef]
- Konur, S.; Fisher, M.; Schewe, S. Combined model checking for temporal, probabilistic, and real-time logics. Theor. Comput. Sci. 2013, 503, 61–88. [Google Scholar] [CrossRef][Green Version]
- Al-Saqqar, F.; Al-Shatnawi, A.M. Reasoning about group social commitments in multi-agent systems. J. Ambient Intell. Humaniz. Comput. 2020, 9, 1–17. [Google Scholar] [CrossRef]
- El Menshawy, M.; Bentahar, J.; El Kholy, W.; Dssouli, R. Reducing model checking commitments for agent communication to model checking ARCTL and GCTL*. Auton. Agents Multi-Agent Syst. 2012, 27, 375–418. [Google Scholar] [CrossRef]
- Anger, F.D.; Clarke, E.M. New and used temporal models: An issue of time. Appl. Intell. 1993, 3, 5–15. [Google Scholar] [CrossRef]
- Clarke, E.; Grumberg, O.; Peled, D. Model Checking; The MIT Press: Cambridge, CA, USA, 1999. [Google Scholar]
- Fagin, R.; Halpern, J.Y.; Moses, Y.; Vardi, M.Y. Reasoning About Knowledge; The MIT Press: Cambridge, CA, USA, 1995. [Google Scholar]
- Pecheur, C.; Raimondi, F. Symbolic model checking of logics with actions. In MoChArt; Edelkamp, S., Lomuscio, A., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4428, pp. 113–128. [Google Scholar]
- Lomuscio, A.; Pecheur, C.; Raimondi, F. Automatic verification of knowledge and time with nusmv. In Proceedings of the 20th International Joint Conference on Artifical Intelligence, IJCAI’07, Hyderabad, India, 6–12 January 2007; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2007; pp. 1384–1389. [Google Scholar]
- Souri, A.; Rahmani, A.M.; Navimipour, N.J.; Rezaei, R. A symbolic model checking approach in formal verification of distributed systems. Hum. -Cent. Comput. Inf. Sci. 2019, 9, 4. [Google Scholar] [CrossRef]
- Khattabi, G.; Benelallam, I.; Bouyakhf, E. Maintaining ethical resolution in distributed constraint reasoning. J. Ambient Intell. Humaniz. Comput. 2020, 11, 5065–5081. [Google Scholar] [CrossRef]
- Al-Saqqar, F.; Bentahar, J.; Sultan, K.; El Menshawy, M. On the interaction between knowledge and social commitments in multi-agent systems. Appl. Intell. 2014, 41, 235–259. [Google Scholar] [CrossRef]
- FAl-Saqqar; Bentahar, J.; Sultan, K.; Wan, W.; Asl, E.K. Model checking temporal knowledge and commitments in multi-agent systems using reduction. Simul. Model. Pract. Theory 2015, 51, 45–68. [Google Scholar] [CrossRef]
- Dignum, F.; Greaves, M. (Eds.) Issues in Agent Communication, Volume 1916 of Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Dourlens, S.; Ramdane-Cherif, A.; Monacelli, E. Multi levels semantic architecture for multimodal interaction. Appl. Intell. 2012, 38, 586–599. [Google Scholar] [CrossRef]
- El Menshawy, M.; Bentahar, J.; El Kholy, W.; Laarej, A. Model checking real-time conditional commitment logic using transformation. J. Syst. Softw. 2018, 138, 189–205. [Google Scholar] [CrossRef]
- El Kholy, W.; Bentahar, J.; El Menshawy, M.; Qu, H.; Dssouli, R. SMC4AC: A New Symbolic Model Checker for Intelligent Agent Communication. Fundam. Inform. 2017, 152, 223–271. [Google Scholar] [CrossRef]
- Dignum, F.; van Eijk, R.M. Agent communication and social concepts. Auton. Agents Multi-Agent Syst. 2007, 14, 119–120. [Google Scholar] [CrossRef]
- El-Menshawy, M. Model Checking Logics of Social Commitments for Agent Communication. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2012. [Google Scholar]
- Singh, M. Agent communication languages: Rethinking the principles. Computer 1998, 31, 40–47. [Google Scholar] [CrossRef]
- Singh, M.P. A social semantics for agent communication languages. In Issues in Agent Communication; Springer: Berlin/Heidelberg, Germany, 2000; pp. 31–45. [Google Scholar]
- Woźna-Szcześniak, B.; Szcześniak, I. Real-time conditional commitment logic and duration communication interpreted systems. In Proceedings of the Distributed Computing and Artificial Intelligence, 15th International Conference, DCAI 2018, Toledo, Spain, 20–22 June 2018; pp. 103–111. [Google Scholar]
- Forestiero, A.; Mastroianni, C.; Spezzano, G. Building a Peer-to-peer Information System in Grids via Self-organizing Agents. J. Grid Comput. 2008, 6, 125–140. [Google Scholar] [CrossRef]
- Searle, J.R. Speech Acts: An Essay in the Philosophy of Language; Cambridge University Press: Cambridge, CA, USA, 1969. [Google Scholar]
- Acay, D.; Sonenberg, L.; Tidhar, G. Formalizing tool use in intelligent environments. J. Ambient Intell. 2019, 10, 1597–1610. [Google Scholar] [CrossRef]
- Wooldridge, M. Introduction to Multiagent Systems; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Agha, G.; Palmskog, K. A survey of statistical model checking. ACM Trans. Model. Comput. Simul. 2018, 28, 1–39. [Google Scholar] [CrossRef]
- Souri, A.; Nourozi, M.; Rahmani, A.M.; Navimipour, N.J. A model checking approach for user relationship management in the social network. Kybernetes 2019, 48, 407–423. [Google Scholar] [CrossRef]
- Telang, P.R.; Singh, M.P.; Yorke-Smith, N. A Coupled Operational Semantics for Goals and Commitments. J. Artif. Intell. Res. 2019, 65, 31–85. [Google Scholar] [CrossRef]
- Yolum, P.; Singh, M.P. Reasoning about Commitments in the Event Calculus: An Approach for Specifying and Executing Protocols. Ann. Math. Artif. Intell. 2004, 42, 227–253. [Google Scholar] [CrossRef]
- Bhat, G.; Cleaveland, R.; Groce, A. Efficient Model Checking Via Büchi Tableau Automata? In Computer Aided Verification; Berry, G., Comon, H., Finkel, A., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2001; pp. 38–52. [Google Scholar]
- Drawel, N.; Bentahar, J.; El-Menshawy, M.; Laarej, A. Verifying temporal trust logic using CTL model checking. In Proceedings of the 20th International Trust Workshop Co-Located with AAMAS/IJCAI/ECAI/ICML 2018, Stockholm, Sweden, 14 July 2018; pp. 62–74. [Google Scholar]
- Forestiero, A.; Mastroianni, C.; Spezzano, G. Antares: An ant-inspired P2P information system for a self-structured grid. In Proceedings of the 2007 2nd Bio-Inspired Models of Network, Information and Computing Systems, Budapest, Hungary, 10–12 December 2007; pp. 151–158. [Google Scholar]
- Christie, S.H.; V; Chopra, A.K.; Singh, M.P. Compositional correctness in multiagent interactions. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, AAMAS ’18, Stockholm, Sweden, 10–15 July 2018; International Foundation for Autonomous Agents and Multiagent Systems: Richland, SC, USA, 2018; pp. 1159–1167. [Google Scholar]
- Singh, M.P. An ontology for commitments in multiagent systems. Artif. Intell. Law 1999, 7, 97–113. [Google Scholar] [CrossRef]
- Al-humaikani, M.A.S.; Rahim, L.B.A. A review on the verification approaches and tools used to verify the correctness of security algorithms and protocols. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 146–152. [Google Scholar] [CrossRef][Green Version]
- Baldoni, M.; Baroglio, C.; Marengo, E. Behavior-oriented commitment-based protocols. In Proceedings of the 19th European Conference on Artificial Intelligence, Lisbon, Portugal, 16–20 August 2010; pp. 137–142. [Google Scholar]
- Desai, N.; Cheng, Z.; Chopra, A.K.; Singh, M.P. Toward verification of commitment protocols and their compositions. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems (AAMAS), Honolulu, HI, USA, 14–18 May 2007; pp. 144–146. [Google Scholar]
- Gunay, A.; Chopra, A.K.; Singh, M.P. Supple: Multiagent communication protocols with causal types. In Proceedings of the 18th International Conference on Autonomous Agents and Multiagent Systems, AAMAS ’19, Montreal, QC, Canada, 13–17 May 2019; International Foundation for Autonomous Agents and Multiagent Systems: Richland, SC, USA, 2019; pp. 781–789. [Google Scholar]
- Bataineh, A.S.; Bentahar, J.; El Menshawy, M.; Dssouli, R. Specifying and verifying contract-driven service compositions using commitments and model checking. Expert Syst. Appl. 2017, 74, 151–184. [Google Scholar] [CrossRef]
- Bentahar, J.; Yahyaoui, H.; Kova, M.; Maamar, Z. Symbolic model checking composite Web services using operational and control behaviors. Expert Syst. Appl. 2013, 40, 508–522. [Google Scholar] [CrossRef]
- Venkatraman, M.; Singh, M.P. Verifying Compliance with Commitment Protocols. Auton. Agents Multi-Agent Syst. 1999, 2, 217–236. [Google Scholar] [CrossRef]
- Desai, N.; Chopra, A.K.; Singh, M.P. Amoeba: A methodology for modeling and evolving crossorganizational business processes. ACM Trans. Softw. Eng. Methodol. 2009, 19, 1–45. [Google Scholar] [CrossRef]
- Fornara, N.; Vigano, F.; Verdicchio, M.; Colombetti, M. Artificial institutions: A model of institutional reality for open multiagent systems. Artif. Intell. Law 2008, 16, 89–105. [Google Scholar] [CrossRef]
- Günay, A.; Chopra, A.K. Stellar: A programming model for developing protocol-compliant agents. In Proceedings of the Engineering Multi-Agent Systems—6th International Workshop, EMAS 2018, Stockholm, Sweden, 14–15 July 2018; pp. 117–136, Revised Selected Papers. [Google Scholar]
- Winikoff, M. Implementing commitment-based interactions. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems (AAMAS), Honolulu HI, USA, 14–18 May 2007; pp. 873–880. [Google Scholar]
- Singh, M.P.; Chopra, A.K. Violable contracts and governance for blockchain applications. arXiv 2018, arXiv:1801.02672. [Google Scholar] [CrossRef]
- Boella, G.; Pigozzi, G.; Slavkovik, M.; van der Torre, L.W.N. Group intention is social choice with commitment. In Proceedings of the Coordination, Organizations, Institutions, and Norms in Agent Systems VI-COIN 2010 International Workshops, COIN@AAMAS 2010, Toronto, ON, Canada, May 2010; N@MALLOW: Lyon, France, 2010; pp. 152–171, Revised Selected Papers. [Google Scholar]
- Castelfranchi, C. Commitments: From individual intentions to groups and organizations. In Proceedings of the First International Conference on Multiagent Systems, San Francisco, CA, USA, 12–14 June 1995; pp. 41–48. [Google Scholar]
- Dunin-Keplicz, B.; Verbrugge, R. Calibrating collective commitments. In Proceedings of the Multi-Agent Systems and Applications III, 3rd International Central and Eastern European Conference on Multi-Agent Systems, CEEMAS 2003, Prague, Czech Republic, 16–18 June 2003; pp. 73–83. [Google Scholar]
- Garion, C.; Cholvy, L. Deriving individual obligations from collective obligations. In Proceedings of the Second International Joint Conference on Autonomous Agents and Multiagent System, Melbourne, Australia, 18–23 March 2007. [Google Scholar]
- Wright, B. Together, is anything possible? A look at collective commitments for agents. In Proceedings of the Technical Communications of the 28th International Conference on Logic Programming, ICLP 2012, Budapest, Hungary, 4–8 September 2012; pp. 476–480. [Google Scholar]
- Bryant, R.E. Graph-Based Algorithms for Boolean Function Manipulation. Comput. IEEE Trans. Comput. 1986, 35, 677–691. [Google Scholar] [CrossRef]
- Kholy, W.E.; El-Menshawy, M.; Laarej, A.; Bentahar, J.; Al-Saqqar, F.; Dssouli, R. Real-time conditional commitment logic. In Proceedings of the PRIMA 2015: Principles and Practice of Multi-Agent Systems—18th International Conference, Bertinoro, Italy, 26–30 October 2015; pp. 547–556. [Google Scholar]
- Sultan, K.; Bentahar, J.; Yahyaoui, H.; Mizouni, R. Model checking agent-based communities against uncertain group commitments and knowledge. Expert Syst. Appl. 2021, 177, 114792. [Google Scholar] [CrossRef]
- Bentahar, J.; El-Menshawy, M.; Qu, H.; Dssouli, R. Communicative commitments: Model checking and complexity analysis. Knowl. -Based Syst. 2012, 35, 21–34. [Google Scholar] [CrossRef]
- ALomuscio; Qu, H.; Raimondi, F. MCMAS: A model checker for the verification of multi-agent systems. In Computer Aided Verification; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; pp. 682–688. [Google Scholar]
- Raimondi, F. Model Checking Multi-Agent Systems. Ph.D. Thesis, University College London, London, UK, 2006. [Google Scholar]
- El-Menshawy, M.; Bentahar, J.; Qu, H.; Dssouli, R. On the verification of social commitments and time. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems (AAMAS), Taipei, Taiwan, 2–6 May 2011; pp. 483–490. [Google Scholar]
- Lomuscio, A.; Penczek, W. Symbolic model checking for temporal-epistemic logic. In Logic Programs, Norms and Action; Springer: Berlin/Heidelberg, Germany, 2012; pp. 172–195. [Google Scholar]
- Wan, W.; Bentahar, J.; Hamza, A.B. Model checking epistemic and probabilistic properties of multi-agent systems. In International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 68–78. [Google Scholar]
- Wan, W.; Bentahar, J.; Ben Hamza, A. Model checking epistemic–probabilistic logic using probabilistic interpreted systems. Knowledge-Based Syst. 2013, 50, 279–295. [Google Scholar] [CrossRef]
- Cimatti, A.; Clarke, E.M.; Giunchiglia, E.; Giunchiglia, F.; Pistore, M.; Roveri, M.; Sebastiani, R.; Tacchella, A. Nusmv 2: An opensource tool for symbolic model checking. In Computer Aided Verification; Brinksma, E., Larsen, K.G., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2404, pp. 359–364. [Google Scholar]
- Sirbu, M. Credits and debits on the Internet. IEEE Spectr. 1997, 34, 23–29. [Google Scholar] [CrossRef]
- Cox, B.; Tygar, J.D.; Sirbu, M. Netbill security and transaction protocol. In Proceedings of the First USENIX Workshop on Electronic Commerce, New York, NY, USA, 11–12 July 1995; pp. 77–88. [Google Scholar]
- Mallya, A.U.; Singh, M.P. An algebra for commitment protocols. Auton. Agents Multi-Agent Syst. 2007, 14, 143–163. [Google Scholar] [CrossRef]
- Yolum, P.; Singh, M.P. Commitment machines. In Proceedings of the 8th International Workshop on Agent Theories, Architectures, and Languages, Seattle, WA, USA, 1–3 August 2001; Springer: Berlin/Heidelberg, Germany, 2000; pp. 235–247, ATAL-01. [Google Scholar]
- Bentahar, J.; Meyer, J.-J.; Wan, W. Model checking communicative agent-based systems. Knowledge-Based Syst. 2009, 22, 142–159. [Google Scholar] [CrossRef]
- Cheng, Z. Verifying Commitment-Based Business Protocols and Their Compositions: Model Checking Using Promela and Spin. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2006. [Google Scholar]
- Mizouni, R.; Salah, A. Towards a framework for estimating system NFRs on behavioral models. Knowledge-Based Syst. 2010, 23, 721–731. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).